Experimental (FT-IR and FT-Raman) and spectroscopic investigations, electronic properties and conformational analysis by PES scan on 2-methoxy-5-nitrophenol and 2-methoxy-4-methylphenol

Abstract

A complete vibrational and molecular structure analysis is performed based on the quantum mechanical approach by HF and DFT calculations. On the basis of the calculated and experimental results the assignments of the fundamental frequencies are examined. The available experimental results are compared with the theoretical data. A low value of HOMO LUMO energy gap suggests the possibility of intramolecular charge transfer in the molecule. This plays an important role in the significant increase of the β value, which is a property to exhibit nonlinear optical (NLO) activity. The NBO result reflects the charge transfer mainly due to lone pairs. Theoretical ¹H and ¹³C chemical shift values (with respect to TMS) are reported and compared with experimental data which shows the agreement for both ¹H and ¹³C. Predicted electronic absorption spectra from TD-DFT calculations are analysed and they are mainly derived from the contribution of the π → π* band. The predicted NLO properties are much greater than those of urea.

---

1. Introduction

Phenol derivatives are motivating molecules for theoretical studies due to their relatively small size and similarity to biological species. Unlike normal alcohols, phenols are acidic because of the influence of the aromatic ring. The free phenol is liberated by adding sulphuric acid. It is used as anti-bacterial and anti-septic and also for the treatment of surgical instruments and bandaging materials.¹ Various spectroscopic studies of chloro and methyl phenols have been reported in the literature.^2–4 Sing et al. have studied the infrared and the electronic absorption spectra of 4-chloro-2-methyl, 4-chloro-3-methyl and 6-chloro-3-methyl phenols. The vibrational spectra of p-cresol and its deuterated derivatives have been studied by Jakobsen,⁵ who gave detailed interpretations of the vibrational bands. The assignment of the vibrational frequencies for substituted phenols is complicated because of the superposition of several vibrations due to fundamentals and substituents. However, a comparison of the spectra with that of the parent compound gives some definite clues about the nature of the molecular vibrations. The Raman spectra of this compound and its three deuterated derivatives in the liquid state and the infrared spectra in the liquid, vapour and solid state have been reported partially by Jakobsen,⁵ the vibrational spectra of p-nitrophenol in the region 300–1600 cm⁻¹ were studied by Jakobsen and Brewer.⁶ Kishore et al.⁷ recorded the infrared absorption spectra of o-, m- and p-nitrophenols in the region 200–4000 cm⁻¹ using the KBr pellet technique.

In conjunction with the development of technology, among the computational methods for calculating the structure of molecular systems, DFT has been a favourite due to its great accuracy in reproducing the experimental values of molecular geometry, vibrational frequencies, atomic charges, dipole moment, etc.

By considering the above mentioned points this study deals the molecular geometry, optimized parameters and vibrational frequencies of 2-methoxy-5-nitrophenol (MNP) and 2-methoxy-4-methylphenol (MMP) and the performance of the computational methods (HF and B3LYP) at the 6-31G (d,p) basis set.

2. Experimental details

The compounds under investigation namely 2-methoxy-5-nitrophenol (MNP) and 2-methoxy-4-methylphenol (MMP) are purchased from Sigma-Aldrich chemicals, USA which is of spectroscopic grade and hence used for recording the spectra as such without any further purification. The FT-IR spectrum is recorded using a Bruker IFS 66V spectrometer in the range of 4000–400 cm⁻¹. The spectral resolution is ±2 cm⁻¹. The FT-Raman spectrum was also recorded with the same instrument with a FRA 106 Raman module equipped with a Nd:YAG laser source operating at 1064 nm excitation wavelengths, line widths with 200 mW power in the range of 3500–50 cm⁻¹ with scanning speed of 30 cm⁻¹ min⁻¹ of spectral width 2 cm⁻¹. The frequencies of all sharp bands are accurate to ±1 cm⁻¹.

3. Theoretical methods

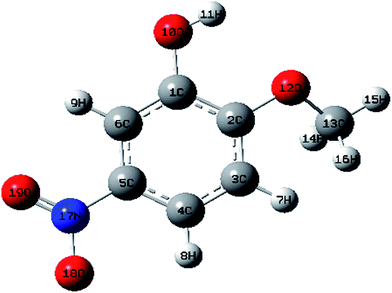
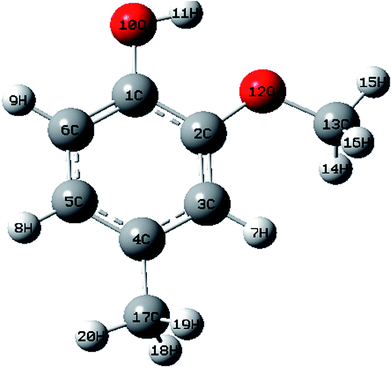
The optimized structures of MNP and MMP in the ground state (Fig. 1 and 2) are computed by performing both ab initio/HF and DFT/B3LYP with the 6-31G (d,p) basis set with the Gaussian 09W software package⁸ and Gauss view visualization program.⁹ The optimized structural parameters are used in the vibrational frequency calculations in HF and DFT methods. The total energy distribution (TED) corresponding to each of the observed frequencies is calculated using the MOLVIB program¹⁰ and it shows the reliability and accuracy of the spectral analysis. The isotropic chemical shifts are frequently used as an aid for the identification of organic compounds. The GIAO method is one of the most common approaches for calculating nuclear magnetic shielding tensors. The ¹³C and ¹H NMR isotropic shielding were calculated with the GIAO method using the optimized parameters obtained from B3LYP/6-31G(d,p) method. UV-vis spectra, electronic transitions, vertical excitation energies, absorbance and oscillator strengths were computed with the time-dependent DFT method. The electronic properties such as HOMO and LUMO energies were determined by time-dependent DFT approach.

Fig. 1 Molecular structure of 2-methoxy-5-nitrophenol.

Fig. 2 Molecular structure of 2-methoxy-4-methylphenol.

The natural bonding orbital (NBO) calculations were performed in order to understand various second order interactions between the filled and vacant orbitals of the system, which is a measure of the intermolecular and intramolecular delocalization or hyper conjugation. Next, first hyperpolarizabilities of the title compounds were obtained based on theoretical calculations.

4. Results and discussion

4.1. Structural analysis and potential energy surface scan

The optimized structural parameters such as bond lengths and bond angles of the title compounds are determined at the above mentioned level of theory. The optimized parameters are collected in Tables S1 and S2† in accordance with the atom numbering scheme shown in Fig. 1 and 2.

According to the calculated values, the order of the optimized bond lengths of the six C–C bonds of the ring as C5–C6 < C3–C4 < C1–C6 < C4–C5 < C2–C3 < C1–C2 in MNP and as C2–C3 < C4–C5 < C1–C6 < C5–C6 < C3–C4 < C1–C2 in MMP. From the order of the bond lengths, it is clear that the phenyl ring appears a little distorted from the perfect hexagonal structure. It is due to the substitutions of the OH, NO₂, O–CH₃ and CH₃ groups in the place of H atoms. It is also evident that the bond lengths of C5–C6, C1–C2 and C3–C4 (1.3893, 1.4152 and 1.3955 Å cal by B3LYP) are more extended than the bond lengths C1–C6, C4–C5 and C2–C3 (1.3822, 1.3877 and 1.3889 Å). A similar effect is also observed as mentioned above in calculated bond lengths by the HF method. The bond length O10–H11 (0.9987 Å) calculated by B3LYP/6-31G(d,p) is just 0.0317 Å higher than the reported experimental value of 0.969 Å (ref. 11) in both the compounds. The experimental value of the C–H bond of methyl group is 1.090 Å (ref. 12) differed by 0.0071 and 0.0042 Å (calculated by B3LYP/6-31G(d,p)) in MMP.

In order to describe the conformational flexibility of the title compounds, the potential energy profile was achieved for the rotations of hydroxy, methoxy and methyl groups with the B3LYP/6-31G(d,p) method (Fig. S1 and S2†). The conformational energy profiles of MNP (Fig. S1†) show that there are three local minima observed at 0°, 90° and 360° (−623.017214198 for 0°, −623.00807271 hartree for 90°, −623.017214195 hartree for 360°) for T (C2–C1–O10–H11); for C1–O12–C13–H14, there are also three minima obtained at 60° (−623.017211684 hartree), 180° (−623.017214196 hartree) and 300° (−623.017211683 hartree); therefore, the most stable conformer is obtained for a 0° torsion angle of the OH group in MNP.

Furthermore, the conformational energy profiles of MMP (Fig. S2†) show that there are three local minima observed at 0°, 90° and 360° (−458.777154441 hartree for 0°, −458.766129262 hartree for 90°, −458.77715444 hartree for 360°) for T (C2–C1–O10–H11); for T (C1–012–C13–H14), there are also three minima obtained at 60° (−458.777152104 hartree), 180° (−458.777154046 hartree) and 300° (−458.777152234 hartree); for T (C3–C4–C17–H19), three minimum energies are also obtained at 60° (−458.777154422 hartree), 180° (−458.777154385 hartree) and 300° (−458.777154433 hartree). Therefore, the most stable conformer is obtained for a 0° torsion angle of the OH group in MMP also.

4.2. Vibrational assignments

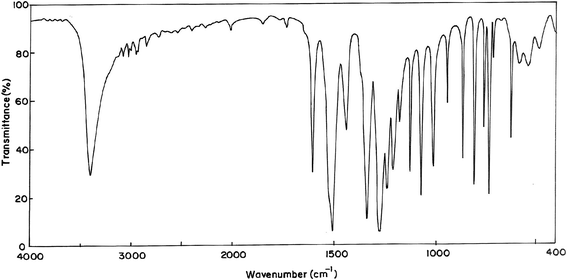
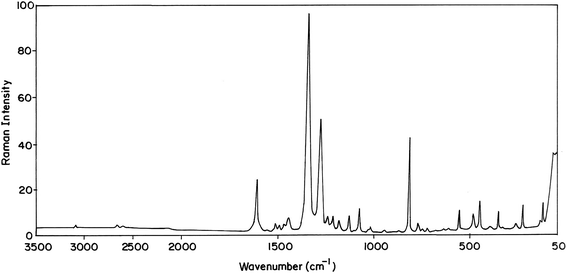
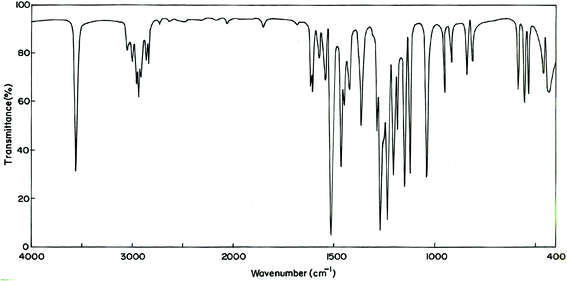
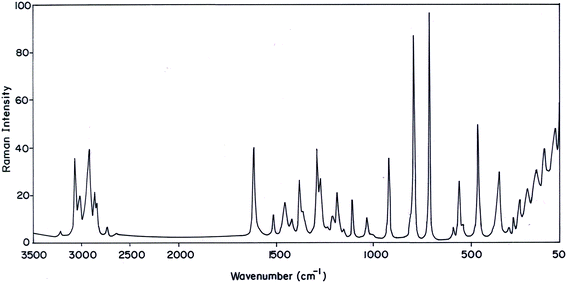
The MNP and MMP consist of 19 and 20 atoms, respectively, hence the number of normal modes of vibrations are 51 and 54 for MMP and MNP, respectively. Experimental FT-IR and FT-Raman spectra of the title compounds are presented in Fig. 3–6. Observed and calculated frequencies are quoted in Tables 1 and 2.

Fig. 3 FT-IR spectrum of 2-methoxy-5-nitrophenol.

Fig. 4 FT-Raman spectrum of 2-methoxy-5-nitrophenol.

Fig. 5 FT-IR spectrum of 2-methoxy-4-methylphenol.

Fig. 6 FT-Raman spectrum of 2-methoxy-4-methylphenol.

Table 1 Vibrational assignments of experimental frequencies of 2-methoxy-5-nitrophenol along with calculated frequencies by HF and B3LYP methods using 6-31G(d,p) basis set^a

S. No	Experimental frequency (cm^−1)		Calculated frequency (cm^−1)				Assignments with TED (%)
	FT-IR	FT-Raman	HF/6-31G(d,p)		B3LYP/6-31G(d,p)
			Unscaled	Scaled	Unscaled	Scaled
a Abbreviations: ν – stretching; b – bending; symd – symmetric deformation; asymd – asymmetric deformation; trigd – trigonal deformation; δ-out-of plane bending; t – torsion; twist – twisting; ss – symmetric stretching; ass – asymmetric stretching; ips – in-plane stretching; ops-out-of plane stretching; sb – symmetric bending; ipb – in plane bending; opb – out of plane bending; ipr – in plane rocking; opr – out of plane rocking; scis – scissoring; rock – rocking; wag – wagging.
1	3407	—	3477	3425	3448	3419	νOH (99)
2	—	3100	3305	3108	3300	3105	νCH (97)
3	3087	—	3294	3100	3272	3099	νCH (96)
4	3036	—	3257	3053	3235	3042	νCH (97)
5	3013	—	3173	3029	3168	3021	CH3ips (98)
6	2968	—	3118	2982	3104	2972	CH3ss (98)
7	2946	—	3049	2963	3043	2951	CH3ops (98)
8	1607	1610	1766	1621	1652	1614	νC=C (84), Rsymd (13)
9	1528	—	1750	1553	1628	1542	νC=C (73), Rasymd (29)
10	1513	—	1665	1534	1569	1521	NO2ass (80)
11	1459	—	1656	1472	1553	1464	νC–O (79), bCH (17)
12	1449	—	1655	1472	1544	1461	νC–O (79), bCO (19)
13	1444	—	1637	1463	1509	1459	νC=C (79), bCH (17)
14	—	1402	1613	1419	1498	1413	νC–C (83), Rsymd (11)
15	—	1388	1538	1399	1416	1392	νC–C (87), Rsymd (11)
16	1345	1347	1419	1351	1347	1347	νC–C (84), Rasymd (11)
17	—	1330	1380	1351	1333	1344	NO2ss (80), bCN (12)
18	1280	—	1341	1299	1295	1294	bCH (78), Rtrigd (15)
19	—	1268	1301	1280	1254	1277	bCH (79), Rasymd (12)
20	1242	—	1297	1251	1243	1249	bCH (75), Rsymd (14)
21	1214	1211	1279	1221	1193	1219	bOH (69), Rasymd (21)
22	1182	—	1260	1196	1189	1190	CH3ipb (98)
23	1130	—	1230	1147	1163	1141	CH3sb (97)
24	1116	—	1165	1128	1162	1121	CH3opb (98)
25	—	1080	1151	1101	1088	1094	νCN (77), bCH (12)
26	1077	—	1144	1088	1044	1081	Rtrigd (71), bCC (19)
27	—	1020	1072	1032	1029	1029	νO–CH3 (81)
28	1017	—	1057	1021	1001	1009	Rsymd (72), bCH (18)
29	949	—	994	959	936	953	Rasymd (74), bCN (15)
30	870	—	976	881	892	879	CH3ipr (78)
31	816	819	930	821	799	802	NO2scis (75)
32	769	—	811	777	771	771	CH3opr (76)
33	744	—	789	751	748	748	δCH (65), δCN (20)
34	723	—	778	733	704	711	δCH (64), tRasymd (21)
35	634	—	759	649	644	644	δCH (64), δCO (16)
36	607	—	679	613	602	602	NO2rock (68)
37	593	—	642	599	595	595	bC–N (69), Rasymd (21)
38	—	560	625	571	558	559	NO2wag (64), δCN (20)
39	543	—	586	552	546	546	δOH (59), δCC (17)
40	486	—	522	491	489	489	bC–O (67), bO–H (15)
41	—	450	508	461	467	459	bC–O (69), Rasymd (22)
42	—	390	439	399	378	387	bO–CH3 (66)
43	—	360	423	369	377	363	δCN (67), tRtrigd (20)
44	—	330	401	334	323	327	tRtrigd (63), δCN (18)
45	—	250	353	252	240	248	tRsymd (64), δCH (21)
46	—	225	295	231	235	229	tRasymd (65), δCH(22)
47	—	210	261	217	206	206	t(O–CH3) (59)
48	—	165	228	171	176	169	δC–O (67)
49	—	125	224	137	137	129	δC–O (63)
50	—	68	210	88	85	71	tCH3 (55)
51	—	29	126	42	67	32	NO2twist (58)

---

Table 2 Vibrational assignments of experimental frequencies of 2-methoxy-4-methylphenol along with calculated frequencies by HF and B3LYP methods using the 6-31G(d,p) basis set^a

S. No	Experimental frequency (cm^−1)		Calculated frequency (cm^−1)				Assignments with TED (%)
	FT-IR	FT-Raman	HF/6-31G(d,p)		B3LYP/6-31G(d,p)
			Unscaled	Scaled	Unscaled	Scaled
a Abbreviations: ν – stretching; b – bending; symd – symmetric deformation; asymd – asymmetric deformation; trigd – trigonal deformation; δ-out-of-plane bending; t – torsion; twist – twisting; ss – symmetric stretching; ass – asymmetric stretching; ips – in plane stretching; ops – out-of-plane stretching; sb – symmetric bending; ipb – in plane bending; opb – out of plane bending; ipr – in plane rocking; opr – out of plane rocking; scis – scissoring; rock – rocking; wag – wagging.
1	3662	—	3404	3582	3445	3599	νOH (99)
2	—	3067	3300	3079	3232	3072	νCH (99)
3	3005	—	3275	3020	3210	3012	νCH (98)
4	2961	—	3262	2981	3197	2973	νCH (98)
5	2939	—	3208	2952	3155	2947	CH3ips (98)
6	—	2921	3160	2944	3120	2933	CH3ips (98)
7	2919	—	3146	2931	3089	2922	CH3ss (98)
8	—	2865	3127	2881	3086	2874	CH3ss (98)
9	2855	—	3081	2877	3041	2864	CH3ops (98)
10	2843	—	3078	2870	3031	2857	CH3ops (98)
11	1616	—	1795	1635	1653	1622	νC=C (84), Rsymd (13)
12	1610	—	1780	1622	1638	1619	νC=C (73), Rasymd (29)
13	—	1600	1682	1617	1576	1609	νC–O (79), bCH (17)
14	1565	—	1670	1579	1562	1571	νC–O (79), bCO (19)
15	1540	—	1667	1560	1557	1552	νC=C (79), bCH (17)
16	—	1532	1664	1557	1553	1547	νC–C (83), Rsymd (11)
17	1523	—	1653	1540	1549	1531	νC–C (87), Rsymd (11)
18	1515	—	1642	1533	1510	1524	νC–C (84), Rasymd (11)
19	1466	1466	1612	1481	1471	1477	νC–Cme (59), bCH (17)
20	1451	—	1596	1471	1463	1461	CH3ipb (98)
21	1425	—	1564	1439	1433	1431	CH3ipb (98)
22	1367	—	1438	1382	1355	1376	CH3sb (97)
23	1288	1290	1392	1301	1283	1293	CH3sb (98)
24	1272	1275	1361	1289	1266	1280	CH3opb (98)
25	1256	—	1329	1278	1251	1261	CH3opb (98)
26	1206	—	1297	1211	1195	1202	bCH (78), Rtrigd (15)
27	1188	1189	1284	1197	1174	1181	bCH (79), Rasymd (12)
28	1151	—	1244	1177	1166	1162	bCH (75), Rsymd (14)
29	1123	—	1242	1141	1165	1132	bOH (69), Rasymd (21)
30	—	1110	1227	1122	1101	1119	Rtrigd (71), bCC (19)
31	1045	—	1144	1073	1056	1051	νOCH3 (81)
32	—	1036	1138	1055	1044	1042	Rsymd (72), bCH (18)
33	954	—	1093	975	989	961	Rasymd (74), bCH (15)
34	—	922	1057	944	927	931	bCCme (42), bCH (27)
35	918	—	1000	934	926	926	CH3ipr (78)
36	845	—	975	867	855	855	CH3ipr (78)
37	810	—	928	819	801	801	CH3opr (76)
38	—	794	848	808	781	781	CH3opr (76)
39	—	715	825	723	719	719	δCH (65), δCO (20)
40	599	—	770	610	608	608	δCH (64), tRasymd (21)
41	—	562	688	588	562	562	δCH (64), δCO (16)
42	557	—	604	577	558	558	bCO (69), Rasymd (21)
43	530	—	598	550	549	543	δOH (59), δCC (17)
44	460	—	533	487	477	469	bCO (67), bOH (15)
45	435	—	509	451	475	442	bCO (69), Rasymd (22)
46	—	366	434	389	372	372	bOCH3 (66)
47	—	361	413	377	360	360	tRtrigd (63), δCN (18)
48	—	276	408	299	285	285	tRsymd (64), δCH (21)
49	—	249	350	266	253	253	tRasymd (65), δCH (22)
50	—	188	336	201	197	196	δCCme (54), bCH (21)
51	—	173	299	188	189	179	t(OCH3) (59)
52	—	135	237	149	152	141	δCO (67)
53	—	61	187	87	74	71	δCO (63)
54	—	43	169	76	55	49	tCH3 (55)

---

4.2.1 C–H vibrations. The existence of one or more aromatic rings in a structure is normally readily determined from the C–H and C–C–C related vibrations. Aromatic compounds commonly exhibit multiple bands in the region 3100–3000 cm⁻¹ due to aromatic C–H stretching vibrations¹³ and are typically exhibited as a multiplicity of weak to moderate bands, compared with the aliphatic C–H stretch. Scaled vibrations assigned to the aromatic C–H stretchings at 3108, 3099, 3042 cm⁻¹ by the B3LYP/6-31G(d,p) method along with the TED contribution of 94, 96, 97% respectively show good agreement with the recorded FT-IR at 3100, 3087, 3036 cm⁻¹ and 3100 cm⁻¹ in FT-Raman spectrum in MNP. In MMP IR bands at 3005, 2961 cm⁻¹ and the band observed in FT-Raman spectrum at 3067 cm⁻¹ are due to C–H stretching vibrations. The C–H in-plane bending vibrations lie in the region 1230–970 cm⁻¹.¹⁴ In MNP, the bands at 1280, 1242 cm⁻¹ in the FT-IR spectrum and the bands observed at 1268 cm⁻¹ in the FT-Raman spectrum are assigned to the C–H in-plane bending vibrations, they show good agreement with the theoretically computed values with the contributions of 78, 79 and 75%, respectively. The IR bands at 1206, 1188, 1151 cm⁻¹ in MMP are assigned to C–H in-plane bending vibrations. The C–H out of plane bending modes usually medium to strong in intensity arise in the region 950–600 cm⁻¹.¹⁵ Hence the C–H out of plane bending modes of MNP and MMP are observed at 744, 723, 634 cm⁻¹ and 715, 599, 562 cm⁻¹, respectively.

4.2.2 O–H vibrations. Bands due to OH stretching are of medium to strong intensity in the infrared spectrum, even though it may be broad. In Raman spectra the band is generally weak. Unassociated hydroxyl group absorbs strongly in the region 3670–3580 cm⁻¹. The band due to the free hydroxyl group is sharp and its intensity increases. The observed band due to O–H stretching is broad in the case of MNP compared with that of MMP which indicates stronger intermolecular hydrogen bonding in MNP. The O–H stretching band in MMP is sharp and it indicates the absence of intermolecular hydrogen bonding. The isomer under investigation shows strong broad and strong sharp stretching of the hydroxyl group at 3407 cm⁻¹ in MNP and 3662 cm⁻¹ in MMP, respectively, in the infrared spectrum which are assigned as O–H stretching vibrations. A broad stretching of O–H also indicates the presence of intramolecular hydrogen bonding.¹⁶ The O–H in-plane and out-of-plane bending vibrations are usually observed in the regions 1350–1200 cm⁻¹ and 720–590 cm⁻¹,^17,18 respectively. In view of that the O–H in-plane and out-of-plane bending vibrations are found at 1214, 1123 cm⁻¹ and 543, 530 cm⁻¹ in MNP and MMP, respectively. These assignments are also in line with the literature.¹⁹

4.2.3 Ring vibrations. The aromatic ring vibrational modes of the title compounds have been analyzed based on the vibrational spectra of previously published vibrations of the benzene molecule which are helpful in the identification of the phenyl ring modes.²⁰ The carbon–carbon stretching modes of the phenyl group are expected in the range from 1650 to 1200 cm⁻¹. In general, the bands of variable intensities are observed at 1625–1590, 1590–1575, 1540–1470, 1465–1430 and 1380–1280 cm⁻¹ from the wavenumber ranges given by Varsanyi.²¹ In the present work, the wavenumbers observed in the FTIR spectrum at 1607, 1528, 1444, 1345 cm⁻¹ and in FT-Raman spectrum at 1610, 1402, 1338, 1347 cm⁻¹ are assigned to C–C stretching vibrations for MNP. The FT-IR bands at 1616, 1610, 1540, 1523, 1515 cm⁻¹ and the FT-Raman bands at 1600, 1532 cm⁻¹ are ascribed as stretching vibrations for MMP. In MNP and MMP, bands found at 1077, 1017, 949 cm⁻¹ and 1110, 1036, 954 cm⁻¹ are assigned to C–C–C in-plane bending, respectively. The bands assigned at 330, 250, 225 cm⁻¹ and 361, 276, 249 cm⁻¹ are due to C–C–C out-of-plane bending. These assignments are in line with the assignments proposed by the theoretical values (B3LYP).

4.2.4 Methoxy group vibrations. For MNP the peaks identified at 3013, 2968 and 2946 cm⁻¹ are ascribed to CH₃ips, CH₃ss, and CH₃ops vibrations of the methyl group attached to O12, whereas for the methyl group attached to O12 of MMP, they are observed at 2921, 2865 and 2843 cm⁻¹, respectively. The corresponding calculated values (scaled) are 3021, 2972, 2951 cm⁻¹ and 2933, 2874, 2857 cm⁻¹ for MNP and MMP, respectively. The FT-Raman band at 1020 cm⁻¹ and FT-IR band at 1045 cm⁻¹ are assigned to stretching vibrations of O–CH₃ for MNP and MMP, respectively. FT-IR bands established at 1182, 1130, 1116, 870 and 769 cm⁻¹ are attributed to CH₃ipb, CH₃sb, CH₃opb, CH₃ipr, and CH₃opr vibrational modes for MNP and they are established at 1425, 1288, 1256, 845 in FT-IR spectrum and 794 cm⁻¹ in FT-Raman spectrum for MMP, respectively. The bands at 210, 68 and 173, 43 cm⁻¹ are assigned as tO–CH₃ and tCH₃ modes for MNP and MMP, respectively.

4.2.5 Nitro group vibrations. Generally aromatic nitro compounds have strong absorptions due to asymmetric and symmetric stretching vibrations of the NO₂ group at 1570–1485 and 1370–1320 cm⁻¹, respectively. Hydrogen bonding has little effect on the NO₂ asymmetric stretching vibrations.²² Hence the bands at 1513 and 1330 cm⁻¹ are assigned to asymmetric and symmetric stretching modes of NO₂ in the MNP. The NO₂ scissoring mode is designated to the band at 816 and 819 cm⁻¹ in FT-IR and FT-Raman spectra, respectively. The deformation vibrations of NO₂ group (rocking, wagging and twisting) contribute to several normal modes in the low frequency region.²³ These bands are also found well within the characteristic region and summarized in Table 1.

4.2.6 Methyl group vibrations. The position of the CH₃ vibration is almost entirely dependent upon the nature of the element to which the methyl groups are attached. For the assignments of CH₃ group frequencies, nine fundamentals can be associated to each CH₃ group. The C–H stretching in CH₃ occurs at lower frequencies than those of aromatic rings (3100–3000 cm⁻¹). Moreover, the asymmetric stretch is usually at higher wavenumbers than the symmetric stretch. The presence of C–H vibrations confirms the position of the methyl group in the benzene ring. The asymmetric C–H vibration for the methyl group generally occurs in the region between 2975 and 2920 cm⁻¹ (ref. 24) and the symmetric C–H vibration for the methyl group typically occurs in the region of 2870–2840 cm⁻¹. In MMP, the C–H stretching vibrational frequencies are observed at 2939, 2919 and 2855 cm⁻¹. From the above assignments, it is clear that the two bands are asymmetric and one is symmetric. The vibrational bands at 1451, 1367 and 1272 cm⁻¹ are assigned to C–H bending modes and the bands are identified at 918 and 810 cm⁻¹ for C–H in-plane and out-of-plane rocking vibrations, respectively. The theoretically computed values (scaled) by the B3LYP/6-31G(d,p) method for CH₃ stretching nearly coincide with the FT-IR and FT-Raman experimental values.

5. NBO analysis

NBO theory allows the assignment of the hybridization of atomic lone-pairs and of the atoms involved in bond orbitals. These are significant data in spectral interpretation since the frequency ordering is interrelated to the bond hybrid composition. The NBO analysis allows us to estimate the energy of the molecule with the same geometry but in the absence of electronic delocalization. Moreover, only the steric and electrostatic interactions through the E_Lewis are taken into account.

The most important interactions between ‘filled’ (donors) Lewis-type NBO’s and ‘empty’ (acceptors) non-Lewis NBO’s of title compounds are reported in Tables S3 and S4.† The lone pair of n₃ (O18) with π* (N17–O19) and n₂ (O10) with π* (C1–C6) are identified as the strongest interaction (180.46 and 20.57 kcal mol⁻¹) for MNP and MMP, respectively. The lone pair interactions such as n₂ (O10) → π* (C1–C2) in MNP, n₂ (O12) → π* (C2–C3) in MMP provide evidence for charge transfer interactions from the OH moiety to the ring. The energy contribution of these interactions are 34.06 and 20.37 kcal mol⁻¹, respectively. The π-electron cloud movement from donor to acceptor can make the molecule highly polarized and this CT must be responsible for the NLO properties.

6. HOMO–LUMO analysis on the most stable structures

The analysis of the wave function indicates that the electron adsorption corresponds to the transition from the ground state to the first excited state and is mainly described by one-electron excitation from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO). The HOMO and LUMO orbitals for the most stable conformers of MNP and MMP are shown in Fig. 7. The HOMO–LUMO energy gaps are calculated at the B3LYP/6-31G(d,p) level (see Fig. 7) and these energy gaps reflect the chemical activity of the molecule. The LUMO as an electron acceptor represents the ability to obtain an electron, and HOMO refers to the ability to donate an electron. The energy gaps of HOMO–LUMO (Fig. 7) explain the eventual charge transfer interactions within the conformers. Consequently, the lowering of the HOMO–LUMO band gap is basically a consequence of the large stabilization of the LUMO. This is due to the strong electron-acceptor ability of the electron-acceptor group. For these conformers, the HOMO and LUMO have π and π* characters, respectively. The HOMO of MNP conformer shows antibonding character at O–CH₃, O–H and NO₂ moieties and bonding character on the ring. There is no electronic projection over the C–H group. The LUMO of MNP has a larger electronic projection over NO₂. Similarly, the HOMO of MMP conformer shows antibonding character at O–CH₃, O–H and CH₃ moieties and bonding character on ring. In LUMO of both the compounds there is no charge localization towards the C–H group of the O–CH₃ moiety.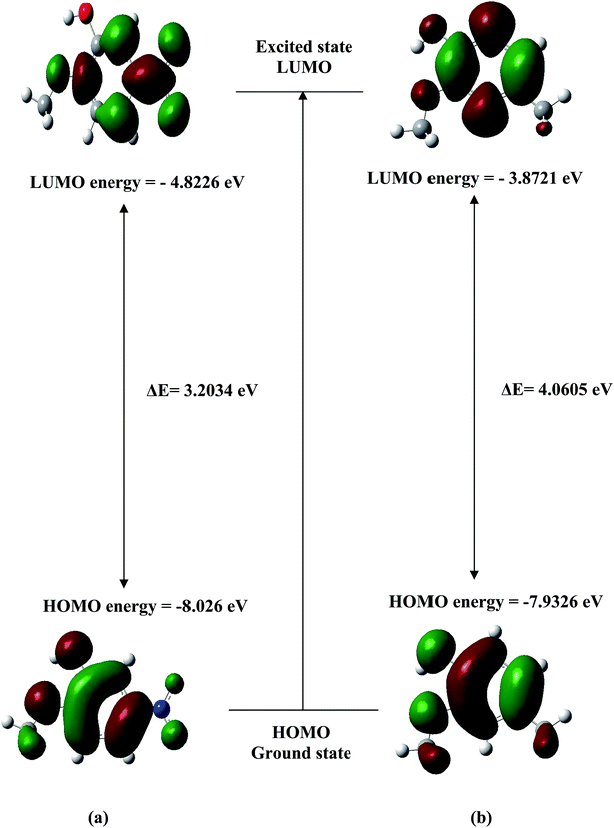

Fig. 7 HOMO–LUMO surface pictorial of (a) most stable conformer of MNP (b) most stable conformer of MMP.

7. NMR spectra

It is well recognized that accurate predictions of molecular geometries are essential for reliable calculations of magnetic properties. Therefore, full geometry optimization of both the compounds are performed using the B3LYP method with the 6-31G(d,p) basis set. The ¹³C chemical shifts for both the compounds are calculated by the GIAO (gauge-including atomic orbital) method in two different solvents such as DMSO, CDCl₃. The relative chemical shifts are then estimated using TMS shielding as the reference. Calculated ¹³C and ¹H isotropic chemical shielding for TMS are 182.4656 and 31.8821 ppm by B3LYP/6-311 + G(2d,p), respectively. The calculated ¹H and ¹³C NMR chemical shifts of MNP and MMP are compared with the experimental data. All the calculated ¹H and ¹³C chemical shifts of title the compounds are tabulated in Tables S5 and S6.†

C2 of MNP and MMP in the phenyl ring appears at higher chemical shifts of 112.4858 and 117.4975 ppm due to a neighbouring electronegative oxygen atom, respectively. Hence C2 seems to be shielded due to delocalization of electrons from the nitrogen atom. A peak at 112.5195 ppm is due to the nitro group. The deviation of the chemical shift of carbon atoms between the given experimental²⁵ and computed chemical shifts may be due to the presence of intermolecular hydrogen bonding.

Vacuum phase peaks at 5.0212, 6.5672, 6.4004 ppm and 4.7539, 5.335, 5.1463 ppm indicate the presence of aromatic hydrogen atoms in MNP and MMP, respectively. The average peak values at 3.044 and 2.8524 ppm indicate the O–CH₃ protons. These values are compared with the experimental value of 2-methoxy phenol.²⁶ In MMP, the average peak value at 1.1908 ppm belongs to the methyl group proton which is compared with the experimental value of 2-methylphenol.²⁶ The chemical shifts obtained and calculated for the hydrogen atoms of methyl groups are quite low. All values are ≤3 ppm due to shielding effects. In line with the above literature data, in our present study the methyl protons at C17 appear at 1.2772 ppm in DMSO showing good agreement with the computed chemical shift values.

8. Electronic spectra

The electronic transition energies and oscillator strengths at the excitation or emission processes are calculated by the TDDFT method in combination with PCM. In the excitation energy calculations, the PBE0 hybrid functional (PBE1PBE keyword in Gaussian) is selected. Generally the solvent plays an important role in absorption or emission spectrum of the title compounds. In this paper, the polarisable continuum model (PCM) including the solvent effect is preferred in excitation energy calculations. The PCM/TDDFT calculations is used for the solute molecule in solvents of different polarity such as a weakly polar cyclohexane (CHX), medium polar tetrahydrofuran (THF) and strongly polar acetonitrile (ACN). The vertical excitation energy and oscillator strength along with the main excitation configuration are listed in Table S7.† Major electronic absorption bands are assigned to those excitations with significant oscillator strengths as π → π* in all solvents.

9. First hyperpolarizability

The electronic and vibrational contributions to the first hyperpolarizabilities have been studied theoretically for many organic and inorganic systems. The values of the first hyperpolarizability were found to be quite large for the so-called push–pull molecules, i.e. p-conjugated molecules with the electron donating and the electron withdrawing substituents attached to a ring, compared to the monosubstituted systems. This type of functionalization of organic materials, with the purpose of maximizing NLO properties, is still a commonly followed route.

The first hyperpolarizabilities of these molecular systems are calculated using the B3LYP/6-31G(d,p) method, based on the finite-field approach. In the presence of an applied electric field, the energy of a system is a function of the electric field. First order hyperpolarizability (β) is a third rank tensor that can be described by 3 × 3 × 3 matrices. The components of which are defined as the coefficients in the Taylor series expansion of the energy in the external electric field. When the external electric field is weak and homogeneous, this expansion becomes:

where E⁰ is the energy of the unperturbed molecule, F_α is the field at the origin, and μ_α, α_αβ and β_αβγ are the components of dipole moment, polarizability and the first order hyperpolarizabilities, respectively. The total static dipole moment μ, and the mean first hyperpolarizability (β) using the x, y, z components, are defined as:μ = (μ_x² + μ_y² + μ_z²)^1/2whereβ = (β_x² + β_y² + β_z²)^1/2

β_x = β_xxx + β_xyy + β_xzz

β_y = β_yyy + β_xxy + β_yzz

β_z = β_zzz + β_xxz + β_yyz

Since the value of hyperpolarizability (β) of the Gaussian 09W output is reported in atomic units (au.), the calculated values have been converted into electrostatic units (esu) (β: 1 au. = 8.639 × 10⁻³³ esu). The total molecular dipole moment and first hyperpolarizability of MNP and MMP are 7.5450 and 3.2974 debye and 2.3332 × 10⁻³⁰ and 1.678 × 10⁻³⁰ esu, respectively and are depicted in Table 3. Total dipole moment and first hyperpolarizability of the title compounds are greater than those of urea (μ and β of urea are 1.3732 debye and 0.3728 × 10⁻³⁰ esu obtained by the HF/6-311G(d,p) method).

Table 3 Theoretical first hyperpolarizability of 2-methoxy-5-nitrophenol and 2-methoxy-4-methylphenol using the DFT/B3LYP/6-31G(d,p) method and basis set

Parameters	Values (au.)
	2-Methoxy-5-nitrophenol	2-Methoxy-4-methylphenol
βxxx	194.7	176.2
βxxy	668 933	8.5
βyyy	−0.0030211	8.7
βxxz	14.3614282	−84
βxyz	0.0149988	−430
βyyz	16.305164	−9.1
βxzz	61.8314414	5.7
βyzz	60.5510057	299.6
βzzz	−0.0072881	202.7
β	2.3332 × 10^−30 esu	1.678 × 10^−30 esu

---

10. Conclusion

A complete vibrational and molecular structure analyses is performed based on the quantum mechanical approach by HF and DFT calculations. On the basis of the calculated and experimental results the assignment of the fundamental frequencies are examined. The available experimental results were compared with theoretical data. A low value of HOMO LUMO energy gap suggests the possibility of intramolecular charge transfer in the molecule. This plays an important role in the significant increase of the β value, which is an important property to exhibit nonlinear optical activity. NBO result reflects the charge transfer mainly due to lone pairs. Theoretical ¹H and ¹³C chemical shift values (with respect to TMS) are reported and compared with experimental data, show agreement for both ¹H and ¹³C. Predicted electronic absorption spectra from TD-DFT calculations are analysed and they are mainly derived from the contribution of the π → π* band. The predicted NLO properties are much greater than those of urea.

References

1. B. S. Bhal and A. Bhal, Advanced Organic Chemistry, S. Chand and Company, 4th edn, 1995.
2. J. H. S. Green and D. J. Harrison, Spectrochim. Acta, Part A, 1971, 27, 93.
3. R. K. Rai, Proc. Indiana Acad. Sci., 1962, 55, 232.
4. R. B. Singh and D. K. Rai, Indian J. Pure Appl. Phys., 1980, 20, 330.
5. R. J. Jakobsen, Spectrochim. Acta, Part A, 1965, 21, 433.
6. R. J. Jakobsen and E. J. Brewer, Appl. Spectrosc., 1962, 17, 32.
7. Y. Kishore, S. N. Sharma and C. P. D. Dwivedi, Indian J. Phys., 1974, 48, 412.
8. Gaussian 09W Program, Gaussian Inc., Wallingford, 2004.
9. R. Dennington, I. I. T. Keith and J. Millam, Gauss View, Semichem, Inc., Shawnee Mission, KS, 2007.
10. MOLVIB (V.7.0), Calculation of Harmonic Force Fields and Vibrational Modes of Molecules, QCPE Program No. 807, 2002.
11. S. Kashino, M. Tomita and M. Haisa, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1988, 44, 730.
12. M. Bakiler, I. V. Maslov and S. Akyuz, J. Mol. Struct.: THEOCHEM, 1999, 475, 83–87.
13. G. Varsanyi, Assignments for Vibrational Spectra of Seven Hundred Benzene Derivatives, Acacemiai Kiado, Budapest, 1973, vol. 1 and 2.
14. A. J. Barnes, Spectrochim. Acta, Part A, 1985, 41, 629.
15. I. F. Shishkov, N. I. Sadova, V. P. Novikov and L. V. Vilkov, Zh. Strukt. Khim., 1984, 25, 98–102.
16. R. M. Silverstein, G. C. Bassler and T. C. Morrill, Spectrometric Identification of Organic Compounds, John Wiley & Sons, Inc., New York, 5th edn, 1981.
17. J. Coates, Interpretation of infrared spectra: a practical approach, in Encyclopedia of Analytical Chemistry, ed. R. A. Meyers, John Wiley & Sons Ltd, Chichester, 2000.
18. S. Ahmad, S. Mathew and P. K. Verma, Indian J. Pure Appl. Phys., 1992, 30, 764–770.
19. D. Mahadevan, S. Periandy and S. Ramalingam, Spectrochim. Acta, Part A, 2011, 78, 575–581.
20. N. B. Colthup, L. H. Daly and S. E. Wiberley, Introduction to Infrared and Raman Spectroscopy, Academic Press, New York, 1990.
21. G. Varsanyi, Assignments of Vibrational Spectra of Seven Hundred Benzene Derivatives, Adam Hilger, 1974, vol. 1 and 2.
22. N. Sundaraganesan, S. Ilakiamani, H. Saleem, P. M. Wojieehowski and D. Michalska, Spectrochim. Acta, Part A, 2005, 61, 2995.
23. A. Kovács, G. Keresztury and V. Izvekov, Chem. Phys., 2000, 253, 193–204.
24. D. N. Sathyanarayana, Vibrational Spectroscopy–Theory and Applications, Newage International (P) Limited Publishers, New Delhi, 2nd edn, 2004.
25. G. Crisponi, et al., Talanta, 2002, 56, 441–449.
26. R. J. Abraham and M. Mobli, Magn. Reson. Chem., 2007, 45, 865–877.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra00092d

---