Computational study on thermally activated delayed fluorescence of donor–linker–acceptor network molecules†
Talapunur Vikramaditya,
Mukka Saisudhakar and
Kanakamma Sumithra*
Birla Institute of Technology and Science (BITS), Pilani, Hyderabad Campus, Shamirpet, Telangana State, India 500078. E-mail: sumithra@hyderabad.bits-pilani.ac.in
First published on 24th March 2016
Abstract
Using Density Functional Theory (DFT) and time-dependent DFT calculations, we have investigated the structure–property relationships of organic molecules with donor–linker–acceptor (DLA) frameworks which can be used as precursors of OLED materials. Two types of linkers, thiophene (π-conjugated) and ethylene (non-π-conjugated), with carbazole as the electron donor and cyano-substituted benzene as the electron acceptor in the DLA framework were chosen. The donor–linker–acceptor network allows the HOMO and LUMO orbitals to be spatially separated, reducing the overlap of the frontier orbitals and decreasing the exchange energy (J); this results in a smaller ΔEST (energy gap between the excited singlet and triplet states), thus allowing us to realize metal-free molecules suitable for OLED applications. Incorporation of donor and acceptor groups in the same moiety helps reduce the number of layers conventionally used in OLEDs, reducing the cost and simplifying the fabrication of the device. By enhancing the electron donating nature of the donor group and increasing the electron withdrawing nature of the acceptor group, we observed a decrease in exchange energy, which was further decreased by the non-conjugated linker. Important properties such as the changes in dipole moments, absorption and emission energies and their corresponding oscillator strengths, transport energy gaps, electron affinities, ionization potentials (vertical and adiabatic), reorganization energies, and exciton binding energies of various substituted molecules were investigated and their roles in determining the efficiencies are discussed. In order to account for the effects of solvents and their role in altering various properties, the studies were carried out for polar and non-polar solvent phases in addition to the gas phase calculations.
Introduction
Ever-increasing energy demands and the depletion of non-renewable resources are creating a great necessity to devise more efficient technologies which harness power from renewable sources, consume less power and conserve the environment. Light emitting diodes (LEDs) have been widely investigated and have attained commercial-scale usage. Current research is focused on organic light emitting diodes (OLEDs), especially small molecule organic semiconductors, as they offer many advantages over their inorganic counterparts,1 such as fabrication of devices with high uniformity and large surface areas. However, lower efficiencies and shorter lifetimes are the main drawbacks associated with these devices (OLEDs), and many new materials are being synthesized and tested every year.1–11 In OLEDs, electrically injected charge carriers recombine to form singlet and triplet excitons in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio;2 as the transition between the triplet to singlet states is spin forbidden, it imposes a theoretical quantum efficiency of 25%. In order to overcome this problem, phosphorescent metal–organic complexes of heavy transition metals, such as Os, Pt, Ru, Re and Ir, are employed.3–6 The heavy atom induces a spin–orbit coupling effect which can partially decrease the spin–orbit forbidden nature of the T1 → S0 transition. However, the usage of heavy metals imposes a challenge of high cost in addition to many environmental concerns.
3 ratio;2 as the transition between the triplet to singlet states is spin forbidden, it imposes a theoretical quantum efficiency of 25%. In order to overcome this problem, phosphorescent metal–organic complexes of heavy transition metals, such as Os, Pt, Ru, Re and Ir, are employed.3–6 The heavy atom induces a spin–orbit coupling effect which can partially decrease the spin–orbit forbidden nature of the T1 → S0 transition. However, the usage of heavy metals imposes a challenge of high cost in addition to many environmental concerns.
Another way to increase the efficiency of OLEDs is by efficient spin upconversion from non-radiative triplet states (which are formed at a rate of 75%) to radiative singlet states.4 This can be achieved by minimizing the energy gap between S1 and T1. Thermally activated delayed fluorescence (TADF), or E-type delayed fluorescence, is directly proportional to the energy gap between the triplet and singlet states (ΔEST7), which is dependent on the electron exchange energy. Intramolecular charge transfer states (ICT), where the electrons and holes are decoupled on different orbitals, have zero to first order exchange energy, giving rise to E-type delayed fluorescence.8 Recently, Adachi and co-workers9 have synthesized metal-free, environmentally benign organic molecules which harness both singlet and triplet excitons for light emission through fluorescence decay channels with very high efficiencies.
OLEDs have a three-layered structure that consists of a hole transporting layer (HTL), an emitting layer (EL) and an electron transporting layer (ETL). Hole transporting materials should contain electron donating moieties which can form stable cation radicals, whereas electron-transporting materials should have electron withdrawing groups which can form stable anion radicals.10 A single layer structure is possible if the emitting material has balanced electron and hole mobilities. Such a structure would have a lower overall cost and simplified device fabrication.11 Recently, Huang et al.11 synthesized dipolar dibenzothiophene S,S-dioxide derivatives for use as materials for single layer OLED devices. However, such studies are rare, and there is great scope to model and synthesize these molecules.
In the current work, we have considered some important donor–linker–acceptor framework structures and investigated their electronic properties. This type of framework helps reduce the cost of OLEDs in two ways: first, the electron donating and withdrawing groups are separated, which allows the HOMO and LUMO to separate; this minimizes the overlap of the frontier orbitals and reduces the exchange energy (J), resulting in a small ΔEST and thus allowing the realization of metal free molecules suitable for OLED applications. Moreover, the incorporation of donor and acceptor groups in the same moiety helps reduce the number of layers. Excited state angular materials have stronger charge transfer character than the excited state of their linear analogues;12 this enhances the charge transfer character of the lowest singlet excited state, favouring higher intersystem crossing yields.13 We have chosen carbazole as the electron donor and different cyano-substituted benzene groups as the acceptors. Thiophene and ethylene molecules were chosen as linkers. This type of framework allows the compound to adopt an angular geometry where the donor and acceptor moieties are separated by the linkers.14
Computational methodology
Ground state optimizations were carried out employing DFT with the hybrid functional B3LYP and the valence triple zeta polarized 6-311G(d) basis set. Excited state properties were determined by employing TD-DFT, using the same functional and basis set. B3LYP combines the Becke generalized gradient approximation (GGA) and exchange potential based upon Hartree Fock (HF) exchange along with the Lee–Yang–Parr correlation functional.15,16 The hybrid functional B3LYP is found to give better results in calculating HOMO and LUMO energies, ionization potentials and electron affinities in comparison with regular local density and generalized gradient approximations.17 It is found to provide accurate ionization potentials, electron affinities and cohesive energies for a range of finite molecules.17,18 B3LYP typically employs 20% of orbital exchange, which is accurate enough to calculate excitonic properties for organic molecules.19 Basis set effects in calculating excitation energies19 and other ground state properties17–19 are found to be negligible beyond the 6-31G(d) basis set. Recent theoretical investigations by Gierschner et al.14 and a few other groups20,21 have suggested that B3LYP gives a very good description of the singlet and triplet states of medium-sized molecules. Hence, we expected that various properties calculated employing the B3LYP functional and 6-311G(d) basis set would predict the properties of medium-sized organic molecules with reasonable accuracy. We employed the polarizable continuum model (PCM)22–24 to model the bulk solvent effects. This model accounts for the solvent effect by considering the solute inside a cavity that is surrounded by structureless media which has the macroscopic characteristics of the solvent. To compute transition energies within the PCM framework, we employed the Linear-Response (LR) approach, which is computationally efficient and has well-defined transition properties.24 All the calculations are performed employing Gaussian 09 software.25We investigated the excited singlet–triplet gaps (ΔEST), changes in dipole moments, absorption and emission energies and their corresponding oscillator strengths, HOMO–LUMO energies, electron affinities, ionization potentials, reorganization energies, and exciton binding energies for the chosen molecules to understand their properties for application in OLEDs. All the calculations were carried out in the gas phase as well as in solvent phases to understand how solvent effects alter the properties of the molecules under consideration. To account for the effects of polarity, we chose two different solvents, namely cyclohexane (non-polar, ε = 2.0165) and methanol (polar, ε = 32.613).
The preliminary strategy adopted to design molecules which exhibit low singlet–triplet energy gaps is as follows. The molecular energies of the lowest singlet energy (ES) and the triplet energy (ET) are given by
| ES = ES + K + J | (1) |
| ET = ET + K − J | (2) |
| ΔEST = ES − ET = 2J | (3) |
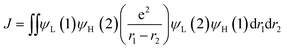 | (4) |
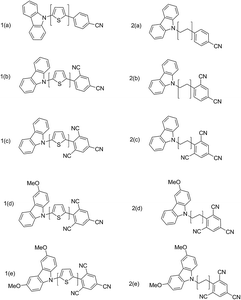 | ||
| Fig. 1 Donor–linker–acceptor (DLA) molecules with thiophene (1a–e) and ethylene (2a–e) as linkers (linkers are shown in brackets). | ||
The advantage of considering cyano groups is that they act as strong electron-withdrawing groups, enhancing the electron affinities of the resulting cyano-substituted aromatophors;29,30 incorporation of alkyl or alkoxy groups enhances the solubility, which facilitates processing.10 Two types of linkers, a π-conjugated group, thiophene (C4H4S), and a non-conjugated group, ethylene (–CH2–CH2–), were considered.
Results and discussion
As a first step, we calculated ΔEST, which is crucial in determining the efficiencies of OLED materials, since the energy gap affects the rate of intersystem crossing. The emission quantum yield (Ø) is given by eqn (5), where kr and knr correspond to the radiative and non-radiative rate constants given by eqn (6) and (7).31–33
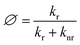 | (5) |
knr ≈ α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βET) exp(−βET)
| (6) |
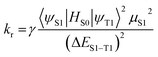 | (7) |
| Molecules | Gas phase | Cyclohexane | Methanol |
|---|---|---|---|
| 1a | 1.05 | 1.20 | 1.14 |
| 1b | 0.72 | 0.77 | 0.88 |
| 1c | 0.29 | 0.39 | 0.66 |
| 1d | 0.01 | −0.14 | 0.06 |
| 1e | 0.00 | −0.10 | 0.04 |
| 2a | 0.65 | 0.68 | 0.71 |
| 2b | 0.01 | 0.01 | 0.05 |
| 2c | −0.12 | −0.08 | 0.01 |
| 2d | 0.01 | 0.01 | 0.01 |
| 2e | 0.01 | 0.01 | 0.01 |
From Table 1, it is evident that with the increase in substitution of electron-withdrawing and donating groups, the energy gap between the excited state singlet and triplets decreases. The energy gaps (ΔEST) of molecules with thiophene as a linker are larger (1a–c) than those of the molecules having ethylene as a linker (2a–c).
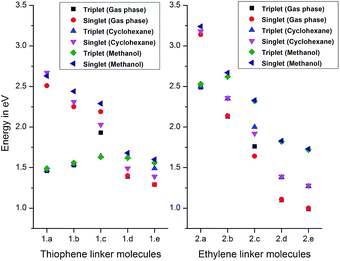
As the number of cyano groups attached to the benzene ring increased (1a to c), we observed a decrease in the ΔEST values. In the case of the thiophene linker molecules (TLMs), we noticed a steep decrease in ΔEST values with the substitution of electron donating methoxy groups (1d and e). Unlike the TLMs, the ΔEST values of the ethylene linker molecules (ELMs) were found to be very sensitive with respect to substitution. We observed a steep decrease in ΔEST from 0.65 eV to 0.01 eV (in the gas phase from 2a to b), and a similar trend is observed in the solvent phases, as shown in Table 1. The overall trend of decreasing ΔEST energies in the gas phase was found to be similar with respect to the solvent phases (cyclohexane and methanol). However, we noticed that in most cases, the ΔEST energies are higher (or equal) in polar media (methanol) in comparison with cyclohexane, which in turn are higher than the gas phase energies. The excited singlet and triplet energy states in the different phases are shown in Fig. 2.
To understand this effect of decreasing ΔEST energies, we plotted the HOMOs and LUMOs (gas phase) for the TLMs and ELMs, as shown in Fig. 3. From Fig. 3, it is clear that in the molecules where thiophene is the linker (TLMs), the HOMO and LUMO orbitals are slightly overlapped at the linker. On the other hand, in the case of the molecules where ethylene is the linker, the overlap is minimal or negligible. For example, in the case of 1a, the contribution of the donor, linker and acceptor towards the HOMO were found to be 89%, 9% and 2%, and those for the LUMO were 2%, 35% and 63%. For 2a, the contributions of the donor, linker and acceptor towards the HOMO were found to be 95%, 4% and 1%, and for the LUMO, they were 1%, 4% and 95%.
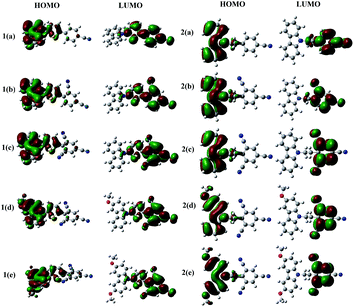 | ||
| Fig. 3 HOMO and LUMO orbitals of molecules with thiophene linkers (1a–e) and ethylene linkers (2a–e). Grey, white, blue, red and yellow indicate carbon, hydrogen, nitrogen, oxygen and sulphur atoms. | ||
This can be understood by the π-conjugation in thiophene, which allows electronic information to be shared between the HOMO and LUMO with the π electron network, whereas in the ELMs, the electronic information is blocked by the non-conjugated linker ethylene. Hence, the energy gaps of the excited state singlet and triplet are lower for the ELMs in comparison with the conjugated TLMs. We observed that with increasing strength of the electron donating and withdrawing substituents, there was a decrease in the ΔEST energies in the compounds with donor–linker–acceptor frameworks. The contributions of the donor, linker and acceptor towards the HOMOs and LUMOs for all the molecules in the gas phase are given in the ESI.†
From eqn (6) and (7), we can observe that for efficient OLED materials, higher energy T1 states are required. With the increasing substitution of cyano groups on the benzene moiety for the TLMs, we observed an increase in the level of the T1 states, as shown in Fig. 2 (1a–c); however, no such trend is observed for the ELMs (2a–c). With the substitution of electron donating methoxy groups on the carbazole moiety, we observed a decrease in both the S1 and T1 states (1d, e, 2d and e).
We calculated the dipole moments corresponding to the optimized ground (S0) and excited states (S1) in order to understand the structural changes which the molecules underwent upon excitation. The differences in the dipole moments from the ground state to the excited singlet state (S0–S1) are shown in Fig. 4. Negative dipole moments suggest larger dipole moments in the excited state, and positive values suggest higher dipole moments in the ground state. From Fig. 4, it is evident that the polarity of the solvent plays a significant role in altering the dipole moments of the molecules from the ground state to the excited state. The gas phase and cyclohexane solvent phase (ε = 2.0165) calculation results were found to be closer; on the other hand, in the solvent phase calculations with methanol, the changes in the dipole moments are significantly different from the gas phase. In the case of the TLMs, with increasing substitution, we observed an increase in the change in the dipole moment in the gas phase. The cyclohexane phase results were closer to the gas phase calculations; however, the magnitudes of the dipoles are slightly different. We did not observe any particular trend in the case of methanol medium for TLMs. The dipole moments of TLMs in the excited state are significantly higher compared to the ground state in methanol medium (negative dipole moment, as shown in Fig. 4). If the solute dipole moment in the excited state is greater than in the ground state, then the excited state is better stabilized compared to the ground state.34 Hence, it can be concluded that the excited states of TLMs are more stabilized in polar media such as methanol, offering longer lifetimes for the corresponding singlet excitons. In contrast to the TLMs, the ELMs exhibit a different trend where the gas phase and non-polar solvent (cyclohexane) stabilize the excited state (2c–e) when compared to methanol medium. Another important conclusion which can be drawn based on the change in dipole moments is the geometrical relaxation experienced by the molecule upon excitation. The larger the difference in the dipole moments (between the ground state and the excited state), the greater the structural change the molecule undergoes. From Fig. 4, we observed that the TLMs undergo greater structural changes in comparison with the ELMs; this effect is greatly influenced by the solvent medium.
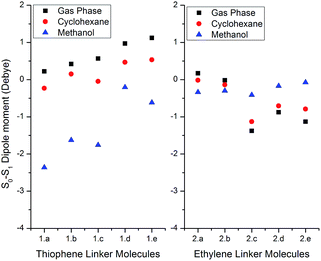 | ||
| Fig. 4 Differences in dipole moments (in Debye) from S0 → S1 for thiophene and ethylene linker molecules (optimized ground and excited state dipole moments are considered). | ||
We calculated the absorption and fluorescence energies and corresponding oscillator strengths (f), which give us information about the molecule aggregation, intensities and rates of transition dipole moments (in the solvent phases). From Table 2, it is clear that the absorption energies decrease with substitution due to the increasing conjugation, resulting in a bathochromic shift of the absorption maxima. The absorption energies of the TLMs decreased from 3.16 to 2.08 eV in non-polar media and from 3.24 to 2.24 eV in polar media. A similar trend was observed in the case of the ELMs. The increase in the intensity of the absorption indicates that the solute is most soluble in the solvent and that there is the lowest degree of aggregation.35 The oscillator strength suggests the intensity of absorption or emission. Compared to the ELMs, the oscillator strengths of the TLMs were found to be higher, indicating that the aggregation of the TLMs is lower than that of the ELMs. The oscillator strengths of the TLMs are mostly higher (except 1a) in non-polar media than in polar media, whereas the ELMs exhibit higher oscillator strengths in polar media than in non-polar media (gas phase calculation results are given in the ESI†).
| Molecule | (A) NP | (f) NP | (A) P | (f) P |
|---|---|---|---|---|
| 1a | 3.16 | 0.0572 | 3.24 | 0.0631 |
| 1b | 2.81 | 0.2178 | 2.93 | 0.2069 |
| 1c | 2.50 | 0.2117 | 2.71 | 0.1524 |
| 1d | 2.23 | 0.2186 | 2.42 | 0.1342 |
| 1e | 2.08 | 0.1783 | 2.24 | 0.1790 |
| 2a | 3.60 | 0.0870 | 3.67 | 0.0885 |
| 2b | 2.87 | 0.0551 | 3.10 | 0.0564 |
| 2c | 2.42 | 0.0010 | 2.77 | 0.0593 |
| 2d | 2.10 | 0.0017 | 2.47 | 0.0512 |
| 2e | 1.89 | 0.0007 | 2.27 | 0.0105 |
Another important factor which enhances the radiative rate constants is the transition dipole moment (eqn (7)). μS1 corresponds to the transition dipole moment (S0 → S1), which is correlated with the oscillator strengths of absorption. Quantum mechanical oscillator strengths (f) and transition dipole moments are related as36
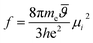 | (8) |
![[small variant theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e1f3.gif) is the energy of the transition, “h” is Planck's constant and μi2 corresponds to the square of the transition dipole moment to the ith state (here, it is to the S1 state from the ground state). From eqn (8), we noted that higher oscillator strengths and larger energies of excitation favour larger transition dipole moments, thus enhancing the radiative rate constants. From the oscillator strengths corresponding to the absorption shown in Table 2, we observed that the TLMs exhibited higher oscillator strengths compared to the ELMs in both polar and non-polar media.
is the energy of the transition, “h” is Planck's constant and μi2 corresponds to the square of the transition dipole moment to the ith state (here, it is to the S1 state from the ground state). From eqn (8), we noted that higher oscillator strengths and larger energies of excitation favour larger transition dipole moments, thus enhancing the radiative rate constants. From the oscillator strengths corresponding to the absorption shown in Table 2, we observed that the TLMs exhibited higher oscillator strengths compared to the ELMs in both polar and non-polar media.
Absorption and fluorescence intensities are generally similar if there are negligible structural changes associated with the excitation. However, from Fig. 4, we observed significant changes in the dipole moments corresponding to the ground state and excited state, which in turn alters the intensity of fluorescence (oscillator strength) differently from the absorption, as shown in Table 3. The fluorescence intensity was higher in polar solvent compared to non-polar solvent, as is evident from the corresponding oscillator strengths shown in Table 3. TLMs exhibit higher oscillator strengths in comparison with ELMs. With increasing substitution, we observed a decrease in fluorescence intensity.
| Molecule | (F) NP | (f) NP | (F) P | (f) P |
|---|---|---|---|---|
| 1a | 2.67 | 0.0046 | 2.63 | 0.9914 |
| 1b | 2.31 | 0.0003 | 2.44 | 0.6013 |
| 1c | 2.03 | 0.0001 | 2.29 | 0.4003 |
| 1d | 1.49 | 0.0004 | 1.68 | 0.0008 |
| 1e | 1.39 | 0.0005 | 1.60 | 0.0005 |
| 2a | 3.18 | 0.0630 | 3.24 | 0.1024 |
| 2b | 2.36 | 0.0246 | 2.67 | 0.0493 |
| 2c | 1.92 | 0.0005 | 2.33 | 0.0258 |
| 2d | 1.39 | 0.0033 | 1.83 | 0.0189 |
| 2e | 1.28 | 0.0003 | 1.73 | 0.0192 |
The HOMO and LUMO energies are crucial because they are related to the hole and electron injection abilities,37 and the values of the energy levels must be determined for choosing anodes and cathodes in the OLED set-up.38 We calculated the HOMO and LUMO energies (or transport energy levels) in different media, as depicted in Fig. 5 (the energy values are provided in the ESI†). The transport energy gaps were found to decrease with the substitution of both electron withdrawing and electron donating groups in all the phases. In the case of the TLMs, the highest transport energy gap was found to be 3.64 eV (1a, gas phase) with a significant decrease in energy gap upon substitution from 1a to e; the lowest energy gap was 2.43 eV (1e, gas phase). Similar findings were observed in the ELMs with the highest transport energy gap of 4.02 eV (2a, gas phase) and the lowest energy gap of 2.12 eV (2e, gas phase).
The solvent effects on the transport energy gaps were found to be profound, as is evident from Fig. 5, where we observed that the LUMO energy levels in solvent media are higher than in the gas phase calculations, resulting in larger energy gaps. The transport energy gaps in various media are given in Table 4. As the polarity of the solvent increases, the transport gap increases. For example, in the case of the ELMs with an increase in substitution, the difference in the transport gaps of the gas phase and the methanol phase was found to increase from 0.08 eV (2a) to 0.58 eV (2e). In the case of the TLMs, we observed that the difference between the transport energy gaps of the methanol and gas phases increased from 0.12 to 0.27 eV (from 1a to c) and slightly decreased to 0.24 and 0.21 eV for 1d and e. In the case of cyclohexane media, the transport energy gaps of all the molecules studied were found to be intermediate between the gas phase and methanol media.
| Molecules | Gas phase | Cyclohexane | Methanol |
|---|---|---|---|
| 1a | 3.64 | 3.68 | 3.76 |
| 1b | 3.23 | 3.27 | 3.39 |
| 1c | 2.87 | 2.93 | 3.14 |
| 1d | 2.58 | 2.62 | 2.82 |
| 1e | 2.43 | 2.46 | 2.64 |
| 2a | 4.02 | 4.04 | 4.10 |
| 2b | 3.21 | 3.33 | 3.57 |
| 2c | 2.69 | 2.88 | 3.22 |
| 2d | 2.34 | 2.53 | 2.90 |
| 2e | 2.12 | 2.32 | 2.70 |
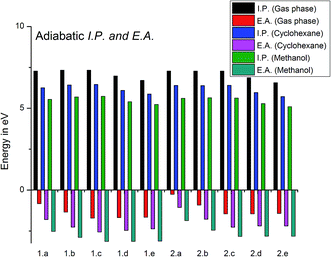
Ionization potentials and electron affinities give us information about the hole injection and electron injection capabilities of molecules. The ionization potentials (IP) and electron affinities (EA) (only adiabatic IP and EA are discussed here; vertical and adiabatic IP and EA values are provided in the ESI†) were calculated in order to understand the performance of the proposed molecules. Smaller ionization potentials favour easier hole injection, and larger electron affinities facilitate electron injection.37 Fig. 6 depicts the trends of the IPs and EAs (adiabatic) of the TLMs and ELMs. The IP values depend on the HOMO energy levels, and the EA values depend on the LUMO levels. The electron withdrawing groups decrease the LUMO energies, and the electron donating groups increase the HOMO levels by donating electrons (Fig. 5).
The ionization potential energies (shown in Fig. 6) were found to be slightly altered with the substitution of electron withdrawing groups; however, we observed a significant reduction in IP values from 7.274 to 6.708 eV (1c to e, gas phase) with the substitution of electron donating groups, as they increase the HOMO energy levels, thus favouring the easy removal of electrons. The ionization potential increases from 7.274 to 7.328 eV (1a to c) and decreases to 6.708 eV (1e) for the TLMs; the ELMs also exhibit the same trend. From the histogram in Fig. 6, it is evident that the IP values are highest in the gas phase and lowest in the polar medium methanol, as the cations are stabilized by the polar media. A significant difference in the magnitude of the IP energy is observed between the gas phase and the polar medium methanol; they were found to be in the range of 1.4 to 1.7 eV. From Fig. 6, we observed that the magnitude of the electron affinities increased with increasing substitution of cyano groups (1a to c and 2a to c) from −0.829 to −1.714 eV (1a to c, gas phase) and a slight decrease upon substitution with electron donating groups from −1.687 to −1.657 (1d to e, gas phase). The electron affinities of the ELMs were found to be lower in comparison with the TLMs; however, the trend was found to be similar to that of the TLMs. Compared to the IP energies, a contrasting trend was observed, where the EAs were higher in energy in the polar solvent methanol compared to the gas phase. The cyclohexane IPs and EAs were found to be intermediate between the gas phase and methanol.
One of the important factors which determine the efficiencies of OLED materials is the reorganization energy (λ). “λ” is related to the rate of intermolecular charge transfer (ket) from Marcus–Hush theory,39 given by the formula
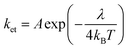 | (9) |
| λe = (E−0 − E−−) + (E0− − E00) | (10) |
| λh = (E+0 − E++) + (E0+ − E00) | (11) |
From Fig. 7, we observe that λhole is found to be lower in comparison with λelectron (except 1a), indicating that the hole transporting ability of these molecules is superior to that of electron transport. Compared to TLMs, ELMs exhibit lower reorganization energies (both λhole and λelectron). From Fig. 7, we observed a significant difference in the magnitude of reorganization energies corresponding to the electrons and holes in different media; however, the trend was found to be similar in all the phases.
Lower ΔE values (ΔE corresponds to the modulus of energy difference between the reorganization of electrons and holes) are required for efficient balance of electrons and holes in the emitting layer.37 The ΔE values of the studied molecules in different phases are given in Table 5.
| Molecules | Gas phase | Cyclohexane | Methanol |
|---|---|---|---|
| 1a | 0.011 | 0.068 | 0.092 |
| 1b | 0.189 | 0.190 | 0.159 |
| 1c | 0.261 | 0.237 | 0.217 |
| 1d | 0.184 | 0.148 | 0.117 |
| 1e | 0.235 | 0.208 | 0.103 |
| 2a | 0.036 | 0.154 | 0.271 |
| 2b | 0.165 | 0.184 | 0.213 |
| 2c | 0.182 | 0.203 | 0.214 |
| 2d | 0.017 | 0.033 | 0.030 |
| 2e | 0.099 | 0.092 | 0.104 |
With the increase in substitution of cyano groups in the TLMs, we observed increases in the ΔE values from 0.011 to 0.261 eV (in the gas phase). With the substitution of electron donating methoxy groups, the ΔE value slightly decreases to 0.184 (1d, gas phase) and increases to 0.235 (1e, gas phase) with the substitution of an additional methoxy group. ELMs also followed a similar trend to that of the TLMs. The ΔE values in the solvent phases mostly followed a similar trend to that of the gas phase; however, they slightly differed in magnitude, as shown in Table 5.
Larger exciton binding energies are required in OLED materials to increase the probability of electron hole pair recombination.41 From eqn (12), we observed that the exciton binding energy is dependent on the transport gap and the optical energy. ET is called the transport gap, which is the energy difference between the HOMO and LUMO; Eopt corresponds to the optical gap (S0 to S1). Exciton binding energy helps us understand the attraction–repulsion interplay between electrons and holes by comparing the variation of S1 energy with respect to the HOMO–LUMO energy gap.42 The exciton binding energy is calculated by the formula given in eqn (12).
| E.B.E. = ET − Eopt | (12) |
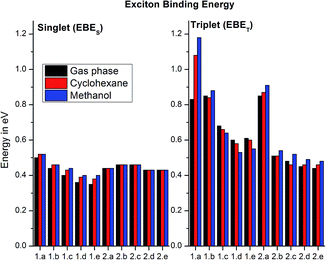
In larger chains (and solids), the electrons and holes are well separated; their localized repulsions are negligible, and the HOMO–LUMO gap coincides with the optical gap.43,44 However, in small and medium-sized molecules, we observe appreciable exciton binding energies due to the strong attraction between electrons and holes. From Fig. 8, we found that the HOMO–LUMO energy gaps are greater than the optical gaps due to the effective electron–hole attraction which stabilizes the HOMO–LUMO gaps. In solar cells, the excitation is optical (the transition is from S0 to S1); however, in the case of OLEDs, the injection is electrical, which results in the formation of triplet and singlet excitons (75% triplet and 25% singlet). Hence, we calculated the exciton binding energies corresponding to the triplet states (EBET) along with the singlet states (EBES), as shown in Fig. 8.
In general, excited triplet states are found to be lower compared to the corresponding singlets; hence, we observed (in Fig. 8) higher exciton binding energies for the triplets than for their corresponding singlets. In the case of the TLMs, the EBES were found to be higher in the solvent phase than in the gas phase, and we observed a decrease in the EBES from 1a to e (0.5 to 0.35 eV – gas phase; 0.52 to 0.38 eV – methanol medium). On the other hand, for the ELMs, the EBES were insensitive to both solvent media and substitution (2a to e); they remained close to ∼0.4 eV. In the case of the triplet exciton binding energies, there is a gradual decrease in the exciton binding energies for the TLMs (from 1a to e) from 0.83 to 0.61 eV in the gas phase and from 1.18 to 0.60 eV in methanol media. The ELMs exhibited lower EBET values compared to the TLMs, ranging from 0.85 to 0.44 eV in the gas phase and 0.91 to 0.48 eV in methanol.
Conclusions
We have considered donor–linker–acceptor framework molecules to study the properties of OLEDs. Various properties which effect the efficiencies of emission quantum yields (Ø), such as the energy gaps between the excited singlet and triplet states (ΔEST), dipole moments, HOMO and LUMO energies, transport energy gaps, ionization potentials, electron affinities, reorganization energies and exciton binding energies, were investigated. Calculations were carried out with a regular gas phase along with non-polar cyclohexane and polar methanol solvent media in order to understand the effects of solvent on these properties. The singlet–triplet energy gap, which is dependent on the exchange energy, can be reduced by separating the HOMO and LUMO with a linker. By enhancing the donating ability of the electron donors and the withdrawing capability of the electron acceptors, the energy gaps of the S1 and T1 states can be reduced to almost zero eV. A non-conjugated linker (ethylene) was found to be more efficient in decreasing the energy gap (ΔEST) compared to the conjugated linker thiophene, since the non-conjugated linker blocks the electronic information between the frontier orbitals more efficiently than the conjugated linker thiophene. Although the gas phase calculations in most of the cases (except the dipole moment changes from S0 to S1) predicted the trend of variation in properties with respect to substitution, the magnitude of the difference is appreciable in many of the cases. The solvent effects were found to be profound due to the polarity difference, and it was found that the transport energy gaps (HOMO–LUMO gaps) increased with increasing solvent polarity. Significant differences in the magnitudes of IP and EA in various media were found, as the frontier orbital energy levels varied in the different media due to the changes associated with polarity. The reorganization energies were calculated; we observed that λhole was lower in comparison with λelectron (except in 1a), indicating that the hole transporting abilities of these molecules are superior to their electron transporting abilities. Compared to the TLMs, the ELMs exhibit lower reorganization energies (both λhole and λelectron). Exciton binding energies (EBE) corresponding to the first excited singlet and triplet states were calculated. The EBET values of the triplets were higher than their corresponding singlets due to the lower energies of the triplets compared to their respective singlets. In the case of the TLMs, we observed a gradual decrease in the exciton binding energies with respect to substitution corresponding to both singlets and triplets. The ELMs exhibited a different trend compared to the TLMs, where we do not observe any significant changes corresponding to the EBES upon substitution; on the other hand, there is a gradual decrease in the exciton binding energy corresponding to the triplets.Acknowledgements
K. Sumithra gratefully acknowledges the Council of Scientific and Industrial Research (CSIR), Government of India, New Delhi for financial support in the form of a project grant (01 (2748)/13/EMR-II), T. Vikramaditya thanks the University Grants Commission, New Delhi for providing a senior research fellowship and M. Saisudhakar acknowledges support from the same CSIR project for funding in the form of a senior research fellowship.References
- D. Yokoyama, J. Mater. Chem., 2011, 21, 19187 RSC.
- M. Pope, H. P. Kallmann and P. Magnante, J. Chem. Phys., 1963, 38, 2042 CrossRef CAS.
- M. A. Baldo, S. Lamansky, P. E. Burrows, M. E. Thompson and S. R. Forrest, Appl. Phys. Lett., 1999, 75, 4 CrossRef CAS.
- C. Adachi, M. A. Baldo, M. E. Thompson and S. R. Forrest, J. Appl. Phys., 2001, 90, 5048 CrossRef CAS.
- T. Tsutsui and S. Saito, Organic Multilayer-Dye Electroluminescent Diodes: Is There Any Difference with Polymer LED? 127–131, Kluwer, 1993.
- L. J. Rothberg and A. J. Lovinger, J. Mater. Res., 1996, 11, 3174 CrossRef CAS.
- C. A. Parker and C. G. Hatchard, Trans. Faraday Soc., 1961, 57, 1894 RSC.
- H. Beens and A. Weller, Acta Phys. Pol., 1968, 34, 593 CAS.
- A. Endo, K. Sato, K. Yoshimura, T. Kai, A. Kawada, H. Miyazaki and C. Adachi, Appl. Phys. Lett., 2011, 98, 083302 CrossRef.
- L. Duan, L. Hou, T. W. Lee, J. Qiao, D. Zhang, G. Dong, L. Wang and Y. Qiu, J. Mater. Chem., 2010, 20, 6392 RSC.
- T.-H. Huang, J. T. Lin, L.-Y. Chen, Y.-T. Lin and C.-C. Wu, Adv. Mater., 2006, 18, 602 CrossRef CAS.
- K. C. Moss, K. N. Bourdakos, V. Bhalla, K. T. Kamtekar, M. R. Bryce, M. A. Fox, H. L. Vaughan, F. B. Dias and A. P. Monkman, J. Org. Chem., 2010, 75, 6771 CrossRef CAS PubMed.
- S. King, R. Matheson, F. B. Dias and A. P. Monkman, J. Phys. Chem. B, 2008, 112, 8010 CrossRef CAS PubMed.
- B. Milián-Medina and J. Gierschner, Org. Electron., 2012, 13, 985 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 37, 785 CrossRef.
- G. Zhang and C. B. Musgrave, J. Phys. Chem. A, 2007, 111, 1554 CrossRef CAS PubMed.
- T. Vikramaditya, M. Sai Sudhakar and K. Sumithra, J. Mol. Struct., 2014, 1081, 114 CrossRef.
- S. Kilina, E. Badaeva, A. Piryatinski, S. Tretiak, A. Saxenaa and A. R. Bishopa, Phys. Chem. Chem. Phys., 2009, 11, 4113 RSC.
- M. Parac and S. Grimme, Chem. Phys., 2003, 292, 11 CrossRef CAS.
- K. A. Nguyen, J. Kennel and R. Pachter, J. Chem. Phys., 2002, 117, 7128 CrossRef CAS.
- J. S. Bader and B. A. Berne, J. Chem. Phys., 1996, 104, 1293 CrossRef CAS.
- J. Thonasi, B. Menucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef PubMed.
- G. Scalmani, M. J. Frisch, B. Menucci, J. Thomasi, R. Cammi and V. Barone, J. Chem. Phys., 2006, 124, 94107 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- G. Mehes, H. Nomura, Q. S. Zhang, T. Nakagawa and C. Adachi, Angew. Chem., Int. Ed., 2012, 51, 11311 CrossRef CAS PubMed.
- A. Köhler, J. S. Wilson, R. H. Friend, M. K. Al-Suti, M. S. Khan, A. Gerhard and H. Bässler, J. Chem. Phys., 2002, 116, 9457 CrossRef.
- A. Köhler and H. Bässler, Mater. Sci. Eng., R, 2009, 66, 71 CrossRef.
- A. Yassar, F. Demanze, A. Jaafari, M. El Idrissi and C. Coupry, Adv. Funct. Mater., 2002, 12, 699 CrossRef CAS.
- K. Thomas, M. Velusamy, J. T. Lin, Y. T. Tao and C. H. Cheun, Adv. Funct. Mater., 2004, 14, 387 CrossRef CAS.
- G. Tong and C. Che, Chem.–Eur. J., 2009, 15, 7225 CrossRef CAS PubMed.
- J. S. Wilson, N. Chawdhury, M. R. A. Al-Mandhary, M. Younus, M. S. Khan, P. R. Raithby, A. Kohler and R. H. Friend, J. Am. Chem. Soc., 2001, 123, 9412 CrossRef CAS PubMed.
- H. Yersin, Highly Efficient OLEDs with Phosphorescent Materials, Wiley-VCH, Weinheim, Germany, 2008 Search PubMed.
- B. Valeur, Molecular fluorescence principles and applications, Wiley-Vch Verlag GmbH, Weinheim, 2002 Search PubMed.
- M. Homocianu, A. Airinei and D. O. Dorohoi, Journal of Advanced Research in Physics, 2011, 2, 011105 Search PubMed.
- N. J. Turro, V. Ramamurthy and J. C. Scaiano, Principles of Molecular Photochemistry: An Introduction, University Science Books, 2009 Search PubMed.
- X. Shang, N. Wan, D. Han and G. Zhang, Photochem. Photobiol. Sci., 2014, 13, 574 CAS.
- Y. Tao, K. Yuan, T. Chen, P. Xu, H. Li, R. Chen, C. Zheng, L. Zhang and W. Huang, Adv. Mater., 2014, 26, 7931 CrossRef CAS PubMed.
- R. A. Marcus, Rev. Mod. Phys., 1958, 28, 962 Search PubMed.
- G. R. Hutchison, M. A. Ratner and T. J. Marks, J. Am. Chem. Soc., 2005, 127, 2339 CrossRef CAS PubMed.
- J. H. Seo, Y. Jin, J. Z. Brzezinski, B. Walker and T. Q. Nguyen, ChemPhysChem, 2009, 10, 1023 CrossRef CAS PubMed.
- K. I. Igumenshchev, J. Chem. Phys., 2007, 127, 114902 CrossRef PubMed.
- L. Reining, V. Olevano, A. Rubio and G. Onida, Phys. Rev. Lett., 2002, 88, 066404 CrossRef PubMed.
- F. Sottile, V. Olevano and L. Reining, Phys. Rev. Lett., 2003, 91, 056402 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra00053c |
| This journal is © The Royal Society of Chemistry 2016 |