Temperature and composition dependence of the density, viscosity and refractive index of binary mixtures of a novel gemini ionic liquid with acetonitrile
Abstract
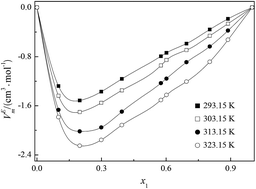
A novel asymmetrical gemini ionic liquid, 1-(1-methypiperidinium-1-yl)hexane-(1-pyridinium)bi[bis(trifluoromethanesulfonyl)imide] ([MPiC6Py][NTf2]2) was synthesized and characterized by 1H NMR, 13C NMR and IR. Elemental analysis was performed on a Vario EL III instrument. Densities, viscosities and refractive indexes were measured for the binary mixture of [MPiC6Py][NTf2]2 with acetonitrile over the entire range of mole fractions at temperatures from T = (293.15 to 323.15) K under the atmospheric pressure of 0.1 MPa. Using the basic experimental data, the excess molar volumes (VEm), the viscosity deviations (Δη) and the refractive index deviations (ΔnD) for the binary systems were calculated and correlated to the Redlich–Kister polynomial to estimate coefficients and the standard deviation between the experimental and calculated values. The negative values of VEm and Δη result from strong self-association and weak hydrogen bonding interactions between the molecules of [MPiC6Py][NTf2]2 and acetonitrile. The values of ΔnD are all positive for the binary mixtures and increase with increasing temperature. The enthalpy, entropy and excess Gibbs energy of activation of the viscous flow of the binary mixtures also have been determined. The values of molar refraction and polarizability indicate that the dominant interactions between [MPiC6Py][NTf2]2 and acetonitrile are dipole–dipole molecular interactions. The obtained results are hoped to provide helpful information for the fundamental physicochemical properties of asymmetrical gemini ionic liquids and their further industrial applications.

 Please wait while we load your content...
Please wait while we load your content...