A kinetic model for diffusion and chemical reaction of silicon anode lithiation in lithium ion batteries
Abstract
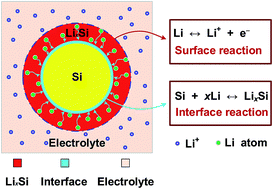
In this paper, a kinetic model is proposed that combines lithium ion diffusion through a lithiated phase with chemical reaction at the interface between lithiated amorphous and crystalline silicon. It is found out that a dimensionless parameter, relating the concentration distribution of lithium ions to the movement velocity of phase interface, can be used to describe the lithiation process. Based on the stress distributions and lithium ion diffusion profiles calculated by an elastic and perfectly plastic model, it is shown that, as lithiation proceeds, the hoop stress that changes from initial compression to tension in the surface layer of silicon particles may lead to surface cracking.

 Please wait while we load your content...
Please wait while we load your content...