Evolution of shape, size, and areal density of a single plane of Si nanocrystals embedded in SiO2 matrix studied by atom probe tomography
Abstract
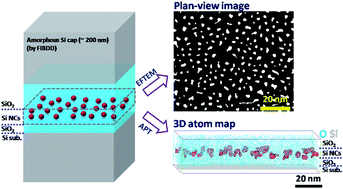
Single planes of Si nanocrystals (NCs) embedded in a SiO2 matrix were synthesized by annealing SiO2/SiO/SiO2 multilayer structures deposited on Si (100) substrates by e-beam evaporation. The dependence of the shape, size, and areal density of Si NCs on the thickness of the initial SiO layer was investigated using atom probe tomography and validated by energy filtered transmission electron microscopy. Three kinds of samples were prepared with SiO layer thicknesses of 4, 6, and 10 nm. The size of Si NCs enlarged with increasing SiO layer thickness. The shape of Si NCs was mainly extended spheroid in all three kinds of samples. In the sample with the 4 nm-thick SiO layer, the Si NCs were more prolate than those in the other two samples. Moreover, many rod-shaped Si NCs appeared in the sample with the 10 nm-thick SiO layer. These rod-shaped Si NCs were found to be connected by small Si NCs. The areal densities of Si NCs were in the order of 1012 NCs per cm2 in all samples.


 Please wait while we load your content...
Please wait while we load your content...