Growth of thiol-coated Au-nanoparticle Langmuir monolayers through a 2D-network of disk-like islands†
Mala Mukhopadhyay and
S. Hazra*
Saha Institute of Nuclear Physics, 1/AF Bidhannagar, Kolkata 700064, India. E-mail: satyajit.hazra@saha.ac.in
First published on 18th January 2016
Abstract
Formation of 2D-networked structures of disk-like islands for ultrathin Langmuir–Schaefer (LS) films of thiol-coated Au-nanoparticles (DT-AuNPs) on H-passivated Si substrates is evidenced for the first time, directly from a broad peak in grazing incidence small angle X-ray scattering data and also from atomic force microscopy images. Theoretical modeling of the system, carried out based on density–density and height–height correlation functions, supports well the formation of such structures. The structural information of the LS films, obtained at different surface pressure, helps to infer the growth of Langmuir monolayers of DT-AuNPs, which is very important in understanding the self-assembly process of nanoparticles at the air–water interface and in controlling the growth of 2D-networked nanostructures in large areas. On the surface of water, DT-AuNPs first self-assembled around different points to form disk-like islands of nanometer size and monolayer height, due to the complex balance of long range van der Waals attractions and short-range steric repulsion of the DT-AuNPs, initiated by solvent evaporation and also to optimize the hydrophobic repulsive force of water. On barrier compression, the size and 2D-network of the islands grow due to a combined effect of collision induced coalescence and solid-like behavior resisting deformation of the islands. On the other hand, the separation between the DT-AuNPs either decreases or increases depending upon the competitive effects of packing or buckling.
1 Introduction
Metal nanoparticles attract significant attention because of their unusual optical, magnetic, electronic and catalytic properties.1–8 Among them, thiol-capped gold nanoparticles (DT-AuNPs) have attracted considerable interest due to their ease of preparation and ability to spontaneously self-assemble into large arrays that offers an accessible route to design regular macroscopic AuNP layers.6,9,10 New collective phenomena can be explored for such organized structures due to an interparticle coupling effect in both in-plane and out-of-plane directions.4,6,9,11,12 In this sense, separation between particles and their local ordering, as well as long-range ordering and/or connectivity, becomes very important, especially for the preparation of organized structures in large areas.There are several techniques to prepare packed 2D arrays or 2D-network patterns from colloidal DT-AuNP solutions such as drop casting, spin coating, Langmuir–Blodgett (LB) and Langmuir–Schaefer (LS) depositions, etc.4,13,14 The LB and LS techniques are especially suitable for the fabrication of uniform nanostructures over large areas, where an ordered nanoparticle array formed at the air–water interface in an LB trough at an appropriate surface pressure (known as Langmuir film) is transferred onto a solid substrate.15 The structures of such LB or LS films depend on the initial structures of the Langmuir films, the transfer process and the film–substrate interactions.
The structures of the Langmuir films of DT-AuNPs have been studied using microscopy and scattering techniques. Optical microscopy or Brewster angle microscopy (BAM) have been used to monitor the structures of such films on the micrometer scale,16,17 while scattering, especially grazing incidence small angle X-ray scattering (GISAXS), has been used mainly to monitor the particle arrangement and interparticle separation. In some cases, the presence of islands or domains have been predicted indirectly from the width of the interparticle separation peak18,19 or from the analyzed correlation length,20 as expected.21 However, the complete structures of the Langmuir films (i.e. the size of the islands and their separation or connectivity) at different surface pressures (Π) have never been evidenced clearly, which is particularly important for small size AuNPs where the long range van der Waals (vdW) attractions are weak compared to the thermal energies.
The structures of the LB and LS films of DT-AuNPs have also been studied directly. The LB films on hydrophilic Si substrates show nanopattern formation due to the drying mediated agglomeration of AuNPs in the presence of hydrophobic–hydrophilic interactions between thiols and substrate.22 The LS films on carbon coated grids have been studied mainly using transmission electron microscopy (TEM), which show the ordering of the AuNPs. However, the LS films on a large hydrophobic substrate, which is expected to mimic the Langmuir film structure better, have never been studied in detail using statistically meaningful techniques, such as GISAXS,23–26 to obtain better structural information for the AuNP Langmuir films, which is otherwise not possible.
The fact that the complete structures of the AuNP Langmuir or LS films have not been evidenced so far is mainly associated with the poor resolution limit of X-ray beams and/or beam induced damage. The poor resolution limit arises from the relatively broad beam size (used to enhance the beam intensity), relatively large beam divergence (as obtained from most of the sources itself and also due to the use of an additional reflecting mirror to impinge the X-ray beam onto the horizontal air–water interface) and relatively small sample-to-detector distance (required to capture the low scattering intensity). A high intensity and small divergence beam of advanced synchrotron sources can, however, create a better resolution limit. Even then, the requirement of an additional reflecting mirror for the study of the Langmuir film, is still a problem. Additionally, the intense beams of the advanced source can create beam induced damage, especially considering the time required to align the beam to the sample. To minimize the effect of damage, lateral movement of the beam (or sample) with respect to the sample (or beam) is required for the actual measurements after alignment, which has somehow never been considered.
Here, we have tried to overcome all such problems by transferring DT-AuNP Langmuir films on H-passivated Si substrates using LS techniques, which closely resemble Langmuir monolayers, and then carrying out measurements using GISAXS techniques27,28 with a high intensity small divergence X-ray beam (which has a better resolution limit) and by moving the samples laterally before actual measurements (to minimize beam induced damage). Indeed, a broad peak or shoulder (related to island separation and/or size), the position of which varies with Π, is observed from such measurements for the first time. Detailed analysis of the GISAXS data corresponds to the structures of networked disk-like islands, which is well supported by atomic force microscopy (AFM) images. Further, the present study also infers that the growth of DT-AuNP Langmuir films is through networked disk-like islands, the size and networking of which increases while the interparticle separation decreases or increases due to further interdigitation or buckling with Π. This information is important for understanding the self-assembly process and for controlling nanostructure formation.
2 Experimental section
2.1 Synthesis of DT-AuNPs
Colloidal AuNPs were synthesized following the Brust method,29 i.e. a two-phase (water–toluene) reduction of hydrogen tetrachloroaurate by sodium borohydride in the presence of dodecanethiol. Further, considering that the mean diameter of the particles is controlled by the Au/thiol molar ratio,30 we used a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio to prepare particles with a mean core diameter of around 2 nm. For the synthesis, hydrogen tetrachloroaurate trihydrate [HAuCl4·3H2O], sodium borohydride [NaBH4], dodecanethiol [C12H25SH] and tetraoctylammonium bromide (TOABr) were obtained from Sigma Aldrich and used without further purification. Milli-Q water (Millipore) and toluene (Merck) were used as solvents. First, 4.4 ml of a solution (0.1 M) of TOABr in toluene was added to 5 ml of an aqueous solution (0.04 M) of HAuCl4. TOABr acted as a phase transfer reagent, which transferred HAuCl4 from the aqueous to the organic phase. About 2.4 ml of a solution (0.04 M) of dodecanethiol in toluene was then added and the mixture was stirred vigorously with a magnetic stirrer until the mixture turned milky. At the end, 5.5 ml of a solution (0.4 M) of sodium borohydride (reducing agent) in water was added to the mixture. The mixture was left for an hour. The upper deep brown part containing the nanoparticles was separated and excess ethanol was added. This mixture was left overnight for precipitation. The precipitate of thiol coated AuNPs (DT-AuNPs) was then collected on a filter paper for further use. The formation and size of the AuNPs were verified and estimated from an optical absorption spectrum and transmission electron microscopy image (see Fig. S1 of ESI†). The estimated size of AuNPs (2R) is about 2.5 ± 0.6 nm and that of DT-AuNPs is 4.5 ± 0.6 nm.
1 ratio to prepare particles with a mean core diameter of around 2 nm. For the synthesis, hydrogen tetrachloroaurate trihydrate [HAuCl4·3H2O], sodium borohydride [NaBH4], dodecanethiol [C12H25SH] and tetraoctylammonium bromide (TOABr) were obtained from Sigma Aldrich and used without further purification. Milli-Q water (Millipore) and toluene (Merck) were used as solvents. First, 4.4 ml of a solution (0.1 M) of TOABr in toluene was added to 5 ml of an aqueous solution (0.04 M) of HAuCl4. TOABr acted as a phase transfer reagent, which transferred HAuCl4 from the aqueous to the organic phase. About 2.4 ml of a solution (0.04 M) of dodecanethiol in toluene was then added and the mixture was stirred vigorously with a magnetic stirrer until the mixture turned milky. At the end, 5.5 ml of a solution (0.4 M) of sodium borohydride (reducing agent) in water was added to the mixture. The mixture was left for an hour. The upper deep brown part containing the nanoparticles was separated and excess ethanol was added. This mixture was left overnight for precipitation. The precipitate of thiol coated AuNPs (DT-AuNPs) was then collected on a filter paper for further use. The formation and size of the AuNPs were verified and estimated from an optical absorption spectrum and transmission electron microscopy image (see Fig. S1 of ESI†). The estimated size of AuNPs (2R) is about 2.5 ± 0.6 nm and that of DT-AuNPs is 4.5 ± 0.6 nm.
2.2 Preparation of DT-AuNP/H-Si LS films
A 1.5 ml toluene solution of DT-AuNPs (0.5 mg ml−1) was spread uniformly, using a micropipette, on the surface of Milli-Q water in a Langmuir trough (KSV 5000). It was kept undisturbed for some time to let the toluene evaporate and the hydrophobic DT-AuNPs lay suspended at the air–water interface (at 23 °C). A pressure–area (Π–A) isotherm of the DT-AuNP Langmuir film on water surface was recorded (as shown in Fig. 1) by regulating barrier movement. Π was measured using a Wilhelmy plate. Prior to DT-AuNP monolayer deposition, H-terminated Si (H-Si) substrates were prepared through a standard pre-treatment method.31,32 In short, Si(001) substrates (of size about 15 × 15 mm2) were first sonicated in acetone and ethanol solutions to remove organic contaminants and subsequently etched with hydrogen fluoride [HF, Merck, 10%] solution for 60 s at room temperature (25 °C) to terminate the Si surface with H after removing the native oxide layer. The DT-AuNP Langmuir monolayers formed at different pressures were then transferred onto the H-Si substrates using the LS deposition technique.33 DT-AuNP/H-Si LS films prepared at Π = 2, 4, 6, 10 and 14 mN m−1, as shown in the Π–A isotherm of Fig. 1, were used for further analysis.2.3 Characterization of DT-AuNP/H-Si LS films
The characterization of the DT-AuNP/H-Si LS films, in reciprocal and real space, was carried out using X-ray scattering and AFM techniques, respectively. The scattering geometry used for the characterization of samples is shown schematically in Fig. 2. The surface of the sample is in the x–y plane and the incident X-ray beam (of wavelength λ) is in the x–z plane. α and β are the incident and exit angles with the x–y plane and α + β is the scattering angle along the z-direction, while φ is the exit angle with the x–y plane and also the scattering angle along the y-direction. In this reflection geometry, the components of the wave vector transfer, q (qx, qy, qz), can be expressed in terms of X-ray wavelength and different angles, as indicated in Fig. 2.X-ray reflectivity (XR) measurements of the films were performed using a versatile X-ray diffractometer (VXRD) setup.34 VXRD consists of a diffractometer (D8 Discover, Bruker AXS) with a Cu source (sealed tube) followed by a Göbel mirror to select and enhance Cu Kα radiation (λ = 1.54 Å). The diffractometer has a two-circle goniometer [θ(ω) − 2θ] with a quarter-circle Eulerian cradle as a sample stage. The latter has two circular (χ and ϕ) and three translational (X, Y, and Z) motions. The scattered beam was detected using a NaI scintillation (point) detector. Data were taken under specular conditions, i.e. for φ = 0 and α = β = θ. Under such conditions there exists a nonvanishing wave vector component, qz, which is equal to (4π/λ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ with resolution 0.002 Å−1. An XR technique essentially provides an electron–density profile (EDP), i.e. in-plane (x–y) average electron density (ρ) as a function of depth (z) in high resolution.32 From EDP it is possible to estimate film thickness, electron density, and interfacial roughness.
θ with resolution 0.002 Å−1. An XR technique essentially provides an electron–density profile (EDP), i.e. in-plane (x–y) average electron density (ρ) as a function of depth (z) in high resolution.32 From EDP it is possible to estimate film thickness, electron density, and interfacial roughness.
GISAXS measurements of the films were carried out using a synchrotron source (MiNaXS beam line, PETRA III)35 at λ = 0.94 Å. The scattered beam was detected using a 2D detector (PILATUS 300k, Dectris, with 619 × 487 pixels of pixel size 172 × 172 μm2). To avoid saturation of the detector, the direct beam was stopped and the specular reflected beam was attenuated by two separate point-like beam stops. The sample-to-detector distance was 1721 mm. The corresponding angular resolution (given by the ratio of pixel size and the sample-to-detector distance) is 0.1 mrad. The resolution limit along the qy-direction is less than 0.002 Å−1, for the present setup (see Fig. S2 of ESI†). It is necessary to mention that such a low value, which is mainly achievable in this beamline (due to very small divergence of the micro-focused beam), is absolutely essential for the direct estimation of the long-range in-plane correlations, such as the domains, if any, along with the short-range in-plane correlations, such as the separation between AuNPs. For data collection, the incident angle α was kept at 0.25°, slightly greater than the critical angle, αc, of the sample. Under such grazing incidence, the footprint of the micro-focused beam on the sample, along the x-direction, is quite large, as is necessary for any statistically relevant information, while along the y-direction, it is small, which can be used to map the in-plane inhomogeneity, if any. To minimize the effect of radiation damage of the sample (due to the high intensity beam), the GISAXS pattern, at a single position, was collected for a small length of time (10 s). To check the in-plane inhomogeneity and/or enhance the statistics, similar GISAXS patterns were also collected at different positions by moving the sample laterally.
The detailed top surface morphologies of the films were mapped using an AFM (5500 AFM, Agilent) technique, a few days after deposition. Topographic images were collected in a noncontact (or intermittence contact) mode to minimize silicon-tip-induced damage of the soft film. Scans of different sizes and in different portions of the sample were carried out to get statistically meaningful information about the topography. WSXM software36 was used for AFM image processing and analysis.
3 Results and discussion
3.1 Out-of-plane structure from XR
XR data of the DT-AuNP/H-Si LS films deposited at different Π-values are shown in Fig. 3. Oscillations with more than a single periodicity are observed in all the XR profiles. The periodicity even changes with the films, readily suggesting that the film changes with the deposition pressure. However, to get quantitative information about the films, all XR profiles were analyzed using Parratt’s formalism,37 after incorporating roughness at each interface.32 An instrumental resolution in the form of a Gaussian function and a constant background were also included at the time of data analysis. For the analysis, we started with a monolayer of DT-AuNPs of a certain thickness and coverage on the Si substrate and then replaced some coverage with bilayer and/or trilayer, according to the fitting requirements. Further, each DT-AuNP monolayer is divided into three layers, namely a thiol-rich low density bottom layer, a Au-rich high density middle layer and a thiol-rich low density top layer. The best fit XR profiles along with the corresponding EDPs for all the films are shown in Fig. 3.It is evident from the EDPs that only a monolayer structure is present in the film deposited at Π = 2 mN m−1. For the films deposited at Π = 4, 6 and 10 mN m−1, a very small amount of bilayer structure and for the film deposited at Π = 14 mN m−1, even a very small amount of trilayer structure are also present in the films in addition to the monolayer structure. In the film deposited at Π = 2 mN m−1, the monolayer coverage is partial (low peak ρ-value) and the monolayer fluctuation along the z-direction is almost negligible (low thickness). In the film deposited at Π = 4 mN m−1, there is no increase in the monolayer coverage, rather a decrease at the expense of some bilayer structure and some monolayer fluctuation (increase in monolayer thickness). In the films deposited at Π = 6 and 10 mN m−1, only the monolayer coverage increases further with the Π-value. In the film deposited at Π = 14 mN m−1, some trilayer structure is also formed in addition to the further small increase in monolayer coverage.
3.2 In-plane structure from GISAXS
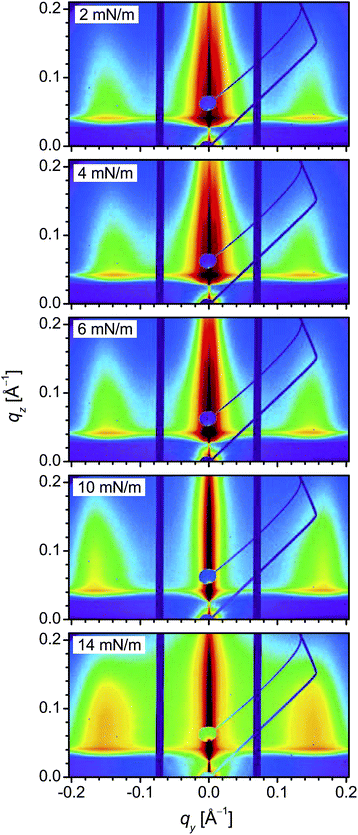
GISAXS patterns of the DT-AuNP/H-Si LS films deposited at different surface pressures are shown in Fig. 4. It can be noted that for each film, the in-plane homogeneity was first ascertained from the similar GISAXS patterns observed after moving the sample laterally and then the averaging of such similar patterns was carried out to have better statistics, which are actually presented in Fig. 4. Bragg rods around qy = ± 0.15 Å−1 are observed in all the patterns, the intensity of which varies with the Π value. Also, a strong intensity is observed near qy = 0, the nature of which again changes with Π. To have a better idea about the position and intensity of the Bragg rods and also the variation of the intensity near qy = 0, GISAXS line profiles along the qz and qy directions and through the Bragg rods, for all the films, are plotted in Fig. 5 and 6. The line profiles along the qz-direction (in Fig. 5) only show an increase in absolute intensity with Π value, which is expected due to the increase in the number of AuNPs in the films with increasing Π (as observed from the Π–A isotherm and EDPs). The line profiles along the qy-direction (in Fig. 6) not only show peaks at around qy = ± 0.15 Å−1 due to AuNP separation but also broad peaks or shoulders within qy = ±0.02 Å−1. The latter is quite prominent in the magnified view of the central portion, as shown in the inset of Fig. 6. The position of the shoulder moves toward the center with an increase in the Π value and is only evident for the three low Π value films. The position of the shoulder, however, remains unchanged with the qz value (as evidenced by Fig. S3 of the ESI†) and thus the value of qz is not very important for the extraction of the horizontal line profile from the GISAXS image. The observation of such a shoulder is direct evidence of the presence of a certain long range correlation, which has never been observed before. It is clear that the horizontal line profiles are of actual interest and need further analysis and discussion.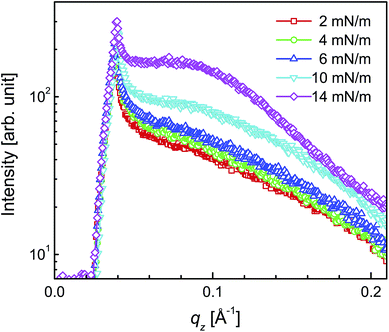 | ||
| Fig. 5 GISAXS line profiles along the qz direction (i.e. vertical cut along the first Bragg rod at qy ≈ 0.15 Å−1) of the DT-AuNP/H-Si LS films deposited at different surface pressures (Π). | ||
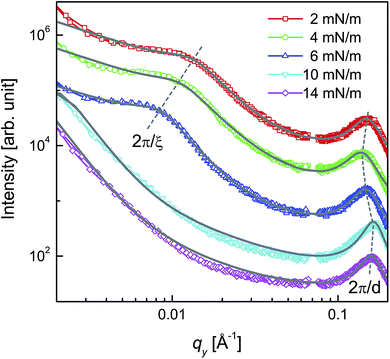
The horizontal line profiles, on a log–log scale, are shown in Fig. 7, where both a peak at large qy values and a broad hump at low qy values (if present) are clearly visible; the positions of which are marked by dashed lines and provide a rough estimate of in-plane AuNP separation (d) and in-plane correlation length (ξ). For better estimation of these parameters, quantitative analysis of the horizontal line profiles is necessary. It is known that in the kinematic or Born approximations the measured scattering intensity can be expressed as the square of total scattering amplitude, which is the Fourier transform of the electron density in the film, as
| I(q) = |∫drρ(r)e−iq·r|2 = |FT[ρ(r)]|2 | (1) |
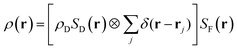 | (2) |
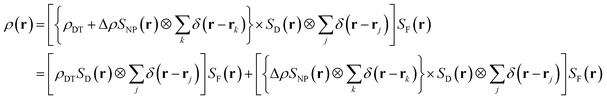 | (3) |
 | (4) |
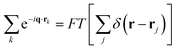 gives rise to the structure factor and can be determined considering the distribution of the islands or AuNPs. It is known that the limited dimensions can create a smearing (broadening) effect on the delta-like function, arising from the perfectly ordered arrangement. However, if we consider that the islands have polydispersity in size as well as in separation then the island distribution term should not have sharp maxima. In such a case, the square of the island distribution term convoluted with the sample dimensions term can be expressed as the Fourier transform of the position–position auto-correlation or pair correlation function of the islands. Similarly, polydispersity in the size of the AuNPs is present, which will certainly give rise to polydispersity in the separation. Even if such polydispersity is less, it is sufficient to destroy any correlation beyond the island length scale. In such a case, again the square of the AuNP distribution term convoluted with the island dimensions term can be expressed as the Fourier transform of the pair correlation function of AuNPs. Considering cylindrical islands and spherical AuNPs, the ID and IP along in-plane direction can be expressed as
gives rise to the structure factor and can be determined considering the distribution of the islands or AuNPs. It is known that the limited dimensions can create a smearing (broadening) effect on the delta-like function, arising from the perfectly ordered arrangement. However, if we consider that the islands have polydispersity in size as well as in separation then the island distribution term should not have sharp maxima. In such a case, the square of the island distribution term convoluted with the sample dimensions term can be expressed as the Fourier transform of the position–position auto-correlation or pair correlation function of the islands. Similarly, polydispersity in the size of the AuNPs is present, which will certainly give rise to polydispersity in the separation. Even if such polydispersity is less, it is sufficient to destroy any correlation beyond the island length scale. In such a case, again the square of the AuNP distribution term convoluted with the island dimensions term can be expressed as the Fourier transform of the pair correlation function of AuNPs. Considering cylindrical islands and spherical AuNPs, the ID and IP along in-plane direction can be expressed as
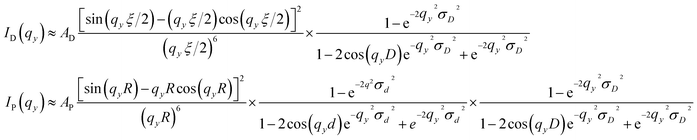 | (5) |
| Π (mN m−1) | 2R ± σ2R (nm) | d ± σd (nm) | ξ ± σξ (nm) | D ± σD (nm) | ξh ± σξh (nm) | Dh ± σDh (nm) |
|---|---|---|---|---|---|---|
| 2 | 2.5 ± 0.6 | 3.8 ± 0.7 | 32 ± 12 | 33 ± 12 | 33 ± 07 | 47 ± 16 |
| 4 | 2.5 ± 0.6 | 4.1 ± 0.8 | 39 ± 15 | 44 ± 16 | 45 ± 12 | 59 ± 18 |
| 6 | 2.5 ± 0.6 | 3.9 ± 0.7 | 54 ± 18 | 56 ± 19 | 65 ± 19 | 80 ± 25 |
| 10 | 2.5 ± 0.6 | 3.6 ± 0.6 | >100 | >100 | 79 ± 23 | 85 ± 30 |
| 14 | 2.5 ± 0.6 | 3.7 ± 0.6 | >200 | >200 | 30 ± 09 | 30 ± 30 |
It is clear from Table 1 that the values of ξ, D and their distributions increase with the increase of Π-value. Also, it is found that the value of D is quite close to the value of ξ. However, for the films with a high (10 and 14 mN m−1) Π-value, as there is no shoulder in the GISAXS line profiles, no definitive values, rather the lower limits of these parameters, are obtained. The d-values for all the films are found to be less than those of the free DT-AuNPs, while the variation of d-value with surface pressure, although small, shows an interesting variation. With an increase of the Π-value, the d-value of the film first increases (when Π changes from 2 to 4 mN m−1) then decreases gradually (when Π changes from 4 to 10 mN m−1) and then again increases (when Π changes from 10 to 14 mN m−1). Such a variation is quite consistent with the observed EDPs of the films, namely only a monolayer structure for the film deposited at Π = 2 mN m−1, while partial bilayer structures for the films deposited at Π = 4 to 10 mN m−1 (i.e. monolayer structure first relaxed and then compressed with pressure) and a partial trilayer structure for the film deposited at Π = 14 mN m−1 (thus monolayer structure again slightly relaxed).
3.3 Topography from AFM
So far, we have presented the structures of the films obtained from the X-ray scattering study. Although the structures obtained from such reciprocal space mapping are quite complete, nonetheless, it is always demanding to validate them with real space mapping. The topographies of the films obtained from scanning electron microscopy (see Fig. S4 of ESI†) show no increase in the coverage of the film, on the large scale, but only an increase in the thickness and/or coverage on the small scale with surface pressure. Such small scale topography of the films is best viewed using AFM. Typical AFM images of the films in different scan ranges are shown in Fig. 9. In a relatively large (5 × 5 μm2) scan size, large voids are observed for the film deposited at Π = 2 mN m−1, otherwise the film is found to be uniform. Such a uniform portion when magnified (i.e. images of scan size ≤ 2 × 2 μm2) clearly shows the presence of networked 2D-islands of monolayer height. Large voids, however, decrease in size and number with an increase of the surface pressure (see the 5 × 5 μm2 scan size images) and almost vanish for the films deposited at Π = 10 mN m−1. The presence of networked 2D-islands of monolayer height is also evident (in the images of scan size ≤ 2 × 2 μm2) for the films deposited at higher pressures (Π = 4 to 10 mN m−1), the size of which increases with the pressure. However, separate islands are almost invisible for the film deposited at Π = 14 mN m−1. | ||
| Fig. 9 AFM images of the DT-AuNP/H-Si LS films deposited at different surface pressures (Π) showing topography in three different scan sizes. | ||
To give a better idea about the average size of the islands, power spectral density (PSD),40,41 extracted from the AFM images of different scan size, is plotted in Fig. 10 for all of the films. It can be noted that the PSD is the angular averaged radial distribution of the Fourier transformed AFM image, which can be expressed as
 | (6) |
 | (7) |
The values of parameters ξh and Dh are found to increase with an increase of Π-value similar to the values of ξ and D, with the exception of the film deposited at Π = 14 mN m−1. The values of ξh and Dh (and their differences) are found to be more comparable to the definitive values of ξ and D (and their differences) for the films deposited at low Π-values (2 to 6 mN m−1), which may be related to time evolution and/or tip convolution effects. Additionally, AFM is able to estimate island size, which GISAXS cannot, for the films deposited at high Π-values (10 and 14 mN m−1) having large monolayer coverage (as predicted from EDPs). This is probably related to the relatively enhanced height fluctuation of the islands with time due to interfacial instability. For the film deposited at Π = 10 mN m−1, the value of ξh is however systematic, which is not the case for the film deposited at Π = 14 mN m−1. The small size islands in the latter film are actually within the large size island. The imaging of a single large size island essentially allows us to observe small size discrete islands with a very small height fluctuation, which evolve with time. The appearance of such small islands may be associated with the pressure independent characteristic island size of the DT-AuNPs system on water surface. Such a finding is quite interesting and needs further verification.
3.4 Structures of LS and Langmuir films
Let us now first try to visualize the overall structures of the DT-AuNP/H-Si LS films, by combining the information obtained from different techniques and then discuss its implication in understanding the structures of the DT-AuNP Langmuir monolayers. It is clear (from EDP and topography) that the DT-AuNP/H-Si LS films, deposited at different Π-values, are predominantly of a monolayer structure. Considering the coverage of the monolayer (as obtained from the EDPs), such films can be categorized into two groups, namely low coverage (for Π = 2 to 6 mN m−1) and high coverage (for Π = 10 to 14 mN m−1), which is consistent with the classification of the liquid expanded (LE) and liquid condensed (LC) phase diagram of the Π–A isotherm.22,42 However, considering the presence of other structures (namely bilayer, trilayer, etc.), the films can be categorized into three groups, namely only monolayer structure (for Π = 2 mN m−1), monolayer plus a very small amount of bilayer structure (for Π = 4 to 10 mN m−1) and monolayer plus very small amounts of bilayer and trilayer structures (for Π = 14 mN m−1), which is again consistent with the observed very small decrease in the d-value associated with the flipping of some DT-AuNPs from the monolayer to form a bilayer or trilayer.On the other hand, it is clear (from the in-plane density–density and height–height correlations) that the monolayers are made of networked disk-like islands; the size and separation of which however varies with the Π-value. The size distributions of the islands, for the films deposited at different surface pressures (Π), are shown in Fig. 11 along with the size distribution of the AuNPs. An increase in the size of the islands (ξ) is clearly evident from the GISAXS study, although the size estimation is only accurate for the films deposited at low Π-values and approximate for the films deposited at high Π-values, due to the resolution limit. Such a variation is also confirmed from the AFM study, however the sizes, ξh, are found to be slightly more comparable to the corresponding sizes, ξ (for the low Π-value films) and can be understood considering time evolution and/or tip convolution effects. The signature of small size islands is found in the film deposited at Π = 14 mN m−1 from the AFM study, which is not visible from the GISAXS study, suggesting that such small size islands are formed with time within a large size island.
Let us now consider the fact that DT-AuNP films have been prepared by transferring Langmuir films on H-Si substrates using LS techniques. Such a transfer technique and hydrophobic–hydrophobic interactions (between the Langmuir film and H-Si substrate) are expected to create least disturbance. Thus it can be considered that the observed structures of the LS films, at least in the initial stages, are in close resemblance to the Langmuir films. Accordingly, at Π = 2 mN m−1, only perfect monolayer height networked islands (of size around 30 nm) that have large voids are formed at the air–water interface. Upon the increase of Π from 2 to 4 mN m−1, the size of the islands increases (to about 40 nm), the size and number of voids decreases and a very small amount of bilayer is formed along with monolayer height fluctuation along the z-direction through the buckling and flipping of the DT-AuNPs. Upon a further increase of Π from 4 to 10 mN m−1, the size of the islands increases, while the size and number of voids decreases and almost vanishes at Π = 10 mN m−1 but the amount of bilayer remains almost the same. Upon an increase of Π from 10 to 14 mN m−1, the size of the islands increases appreciably and a very small amount of trilayer is also formed through further buckling and flipping of the DT-AuNPs.
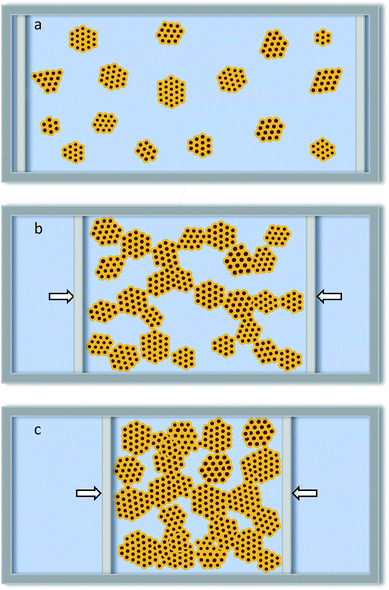
The growth of the of DT-AuNP Langmuir monolayers predicted from the structures of the Langmuir films is shown schematically in Fig. 12. The DT-AuNPs at the water surface first assembled (in a hexagonal close pack) around different points (which act as nucleation centers) to form disk-like islands of monolayer height (Fig. 12a), probably due to the complex balance of vdW attraction and steric repulsion of the DT-AuNPs.18,21,43–46 It is known that the evaporation of solvent (toluene) creates an attractive force between the DT-AuNPs, which in the presence of the hydrophobic repulsion of water can freely organize to form a 2D-structure.11,43,47,48 Formation of a 2D-structure also minimizes the DT-AuNP–water interfacial energy (or repulsive hydrophobic force) by minimizing the interfacial area. Short range interactions which decide the hexagonal close pack-like organization are AuNP–AuNP vdW, thiol–thiol hydrophobic attractions and steric repulsion. While interdigitation of thiols can take place due to the low packing density of thiols on the curved AuNPs surface,19,42 and can be quite appreciable for very small size particles having large curvature. On the other hand, a lack of real long range interactions (due to the small size and limited local concentration of DT-AuNPs) only allows 2D organization up to limited dimensions to form disk-like islands of monolayer height;21 the critical size of which is related to the local concentration and size of the AuNPs, the length of the thiols, the evaporation rate of solvent, the temperature, etc.11,43,48 On compression of the barriers, the monolayer islands collide with each other (due to in-plane diffusion of freely floating islands) and try to coalesce, while in the absence of the solvent, these nanoparticle islands typically exhibit solid-like behavior and try to resist deformation.21 As a result, networking (Fig. 12b), some in-plane deformation (contraction and expansion along contact and its perpendicular directions, respectively) and/or buckling of the islands take place. The size of the islands increases (Fig. 12c) to some extent (due to the deformation and increase in the local DT-AuNP concentration). Such behavior (i.e. an increase in size and connectivity) is reversible with the surface pressure when the compression of the barriers is not beyond the collapse of the Langmuir films. Also the separation between AuNPs (or d-value) decreases (due to the increase in their packing through further thiol-interdigitation) with a sudden increase (due to some buckling of DT-AuNPs20). Monolayer fluctuations are formed through buckling, while bilayer and trilayer structures are formed through buckling and flipping. Considering the shape, the buckling of DT-AuNPs (which are spherically symmetric) can be considered slightly favorable compared to any amphiphilic molecules (which are spherically asymmetric). It can be noted that the formation of 2D-networks patterned on solid substrates has been well simulated using a coarse-grained model of nanoparticle self-assembly that explicitly includes the dynamics of the evaporating solvent.47,49 However, in the present case the networking is predominantly due to the barrier driven in-plane diffusion of the islands rather then the individual nanoparticles.
It is interesting to note that, in spite of a large number of in situ structural studies of organic-coated metal nanoparticles, Langmuir films in general and DT-AuNP Langmuir films in particular, the formation of their networked island structures at an air–water interface has never been observed directly, which can be understood as follows. Optical microscopy or BAM, which have been used extensively to study the structures of such films at the micrometer length scale,16,17 cannot resolve the structures at the nanometer length scale, due to their limited spatial resolution. On the other hand, scattering, especially GISAXS, has been used extensively, mainly to monitor particle arrangement and interparticle separation. In some cases, the presence of islands or domains has been predicted indirectly from the width of the interparticle separation peak18,19 or from the analyzed correlation length,20 which has large uncertainties. However, the presence of islands has never been evidenced by the island separation peak directly, which is very important for understanding the structures and growth of such Langmuir films. As mentioned before, the problem is mainly associated with the poor resolution limit and/or beam induced damage. The poor resolution limit arises from the relatively broad beam size (used to enhance beam intensity), relatively large beam divergence (as obtained from most of the sources itself and also due to the use of an additional reflecting mirror to impinge the X-ray beam onto the horizontal air–water interface) and relatively small sample-to-detector distance (required to capture the low scattering intensity). High intensity and small divergence beams of advanced synchrotron sources can, however, create a better resolution limit. Even then the requirement of an additional reflecting mirror, for the study of Langmuir monolayers, is still a problem. Additionally, the intense beam of the advance source can create beam induced damage, especially considering the time required to align the beam to the Langmuir monolayer. To minimize the effect of damage, lateral movement of the beam (or sample) with respect to the sample (or beam) is required for the actual measurements after alignment, which is usually a problem.
4 Conclusions
The structures of the DT-AuNP/HSi LS films, deposited at different Π-values were first estimated using XR and GISAXS techniques and then confirmed using an AFM technique. The GISAXS measurements were carried out using an intense X-ray beam of small divergence (from the P03 beamline of PETRA III) to enhance the in-plane resolution limit and by shifting the sample in-plane to minimize the effect of beam induced damage. It is clear (from XR and AFM) that the films are predominantly of a monolayer structure. Such a monolayer is made of networked disk-like islands with some voids (as evidenced by GISAXS and AFM). The size of the islands (ξ or ξh) increases, while the size and amount of voids decreases with an increase in the Π-value. The islands are again made of DT-AuNPs, self-assembled into a hexagonal-like close pack with interdigitation. The average separation between DT-AuNPs (d) either decreases or increases with Π-value depending upon the competitive effects of packing and flipping due to compression. Owing to the least disturbance of the Langmuir films during transfer (using a LS technique) onto the H-Si substrates (due to the hydrophobic–hydrophobic interactions between the Langmuir film and H-Si substrate), the observed structures of the LS films, at least in the initial stages, can be considered to represent the structures of the Langmuir films, which are of immense importance not only for the understanding of the self-assembly process of nanoparticles at the air–water interface but also for their use as a template to grow nanodevices with interesting properties arising from collective phenomena.Acknowledgements
The authors thank Dr S. V. Roth for his support with GISAXS measurements. The financial support received from the Saha Institute of Nuclear Physics under the DST-DESY project to carry out GISAXS experiments at PETRA III is thankfully acknowledged.References
- W. P. Halperin, Rev. Mod. Phys., 1986, 58, 533 CrossRef CAS.
- C. P. Collier, R. J. Saykally, J. J. Shiang, S. E. Henrichs and J. R. Health, Science, 1997, 277, 1978 CrossRef CAS.
- S. Link, M. B. Mohamed and M. A. El-Sayed, J. Phys. Chem. B, 1999, 103, 3073 CrossRef CAS.
- C. B. Murray, C. R. Kagan and M. G. Bawendi, Annu. Rev. Mater. Sci., 2000, 30, 545 CrossRef CAS.
- Z. Tang, N. A. Kotov and M. Giersig, Science, 2002, 297, 237 CrossRef CAS PubMed.
- M. C. Daniel and D. Astruc, Chem. Rev., 2004, 104, 293 CrossRef CAS PubMed.
- Clusters and Colloids: From Theory to Applications, ed. G. Schmid, John Wiley & Sons, 2008 Search PubMed.
- Z. Nie, A. Petukhova and E. Kumacheva, Nat. Nanotechnol., 2010, 5, 15 CrossRef CAS PubMed.
- S. Liu, R. Maoz and J. Sagiv, Nano Lett., 2004, 4, 845 CrossRef CAS.
- M. A. Mezour, I. I. Perepichka, J. Zhu, R. B. Lennox and D. F. Perepichka, ACS Nano, 2014, 8, 2214 CrossRef CAS PubMed.
- T. P. Bigioni, X.-M. Lin, T. T. Nguyen, E. I. Corwin, T. A. Witten and H. M. Jager, Nat. Mater., 2006, 5, 265 CrossRef CAS PubMed.
- Y. Min, M. Akbulut, K. Kristiansen, Y. Golan and J. Israelachvili, Nat. Mater., 2008, 7, 527 CrossRef CAS PubMed.
- J. F. Galisteo-López, M. Ibisate, R. Sapienza, L. S. Froufe-Pérez, A. Blanco and C. López, Adv. Mater., 2011, 23, 30 CrossRef PubMed.
- P. Colson, R. Cloots and C. Henrist, Langmuir, 2011, 27, 12800 CrossRef CAS PubMed.
- Handbook of Applied Surface and Colloid Chemistry, ed. K. Holmberg, D. O. Shah and M. J. Schwuger, John Wiley & Sons Ltd., 2002, vol. 1 Search PubMed.
- R. K. Gupta, K. A. Suresh and S. Kumar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 032601 CrossRef PubMed.
- K. Vegso, P. Siffalovic, E. Majkova, M. Jergel, M. Benkovicova, T. Kocsis, M. Weis, S. Luby, K. Nygard and O. Konovalov, Langmuir, 2012, 28, 10409 CrossRef CAS PubMed.
- M. Fukuto, R. K. Heilmann, P. S. Pershan, A. Badia and R. B. Lennox, J. Chem. Phys., 2004, 120, 3446 CrossRef CAS PubMed.
- D. G. Schultz, X.-M. Lin, D. Li, J. Gebhardt, M. Meron, P. J. Viccaro and B. Lin, J. Phys. Chem. B, 2006, 110, 24522 CrossRef CAS PubMed.
- M. K. Bera, M. K. Sanyal, S. Pal, J. Daillant, A. Datta, G. U. Kulkarni, D. Luzet and O. Konovalov, Europhys. Lett., 2007, 78, 56003 CrossRef.
- V. Santhanam, J. Liu, R. Agarwal and R. P. Andres, Langmuir, 2003, 19, 7881 CrossRef CAS.
- R. Banerjee, S. Hazra, S. Banerjee and M. K. Sanyal, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 056204 CrossRef CAS PubMed.
- S. Hazra, A. Gibaud, A. Désert, C. Sella and A. Naudon, Phys. B, 2000, 283, 97 CrossRef CAS.
- P. Du, M. Li, K. Douki, X. Li, C.-B.-W. Garcia, A. Jain, D.-M. Smilgies, L.-J. Fetters, S.-M. Gruner, U. Wiesner and C.-K. Ober, Adv. Mater., 2004, 16, 953 CrossRef CAS.
- R. Lazzari, F. Leroy and G. Renaud, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 125411 CrossRef.
- P. Chatterjee and S. Hazra, J. Phys. Chem. C, 2014, 118, 11350 CAS.
- S. V. Roth, G. Herzog, V. Körstgens, A. Buffet, M. Schwartzkopf, J. Perlich, M. M. A. Kashem, R. Döhrmann, R. Gehrke, A. Rothkirch, K. Stassig, W. Wurth, G. Benecke, C. Li, P. Fratzl, M. Rawolle and P. Müller-Buschbaum, J. Phys.: Condens. Matter, 2011, 23, 254208 CrossRef CAS PubMed.
- P. Chatterjee and S. Hazra, Soft Matter, 2013, 9, 9799 RSC.
- M. Brust, M. Walker, D. Bethell, D. J. Schiffrin and R. Whyman, J. Chem. Soc., Chem. Commun., 1994, 801 RSC.
- D. V. Leff, P. C. Ohara, J. R. Heath and W. M. Gelbart, J. Phys. Chem., 1995, 99, 7036 CrossRef CAS.
- H. F. Okorn-Schmidt, IBM J. Res. Dev., 1999, 43, 351 CrossRef CAS.
- J. K. Bal and S. Hazra, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 155412 CrossRef.
- I. Langmuir and V. J. Schaefer, J. Am. Chem. Soc., 1938, 60, 1351 CrossRef CAS.
- S. Hazra, Appl. Surf. Sci., 2006, 253, 2154 CrossRef CAS.
- I. Roy and S. Hazra, RSC Adv., 2015, 5, 665 RSC.
- I. Horcas, R. Fernández, J. M. Gómez-Rodriguez, J. Colchero, J. Gómez-Herrero and A. M. Baro, Rev. Sci. Instrum., 2007, 78, 013705 CrossRef CAS PubMed.
- L. G. Parratt, Phys. Rev., 1954, 95, 359 CrossRef.
- M. Mâaza, A. Gibaud, C. Sella, B. Pardo, F. Dunsteter, J. Corno, F. Bridou, G. Vignaud, A. Désert and A. Menelle, Eur. Phys. J. B, 1999, 7, 339 CrossRef.
- S. Hazra, A. Gibaud and C. Sella, J. Appl. Phys., 2007, 101, 113532 CrossRef.
- J. M. Elson and J. M. Bennett, Appl. Opt., 1995, 34, 201 CrossRef CAS PubMed.
- S. J. Fang, S. Haplepete, W. Chen, C. R. Helms and H. Edwards, J. Appl. Phys., 1997, 82, 5891 CrossRef CAS.
- J. R. Heath, C. M. Knobler and D. V. Leff, J. Phys. Chem. B, 1997, 101, 189 CrossRef CAS.
- B. Kim, M. A. Carignano, S. L. Tripp and A. Wei, Langmuir, 2004, 20, 9360 CrossRef CAS PubMed.
- S. J. Khan, F. Pierce, C. M. Sorensen and A. Chakrabarti, Langmuir, 2009, 21, 487 Search PubMed.
- M. N. Martin, J. I. Basham, P. Chando and S.-K. Eah, Langmuir, 2010, 26, 7410 CrossRef CAS PubMed.
- C. P. Joshi, Y. Shim, T. P. Bigioni and J. G. Amar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 032406 CrossRef PubMed.
- P. L. G. E. Rabani, D. R. Reichman and L. E. Brus, Nature, 2003, 426, 271 CrossRef PubMed.
- S. Narayanan, J. Wang and X.-M. Lin, Phys. Rev. Lett., 2004, 93, 135503 CrossRef PubMed.
- C. P. Martin, M. O. Blunt and P. Moriarty, Nano Lett., 2004, 4, 2389 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra26267d |
| This journal is © The Royal Society of Chemistry 2016 |