Interband-transition-modified third-order nonlinear optical properties of Al nanoshells in carbon disulfide†
Abstract
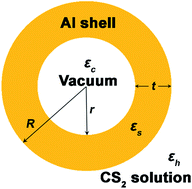
Interband transitions have important impacts on the nonlinear responses of metal nanoparticles. This work calculated the third-order nonlinear refraction index n2eff and absorption coefficient βeff of Al nanoshells in liquid carbon disulfide (CS2) by using Maxwell-Garnett effective medium theory. Calculation results reveal that the interband-transition-induced absorption (IA) of Al nanoshells can enhance the nonlinear refraction index and absorption coefficient of composites in the near-infrared region. The peak values of n2eff and βeff deviate from the IA peak and occur on the long-wavelength side of the interband transitions, which could be qualitatively interpreted by the increase in the linear refraction index of the CS2 induced by the irradiation of incident light. With decreasing nanoshell thickness, the n2eff and βeff peaks shift toward longer wavelengths and their deviations from the IA position become more noticeable. Besides, by controlling the nanoshell thickness together with the volume fraction of Al nanoparticles, one can optimize the nonlinear optical response of Al–CS2 composites.

 Please wait while we load your content...
Please wait while we load your content...