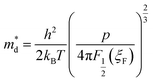DOI:
10.1039/C5RA25012A
(Paper)
RSC Adv., 2016,
6, 12243-12248
Enhanced thermoelectric figure of merit in p-type β-Zn4Sb3/Bi0.4Sb1.6Te3 nanocomposites
Received
25th November 2015
, Accepted 20th January 2016
First published on 25th January 2016
Abstract
The thermoelectric properties of Bi0.4Sb1.6Te3-based composites incorporated with β-Zn4Sb3 nanoparticles are investigated in the temperature range from 300 K to 500 K. The results show that ∼5% increase in Seebeck coefficient and ∼32% reduction of lattice thermal conductivity at 443 K are concurrently realized in the nanocomposite system with 1.3 vol% of β-Zn4Sb3, which originates from energy filtering effect as well as enhanced phonon scattering at dispersed nanoparticles and phase boundaries, respectively. As a result, the largest figure of merit ZT = 1.43 is achieved at 443 K for the sample with 1.3 vol% of β-Zn4Sb3 nanoinclusions, which is ∼18% larger than that (=1.21) of the Bi0.4Sb1.6Te3 matrix.
1. Introduction
Thermoelectric (TE) material is a type of functional material with good prospects in the future due to its unique properties to be applied as a power generator and waste heat pump.1,2 The performance of TE materials is evaluated with a dimensionless figure of merit (ZT), expressed as ZT = (S2T)/ρ(κc + κL), being dependent on the electrical resistivity (ρ), Seebeck coefficient (S), the carrier thermal conductivity (κc), the lattice thermal conductivity (κL) and absolute temperature (T).3,4 Among various TE materials, Bi2Te3-based alloys play a dominant role in commercial applications in the fields of thermoelectric energy generation and solid state cooling near room temperature.5,6 Therefore, great efforts have been made to improve their ZT values. For instance, p-type BixSb2−xTe3 nanocomposites prepared by high energy ball milling combined with hot pressing have the maximum ZT value of 1.4 (at ∼373 K).7 Moreover, in order to improve its thermoelectric properties, an excellent alternative approach, incorporating nanoinclusions into matrices to form composites, was used. For instance, incorporating D-ATP,8 SiC,9 SiO2,10 SI3N4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11 and C60
11 and C60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 into matrices has been investigated so far. However, the obtained ZT values are still not large enough. In the composites, κL can be reduced further through scattering of phonons at interfaces formed in the host materials due to embedded nanoinclusions. Although ρ is increased owing to the scattering of electrons on the interfaces, it is partially compensated by an increase in S, for energy filtering effect (EFE) would be enhanced through carrier scattering at the interface potentials.13,14 The Seebeck coefficient of a degenerate semiconductor can be expressed by the Mott formula:15
12 into matrices has been investigated so far. However, the obtained ZT values are still not large enough. In the composites, κL can be reduced further through scattering of phonons at interfaces formed in the host materials due to embedded nanoinclusions. Although ρ is increased owing to the scattering of electrons on the interfaces, it is partially compensated by an increase in S, for energy filtering effect (EFE) would be enhanced through carrier scattering at the interface potentials.13,14 The Seebeck coefficient of a degenerate semiconductor can be expressed by the Mott formula:15| |
 | (1) |
with carrier mobility μ(E) = qτ/m*d, where σ, q, E, p(E), μ(E), m*d and Ef are the electrical conductivity, the carrier charge, the energy, the energy dependent carrier density, the mobility, the effective mass and the Fermi energy, respectively. Under the approximation of free-electron gas and assuming relaxation time τ has power law relation to scattering parameter λ, i.e. τ = τ0Eλ−1/2 (here τ0 an energy-independent constant),16 formula (1) can be written as:| |
 | (2) |
where N(E) is electronic density of states. Formula (2) means that S can be enhanced through increasing scattering parameter λ. In the present work, β-Zn4Sb3 nanoinclusions were chosen to be incorporated into to Bi0.4Sb1.6Te3 (BST) matrix to explore possible EFE to enhance thermopower, for β-Zn4Sb3 is one of the most attractive p-type thermoelectric semiconductors with a wider band gap of 0.26 eV,17 while BST has a band gap of ∼0.13–0.15 eV.18 As they contact each other, p–p type heterojunction potentials at the interfaces would form and EFE would take place.
2. Experimental
Elemental Bi (99.99%, Alfa Aesar), Sb (99.5%, Sigma Aldrich), and Te (99.999%, Alfa Aesar) powders were weighted in stoichiometric proportions as starting materials. The powder mixture was loaded into quartz ampoule pumped under vacuum of 10−2 Pa and then heated to 1073 K for 10 h. Then the ingot was grinded into powders. In order to obtain p-type β-Zn4Sb3 compounds, constituent elements Zn (99.999%, Alfa Aesar) and Sb (99.5%, Sigma Aldrich) were sealed into evacuated quartz tubes corresponding to their stoichiometry. The mixture of elements Zn and Sb were heated slowly to 1023 K and isothermally kept for 12 h before quenching in water. The obtained β-Zn4Sb3 alloys ingots were ground into pieces and then were ball-milled in a high-energy planetary mill (QM-SB) with a speed of 260 rpm under Ar atmosphere for 30 h. The nanometer-sized β-Zn4Sb3 and BiSbTe powders were mixed in a planetary mill for 2 h in accordance with the volume ratios of 1.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 98.7, 2.6
98.7, 2.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 97.4, 3.9
97.4, 3.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 96.1 and 5.0
96.1 and 5.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95.0. Then the bulk composite samples were obtained by hot-pressing the blended powders under a pressure of 600 MPa in vacuum at 623 K for 1 h.
95.0. Then the bulk composite samples were obtained by hot-pressing the blended powders under a pressure of 600 MPa in vacuum at 623 K for 1 h.
X-ray diffraction (Philips diffractometer, Cu Kα radiation) was used to study the phase structure of the obtained samples at room temperature. Microstructures of the obtained powders and fracture surface of the bulk samples were observed by using field emission scanning microscopy (FE-SEM). Electrical resistivity and Seebeck coefficient were measured by the ZEM-3 system from ULVAC under Helium atmosphere from 293 to 493 K. The thermal diffusivity D was measured using the laser flash method (Netzsch, LFA-457). It should be pointed out that due to the anisotropic characteristic of BiSbTe alloys, D is measured in the perpendicular direction to the pressing direction, ensuring that the thermal and electrical properties are measured in the same direction. The specific heat, Cp, was determined by differential scanning calorimetry (DSC Pyris Diamond). The density d was measured by the Archimedes' method. The resulting total thermal conductivity was calculated from the measured thermal diffusivity D, specific heat Cp, and density d according to the relationship κ = DdCp. The Hall coefficients were measured using the Van der Pauw technique under a magnetic field of 0.72 T.
3. Results and discussion
Fig. 1 shows the XRD patterns of BST, β-Zn4Sb3 and f(β-Zn4Sb3)/BST composite samples (f = 1.3, 2.6, 3.9 and 5.0 vol%). The main diffraction peaks correspond well to the standard JCPDS cards (Bi0.5Sb1.5Te3: no. 72-1836, β-Zn4Sb3: no. 89-1969), as shown in Fig. 1(curve (a) and curve (b)). Moreover, several diffraction peaks from the β-Zn4Sb3 phase appear in XRD patterns of the composites, and the intensity of these peaks increases with increasing β-Zn4Sb3 content, which indicates that other than the two constituent phases (BST and β-Zn4Sb3) no obvious impurity phase forms, as shown in Fig. 1(c)–(f).
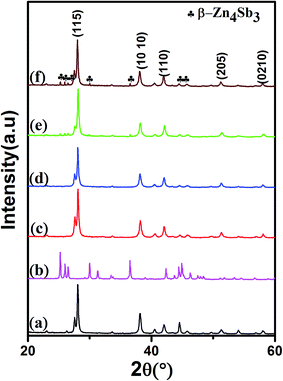 |
| | Fig. 1 XRD patterns at room temperature of (a) BST, (b) β-Zn4Sb3 and (c–f) f(β-Zn4Sb3)/BST (f = 1.3, 2.6, 3.9 and 5.0 vol%). | |
Fig. 2(a) and (b) shows the particle morphologies of BST (a) and β-Zn4Sb3 (b) powders. One can see that the typical particle size of BST powders is ∼500–1000 nm, while the typical particle sizes of β-Zn4Sb3 powders range from ∼40 nm to ∼250 nm. The FE-SEM images of composite β-Zn4Sb3/BST powders are shown in Fig. 2(c) and (d). It can be seen from Fig. 2(c) and (d) that some small spots existed in the big grains, which were attributed to β-Zn4Sb3 nanoparticles. Fig. 2(e) and (f) shows the fracture surface of β-Zn4Sb3/BST bulk composite sample. One can see that some small particles distributed on the smooth fracture surface, which could be β-Zn4Sb3 nanoinclusions.
 |
| | Fig. 2 FE-SEM micrographs of (a) BST powders, (b) β-Zn4Sb3 powders, (c) and (d) nanocomposite β-Zn4Sb3/BST powders, (e) and (f) the fracture surface of β-Zn4Sb3/BST bulk composite sample. | |
The thermoelectric properties (ρ and S) of composites f(β-Zn4Sb3)/BST (f = 0, 1.3, 2.6, 3.9 and 5.0 vol%) are shown in Fig. 3. It can be seen from Fig. 3(a) that ρ for all the composite samples f(β-Zn4Sb3)/BST (f = 0, 1.3, 2.6, 3.9 and 5.0 vol%) increases with increasing temperature, showing degenerate semiconductor behavior.19 In comparison, ρ increases monotonically with increasing β-Zn4Sb3 content. For instance, at 298 K, ρ increases from 0.87 to 1.34, 1.48, 1.56 and 1.69 × 10−5 Ω m as f increases from 0 to 1.3, 2.6, 3.9 and 5.0 vol%, respectively.
 |
| | Fig. 3 Temperature dependences of (a) electrical resistivity and (b) Seebeck coefficient for composite samples f(β-Zn4Sb3)/BST (f = 0, 1.3, 2.6, 3.9 and 5.0 vol%). | |
Fig. 3(b) shows the temperature dependences of S. S values for all of the samples are positive, indicating that the major charge carriers are holes. The temperature behaviors of S for the all the samples are similar: S increases first with increasing temperature at T < ∼403 K and then it decreases with further increase in temperature, which can be ascribed to the excitation of minority carriers (i.e. electrons) at high temperatures.20 For the sample with f = 1.3 vol%, S is smaller at beginning and then becomes larger than that of the BST matrix with further increasing temperature. For instance, ∼5% increase in Seebeck coefficient for the sample with f = 1.3 vol% is found as compared with the BST matrix at 443 K. While for the sample with f = 2.6 and 3.9 vol%, S increases with increasing β-Zn4Sb3 content at T < ∼400 K. Furthermore, S for the samples with f = 3.9 and 5.0 vol% shows small changes at T < ∼400 K.
As listed in Table 1, the carrier concentration p, determined by the Hall coefficient measurements, increases from 4.41 to 5.05, 5.23, 5.57 and 6.11 × 1019 cm−3 as f increases from 0 to 1.3, 2.6, 3.9 and 5.0 vol%. Simultaneously, the mobility μ decreases moderately from 163.6 to 60.4 cm2 V−1 s−1. Present results indicate that the increase in ρ of the composite samples originates from decrease in μ due to the relation ρ = (peμ)−1 (see Fig. 3(a)).
Table 1 List of Hall mobility μ, carrier concentration p, scattering parameter λ, the relative density dr and the Lorenz number L at room temperature for f(β-Zn4Sb3)/BST (f = 0, 1.3, 2.6, 3.9 and 5.0 vol%)
| f (vol%) |
μa (cm2 V−1 s−1) |
pb (1019 cm−3) |
λc |
drd (%) |
Le |
| μ is Hall mobility. p is carrier concentration. λ is scattering parameter. dr is relative density, defined as dr = d/d0, where d is measured density and d0 (=6.76 g cm−3) is theoretical density of BST. For the composite samples f(β-Zn4Sb3)/BST, its theoretical density is modified as: d0 = (1 − f)d1 + fd2, here d1 = d0 for BST and d2(=6.36 g cm−3) is theoretical density of β-Zn4Sb3. L is the Lorenz number. |
| 0 |
163.6 |
4.41 |
0 |
97 |
1.90 |
| 1.3 |
92.7 |
5.05 |
0.05 |
96 |
1.93 |
| 2.6 |
80.6 |
5.23 |
0.19 |
96 |
1.93 |
| 3.9 |
72.1 |
5.57 |
0.43 |
97 |
1.94 |
| 5.0 |
60.4 |
6.11 |
0.53 |
96 |
1.96 |
Obviously, the increase in p can qualitatively explain why S of composite samples decrease with increasing f. However, quantitative analysis indicates that energy-dependent scattering (or EFE) has occurred, as manifested by the increase in the scattering parameter λ. By using a single parabolic band model, the density of state effective mass m*d and the Seebeck coefficient S can be expressed as:21,22
| |
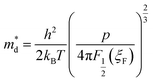 | (3) |
| |
 | (4) |
with Fermi integral of order
i| |
 | (5) |
where
h is the Planck constant and
ξF is the reduced Fermi level
Ff/(
kBT). Then, we obtain
m*d = 1.58
me (where
me is the free electron mass) for BST at 300 K by assuming that
λ = 0 for the BST matrix (
i.e. acoustic scattering is dominant in BST). Moreover, in our calculation, we assume that
m*d do not change in different samples, and then we obtain the
λ values for all the samples (see
Table 1).
Table 1 shows that
λ increases with increasing β-Zn
4Sb
3 content, and this increase of
λ leads to ∼5, ∼16, ∼34 and ∼41 μV K
−1 rise in
S at 300 K for the samples with
f = 1.3, 2.6, 3.9 and 5.0 vol%, respectively, as shown in
Fig. 4 (where the solid line is the Pisarenko relation of BST at
T = 300 K and shows the dependence of
S on
p calculated by using formulae
(3)–(5)).
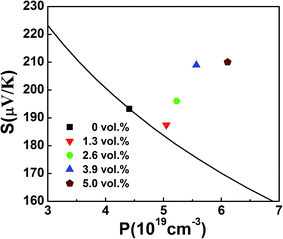 |
| | Fig. 4 Variation of Seebeck coefficient with carrier concentration for f(β-Zn4Sb3)/BST (f = 0, 1.3, 2.6, 3.9 and 5.0 vol%) at 300 K. The solid line is Pisarenko relation for BST at 300 K. | |
Fig. 5 shows PF of f(β-Zn4Sb3)/BST as functions of temperature. One can see that PF of the BST matrix decreases with increasing temperature, while PF of the composite samples (f = 1.3 and 2.6 vol%) increases at T < ∼403 K and then PF decreases with further increase in temperature. For the samples with f = 3.9 and 5.0 vol%, PF almost decreases with increasing temperature in the whole temperature range investigated here. Although PF of all the heavily incorporated samples (f = 2.6, 3.9 and 5.0 vol%) are smaller than that of the BST matrix, PF of the lightly incorporated sample with f = 1.3 vol% is almost the same to that of the BST matrix after T > 443 K, which comes from the increase in S due to the EFE.
 |
| | Fig. 5 Temperature dependences of power factor for composite samples f(β-Zn4Sb3)/BST (f = 0, 1.3, 2.6, 3.9 and 5.0 vol%). | |
The total thermal conductivity κ for all the samples is given in Fig. 6(a) as a function of temperature. As shown in Fig. 6(a), κ for all the samples decreases with increasing temperature and then slightly increase with further increasing temperature. One can also see that κ becomes smaller with the increasing β-Zn4Sb3 content in the whole temperature range investigated. For instance, at 443 K, κ decreases from 1.22 to 0.95, 0.90 0.85 and 0.78 W (m K)−1 as f increases from 0 to 1.3, 2.6, 3.9 and 5.0 vol%. The lattice thermal conductivity κL can be obtained by removing the carrier thermal conductivity κc from κ, where the carrier thermal conductivity κc can be estimated by the Wiedemann–Franz relation (κc = L0T/ρ) (see the inset of Fig. 6(a)), in which the Lorenz number L is estimated using formula (6) with the assumption of transport dominated by acoustic scattering and a single parabolic band:23
| |
 | (6) |
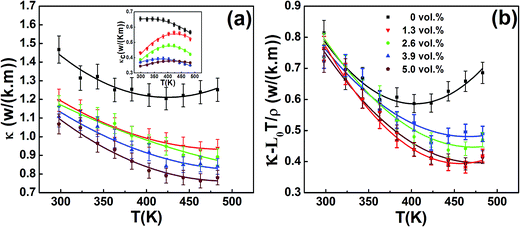 |
| | Fig. 6 Temperature dependences of (a) total thermal conductivity κ (carrier thermal conductivity κc in inset) and (b) κ − L0T/ρ for composite samples f(β-Zn4Sb3)/BST (f = 0, 1.3, 2.6, 3.9 and 5.0 vol%). | |
The obtained values of L are 1.90–1.96 × 10−8 V2 K−2, as listed in Table 1. The calculated (κ − L0T/ρ) for all the samples decrease with increasing temperature due to the phonon–phonon Umklapp scattering (U-scattering); however they increase at elevated temperature which can be due to the bipolar contribution. For a semiconductor with U-scattering as the dominant phonon scattering mechanism, κL should vary as 1/T. The portion that deviates from such a temperature dependence can be ascribe to the bipolar diffusion contribution κbipolar, as shown in Fig. 7. It can be seen that the obtained κbipolar becomes smaller with the increasing β-Zn4Sb3 content. For instance, κbipolar decreases from 0.23 to 0.12, 0.10, 0.09 and 0.08 W (m K)−1 as f increases from 0 to 1.3, 2.6, 3.9 and 5.0 vol% at 483 K. In addition, as shown in the inset of Fig. 7, the incorporation of β-Zn4Sb3 leads to substantial reduction of κL as compared to that of BST. According to Callaway mode, the lattice thermal conductivity κL can be written as:24
| |
 | (7) |
where
h is plank constant,
θD Debye temperature,
v phonon velocity,
ξ usual dimensionless variable and
τ phonon relaxation time. Furthermore, according to Matthiessen's rule,
τ is mainly related to scattering from multiple scattering centers in the materials and can be expressed as:
| | |
τ−1 = τPD−1 + τNP−1 + τp–p−1 + τIF−1
| (8) |
where
τPD,
τNP,
τp–p and
τIF are the relaxation times correspond to scattering from point defect, nanoinclusions, phonon–phonon interactions and interfaces, respectively. Therefore, the reduction in
κL for the composite samples can be ascribed to the additional phonon scattering from nanoinclusions (
τNP) and the formed interfaces (
τIF).
 |
| | Fig. 7 Variation of κ − L0T/ρ with the reciprocal of temperature for f(β-Zn4Sb3)/BST (f = 0, 1.3, 2.6, 3.9 and 5.0 vol%). Deviation of the thermal conductivity from straight lines indicates a significant bipolar contribution. The inset is the temperature dependences of estimated lattice thermal conductivity for composite samples f(β-Zn4Sb3)/BST (f = 0, 1.3, 2.6, 3.9 and 5.0 vol%). | |
Fig. 8 shows ZT for all the nanocomposite samples. For comparison, the ZT for BST matrix and for β-Zn4Sb3 studied here is also depicted in Fig. 8. One can see that ZT for all the samples increases with increasing temperature, and after reaching maximum values, they decrease with further increasing temperature. Specially, the composite samples with f = 1.3, 2.6, 3.9 and 5.0 vol% reach their high ZT values at elevated temperatures. Especially, ZT of the sample with f = 1.3 vol% reaches 1.43 at 443 K, which is ∼18% larger than that (=1.21) of BST matrix and is larger than the ZT values reported in ref. 7 (1.4), ref. 8 (1.3), ref. 9 (1.33), ref. 10 (1.27) and ref. 11 (1.38), resulting from both increased S and reduced κL through interface scattering of both carriers and phonons. Moreover, ZT for all the nanocomposite samples are much larger than that of β-Zn4Sb3 in the whole temperature range investigated here. With such ZT characteristics, the present composite material system is attractive for power generation applications from low-grade waste heat.
 |
| | Fig. 8 Temperature dependences of ZT for composite samples f(β-Zn4Sb3)/BST (f = 0, 1.3, 2.6, 3.9 and 5.0 vol%) and β-Zn4Sb3 sample. | |
4. Conclusions
In summary, the incorporation of 1.3 vol% β-Zn4Sb3 nanoparticles into BST matrix can concurrently result in ∼5% increase in S and ∼32% reduction in κL at 443 K. The increase in S results from the EFE, while the reduction of κL in the composite samples is attributed to the enhanced phonon scattering at dispersed nanoparticles and the phase boundaries. Owing to increase in S and reduction in κL, ZT = 1.43 is achieved at 443 K in the composite system with 1.3 vol% of β-Zn4Sb3. Present study demonstrates that the thermoelectric performance of BST can be effectively improved by incorporating proper amount of nanophase β-Zn4Sb3.
Acknowledgements
Financial supports from the National Natural Science Foundation of China (no. 11374306, 11174292, 51101150, 50972146, and 10904144) are gratefully acknowledged.
References
- L. E. Bell, Science, 2008, 321, 1457 CrossRef CAS PubMed.
- Y. Z. Pei, X. Y. Shi and A. LaLonde, Nature, 2011, 473, 66 CrossRef CAS PubMed.
- T. C. Harman, P. J. Taylor and M. P. Walsh, Science, 2002, 297, 2229 CrossRef CAS PubMed.
- J. Zhang, X. Y. Qin and D. Li, J. Mater. Chem. A, 2004, 2, 2891 RSC.
- S. V. Dordevic, M. S. Wolf and N. Stojilovic, J. Phys.: Condens. Matter, 2013, 25, 075501 CrossRef CAS PubMed.
- I. H. Kim, S. M. Choi, W. S. Seo and D. I. Cheong, Nanoscale Res. Lett., 2012, 7, 2 CrossRef PubMed.
- B. Poudel, Q. Hao and Y. Ma, Science, 2008, 320, 634 CrossRef CAS PubMed.
- T. Zhang, J. Jiang and Y. K. Xiao, RSC Adv., 2013, 3, 4951 RSC.
- J. H. Li, Q. Tan and J. F. Li, Adv. Funct. Mater., 2013, 10, 1002 Search PubMed.
- Y. C. Dou, X. Y. Qin and D. Li, J. Appl. Phys., 2013, 114, 044906 CrossRef.
- Y. C. Dou, X. Y. Qin and D. Li, RSC Adv., 2015, 5, 34251 RSC.
- V. D. Blank, S. G. Buga and V. A. Kulbachinskii, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075426 CrossRef.
- J. Martin, L. Wang, L. Chen and G. S. Nolas, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115311 CrossRef.
- J. P. Heremans, C. M. Thrush and D. T. Morelli, J. Appl. Phys., 2005, 98, 063703 CrossRef.
- P. H. Joseph and T. M. Donald, J. Appl. Phys., 2005, 98, 063703 CrossRef.
- J. P. Heremans, C. M. Thrush and D. T. Morelli, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 115334 CrossRef.
- G. J. Snyder, M. Christensen and E. Nishibori, Nat. Mater., 2004, 3, 458 CrossRef CAS PubMed.
- W. Xie, J. He and H. J. Kang, Nano Lett., 2010, 10, 3283 CrossRef CAS PubMed.
- D. Li and X. Y. Qin, Intermetallics, 2011, 19, 2002 CrossRef CAS.
- V. D. Blank, S. G. Buga and V. A. Kulbachinskii, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075426 CrossRef.
- Q. Q. Wang and X. Y. Qin, J. Appl. Phys., 2013, 113, 124901 CrossRef.
- T. Caillat, J. P. Fleurial and A. Borshevsky, J. Phys. Chem. Solids, 1997, 58, 1119 CrossRef CAS.
- E. S. Toberer, P. Rauwel and S. Gariel, J. Mater. Chem., 2010, 20, 9877 RSC.
- Y. B. Luo, J. Y. Yang and M. Liu, J. Mater. Chem. A, 2015, 3, 1251 CAS.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  ,
Tianhua Zou,
Yongfei Liu and
Cong Li
,
Tianhua Zou,
Yongfei Liu and
Cong Li
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11 and C60
11 and C60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 into matrices has been investigated so far. However, the obtained ZT values are still not large enough. In the composites, κL can be reduced further through scattering of phonons at interfaces formed in the host materials due to embedded nanoinclusions. Although ρ is increased owing to the scattering of electrons on the interfaces, it is partially compensated by an increase in S, for energy filtering effect (EFE) would be enhanced through carrier scattering at the interface potentials.13,14 The Seebeck coefficient of a degenerate semiconductor can be expressed by the Mott formula:15
12 into matrices has been investigated so far. However, the obtained ZT values are still not large enough. In the composites, κL can be reduced further through scattering of phonons at interfaces formed in the host materials due to embedded nanoinclusions. Although ρ is increased owing to the scattering of electrons on the interfaces, it is partially compensated by an increase in S, for energy filtering effect (EFE) would be enhanced through carrier scattering at the interface potentials.13,14 The Seebeck coefficient of a degenerate semiconductor can be expressed by the Mott formula:15

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 98.7, 2.6
98.7, 2.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 97.4, 3.9
97.4, 3.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 96.1 and 5.0
96.1 and 5.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95.0. Then the bulk composite samples were obtained by hot-pressing the blended powders under a pressure of 600 MPa in vacuum at 623 K for 1 h.
95.0. Then the bulk composite samples were obtained by hot-pressing the blended powders under a pressure of 600 MPa in vacuum at 623 K for 1 h.