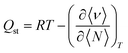DOI:
10.1039/C5RA24933C
(Paper)
RSC Adv., 2016,
6, 21517-21525
Predicting 1,3,5,7-tetrakis(4-aminophenyl)adamantine based covalent-organic frameworks as hydrogen storage materials
Received
24th November 2015
, Accepted 17th February 2016
First published on 17th February 2016
Abstract
Four types of 1,3,5,7-tetrakis(4-aminophenyl)adamantine based covalent-organic frameworks (tapa-COFs) have been designed with diamond, ctn and bor net topologies using the methods of molecular mechanics and density function theory. Their low density (0.096–0.258 g cm−3), high porosity (90–96%) and large H2 accessible surface area (5511–6810 m2 g−1) forecast excellent hydrogen uptake capacities. The grand canonical Monte Carlo (GCMC) simulation revealed that at 77 K tapa-COF-1 possesses the highest gravimetric hydrogen storage capacity at 49.10 wt%, while tapa-COF-3 has the highest volumetric hydrogen storage capacity at 58.66 g L−1. Impressively, at 298 K, tapa-COF-1 and tapa-COF-2 possess rather high gravimetric hydrogen uptake capacities, which exceed both the U.S. Department of Energy’s goal (5.5 wt%) for onboard light-duty vehicles for 2020 and the criterion of 6 wt% for commercial use of hydrogen at room temperature. In addition, the possible schemes are also proposed to synthesize the tapa-COFs.
1. Introduction
The continued growth in worldwide demand for energy sources and a better environment has led to increasing pursuit of clean energy. Hydrogen has long been identified as a promising candidate due to its inherent advantages in comparison with other possible fuels.1,2 However, the safe and effective storage of hydrogen is one of the main challenges in a hydrogen economy because of the drawbacks of traditional high pressure gas or cryogenic liquefaction storage methods.2,3 In recent decades, material-based hydrogen storage has attracted more and more attention both experimentally and theoretically. Consequently, a great number of materials such as porous frameworks,4–7 hydrides,8,9 hydrogen clathrates,10,11 and so on,12,13 have been proposed as hydrogen storage media. The U.S. Department of Energy (DOE) has set a series of goals for commercialized on-board hydrogen storage systems.14 The goal for onboard light-duty vehicles for 2020 is a hydrogen gravimetric density of 4.5 wt% and volumetric capacity of 40 g L−1 at near ambient temperature and applicable pressure less than 100 bar. Unfortunately, no existing material has met all the application requirements set by the U. S. DOE. Therefore, the search for novel materials with better hydrogen storage properties is still an urgent priority in the field of hydrogen storage.
Currently, porous covalent-organic materials (COMs) including covalent-organic frameworks (COFs),15–18 porous aromatic frameworks (PAFs),19,20 polymers of intrinsic microporosity (PIMs),21,22 conjugated microporous polymers (CMPs)23,24 and so on, have been considered as new star materials with promising prospects in the hydrogen storage field. Constructed by strong covalent bonds between light elements such as C, H, O, B, N, Si, etc.,15,25 versatile COMs possess low density, tunable pore size, high porosity, and large specific surface area which are advantages for hydrogen storage. Therefore, many investigations have been performed to study the hydrogen storage properties of pristine COMs or their modified counterparts.25–29 For example, Furukawa and Yaghi measured the H2 adsorption isotherms of a series of COFs at pressures of 1–85 bar and temperatures of 77–298 K in their experiments.26 Garberoglio simulated the hydrogen adsorption isotherms of several COFs with the GCMC method and found that these COFs might attain a 30% increase in hydrogen uptake compared with the analogous simulations performed for metal organic frameworks at 77 K and 298 K.27 Cao et al. studied the hydrogen storage capacities of lithium doped COFs and demonstrated that the gravimetric adsorption capacities for hydrogen in Li-doped COF-105 and COF-108 can reach 6.84 wt% and 6.73 wt% at 298 K and 100 bar, meeting the requirements for commercial use set by the U. S. DOE.29 Zhu et al. designed a series of PAFs and investigated their advanced applications in hydrogen storage, carbon dioxide capture, drug release and so on.25,30 Moreover, Xiang et al. first synthesized a covalent organic polymer (COP) experimentally, and then they proposed a novel lithium-decorating approach to enhance its H2 adsorption properties.28 Surprisingly, the H2 uptake of the lithium-modified COPs increased by 70.4% compared with the unmodified compounds. All these vivid examples indicate the potential of COMs as practical hydrogen storage media. However, none of the existing COMs can be used as practical hydrogen storage media for commercial use and hence the study on COMs as hydrogen storage materials still has a long way to go.
Probing into the structures of crystalline COMs, one can easily find that COMs are combined by ever-changing organic linkers with regular geometric shapes under various net topologies. At the same time, different structures can be formed by the same organic linkers under different net topologies. Typically, COF-102, COF-103, COF-105 have ctn topology while COF-108 has a bor topology, and, furthermore, COF-105 and COF-108 contain the same building blocks but different topology nets.17 Also, PAFs are mainly constructed by various aromatic organic linkers under different net topologies.20,25,31,32 Relying on this feature, many novel COMs with targeted properties have been predicted by theoretical design. Huang et al. proposed a series of PAFs by replacing the silicon in zeolites with tetrakis(4-bromophenyl)methane. Marvelously, hydrogen uptake can reach up to 5.9 wt% at 100 bar and 298 K, exceeding the DOE 2017 target (4.5 wt%).20 Also, Mendoza-Cortes designed 14 COFs which can adsorb large amounts of methane at 298 K and up to 300 bar.32 Similarly, Farha et al. first used computational design to predict and characterize a metal–organic framework. Then, they synthesized and tested it for its hydrogen storage properties experimentally.33 All these investigations indicate that the design of new COMs with computational methods prior to experimental synthesis can not only save time and effort but also make the experimental synthesis goal-directed.
Motivated and inspired by these studies, four types of novel covalent-organic frameworks were designed as hydrogen storage medium based on 1,3,5,7-tetrakis(4-aminophenyl)adamantine (TAPA) and three anhydrides. Adamantane is a cycloaliphatic hydrocarbon with a diamond-like cage structure that contains six secondary carbons and four tertiary carbons. Its bulky molecular volume, rigidity and highly symmetrical tetrahedral shape render it an ideal building block for the construction of porous materials. The four hydrogen atoms attached to the tertiary carbons can be substituted by phenyls through arylation to form 1,3,5,7-tetraphenyladamantane (TPA).34 Moreover, 1,3,5,7-tetrakis(4-aminophenyl)adamantine (TAPA) can be generated from the nitration of TPA with a sequence of reaction procedures.35,36 The amino in TAPA is chemically active for polymerization to generate different kinds of function materials. However, polyimides constructed from TAPA have rarely appeared in the literature up to now. Also, there are few investigations on the hydrogen storage properties of polyimides. Therefore, four types of TAPA based polyimides were theoretically designed and their hydrogen storage properties studied in the present work. We hope our design can provide some new thinking for the experiment synthesis of novel high-capacity hydrogen storage materials.
2. Design schemes and computation details
The structures of 1,3,5,7-tetrakis(4-aminophenyl)adamantine (TAPA) and three other anhydride monomers A, B and C are depicted in Fig. 1. As can be seen in Fig. 1, TAPA possesses a tetrahedral structure and four amino groups sit at the vertices of the tetrahedral. The amino group is reactive and can react with the anhydrides A, B and C. A and B are linear monomers while C has a planar triangular shape. Four types of polyimides can be formed between TAPA and the three chemical monomers and the possible synthesis schemes are depicted in Fig. 1. Here, for convenience, we term the TAPA based polyimides as tapa-COFs and the four types of tapa-COF networks are respectively named tapa-COF-1, tapa-COF-2, tapa-COF-3 and tapa-COF-4. Here, the possible schemes to synthesize these tapa-COFs are proposed and shown in Fig. 1. As depicted in Fig. 1, tapa-COF-1 and tapa-COF-2 are possibly generated through polycondensation between A or B and TAPA while tapa-COF-3 and tapa-COF-4 can be both formed through polycondensation between TAPA and C but possess different topological structures. Similar schemes to synthesize other porous materials have been performed in experiments in previous work.36–38 As shown in Fig. 1, tapa-COF-1 and tapa-COF-2 are designed with the topological structure of diamond (dia). For these two networks, TAPA is equivalent to the carbon atom and the linear monomers A and B are equivalent to the C–C bond in diamond. As we all know, for design frameworks with tetrahedral and triangular units, the ctn (a hypothetical C3N4 structure, I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m space group) and bor (boracite, P
3m space group) and bor (boracite, P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m space group) topology nets are considered to be the most stable.17,32,39 Hence, we designed tapa-COF-3 and tapa-COF-4 with the same chemical monomers with the corresponding ctn and bor net topologies. The optimized structures of the four tapa-COFs are shown in Fig. 2.
3m space group) topology nets are considered to be the most stable.17,32,39 Hence, we designed tapa-COF-3 and tapa-COF-4 with the same chemical monomers with the corresponding ctn and bor net topologies. The optimized structures of the four tapa-COFs are shown in Fig. 2.
 |
| | Fig. 1 The possible schemes to synthesize four 1,3,5,7-tetrakis(4-aminophenyl)adamantine (TAPA) based polyimide (tapa-COF) networks. | |
 |
| | Fig. 2 The optimized structures of (a) tapa-COF-1, (b) tapa-COF-2, (c) tapa-COF-3 and (d) tapa-COF-4. | |
To construct the tapa-COF networks, first, we optimized four chemical monomers using a generalized gradient approximation within the framework of density function theory. Then we assembled the four tapa-COFs by adding irreducible representations of the ligands into the topological structures of the corresponding space groups. Based on the preliminary design, subsequently, we optimized the tapa-COF networks using the classical molecular mechanics method with a COMPASS40,41 force field. Most parameters of the COMPASS force field were derived from ab initio results and the COMPASS force field was parameterized to predict various properties for a variety of materials including the most common organics, small inorganic molecules, and polymers in isolation and in condensed phases. During the optimized process, the conjugate gradient method was implemented to begin with the steepest descent method as the first step. To get the best geometrical structures, no space group symmetry constraints were imposed on the networks and all the bond lengths, angles, and cell parameters were optimized to get the best framework structures. The geometrical structures were optimized until the remaining atomic forces were less than 0.001 kcal (mol−1 Å−1) on each atom and the energy convergence criterion was chosen as 1.0 × 10−7 kcal mol−1 between two steps.
On the basis of the optimized structures, the hydrogen adsorption properties of these tapa-COF networks were investigated by the method of grand canonical Monte Carlo (GCMC) simulation. The 12-6 Lennard-Jones (L-J) potential shown in eqn (1) was used to describe the van der Waals (VDW) interactions between the H2 molecules and the networks. The potential parameters for the network atoms were from the DREIDING force field of Mayo et al.42 The potential parameters of the H2 molecule were from the work of Buch,43 where a united-atom model for H2 was employed. All the potential parameters used in the present work are listed in Table 1. The cross-interaction parameters between two different atoms were treated using the Lorentz–Berthelot mixing rules shown in eqn (2) and (3).
| |
 | (1) |
| |
 | (3) |
Table 1 The L-J potential parameters of the H2 and He molecules and all the network atoms used in the present work
| |
H2 |
He |
C |
H |
O |
N |
| σ (Å) |
2.956 |
2.64 |
3.473 |
2.846 |
3.033 |
3.263 |
| ε/kB (K) |
36.7 |
10.9 |
47.856 |
7.649 |
48.156 |
38.948 |
The GCMC simulations were carried out using the code MuSic.44 2 × 2 × 2 simulation cells of frameworks were adopted in the simulations and periodic boundary conditions were applied in all three dimensions. The frameworks were kept rigid with frozen atoms during the simulation processes. The L-J interactions were evaluated with a spherical cut off of 12.9 Å. The number of trial moves in a typical GCMC simulation was 2 × 107. The first 1 × 107 steps were used for equilibration and the subsequent 1 × 107 steps were used for ensemble averages. Three different trial moves were attempted in the GCMC simulation, namely, translation, random insertion, and deletion. In many studies, the excess adsorbed amounts were calculated from absolute adsorbed amounts to compare with the experiments. In this work, the excess adsorbed amounts (Nexc) were computed by the following eqn (4)
where
Nabs denotes the amount of absolute H
2 molecules adsorbed,
ρ refers to the density of the hydrogen under the thermodynamics condition studied, and
Vp represents the pore volume of adsorbent. The density of the hydrogen is calculated by the Peng–Robinson equation of state
45 at a given temperature and pressure. The pore volumes of these materials were estimated with the method proposed by Talu and Myers.
46 They suggested that the pore volume could be calculated by the amounts of helium molecules contained in a unit mass adsorbent (
Na) from GCMC simulation at low pressures (
P) and room temperature (
T0) with
eqn (5)where
kB refers to the Boltzmann constant.
3. Results and discussions
Based on geometry optimization, the final structures of the four tapa-COFs were obtained. Under the tolerance of 10−2 Å, the optimized tapa-COF-1 and tapa-COF-2 belong to cubic lattices without more symmetry, while tapa-COF-3 retains the I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m space group symmetry and tapa-COF-4 retains the P
3m space group symmetry and tapa-COF-4 retains the P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m space group symmetry. The cell and physical parameters of the four tapa-COF networks are listed in Table 2 and the structure models are shown in Fig. 2. As shown in Table 2, tapa-COF-1 and tapa-COF-2 possess almost the same cell length due to the same dia topology structures and nearly equally sized building units. On the other hand, although having the same build unit, the cell length of tapa-COF-3 is much larger than that of tapa-COF-4, which is attributed to their different space group symmetry. It can be found in Table 2 that all four tapa-COF networks possess very low densities (0.096–0.258 g cm−3), especially tapa-COF-1 and tapa-COF-2 whose densities are nearly the same as water. It is well known that COFs are some of the lowest density COMs. To the best of our knowledge, the lowest densities reported for three-dimensional COFs are COF-108 (0.17 g cm−3) and COF-105 (0.18 g cm−3). Here, the densities of tapa-COF-1 and tapa-COF-2 are even lower than that of COF-108 and COF-105, which shows that the tapa-COFs designed in this work can be ranked amongst the members of COMs with the lowest density.
3m space group symmetry. The cell and physical parameters of the four tapa-COF networks are listed in Table 2 and the structure models are shown in Fig. 2. As shown in Table 2, tapa-COF-1 and tapa-COF-2 possess almost the same cell length due to the same dia topology structures and nearly equally sized building units. On the other hand, although having the same build unit, the cell length of tapa-COF-3 is much larger than that of tapa-COF-4, which is attributed to their different space group symmetry. It can be found in Table 2 that all four tapa-COF networks possess very low densities (0.096–0.258 g cm−3), especially tapa-COF-1 and tapa-COF-2 whose densities are nearly the same as water. It is well known that COFs are some of the lowest density COMs. To the best of our knowledge, the lowest densities reported for three-dimensional COFs are COF-108 (0.17 g cm−3) and COF-105 (0.18 g cm−3). Here, the densities of tapa-COF-1 and tapa-COF-2 are even lower than that of COF-108 and COF-105, which shows that the tapa-COFs designed in this work can be ranked amongst the members of COMs with the lowest density.
Table 2 Unit cell parameters, chemical formula, molar mass (M), density, pore volume (Vp) and H2 accessible surface (S) of four tapa-COF networks
| Materials |
a = b = c (Å) |
Chemical formula |
M (g mol−1) |
Density (g cm−3) |
Vp (cm3 g−1) |
S (m2 g−1) |
| tapa-COF-1 |
49.35 |
C432H256N32O64 |
6918.93 |
0.096 |
10.05 |
6810.19 |
| tapa-COF-2 |
50.34 |
C496H288N32O64 |
7719.89 |
0.100 |
9.51 |
6755.06 |
| tapa-COF-3 |
39.74 |
C600H336N48O96 |
9753.49 |
0.258 |
3.49 |
5654.44 |
| tapa-COF-4 |
25.91 |
C150H84N12O24 |
2438.37 |
0.233 |
3.95 |
5511.10 |
Surface area and pore size are two important indices determining the gas adsorption capacity of porous materials. The surface areas of the four tapa-COFs were evaluated by using a numerical Monte Carlo integration technique proposed by Frost et al.47 It was performed by “rolling” a probe molecule with a diameter equal to the L-J σ parameter for H2 (2.958 Å) over the network surface. The probe was inserted randomly around the surface of each network atom with a diameter equal to the LJ σ parameters one by one. The ratio of probes that did not overlap with other network atoms was used to calculate the accessible surface area. It is obvious that surface area calculated in this way is highly dependent on the probe size used for measurement and calculating the surface area with a H2 probe provides the amount of area accessible to H2 molecules. The calculated H2 accessible surface areas of the four tapa-COFs are listed in Table 2. As shown in Table 2, for tapa-COF-1 and tapa-COF-2 with diamond net topologies, tapa-COF-1 exhibits a larger H2 accessible surface area than tapa-COF-2, attributed to the different linear building units depicted in Fig. 1. For tapa-COF-3 and tapa-COF-4 with the same building units, tapa-COF-3 has a larger H2 accessible surface area than tapa-COF-4, since the network with the ctn net topology has a larger surface area than that with the bor net topology. Nevertheless, all tapa-COFs have quite large surface areas. Up to now, the highest surface area reported for COF materials was COF-103 with a Brunauer–Emmett–Teller (BET) surface area of 4210 m2 g−1.17 Moreover, PAF-1 has a very high BET surface area of 5600 m2 g−1 and a Langmuir surface area of 7100 m2 g−1.30 The accessible surface areas of the four tapa-COFs in Table 2 reflect that all the designed tapa-COFs here are on a par with porous materials with the highest surface area. Using the method mentioned before, the pore volumes of the four tapa-COFs were estimated by the amounts of helium molecules adsorbed at the temperature of 298 K and the pressure of 0–1 bar through eqn (5). As revealed in Table 2, the sequence for pore volume is opposite that of density, that is, tapa-COF-1 (tapa-COF-3) has a larger pore volume than tapa-COF-2 (tapa-COF-4). To gain a concrete concept of the pore size, we also calculated the percent pore volumes of the four tapa-COFs and they are 96%, 95%, 90% and 92% for tapa-COF-1 to tapa-COF-4, respectively. To our knowledge, the percent pore volumes of COF-105 (88.22%), COF-108 (88.84%) and PAF-1 (77.60%)17,29,30 are among the highest ones reported for COMs experimentally. Obviously, the percent pore volume of the tapa-COFs means they can join the rank of porous materials with the highest porosity up to now. The high porosity and the large surface area implies an excellent hydrogen storage capacity of these tapa-COFs.
In order to verify the rationality of the GCMC simulation and the employed force field based on the L-J potential mode, the hydrogen adsorption isotherm of COF-102 was simulated at 77 K and the result was compared with the experimental data by Furukawa and Yaghi26 and the simulated results by Han et al.48 and Klontzas et al.49 with different parameters, as depicted in Fig. 3. As displayed in Fig. 3, the trend of our simulated results is consistent with the experimental data but the hydrogen uptake is a little larger. Therefore, the force field based GCMC simulation can accurately predict the hydrogen storage capacities of the tapa-COF networks in the present work.
 |
| | Fig. 3 Comparison of the simulated absolute H2 adsorption isotherm in COF-102 at 77 K with experimental data by Furukawa et al.26 and other simulated results by Han et al.48 and Klontzas et al.49 with different methods or parameters. | |
The hydrogen uptake capacities of the four tapa-COF networks at 77 K were calculated using the GCMC simulation and the results are shown in Fig. 4. As shown by the hydrogen adsorption isotherms in Fig. 4, the absolute gravimetric and volumetric H2 uptake capacities increase gradually with increasing H2 gas pressure from 0.1 bar to 100 bar. However, the situation is not the same for excess H2 uptake capacities. For tapa-COF-1 and tapa-COF-2, the excess H2 uptake capacities also increase gradually in the range of pressure studied while for tapa-COF-3 and tapa-COF-4, the excess H2 uptake capacities reach a maximum at a moderate H2 gas pressure. This implies that tapa-COF-1 and tapa-COF-2 possess a larger pore volume and surface area than tapa-COF-3 and tapa-COF-4, which is consistent with the results displayed in Table 2. Fig. 4(a) shows that the H2 gravimetric adsorption capacity of tapa-COF-1 (tapa-COF-4) is higher than that of tapa-COF-2 (tapa-COF-3) at all H2 gas pressures studied. The maximum gravimetric H2 uptake capacities are 49.10 wt%, 46.30 wt%, 22.90 wt% and 24.80 wt% for tapa-COF-1, tapa-COF-2, tapa-COF-3 and tapa-COF-4, respectively. In addition, the excess gravimetric H2 uptake capacities are 14.80 wt% at 100 bar for tapa-COF-1, 13.90 wt% at 100 bar for tapa-COF-2, 12.50 wt% at 50 bar for tapa-COF-3 and 12.60 wt% at 50 bar for tapa-COF-4. From Fig. 4(b), we can see that tapa-COF-1 and tapa-COF-2 possess almost the same absolute and excess volumetric H2 uptake capacities. At the same time, tapa-COF-3 has higher absolute and excess volumetric H2 uptake capacities than tapa-COF-4, which is contrary to the gravimetric H2 uptake capacities. The maximum absolute (excess) volumetric H2 uptake capacities are 46.60 g L−1 (23.80 g L−1 at 100 bar), 46.20 g L−1 (13.60 g L−1 at 40 bar), 58.66 g L−1 (31.80 g L−1 at 50 bar) and 57.30 g L−1 (28.90 g L−1 at 50 bar) for tapa-COF-1 to tapa-COF-4, respectively. On the whole, tapa-COF-1 and tapa-COF-2 have much higher gravimetric H2 uptake capacities than tapa-COF-3 and tapa-COF-4, while tapa-COF-3 and tapa-COF-4 have higher volumetric H2 uptake capacities than tapa-COF-1 and tapa-COF-2. Nevertheless, the simulation results show the excellent H2 storage capacities of these tapa-COFs at 77 K.
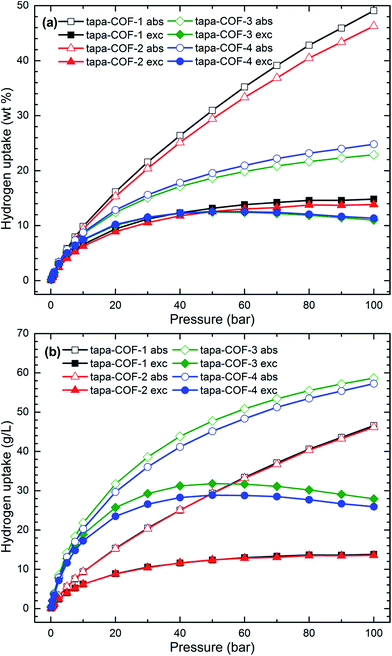 |
| | Fig. 4 The computed absolute (abs) and excess (exc) H2 adsorption isotherms in four tapa-COFs at 77 K. (a) Gravimetric H2 adsorption isotherms and (b) volumetric H2 adsorption isotherms. | |
Since the practical application of hydrogen should be at room temperature, we also simulated the hydrogen adsorption isotherms of the four tapa-COFs at 298 K and the results are depicted in Fig. 5. As shown by the hydrogen adsorption isotherms, both the gravimetric and volumetric H2 uptake capacities increase linearly with rising H2 gas pressure at room temperature. This tendency conforms to the characteristic of Henry’s linear isotherm equation.50,51 The Henry law constant can be expressed by the slope of the linear isotherm. The Henry’s linear isotherm equation is n = KP, where n is the absolute adsorbed amount per unit weight of adsorbent (wt%), P is the adsorbate H2 gas pressure at equilibrium (bar), and K is the Henry’s law constant (wt% per bar). The linear fits were done for the absolute gravimetric hydrogen adsorption isotherms and the fitted equations are listed in Fig. 5(a), including the respective degree of linear correlation (r). The subscripts 1 to 4 in these equations denote the corresponding equations and degrees of linear correlation for tapa-COF-1 to tapa-COF-4. From these equations, the isotherms have good linearity, which reveals that the H2 uptake capacity of these tapa-COFs is mainly related to the pore volume and is virtually independent of binding energy or surface area at room temperature. As can be seen from Fig. 5 and Table 2, tapa-COF-1 (tapa-COF-4) does possess higher gravimetric H2 uptake capacities than that of tapa-COF-2 (tapa-COF-3) at all H2 pressure studied, which is consistent with the size of their pore volume. The highest absolute gravimetric (volumetric) H2 uptake capacities of tapa-COF-1 to tapa-COF-4 are 8.06 wt% (7.64 g L−1), 7.53 wt% (7.51 g L−1), 3.13 wt% (8.03 g L−1), and 3.49 wt% (8.05 g L−1), respectively. Surprisingly, the maximum gravimetric H2 uptake capacities for tapa-COF-1 and tapa-COF-2 exceed the U.S. Department of Energy’s goal (4.5 wt%) for 2017 and also the capacity (6 wt%) for practical application of hydrogen storage at room temperature.14 The only disadvantage is that the four tapa-COFs have low absolute volumetric H2 uptake capacities and the capacities are almost the same at 298 K, which also indicates that the amount of hydrogen adsorbed is mainly dependent on pore volume. In order to use the tapa-COFs as practical hydrogen storage media, some modification methods such as doping metals or introducing functionalized groups15,28,52 can be adopted to improve the volumetric H2 uptake capacity at room temperature. For most investigations, excess H2 uptake capacity is rarely mentioned at room temperature, since it is always very low. To make the studies more comprehensive, we also calculated the excess H2 adsorption capacities at 298 K. As shown in Fig. 4, the maximum excess gravimetric (volumetric) H2 uptake capacities of tapa-COF-1 to tapa-COF-4 are 0.21 wt% (0.16 g L−1), 0.11 wt% (0.08 g L−1), 0.39 wt% (0.95 g L−1) and 0.39 wt% (0.84 g L−1), respectively. Here, the excess H2 adsorption capacities of tapa-COF-3 and tapa-COF-4 are higher than those of tapa-COF-1 and tapa-COF-2, which implies that tapa-COF-3 and tapa-COF-4 can adsorb H2 molecules more strongly than tapa-COF-1 and tapa-COF-2.
 |
| | Fig. 5 The computed absolute (abs) and excess (exc) H2 adsorption isotherms of the four tapa-COFs at 298 K. (a) Gravimetric H2 adsorption isotherms and (b) volumetric H2 adsorption isotherms. | |
In order to study the energetics of the adsorbed H2 molecules, we calculated the isosteric heat of adsorption (Qst) as a function of H2 loading from eqn (6).53
| |
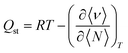 | (6) |
Here,
R is the ideal gas constant,
T is the temperature, 〈
ν〉 is the average potential energy of the adsorbed phase, and 〈
N〉 is the average number of molecules in the adsorbed phase.
Table 3 lists the isosteric heat of adsorption for H
2 of each tapa-COF at 77 K and 298 K. Also, the average isosteric heat of adsorption for H
2 of each tapa-COF at 77 K and 298 K was calculated. As shown in
Table 3, the isosteric heats of adsorption for H
2 at 298 K is larger than that of 77 K for the each tapa-COF as a whole. This is related to the fact that much more H
2 is adsorbed on the same tapa-COF at 77 K than at 298 K. Hence, at 298 K the H
2 molecules are mainly adsorbed near the surface of the tapa-COFs, while more H
2 molecules fill the pore cavities far from the network surface at 77 K. Since the isosteric heat of adsorption for H
2 mainly comes from the Van der Waals interactions between the H
2 molecules and the network surface, it was smaller at 77 K than at 298 K. On the other hand, tapa-COF-3 and tapa-COF-4 possess a little larger isosteric heat of adsorption for H
2 than that of tapa-COF-1 and tapa-COF-2. This can be explained by the size of the pore volume of the networks. Since tapa-COF-1 and tapa-COF-2 have larger pore volumes than tapa-COF-3 and tapa-COF-4, the average distance between the adsorbed H
2 molecule and the network surface in tapa-COF-1 and tapa-COF-2 is longer than that in tapa-COF-3 and tapa-COF-4 and hence larger energetics is attained. Unfortunately, the isosteric heats of adsorption for H
2 in the four tapa-COFs are all rather small. A previous study has pointed out that the value of the isosteric heat of adsorption needs to be larger than 15 kJ mol
−1 for practical hydrogen storage application.
54 The low isosteric heats of adsorption for H
2 in COFs is a common problem. In a previous feature article, Xiang and Cao summarized the hydrogen adsorption properties of porous COFs and the isosteric heats of adsorption for H
2 in COFs lies between 3.9–9.5 kJ mol
−1.
15 Therefore, to enhance the isosteric heats of adsorption for H
2 in the tapa-COFs, some modified methods can be adopted, which was mentioned in the previous paragraph to improve the volumetric H
2 uptake capacity at room temperature.
Table 3 The isosteric heat of H2 adsorption (kJ mol−1) in four tapa-COF networks under pressures from 0.1–100 bar and their average values at both 77 K and 298 K
| Pressure (bar) |
tapa-COF-1 |
tapa-COF-2 |
tapa-COF-3 |
tapa-COF-4 |
| 77 K |
298 K |
77 K |
298 K |
77 K |
298 K |
77 K |
298 K |
| 0.1 |
2.88 |
2.67 |
2.16 |
2.48 |
4.15 |
3.47 |
3.43 |
3.29 |
| 0.5 |
3.05 |
2.94 |
2.89 |
2.90 |
3.48 |
3.43 |
3.21 |
4.06 |
| 1 |
3.07 |
3.24 |
3.31 |
2.88 |
3.84 |
3.98 |
3.08 |
2.99 |
| 2.5 |
2.92 |
3.63 |
2.69 |
2.54 |
3.28 |
3.72 |
3.28 |
3.85 |
| 5 |
2.63 |
2.47 |
3.68 |
2.40 |
2.26 |
2.54 |
2.56 |
3.58 |
| 7.5 |
2.55 |
2.61 |
2.87 |
2.89 |
3.22 |
4.32 |
2.46 |
3.95 |
| 10 |
1.53 |
2.85 |
2.27 |
3.19 |
2.64 |
3.83 |
3.34 |
4.22 |
| 20 |
2.16 |
3.31 |
2.83 |
3.74 |
3.06 |
3.16 |
3.00 |
3.33 |
| 30 |
2.31 |
2.59 |
1.65 |
2.96 |
3.24 |
3.85 |
2.92 |
4.59 |
| 40 |
1.80 |
2.80 |
1.89 |
3.60 |
3.15 |
3.46 |
3.39 |
3.96 |
| 50 |
1.26 |
2.89 |
2.27 |
2.32 |
2.25 |
3.46 |
3.36 |
4.12 |
| 60 |
1.01 |
2.53 |
2.38 |
3.81 |
2.89 |
4.29 |
2.85 |
4.33 |
| 70 |
2.58 |
3.68 |
2.01 |
3.14 |
3.05 |
3.78 |
2.91 |
4.00 |
| 80 |
2.11 |
3.44 |
2.06 |
3.02 |
3.66 |
3.96 |
2.58 |
3.47 |
| 90 |
2.04 |
2.96 |
1.98 |
3.29 |
3.19 |
3.58 |
2.96 |
4.84 |
| 100 |
2.17 |
3.47 |
2.22 |
3.01 |
3.56 |
4.19 |
2.69 |
3.77 |
| Average |
3.18 |
3.69 |
3.00 |
3.90 |
2.25 |
3.01 |
2.45 |
3.01 |
To understand the adsorption process of H2 molecules in these tapa-COF frameworks, we investigated their adsorption behavior at a molecular level by detecting snapshots of the four tapa-COFs with H2 molecules adsorbed at both 77 K and 298 K. Fig. 6 shows typical snapshots of the four tapa-COFs with adsorbed H2 molecules at 77 K and 100 bar. By studying the adsorption behavior of the H2 molecules in these tapa-COFs, we found that the monomers A, B and C (seen in Fig. 1) are the preferential adsorption sites for H2 molecules, which is consistent with studies in previous work by ab initio calculations. During the process, the H2 molecules are first adsorbed near the monomers A, B and C at low H2 pressure. With rising H2 pressure, the H2 molecules begin to occupy the corner sites near the TAPA units. Finally, the H2 molecules accommodate the pore space far from the framework surface at high H2 pressure.
 |
| | Fig. 6 Equilibrium snapshots of the four tapa-COFs with H2 molecules adsorbed under the pressure of 100 bar at 77 K. (a) tapa-COF-1, (b) tapa-COF-2, (c) tapa-COF-3 and (d) tapa-COF-4. | |
4. Conclusions
In this work, four novel covalent-organic frameworks have been designed based on 1,3,5,7-tetrakis(4-aminophenyl)adamantine and proposed as hydrogen storage materials. The simulated results reveal that the tapa-COFs have high pore volumes, large H2 accessible surface areas and very low densities. The GCMC simulations show that tapa-COF-1 has the highest gravimetric hydrogen uptake while tapa-COF-3 possesses the highest volumetric hydrogen uptake at both 77 K and 298 K. The good hydrogen uptake capacities of these tapa-COFs implies their potential as hydrogen storage materials. At the same time, possible schemes to synthesize the tapa-COFs were also proposed. Although the experimental synthesis of these tapa-COFs is still to be achieved, we expect that the ideas gained from this work may motivate inspiration for the corresponding experiments in future.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 11447142, 11504088, 11304079 and 51201059). X.-D. Li also acknowledges financial support from the Talent Introduction Fund (No. 2013BS039) and the Plan of Nature Science Fundamental Research (No. 2013JCYJ10) in Henan University of Technology and the support from the Fundamental Research Funds for the Henan Provincial Colleges and Universities (No. 2014YWQN07, 16A140005 and 14A140027).
References
- C.-J. Winter, Int. J. Hydrogen Energy, 2009, 34, S1–S52 CrossRef CAS.
- L. Schlapbach and A. Zuttel, Nature, 2001, 414, 353–358 CrossRef CAS PubMed.
- K. Mazloomi and C. Gomes, Renewable Sustainable Energy Rev., 2012, 16, 3024–3033 CrossRef CAS.
- V. C. Menon and S. Komarneni, J. Porous Mater., 1998, 5, 43–58 CrossRef CAS.
- S. Ma and H. C. Zhou, Chem. Commun., 2010, 46, 44–53 RSC.
- B. Assfour and G. Seifert, Microporous Mesoporous Mater., 2010, 133, 59–65 CrossRef CAS.
- E.-Y. Chen, Y.-C. Liu, M. Zhou, L. Zhang and Q. Wang, Chem. Eng. Sci., 2012, 71, 178–184 CrossRef CAS.
- S. Orimo, Y. Nakamori, J. R. Eliseo, A. Zuttel and C. M. Jensen, Chem. Rev., 2007, 107, 4111–4132 CrossRef CAS PubMed.
- B. Sakintuna, F. Lamari-Darkrim and M. Hirscher, Int. J. Hydrogen Energy, 2007, 32, 1121–1140 CrossRef CAS.
- P. K. Chattaraj, S. Bandaru and S. Mondal, J. Phys. Chem. A, 2011, 115, 187–193 CrossRef CAS PubMed.
- V. V. Struzhkin, B. Militzer, W. L. Mao, H.-k. Mao and R. J. Hemley, Chem. Rev., 2007, 107, 4133–4151 CrossRef CAS PubMed.
- Y. Zhao, Y.-H. Kim, A. C. Dillon, M. J. Heben and S. B. Zhang, Phys. Rev. Lett., 2005, 94, 155504 CrossRef PubMed.
- J. Carrete, R. C. Longo, L. J. Gallego, A. Vega and L. C. Balbás, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125435 CrossRef.
- http://www.hydrogen.energy.gov/roadmaps_vision.html.
- Z. Xiang and D. Cao, J. Mater. Chem. A, 2013, 1, 2691–2718 CAS.
- E. Tylianakis, E. Klontzas and G. E. Froudakis, Nanoscale, 2011, 3, 856–869 RSC.
- H. M. El-Kaderi, J. R. Hunt, J. L. Mendoza-Cortes, A. P. Cote, R. E. Taylor, M. O’Keeffe and O. M. Yaghi, Science, 2007, 316, 268–272 CrossRef CAS PubMed.
- A. P. Cote, A. I. Benin, N. W. Ockwig, M. O’Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170 CrossRef CAS PubMed.
- T. Ben and S. Qiu, CrystEngComm, 2013, 15, 17–26 RSC.
- L. Huang, X. Yang and D. Cao, J. Phys. Chem. C, 2015, 119, 3260–3267 CAS.
- N. B. McKeown and P. M. Budd, Macromolecules, 2010, 43, 5163–5176 CrossRef CAS.
- N. B. McKeown and P. M. Budd, Chem. Soc. Rev., 2006, 35, 675–683 RSC.
- A. I. Cooper, Adv. Mater., 2009, 21, 1291–1295 CrossRef CAS.
- J. X. Jiang, F. Su, A. Trewin, C. D. Wood, H. Niu, J. T. Jones, Y. Z. Khimyak and A. I. Cooper, J. Am. Chem. Soc., 2008, 130, 7710–7720 CrossRef CAS PubMed.
- X. Zou, H. Ren and G. Zhu, Chem. Commun., 2013, 49, 3925–3936 RSC.
- H. Furukawa and O. M. Yaghi, J. Am. Chem. Soc., 2009, 131, 8875–8883 CrossRef CAS PubMed.
- G. Garberoglio, Langmuir, 2007, 23, 12154–12158 CrossRef CAS PubMed.
- Z. Xiang, D. Cao, W. Wang, W. Yang, B. Han and J. Lu, J. Phys. Chem. C, 2012, 116, 5974–5980 CAS.
- D. Cao, J. Lan, W. Wang and B. Smit, Angew. Chem., Int. Ed., 2009, 48, 4730–4733 CrossRef CAS PubMed.
- T. Ben, H. Ren, S. Ma, D. Cao, J. Lan, X. Jing, W. Wang, J. Xu, F. Deng, J. M. Simmons, S. Qiu and G. Zhu, Angew. Chem., Int. Ed., 2009, 48, 9457–9460 CrossRef CAS PubMed.
- S. Amirjalayer, R. Q. Snurr and R. Schmid, J. Phys. Chem. C, 2012, 116, 4921–4929 CAS.
- J. L. Mendoza-Cortes, T. A. Pascal and W. A. Goddard, J. Phys. Chem. A, 2011, 115, 13852–13857 CrossRef CAS PubMed.
- O. K. Farha, A. O. Yazaydin, I. Eryazici, C. D. Malliakas, B. G. Hauser, M. G. Kanatzidis, S. T. Nguyen, R. Q. Snurr and J. T. Hupp, Nat. Chem., 2010, 2, 944–948 CrossRef CAS PubMed.
- I. Boldog, A. B. Lysenko, E. B. Rusanov, A. N. Chernega and K. V. Domasevitch, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2009, 65, O248–O252 CAS.
- V. R. Reichert and L. J. Mathias, Macromolecules, 1994, 27, 7015–7023 CrossRef CAS.
- C. Shen, Y. Bao and Z. Wang, Chem. Commun., 2013, 49, 3321–3323 RSC.
- Y. Luo, B. Li, L. Liang and B. Tan, Chem. Commun., 2011, 47, 7704–7706 RSC.
- J. Weber, M. Antonietti and A. Thomas, Macromolecules, 2008, 41, 2880–2885 CrossRef CAS.
- O. Delgado-Friedrichs, M. O’Keeffe and O. M. Yaghi, Acta Crystallogr., Sect. A: Found. Crystallogr., 2006, 62, 350–355 CrossRef PubMed.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef CAS.
- D. Rigby, H. Sun and B. E. Eichinger, Polym. Int., 1997, 44, 311–330 CrossRef CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- V. Buch, J. Chem. Phys., 1994, 100, 7610–7629 CrossRef CAS.
- A. Gupta, S. Chempath, M. J. Sanborn, L. A. Clark and R. Q. Snurr, Mol. Simul., 2003, 29, 29–46 CrossRef CAS.
- D. Y. Peng and D. B. Robinson, Ind. Eng. Chem. Fundam., 1976, 15, 59–64 CAS.
- O. Talu and A. L. Myers, AIChE J., 2001, 47, 1160–1168 CrossRef CAS.
- H. Frost, T. Duren and R. Q. Snurr, J. Phys. Chem. B, 2006, 110, 9565–9570 CrossRef CAS PubMed.
- S. S. Han, H. Furukawa, O. M. Yaghi and W. A. Goddard, J. Am. Chem. Soc., 2008, 130, 11580–11581 CrossRef CAS PubMed.
- E. Klontzas, E. Tylianakis and G. E. Froudakis, J. Phys. Chem. C, 2008, 112, 9095–9098 CAS.
- J. Palgunadi, H. S. Kim, J. M. Lee and S. Jung, Chem. Eng. Process., 2010, 49, 192–198 CrossRef CAS.
- L. Zhou and Y. P. Zhou, Ind. Eng. Chem. Res., 1996, 35, 4166–4168 CrossRef CAS.
- J. Lan, D. Cao, W. Wang and B. Smit, ACS Nano, 2010, 4, 4225–4237 CrossRef CAS PubMed.
- R. Q. Snurr, A. T. Bell and D. N. Theodorou, J. Phys. Chem., 1993, 97, 13742–13752 CrossRef CAS.
- A. W. C. van den Berg and C. O. Arean, Chem. Commun., 2008, 668–681 RSC.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m space group) and bor (boracite, P
3m space group) and bor (boracite, P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m space group) topology nets are considered to be the most stable.17,32,39 Hence, we designed tapa-COF-3 and tapa-COF-4 with the same chemical monomers with the corresponding ctn and bor net topologies. The optimized structures of the four tapa-COFs are shown in Fig. 2.
3m space group) topology nets are considered to be the most stable.17,32,39 Hence, we designed tapa-COF-3 and tapa-COF-4 with the same chemical monomers with the corresponding ctn and bor net topologies. The optimized structures of the four tapa-COFs are shown in Fig. 2.




![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m space group symmetry and tapa-COF-4 retains the P
3m space group symmetry and tapa-COF-4 retains the P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m space group symmetry. The cell and physical parameters of the four tapa-COF networks are listed in Table 2 and the structure models are shown in Fig. 2. As shown in Table 2, tapa-COF-1 and tapa-COF-2 possess almost the same cell length due to the same dia topology structures and nearly equally sized building units. On the other hand, although having the same build unit, the cell length of tapa-COF-3 is much larger than that of tapa-COF-4, which is attributed to their different space group symmetry. It can be found in Table 2 that all four tapa-COF networks possess very low densities (0.096–0.258 g cm−3), especially tapa-COF-1 and tapa-COF-2 whose densities are nearly the same as water. It is well known that COFs are some of the lowest density COMs. To the best of our knowledge, the lowest densities reported for three-dimensional COFs are COF-108 (0.17 g cm−3) and COF-105 (0.18 g cm−3). Here, the densities of tapa-COF-1 and tapa-COF-2 are even lower than that of COF-108 and COF-105, which shows that the tapa-COFs designed in this work can be ranked amongst the members of COMs with the lowest density.
3m space group symmetry. The cell and physical parameters of the four tapa-COF networks are listed in Table 2 and the structure models are shown in Fig. 2. As shown in Table 2, tapa-COF-1 and tapa-COF-2 possess almost the same cell length due to the same dia topology structures and nearly equally sized building units. On the other hand, although having the same build unit, the cell length of tapa-COF-3 is much larger than that of tapa-COF-4, which is attributed to their different space group symmetry. It can be found in Table 2 that all four tapa-COF networks possess very low densities (0.096–0.258 g cm−3), especially tapa-COF-1 and tapa-COF-2 whose densities are nearly the same as water. It is well known that COFs are some of the lowest density COMs. To the best of our knowledge, the lowest densities reported for three-dimensional COFs are COF-108 (0.17 g cm−3) and COF-105 (0.18 g cm−3). Here, the densities of tapa-COF-1 and tapa-COF-2 are even lower than that of COF-108 and COF-105, which shows that the tapa-COFs designed in this work can be ranked amongst the members of COMs with the lowest density.