Mechanistic outlook on thermal degradation of 1,3-dialkyl imidazolium ionic liquids and organoclays†
Eapen Thomas,
Deepthi Thomas,
Kunduchi Periya Vijayalakshmi* and
Benny Kattikkanal George
Analytical and Spectroscopy Division, Analytical, Spectroscopy and Ceramics Group, Propellants, Polymers, Chemicals and Materials Entity, Vikram Sarabhai Space Centre, Thiruvananthapuram-695022, India. E-mail: vijisura@gmail.com; kp_vijayalakshmi@vssc.gov.in
First published on 11th January 2016
Abstract
The thermal degradation mechanisms of ionic liquids (ILs) 1-butyl-3-methylimidazolium chloride (BMImCl) and 1-butyl-3-methylimidazolium tetrafluoroborate (BMImBF4) have been established using pyrolysis-GC-MS (Py-GC-MS) and B3LYP/6-311+G(d,p) level of density functional theory (DFT). BMImCl decompose through a bimolecular nucleophilic substitution (SN2) while BMImBF4 exhibit SN2 along with a competitive E2 elimination pathway. Activation energy parameters obtained using Kissinger–Akahira–Sunose method and Ozawa–Flynn–Wall method is compared with the computed activation barriers. The montmorillonite based organoclay prepared using these ionic liquids exchange only the cation part ([BMIm]+) into the clay gallery leading to an expansion of d-spacing from 12.08 to 13.64 Å. The organoclay showed the maximum decomposition at 462 °C in the TGA experiment and the decomposition products were identified as methyl imidazole and 1-butene using Py-GC-MS. DFT studies employing a model compound Si(OH)3O− suggested a mechanism involving an imidazole-2-ylidine (carbene) intermediate for the decomposition of [BMIm]+ in the clay. Theoretical results were further supported by 13C NMR analysis of IL in presence of colloidal silica which showed a characteristic carbene NMR signal at 187.6 ppm.
1 Introduction
Ionic liquids (ILs) are a class of novel compounds typically composed of organic cations and inorganic or organic anions. ILs have large liquid ranges determined by their low melting point and high decomposition temperature. The high thermal stability of ILs attracted intense research interest owing to their applications in various fields such as energetic materials,1,2 solvents for organic reactions,3 solvents for cellulose,4 thermal energy storage,5 clay modifiers to form thermally stable polymer composites,6 heat-transfer fluids,7 high-temperature lubricants,8 curing of ionogels9 and as a stationary phase in gas chromatography.10 It is well known that the physical and chemical properties of ILs vary with the choice of anion and cation while thermal stability is often tuned by the choice of anions.For safe application of ILs at elevated temperatures, it is important to understand the degradation mechanism. The nucleophilic attack of the halide at primary alkyl substituents in imidazolium ring is known to be the major degradation pathway in N,N-dialkyl imidazolium halides.11–16 Chowdhury et al.17 showed that imidazolium based ILs decompose at lower temperatures in the presence of nucleophiles. Baranyai et al.18 investigated the thermal decomposition mechanism of 1,3-dialkyl imidazolium bis(trifluoromethylsulfonyl)imide ILs, and suggested degradation of the anion as possible thermal decomposition pathway, but the anion degradation products were not detected. Lazzús19 introduced a group contribution method and Yan et al.20 used quantitative structure property relationship method to predict the thermal decomposition temperature of ILs. Ohtani et al.21 studied decomposition of imidazolium ILs using Py-GC-MS and proposed mechanism based on the products formed. Quantum mechanical tools have also been extensively used to understand the degradation mechanism of compounds.22–26
In spite of the several reports on the thermal stability of ILs,27–30 systematic studies correlating the structural features as well as the degradation mechanism to understand the thermal stability of ILs are scarce. In the present study, the degradation reactions of 1-butyl-3-methylimidazolium chloride (BMImCl), 1-butyl-3-methylimidazolium tetrafluoroborate (BMImBF4) and 1-butyl-3-methylimidazolium modified montmorillonite clay (Clay-BMIm) are analyzed using Py-GC-MS and formation of pyrolysis products are rationalized using density functional theory (DFT). We have proposed a new mechanism for decomposition of 1,3-dialkylimidazolium modified clays in general by taking into consideration of Clay-BMIm. To the best of our knowledge, this is the first report on thermal decomposition mechanism of 1,3-dialkylimidazolium incorporated montmorillonite clay.
2 Methodology
2.1 Materials
BMImCl and BMImBF4 of purity > 99% were procured from M/s Otto Chemie Pvt. Ltd, Mumbai, India. Clay used was sodium montmorillonite (trade name: Cloisite-Na+, CAS no. 1318-93-0, Southern Clay Products, Inc., USA) for the ion exchange modification with ILs. Colloidal silica (30% suspension of SiO2 in water, CAS no. 7631-86-9) was obtained from Sigma-Aldrich.2.2 Functionalization of clay
Standard ion exchange procedures were employed for the functionalization of sodium montmorillonite clay (MMT) with ILs.31 Aqueous suspension of MMT clay (2%) was prepared by sonicating for 10 minutes using Hielscher-UIP1000hd probe sonicator at amplitude of 80%. To this, BMImCl (or BMImBF4, both yield same product Clay-BMIm) was added and the exchange reactions were carried out by sonicating for 15 minutes. It was allowed to settle and filtered. The residue was repeatedly (5–8 times) washed with distilled water until no chloride traces were detected with silver nitrate solution. The residue (modified MMTs) was dried at room temperature for 4 h and then at 100 °C for 2 hour under vacuum. Characterisation of modified clay is included in the (ESI).†2.3 Instrumental
Thermal stability of ILs and Clay-BMIm were studied using Perkin-Elmer, Pyris-1 TGA (Shelton, USA) in He atmosphere at a heating rate of 10 °C min−1. Py-GC-MS studies were carried out using a system consists of a Thermo Electron Trace ultra GC directly coupled to a Thermo Electron PolarisQ (Quadrupole ion trap) mass spectrometer (Thermo Electron Corporation, Waltham, Massachusetts, USA) and SGE pyrolyser (Pyrojector II, SGE Analytical Science Pty Ltd, Ringwood, Victoria, Australia). The GC is equipped with 30 m, 0.25 mm ID capillary column (PDMS with 5% phenyl, SLB-5MS, Supelco). The Py-GC-MS conditions were set with ion source at 200 °C, inlet at 250 °C, transfer line at 280 °C, column temperature programme 40 °C to 250 °C with heating rate of 10 °C min−1. The m/z range used was 20–600 amu and the pyrolysis was carried out at 350 °C and 600 °C. 13C NMR analysis was done using Bruker Avance-III 400 MHz spectrometer operated at 100.2 MHz with power 54 W, pulse width 8.9 μs and D2O as locking solvent.2.4 Computational method
Geometries of gaseous ion pairs of BMImCl, BMImBF4, transition states and products were optimized at B3LYP32 level of DFT using 6-311+G(d,p) basis set as implemented in Gaussian09.33 All the transition states were confirmed by the presence of single imaginary frequency. The single step conversion is further analysed using IRC calculations (ESI†). Molecular electrostatic potential (MESP) derived Merz–Singh–Kollman charge (MK charge)34,35 was computed at the same level of theory. Basis set superposition error corrected binding energy36 for the ion-pairs ([BMIm]+[X]−) was calculated using eqn (1).| [BMIm]+ + [X]− ⇌ [BMIm]+[X]− | (1) |
2.5 Kinetic studies
Kinetic parameters for the thermal decomposition of ILs were calculated using two methods, Kissinger–Akahira–Sunose (KAS) method37–39 and Ozawa–Flynn–Wall (FWO) method.40–42 KAS is a multiple heating rate method and we have selected heating rate of 2, 5, 10 and 15 °C min−1. KAS method is based on the following eqn (2)
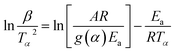 | (2) |
 versus 1/Tα. FWO method for determination of kinetic parameters is based on the assumption that the decomposition obeys first order kinetics using a point of constant conversion from a series of decomposition curves obtained at different heating rates. It helps in calculating the Ea for a desired conversion (eqn (3)).
versus 1/Tα. FWO method for determination of kinetic parameters is based on the assumption that the decomposition obeys first order kinetics using a point of constant conversion from a series of decomposition curves obtained at different heating rates. It helps in calculating the Ea for a desired conversion (eqn (3)).
 | (3) |
3 Results and discussion
3.1 Electronic structure and properties of ion pairs
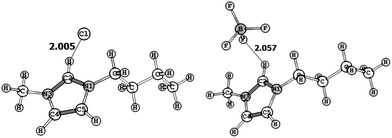
Optimized structures of BMImCl and BMImBF4 at B3LYP/6-311+G(d,p) level of DFT are shown in Fig. 1. In BMImCl, the distances of the C2H⋯Cl (2.005 Å) are much longer than the covalent bond distance of H–Cl (1.31 Å) and shorter than the van der Waals distance of H⋯Cl (2.95 Å). Similarly in BMImBF4, the shortest distance of C2H⋯F between the imidazolium cation and the anion (2.057 Å) are higher than covalent bond distance of H–F (1.07 Å) and smaller than the van der Waals distance of H–F (2.67 Å). The non-covalent binding energy (Eb) computed for ILs are very high, 373.4 kJ mol−1 and 340.2 kJ mol−1 respectively for BMImCl and BMImBF4, indicating strong electrostatic interactions in ion pairs. The geometric features as well as the Eb values of these ion pairs agreed very well with those reported by Dong et al.43 and Fumino et al. at B3LYP/6-31+G(d) level.44 The MK charge can be considered as a measure of charge transfer from the anion to the cation. Higher charge transfer was observed for BMImCl (23%) than BMImBF4 (12%) (Table 1).Generally the stability of a salt system is assessed by the large energy gap between the highest occupied molecular orbital and the lowest unoccupied molecular orbital (HOMO–LUMO gap).45 Since, the charge transfer is more conducive in BMImCl than BMImBF4, the latter with higher HOMO–LUMO gap (6.88 eV) can be considered as a more stable salt than BMImCl, which is further supported by TG analysis.
3.2 TG analysis
Fig. 2 shows the TG curves for BMImCl, BMImBF4 and Clay-BMIm. The higher initial decomposition temperature observed for BMImBF4 (260 °C) compared to BMImCl (180 °C), suggests the role of counter anion on thermal stability of ILs. The maximum decomposition temperatures (Ts) are 297, 427 and 462 °C respectively for BMImCl, BMImBF4 and Clay-BMIm. The differences in the decomposition of selected ILs with different anions and Clay-BMIm, without an anion suggests the possibility of different mechanisms for their thermal decomposition reactions. In Clay-BMIm the weight loss observed between 500 °C and 600 °C was attributed to the dehydroxylation of structural hydroxyl groups.46 | ||
| Fig. 2 TG curves for BMImCl, BMImBF4 and Clay-BMIm in He atmosphere at a heating rate of 10 °C min−1. | ||
Ea for thermal decomposition of BMImCl, BMImBF4 and Clay-BMIm were calculated using KAS method and FWO method (Table 2). The calculated Ea values showed 6% deviation for BMImCl, 8% for BMImBF4 and 9% for Clay-BMIm (ESI†).
| β (°C min−1) | KAS method | FWO method | ||||
|---|---|---|---|---|---|---|
| Ts (°C) | Ea (kJ mol−1) | Ea (kJ mol−1) | ||||
| 2 | 5 | 10 | 15 | |||
| BMImCl | 257 | 285 | 297 | 300 | 101.5 | 107.4 |
| BMImBF4 | 402 | 411 | 427 | 432 | 236.8 | 258.0 |
| Clay-BMIm | 437 | 442 | 462 | 468 | 229.3 | 208.5 |
3.3 Decomposition mechanism
The dealkylation reaction is initiated by the nucleophilic attack of chloride anion at the alkyl group of imidazolium cation which passes through the bimolecular nucleophilic (SN2) transition state. Kroon et al.22 used B3LYP at 6-31G** level to predict the decomposition products of BMImCl. For pathway-I, Ea was 127 kJ mol−1 while for pathway-II, a higher value 136 kJ mol−1 was observed.
Semi quantitative estimation using standard solutions of 1-butylimidazole and 1-methylimidazole shows that 90% of the products are from pathway-1 (ESI†). We have calculated Ea of reaction pathways shown in Scheme 1 at a higher level, B3LYP/6-311+G(d,p) to confirm the product distribution as calculated from Py-GC-MS. Transition states identified and energy profile are shown in Fig. 4.
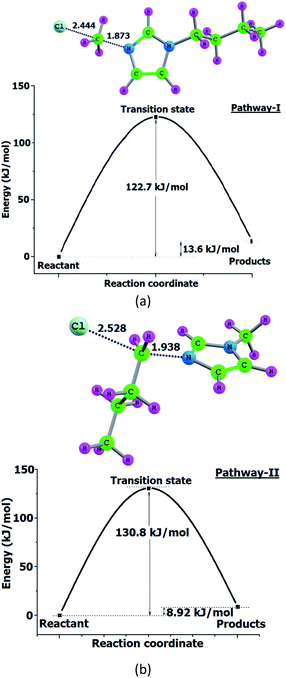 | ||
| Fig. 4 Energy profile and transition states of BMImCl decomposition shown in Scheme 1. (a) Pathway-I and (b) pathway-II. Bond lengths in Å. | ||
Demethylation reaction (pathway-I) proceed with an Ea of 122.7 kJ mol−1 while debutylation reaction proceed with an Ea of 130.8 kJ mol−1 (Fig. 4). These results match with Kroon et al.22 and shows the selectivity for pathway-I even though the Ea differ only by 8 kJ mol−1 and the higher percentage of butylimidazole is accounted. Consequently the net Ea for the reaction was 123.5 kJ mol−1 (Table 3) and experimental values for Ea were 101.5 kJ mol−1 and 107.4 kJ mol−1 calculated using KAS and FWO methods respectively. The results showed a deviation of 13% with FWO method and 18% with KAS method (Table 3). DFT studies also predict that both demethylation and debutylation reactions of BMImCl are endothermic by ∼10 kJ mol−1 and DSC analysis shows endotherm for the same (ESI†).
| Computational study | Experimental | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| SN2(I) | SN2(II) | Avg. Ea (kJ mol−1) | KAS method | FWO method | |||||
| Ea (kJ mol−1) | Rn (%) | Ea (kJ mol−1) | Rn (%) | Ea (kJ mol−1) | Deviation (%) | Ea (kJ mol−1) | Deviation (%) | ||
| BMImCl | 122.7 | 90 | 130.8 | 10 | 123.5 | 101.5 | 17.8 | 107.4 | 13.0 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| E2 | |||||||||
| BMImBF4 | 188.5 | 51 | 237.0 | 49 | 212.1 | 236.8 | 10.4 | 258.0 | 17.8 |
Owing to the steric bulkiness of BF4− compared to Cl−, the SN2 reactions are likely to happen only at the N3–CH3 site (Scheme 2) and it is unambiguous with the presence of butyl imidazole as the major product in the pyrogram.
Differing from BMImCl, the presence of 1-butene in the pyrogram suggests existence of competitive elimination reactions in the thermal decomposition of BMImBF4. Three different elimination mechanism namely bimolecular E2 elimination, internal elimination and elimination via imidazole-2-ylidene (carbene route)47,48 were analyzed by DFT (ESI†) and transition state was identified only for E2 elimination (pathway-II).
Though the intramolecular elimination reactions (Ei) are common in pyrolysis reactions, in the case of BMImBF4 the basicity of the anion overrules and E2 elimination is found to be preferred over Ei route, as the basicity of BF4− anion is insufficient to form the imidazole-2-ylidene which is expected to undergo further abstraction of β-hydrogen to form the pyrolysis products viz. butene and methyl imidazole (ESI†).
Computed activation barrier for the formation of butyl imidazole, (Fig. 6) is 188.5 kJ mol−1 (195 kJ mol−1 by Kroon et al.22 at B3LYP/6-31** level of DFT) and is higher than the corresponding value for BMImCl (122.7 kJ mol−1, Fig. 4, pathway-I). Transition state for E2 elimination was characterized by a four membered ring with breaking of C–N bond at C⋯N distance 2.537 Å and simultaneous β-hydrogen shift. The activation barrier for this reaction was 237 kJ mol−1 (Fig. 6). The experimental values depicted in Table 2 using KAS method (236.8 kJ mol−1), FWO method (258.0 kJ mol−1) and a higher concentration of 1-butene and 1-methylimidazole in the pyrogram suggest the possibility of interplay of both the mechanisms in decomposition of BMImBF4. The ratio of 1-methylimidazole to 1-butylimidazole was determined by a semi quantitative method as in the case of BMImCl and observed both reactions proceed equally (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) (ESI†). The average Ea predicted using DFT was 212.1 kJ mol−1 (Table 3) and the deviation between computed and experimental Ea may be due to the lattice energy change in experiments where ILs in liquid phase are analysed unlike gas phase calculations in computational method. Both the mechanisms discussed are highly endothermic (172–212 kJ mol−1) as shown in Fig. 6 and confirmed using DSC analysis (ESI†).
1) (ESI†). The average Ea predicted using DFT was 212.1 kJ mol−1 (Table 3) and the deviation between computed and experimental Ea may be due to the lattice energy change in experiments where ILs in liquid phase are analysed unlike gas phase calculations in computational method. Both the mechanisms discussed are highly endothermic (172–212 kJ mol−1) as shown in Fig. 6 and confirmed using DSC analysis (ESI†).
Thermal decomposition of Clay-BMIm was analysed using DFT method. MMT clays own a pyrophyllite structure where the trivalent Al-cation in the octahedral layer is partially substituted by the divalent Mg-cation. Consequent negative charge generated in the clay layer is balanced by hydrated sodium ions adsorbed in the interlayer. The interlayer dimension is determined by the crystal structure of the silicate and the d-spacing is ∼1 nm for MMT clay. From the model of MMT clay given in Fig. 8, it is clear that the ions in the interlayer gallery face SiO4 tetrahedral unit as their immediate neighbour.49 In Clay-BMIm sodium ions are replaced by 1-butyl-3-methylimidazolium cation.
 | ||
| Fig. 8 (a) Model structure of MMT clay, (b) Clay-BMIm, (c–h) optimized structures of species involved in decomposition of Clay-BMIm with transition state and energy profile. | ||
A truncated model for the montmorillonite clay showing the interaction of Na+ with oxygen atoms that bridges two silicon centers is presented in Fig. 8(a). The [BMIm]+ could replace the Na+ cation owing to extended interaction of several CH bonds on to the layer dominated by Si–O bonds. Considering the negatively charged character of the clay and the possible CH⋯O–Si interactions from [BMIm]+ to the clay, we propose the use of the anionic moiety Si(OH)3O− to model the decomposition reaction of [BMIm]+ in the clay.
BMIm–Si(OH)3O− ion pair is found to be marginally higher in energy (9.1 kJ mol−1) than the neutral complex of imidazole-2-ylidene–Si(OH)4 (Fig. 8). Therefore the DFT results suggest that the intercalated imidazolium cations can easily form the imidazole-2-ylidene through a barrier less pathway. The singlet carbenes thus formed on heating can undergo elimination reactions involving beta hydrogen shift from the butyl substituent at N1 to the carbenic centre followed by bond breaking at the quaternary nitrogen. Such a transition state was located in the DFT analysis with single imaginary frequency corresponding to the bond shifting process which is shown in Fig. 8(g).
The activation energy for the decomposition was 195.6 kJ mol−1 (Fig. 8(h)) and the reaction is exothermic by 39.9 kJ mol−1 and DSC analysis shows an exotherm for the same (ESI†). The summarized decomposition mechanism is shown in Fig. 9. Anions with high basicity is capable of deprotonating imidazolium cation at C2 position, resulting in the formation of neutral carbon bases with nucleophilic singlet carbenes that are stabilized by the two neighboring nitrogen atoms at the carbenic centre. The formation of carbene from BMIm cation on heating was confirmed by the NMR analysis of BMImCl in D2O solvent in presence of colloidal silica. Colloidal silica is 30% suspension of SiO2 in water, which contains –SiOH species similar to our model compound Si(OH)3O− used in DFT study. 13C NMR spectra of BMImCl and BMImCl with colloidal silica heated at 90 °C for 5 minutes are shown in Fig. 10. The additional NMR signal observed at 187.64 ppm is attributed to singlet carbene carbon in imidazolium ring.
4 Conclusions
Thermal stability of BMImCl and BMImBF4 were compared using TGA and decomposition products were identified using Py-GC-MS experiments. The inherent stability of BMImBF4 is attributed to their very high HOMO–LUMO gap as well as the higher MK charge computed for ion-pair counterparts. Bimolecular nucleophilic substitution reactions are identified to be the lowest energy pathway for decomposition of both the ions pairs. However, BF4− anion facilitates competitive E2 elimination reactions in imidazolium based ILs. The extend of reactions were calculated from Py-GC-MS and DFT results. Demethylation reaction of BMImCl constitutes 90% of the reaction. Decomposition of BMImBF4 proceeds with 50% demethylation and 50% elimination reaction. For the first time the thermal degradation of ionic liquid modified clay was elucidated using DFT and experimentally rationalized using Py-GC-MS and 13C-NMR experiments.Abbreviations
| IL | Ionic liquid |
| [BMIm]+ | 1-Butyl-3-methylimidazolium cation |
| BMImCl | 1-Butyl-3-methylimidazolium chloride |
| BMImBF4 | 1-Butyl-3-methylimidazolium tetrafluoroborate |
| MMT | Montmorillonite clay |
| Clay-BMIm | Clay modified with ILs |
| DFT | Density functional theory |
| [BF4]− | Tetrafluoroborate anion |
| Ea | Activation energy |
| Eb | Binding energy |
| Ts | Maximum decomposition temperature |
| HOMO | Highest occupied molecular orbital |
| LUMO | Lowest unoccupied molecular orbital |
| ΔE* | Energy gap between the HOMO and LUMO |
| MK charge | Merz–Singh–Kollman charge |
| KAS | Kissinger–Akahira–Sunose method |
| FWO | Osawa–Flynn–Wall method |
Acknowledgements
The authors thank Director, Vikram Sarabhai Space centre for granting permission to publish this work. One of the authors (ET) thanks Indian Space Research Organization for providing research fellowship. The authors also thank Dr Suresh C. H., CSIR-National Institute for Interdisciplinary Science and Technology, Trivandrum for his valuable comments.References
- E. Sebastiao, C. Cook, A. Hu and M. Murugesu, J. Mater. Chem. A, 2014, 2, 8153–8173 CAS.
- E. Thomas, K. P. Vijayalakshmi and B. K. George, RSC Adv., 2015, 5, 71896–71902 RSC.
- R. H. Wang, C. M. Jin, B. Twamley and J. M. Shreeve, Inorg. Chem., 2006, 45, 6396–6403 CrossRef CAS PubMed.
- F. Wendler, L. N. Todi and F. Meister, Thermochim. Acta, 2012, 528, 76–84 CrossRef CAS.
- L. Bai, X. Li, J. Zhu and B. Chen, Energy Fuels, 2011, 25, 1811–1816 CrossRef CAS.
- J. Gilman, W. H. Awad, R. D. Davis, J. Shields, R. H. Harris, C. Davis, A. B. Morgan, T. E. Sutto, J. Callahan, P. C. Trulove and H. C. DeLong, Chem. Mater., 2002, 14, 3776–3785 CrossRef CAS.
- E. B. Fox, A. E. Visser, N. J. Bridges and J. W. Amoroso, Energy Fuels, 2013, 27, 3385–3393 CrossRef CAS.
- Z. Zeng, B. S. Phillips, J. C. Xiao and J. M. Shreeve, Chem. Mater., 2008, 20, 2719–2726 CrossRef CAS.
- J. L. Bideau, L. Viau and A. Vioux, Chem. Soc. Rev., 2011, 40, 907–925 RSC.
- Z. Breitbach and D. Armstrong, Anal. Bioanal. Chem., 2008, 390, 1605–1617 CrossRef CAS PubMed.
- H. L. Ngo, K. LeCompte, L. Hargens and A. B. McEwen, Thermochim. Acta, 2000, 357–358, 97–102 CrossRef CAS.
- T. Erdmenger, J. Vitz, F. Wiesbrock and U. S. Schubert, J. Mater. Chem., 2008, 18, 5267–5273 RSC.
- A. G. Glenn and P. B. Jones, Tetrahedron Lett., 2004, 45, 6967–6969 CrossRef CAS.
- L. Bai, X. Li, J. Zhu and B. Chen, Energy Fuels, 2011, 25, 1811–1816 CrossRef CAS.
- C. Maton, N. D. Vos and C. V. Stevens, Chem. Soc. Rev., 2013, 42, 5963–5977 RSC.
- K. R. J. Lovelock, J. P. Armstrong, P. Licence and R. G. Jones, Phys. Chem. Chem. Phys., 2014, 16, 1339–1353 RSC.
- A. Chowdhury and S. T. Thynell, Thermochim. Acta, 2006, 443, 159–172 CrossRef CAS.
- K. J. Baranyai, G. B. Deacon, D. R. MacFarlane, J. M. Pringle and J. L. Scott, Aust. J. Chem., 2004, 57, 145–147 CrossRef CAS.
- J. A. Lazzús, J. Mol. Liq., 2012, 168, 87–93 CrossRef.
- F. Yan, S. Xia, Q. Wang and P. Ma, J. Chem. Eng. Data, 2012, 57, 805–810 CrossRef CAS.
- H. Ohtani, S. Ishimura and M. Kumai, Anal. Sci., 2008, 24, 1335–1340 CrossRef CAS PubMed.
- M. C. Kroon, W. Buijs, C. J. Peters and G. J. Witkamp, Thermochim. Acta, 2007, 465, 40–47 CrossRef CAS.
- S. Reshmi, K. P. Vijayalakshmi, D. Thomas, B. K. George and C. P. Reghunadhan Nair, J. Anal. Appl. Pyrolysis, 2013, 104, 603–608 CrossRef CAS.
- Z. Xue, Y. Zhang, X. Zhou, Y. Cao and T. Mu, Thermochim. Acta, 2014, 578, 59–67 CrossRef CAS.
- P. Ballone and R. C. Huerto, Faraday Discuss., 2012, 154, 373–389 RSC.
- Y. Hao, J. Peng, S. Hu, J. Li and M. Zhai, Thermochim. Acta, 2010, 501, 78–83 CrossRef CAS.
- Y. Cao and T. Mu, Ind. Eng. Chem. Res., 2014, 53(20), 8651–8664 CrossRef CAS.
- W. H. Awad, J. W. Gilman, M. Nyden, R. H. Harris, T. E. Sutto, J. Callahan, P. C. Trulove, H. C. DeLong and D. M. Fox, Thermochim. Acta, 2004, 409, 3–11 CrossRef CAS.
- C. P. Fredlake, J. M. Crosthwaite, D. G. Hert, S. N. V. K. Aki and J. F. Brennecke, J. Chem. Eng. Data, 2004, 49, 954–964 CrossRef CAS.
- M. E. Van Valkenburg, R. L. Vaughn, M. Williams and J. S. Wilkes, Thermochim. Acta, 2005, 425, 181–188 CrossRef CAS.
- L. B. de Paiva, A. R. Morales and F. R. V. Diaz, Appl. Clay Sci., 2008, 42, 8–24 CrossRef.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.1, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145 CrossRef CAS.
- B. H. Besler, K. M. Merz Jr. and P. A. Kollman, J. Comput. Chem., 1990, 11, 431–439 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- H. Tanaka, Thermochim. Acta., 1995, 267, 29–44 CrossRef CAS.
- S. Vyazovkin, K. Chrissafis, M. L. Di Lorenzo, N. Koga, M. Pijolat and B. Roduit, Thermochim. Acta, 2014, 590, 1–23 CrossRef CAS.
- B. V. L'Vov, Spectrochim. Acta, Part B, 2011, 66(7), 557–564 CrossRef.
- ASTM, Standard Test Method for Decomposition Kinetics by Thermogravimetry, E-1641–1699.
- T. Ozawa, Bull. Chem. Soc. Jpn., 1965, 88, 1881–1886 CrossRef.
- J. H. Flynn and L. A. wall, Polym. Lett., 1966, 4, 323–328 CrossRef CAS.
- K. Dong, S. Zhang, D. Wang and X. Yao, J. Phys. Chem. A, 2006, 110, 9775–9782 CrossRef CAS PubMed.
- K. Fumino, A. Wulf and R. Ludwig, Phys. Chem. Chem. Phys., 2009, 11, 8790–8794 RSC.
- G. Zhao and M. Lu, J. Mol. Model., 2012, 16, 2443–2451 CrossRef PubMed.
- P. Singla, R. Mehta and S. N. Upadhyay, Green Sustainable Chem., 2012, 2, 21–25 CrossRef CAS.
- O. Holloczki, D. Gerhard, K. Massone, L. Szarvas, B. Nemeth, T. Veszpremi and L. Nyulaszi, New J. Chem., 2010, 34, 3004–3009 RSC.
- E. A. Turner, C. C. Pye and R. D. Singer, J. Phys. Chem. A, 2003, 107, 2277–2288 CrossRef CAS.
- S. Cadars, R. Guegan, M. N. Garaga, X. Bourrat, L. L. Forestier, F. Fayon, T. V. Huynh, T. Allier, Z. Nour and D. Massiot, Chem. Mater., 2012, 24, 4376–4389 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra24907d |
| This journal is © The Royal Society of Chemistry 2016 |