Modification of abandoned fine blue-coke: optimization study on removal of p-nitrophenol using response surface methodology
Fengyu Wei*,
Bo Wu,
Jincheng Zhang and
Wanting Zhang
School of Chemistry and Chemical Engineering, Hefei University of Technology, Hefei 230009, China. E-mail: weifyliuj@hfut.edu.cn; Fax: +86 551 62901450; Tel: +86 551 62901548
First published on 26th January 2016
Abstract
Abandoned fine blue-coke was modified with a physicochemical method including nitric acid (HNO3) treatment and nitrogen gas (N2) calcination, and used as an adsorbent for p-nitrophenol (PNP) removal. The preparation process was optimized to improve the adsorption ability based on the 2IV6–2 fractional factorial design, steepest ascending method and the Box–Behnken design (BBD) of the response surface methodology (RSM) technique. The significant factors on each experimental design response were identified by means of analysis of variance (ANOVA). The predicted adsorption capacity of PNP on MFBC was found to agree with the experimental values. The optimum experimental conditions were as follows: HNO3 concentration: 4.46 mol L−1, modification temperature: 87.8 °C, modification time: 20.3 h, impregnation ratio of HNO3 to MFBC: 10 mL/1 g, calcination time: 2 h, and calcination temperature: 716 °C. Moreover, surface roughness of the MFBC was found to increase obviously after the modification by FESEM and HRTEM analysis, and the total pore volume and specific surface area increased by 0.8 and 1.2 times, respectively. The PNP equilibrium adsorption capacity of MFBC was found to be 156.9 mg g−1 at 328 K, which highlights its potential application in wastewater treatment.
1. Introduction
p-Nitrophenol (PNP) as a toxic substance is widely present in the wastewater of chemical, medicine, pesticide, dye and washing industries.1 It has strong stimulation to the skin and can be absorbed through skin and digestive tract.2,3 The adsorption method has been widely adopted to treat phenolic wastewater due to its good treatment effect.4 Among the adsorbents, activated carbons are widely used because of their high adsorption capacity.5 However, their high cost limits the wide application in the field of wastewater treatment.6 Recently, many researchers have tried to prepare low-cost adsorbents using industrial and agricultural by-products, such as abandoned tea,1 coconut husks,7 bagasse,8 etc. However, these raw materials are hard to collect and a carbonization process is necessary in the preparation, resulting in a low yield, which is not suitable for industrial production. Therefore, cheap, high-yield, and efficient adsorbents are developed for the treatment of phenolic wastewater.Fine blue-coke, with a particle size of less than 6 mm, is a by-product of coal pyrolysis, produced at a relatively low temperature (600–700 °C).9,10 It is mostly disposed as low-grade fuel material or abandoned in rivers and fields since it cannot meet the iron alloy, ferrosilicon, silicon carbide, or calcium carbide production requirements.10,11 The investigation revealed that millions of tons of fine blue-coke are abandoned annually in China, which accounts for about 10% of the total blue-coke.12 This not only causes the waste of large amounts of energy, but also heavy contamination of the environment. On account of their high carbon content and certain pore size distributions, if modified moderately, fine blue-coke will possess a relatively large specific surface area and thus can be recognized as a potential adsorption material.
Currently, many physical and chemical activation methods are employed to modify blue-coke, which is specially used as the catalyst carrier for desulfurization and denitrification.13–15 However, it is not reported in the literature that the modified fine blue-coke was directly used for wastewater treatment.9 In our previous work, it was found that fine blue-coke can adsorb phenol and p-nitrophenol and the adsorption capacity was increased significantly after nitric acid treatment and subsequent high temperature modification.16 The objectives of this research are to use abandoned fine blue-coke as a raw material to produce adsorbents for the treatment of PNP in wastewater. The operating conditions of the modification process are determined, which influence the type and distribution of the surface functional groups and the adsorption capacity of fine blue-coke for various substances. Response surface methodology (RSM) was adopted to optimize the modification process for abandoned fine blue-coke in this work, as it is a useful experimental design method to study two or more variables including the effect of their interaction on the response value.17 This research provides an environmentally friendly method to remove PNP using abandoned fine blue-coke as an adsorbent, which has a potential application in other phenolic wastewater treatments.
2. Materials and methods
2.1 Preparation of modified fine blue-coke
Shenmu fine blue-coke (FBC) was selected as a raw material and obtained from Yulin City, Shanxi Province, China. The FBC was firstly washed with warm water and subsequently dried at 105 °C for 24 h to remove surface dirt and other impurities. The dried FBC was crushed and sieved to fewer than 100 meshes. The samples obtained were then mixed and reacted with a nitric acid aqueous solution at a certain ratio of HNO3 to FBC. The mixture was filtered. The solid was dried at 105 °C and heated at different temperatures for different times under the protection of nitrogen in a tube furnace, then cooled to room temperature. The modified fine blue-coke (MFBC) was thus obtained and kept in a hermetic bottle for subsequent use.2.2 Adsorption studies
For batch adsorption studies, 250 mg of MFBC was mixed with 50 mL PNP aqueous solutions of 400 mg L−1 initial concentration in a set of 100 mL Erlenmeyer flasks. The pH of the solution was natural without any pH adjustment. The mixture was agitated at 200 rpm at 25 °C for 4 h until equilibrium was reached. The concentrations of PNP in the supernatant solutions before and after adsorption were determined using a double beam UV-vis spectrophotometer (722S, China) at its maximum absorption wavelength of 400 nm. The PNP uptake at equilibrium, qe (mg g−1), was calculated using eqn (1):
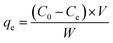 | (1) |
2.3 Design of experiments
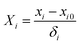 | (2) |
| Factor | Code | Units | Coded variable levels | ||
|---|---|---|---|---|---|
| −1 | 0 | +1 | |||
| CHNO3 | x1 | mol L−1 | 0.1 | 1.55 | 3 |
| Tm | x2 | °C | 25 | 57.5 | 90 |
| tm | x3 | h | 3 | 13.5 | 24 |
| IR | x4 | mL g−1 | 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
12.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
| TC | x5 | °C | 400 | 550 | 700 |
| tc | x6 | h | 0.5 | 2.25 | 4 |
The experimental design, data analysis and modeling were performed by Design-Expert 8.0.6. Its statistical significance was determined by an F-test and the significance of the regression coefficients was analyzed by a t-test. The model obtained is expressed as eqn (3).18 From the regression analysis, the significant variables (p < 0.05) were considered to have a greater impact on the PNP uptake and were screened out to conduct the next experiments.
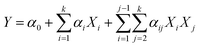 | (3) |
| N = 2n + 2n + cp = 24 + 2 × 4 + 3 = 27 | (4) |
 | (5) |
| Factor | Code | Units | Coded variable levels | ||
|---|---|---|---|---|---|
| −1 | 0 | +1 | |||
| CHNO3 | x1 | mol L−1 | 3 | 3.73 | 4.46 |
| Tm | x2 | °C | 72.6 | 80.2 | 87.8 |
| tm | x3 | h | 18.1 | 20.5 | 22.8 |
| TC | x5 | °C | 692 | 763 | 834 |
2.4 Characteristics
A field emission scanning electron microscopy (FESEM) instrument (SU8020, Japan) was employed to estimate the surface morphology of the raw material and MFBC at an accumulation voltage of 5 kV with 20 K and 100 K magnification. A high-resolution transmission electron microscopy (HRTEM) unit (JEM-2100F, Japan) was employed to intuitively depict the microstructure and morphology of the raw material and MFBC. A specific surface area and porosity analyzer (Coulter SA3100, America) was employed to determine the surface area, pore volume and pore size distribution of the raw material and MFBC. Prior to analysis, the sample was degassed at 200 °C in a vacuum condition for a period of at least 2 h. The nitrogen adsorption isotherm was measured over a relative pressure (P/P0) range from approximately 10−7 to 1. The BET surface area was calculated from the isotherms using the Brunauer–Emmett–Teller (BET) equation. The total pore volume was calculated from the nitrogen adsorption data as the volume of liquid nitrogen at a relative pressure of approximately 0.99 to 1.223. Results and discussion
3.1 2IV6–2 fractional factorial design
According to the preliminary single-factor investigation results of nitric acid concentration (CHNO3, mg L−1), modification temperature (Tm, °C), modification time (tm, h), impregnation ratio of HNO3 to FBC (IR, mL g−1), calcination temperature (TC, °C) and calcination time (tc, h), the independent variables and their coded levels are shown in Table 1. The 16 experimental runs and results of the 2IV6–2 fractional factorial design are shown in Table 3.| Run | Modification variables | PNP uptake qe (mg g−1) | |||||
|---|---|---|---|---|---|---|---|
| CHNO3 (mol L−1) | Tm (°C) | tm (h) | IR (mL g−1) | TC (°C) | tc (h) | ||
| 1 | 3(+1) | 90(+1) | 3(−1) | 5(−1) | 400(−1) | 4(+1) | 15.3 |
| 2 | 3(+1) | 25(−1) | 24(+1) | 5(−1) | 400(−1) | 4(+1) | 13.5 |
| 3 | 0.1(−1) | 25(−1) | 24(+1) | 5(−1) | 700(+1) | 4(+1) | 14 |
| 4 | 0.1(−1) | 25(−1) | 24(+1) | 20(+1) | 700(+1) | 0.5(−1) | 15.4 |
| 5 | 3(+1) | 25(−1) | 3(−1) | 20(+1) | 700(+1) | 4(+1) | 33.2 |
| 6 | 3(+1) | 90(+1) | 24(+1) | 5(−1) | 700(+1) | 0.5(−1) | 63.2 |
| 7 | 3(+1) | 25(−1) | 24(+1) | 20(+1) | 400(−1) | 0.5(−1) | 15.1 |
| 8 | 3(+1) | 90(+1) | 24(+1) | 20(+1) | 700(+1) | 4(+1) | 70.9 |
| 9 | 3(+1) | 90(+1) | 3(−1) | 20(+1) | 400(−1) | 0.5(−1) | 17.2 |
| 10 | 3(+1) | 25(−1) | 3(−1) | 5(−1) | 700(+1) | 0.5(−1) | 30.2 |
| 11 | 0.1(−1) | 90(+1) | 24(+1) | 5(−1) | 400(−1) | 0.5(−1) | 11.3 |
| 12 | 0.1(−1) | 90(+1) | 3(−1) | 5(−1) | 700(+1) | 4(+1) | 14.1 |
| 13 | 0.1(−1) | 25(−1) | 3(−1) | 5(−1) | 400(−1) | 0.5(−1) | 10.7 |
| 14 | 0.1(−1) | 90(+1) | 3(−1) | 20(+1) | 700(+1) | 0.5(−1) | 13.3 |
| 15 | 0.1(−1) | 25(−1) | 3(−1) | 20(+1) | 400(−1) | 4(+1) | 10.7 |
| 16 | 0.1(−1) | 90(+1) | 24(+1) | 20(+1) | 400(−1) | 4(+1) | 11.2 |
According to the data listed in Table 3, the statistical software Design-Expert version 8.0.6 was used to get the significance of each factor analysis and regression model analysis of variance. The results are shown in Table 4.
| Source | Sum of squares | Degree of freedom | Mean square | F-value | p-Valueb Prob > F |
|---|---|---|---|---|---|
| a R-Square value = 0.9947.b Significant at the 5% level. | |||||
| Model | 5194.30 | 13 | 399.56 | 218.27 | 0.0046 |
| X1 | 1558.28 | 1 | 1558.28 | 851.23 | 0.0012 |
| X2 | 339.4806 | 1 | 339.4806 | 185.4452 | 0.0053 |
| X3 | 305.3756 | 1 | 305.3756 | 166.815 | 0.0059 |
| X4 | 13.50563 | 1 | 13.50563 | 7.377603 | 0.1130 |
| X5 | 1393.156 | 1 | 1393.156 | 761.0273 | 0.0013 |
| X6 | 2.640625 | 1 | 2.640625 | 1.442472 | 0.3527 |
| X1X2 | 356.2656 | 1 | 356.2656 | 194.6142 | 0.0051 |
| X1X3 | 253.6056 | 1 | 253.6056 | 138.535 | 0.0071 |
| X1X4 | 11.73063 | 1 | 11.73063 | 6.407989 | 0.1270 |
| X1X5 | 953.2656 | 1 | 953.2656 | 520.7323 | 0.0019 |
| X1X6 | 3.900625 | 1 | 3.900625 | 2.130761 | 0.2818 |
| X2X4 | 0.455625 | 1 | 0.455625 | 0.24889 | 0.6673 |
| X2X6 | 2.640625 | 1 | 2.640625 | 1.442472 | 0.3527 |
| Residual | 3.66 | 2 | 1.83 | ||
| Cor total | 5197.96 | 15 | |||
As can be seen from Table 4, the fitting regression of the model was significant (P < 0.05). The determination coefficient of the model R2 was 0.9947, which means that the regression model and the actual values fitted well. According to the P-value of each independent variable, the nitric acid concentration x1, modification temperature x2, modification time x3 and calcination temperature x5 were the most significant factors for the response value (P < 0.05). The remaining main factors, impregnation ratio of HNO3 to MBC x4 and calcination time x6 were not significant (P > 0.05). On this basis, the nitric acid concentration, modification temperature, modification time and calcination temperature were picked out to conduct further investigation in the next step. The simplified model fitting equation after removal of insignificant factors is obtained as follows:
| Y = 22.456 + 9.869X1 + 4.606X2 + 4.369X3 + 9.331X5 + 4.719X1X2 + 3.981X1X3 + 7.719X1X5 | (6) |
3.2 The steepest ascending method
According to the regression eqn (6) of the 2IV6–2 fractional factorial design model, the fastest rising route direction was obtained as follows:
 | (7) |
Set the center (0, 0, 0, 0) of the 2IV6–2 fractional factorial design as a starting point, and it can be obtained that ∇f = (9.869, 4.606, 4.369, 9.331). X1 was chosen as the standard because its coefficient was bigger. One basal increment (Δ) of CHNO3 (x1) was defined as 0.73 mol L−1. X2, X3, and X5 also increased as the following proportion:
 | (8) |
The design of the steepest ascent path experiment and corresponding results are listed in Table 5. It can be seen from Table 5 that the response value exhibited an increasing tendency from the center to step 3, but all steps beyond this point resulted in a decrease. Therefore, the optimal region of the response value qe was near this point. And the next BBD should select this point as the central level (x1 = 3.73, x2 = 80.2, x3 = 20.5, x5 = 763).
| Steps | Coded variables | Natural variables | Response qe (mg g−1) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X5 | x1 | x2 | x3 | x5 | ||
| Δ | 0.5 | 0.233 | 0.221 | 0.473 | 0.73 | 7.6 | 2.3 | 71 | |
| Center | 0 | 0 | 0 | 0 | 1.55 | 57.5 | 13.5 | 550 | 24.2 |
| Center + Δ | 0.5 | 0.233 | 0.221 | 0.473 | 2.28 | 65.1 | 15.8 | 621 | 40.4 |
| Center + 2Δ | 1 | 0.466 | 0.442 | 0.946 | 3 | 72.6 | 18.1 | 692 | 57.6 |
| Center + 3Δ | 1.5 | 0.699 | 0.663 | 1.419 | 3.73 | 80.2 | 20.5 | 763 | 70.2 |
| Center + 4Δ | 2 | 0.922 | 0.884 | 1.892 | 4.46 | 87.8 | 22.8 | 834 | 69.3 |
| Center + 5Δ | 2.5 | 1.155 | 1.105 | 2.365 | 5.19 | 95.4 | 25.1 | 905 | 60.4 |
In this experiment, the response value qe was remarkably improved, implying that the steepest ascending method was an efficient and effective technique to approximate the optimal conditions.19
3.3 The Box–Behnken design
| Y = 71.80 + 5.13X1 + 9.17X2 − 0.57X3 − 7.38X5 + 0.55X12 − 2.53X22 − 4.31X32 − 6.14X52 − 3.67X1X2 − 1.35X1X2 + 0.55X1X5 + 2.30X2X3 + 3.40X2X5 + 3.20X3X5 | (9) |
| Run | Modification variables | PNP uptake qe (mg g−1) | |||
|---|---|---|---|---|---|
| CHNO3 (mol L−1) | Tm (°C) | tm (h) | TC (°C) | ||
| 1 | 4.46(+1) | 72.6(−1) | 20.45(0) | 763(0) | 69.6 |
| 2 | 3.73(0) | 72.6(−1) | 20.45(0) | 692(−1) | 68.6 |
| 3 | 3(−1) | 80.2(0) | 22.8(+1) | 763(0) | 66.5 |
| 4 | 3.73(0) | 87.8(+1) | 22.8(+1) | 763(0) | 76.9 |
| 5 | 3.73(0) | 72.6(−1) | 22.8(+1) | 763(0) | 47.7 |
| 6 | 3.73(0) | 87.8(+1) | 20.45(0) | 692(−1) | 77.6 |
| 7 | 3.73(0) | 80.2(0) | 22.8(+1) | 834(+1) | 57.4 |
| 8 | 4.46(+1) | 80.2(0) | 20.45(0) | 692(−1) | 78.8 |
| 9 | 3.73(0) | 72.6(−1) | 20.45(0) | 834(+1) | 45.4 |
| 10 | 3.73(0) | 80.2(0) | 20.45(0) | 763(0) | 72 |
| 11 | 3.73(0) | 72.6(−1) | 18.1(−1) | 763(0) | 56.2 |
| 12 | 3.73(0) | 87.8(+1) | 20.45(0) | 834(+1) | 68 |
| 13 | 4.46(+1) | 87.8(+1) | 20.45(0) | 763(0) | 76.9 |
| 14 | 3.73(0) | 80.2(0) | 18.1(−1) | 692(−1) | 69.6 |
| 15 | 3.73(0) | 80.2(0) | 22.8(+1) | 692(−1) | 61.7 |
| 16 | 3.73(0) | 80.2(0) | 20.45(0) | 763(0) | 72.9 |
| 17 | 3(−1) | 80.2(0) | 20.45(0) | 834(+1) | 51.1 |
| 18 | 4.46(+1) | 80.2(0) | 18.1(−1) | 763(0) | 75.8 |
| 19 | 3(−1) | 87.8(+1) | 20.45(0) | 763(0) | 75.3 |
| 20 | 3(−1) | 72.6(−1) | 20.45(0) | 763(0) | 53.3 |
| 21 | 3.73(0) | 80.2(0) | 18.1(−1) | 834(+1) | 52.5 |
| 22 | 3(−1) | 80.2(0) | 20.45(0) | 692(−1) | 69.4 |
| 23 | 4.46(+1) | 80.2(0) | 20.45(0) | 834(+1) | 62.7 |
| 24 | 3(−1) | 80.2(0) | 18.1(−1) | 763(0) | 61.8 |
| 25 | 4.46(+1) | 80.2(0) | 22.8(+1) | 763(0) | 75.1 |
| 26 | 3.73(0) | 87.8(+1) | 18.1(−1) | 763(0) | 76.2 |
| 27 | 3.73(0) | 80.2(0) | 20.45(0) | 763(0) | 70.5 |
Coefficients with one factor represent the effect of the particular factor, while coefficients with two factors and those with second-order terms represent the interaction between the two factors and a quadratic effect, respectively. The positive sign in front of the terms indicates a synergistic effect, whereas a negative sign indicates an antagonistic effect.6
The adequacy of the models was further justified by the analysis of variance (ANOVA). The results of the ANOVA for the quadratic model are listed in Table 7. The model F-value of 14.44 and low p-value < 0.0001 indicate that the model was significant.23 The small F-values of 9.70 and high P-values of 0.0970 obtained for the lack-of-fit for qe were found to be non-significant which further verifies that the quadratic model is statistically valid.
| Source | Sum of squares | Degree of freedom | Mean square | F-value | p-Valueb Prob > F |
|---|---|---|---|---|---|
| a R-Square = 0.9440, Adj R-squared = 0.8786, Pred R-squared = 0.6813.b Significant at the 5% level. | |||||
| Model | 2451.97 | 14 | 175.14 | 14.44 | < 0.0001 |
| X1 | 315.19 | 1 | 315.19 | 25.99 | 0.0003 |
| X2 | 1010.17 | 1 | 1010.17 | 83.30 | < 0.0001 |
| X3 | 3.85 | 1 | 3.85 | 0.32 | 0.5833 |
| X5 | 654.16 | 1 | 654.16 | 53.95 | < 0.0001 |
| X1X2 | 54.02 | 1 | 54.02 | 4.45 | 0.0565 |
| X1X3 | 7.29 | 1 | 7.29 | 0.60 | 0.4531 |
| X1X4 | 1.21 | 1 | 1.21 | 0.100 | 0.7575 |
| X2X3 | 21.16 | 1 | 21.16 | 1.74 | 0.2111 |
| X2X4 | 46.24 | 1 | 46.24 | 3.81 | 0.0746 |
| X3X4 | 40.96 | 1 | 40.96 | 3.38 | 0.0910 |
| X12 | 1.61 | 1 | 1.61 | 0.13 | 0.7216 |
| X22 | 34.00 | 1 | 34.00 | 2.80 | 0.1199 |
| X32 | 99.19 | 1 | 99.19 | 8.18 | 0.0144 |
| X42 | 200.90 | 1 | 200.90 | 16.57 | 0.0016 |
| Residual | 145.52 | 12 | 12.13 | ||
| Lack of fit | 142.58 | 10 | 14.26 | 9.70 | 0.0970 |
| Pure error | 2.94 | 2 | 1.47 | ||
| Cor total | 2597.49 | 26 | |||
The quality of the model developed was evaluated based on the correlation coefficient R2 value. In fact, the developed model seems to be the best at a low standard deviation and high R2 statistics (closer to 1) as it will give the predicted value closer to the actual value for the responses.24 Fig. 1 shows the correlation of the experimental and predicted values of PNP uptake (qe). Good agreement between the actual and predicted values of PNP uptake was confirmed by high values of the coefficient of determination R2 (0.9440) and the adjusted R2 (0.8786). The value of the adjusted R2 suggested that the total variation of 87.86% qe was attributed to the independent variables and only about 12.14% of the total variation cannot be explained by the model. On the basis of these findings, it can be concluded that the model can be applied for further analysis of the effect of the process variables.23
The effect of the nitric acid concentration on the PNP uptake of MBFC is shown in Fig. 2(a)–(c). When the modification temperature, modification time and calcination temperature were fixed at the zero level, the PNP uptake generally increased with the nitric acid concentration increasing from 3 mol L−1 to 4.46 mol L−1. The results were in agreement with the work of Qiu et al.25 which reported that the adsorption amount of the MCs toward BT and DBT increased obviously by increasing the concentration of nitric acid from 35% to 85%. Nitric acid is a typical modifier used for the surface modification of coal-based adsorbents. Shim et al.26 found that nitric acid oxidation treatment gives rise to a large increase in the amount of carbon surface oxide groups such as carboxyl, lactone and anhydride. Most of these acidic groups would be decomposed into basic groups such as hydroxyl, carbonyl, and quinone during the calcination step.27 Haydar et al.28 suggested that an adsorption mechanism of carbon toward PNP involved an interaction between some basic groups located in the graphene layers and the aromatic ring of PNP. Based on the literature, the increase of PNP uptake with nitric acid concentration in our work might be due to the increase of oxygen-containing groups after the oxidative modification, which could be beneficial to the PNP uptake.
As shown in Fig. 2(a), (d) and (e), when the nitric acid concentration, modification time and calcination temperature were fixed at the zero level, the PNP uptake increased on increasing the modification temperature from 72.6 °C to 87.8 °C. As the modification temperature increased to about 80 °C, a great deal of bubbles appeared in the experiment. This phenomenon might be ascribed to the fact that with increasing modification temperature, the reaction between nitric acid and ash impurities such as calcium carbonate in the pores of FBC was accelerated. The impurities inside the pores of FBC were effectively removed, which was beneficial to the PNP uptake of MFBC. Additionally, the increment in temperature might be conducive to the formation of oxygen-containing groups on the MFBC surface, which contributes to a significant increase in the PNP uptake of MFBC after a further calcination step. Qiu et al.25 found that the densities of the oxygen-containing groups on the MCs and the adsorption desulfurization rate increased when the nitric acid oxidation temperature increased from 60 °C to 80 °C.
The effect of modification time on the PNP uptake of MBFC is shown in Fig. 2(b), (d) and (f). As shown in Fig. 2(b), (d) and (f), when the nitric acid concentration, modification temperature and calcination temperature were fixed at the zero level, the PNP uptake firstly increased with the modification time increasing from 18.1 h to 20 h, and then an invariant tendency appeared after 20 h. The modification time was analyzed to be a significant factor in the 2IV6–2 fractional factorial experiment, however, this variable became an insignificant factor in the BBD experiment. This was because in the 2IV6–2 fractional factorial experiment, the large span of modification time ranged from 3 h to 24 h, which had a greater influence on the PNP uptake. On the other hand, in the BBD experiment, the modification time changed from 18.1 h to 22.8 h and the variation range was relatively narrow, resulting in a slighter effect on PNP uptake compared to the other factors. The modification time was thus determined as an insignificant factor in the BBD experiment. However, considering its significant quadratic term examination, it cannot be ignored in equation fitting. The effect of modification time on the PNP uptake was also attributed to the increase in the densities of oxygen-containing groups on MFBC with the increase of modification time.25
As can be seen from Fig. 2(c), (e) and (f), when the nitric acid concentration, modification temperature and modification time were fixed at the zero level, the PNP uptake firstly increased with the calcination temperature increasing from 692 °C to 720 °C, and then exhibited an obviously decreasing tendency above 720 °C. Aber et al.29 also reported that the adsorption ability of the ACF samples increases when the activation temperature increases until 700 °C and then decreases after a further increase in activation temperature. This was perhaps due to the opening of pores of MFBC and an increase of the number of micropores with calcination temperature increasing, but the micropores widen to become mesopores when the temperature continued to increase as Sudaryanto et al.30 reported, which might lead to a decrease of the PNP uptake when the calcination temperature was above 720 °C in this work. On the other hand, Liu et al.27 found that the calcination process resulted in the destruction of most of the acidic groups to form basic groups, which was also beneficial to the PNP uptake. Nian et al.31 reported that oxygen functional groups on an activation carbon surface such as carboxyl, anhydride and lactone groups would be desorbed as CO2 while hydroxyl, carbonyl and quinone groups would be desorbed as CO during a thermal treatment process in an inert environment. The increase in temperature also caused the CO2 and CO to further gasify the carbon, leading to widening of the pores. However, when the calcination temperature was above 750 °C, the majority of the oxygen functional groups including these basic groups would be desorbed as CO2 and CO,31 which led to a decrease of the PNP uptake when the calcination temperature was above 720 °C in this work.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The calcination time was determined as 2 h because a too long or too short calcination time could reduce the surface area and the adsorption capacity of MFBC prepared, as a longer activation time might destroy the pore structure formed previously whereas a shorter calcination time could not enrich the formation of porosity.5 According to the BBD experiment, together with the quadratic equation fitting of these four variables (nitric acid concentration, modification time, modification temperature and calcination temperature), the expected response value was set as 80 mg g−1, the optimal combination of each factor was determined by Design-Expert version 8.0.6 (STAT-EASE Inc., Minneapolis, USA) and the experimental verification values are as follows (Table 8).
1. The calcination time was determined as 2 h because a too long or too short calcination time could reduce the surface area and the adsorption capacity of MFBC prepared, as a longer activation time might destroy the pore structure formed previously whereas a shorter calcination time could not enrich the formation of porosity.5 According to the BBD experiment, together with the quadratic equation fitting of these four variables (nitric acid concentration, modification time, modification temperature and calcination temperature), the expected response value was set as 80 mg g−1, the optimal combination of each factor was determined by Design-Expert version 8.0.6 (STAT-EASE Inc., Minneapolis, USA) and the experimental verification values are as follows (Table 8).
| CHNO3 (mol L−1) | Tm (°C) | tm (h) | IR (mL g−1) | TC (°C) | tc (h) | PNP uptake, qe (mg g−1) | |
|---|---|---|---|---|---|---|---|
| Predicted | Experimental | ||||||
| 4.46 | 20.3 | 87.8 | 10/1 | 716 | 2 | 80 | 79.6 |
The adsorption isotherms of PNP onto MFBC obtained under the optimum conditions at different temperatures were depicted. The maximum equilibrium adsorption capacity of p-nitrophenol onto MFBC was 156.9 mg g−1 at 328 K. The comparison of PNP uptake between MFBC via the above-mentioned optimized process and the materials used in the literature can be seen in Table 9. The comparative data shows that MFBC has quite a high PNP uptake compared to other adsorbent materials, and may be used effectively for the removal of PNP from aqueous streams.
| Materials | The maximum adsorption capacity on PNP (mg g−1) |
|---|---|
| MFBC (in this work) | 156.9 |
| ATW1 | 142.85 |
| Modified pyrophyllite32 | 0.268 |
| Bagasse fly ash8 | 0.77–1.16 |
| Wood fly ash33 | 134.9 |
| Fly ash34 | 7.80–9.61 |
| Microporous cyclodextrin35 | 167.0 |
| Charred saw dust36 | 147.0 |
| Modified bentonite37 | 107.27 |
| Modified starch38 | 131.5 |
| Rice husk39 | 15.31 |
| Rice husk char39 | 39.21 |
| Petroleum coke39 | 11.06 |
| Coke breeze39 | 4.64 |
| Silica beads40 | 116 |
| Pyrolyzed residue from animal bones41 | 111.0 |
| Pyrolyzed oil shale41 | 4.895 |
| ZnCl2 pyrolyzed oil shale41 | 6.026 |
| KOH pyrolyzed oil shale41 | 0.895 |
3.4 Characterization of fine blue-coke modified under optimum conditions
Fig. 3(a) and (b), and (c) and (d), exhibit FESEM images of the precursor (FBC) and the fine blue-coke modified under optimum conditions (MFBC), respectively. As can be seen from Fig. 3(a) and (b), there are very few pores available on the surface of the precursor. However, after HNO3 treatment and high temperature activation under the optimum modification conditions, the surface roughness of fine blue-coke increased obviously and many pores were developed on the surface of MFBC, as clearly shown in Fig. 3(c) and (d). The HRTEM images (Fig. 3(e) and (f)) further exhibit the rougher surface of MFBC compared to that of FBC. This showed that HNO3 and high temperature were effective in creating well-developed pores on the surfaces of the precursor, hence leading to the fine blue-coke with a large surface area and porous structure which had high PNP uptake. Similar observations were reported by other researchers in their works of preparing activated carbons from mangosteen peel6 and coconut husk.7As presented in Fig. 4(a), the N2 adsorption–desorption isotherms exhibit characteristics of type IV curves (according to the IUPAC classification) with a sharp capillary condensation step in the relative pressure range of 0.4–0.7 and an H4-type hysteresis loop. In detail, an increase is shown at a low relative pressure, and the next slow rise of isotherms appears at a medium relative pressure, while the isotherms rising at the relative pressure are close to 1.0 points, indicating the co-existence of micropores, mesopores, and macropores in the FBC and MFBC.43 Furthermore, the total pore volume and specific surface area of the fine blue-coke were increased by 0.8 and 1.2 times after being modified, respectively. Fig. 4(b) shows the pore size distribution of FBC and MFBC estimated using the BJH method, which revealed that the FBC and MFBC almost have the same pore size distribution in the range of 0–5 nm. And most of the pores were in the microporous and mesoporous region according to the IUPAC classification.42 This demonstrates that the physicochemical activation process has contributed to the high surface area and total pore volume of the fine blue-coke, but could not change the pore diameter distribution of the fine blue-coke. This is perhaps due to some new pores being created and some blocked pores were opened under the physicochemical activation process, which make the surface area and total pore volume of MFBC increase obviously. However, the activation temperature of the fine blue-coke is almost the same as the formation temperature of the fine blue-coke at about 700 °C, and it isn’t high to make the pores continue to widen, which results in the pore diameter distribution of the modified blue-coke remaining almost the same as that of the raw fine blue coke. A similar phenomenon has been reported by Qiu et al.25 and Chingombe et al.44 They also found that the specific surface area of activated carbon increased but the pore diameter distribution had not obviously changed after nitric acid oxidation and the high temperature activation process.
4. Conclusions
Based on the application of three types of experimental designs, that is, a fraction factorial design (2IV6–2), a steepest ascent method, and a Box–Behnken design, the effects of the modified processes on PNP uptake of the modified fine blue-coke, such as nitric acid concentration, modification temperature, modification time, impregnation ratio of HNO3 to FBC, calcination temperature and calcination time, were systematically investigated. This study clearly demonstrated that the impregnation ratio of HNO3 to FBC and calcination time had no significant effect on the PNP uptake of the modified fine blue-coke. However, the nitric acid concentration, modification time and temperature, and calcination temperature exhibited a distinctive effect on the PNP uptake. The first- and second-order model fitting was very good. No obvious lack-of-fit phenomenon occurred, and the experimental values were close to the fitting ones. The optimized process for modification was as follows: nitric acid concentration was 4.46 mol L−1, modification temperature was 87.8 °C, modification time was 20.3 h, impregnation ratio of HNO3 to FBC was 10 mL g−1, calcination time was 2 h and calcination temperature was 716 °C. As can be seen from the FESEM and HRTEM results, the surface roughness of MFBC increased obviously. The total pore volume and specific surface area increased by 0.8 and 1.2 times, respectively. The PNP equilibrium adsorption capacity was found to be 156.9 mg g−1 at 328 K. Compared with previous literature, the fine blue-coke modified by the optimized process in this work had excellent adsorption properties for PNP and may have a potential application in wastewater treatment.Acknowledgements
The financial support from Ministry of Education of the People’s Republic of China, Creative Experimental Project of National Undergraduate Students (No. 201410359035) is gratefully acknowledged.References
- A. Alif and P. Boule, J. Photochem. Photobiol., A, 1991, 59, 357–367 CrossRef CAS.
- M. Ahmaruzzaman and S. L. Gayatri, J. Chem. Eng. Data, 2010, 55, 4614–4623 CrossRef CAS.
- A. A. Pradhan and P. R. Gogate, Chem. Eng. J., 2010, 156, 77–82 CrossRef CAS.
- N. K. Amin, J. Hazard. Mater., 2009, 165, 52–62 CrossRef CAS PubMed.
- I. A. W. Tan, A. L. Ahmad and B. H. Hameed, J. Hazard. Mater., 2008, 153, 709–717 CrossRef CAS PubMed.
- M. A. Ahmad and R. Alrozi, Chem. Eng. J., 2010, 165, 883–890 CrossRef CAS.
- I. A. W. Tan, A. L. Ahmad and B. H. Hameed, Chem. Eng. J., 2008, 137, 462–470 CrossRef CAS.
- V. K. Gupta, S. Sharma, I. S. Yadav and D. Mohan, J. Chem. Technol. Biotechnol., 1998, 71, 180–186 CrossRef CAS.
- X. Wang, J. H. Peng and X. H. Duan, Journal of Microwave Power and Electromagnetic Energy, 2013, 47, 110–125 Search PubMed.
- Y. H. Tian, X. Z. Lan, Y. H. Song, C. B. Liu and J. Zhou, Int. J. Energy Res., 2015, 39, 1800–1806 CrossRef CAS.
- X. Z. Lan, Y. Yang, Y. H. Song, Q. L. Zhang, W. Z. Shang and W. J. Luo, Coal Conversion., 2009, 32, 18–21 CAS.
- M. D. Zheng, S. C. Yan and X. J. He, Fuel and Chemical Processes, 2007, 38, 21–23 Search PubMed.
- J. Mi, J. Ren and Y. Y. Zhang, Environ. Eng. Sci., 2012, 29, 1026–1031 CrossRef CAS PubMed.
- Q. Y. Liu, C. H. Li and Y. X. Li, Carbon, 2003, 41, 2217–2223 CrossRef CAS.
- K. Tsuji and I. Shiraishi, Fuel, 1997, 76, 549–553 CrossRef CAS.
- F. Y. Wei, B. Wu, J. C. Zhang, W. T. Zhang and C. Zhang, China Pat., CN104525113A, 2015.
- F. Karacan, U. Ozden and S. Karacan, Appl. Therm. Eng., 2007, 27, 1212–1218 CrossRef CAS.
- Y. N. Min, The design of experiment (DOE) application guide, Mechanical Engineering, Beijing, 2001 Search PubMed.
- G. Q. Xu, J. Chu, Y. P. Zhuang, Y. H. Wang and S. L. Zhang, Biochem. Eng. J., 2008, 38, 189–197 CrossRef CAS.
- N. Esfandiar, B. Nasernejad and T. Ebadi, J. Ind. Eng. Chem., 2014, 20, 3726–3736 CrossRef CAS.
- S. K. R. Kuppireddy, K. Rashid, A. A. Shoaibi and C. Srinivasakannan, Chem. Eng. Commun., 2014, 201, 1021–1040 CrossRef CAS.
- S. B. Lyubchik, R. Benoit and F. Béguin, Carbon, 2002, 40, 1287–1294 CrossRef CAS.
- L. Remenárová, M. Pipíška, E. Florková, M. Horník, M. Rozložník and J. Augustín, Clean Technol. Environ., 2014, 16, 1551–1564 CrossRef.
- A. A. Ahmad, B. H. Hameed and A. L. Ahmad, J. Hazard. Mater., 2009, 170, 612–619 CrossRef CAS PubMed.
- J. H. Qiu, G. H. Wang, Y. C. Bao, D. L. Zeng and Y. Chen, Fuel Process. Technol., 2015, 129, 85–90 CrossRef CAS.
- J. W. Shim, S. J. Park and S. K. Ryu, Carbon, 2001, 39, 1635–1642 CrossRef CAS.
- Q. Y. Liu, J. S. Guan, J. G. Li and C. H. Li, Carbon, 2003, 41, 2225–2230 CrossRef CAS.
- S. Haydar, M. A. Ferro-García, J. Rivera-Utrilla and J. P. Joly, Carbon, 2003, 41, 387–395 CrossRef CAS.
- S. Aber, A. Khataee and M. Sheydaei, Bioresour. Technol., 2009, 100, 6586–6591 CrossRef CAS PubMed.
- Y. Sudaryanto, S. B. Hartono, W. Irawaty, H. Hindarso and S. Ismadji, Bioresour. Technol., 2006, 97, 734–739 CrossRef CAS PubMed.
- Y. R. Nian and H. Teng, J. Electrochem. Soc., 2002, 149, A1008–A1014 CrossRef CAS.
- H. Sayılkan, S. Erdemoğlu, Ş. Şener, F. Sayılkan, M. Akarsu and M. Erdemoğlu, J. Colloid Interface Sci., 2004, 275, 530–538 CrossRef PubMed.
- A. E. Daifullah and H. Gad, Adsorpt. Sci. Technol., 1998, 16, 273–283 CAS.
- B. K. Singh and P. S. Nayak, Adsorpt. Sci. Technol., 2004, 22, 295–309 CrossRef CAS.
- G. Crini, N. Morin, J. C. Rouland, L. Janus, M. Morcellet and S. Bertini, Eur. Polym. J., 2002, 38, 1095–1103 CrossRef CAS.
- S. Dutta, J. K. Basu and R. N. Ghar, Sep. Purif. Technol., 2001, 21, 227–235 CrossRef CAS.
- M. Akçay and G. Akçay, J. Hazard. Mater., 2004, 113, 189–193 CrossRef PubMed.
- F. Delval, G. Crini and J. Vebrel, Bioresour. Technol., 2006, 97, 2173–2181 CrossRef CAS PubMed.
- M. Ahmaruzzaman and D. K. Sharma, J. Colloid Interface Sci., 2005, 287, 14–24 CrossRef CAS PubMed.
- T. N. T. Phan, M. Bacquet and M. Morcellet, J. Inclusion Phenom. Macrocyclic Chem., 2000, 38, 345–359 CrossRef CAS.
- S. Al-Asheh, F. Banat and A. Masad, Environ. Geol., 2004, 45, 1109–1117 CrossRef CAS.
- IUPAC, Pure Appl. Chem., 1972, 31, 587 Search PubMed.
- Y. F. Nie, Q. Wang, H. T. Yi, X. Y. Chen and Z. J. Zhang, RSC Adv., 2015, 80, 65100–65109 RSC.
- P. Chingombe, B. Saha and R. J. Wakeman, Carbon, 2005, 43, 3132–3143 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |




