DOI:
10.1039/C5RA24600H
(Paper)
RSC Adv., 2016,
6, 27060-27067
Lattice dynamics, phonon vibrational spectra, and thermal properties of tetragonal SrPt3P: a first-principles study
Received
20th November 2015
, Accepted 1st March 2016
First published on 7th March 2016
Abstract
The phonon vibrational spectra and thermal properties of the platinum-based superconductor SrPt3P are investigated by the generalized gradient approximation (GGA) plus the PBESOL exchange–correlation functional in the framework of density functional theory (DFT). The calculated structural parameters of SrPt3P at the ground state are in good agreement with the available experimental data and seem to be better than other calculated results. The finite displacement method is used to calculate the phonon vibrational spectra and phonon density of states of SrPt3P. The obtained phonon dispersion curves show that, no imaginary phonon frequency is observed in the whole Brillouin zone, while the imaginary frequencies exist at the gamma point as the pressure is greater than 100 GPa, indicating its structural instability at high pressure. The vibrational modes at the gamma point are analyzed from group theory, and the obtained phonon frequencies are in good agreement with other theoretical and experimental values. The temperature and pressure dependences of the thermal quantities of SrPt3P (such as the thermal expansion, the heat capacity at constant volume, the entropy, and the Grüneisen parameter) are calculated based on the quasi-harmonic approximation (QHA). Our results show that both the thermal expansion coefficient α and the heat capacity CV increase with T3 at low temperatures and gradually turn almost linear as the temperature increases. It is demonstrated that the entropy is sensitive to temperature while the Grüneisen parameter γ is more sensitive to pressure.
1. Introduction
After the discovery of the first Fe-based superconductors,1 enormous efforts were made to seek routes which realize superconductivity at high temperatures. The close proximity to a magnetically ordered state has been widely believed to be one of the most promising routes. When MgB2 was found with critical temperature Tc = 39 K,2 the electron–phonon mediated superconductivity was regarded as another promising route. The relatively high Tc in MgB2 is resulted from the charge carriers enhance the coupling to high energy optical phonons.3 A similar scene might appear in the doped diamonds,4 KOs2O6,5 and the chevrel phase.6 Presently, the phenomenon attracts considerable interest, and a mass of superconductors have been found and investigated.
In the course of intensive search for high-Tc superconductors, some compounds were further investigated, such as BaNi2As2,7 SrNi2As2,8 SrPtAs,9 SrPt2As2,10 and APt3P (A = Sr, Ca, La).11 In 2012, Takayama et al.11 made structural analysis to the Pt-based superconductor (SrPt3P, CaPt3P, LaPt3P) by the X-ray diffraction, and obtained the critical temperature Tc = 8.4 K, 6.6 K and 1.5 K by resistivity measurements, respectively. It is shown that SrPt3P seems to be very special among APt3P since it not only has the highest Tc in the 5d-electron based superconductors, but also has a large 2Δ0/κBTc ∼ 5, manifesting strong-coupling superconductivity. Thus, SrPt3P has been attracted a considerable interest.12–18
By the linearized muffin-tin orbital (LMTO) method, Nekrasov et al.12 demonstrated that the ternary platinum phosphide SrPt3P is an anti-perovskite structure, similar to that of CePt3Si,13 and found that there exists multiple Fermi surfaces in the system, indicating an intricate superconducting gap structure. Jawdat et al.14 investigated the chemical doping and high-pressure effects on the properties of SrPt3P. They selected Si as the dopant to investigate the chemical doping. By means of the X-ray-diffraction, they found that there was a phase separation with the increasing Si doping. As the Si doping increased, the observed Tc decreased through the resistivity and magnetization measurements. Theoretical studies on the pairing mechanism in the new compound15,16 gave partially contradicting results. Chen et al.15 performed first-principles calculations and proposed that the superconductivity of SrPt3P is caused by the proximity to the dynamical charge density wave instability, and a strong spin–orbit coupling leads to exotic pairing. In contrast, Subedi et al.16 suggested the conventional phonon mediated superconductivity from first-principles calculations and Migdal-Eliashberg analysis. Recently, many efforts have been made on investigating the phonon property of SrPt3P. Based on the observation of nonlinear temperature behavior of the Hall resistivity, Kang et al.17 calculated the electron and phonon band structure of SrPt3P, evidencing that it has low-energy two-dimensional phonons and the superconducting charge carriers, which come from the pdπ-hybridized bands between Pt and P ions, which couples to low energy phonon modes. Although Zocco et al.18 provided the results of the phonon band structure via inelastic X-ray scattering, the further analyze to phonon properties is still necessary.
In the work, to give a further and more comprehensive understanding of SrPt3P, we focus on the lattice dynamics, phonon vibrational spectra, and thermal properties of tetragonal SrPt3P by the plane-wave pseudopotential density functional theory (DFT) method as implemented in the CASTEP code.19,20 Thermal properties were obtained from the quasi-harmonic approximation (QHA).21
The rest of this work is organized in the following order. Firstly, the theoretical methods and computational details are introduced in Section 2. The results of the vibrational modes analysis, phonon dispersion curves and related thermal properties of SrPt3P are presented in Section 3. Finally, main points of this work are included in Section 4.
2. Theoretical methods and computation details
In our electronic structure calculations, the generalized gradient approximation (GGA) proposed by Perdew et al.22 was adopted as the exchange–correlation potentials. The ultrasoft pseudopotential was introduced by Vanderbilt23 to describe the interactions between the electrons and the ion cores. The Brillouin-zone integration of the primitive unit cell was performed using 8 × 8 × 8 k-points meshes according to the Monkhorst–Pack method24 with the plane-wave cutoff energy of 480 eV. Pseudo atomic calculations were performed for Sr-3d104p65s2, Pt-5d96s1 and P-3s23p3. These parameters were carefully tested, convergence of the geometry optimization were set to 5 × 10−6 eV per atom for energy, 0.01 eV Å−1 for force, 5 × 10−4 Å for ionic displacement, and 0.02 GPa for stress.
The first-principles investigations of the phonon dispersion relations and phonon modes were performed by using the finite displacement method.25 The phonon frequencies in the Brillouin zone (BZ) center were computed as second-order derivatives of the total energy with respect to atomic displacements. In the phonon calculations, the supercell was defined using a cutoff radius of 5.0 Å. The supercell volume was 16 times that of the unit cell. 14 × 14 × 14 Monkhorst–Pack meshes were used in the calculation of the phonon density of states. Furthermore, phonon related thermal properties such as the thermal expansion, the heat capacity at constant volume, the entropy, and the thermodynamic Grüneisen parameter were evaluated by employing the quasi-harmonic approximation (QHA).21
In the QHA model, the nonequilibrium Gibbs function G*(V; P, T) under a given pressure P and temperature T takes the form:
| | |
G*(V; P, T) = E(V) + PV + F*vib(Θ(V); T)
| (1) |
where the static energy
E(
V) is the total energy,
PV corresponds to the constant hydrostatic pressure condition,
Θ(
V) is the Debye temperature, and the nonequilibrium vibrational contribution to the Helmholtz energy is given by
| |
 | (2) |
where
g(
ω,
x) is the phonon density of state (PDOS) and depends on the crystal geometry. Other trivial contributions to the free energy can be ignored for ideal SrPt
3P crystal. The entropy (
S) and constant-volume heat capacity (
CV) are expressed as
| |
 | (3) |
| |
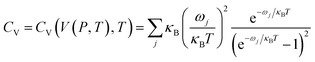 | (4) |
with the obtained phonon density of states at different volumes, we obtained the relevant results for SrPt
3P. In essence, thermal expansion coefficient
α is originated from the non-harmonic effect described with Grüneisen constants
γ. Generally, the coefficient of thermal expansion
α is the function of both
γ and
CV,
| |
 | (5) |
where
K0 is the bulk modulus in the ground state,
V is the volume of unit cell under a given temperature.
3. Results and discussion
3.1. Phonon properties
The obtained structural parameters of SrPt3P at the ground state are listed in Table 1, together with other theoretical data and the available experimental data. Our results (a0 = 5.8223 Å, c0 = 5.4075 Å) are in good agreement with the experimental values (a = 5.8094 Å and c = 5.3833 Å)11 with the errors of 0.22%, 0.45%, 0.88% for a, c, V, respectively. These ensure the reliability of our study.
Table 1 Calculated lattice parameters (a, c, c/a) and primitive cell volume V, together with the experimental data and other calculated results
| Lattice parameters |
a (Å) |
c (Å) |
c/a |
V (Å3) |
References |
| Obtained from quantum-ESPRESSO code. Obtained from VASP code. Obtained from VASP code. Obtained from VASP code, where SOC represents spin–orbit-coupling. Obtained from the X-ray diffraction measurements. |
| Cal. (GGA-PBESOL) |
5.8223 |
5.4075 |
0.9287 |
183.3 |
This work |
| Cal. (GGA-PBE)a |
5.8980 |
5.4700 |
0.9274 |
190.3 |
16 |
| Cal. (GGA-PBE)b |
5.8828 |
5.4426 |
0.9252 |
188.3 |
26 |
| Cal. (GGA-PBE)c |
5.8788 |
5.4313 |
0.9238 |
187.7 |
15 |
| Cal. (GGA-PBE-SOC)d |
5.8852 |
5.4339 |
0.9233 |
188.2 |
15 |
| Exp.e |
5.8094 |
5.3833 |
0.9266 |
181.7 |
11 |
SrPt3P has a strongly exchange-enhanced paramagnetic element Pt, the spin–orbit coupling (SOC) in 5d electrons is strong. In order to understand the puzzling features observed in the SrPt3P, it is necessary and informative to clarify the impact of SOC. Kang et al.17 confirmed that the band structure with and without SOC are essentially the same near the Fermi level (EF), and thus Fermi surface becomes almost the same. Chen et al.15 demonstrated that the SOC effect can be negligible in electron band. We also calculated the phonon properties with and without SOC in this work, and our results show that the impact of SOC is very little. The phonon dispersion curves along the high-symmetry directions in the Brillouin zone, total and partial phonon density of states (DOS) at 0 GPa and 0 K are showed in Fig. 2. From Fig. 2(a), no imaginary phonon frequency is observed in the whole Brillouin zone, indicating that the bulk SrPt3P is dynamically stable. Since the primitive cell of SrPt3P contains ten atoms (Fig. 1), the corresponding numbers of the vibrational modes are thirty. It can be seen that there are thirty phonon branches from 0 to 460 cm−1, two upper and four intermediate branches come from vibration of P atoms, remaining 24 branches in the low frequency region mostly originate from the mixture of vibrations of the Sr and Pt ions in SrPt3P. These low energy phonon modes are indeed consistent with the prediction by Takayama et al.11 Fig. 2(b) shows the existing four main peaks in the low phonon density of state. The first peak (located at ∼180 cm−1) is sharp, which is made up of Sr, Pt and P ions. It is obvious that the vibrations of Sr ions are far outweigh other atoms. Sr ions and Pt ions play a dominant role in producing the second peaks, while the third and fourth peaks originate from the vibrations of Pt ions. Generally speaking, the high phonon DOS peaks in low energy regime are related to the large electron–phonon coupling constant λ and the critical temperature Tc. Since the ionic radius of Sr2+ is larger than those of the Ca2+ and La3+, the vibration modes of Pt ions are localized in SrPt3P, as explains why SrPt3P has the highest critical temperature Tc among APt3P (A = Sr, Ca and La). In Fig. 2(c), we can see that the phonon DOS of Pt1 (0.25, 0.25, 0.5) atoms and Pt2 (0, 0.5, 0.1409) atoms are different, relating to the anti-perovskite structure of SrPt3P.12 Based on the atomic Mulliken populations,27,28 the calculated covalent degrees of P–Pt1 and P–Pt2 are different so that the phonon DOS are distinguishing.
 |
| | Fig. 1 The tetragonal structure of SrPt3P in different direction view. The green, blue and pink spheres in the sketch represent the Sr atoms, Pt atoms and P atoms, respectively. | |
 |
| | Fig. 2 (a) Phonon dispersion; (b) total phonon density of states (DOS); (c) partial phonon DOS of SrPt3P. | |
We next investigate the mechanical stability of SrPt3P under external pressures by showing the evolution of the phonon DOS. Our results are illustrated in Fig. 3. It can be seen that SrPt3P is mechanically stable at the ground state. Chen et al.15 calculated the phonon properties in a unit cell and found that the soft phonon modes located around the (π, π, 0) and (π, π, π) points. When calculating the phonon properties in a 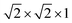 supercell, they found that the soft phonon modes disappear. Thus, Chen et al.15 concluded that the soft phonon modes are due to the charge density wave instability in SrPt3P. However, by the linear response method and Fourier interpolation, Subedi et al.16 and Kang et al.17 demonstrated that SrPt3P is mechanically stable at the ground state. We thought that their calculations did not converge sufficiently. As a whole, the phonon DOS of SrPt3P at different pressures are always distributed in three frequency regions. With the increasing pressure, the first frequency region, primarily contributed by the lowest optical modes, is gradually broaden. It tends to below 0 THz as the pressure is up to 100 GPa, suggesting that SrPt3P is mechanically unstable. The second and third frequency regions shift to higher energies at higher pressure and the peaks in second frequency region change from one into two. The external pressure compresses the interatomic distance, causing stiffer bonds, and thus all phonon modes shift to higher energies.
supercell, they found that the soft phonon modes disappear. Thus, Chen et al.15 concluded that the soft phonon modes are due to the charge density wave instability in SrPt3P. However, by the linear response method and Fourier interpolation, Subedi et al.16 and Kang et al.17 demonstrated that SrPt3P is mechanically stable at the ground state. We thought that their calculations did not converge sufficiently. As a whole, the phonon DOS of SrPt3P at different pressures are always distributed in three frequency regions. With the increasing pressure, the first frequency region, primarily contributed by the lowest optical modes, is gradually broaden. It tends to below 0 THz as the pressure is up to 100 GPa, suggesting that SrPt3P is mechanically unstable. The second and third frequency regions shift to higher energies at higher pressure and the peaks in second frequency region change from one into two. The external pressure compresses the interatomic distance, causing stiffer bonds, and thus all phonon modes shift to higher energies.
 |
| | Fig. 3 Phonon density of states under different pressures. Negative frequency indicates the imaginary phonon modes. | |
As to the three acoustic modes of SrPt3P, we find that the in-plane longitudinal acoustic (LA) and transverse acoustic (TA) modes have a linear behavior near the gamma point, and the out-of-plane acoustic (ZA) mode displays a q2 dependence. This q2 dependence is a consequence of the point group symmetry.29 According to the group theory,30 the irreducible representations of the optical phonon modes at the Brillouin zone center (gamma point) can be classified as
| | |
Goptical = A1g(R) + 3A1u(IR) + 2B1g(IN) + B2u(IN) + 2B2g(IN) + 3Eg(R) + 6Eu(IR)
| (6) |
where R, IR and IN indicate the Raman, infrared, and inactive silent modes, respectively. The subscripts u and g represent the symmetric mode and the anti-symmetric mode. E
g and E
u are double degenerate modes, while A
g and A
u are single degenerate modes. The R and IR modes are mutually exclusive in SrPt
3P due to the presence of inversion symmetry. The A
1g and E
g are Raman active modes while the A
1u and E
u are Infrared active modes, the remaining phonon modes are inactive silent. In
Table 2, we list our calculated frequencies, vibrational modes and the atoms that contribute to these vibrations of SrPt
3P, together with other theoretical values and the available experimental data. It can be found that our results are in good agreement with those reported by Kang
et al.17 and the experimental data.
18 It can be seen from
Table 2 that the A
1g and B
2u modes include one phonon frequency, the A
1g mode results from the vibrations of Sr atoms while the B
2u mode comes from the vibrations of Pt atoms. The B
1g and B
2g modes have two phonon frequencies, and the vibrations of P atoms create two B
1g modes in high phonon while two B
2g modes located in low phonon energy involve the vibrations of Pt atoms. Three A
1u modes main concentrate in intermediate frequency, and are produced by the vibrations of P and Pt atoms, Sr atoms and Pt atoms, respectively. In three E
g modes, two E
g modes in low phonon energy mainly come from Pt atoms, while higher E
g mode includes vibrations of P atoms. The E
u mode distributes in whole phonon frequency so that it possesses the mixture of vibrations of the whole ions in SrPt
3P. To facilitate the discussion, we sketch a part of vibrational modes in
Fig. 4. We note that the listed B
2u, B
2g, and E
g modes respect only the vibrations of Pt atoms, while the vibrations of Sr and P atoms are negligible. The B
2u mode involves Pt atoms moving to the body-center, the B
2g mode includes these Pt atoms move along Pt–P bond direction, the E
g mode results from opposing vibrations of Pt atoms in the same direction. The listed A
1u, A
1g and E
u modes only involve the vibrations of Sr atoms, the A
1u mode is created by the Sr atoms along
z direction, the A
1g mode results from opposing vibrations of the Sr atoms in the lattice point and in the face-center against the crystal structure along
z axis, while Sr atoms in E
u mode oscillate in opposite
y axis. The B
1g mode comes from the opposing motion of Sr atoms while the remaining atoms are stationary.
Table 2 The assignment of the vibrational modes at the gamma point of bulk (point group D4h) SrPt3P with their frequencies and reference data (unit: cm−1)
| D4h |
Character |
Atoms |
Present |
Other theor. |
Exp. |
| Ref. 17 |
Ref. 16 |
Ref. 18 |
| B2u |
Inactive |
Pt |
70.94 |
39.7 |
— |
43.35 |
| 2Eg |
Raman |
Sr + Pt |
74.98 |
71.51 |
— |
59.11 |
| Eg |
Raman |
Pt |
77.79 |
77.3 |
— |
65.02 |
| 2Eu |
Infrared |
Sr + Pt |
79.44 |
93.2 |
— |
76.84 |
| B2g |
Inactive |
Pt |
98.67 |
93.2 |
93.02 |
96.54 |
| 2Eu |
Infrared |
Pt + P |
106.49 |
98.98 |
101.1 |
106.39 |
| B2g |
Inactive |
Pt |
122.66 |
114.88 |
113.24 |
116.25 |
| A1u |
Infrared |
P + Pt |
122.73 |
114.88 |
113.24 |
116.25 |
| 2Eu |
Infrared |
Sr + P + Pt |
126.04 |
123.55 |
137.5 |
125.11 |
| A1u |
Infrared |
Sr |
128.21 |
123.55 |
144.63 |
125.11 |
| A1g |
Raman |
Sr |
152.19 |
132.21 |
144.63 |
153.68 |
| A1u |
Infrared |
Pt |
166.91 |
156.79 |
143.56 |
158.60 |
| 2Eu |
Infrared |
Sr |
182.75 |
166.9 |
153.47 |
166.48 |
| 2Eu |
Infrared |
Sr |
185.26 |
166.9 |
153.67 |
166.48 |
| 2Eu |
Infrared |
P |
298.45 |
321.53 |
270.96 |
291.43 |
| 2Eg |
Raman |
P |
343.00 |
364.90 |
309.37 |
322.95 |
| B1g |
Inactive |
P |
436.54 |
435.70 |
398.34 |
422.94 |
| B1g |
Inactive |
P |
461.37 |
455.95 |
412.5 |
439.69 |
 |
| | Fig. 4 The assigned vibrational modes of SrPt3P. Red arrows represent the directions of the vibrations. | |
3.2. Thermal properties at finite temperatures and pressures
Thermal properties play an important role in understanding the thermal response of solids. Recently, we have investigated the thermal properties of several materials31–35 by the quasi-harmonic Debye (QHD) model.36 However, for some materials, the QHD model may lead to the dissatisfactory or wrong results. For examples, Qi et al.35 obtained better phase transition pressure of CaF2 by quasi-harmonic approximation (QHA) than by QHD model when compared with the experimental data. Zhang et al.37 found that the phase transition pressure and thermal properties calculated from the QHA model were better than those from the QHD model, particularly at high temperature end. Calculations based on various semi-empirical models as well as on first-principles methods demonstrate that the QHA provides a reasonable description of the dynamic properties of many materials below the melting point.38,39 The main reason is described as follows: the QHD model only takes the acoustic branch in the dispersion relation into account, and neglects the contribution of the optical branch. However, the impact of the optical branch is considerable under high temperature in QHA. Thus, we here investigate the thermal properties of SrPt3P through QHA method. Unfortunately, there are no experimental and other theoretical data for our comparison.
Thermal expansion coefficient α is a very important parametric quantity for interpreting the thermodynamic behaviors of solid. The temperature and pressure dependences of the thermal expansion coefficient α of tetragonal SrPt3P are indicated in Fig. 5. The thermal expansion coefficient decreases with the increasing pressures. The effect of pressure on the thermal expansion is very small below 100 K, but as temperature increases, the effect becomes prominent. It is known that the thermal expansion coefficient is proportional to with T3 at low temperatures and gradually turns almost linear as the increasing temperatures. At higher temperatures, the thermal expansions at 0 GPa are relatively lager than those at the higher pressures. When P > 13 GPa, the curves of the thermal expansion coefficient have a limited difference. The effect of temperature on the thermal expansion coefficient at higher temperatures is smaller than that at low temperatures. The thermal expansion coefficient grows rapidly in low temperature, while at high pressure the variation is small. The figure also indicates that the pressure has a big influence on the thermal expansion of SrPt3P. This pressure factor shall be taken into account carefully in designing and assembling thermoelectric devices.
 |
| | Fig. 5 Calculated thermal expansion coefficient a as a function of pressure for SrPt3P at different temperatures. The right bar chart respects the expansion coefficient α. | |
The investigation on the heat capacity of crystal is an old topic of the condensed matter physics.40,41 The heat capacity CV at constant volume of the SrPt3P is plotted for several pressures and temperatures in Fig. 6. From Fig. 6(a), it is found that CV increases steeply when temperature is below 400 K, which may be due to the anharmonic approximations. Vassilieva et al.42 indicated that CV is proportional to T3 at sufficiently low temperature. With the temperature increasing, the anharmonic effect on CV is suppressed so that the heat capacity Cv increases slowly. It is obvious that CV tends to the Dulong–Petit limit 3nNAκB (124.09 J mol−1 K−1) at high temperature, which is common for all solids at high temperatures. Fig. 6(b) shows the heat capacity CV as a function of pressure at different temperatures, the heat capacity CV decreases for a given temperature with the pressure increasing, but when the temperature is enough high, the influence of pressure is negligible. Overall, the influences of the temperature on CV are more significant than that of the pressure. For example, at P = 0 GPa, the calculated CV at T = 300 K and T = 1000 K are 109.25 J mol−1 K−1 and 123.80 J mol−1 K−1, respectively. While at T = 300 K, the calculated CV at P = 10 GPa and P = 30 GPa are 112.53 J mol−1 K−1 and 109.25 J mol−1 K−1, respectively. That is to say, the heat capacity only decreases a bit when the pressure increases. This decrease may indicate the change of the effective phonon mean-free path induced by the applied pressure.
 |
| | Fig. 6 (a) Calculated heat capacity (CV) as a function of pressure for SrPt3P at different temperatures; (b) heat capacity (CV) as a function of temperature for SrPt3P at different pressures. | |
The temperature and pressure dependences of the entropy S of SrPt3P are plotted in Fig. 7. It can be clearly seen that the variation of entropy is relatively small below the temperature of 100 K. However, the value of the entropy S increases quickly when the temperature is greater than 100 K. For a given temperature, the entropy S gradually decreases with the pressure increasing. Fig. 8 shows the temperature and pressure dependences of the thermodynamic Grüneisen parameter γ. From Fig. 8(a), it can be seen that the Grüneisen parameter γ gradually increases at 0 GPa with the temperature increasing, while the value of γ is changeless as the pressure is more than 0 GPa, which indicates the effect of temperature on the Grüneisen parameter γ at high pressure is negligible. In Fig. 8(b), it is obvious that when the pressure increases the value of γ decreases and tends to a limit. From Fig. 7 and 8, we can conclude that the entropies are more sensitive to temperature while the Grüneisen parameter γ are more sensitive to pressure.
 |
| | Fig. 7 Calculated entropy S (a) as a function of pressure for SrPt3P at different temperatures; (b) at different pressures. | |
 |
| | Fig. 8 Variation of the Grüneisen parameter γ at (a) different temperatures; (b) different pressures. | |
4. Conclusions
We have performed first-principles calculations to investigate the phonon vibrational spectra and thermal properties of SrPt3P based on the generalized gradient approximation (GGA) within density functional theory (DFT). The calculated lattice parameters are in good agreement with the available experimental data and other theoretical results. In the phonon calculations, no imaginary phonon frequency is observed in the whole BZ, indicating that SrPt3P is dynamically stable. However, when the external pressure is more than 100 GPa, there exits imaginary frequency at the gamma point, demonstrating its the mechanically unstable. The calculated phonon PDOS shows that the high phonon frequencies are mainly contributed by the vibrations of P atoms due to their smaller mass than the masses of Sr and Pt atoms, while Sr atomic vibrations are dominant in the intermediate frequency region, the low phonon frequencies are produced by the vibrations of Sr atoms and Pt atoms, in particular Pt atoms. Vibrational modes at the gamma point are assigned by group theory, and their eigenvectors are also sketched. We calculated the thermal expansion coefficient, the heat capacity at constant volume, the entropy and the thermodynamic Grüneisen parameter based on the QHA. Our results show that both the heat capacities CV and thermal expansion coefficient of SrPt3P are all proportional to T3 at low temperatures. In addition, we conclude that the entropy S is sensitive to temperature while the thermodynamic Grüneisen parameter γ is more sensitive to pressure.
Acknowledgements
The authors would like to thank the support by the National Natural Science Foundation of China (Grant No. 11204192) and the NSAF (Grant No. U1430117, U1230201). We also acknowledge the support for the computational resources by the State Key Laboratory of Polymer Materials Engineering of China in Sichuan University. Some calculations are performed on the ScGrid of Supercomputing Center, Computer Network Information Center of Chinese Academy of Sciences.
References
- Y. Kamihara, T. Watanabe, M. Hirano and H. Hosono, J. Am. Chem. Soc., 2008, 130, 3296–3297 CrossRef CAS PubMed
 .
. - J. Nagamatsu, N. Nakagawa, T. Muraoka, Y. Zenitani and J. Akimitsu, Nature, 2001, 410, 63 CrossRef CAS PubMed
 .
. - H. J. Choi, D. Roundy, H. Sun, M. L. Cohen and S. G. Louie, Nature, 2002, 418, 758–760 CrossRef CAS PubMed
 .
. - E. A. Ekimov, V. A. Sidorov, E. D. Bauer, N. N. Mel'nik, N. J. Curro, J. D. Thompson and S. M. Stishov, Nature, 2004, 428, 542–545 CrossRef CAS PubMed
 .
. - Z. Hiroi, S. Yonezawa, Y. Nagao and J. Yamaura, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 014523 CrossRef
 .
. - B. Lachal, A. Junod and J. Muller, J. Low Temp. Phys., 1984, 55, 195–232 CrossRef CAS
 .
. - E. D. Bauer, F. Ronning, B. L. Scott and J. D. Thompson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 172504 CrossRef
 .
. - F. Ronning, N. Kurita, E. D. Bauer, B. L. Scott, T. Park, T. Klimczuk, R. Movshovich and J. D. Thompson, J. Phys.: Condens. Matter, 2008, 20, 342203 CrossRef
 .
. - S. Elgazzar, A. M. Strydom and S. L. Drechsler, J. Supercond. Novel Magn., 2012, 25, 1795–1798 CrossRef CAS
 .
. - K. Kudo, Y. Nishikubo and M. Nohara, J. Phys. Soc. Jpn., 2010, 79, 123710 CrossRef
 .
. - T. Takayama, K. Kuwano, D. Hirai, Y. Katsura, A. Yamamoto and H. Takagi, Phys. Rev. Lett., 2012, 108, 237001 CrossRef CAS PubMed
 .
. - I. A. Nekrasov, M. V. Sadovskii and K. M. Huras, JETP Lett., 2012, 96, 227–230 CrossRef CAS
 .
. - E. Bauer, G. Hilscher, H. Michor, C. Paul, E. W. Scheidt, A. Gribanov, Y. Seropegin, H. Noel, M. Sigrist and P. Rogl, Phys. Rev. Lett., 2004, 92, 027003 CrossRef CAS PubMed
 .
. - B. I. Jawdat, B. Lv, X. Y. Zhu, Y. Y. Xue and C. W. Chu, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094514 CrossRef
 .
. - H. Chen, X. F. Xu, C. Cao and J. Dai, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 125116 CrossRef
 .
. - A. Subedi, L. Ortenzi and L. Boeri, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 144504 CrossRef
 .
. - C. J. Kang, K. H. Ahn, K. W. Lee and B. I. Min, J. Phys. Soc. Jpn., 2013, 82, 053703 CrossRef
 .
. - D. A. Zocco, S. Krannich, R. Held, K. P. Bohnen, T. Wolf, T. Forrest, A. Bosak and F. Weber, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 220504 CrossRef
 .
. - M. C. Payne, M. P. Teter, D. C. Allen, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS
 .
. - V. Milman, B. Winkler, J. A. White, C. J. Packard, M. C. Payne, E. V. Akhmatskaya and R. H. Nobes, Int. J. Quantum Chem., 2000, 77, 895–910 CrossRef CAS
 .
. - A. Otero-de-la-Roza, D. Abbasi-Perez and V. Luanea, Comput. Phys. Commun., 2011, 182, 2232–2248 CrossRef CAS
 .
. - J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed
 .
. - D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef
 .
. - H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef
 .
. - G. J. Ackland, M. C. Warren and S. J. Clark, J. Phys.: Condens. Matter, 1997, 9, 7861–7872 CrossRef CAS
 .
. - I. R. Shein and A. L. Ivanovskii, J. Supercond. Novel Magn., 2013, 26, 3167–3170 CrossRef CAS
 .
. - R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS
 .
. - M. D. Segall, R. Shah, C. J. Pickard and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16317–16320 CrossRef CAS
 .
. - R. Saito, G. Dresselhaus and M. S. Dresselhaus, Physical Properties of Carbon Nanotubes, Imperial College Press, London, 1998 Search PubMed
 .
. - M. I. Aroyo, A. Kirov, C. Capillas, J. M. Perez-Mato and H. Wondratschek, Acta Crystallogr., Sect. A: Found. Crystallogr., 2006, 62, 115–128 CrossRef PubMed
 .
. - L. Y. Lu, Y. Cheng, X. R. Chen and J. Zhu, Phys. B, 2005, 370, 236–242 CrossRef CAS
 .
. - X. F. Li, X. R. Chen, C. M. Meng and G. F. Ji, Solid State Commun., 2006, 139, 197–200 CrossRef CAS
 .
. - X. F. Li, G. F. Ji, F. Zhao, X. R. Chen and D. Alfe, J. Phys.: Condens. Matter, 2009, 21, 025505 CrossRef PubMed
 .
. - X. R. Chen, Z. Y. Zeng, Z. L. Liu, L. C. Cai and F. Q. Jing, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 132102 CrossRef
 .
. - Y. Y. Qi, Y. Cheng, M. Liu, X. R. Chen and L. C. Cai, Phys. B, 2013, 426, 13–19 CrossRef CAS
 .
. - M. A. Blanco, E. Francisco and V. Luana, Comput. Phys. Commun., 2004, 158, 57–72 CrossRef CAS
 .
. - T. Zhang, Y. Cheng, Z. L. Lv, G. F. Ji and M. Gong, Int. J. Mod. Phys. B, 2014, 28, 1450026 CrossRef
 .
. - L. Wang, P. F. Yuan, F. Wang, Q. Sun, E. J. Liang and Y. Jia, Mater. Res. Bull., 2012, 47, 1113–1118 CrossRef CAS
 .
. - C. W. Li, X. L. Tang, J. A. Muñoz, J. B. Keith, S. J. Tracy, D. L. Abernathy and B. Fultz, Phys. Rev. Lett., 2011, 107, 195504 CrossRef PubMed
 .
. - P. Debye, Ann. Phys., 1912, 344, 789 CrossRef
 .
. - A. Einstein, Ann. Phys., 1907, 328, 197–198 CrossRef
 .
. - V. P. Vassilieva, W. Gongb, A. F. Taldrikc and S. A. Kulinich, J. Alloys Compd., 2013, 552, 248–254 CrossRef
 .
.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. 

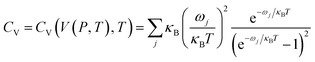



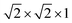 supercell, they found that the soft phonon modes disappear. Thus, Chen et al.15 concluded that the soft phonon modes are due to the charge density wave instability in SrPt3P. However, by the linear response method and Fourier interpolation, Subedi et al.16 and Kang et al.17 demonstrated that SrPt3P is mechanically stable at the ground state. We thought that their calculations did not converge sufficiently. As a whole, the phonon DOS of SrPt3P at different pressures are always distributed in three frequency regions. With the increasing pressure, the first frequency region, primarily contributed by the lowest optical modes, is gradually broaden. It tends to below 0 THz as the pressure is up to 100 GPa, suggesting that SrPt3P is mechanically unstable. The second and third frequency regions shift to higher energies at higher pressure and the peaks in second frequency region change from one into two. The external pressure compresses the interatomic distance, causing stiffer bonds, and thus all phonon modes shift to higher energies.
supercell, they found that the soft phonon modes disappear. Thus, Chen et al.15 concluded that the soft phonon modes are due to the charge density wave instability in SrPt3P. However, by the linear response method and Fourier interpolation, Subedi et al.16 and Kang et al.17 demonstrated that SrPt3P is mechanically stable at the ground state. We thought that their calculations did not converge sufficiently. As a whole, the phonon DOS of SrPt3P at different pressures are always distributed in three frequency regions. With the increasing pressure, the first frequency region, primarily contributed by the lowest optical modes, is gradually broaden. It tends to below 0 THz as the pressure is up to 100 GPa, suggesting that SrPt3P is mechanically unstable. The second and third frequency regions shift to higher energies at higher pressure and the peaks in second frequency region change from one into two. The external pressure compresses the interatomic distance, causing stiffer bonds, and thus all phonon modes shift to higher energies.





.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
