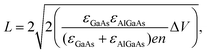Electronic structure investigation of Al_0.7Ga_0.3As/GaAs nanometric heterostructures by Kelvin force microscopy

Abstract

Kelvin force microscopy provides a spatially resolved measurement of the surface potential, which is related to the energetic band structure of a material. The goal of this work is to investigate the surface potential on Al_0.7Ga_0.3As and GaAs heterostructures with a decreasing layer thickness up to a few nanometers. We show that all the Kelvin force microscopy measurements on such a structure show a decreasing contrast relative to the layer thickness which remains the same despite the fact that measurements are done with various atomic force microscopy tip apexes. We prove that this contrast limitation is not due to the resolution limit of the Kelvin force microscopy technique, but is due to an intrinsic property of the sample. We evaluate by a self-consistent simulation, that the depletion layers located at the Al_0.7Ga_0.3As and GaAs interfaces of the narrowest stripes recover each other, which results in the partial or total loss of the contrast between Al_0.7Ga_0.3As and GaAs layers. Consequently, by Kelvin force microscopy we are able to detect the surface potential signal in the nanometer scale which is induced by the band bending between Al_0.7Ga_0.3As and GaAs and does not depend only on the experimental setup.

---

Introduction

Electrical measurements of semiconductor devices with a nanometer-scale are an important challenge for material and device engineers. Among the various measurement techniques,^1–4 Kelvin Force Microscopy (KFM) proposed by Nonnenmacher et al.⁵ is one of the most powerful methods for this purpose due to its exceptional resolution⁶ and high sensitivity.^7,8 Such performances from KFM make a perfect tool to characterize the electrical properties of nano-objects in the function of their size. Some studies were reported on a size-dependent charge transfer process, for example on: GaN nanowires,⁹ Si nanocrystals,^7,10 or KBr islands.¹¹ KFM has also been used on GaAs based devices, like GaAs metal semiconductor field effect transistors,¹² GaAs/AlGaAs heterostructures¹³ or GaAs PN junctions.¹⁴ In this work we will focus on a deeper comprehension and interpretation of KFM signal relative to the Al_0.7Ga_0.3As/GaAs layer thickness (down to 5 nm). First, we will present highly resolved surface potential measurements, and afterwards, we will analyze KFM signal by performing a KFM 3D simulation on the Al_0.7Ga_0.3As/GaAs structure.

Experimental section

In this work we use a BAM-L200 sample,¹⁵ which is mainly used as reference sample for length calibration and lateral resolution testing of imaging techniques like ToF-SIMS or Nano-Esca.¹ Electrical measurements were already performed using KFM system under ambient conditions.¹⁶ The KFM spatial resolution of this system was found to be 10 nm. Here, we analyze the origin of KFM resolution limit on BAM-L200 sample under Ultra-High Vacuum (UHV), and to our knowledge, such origin was never analyzed on AlGaAs/GaAs structure. In parallel, the electronic structure of BAM-L200 sample is analyzed as a function of Al_0.7Ga_0.3As thickness reduction by means of numerical simulations.

BAM-L200 sample [Fig. 1] is fabricated by the “Bundesanstalt für Materialforschung und prüfung” company.¹⁵ It consists in Al_0.7Ga_0.3As layers with decreasing thicknesses, on GaAs substrate. The thickness of each layer is certified by transmission electron microscopy. For this study we will use two regions of BAM-L200 sample represented on Fig. 1(a₁) and (a₂). The Al_0.7Ga_0.3As/GaAs doublet layers indexed from P₁ to P₈ and from P₉ to P₁₄ are respectively certified from 587 to 76.5 nm and from 76.5 nm to 17.5 nm. There is also another area where: the doublet layers indexed from P₁₅ to P₁₇ are certified from 13.3 nm to 6.9 nm and the doublet layers indexed from P₁₈ to P₂₀ are not certified but estimated from 4.6 nm to 2 nm. Separated Al_0.7Ga_0.3As layers indexed W₈, W₁₀ and W₁₁ are certified at 38 nm, 14.2 nm and 3.5 nm. The sample area with In_0.2Ga_0.8As layers will not be analyzed in this work. More information on how the certification was made can be found in the certification report of the sample.¹⁷ The sample is homogeneously n doped (Si), with n = 5 × 10¹⁷ cm⁻³.

Fig. 1 (a₁) and (a₂) Represents two regions of interest on BAM L-200 sample. The Al_0.7Ga_0.3As/GaAs doublet layers indexed from P₁ to P₈ and from P₉ to P₁₄ are respectively certified from 587 to 76.5 nm and from 76.5 nm to 17.5 nm. The separated Al_0.7Ga_0.3As layers indexed W₈, W₁₀ and W₁₁ are certified at 38 nm, 14.2 nm and 3.5 nm. Area with the thinnest doublet layers indexed from P₁₅ to P₁₇ are certified from 13.3 nm to 6.9 nm, the doublet layers indexed from P₁₈ to P₂₀ are not certified but estimated from 4.6 nm to 2 nm. (b) Band diagram for GaAs/Al_0.7Ga_0.3As junction.^18–20

On Fig. 1(b) we present the band diagram for the GaAs/Al_0.7Ga_0.3As heterojunction.^18–20 Specifically, the energy diagram of Al_xGa_1−xAs with respect to the concentration x of aluminum was calculated using the work of Levinstein et al.¹⁹ We obtain χ (electronic affinity), E_g (band gap) and m* (effective electron mass) for Al_0.7Ga_0.3As. The values of χ and m* for both materials are given in the theoretical section. Afterwards, m* is related to N_c (equivalent density of state in the conduction band, in cm⁻³)²⁰ by equation: N_c = 4.83 × 10¹⁵(m* × T)^3/2, where m* is the effective mass in units of the electron mass, and T is the temperature in Kelvins. Knowing the concentration of donor dopants n = 5 × 10¹⁷ cm⁻³, we calculate the difference between the Fermi level E_f and the conduction band energy E_c for GaAs and Al_0.7Ga_0.3As using Fermi–Dirac statistics:²⁰

where k is the Boltzmann constant, [scr F, script letter F]_1/2 is the Fermi–Dirac integral of order 1/2, and T = 300 K. We find E_f − E_c = 0.020 eV for GaAs and −0.015 eV for Al_0.7Ga_0.3As. The work function is given by W = χ − (E_f − E_c). Finally, we find a theoretical work function difference ΔW = 0.50 eV between GaAs and Al_0.7Ga_0.3As. Moreover, the thickness of depletion layer of GaAs/Al_0.7Ga_0.3As junction is calculated using the formula:²⁰
where e is the elementary charge, ΔV is a theoretical electrostatic potential difference between GaAs and Al_0.7Ga_0.3As, ε_GaAs and ε_AlGaAs are respectively the permittivities of the GaAs and AlGaAs materials.

Here we use KFM to investigate BAM L-200 structure, which is one of the techniques used to detect the contact potential difference (CPD) which is equal to the work function difference between sample and atomic force microscopy (AFM) tip (see ref. 21 for further information). In KFM, an electrostatic excitation (DC + AC voltage) is applied to the tip at the cantilever resonance frequency. The electrostatic excitation generates a cantilever oscillation (or resonance frequency shift) if the cantilever DC bias does not match the CPD. To measure CPD, a DC bias feedback is introduced in order to nullify the cantilever oscillation (i.e. amplitude modulation) or frequency shift (i.e. frequency modulation) at the electrostatic excitation angular frequency. This generates a CPD map. Here, we use both amplitude modulation (AM) and frequency modulation (FM) KFM systems, besides, we use non-contact AFM²² and KFM modes simultaneously.

All measurements have been performed with an Omicron Nanotechnology VT-AFM UHV system with a Nanonis controller (SPECS Zürich). In this study we use three kinds of tips. The first is Budgetsensors ElectriMulti75 G (EM75) Cr–Pt coated tips commonly used for electric modes like KFM. Its tip radius is around 25 nm, its fundamental resonant frequency is around 67 kHz. The second consists in an EM75 tip overcame by a tungsten overtip (EM75W), deposited by electron beam-induced deposition in a focused ion-beam microscope. The third is a nanosensors super sharp silicon (SSS) tip often used for high resolution measurements. Its tip radius is between 2 and 5 nm, its fundamental resonance frequency around 300 kHz. SSS tip was sputtered with an argon beam at 4 keV during 20 min in order to get rid of isolating silicon oxide. Using the method derived from the work of Giessibl,²³ we estimate the AFM peak-to-peak oscillation amplitude. Distance between sample and oscillating tip is measured by using approach–retract curves as a function of cantilever detuning frequency Δf.

Theoretical section

The electrostatic potential V(r) is simulated using the finite volumes Poisson solver of the TB_Sim code.²⁴ The electron affinities χ_i of the materials are included explicitly into the simulation through frozen surface dipoles inducing a potential step – χ_i between material i and vacuum, and a potential step (χ_i+1 − χ_i) at the interface between materials i and i + 1. Including these dipoles into the simulation is necessary to account for the CPD contrast. Accordingly, the reference conduction band energy E_c at zero potential is set to zero in all materials. Hence, in absence of volume charge density, the conduction band offset between materials i and i + 1 is determined by the potential step induced by the interface dipoles: ΔE_c = −eV_i+1 + eV_i = (χ_i − χ_i+1). In this study, χ_GaAs = 4.07 eV and χ_AlGaAs = 3.54 eV. The volume charge density is assumed to depend locally of the electrostatic potential and to follow the bulk expression:
where N_d = 5 × 10¹⁷ cm⁻³ is the uniform donor concentration, N_c,i is the equivalent density of states of the conduction band in material i, calculated at T = 300 K with effective masses m* = 0.06 for GaAs and m* = 0.12 for Al_0.7Ga_0.3As. As discussed above, E_c = 0 (the band offsets are included in the potential). E_f is also set to zero by convention. A different choice for E_f would simply lead to a global potential shift, also shifting the potential reference for the tip voltage, but leaving the physics unchanged. The Poisson equation is solved self-consistently with the above expression for the charge density ρ(r̲). This leads to depletion regions at the interfaces and to the band curvatures schematized on Fig. 1(b) and 4(d). The KFM tip is modelled by a portion of sphere extended by a cone (see Fig. 4(b₁)). A constant potential is imposed on the tip surface. The electrostatic force between the tip and the sample is calculated by numerical integration on the surface S of the tip:²⁵

At each position of the tip, the self-consistent calculation is performed for 3 values of the tip potential, which defines a parabola for the tip voltage dependence of the vertical component of the force F_z(V_tip). It has been checked that the parabolic approximation is very good despite the non-linear relation between the free carrier density and the potential. The extremum of the parabola gives the tip voltage which minimizes the force, which is measured in AM-KFM. Simulations were performed at various tip-sample distances ranging from 1 nm to 21 nm. This allowed extracting the tip voltage which minimizes the force derivative dF_z/dz, which is measured in FM-KFM.

Results and discussion

On Fig. 2 we present measurements on the region presented on the Fig. 1(a₁). These measurements are made on the sample without any surface preparation (Fig. 2a₁ and a₂) and after heating under UHV at 150 °C during 30 min (Fig. 2b₁ and b₂) in order to remove the adsorbed water from the sample surface. Firstly, from nc-AFM topography images (Fig. 2a₁ and b₁) we detect that sample surface is very flat (z scale below 5 nm). Secondly, by comparing AM-KFM images before and after sample preparation (Fig. 2a₂ and b₂) we conclude that the surface moisture is totally occulting the KFM Al_0.7Ga_0.3As/GaAs contrast; consequently such a preparation is essential. In Fig. 2(b₂) all the doublet layers indexed from P₁ to P₈ and separated layers indexed W₈, W₁₀ are detected which is in agreement with the work of N. Vorbringer-Dorozhovets et al.¹⁶

Fig. 2 (a₁) and (b₁) Non-contact AFM images on P2–P8 area using EM75 tip with an oscillation amplitude 35 nm and a detuning Δf = −25 Hz. Simultaneously recorded AM KFM images (a₂) on ‘as received’ sample, (b₂) after 150 °C sample heating in UHV conditions. Both AM KFM images are acquired using first cantilever harmonic f₁ = 437 kHz and electrostatically excited with V_ac = 100 mV.

To check the best spatial resolution that our instrument is able to achieve we switch to the sample region presented in the Fig. 1(a₂). A systematic study (not shown here) has been performed to adjust the detuning frequency shift and the oscillation amplitude to maximize the CPD sensitivity. We also adjusted the scan speed and all feedback gains to not have artificial influence on CPD. We present here averaged (20 lines) CPD cross sections in order to compare CPD measurements. At the beginning, we made the measurement by AM KFM [Fig. 3(a)], but finally we choose FM KFM mode, which provides a higher CPD difference (between Al_0.7Ga_0.3As and GaAs layers) comparing to the AM KFM measurement. Such higher CPD difference is due to the fact that the FM mode signal is proportional to the force gradient and not to the force directly as in AM mode.²¹ As described previously, FM KFM sample characterizations were performed with three kinds of AFM tips: EM75, EM75W, SSS [Fig. 3(a–c)].

Fig. 3 KFM measurement on P₉–P₂₀ area. (a) AM KFM, CPD cross section recorded with the Cr–Pt 25 nm tip apex – EM75. AFM frequency detuning is Δf = −25 Hz and oscillation amplitude is 70 nm. AM KFM is acquired using first cantilever harmonic f₁ = 437 kHz and electrostatically excited with V_ac = 100 mV. (b–d) FM KFM, CPD cross sections recorded with the three different tips apexes: (b) Cr–Pt 25 nm – EM75 (c) Cr–Pt 25 nm with W overtip – EM75W (d) Si 5 nm – SSS. Simultaneous non-contact AFM oscillation amplitudes are 35 nm for EM75 and EM75W tips, and 90 nm for SSS tip. AFM frequency detuning Δf = −40 Hz is applied which corresponds to 3 nm tip-sample distance. All FM KFM measurements are acquired using modulation frequency f = 1 kHz and electrostatically excited with V_ac = 500 mV for EM75 and EM75W tips and electrostatically excited with V_ac = 3000 mV for SSS tip.

All KFM measurements show a decreasing contrast relative to the layer thickness. Apart from the AM KFM characterization which is indeed less resolved, we notice that every FM KFM cross-section is very similar in terms of relative differences of CPD. The potential tendency seems to remain the same despite the fact that each of these measurements was done using different AFM tips.

For the better understanding of CPD evolution on BAM-L200 sample we performed 3D simulations of the electrostatic potential. Firstly, we simulate only the sample structure without the AFM tip apex on the same sample region as characterized by KFM on Fig. 3. On Fig. 4(a₁) we present the 2D potential cross-section made perpendicularly to sample surface, through all the layers of interest. The 1D potential cross-sections using 1, 3 and 9 nm distances from the sample surface are shown on Fig. 4(a₂), where decrease of the electrostatic potential as a function of distance is visible due to receding from the Al_0.7Ga_0.3As/GaAs interface dipoles.

Fig. 4 (a₁) Simulated 2D potential cross-section extracted from a 3D simulation on BAM L-200 sample and (a₂) corresponding 1D potential cross-section using 1, 3 and 9 nm distances from the sample surface. (b₁) 2D potential cross-section extracted from a 3D simulation of the sample with the AFM tip at 3 nm from the surface. (b₂) Simulated FM KFM CPD, using 1, 3 and 9 nm distances between the tip apex and the sample surface. (c) Contrast with respect to the layer thickness for P9–P17 regions. (d) Schematic description of the depletion layer and band bending overlap phenomenon.

By comparing experimental CPD and calculated electrostatic potential values we conclude that the decreasing tendency is very similar. Consequently, the assumption that CPD evolution for BAM L-200 sample depends only on the KFM experimental setup is wrong. Here this evolution is intrinsic to the sample electronic properties.

In order to compare the calculated electrostatic potential with a KFM CPD signal, we introduce to our simulation the AFM tip apex and we calculate the CPD signal. To do so, we use the theoretical protocol described elsewhere,²⁵ and we model AFM tip with respect to EM75 geometry. Therefore, we are able to implement tip position anywhere above the sample surface and to calculate CPD. On Fig. 4(b₁) we present the 2D potential cross-section made perpendicularly to sample surface, through all the layers of interest and the AFM tip. FM KFM CPD calculated using 1, 3 and 9 nm distances between the tip and the sample is presented on the Fig. 4(b₂). In that case, the CPD variations are equivalent to the electrostatic potential variations but convoluted with the shape of the tip. Thus, it is natural that CPD variations follow the variations of electrostatic potential.

For the quantitative comparison of the experimental and calculated results we introduce a contrast parameter, defined as:

where CPD_AlGaAs is the maximum of CPD signal measured on Al_0.7Ga_0.3As, CPD_GaAs is the minimum of CPD signal measured in the middle of the GaAs layer located between the corresponding Al_0.7Ga_0.3As twin layers, and ΔW represents the maximum value theoretical work function difference between GaAs and Al_0.7Ga_0.3As layers. As explained before and presented on Fig. 1(b), ΔW = 0.5 eV. Thus, the contrast represents the fraction of the maximal signal that KFM is able to reach on thick GaAs/Al_0.7Ga_0.3As junctions and which is measured outside of depletion region.

On Fig. 4(c) we compare calculated and experimental contrasts for the area designed in Fig. 1(a₂) by using the results presented on Fig. 3(b–d) and Fig. 4(a₂ and b₂) considering 3 nm of distance from the sample surface. Measurements and simulation using FM KFM, as well as, simulation of electrostatic potential without AFM tip show very similar contrast evolution. For the thickest GaAs layer (38.5 nm), the contrast is around 30%, and it decreases to 0 for the smallest layers (<5 nm). The decreasing contrast tendency is the same for each curve. Resemblance of all FM KFM contrasts with electrostatic potential simulated 3 nm above the sample surface confirms that CPD evolution depends mainly on the intrinsic evolution due to the sample electronic properties and not only KFM resolution limit.

We understand that this phenomenon is due to the narrowness of the Al_0.7Ga_0.3As and GaAs layers. A carrier depletion layer creates a band bending at every interface between two semi-conductors. Moreover, in the case of very thin layers, the depletion layers will overlay, creating a band bending covering. Such phenomenon becomes more and more important as the thickness of the layers decreases. Due to the band bending covering, the energy difference (ΔW′) between the local vacuum levels of GaAs and Al_0.7Ga_0.3As becomes smaller than the work function difference between the thick layers (ΔW = 0.5 eV) [Fig. 4(d)]. As we have found before, the thickness of the depletion layer between Al_0.7Ga_0.3As and GaAs is L ≈ 50 nm. Thus, in the case of analyzed area (the regions from P₉ to P₂₀, where the layer thickness changes from 38.5 nm to 1 nm), the band bending covering is affecting our entire FM KFM measurement. Consequently, FM KFM is able to detect changing in the band bending at a nanometer scale, and reliable quantitative contrast values (i.e. not significantly influenced by FM KFM resolution limit) between Al_0.7Ga_0.3As and GaAs layers.

Conclusions

In this study, we performed highly resolved KFM measurements on a reference BAM-L200 sample, composed of Al_0.7Ga_0.3As and GaAs layers with variable thicknesses. The CPD contrast between GaAs and Al_0.7Ga_0.3As showed a decreasing tendency with the layers thickness and it disappears when reaches 5 nm thick layer. In order to fully understand this phenomenon, we made a self-consistency simulation of the electrostatic potential and CPD, on the experimentally observed sample area. The simulation demonstrated that the decreasing tendency is due to an overlay of depletion layers, which causes a band bending overlap. Consequently, CPD evolution for BAM L-200 sample is intrinsic to the sample electronic properties and does not depend only on the KFM experimental setup. Therefore, by KFM measurement we are able detect the CPD signal in the nanometer scale which is induced by the band bending between Al_0.7Ga_0.3As and GaAs.

Acknowledgements

We acknowledge D. Mariolle for helpful discussions and technical help. This work was supported by the French “Recherche Technologique de Base” Program. The measurements and simulations were performed on the CEA Minatec Nanocharacterization Platform (PFNC).

References

1. M. Senoner, T. Wirth, W. E. S. Unger, M. Escher, N. Weber, D. Funnemann and B. Krömker, J. Surf. Anal., 2005, 12, 78–82.
2. M. Niebelschutz, G. Ecke, V. Cimalla, K. Tonisch and O. Ambacher, J. Appl. Phys., 2006, 100, 074909–074903.
3. J. T. Heath, C.-S. Jiang and M. M. Al-Jassim, J. Appl. Phys., 2012, 111, 046103.
4. Z. Wang, M. Zdrojek, T. Mélin and M. Devel, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 085425.
5. M. Nonnenmacher, M. P. O'Boyle and H. K. Wickramasinghe, Appl. Phys. Lett., 1991, 58, 2921–2923.
6. W. Melitz, J. Shen, A. C. Kummel and S. Lee, Surf. Sci. Rep., 2011, 66, 1–27.
7. Ł. Borowik, K. Kusiaku, D. Deresmes, D. Théron, H. Diesinger, T. Mélin, T. Nguyen-Tran, P. Roca and I. Cabarrocas, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 073302.
8. S. Pouch, M. Amato, M. Bertocchi, S. Ossicini, N. Chevalier, T. Mélin, J.-M. Hartmann, O. Renault, V. Delaye, D. Mariolle and Ł. Borowik, J. Phys. Chem. C, 2015, 115, 26776–26782.
9. A. Patsha, P. Sahoo, S. Amirthapandian, A. K. Prasad, A. Das, A. K. Tyagi, M. A. Cotta and S. Dhara, J. Phys. Chem. C, 2015, 119, 21251–21260.
10. Ł. Borowik, T. Nguyen-Tran, P. Roca i Cabarrocas and T. Mélin, J. Appl. Phys., 2013, 114, 204305.
11. F. Krok, J. J. Kolodziej, B. Such, P. Czuba, P. Struski, P. Piatkowski and M. Szymonski, Surf. Sci., 2004, 566, 63–67.
12. K. Matsunami, T. Takeyama, T. Usunami, S. Kishimoto, K. Maezawa, T. Mizutani, M. Tomizawa, P. Schmid, K. M. Lipka and E. Kohn, Solid-State Electron., 1999, 43, 1547–1553.
13. M. Takashi, U. Takao, K. Shigeru and M. Koichi, Jpn. J. Appl. Phys., 1999, 38, L767.
14. M. Takashi, U. Takao, K. Shigeru and M. Koichi, Jpn. J. Appl. Phys., 1999, 38, 4893.
15. M. Senoner, T. Wirth, W. Unger, W. Österle, I. Kaiander, R. L. Sellin and D. Bimberg, Surf. Interface Anal., 2004, 36, 1423–1426.
16. N. Vorbringer-Dorozhovets, B. Goj, T. Machleidt, K. H. Franke, M. Hoffmann and E. Manske, Meas. Sci. Technol., 2014, 25, 044006.
17. M. Senoner, Nanoscale stripe pattern for testing of lateral resolution and calibration of length scale.
18. A. Marty, J. P. Bailbe and G. Rey, Rev. Phys. Appl., 1982, 17, 453–464.
19. M. Levinstein, S. Rumyantsev and M. Shur, Handbook Series on Semiconductor Parameters, World scientific, London, 1999.
20. S. Sze, Physics of semiconductor devices, John Wiley and Sons, Hoboken, 1981.
21. S. Sadewasser and T. Glatzel, Kelvin Probe Force Microscopy, Springer, Berlin, 2012.
22. R. Garcia and R. Pérez, Surf. Sci. Rep., 2002, 47, 197–301.
23. F. J. Giessibl, Rev. Mod. Phys., 2003, 75, 949–982.
24. Y.-M. Niquet and C. Delerue, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075478.
25. Ł. Borowik, K. Kusiaku, D. Théron and T. Mélin, Appl. Phys. Lett., 2010, 96, 103119.

---