Modeling of CO2/CH4 gas mixture permeation and CO2 induced plasticization through an asymmetric cellulose acetate membrane
M. Saberia,
S. A. Hashemifardb and
Ali. A. Dadkhah *a
*a
aDepartment of Chemical Engineering, Isfahan University of Technology, Isfahan 84156-83111, Iran. E-mail: dadkhah@cc.iut.ac.ir; Fax: +98-313391-5644; Tel: +98-313391-5644
bChemical Engineering Department, Persian Gulf University, Bushehr 75169-13817, Iran
First published on 14th January 2016
Abstract
The target of this study is derivation of a mathematical model for permeability and effective diffusivity of mixed gases in glassy polymeric membranes in the presence of plasticization. Diffusion coefficients for all components were assumed to be a function of the plasticizing component. The partial immobilization model was employed to determine the fraction of mobile sorbed gases. The model accurately predicted the mixed gas permeation behavior of CO2 as a plasticizer and CH4 as a second component through the asymmetric cellulose acetate membrane in the presence of plasticization. The model parameters were calculated by fitting experimental data from the literature. The plasticization parameter (β) decreased for both CO2 and CH4 with increasing fraction of CH4 in the feed. This means that plasticization of a glassy polymer was suppressed. This decrease was caused by competitive sorption between CO2 and CH4. Indeed, CH4 in the feed acts as an anti-plasticizer. In addition, permeances of the feed gas components were decreased in comparison to those of the pure gases, which might be attributed to reduction of sorption and the occupation of Langmuir sites by the second component. Moreover, the immobilization factor (F) for CO2 and CH4 decreased with increase in CH4 fraction due to reduction of plasticization. Deff/l for pure CO2 was significantly pressure dependent. However with increasing fraction of CH4 in the feed, this dependency almost disappeared. Finally, the model predicted the decreasing trend of the separation factor for CO2/CH4 mixed gases with pressure accurately. Therefore, the presented model is capable of being a useful tool with which to enhance our knowledge related with permeation behavior of mixed gas systems through glassy polymeric membranes in the presence of plasticization.
1. Introduction
Membranes with different organic and inorganic materials, such as polymers, carbon molecular sieves (CMS), zeolites, ceramics, and graphene sheets, are widely used in gas separation processes.1–5 In addition, nano-structure materials, such as silica nanoparticles, metal oxide nanoparticles, carbon nanotubes (CNTs), and metal–organic frameworks (MOFs), have also been used to produce mixed matrix membranes (MMMs) for gas separation.1 However, polymers are the dominant membrane materials used in natural gas separation processes.3,4 In order to preferentially remove carbon dioxide (CO2), glassy polymeric membranes are often applied rather than rubbery polymeric membranes because of their high CO2/CH4 or CO2/N2 selectivity.4,6–9 It is well known that most of the rubbery polymers exhibit high permeability but at the cost of low selectivity.9 Although some types of glassy membranes have a good performance in CO2 separation, at high-pressure CO2/CH4 or CO2/N2 separation, the performance of these membranes can be hindered by the plasticization phenomenon.7–11 The polymeric matrix usually swells due to the highly sorbed CO2, as a condensable gas. Then, interaction between adjacent segments of the polymer chain is reduced, and the glass transition temperature is depressed.8,10,11 Therefore, it will cause an increase in segmental mobility and free volume of the polymeric matrix.8,10,11 Furthermore, diffusivity and permeability of sorbed gases increase with pressure, and therefore eventually, the membrane loses its selectivity.8,10 In the permeability vs. pressure curves, the permeability goes through a minimum, which is known as the “plasticization pressure”. This is the minimum CO2 pressure necessary to induce plasticization.10,12–16 In some cases in which the membrane has a thin skin (especially asymmetric membranes with a thin skin layer), there is no minimum pressure and permeance increases with pressure monotonously,11,17 which means plasticization pressure decreases with decrease in thickness.18At higher pressures than the plasticization pressure, permeability of pure CO2 in a glassy membrane increases with pressure, whereas for an inert gas, such as N2 or CH4, permeability decreases with pressure; therefore, ideal gas selectivity increases with pressure.19 The mixed gas permeation behavior in glassy polymers, especially in CO2/CH4 or CO2/N2 separation, is significantly different compared with that in pure gas separation.19–21 For example, mixed gas CO2/CH4 selectivity for polyimide (6FDA-mPD) was reported to be about 4 at a feed pressure of 17.5 atm, whereas the ideal selectivity for this was observed to be about 60.21 Moreover, permeation behavior of Matrimid membranes under a mixed gas of CO2/CH4 showed that the selectivity of the membranes plasticized by CO2 dramatically decreased with pressure. Normally, CO2 swelling and plasticization cause permeability of CH4 versus pressure to be increased more than CO2 permeability; therefore, in contrast to that for pure gas, the selectivity of the mixture of gases decreases rapidly.22,23 Moreover, Donohue et al.20 reported that unlike the ideal selectivity, the mixed gas selectivity of a CO2/CH4 mixture by a cellulose acetate membrane decreased with pressure due to plasticization. They interpreted that the presence of CH4 not only reduces CO2 solubility, but also lowers the diffusivity of CO2 for a given partial pressure, which resulted in lowering of the CO2 permeability in the presence of CH4. On the other hand, the presence of CO2 in the feed decreased CH4 solubility in reference to pure CH4, whereas due to the membrane plasticization by dissolved CO2, diffusivity of CH4 increased as well. They reported that the enhancement in CH4 diffusivity was much greater than the decrease in solubility, which finally led to an increase in CH4 permeability.
Furthermore, Visser et al.19 demonstrated that introducing N2 or CH4 to the CO2 feed mixture apparently suppressed plasticization of asymmetric a polyethersulfone (PES)/polyimide (PI) hollow fiber membrane. Its effect was more pronounced at higher concentrations of inert gases. By introducing N2 or CH4 as a second component to the feed, due to lower sorption of CO2, permeances of CO2 were fewer than those of the pure gas one.
As a first study, Koros et al.24 developed a model for permeation of mixed gases in polymeric membranes based on the Dual Mode Sorption (DMS) model of a mixed gas system,23 but they did not consider plasticization. As a result, their model could not predict the permeation of mixed gases when a plasticization phenomenon occurs.19 Lee et al.26 developed a model for permeation of mixed gases in polymeric membranes in the case of plasticization. Based on their model, the diffusion coefficient of each component is dependent on all of the other components and all of the sorbed gases are considered as mobile molecules.
Although the permeation behavior of mixed gases is significantly different from pure gases due to competitive sorption, less attention has been given to mixed gas permeation. Therefore, a simple and comprehensive model is required to simulate this behavior.
In a previous study,27 a mathematical model for permeation of mixed gases in glassy polymeric membranes in presence of plasticization was developed by us. In this study, a model for effective diffusivity for a gas component in a mixed gas feed based upon Fick's first law was developed. Then, permeation behavior of CO2/CH4 mixed gas in an asymmetric cellulose acetate membrane18 was studied and parameters of the model were calculated and discussed.
2. Theory and modeling
2.1. Sorption
Based on the concept that polymers in a glassy state contain some microvoids or “holes” throughout the polymer matrix, two mechanisms of sorption occur in these polymers: (i) ordinary dissolution based on Henry's law and (ii) “hole-filling” according to Langmuir theory. This type of sorption is known as the Dual Mode Sorption (DMS) model.28,29 The equilibrium isotherm for a pure gas “A” is expressed as follows:
 | (1) |
| SA = CA/pA | (2) |
Koros et al.25 extended the DMS model for mixed gas component systems to consider a competitive sorption effect. Based on their assumption, components of a gas mixture in the Henry region of a glassy polymer are sorbed independent of each other, whereas the gas molecules in the mixture compete for sorption on Langmuir sites. The concentration of gas “A” of a binary mixture is obtained by25
 | (3) |
Similarly, the sorption isotherm for component “B” is given by25
 | (4) |
The total sorbed gas concentration is
 | (5) |
Obviously, when either pA or pB approaches zero, eqn (5) reduces to the pure gas relation, i.e. eqn (1).
2.2. Permeation
Based on the partial immobilization model, the total concentration of sorbed gas in glassy polymers is divided into a mobile part with a diffusion coefficient D and concentration Cm, whereas the balance (C − Cm) is totally immobilized. This means that all the gas dissolved in the Henry region is mobile, whereas for the Langmuir sites, a fraction (F) of the adsorbed gas molecules, is mobile and the remainder (1 − F) is immobile.32,33 F is usually called the immobilization factor, which depends on the nature of the penetrant–polymer system as well as the system temperature.18,34 This factor represents the ratio of the diffusivity through the microvoids to that through the polymeric matrix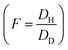 .33
.33
Then, the flux (N) of component “A” of a two component system is expressed as follows:32,35,36
 | (6) |
 | (7) |
Diffusivity of component “A” in the presence of plasticization is given by27,35
DA(CmA) = DA0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(βACmA) exp(βACmA)
| (8) |
Then, eqn (6)–(8) yield the following expression for the flux of penetrant gas in glassy polymers:
 | (9) |
Then, effective diffusivity from eqn (9) is calculated as follows:
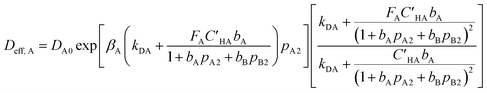 | (10) |
Furthermore, under steady state conditions, the permeability “A” (PA) can be defined as follows:37,38
 | (11) |
By substituting eqn (8) in eqn (6) and then integrating and combining it with eqn (11), permeability of component “A” in a binary mixture through glassy polymers in the presence of plasticization is expressed as follows:27
 | (12) |
It should be noted that negligible downstream pressure of component “A” (pA1 = 0) was assumed in the derivation of eqn (12).
For component “B” in a binary mixture, diffusivity is given by eqn (13):27
DB(CmA) = DB0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(βBCmA) exp(βBCmA)
| (13) |
Moreover, concentration of the mobile part of component “B” is calculated as follows:
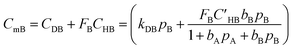 | (14) |
Combining eqn (6), (13), (14) and (11) yielded the permeability of component “B” as follows:27
 | (15) |
Downstream pressure of components was assumed to be zero.
Moreover, by writing eqn (9) for component “B”, effective diffusivity for component “B” is given as follows:
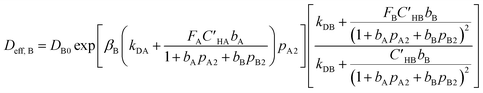 | (16) |
It can be noted that permeability for component “i” in polymeric membranes is defined as the product of diffusivity and solubility:31,39,40
| Pi = Dave,i × Si | (17) |
For a two component system, the selectivity of the membrane is defined as the ratio of their permeability coefficients, which is given by eqn (18):39,41
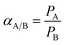 | (18) |
3. Results and discussion
3.1. Model validation and mathematical procedure
To validate the model, the predictions of the proposed model were compared against the permeation of CO2/CH4 mixtures with different compositions in a cellulose acetate membrane.20 The mathematical procedure to predict permeation of a mixed gas in a cellulose acetate membrane was as follows:(i) Calculation of parameters of DMS model (eqn (1)) for pure CO2 and CH4 by fitting this equation using sorption experimental data.
(ii) Parameters obtained from step (i) were combined with eqn (12) and fitted against experimental data for permeation of CO2 to compute parameters β, F and D0/l for CO2.
(iii) Parameters obtained from steps (i) and (ii) (FCO2) were combined with eqn (15) and fitted against experimental data for permeation of CH4 to compute parameters β, F and D0/l for CH4.
It should be noted that the parameters of the DMS model and non-linear proposed models for permeation of CO2 and CH4 were obtained by a least squares regression technique.
3.2. Sorption
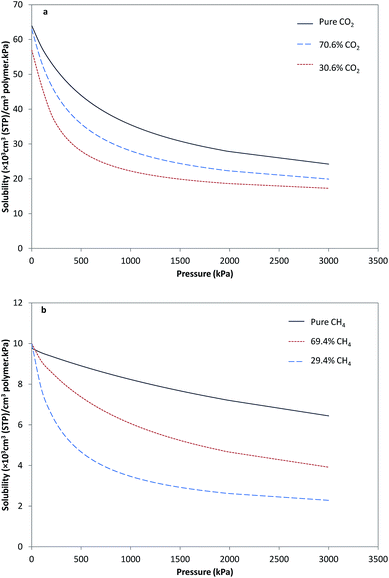
In order to study permeation of a mixed gas system in a cellulose acetate membrane, it was first necessary to estimate the sorption isotherm of the pure gases in the membrane. Then, by using the results of pure gas sorption, combined with the dual mode sorption model for mixed gas systems (eqn (3) and (4)), the mixed gas sorption in the membrane was predicted. Using experimental data, parameters of the dual sorption model (eqn (1)) for pure CO2 and CH4 were calculated, as shown in Table 1.20 Fig. 1a and b show the solubility of pure CO2 and pure CH4 and also the concentration of CO2 and CH4 in the mixed gas (CO2/CH4) with different compositions versus pressure in the membrane. For the sorption of gases in the membrane, at lower pressures, solubility severely decreases; however, for higher pressures, due to occupation of Langmuir sites, decrease in solubility slope occurred. For the sorption of CO2 in the presence of CH4, CO2 was sorbed in the Henry region of the glassy membrane independent of the second component, whereas in Langmuir sites, a competitive sorption occurred and a part of these sites were occupied by CH4 molecules. Then, the sorption of CH4 in Langmuir sites caused less CO2 to be sorbed at these sites at a specific pressure, hence the solubility of CO2 sorbed in the presence of CH4 in the polymer decreased relative to that of pure CO2. By increasing the content of CH4 in the feed, more CH4 was sorbed in Langmuir sites, and then more reduction of CO2 sorption in polymer was observed. Moreover, competitive sorption occurred for CH4 and with increase in CO2 fraction in the feed, the solubility of CH4 was decreased.| Component | kD (cm3 (STP) per cm3 per kPa) | C′H (cm3 (STP) per cm3) | b (kPa−1) |
|---|---|---|---|
| CO2 | 1.43 × 10−2 | 37.29 | 1.32 × 10−3 |
| CH4 | 1.51 × 10−3 | 37 | 2.22 × 10−4 |
3.3. Permeation
Fig. 2 shows the effect of feed composition on the CO2 permeances in a cellulose acetate membrane in binary mixtures of CO2/CH4. This figure compares the experimental data of Donohue et al.20 with the predictions of the proposed model, calculated by eqn (12), using the parameters of CO2 and CH4 shown in Tables 1 and 2. In the case of pure CO2, permeance increases with pressure due to plasticization. This trend was due to the thin skin of asymmetric membranes, in which permeance increases with pressure monotonously.19,20 The presence of CH4 in the feed decreases sorption of CO2 due to competitive sorption, and this decrease in solubility lowers the diffusivity of CO2 for a given pressure and also suppresses plasticization, consequently reducing the CO2 permeance.20 This depression trend was increased with increase in CH4 fraction. Moreover, permeance of CO2 with different amounts of CH4 in the feed was increased with pressure at a lower slope than that for pure CO2, which means that by introducing CH4 into the feed, CO2-induced plasticization was suppressed dramatically. It should be mentioned that although solubility decreased with pressure, diffusivity increased due to plasticization. This increase overcomes the decrease in solubility, therefore permeance increased with pressure for all cases. It was apparent that the model predictions showed good agreement with respect to the experimental points. | ||
| Fig. 2 CO2 permeance in cellulose acetate membrane as a function of pressure with different compositions of the feed.20 | ||
| Composition | βCO2 | FCO2 | D0,CO2/l | R2 |
|---|---|---|---|---|
| Pure CO2 | 0.086 | 0.06 | 0.00253528 | 0.987 |
| 70.6% CO2 | 0.055 | 0.039 | 0.0027093 | 0.967 |
| 30.6% CO2 | 0.036 | 0.028 | 0.00293148 | 0.842 |
As mentioned above, parameters of eqn (12) (β, D0/l and F) were calculated using sorption parameters of pure CO2 and CH4 and also the experimental data20 for CO2 permeances with different fractions in the feed in a cellulose acetate membrane, as shown in Table 2. As can be seen, these parameters are strongly dependent on the feed composition. It can be noted that the experimental data are for an asymmetric membrane and the reported results for permeation are permeability per thickness (permeance in GPU, in which 1 GPU = 10−6 cm3 (STP)/(cm2 s cmHg)). Then, D0/l and D/l were determined in the present study.
For βCO2 with increasing CH4 fraction in the feed, competitive sorption caused less CO2 to be sorbed in the polymer at a specific pressure, hence βCO2 showed decreased plasticization ability. Moreover, with increasing fraction of CH4 in the feed, sorption of CO2 in the membrane and also plasticization decreases.
The diffusion coefficient of CO2 at zero penetrant concentration per unit membrane thickness (D0,CO2/l) decreased with CO2 fraction. With increasing CH4 fraction in the feed and decreasing plasticization, D0/l for CO2 increases. This trend is consistent with the work of Duthie et al.34 and Okamoto et al.,42 which reported that D0 increases with decreasing plasticization.
The immobilization factor for CO2 (FCO2) was decreased with increasing CH4 (decreasing CO2 fraction) in the feed, as shown in Table 2. This means that the diffusivity of CO2 through the microvoids (Langmuir sites) decreased in comparison to the diffusion through the polymer matrix (Henry region). This occurred due to the occupation of a portion of the Langmuir sites by CH4 molecules, therefore CO2 molecules had fewer sites for sorption, whereas sorption of CO2 through the polymer matrix was independent of CH4. The second major reason for the decrease in FCO2 was reduction of the mobility of CO2 molecules due to suppression of plasticization.
The effect of feed composition on the CH4 permeances in a cellulose acetate membrane in a binary mixture of CO2/CH4 is shown in Fig. 3. This figure compares the experimental data of Donohue et al.20 with the predictions of the proposed model, calculated by eqn (15), using the parameters of CO2 and CH4 shown in Tables 1–3. Permeance of CH4 with different fractions of CO2 increased with pressure, and at higher fraction of CH4, the increasing trend had a lower slope. This resulted from higher sorption of CH4 in the membrane, which led to decrease in plasticization. Moreover, at specific pressures, permeances of higher fractions of CH4 in the feed, due to higher sorption of CH4, were higher than those of the lower fractions.
 | ||
| Fig. 3 CH4 permeance in cellulose acetate membrane as a function of pressure with different compositions of the feed.20 | ||
| Composition | βCH4 | FCH4 | D0,CH4/l | R2 |
|---|---|---|---|---|
| 29.4% CH4 | 0.043 | 0.24 | 0.0004369 | 0.978 |
| 69.4% CH4 | 0.036 | 0.13 | 0.0007152 | 0.942 |
Parameters of eqn (15) (β, D0/l and F) were calculated using sorption parameters of pure CO2 and CH4, immobilization factor for CO2 (FCO2) and also the experimental data20 for CH4 permeances with different fractions in the feed in a cellulose acetate membrane, as shown in Table 3. As seen in Table 3, similar to the plasticization ability of CO2, βCH4 decreased as its fraction increased due to suppression in plasticization. D0,CH4/l also increases with CH4 fraction.
Moreover, the immobilization factor for CH4 (FCH4) decreases with fraction of CH4 in the feed. In this case, with an increase in CH4 fraction in the feed, Langmuir sites occupied by CH4 was enhanced; however, plasticization and then mobility of CH4 molecules reduced. This in turn caused a decrease in FCH4.
3.4. Diffusion
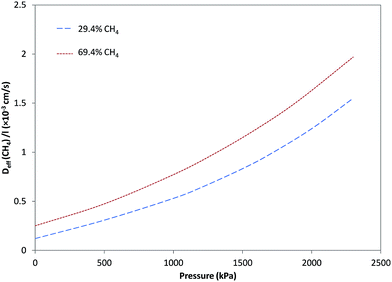
Fig. 4 and 5, respectively, illustrate the estimated effective diffusivity per unit membrane thickness (Deff/l) versus pressure for CO2 and CH4 derived from eqn (10) and (16) utilizing parameters from Tables 1–3. Although D0/l increased as a function of CH4 fraction, variation of effective diffusivity for CO2 with pressure is rapidly overwhelmed by the higher degree of plasticization at lower fractions of CH4, so that the effective diffusivity at higher pressures decreases significantly with increasing CH4 fraction. For pure CO2, stronger dependency of Deff/l on pressure was observed and Deff/l was increased with increasing pressure due to plasticization. In general, for feeds containing different fractions of CH4, the effect of plasticization decreased and the influence of pressure on Deff/l for CO2 became negligible in comparison to the case with pure CO2. By increasing CH4 in the feed, because of less sorption of CO2 and decrease in plasticization, dependency of Deff/l for CO2 on pressure, was more reduced. As can be seen in Fig. 5, Deff/l for CH4 in the feed was enhanced as a result of an increase in pressure due to plasticization. Moreover, for feeds with higher fractions of CH4, because of higher sorption of CH4, Deff/l was higher than in the cases with lower fractions.3.5. Separation factor
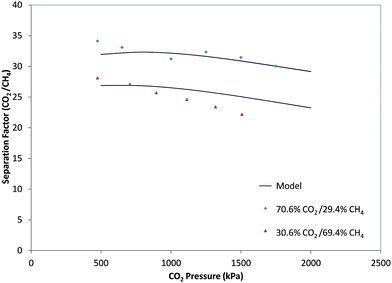
Based on eqn (18), the separation factor for a binary gas mixture is the ratio of the permeability coefficients of the components. In Fig. 6, the experimental separation factor for CO2/CH4 was compared with the predictions of the model using permeances of CO2 and CH4 calculated in Section 3.3. According to this figure, the separation factor of the mixed CO2/CH4 with different compositions decreased with increasing pressure and the model showed this trend accurately. As is observed in Fig. 2 and 3, permeances of CO2 and CH4 increased with pressure, but increase in CH4 permeances was more than that of CO2, and the separation factor decreased with pressure. Moreover, the separation factor for the mixed gas feed at specific pressures was decreased with increasing CH4 fraction. The presence of CH4 led to CO2 permeance reduction with increasing CH4 fraction in the feed at a specific pressure. On the other hand, permeance of CH4 increased with increasing CH4 fraction in the feed. Therefore, with increase in CH4 fraction at a specific pressure, the CO2/CH4 separation factor decreased.4. Conclusion
In the current study, a mathematical model was developed to predict permeation behavior of mixed gases through glassy polymeric membranes in the presence of plasticization. Parameters of the model (β, F, D0/l) were obtained using the experimental data for permeation of a CO2/CH4 mixture feed with different compositions through an asymmetric cellulose acetate membrane. It was shown that these parameters were strongly dependent on the feed composition. The observations revealed that β and F for CO2 and CH4 declined with increasing CH4 fraction in the feed due to reduction in plasticization. D0/l for CO2 and CH4 rose with increasing CH4 fraction. Deff/l for pure CO2 was significantly pressure dependent; however with increasing fraction of CH4 in the feed, this dependency almost disappeared. Moreover, Deff/l for CH4 increased with pressure due to plasticization. Separation factor for CO2/CH4 with different fractions decreased with pressure, and the model showed this trend accurately. In addition, with increase in CH4 fraction in the feed, the separation factor decreased at a specified pressure. In conclusion, the presence of the second component along with CO2 resulted in reduction of sorption of CO2 due to competitive sorption, which eventually led to decrease in plasticization. The presented model was capable of giving a useful tool to enhance our knowledge related to permeation behavior of mixed gas systems through glassy polymeric membranes in the presence of plasticization.References
- H. Vinh-Thang and S. Kaliaguine, Chem. Rev., 2013, 113, 4980–5028 CrossRef CAS PubMed.
- M. G. Buonomenna, RSC Adv., 2013, 3, 5694–5740 RSC.
- C. Ma and W. J. Koros, J. Membr. Sci., 2013, 428, 251–259 CrossRef CAS.
- T. Visser, N. Masetto and M. Wessling, J. Membr. Sci., 2007, 306, 16–28 CrossRef CAS.
- S. P. Koenig, L. Wang, J. Pellegrino and J. S. Bunch, Nat. Nanotechnol., 2012, 7, 728–732 CrossRef CAS PubMed.
- R. W. Baker and K. Lokhandwala, Ind. Eng. Chem. Res., 2008, 47, 2109–2121 CrossRef CAS.
- Y. Liu, R. Wang and T.-S. Chung, J. Membr. Sci., 2001, 189, 231–239 CrossRef CAS.
- S. Kanehashi, T. Nakagawa, K. Nagai, X. Duthie, S. Kentish and G. Stevens, J. Membr. Sci., 2007, 298, 147–155 CrossRef CAS.
- J. Adewole, A. Ahmad, S. Ismail and C. Leo, Int. J. Greenhouse Gas Control, 2013, 17, 46–65 CrossRef CAS.
- A. Bos, I. Pünt, M. Wessling and H. Strathmann, J. Polym. Sci., Part B: Polym. Phys., 1998, 36, 1547–1556 CrossRef CAS.
- G. Kapantaidakis, G. Koops, M. Wessling, S. Kaldis and G. Sakellaropoulos, AIChE J., 2003, 49, 1702–1711 CrossRef CAS.
- A. Bos, I. Pünt, M. Wessling and H. Strathmann, J. Membr. Sci., 1999, 155, 67–78 CrossRef CAS.
- A. Ismail and W. Lorna, Sep. Purif. Technol., 2002, 27, 173–194 CrossRef CAS.
- J. D. Wind, S. M. Sirard, D. R. Paul, P. F. Green, K. P. Johnston and W. J. Koros, Macromolecules, 2003, 36, 6433–6441 CrossRef CAS.
- E. Sanders, J. Membr. Sci., 1988, 37, 63–80 CrossRef CAS.
- J. Chiou, J. W. Barlow and D. Paul, J. Appl. Polym. Sci., 1985, 30, 2633–2642 CrossRef CAS.
- A. Ismail and W. Lorna, Sep. Purif. Technol., 2003, 30, 37–46 CrossRef CAS.
- C. A. Scholes, G. Q. Chen, G. W. Stevens and S. E. Kentish, J. Membr. Sci., 2010, 346, 208–214 CrossRef CAS.
- T. Visser, G. Koops and M. Wessling, J. Membr. Sci., 2005, 252, 265–277 CrossRef CAS.
- M. Donohue, B. Minhas and S. Lee, J. Membr. Sci., 1989, 42, 197–214 CrossRef CAS.
- C. Staudt-Bickel and W. J. Koros, J. Membr. Sci., 1999, 155, 145–154 CrossRef CAS.
- A. Bos, I. Pünt, M. Wessling and H. Strathmann, Sep. Purif. Technol., 1998, 14, 27–39 CrossRef CAS.
- C. Staudt-Bickel and W. J. Koros, J. Membr. Sci., 1999, 155, 145–154 CrossRef CAS.
- W. Koros, R. Chern, V. Stannett and H. Hopfenberg, J. Polym. Sci., Polym. Phys. Ed., 1981, 19, 1513–1530 CrossRef CAS.
- W. Koros, J. Polym. Sci., Polym. Phys. Ed., 1980, 18, 981–992 CrossRef CAS.
- S. Lee, B. Minhas and M. Donohue, AIChE Symp. Ser., 1988, 84, 93 CAS.
- M. Saberi, A. A. Dadkhah and S. A. Hashemifard, J. Membr. Sci., 2016, 499, 164–171 CrossRef CAS.
- P. Meares, J. Am. Chem. Soc., 1954, 76, 3415–3422 CrossRef CAS.
- W. Vieth, J. Howell and J. Hsieh, J. Membr. Sci., 1976, 1, 177–220 CrossRef CAS.
- M. Minelli and G. C. Sarti, J. Membr. Sci., 2013, 435, 176–185 CrossRef CAS.
- T. S. Chung, C. Cao and R. Wang, J. Polym. Sci., Part B: Polym. Phys., 2004, 42, 354–364 CrossRef CAS.
- D. Paul and W. Koros, J. Polym. Sci., Polym. Phys. Ed., 1976, 14, 675–685 CrossRef CAS.
- A. Ahmad, J. Adewole, C. Leo, S. Ismail, A. Sultan and S. Olatunji, J. Membr. Sci., 2015, 480, 39–46 CrossRef CAS.
- X. Duthie, S. Kentish, C. Powell, K. Nagai, G. Qiao and G. Stevens, J. Membr. Sci., 2007, 294, 40–49 CrossRef CAS.
- S. Stern and V. Saxena, J. Membr. Sci., 1980, 7, 47–59 CrossRef CAS.
- S. Y. Bae, H.-T. Kim and H. Kumazawa, Korean J. Chem. Eng., 1994, 11, 211–215 CrossRef CAS.
- G. Q. Chen, C. A. Scholes, C. M. Doherty, A. J. Hill, G. G. Qiao and S. E. Kentish, J. Membr. Sci., 2012, 409, 96–104 CrossRef.
- B. Seoane, J. Coronas, I. Gascon, M. E. Benavides, O. Karvan, J. Caro, F. Kapteijn and J. Gascon, Chem. Soc. Rev., 2015, 44, 2421–2454 RSC.
- M. Buonomenna, W. Yave and G. Golemme, RSC Adv., 2012, 2, 10745–10773 RSC.
- R. Wang, C. Cao and T.-S. Chung, J. Membr. Sci., 2002, 198, 259–271 CrossRef CAS.
- S. N. Shoghl, A. Raisi and A. Aroujalian, RSC Adv., 2015, 5, 38223–38234 RSC.
- K. I. Okamoto, K. Tanaka, H. Kita, A. Nakamura and Y. Kusuki, J. Polym. Sci., Part B: Polym. Phys., 1989, 27, 2621–2635 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |