Chemical fragment-based CDK4/6 inhibitors prediction and web server

Abstract

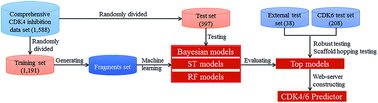
Cyclin-dependent kinases (CDKs), a family of mammalian heterodimeric kinases, play central roles in the regulation of cell cycle progression, transcription, neuronal differentiation, and metabolism. Among these CDKs, CDK4 and CDK6 are considered to be highly validated anticancer drug targets due to their essential role in regulating cell cycle progression at the G1 restriction point. In this study, in silico models derived from 1588 diverse CDK4 enzyme assay data were developed using three machine learning methods, including naïve Bayesian (NB), single tree (ST), and random forest (RF). A total of 1006 models were constructed based on chemical fragments, including fingerprints and atom center fragments (ACFs). The overall predictive accuracies of the best models exceeded 90% for both the training and test sets. The scaffold-hopping abilities of the best models were successfully evaluated by the external test set. Moreover, in silico model-derived CDK4 assay data can predict CDK6 inhibitors (overall predictive accuracies of ∼70–86%). Among all the 1006 models, ACF-based models showed the best performance. A web server was developed based on ACFs and the Bayesian method to predict or design new CDK4/6 inhibitors (CDK4/6 predictor, http://rcidm.org/cdk/).

---

Introduction

Cancer is now believed to result from perturbations in the cell cycle that result in unlimited proliferation and the inability of a cell to undergo differentiation and/or apoptosis.^1–3 The cell cycle typically has four functional phases, G1, S, G2, and M, and the order and timing of each phase of the cell cycle is critical for accurate transmission of genetic information for cell replication.⁴ Progression of cells through the cell cycle is regulated by the expression and assembly of different kinase holoenzymes that includes a family of serine/threonine kinases (CDKs) and a regulatory partner, called cyclin.^2,5 Different combinations of cyclin/CDK complexes regulate each of the cell cycle transitions. In the G1-S phase transition of the mammalian cell cycle, CDK4/6 in complex with D-type cyclins (D1, D2, or D3) control progression through the G1 phase when the cell prepares for the transcription of genes required for DNA synthesis. Activation of CDK4/6/cyclin D complexes can phosphorylate the retinoblastoma (Rb) gene family of proteins, which results in the release of associated protein factors.^6,7 Phosphorylation of Rb activates one key Rb binding partner, called the E2F-1 transcription factor, leading to the transcription of genes required for DNA synthesis and S-phase progression.²

Increasing evidence indicates that the CDK4/6-cyclin D-Rb pathway is deregulated in more than 80% of human tumors.^1–3 For example, CDK4/6 is hyperactivated in a majority of human cancers because positive regulators such as cyclin D or deletion and/or epigenetic alterations of substrates such as Rb are overexpressed.^1–3 Mutations and chromosomal translocations in the CDK4 locus have been identified. For example, mutants of CDK4 that are resistant to p16 have been found in melanoma, whereas loss of p16 activity as a result of mutations, deletions, or gene silencing has been observed in pancreatic cancers, glioblastoma, and NSCLC.⁸ CDK4 is overexpressed in osteosarcomas, and Rb is mutated in retinoblastomas and SCLC.⁸ Endogenous cyclin D1 or CDK4 expression was inhibited by RNA interference in MCF-7 breast cancer cells, which resulted in the inhibition of cell growth, hypophosphorylation of Rb, and accumulation of cells in the G1 phase. The CDK4 mutation (R24C) was first observed in patients with familial melanoma, which resulted in insensitivity of CDK4 to INK4 family inhibitors.^9,10 Finally, CDK4/6 amplification or overexpression has been observed in a wide spectrum of tumors, including gliomas, sarcomas, lymphomas, melanomas, breast carcinomas, squamous cell carcinomas, and leukemias.^2,11 All these results demonstrated that pharmacological inhibition of cyclin D-CDK4/6 complexes was a useful strategy for developing anticancer drugs.

In recent years, many potential CDK4 inhibitors have been discovered and reviewed.^12–14 Based on their inhibition mechanisms, these compounds are classified into two varieties, namely, ATP-competitive and ATP-noncompetitive inhibitors. However, the focus has been on the development of ATP-competitive inhibitors in both academic and industry drug discovery programs.^12,14,15 In February 2015, the US Food and Drug Administration granted accelerated approval to palbociclib (Ibrance®, formerly termed PD-0332991, Pfizer).¹⁶ Some ATP-competitive CDK4/6 inhibitors (e.g. abemaciclib,¹⁷ ribociclib,¹⁴ alvocidib,¹⁸ and G1T28-1 (ref. 19)) are in clinical trials.

To date, the assessment of inhibition by anti-CDK4/6 agents (i.e., ATP-competitive CDK4/6 inhibitors) can be achieved experimentally via in vitro or in vivo assays.^{2,16–18,20–22} However, these experimental assays are expensive, laborious and time-consuming. Thus, the development of computational methods that provide a rapid and efficient screening platform to identify CDK4/6 inhibitors is vital in the early stages of lead design or optimization.

Several computational 3D-QSAR and pharmacophore models have been developed to predict ATP-competitive CDK4 inhibitors. For example, Lu and coworkers constructed 3D-QSAR models based on an isoquinoline-1,3-(2H,4H)-dione scaffold using CoMFA and CoMSIA methods.²³ Their models showed potential predictions that helped in understanding the structure activity relationship of isoquinoline-1,3-(2H,4H)-dione derivatives. Some similar studies were conducted based on the scaffolds of indenopyrazole,²⁴ bisarylmaleimide,²⁵ and thieno[2,3-d]pyramidin-4-yl hydrazine.²⁶ In 2015, Kawade and coworkers predicted CDK4 inhibitors using a pharmacophore modeling approach based on pyrimidine analogs.²⁷ A disadvantage of 3D-QSAR or pharmacophore models for CDK4 inhibitors is the use of a series of compounds based on a single scaffold. The ATP binding pocket of CDK4 is flexible, which makes it difficult to predict new inhibitors based on traditional 3D methods.^28,29 Thus, there is a need for models based on various known CDK4/6 scaffolds to predict CDK4/6 inhibitors with broader chemical structure diversity.

In the present study, we present a large data set of 1588 molecules that are categorized into ATP-competitive CDK4 inhibitors and non-inhibitors. Then, in silico classification models were constructed using single tree (ST), random forest (RF), and naïve Bayesian (NB) techniques. The performance and scaffold-hopping abilities of in silico models were successfully validated by test sets and external test sets. Moreover, the top models based on CDK4 assay data can discriminate CDK6 inhibitors from non-inhibitors. Finally, a web server was developed based on ACFs and the Bayesian method to predict or design new CDK4/6 inhibitors (CDK4/6 predictor, http://rcidm.org/cdk/). The flowchart of the process is depicted in Fig. 1. We anticipate that this will be a useful tool for the research community.

Fig. 1 A flowchart for generating chemical fragment-based models to predict CDK4/6 inhibitors.

Materials and methods

Compound activity data

CDK4 assay data was extracted from ChEMBL (version 18).³⁰ ChEMBL currently represents the most comprehensive public repository of compound data from medicinal chemistry sources and includes information from other databases. The data set was refined with the criteria as follows: (1) only human CDK4 inhibition assay data were selected; (2) only CDK4 assay data based on enzymes or enzyme regulation were kept, and allosteric inhibitors (ATP-noncompetitive inhibitors) were excluded; (3) duplicated compounds, compounds without detailed assay values (K_i or IC₅₀), and compounds with a high molecular weight (>1000 Da) were removed. After applying these criteria, the whole CDK4 data set consisted of 1588 structurally diverse compounds. There were 1019 active compounds in the data set below the K_i/IC₅₀ threshold of 5 μM (a cutoff for hit-to-lead activity studies). The detailed results of choosing an active threshold are available in Fig. S1.†

All chemical structures of the data set were checked against the original published papers. Then, each molecular structure record experienced preprocessing, including removing the counterions, solvent moieties and salts, adding hydrogen atoms, and optimizing the structures based on the MMFF94 force field using MOE (version 2010.10, Chemical Computing Group, Inc., Canada). Finally, the entire data set was divided into a training set (1191) and a test set (397) using a randomized algorithm in DS 3.5 (Discovery Studio version 3.5, Accelrys Inc., USA). The proportion of training set to test set was about 3 to 1, which was employed in references. ^31–36 The data are available online: http://rcidm.org/cdk/.

Structural fingerprint calculation

Two sets of fingerprints, SciTegic extended-connectivity fingerprints (ECFP, FCFP and LCFP) and daylight-style path-based fingerprints (EPFP, FPFP and LPFP), were calculated using DS 3.5. Each type of fingerprint was used in five diameters as follows: 4, 6, 8, 10, and 12, if applicable. All of these fingerprints are frequently applied in ADMET, QSAR, and QSPR models.^31–33,37

Atom center fragments (ACFs) calculation

The ACFs of a given compound were generated using the steps as follows:

(1) A heavy atom (non-hydrogen atom) was chosen as an atom center for an ACF;

(2) Atoms n-bonds (n ≥ 1) away from the center atom were selected, keeping the bonding topology inside the ACF.

In general, ACF_n+1 is larger than ACF_n. Larger ACFs can result in more accurate prediction because they are structurally more specific, but they lose universality. To find a balance point between accuracy and universality, we generated ACF_1–6 fragments from the CDK4 data set using an in-house program.^32,38,39

Single tree (ST) and random forest (RF)

ST and RF are two basic models in the recursive partitioning (RP) method. Recursive partitioning (RP) is a data classification method used to uncover the relationship between a dependent property (Y variable, e.g. inhibition class) and a set of independent properties (X variables, e.g. molecular properties and fingerprints). RP creates a decision tree that strives to correctly classify members of a population based on the dichotomous splitting of a dependent property. Once a model is built, it can be used to make predictions about novel data. In this study, a total of 972 ST and RF models were constructed based on 27 fingerprints. Detailed descriptions of the RP method can be found in the literature.^40,41

Naïve Bayesian (NB)

NB inference derives the posterior probability as a consequence of two antecedents, a prior probability and a “likelihood function” derived from a probability model for the data to be observed. NB inference computes the posterior probability directly, based on the Bayesian law as follows:where P(A) is the initial degree of belief in A; P(B) is the initial degree of belief in B; P(A|B) is the degree of belief in A having accounted for B; and P(B|A) is the degree of belief in B having accounted for A. Detailed descriptions of the NB method can be found in previously published literature.⁴² In this study, we used DS 3.5 to build NB models based on 28 fingerprints. Moreover, ACFs were used as a descriptor that encoded the Bayesian law to construct a classification model (called the ACFs-NB model) based on the in-house program. Detailed information about the ACFs-NB algorithm is described in our previous studies.^32,39 The program can be obtained on request.

Validating performances of models

To evaluate the accuracy and robustness of stability prediction models, a 5-fold cross validation scheme was employed. True positives (TP), true negatives (TN), false positives (FP), false negatives (FN), sensitivity (SE), specificity (SP), overall predictive accuracy (Q) and the Matthews correlation coefficient (MCC) were calculated.

The MCC is the most important indicator for the classification accuracy of the models. In addition, a receiver operating characteristic (ROC) curve was also plotted to present the model behavior in a visual way.⁴³

Results and discussion

Optimizing an active threshold and proportion of training and test sets

The training and testing sets were constructed by splitting from the 1588 data set, which was employed via a random algorithm in DS 3.5. The proportion of the training set (1191) to the test set (397) was ∼3 : 1, which was suggested in other studies.^31–36 Then, the active cutoff values of K_i/IC₅₀ were set to 1, 5, 10, 15, 20, 25, and 30 μM. 14 NB models based on ECFP_4 and ECFP_6 fingerprints were constructed. According to the MCC values of the test set, NB models based on an active threshold of 5 μM have better performances than other cutoff values of K_i/IC₅₀ (ESI Fig. S1a†). Similar results can be found in the curves of Q and the AUC values (ESI Fig. S1b and c†). Therefore, such a cutoff value appeared to be a reasonable starting point for a hit-to-lead activity and, in view of the noise level in the data set, the choice of 5 μM would seem to be justified.

During the process of choosing the active threshold, the proportion of the training set to the test set was ∼3 : 1. To confirm that this proportion is reasonable and reliable for the CDK4 system when the active threshold is set to 5 μM, the proportions of the training set and test set were set to values from 1 : 1 to 10 : 1. 14 NB models based on ECFP_4 and ECFP_6 fingerprints were also constructed. According to AUC values from the test set, NB models based on a training set to test set proportion of ∼3 : 1 have better performances than models based on other proportions (ESI Fig. S2c†). The curves of MCC and Q values of these models show similar results (ESI Fig. S2a and b†). All these results indicate that the predefined proportion of training set to test set (∼3 : 1) is reasonable for the CDK4 data set.

Chemical space and structural diversity analysis

The structural diversity of the training and testing data has a significant influence on the reliability and predictive ability of the models. One way to view the chemical space is to depict compounds in a two-dimensional space using molecular weight (MW) and A log P (Fig. 2). Fig. 2 indicates that the training and the test compounds are distributed over a wide range of MW (100–1000 Da) and A log P (−4 to 8) values. By comparing the chemical diversity of the 1588 CDK4 data set against the chemical diversity of the Drugbank⁴⁴ and the World Drug Index (WDI) databases, a S-cluster approach (SCA)⁴⁵ was employed to measure the structural diversity. The SCA results confirm that the CDK4 data set is structurally more diverse than the compounds in the WDI database and similar to the compounds in the DrugBank database (ESI Table S1†).

Fig. 2 Diversity analysis of the entire CDK assay data set (1588 compounds). Chemical space was defined by molecular weight (MW) as X-axis, and A log P as Y-axis. MW and A log P were calculated using DS 3.5.

Performance of single tree and random forest models

The single tree (ST) and random forest (RF) models generated with the recursive partitioning (RP) method are more intuitive compared with “blind modeling” approaches such as the artificial neural network (ANN) and the support vector machine (SVM). In the RP method, the depths of the ST and RF models are key parameters that control the complexity of a model. Increasing the depth may improve accuracy but may also result in overfitting, whereas a shorter depth may increase the possibility of applying the tree to new data sets but may decrease the accuracy of the prediction.^31–33,37 The optimum depth can be identified by recursively validating the models with different combinations of training and testing data. To optimize the depth of a decision tree for the best prediction performance, tree depths between 3 and 20 were tried. A total of 972 ST and RF models were built and evaluated with evaluation indexes (Fig. 3 and 4, ESI Fig. S3 and S4†). The LPFP_12 fingerprint is not adopted because it is time-consuming to establish a ST or RF model based on this fingerprint. The 5-fold cross-validation method was used to measure the robustness of these models.

Fig. 3 The MCC, Q, and AUC of single tree models versus the tree depth of the fingerprint set (FPFP, LCFP, and LPFP) for (a–c) training set and (d–f) test set. MCC: Matthews correlation coefficient; Q: the overall predictive accuracy; AUC: the area under the receiver operating characteristic curve.

Fig. 4 The MCC, Q, and AUC of random forest models versus the tree depth of the fingerprint set (FPFP, LCFP, and LPFP) for (a–c) training set and (d–f) test set. MCC: Matthews correlation coefficient; Q: the overall predictive accuracy; AUC: the area under the receiver operating characteristic curve.

As shown in Fig. 3, the MCC, Q, and AUC values vary with the decision tree depth. The optimum tree depth varies with the fingerprints. According to the predictions for the test data, the top ten ST models derived from the 27 fingerprints are listed in Table 1. Table 1 suggests that the most favored fingerprint set for ST models is FPFP_8. The best tree depth is 8 for this ST model. The corresponding ST_FPFP_8 model from the testing set has a sensitivity of 0.909, a specificity of 0.869, and an overall prediction accuracy of 89.4%. The model evaluation results from both the training set and testing set are consistent (Table 1). The AUC values for the training and testing sets are 0.924 and 0.942, respectively (Table 1). The ST_FPFP_6 model performs in a similar way to the ST_FPFP_8 model at a tree depth of 8 (except for a slightly lower AUC value from the test set, Table 1). The best single tree model based on FPFP_8 can be easily interpreted, as shown in Fig. 5. The 29 fragments based on the FPFP_8 fingerprint play a key role in discriminating CDK4 inhibitors from non-inhibitors, suggesting that these fragments will be helpful for lead optimization or the design of new CDK4 inhibitors.

Table 1 Performance validation results of top ten single tree (ST) models^a

Models	Training set									Test set
	TP	FN	TN	FP	SE	SP	MCC	Q	AUC	TP	FN	TN	FP	SE	SP	MCC	Q	AUC
a ST: single tree; TP: true positives; TN: true negatives; FP: false positives; FN: false negatives; SE: sensitivity; SP: specificity; Q: the overall predictive accuracy; MCC: Matthews correlation coefficient; AUC: the area under the receiver operating characteristic curve. The best tree depth is 8 for ST models (FPFP_6, FPFP_8, and FPFP_10), 7 for ST models (ECFP_8 and ECFP_10), 20 for ST models (LCFP_4, LCFP_6, LCFP_8, LCFP_10, and LCFP_12), 20 for RP model (LPFP_10), and 26 for RP model (EPFP_4).
ST_FPFP_6	652	115	372	52	0.850	0.877	0.708	0.860	0.930	229	23	126	19	0.909	0.869	0.773	0.894	0.935
ST_FPFP_8	644	123	381	43	0.840	0.899	0.715	0.861	0.924	229	23	126	19	0.909	0.869	0.773	0.894	0.942
ST_FPFP_10	636	131	389	35	0.829	0.917	0.721	0.861	0.935	222	30	127	18	0.881	0.876	0.745	0.879	0.919
ST_EPFP_8	640	127	376	48	0.834	0.887	0.699	0.853	0.922	217	35	125	20	0.861	0.862	0.710	0.861	0.896
ST_EPFP_10	640	127	376	48	0.834	0.887	0.699	0.853	0.922	217	35	125	20	0.861	0.862	0.710	0.861	0.899
ST_LCFP_4	647	120	367	57	0.844	0.866	0.691	0.851	0.923	216	36	125	20	0.857	0.862	0.705	0.859	0.922
ST_LCFP_6	649	118	367	57	0.846	0.866	0.694	0.853	0.925	216	36	125	20	0.857	0.862	0.705	0.859	0.920
ST_LCFP_8	649	118	367	57	0.846	0.866	0.694	0.853	0.925	216	36	125	20	0.857	0.862	0.705	0.859	0.920
ST_LCFP_10	649	118	367	57	0.846	0.866	0.694	0.853	0.925	216	36	125	20	0.857	0.862	0.705	0.859	0.920
ST_LCFP_12	649	118	367	57	0.846	0.866	0.694	0.853	0.9252	216	36	125	20	0.857	0.862	0.705	0.859	0.920

---

Fig. 5 Single tree to discriminate CDK4 inhibitors from non-inhibitors based on FPFP_8 fingerprint. The tree depth is 8. FP: Fingerprint; yes: contains this fingerprint; not: does not contain; red font represents non-inhibitors; black font represents inhibitors.

According to the MCC values from the test set (Fig. 4 and ESI Fig. S4†), the validation parameters of the top ten RF models are listed in Table 2. Similar to the ST models analysis, the values of the validation parameters vary with the tree depth and the optimum tree depth varies along with the fingerprints. As shown in Table 2, the RF model based on the FPFP_8 fingerprint has the highest MCC value (0.794) for the test set. The best tree depth of the RF_FPFP_8 model is 15. This model achieves a sensitivity of 0.925, a specificity of 0.869, and an overall prediction of 90.4% for the test set.

Table 2 Performance validation results of top ten random forest (RF) models^a

Models	Training set									Test set
	TP	FN	TN	FP	SE	SP	MCC	Q	AUC	TP	FN	TN	FP	SE	SP	MCC	Q	AUC
a RF: random forest; TP: true positives; TN: true negatives; FP: false positives; FN: false negatives; SE: sensitivity; SP: specificity; Q: the overall predictive accuracy; MCC: Matthews correlation coefficient; AUC: the area under the receiver operating characteristic curve. The best tree depth is 6 for RF model (EPFP_4), 7 for RF model (FPFP_6), 9 for RF model (FPFP_8), 10 for RF model (FPFP_4), 13 for RF model (EPFP_8), 15 for RF model (FPFP_8), 16 for RF models (LPFP_8, LPFP_10, and LPFP_12), and 19 for RF model (LPFP_4).
RF_FPFP_8	687	80	390	34	0.896	0.920	0.799	0.904	0.971	233	19	126	19	0.925	0.869	0.794	0.904	0.947
RF_FPFP_6	691	76	385	39	0.901	0.908	0.795	0.903	0.958	235	17	123	22	0.933	0.848	0.787	0.902	0.948
RF_LPFP_4	709	58	381	43	0.924	0.899	0.817	0.915	0.973	235	17	123	22	0.933	0.848	0.787	0.902	0.944
RF_LPFP_12	702	65	384	40	0.915	0.906	0.811	0.912	0.975	232	20	123	22	0.921	0.848	0.771	0.894	0.943
RF_LPFP_8	701	66	385	39	0.914	0.908	0.811	0.912	0.974	231	21	123	22	0.917	0.848	0.766	0.892	0.942
RF_LPFP_10	700	67	384	40	0.913	0.906	0.808	0.910	0.974	232	20	122	23	0.921	0.841	0.765	0.892	0.943
RF_FPFP_10	689	78	393	31	0.898	0.927	0.808	0.908	0.969	233	19	121	24	0.925	0.834	0.765	0.892	0.946
RF_EPFP_8	687	80	387	37	0.896	0.913	0.793	0.902	0.971	234	18	120	25	0.929	0.828	0.765	0.892	0.938
RF_FPFP_4	694	73	382	42	0.905	0.901	0.794	0.903	0.967	236	16	118	27	0.937	0.814	0.764	0.892	0.935
RF_EPFP_4	679	88	368	56	0.885	0.868	0.742	0.879	0.949	236	16	117	28	0.937	0.807	0.758	0.889	0.933

---

Compared with the predictive accuracies of ST models, the RF classifier performs better for most of the given fingerprints (Fig. 3 and 4, ESI Fig. S3 and S4†). Taking FPFP_8 as an example, the best ST and RF models are constructed based on the FPFP_8 fingerprint, but the RF_FPFP_8 model performs better than the ST_FPFP_8 model (Tables 1 and 2).

Performance of naïve Bayesian models

The naïve Bayesian (NB) method is an unsupervised learner that does not have a fitting process or tuning parameters. 28 NB models were derived from molecular fingerprints. Similar to ST and RF analysis, the performances of the NB classifiers are different for different fingerprints and the fingerprint diameters (Fig. 6). According to the MCC values determined by the leave-one-out (LOO) cross-validation from the test set, the performance parameters for the top ten NB models are listed in Table 3. The best NB classifier based on the LCFP_10 fingerprint has a sensitivity of 0.898, a specificity of 0.934, and an overall prediction accuracy of 91.1% for the training set. For the 397 tested compounds, this model retrieves a sensitivity of 0.925, a specificity of 0.841, and an overall prediction accuracy of 89.4%. The AUC values for the training and testing sets are 0.921 and 0.955, respectively (Table 3 and ESI Fig. S5†).

Fig. 6 The MCC, Q, and AUC of naïve Bayesian models versus the diameter of the fingerprint set for (a–c) training set and (d–f) test set. A total of 28 NB models were constructed based on 28 different fingerprint sets. MCC: Matthews correlation coefficient; Q: the overall predictive accuracy; AUC: the area under the receiver operating characteristic curve.

Table 3 Performance validation results of the top ten NB models^a

Models	Training set									Test set
	TP	FN	TN	FP	SE	SP	MCC	Q	AUC	TP	FN	TN	FP	SE	SP	MCC	Q	AUC
a NB: naïve Bayesian; TP: true positives; TN: true negatives; FP: false positives; FN: false negatives; SE: sensitivity; SP: specificity; Q: the overall predictive accuracy; MCC: Matthews correlation coefficient; AUC: the area under the receiver operating characteristic curve.
NB_LCFP_10	689	78	396	28	0.898	0.934	0.814	0.911	0.921	233	19	122	23	0.925	0.841	0.771	0.894	0.955
NB_LCFP_12	692	75	401	23	0.902	0.946	0.829	0.918	0.922	227	25	127	18	0.901	0.876	0.769	0.892	0.956
NB_ECFP_12	674	93	404	20	0.879	0.953	0.807	0.905	0.925	228	24	126	19	0.905	0.869	0.768	0.892	0.954
NB_LCFP_8	710	57	376	48	0.926	0.887	0.809	0.912	0.92	228	24	125	20	0.905	0.862	0.763	0.889	0.954
NB_LCFP_6	701	66	372	52	0.914	0.877	0.786	0.901	0.918	225	27	126	19	0.893	0.869	0.754	0.884	0.951
NB_ECFP_8	656	111	399	25	0.855	0.941	0.771	0.886	0.922	228	24	123	22	0.905	0.848	0.751	0.884	0.952
NB_ECFP_10	667	100	402	22	0.870	0.948	0.793	0.898	0.924	223	29	127	18	0.885	0.876	0.750	0.882	0.953
NB_FCFP_12	690	77	396	28	0.900	0.934	0.816	0.912	0.921	219	33	130	15	0.869	0.897	0.749	0.879	0.956
NB_LPFP_12	649	118	403	21	0.846	0.950	0.769	0.883	0.908	213	39	134	11	0.845	0.924	0.747	0.874	0.944
NB_FCFP_10	683	84	392	32	0.890	0.925	0.797	0.903	0.92	217	35	131	14	0.861	0.903	0.746	0.877	0.955

---

The Bayesian score based on LCFP_10 was employed to discriminate CDK4 inhibitors from non-inhibitors via a bimodal histogram (Fig. 7). As shown in Fig. 7a, the p value associated with the difference in the mean Bayesian score of CDK4 inhibitors versus non-inhibitors was 5.49 × 10⁻¹²³ at the 95% confidence level, suggesting the two distributions are significantly different in the training test. The Bayesian score of the CDK4 inhibitor tends to have a more positive value, whereas the Bayesian score of the CDK4 non-inhibitor tends to have a more negative value. Similar results can be found in the 397 tested compounds (Fig. 7b).

Fig. 7 The distributions of Bayesian score predicted by the Bayesian classifier based on the LCFP_10 fingerprint for the CDK4 inhibitor and non-inhibitor classes for (a) the training set and (b) the test set.

Performance of ACFs-NB models

Recently, a virtual screening tool, which can discriminate actives from inactives, was developed based on atom center fragments (ACFs) and Bayesian rules in our lab. Detailed information on the ACFs-NB algorithm was given in our previous studies.^32,39 Herein, we constructed classifiers that discriminate between CDK4 inhibitors and non-inhibitors using the ACFs-NB algorithm. The 5-fold cross-validation technique was also used to evaluate the accuracy and robustness of stability prediction models. The detailed results of the ACFs-NB method are listed in Table S2.† Table S2† indicates that the different C values were obtained based on different ACF layers. The best ACFs-NB model (ACF layers = 6) achieves a MCC of 0.803, a sensitivity of 0.952, a specificity of 0.834, and an overall predictivity of 90.9% for the test set.

Validating the models with external test data

To validate our models, we predicted 38 compounds with CDK4 inhibition activity that were published recently (available online).^2,46 The external data have novel scaffolds, such as novel cyano pyridopyrimidine compounds targeting both CDK4 and ARK5,² and novel pyrido[4′,3′:4,5]pyrrolo[2,3-d]pyrimidine derivatives targeting FLT3 and CDK4,⁴⁶ which are not found in the training and test sets.

The top eight models were validated with the external data and the results are summarized in Table 4. As shown in Table 4, all the models achieved accuracy rates of approximately 89–97%. These results demonstrate that our models are reliable and useful. Moreover, all the compounds have structural novelty, indicating that scaffold hopping can be carried out in a virtual screening project based on our models.

Table 4 Performance validated results of the 38 external test data using top-8 models^a

Models	Test set
	TP	FN	TN	FP	SE	SP	MCC	Q	AUC
a NB: naïve Bayesian; RF: random forest; ST: single tree; TP: true positives; TN: true negatives; FP: false positives; FN: false negatives; SE: sensitivity; SP: specificity; Q: the overall predictive accuracy; MCC: Matthews correlation coefficient; AUC: the area under the receiver operating characteristic curve. The tree depth is 8 for ST models (FPFP_6 and FPFP_8), 7 for RF model (FPFP_6), and 15 for RF model (FPFP_8). The bracket represents the ACF layer.
NB_LCFP_10	36	1	1	0	0.973	1.000	0.697	0.974	1
NB_ECFP_12	34	3	1	0	0.919	1.000	0.479	0.921	1
ST_FPFP_6	33	4	1	0	0.892	1.000	0.422	0.895	0.986
ST_FPFP_8	33	4	1	0	0.892	1.000	0.422	0.895	0.973
RF_FPFP_8	35	2	1	0	0.946	1.000	0.562	0.947	1
RF_FPFP_6	36	1	1	0	0.973	1.000	0.697	0.974	1
ACFs-NB (5)	35	2	1	0	0.946	1.000	0.562	0.947	1
ACFs-NB (6)	35	2	1	0	0.946	1.000	0.562	0.947	1

---

Validating models with CDK6 assay data

CDK6 and CDK4 share 71% amino acid identity (in particular, they have similar pockets of ATP binding sites), suggesting that direct targeting of CDK6 and CDK4 should be used for cancer treatment. For example, palbociclib is a dual CDK4 and CDK6 inhibitor that was granted accelerated approval by the US Food and Drug Administration.¹⁶ Therefore, we validated the top eight models with CDK6 assay data to confirm that the models are indeed predictive.

The CDK6 assay data were extracted from the ChEMBL database (version 18) and reconfigured in the same format as the CDK4 assay data used in the previous training and test sets. Consequently, we collected 52 compounds with CDK6 assay data (these compounds are not included in CDK4 assay data, available online). As with the CDK4 assay data, the active threshold for CDK6 is set to 5 μM (27 actives and 25 inactives). The performance results for CDK6 data are shown in Fig. S6.† All models can achieve MCC values of 0.39–0.73 and overall prediction accuracies of approximately 70–86% (ESI Fig. S6a and b†), suggesting that models developed in the present study can predict both CDK4 and CDK6 assay results and exhibit good prediction ability.

Web implementation

A direct comparison of our results (binary classification models) with previous studies^23–27 (linear models based on a single scaffold) may not be fair with respect to the previous methods as their data sets were smaller. Compared with the best ST, RF, and NB models (Tables 1–3), the ACFs-NB model (ACF layers = 6) showed good prediction abilities because it has slightly better MCC and Q values (0.803 and 0.909, ESI Table S2†). Y-scrambling was investigated to prove that this was not a result of chance correlation. The performance results of 200 scrambled models from the test set are visualized in Fig. 8. The MCC, Q, and AUC values of the ACFs-NB model (ACF layers = 6) are significantly higher than any of the Y-scrambled models, indicating that the models are not the results of chance correlation.

Fig. 8 Y-scrambling results for the ACFs-NB model (ACF layers = 6) from the test set. (a) Structure-activity tables of the training set were scrambled, whereas structure-activity tables of the test set were unscrambled; (b) structure-activity tables of the training set were unscrambled, whereas structure-activity tables of the test set were scrambled. A total of 200 scrambled experiments were carried out. The 5-fold cross-validation technique was used to evaluate the accuracy and robustness of the stability prediction models. MCC: Matthews correlation coefficient; Q: the overall predictive accuracy; AUC: the area under the receiver operating characteristic curve.

The prediction of the ACFs-NB algorithm presented in this study is implemented as a freely accessible web server at http://rcidm.org/cdk/ (CDK4/6 predictor, Fig. 9). The input chemical structures can be drawn online or provided in SDF or MOL format. The program output returns the Bayesian score based on the number of ACF layers chosen (the default number of ACFs layers was set to 6). We anticipate that this would be a useful tool for predicting or designing new CDK4/6 inhibitors.

Fig. 9 Image of CDK4/6 predictor. The web server was constructed based on the ACFs-NB algorithm. The server accepts SDF or MOL formatted structures and allows users to draw structures online.

Conclusion

It is a significant challenge to predict new CDK4 inhibitors based on diverse scaffolds because the ATP binding site of CDK4 is highly flexible. In this study, we report an extensive ATP-competitive CDK4 inhibition database consisting of 1588 molecules. On the basis of the diversity set of CDK4 inhibition data, a total of 1006 ST, RF, NB, and ACFs-NB classifiers were constructed based on chemical fragments, including fingerprints and atom center fragments (ACFs). The overall predictive accuracies of the best models exceeded ∼90% for both training and test sets. The best models were successfully cross-validated with internal and external data sets. Moreover, the top eight models based on CDK4 assay data can discriminate CDK6 inhibitors from non-inhibitors (overall prediction accuracies of approximately 70–86%), suggesting that these models can predict both CDK4 and CDK6 assay results and exhibit a good prediction ability. Finally, a web server for predicting CDK4/6 inhibitors or non-inhibitors was developed based on the best model (ACFs-NB model, ACF layers = 6). This can be as a useful tool for predicting or designing new CDK4/6 inhibitors.

Acknowledgements

This study was funded in part by the Science and Technology Planning Project of Guangdong Province (No. 2015B010109004), the National Natural Science Foundation of China (No. 81502984), the Fundamental Research Funds for the Central Universities (No. 2015ZM049), the China Postdoctoral Science Foundation (No. 2015M572325), Guangdong Provincial Key Laboratory of Construction Foundation (No. 2011A060901014), and the Open Project Program of Guangdong Key Laboratory of Fermentation and Enzyme Engineering, SCUT (FJ2015006).

Notes and references

1. M. Malumbres and M. Barbacid, Nat. Rev. Cancer, 2009, 9, 153–166.
2. M. V. R. Reddy, B. Akula, S. C. Cosenza, S. Athuluridivakar, M. R. Mallireddigari, V. R. Pallela, V. K. Billa, D. R. C. V. Subbaiah, E. V. Bharathi, R. Vasquez-Del Carpio, A. Padgaonkar, S. J. Baker and E. P. Reddy, J. Med. Chem., 2014, 57, 578–599.
3. M. Malumbres and M. Barbacid, Nat. Rev. Cancer, 2001, 1, 222–231.
4. C. Sanchez-Martinez, L. M. Gelbert, M. J. Lallena and A. de Dios, Bioorg. Med. Chem. Lett., 2015, 25, 3420–3435.
5. J. Massague, Nature, 2004, 432, 298–306.
6. N. Dyson, Genes Dev., 1998, 12, 2245–2262.
7. J. W. Harbour and D. C. Dean, Genes Dev., 2000, 14, 2393–2409.
8. M. Hall and G. Peters, Adv. Cancer Res., 1996, 68, 67–108.
9. L. Zuo, J. Weger, Q. Yang, A. M. Goldstein, M. A. Tucker, G. J. Walker, N. Hayward and N. C. Dracopoli, Nat. Genet., 1996, 12, 97–99.
10. T. Wolfel, M. Hauer, J. Schneider, M. Serrano, C. Wolfel, E. Klehmann-Hieb, E. De Plaen, T. Hankeln, K. H. Meyer zum Buschenfelde and D. Beach, Science, 1995, 269, 1281–1284.
11. S. Ortega, M. Malumbres and M. Barbacid, Biochim. Biophys. Acta, 2002, 1602, 73–87.
12. U. Asghar, A. K. Witkiewicz, N. C. Turner and E. S. Knudsen, Nat. Rev. Drug Discovery, 2015, 14, 130–146.
13. M. Peyressatre, C. Prevel, M. Pellerano and M. C. Morris, Cancers, 2015, 7, 179–237.
14. C. Sanchez-Martinez, L. M. Gelbert, M. J. Lallena and A. de Dios, Bioorg. Med. Chem. Lett., 2015, 25, 3420–3435.
15. G. Mariaule and P. Belmont, Molecules, 2014, 19, 14366–14382.
16. D. W. Fry, P. J. Harvey, P. R. Keller, W. L. Elliott, M. Meade, E. Trachet, M. Albassam, X. Zheng, W. R. Leopold, N. K. Pryer and P. L. Toogood, Mol. Cancer Ther., 2004, 3, 1427–1438.
17. L. M. Gelbert, S. F. Cai, X. Lin, C. Sanchez-Martinez, M. del Prado, M. J. Lallena, R. Torres, R. T. Ajamie, G. N. Wishart, R. S. Flack, B. L. Neubauer, J. Young, E. M. Chan, P. Iversen, D. Cronier, E. Kreklau and A. de Dios, Invest. New Drugs, 2014, 32, 825–837.
18. G. I. Shapiro, Clin. Cancer Res., 2004, 10, 4270s–4275s.
19. H. S. W. John, E. Bisi, J. A. Sorrentino, P. J. Roberts and J. C. Strum, Cancer Res., 2015, 75, 1784.
20. H. R. Tsou, M. Otteng, T. Tran, M. B. Floyd, M. Reich, G. Birnberg, K. Kutterer, S. Ayral-Kaloustian, M. Ravi, R. Nilakantan, M. Grillo, J. P. McGinnis and S. K. Rabindran, J. Med. Chem., 2008, 51, 3507–3525.
21. H. R. Tsou, X. Liu, G. Birnberg, J. Kaplan, M. Otteng, T. Tran, K. Kutterer, Z. L. Tang, R. Suayan, A. Zask, M. Ravi, A. Bretz, M. Grillo, J. P. McGinnis, S. K. Rabindran, S. Ayral-Kaloustian and T. S. Mansour, J. Med. Chem., 2009, 52, 2289–2310.
22. P. L. Toogood, P. J. Harvey, J. T. Repine, D. J. Sheehan, S. N. VanderWel, H. R. Zhou, P. R. Keller, D. J. McNamara, D. Sherry, T. Zhu, J. Brodfuehrer, C. Choi, M. R. Barvian and D. W. Fry, J. Med. Chem., 2005, 48, 2388–2406.
23. X. Y. Lu, Y. D. Chen, N. Y. Sun, Y. J. Jiang and Q. D. You, J. Mol. Model., 2010, 16, 163–173.
24. S. K. Singh, N. Dessalew and P. V. Bharatam, Eur. J. Med. Chem., 2006, 41, 1310–1319.
25. N. Dessalew and P. V. Bharatam, Eur. J. Med. Chem., 2007, 42, 1014–1027.
26. B. Q. Cai, H. X. Jin, X. J. Yan, P. Zhu and G. X. Hu, Acta Pharmacol. Sin., 2014, 35, 151–160.
27. K. S. Silva, V. S. Kawade, P. B. Choudhari and M. S. Bhatia, J. Asian Nat. Prod. Res., 2015, 8, 231–235.
28. L. Delgado-Soler, J. Arinez-Soriano, J. M. Granadino-Roldan and J. Rubio-Martinez, Theor. Chem. Acc., 2011, 128, 807–823.
29. A. A. Russo, L. Tong, J. O. Lee, P. D. Jeffrey and N. P. Pavletich, Nature, 1998, 395, 237–243.
30. A. Gaulton, L. J. Bellis, A. P. Bento, J. Chambers, M. Davies, A. Hersey, Y. Light, S. McGlinchey, D. Michalovich, B. Al-Lazikani and J. P. Overington, Nucleic Acids Res., 2012, 40, D1100–D1107.
31. L. Chen, Y. Y. Li, Q. Zhao, H. Peng and T. J. Hou, Mol. Pharm., 2011, 8, 889–900.
32. L. Wang, L. Chen, Z. H. Liu, M. H. Zheng, Q. Gu and J. Xu, PLoS One, 2014, 9, e95221.
33. L. Wang, X. Le, L. Li, Y. C. Ju, Z. X. Lin, Q. Gu and J. Xu, J. Chem. Inf. Model., 2014, 54, 3186–3197.
34. Y. L. Li, L. Wang, Z. H. Liu, C. J. Li, J. K. Xu, Q. Gu and J. Xu, Mol. BioSyst., 2015, 11, 1241–1250.
35. J. Fang, R. Yang, L. Gao, D. Zhou, S. Yang, A. L. Liu and G. H. Du, J. Chem. Inf. Model., 2013, 53, 3009–3020.
36. Q. Z. Ding, C. J. Li, L. Wang, Y. L. Li, H. H. Zhou, Q. Gu and J. Xu, Med. Chem. Commun., 2015, 6, 1393–1403.
37. S. Tian, Y. Li, J. Wang, J. Zhang and T. Hou, Mol. Pharm., 2011, 8, 841–851.
38. J. Xu, Molecules, 1997, 2, 114–128.
39. Z. H. Liu, M. H. Zheng, X. Yan, Q. Gu, J. Gasteiger, J. Tijhuis, P. Maas, J. B. Li and J. Xu, J. Comput.-Aided Mol. Des., 2014, 28, 941–950.
40. T. P. Stockfisch, J. Chem. Inf. Comput. Sci., 2003, 43, 1608–1613.
41. G. De'ath and K. E. Fabricius, Ecology, 2000, 81, 3178–3192.
42. P. Watson, J. Chem. Inf. Model., 2008, 48, 166–178.
43. P. Baldi, S. Brunak, Y. Chauvin, C. A. F. Andersen and H. Nielsen, Bioinformatics, 2000, 16, 412–424.
44. C. Knox, V. Law, T. Jewison, P. Liu, S. Ly, A. Frolkis, A. Pon, K. Banco, C. Mak, V. Neveu, Y. Djoumbou, R. Eisner, A. C. Guo and D. S. Wishart, Nucleic Acids Res., 2011, 39, D1035–D1041.
45. J. Xu, J. Med. Chem., 2002, 45, 5311–5320.
46. Z. H. Li, X. H. Wang, J. Eksterowicz, M. W. Gribble, G. Q. Alba, M. Ayres, T. J. Carlson, A. Chen, X. Q. Chen, R. Cho, R. V. Connors, M. DeGraffenreid, J. T. Deignan, J. Duquette, P. C. Fan, B. Fisher, J. S. Fu, J. N. Huard, J. Kaizerman, K. S. Keegan, C. Li, K. X. Li, Y. X. Li, L. M. Liang, W. Liu, S. E. Lively, M. C. Lo, J. Ma, D. L. McMinn, J. T. Mihalic, K. Modi, R. Ngo, K. Pattabiraman, D. E. Piper, C. Queva, M. L. Ragains, J. Suchomel, S. Thibault, N. Walker, X. D. Wang, Z. L. Wang, M. Wanska, P. M. Wehn, M. F. Weidner, A. J. Zhang, X. N. Zhao, A. Kamb, D. Wickramasinghe, K. Dai, L. R. McGee and J. C. Medina, J. Med. Chem., 2014, 57, 3430–3449.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra23289a

---