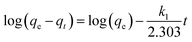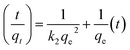DOI:
10.1039/C5RA22851D
(Paper)
RSC Adv., 2016,
6, 5837-5847
Kinetics, equilibrium isotherm and neural network modeling studies for the sorption of hexavalent chromium from aqueous solution by quartz/feldspar/wollastonite
Received
31st October 2015
, Accepted 24th December 2015
First published on 6th January 2016
Abstract
A three layer feed forward artificial neural network (ANN) with back propagation training algorithm was developed to model the adsorption process of Cr(VI) in aqueous solution using riverbed sand containing Quartz/Feldspar/Wollastonite (QFW) as adsorbent. The effect of operational parameters such as adsorbent dosage, initial concentration of Cr(VI) ions, initial pH, agitation speed and contact time was studied to optimize the conditions for maximum removal of Cr(VI) ions in the laboratory batch adsorption experiment. The maximum adsorption efficiency was found at an initial concentration of 10 mg L−1, an adsorbent dosage of 0.75 g L−1 and pH of the solution of 2. Experimental results revealed that a contact time of 90 min was generally sufficient to accomplish equilibrium. The experimental equilibrium data were fitted to various isotherm models. The maximum adsorption capacity of Cr(VI) was found to be 9.812 mg g−1. The kinetic data agreed well with the pseudo-second order model with rate constant value of 4.8 × 10−2. Ninety one experimental data were used to construct an ANN model to predict removal efficiency of Cr(VI). A three-layer ANN, an input layer with five neurons, a hidden layer with 15 neurons and an output layer with one neuron is constructed. The Levenberg–Marquardt algorithm (LMA) was found as the best algorithms with a minimum mean squared error (MSE) of 0.0056. The linear regression between the network outputs and the resultant targets were established to be reasonable with a correlation coefficient of about 0.985 and the experimental data were best fitted to the artificial neural network model.
1. Introduction
The presence of heavy metals is dangerous to the environment and human health. These inorganic pollutants are not biodegradable, thus researchers should find some ways to eliminate these toxic metal ions from surface waters. Various heavy metals exist in surface waters such as Cr, Cd, Cu, Zn, and Ni. Cr(VI) is one of the most toxic and important heavy metals that pollutes the environment.1 Cr(VI) is a strong oxidizing agent which is extremely mobile in soil and aquatic environments and readily absorbed through skin. It is a known carcinogen and an irritant to plant and animal tissues. Due to the health and environmental dangers, hexavalent chromium in industrial wastewater is strictly regulated.2–4 Chromium is considered as one of the most significant pollutant in many countries of the world. Due to chromium wide usage by different industries such as metal plating, paints and pigments, leather tanning, textile dyeing, printing inks and wood preservation, huge quantity of wastewater containing chromium are discharged into the environment in trivalent (Cr(III)) and hexavalent (Cr(VI)) forms. The hexavalent chromium compounds are toxic and carcinogenic. In contrast, relative toxicity of Cr(III) is low and in its trace amounts, it is not a problem for the environment.5 Cr(VI) exists as extremely soluble and highly toxic chromate ions (HCrO4− or Cr2O72−) which can transfer freely in aqueous environments.6 Persistent exposure to Cr(VI) causes cancer in the digestive tract and lungs, and may cause other health problems for instance skin dermatitis, bronchitis, perforation of the nasal septum, severe diarrhea, and hemorrhaging.7–10 Therefore, it is essential to remove Cr(VI) from wastewater before disposal. The permitted limit for Cr(VI) in potable water is 0.05 mg L−1 in both of Iran and USA.11,12 Research in water purification is considered a hot area of research due to the storage in the supply of fresh drinking water and which is at present a serious concern worldwide.13
Various treatment methods are available for removal of heavy metals which include adsorption, ion exchange, reverse osmosis, chemical oxidation, precipitation, distillation, gas stripping, solvent extraction, complexation and bioremediation.14 However, adsorption process is considered to be the cost effective method for treating Cr(VI) containing water and wastewater potentially.15–18 Adsorbent used in the adsorption processes are various materials, including activated carbons prepared from some agricultural by-products, some cellulosic wastes and their carbonization products, bituminous coal and commercial activated carbons.19 However, the high cost of the activation process limits the use in wastewater treatment, particularly for the needs of developing countries. Therefore, over the last few years number of investigations has been conducted to test the low-cost adsorbents for heavy metal ion removal.
New economical, easily available and highly effective adsorbents are still needed. Riverbed sand has the potential to sequester heavy metal ions from solutions. Abundant availability, high sorption capacity, cost-effectiveness, high cation exchange capacity and renewability are the important factors making these materials as economical alternatives for water treatment and waste remediation.20,21 The mechanism of adsorption is highly complex and is difficult to model and simulate using conventional mathematical modeling. This is mainly due to the interaction of more number of adsorption process variables, and hence the resulting relationships are highly non-linear.22
ANN is one of the data based non-traditional tools for modeling the adsorption process. ANN modeling has been successfully used for the adsorption process in the past decade. The objective of ANN model is to compute the output values from input values by some internal manipulated calculations. These models have three layers, such as input, hidden and output layers. Each of these layers contains nodes and these nodes are connected to nodes at adjacent layer(s). The hidden layer(s) contain two processes, i.e., weighted summation functions and transformation function. Both these functions rationalized values from input data to the output measures. The weighted summation function is typically used in a feed-forward back propagation neural network model. The removal efficiency of the adsorbent is to be considered an output layer of the ANN model. Application of ANN has been considered as a promising tool because of their simplicity towards simulation, prediction and modeling. The advantages of ANN are that they require less time for development than the traditional mathematical models, the need for extensive experimentation is avoided as limited numbers of experiments are sufficient to predict the degree of non-linearity and their ability to learn complex relationships without requiring the knowledge of the model structure.23
The ANN's ability to recognize and reproduce and effect relationships through training, for multiple input/output systems, makes it efficient to represent even the most complex systems.24 Because of their reliable, robust and salient characteristics in capturing the non-linear relationships existing between variables (multi-input/output) in complex systems, numerous applications of ANN has been successfully conducted to solve environmental engineering problems.25–30
The present work investigates the implementation of neural networks for the prediction of adsorption efficiency for the removal of chromium using an effective and cheap adsorbent namely QFW. The effects of various operational parameters, such as initial Cr(VI) concentration, initial pH, adsorbent dosage, contact time and agitation speed on the removal of Cr(VI) are also investigated. On the basis of batch adsorption experiments, a three-layer ANN model to predict the Cr(VI) removal efficiency of riverbed sand as adsorbent was applied in this work. Adsorption of Cr(VI) ions using QFW was optimized to determine the optimal network structure. Finally, outputs obtained from the models are compared with the experimental data are also discussed. The adsorption kinetics and isotherms of Cr(VI) on this adsorbent were also studied.
2. Materials and method
2.1. Materials
Stock solution (100 mg L−1) of Cr(VI) ions was prepared by using K2Cr2O7 purchased from Merck Ltd., India. The reagents HNO3, NaOH, HCl and pottasium hydroxide were purchased from Merck Ltd., India. Chemicals and reagents used were of analytical reagent grade.
2.2. Preparation of adsorbent and adsorbate
The QFW samples were collected from Kumbakkarai Falls, Periyakulam, Theni District, Tamilnadu, India. The QFW samples were initially sun dried for 7 days followed by drying in hot air oven at 383 ± 1 K for 2 days. The dried QFW was crushed and sieved and then stored in sterile, closed glass bottles till further investigation.31 A stock solution of Cr(VI) ions with concentration 100 mg L−1 was prepared by dissolving 0.2828 g of K2Cr2O7 in deionised (D.I) water. The stock solution was further diluted to desired concentrations.
2.3. Characterization of QFW
The FT-IR studies of the prepared QFW adsorbent were characterized using a JASCO spectrophotometer with KBr pelletisation in a wide range wavelength ranging from 400 cm−1 and 4000 cm−1. Scanning electron microscope (JEOL JSM-6100) was used to study the surface morphology of the adsorbent at the required magnification at room temperature. UV-vis spectrophotometer (JASCO V-530) was used to record the concentration of the Cr(VI) in the different samples. The Cation Exchange Capacity (CEC) of QFW was estimated using the copper bis-ethylenediamine complex method.32 The zero point charge (pHZPC) for the adsorbent was determined by introducing 1.0 g of QFW into six 100 mL Erlenmeyer flasks containing 100 mL of 0.1 M potassium nitrate solution. Initial pH values of the six solutions were adjusted to 2, 4, 6, 8, 10 and 12 by either adding few drops of nitric acid or potassium hydroxide. The solution mixtures were allowed to equilibrate in an isothermal shaker (25 ± 1 °C) for 24 h. Then the suspension in each sample was filtered and the final pH was measured again. The procedure was repeated by varying the mass of QFW introduced into the solution from 0.1–1.0 g. The value of pHZPC can be determined from the curve that cuts the pH0 lines of the plot ΔpH versus pH0. Adsorbent characterization was performed by means of spectroscopic and quantitative analysis. The results are represented in Table 1.
Table 1 Physicochemical characteristics of QFW
| S. no. |
Parameter |
Value |
| 1 |
pH |
8.78 |
| 2 |
pHzpc |
2.1 |
| 3 |
Specific surface area |
5.8343 m2 g−1 |
| 4 |
Pore volume |
1.099 × 10−2 cm3 g−1 |
| 5 |
Cation exchange capacity |
8. 4 meq g−1 |
| 6 |
SiO2 |
90.05 (%) |
| 7 |
Al2O3 |
0.25% |
| 8 |
Fe2O3 |
3.0% |
| 9 |
CaO |
0.28% |
| 10 |
MgO |
3.6% |
| 11 |
MnO |
0.03% |
| 12 |
Na2O |
0.5% |
| 13 |
K2O |
1.6% |
| 14 |
TiO2 |
0.2% |
2.4. Batch adsorption studies
The batch tests were carried out in glass-stoppered, Erlenmeyer flasks with 200 mL working volume, with a concentration of 10 mg L−1. A weighed amount (0.75 g) of adsorbent was added to the solution. The flasks were agitated at a constant speed of 500 rpm for 90 minutes in an arbitrary shaker at 303 K. The influence of pH (2.0–8.0), initial Cr(VI) concentration (10, 20, 30, 40, 50, 60, 70, 90, 100 mg L−1), contact time (15, 30, 45, 60, 75, 90, 105, 120, 135, 150 min), adsorbent dosage (0.25, 0.5, 0.75, 1, 1.5, 2, 2.5, 3 g) and agitation speed (100, 200, 300, 400, 500, 600, 700, 800 rpm) were evaluated during the present study. Samples were collected from the flasks at predetermined time intervals for analyzing the residual chromium concentration in the solution. After attaining the equilibrium, adsorbent was separated by filtration using Whatman filter paper and the aqueous-phase concentration of metal was determined by UV-vis spectrophotometer. The concentration of chromium left in the solution was determined by the standard spectrophotometric method using diphenylcarbazide as the complexant for chromium.33 Diphenylcarbazide reacts with Cr(VI) in acidic medium to give a red-violet complex at 540 nm. The color intensity is proportional to the concentration of Cr(VI) in the solution. The Cr(VI) concentration in solution was determined by the colorimetric method by using the obtained standard fitting equation.34,35 The percentage of removal of chromium ions was calculated from the following equation:| |
 | (1) |
The effect of initial concentration of Cr(VI), contact time, initial pH, adsorbent dosage and agitation speed was investigated by varying any one of the parameters and keeping other parameter constant.
2.5. Definition of the ANN model
The prediction of removal efficiency of Cr(VI) ions from an aqueous system using QFW is a complex proposition and hence, a neural network approach is adopted. Fig. 1 shows the network architecture with three layers (a single hidden layer). A three layer ANN with a tangent sigmoid transfer function (tansig) at hidden layer, and a linear transfer function (purelin) at output layer were used. Levenberg–Marquardt backpropagation (trainlm) with 1000 iterations was selected for training the designed networks. The number of neurons was optimized between 1–20 neurons in the hidden layer. The data obtained from the experimental values for the removal percentage of Cr(VI) were applied for network training to construct the network model that could compute the predicted removal percentage values from the inputs using MATLAB R20011a software. Ninety one experimental sets were used to develop the ANN model. For Cr(VI) ions, all experimental data were divided randomly into three groups (70%; 63 data for training and 15%; 14 data for testing set and 15%; 14 data for validation set). The initial Cr(VI) concentration, adsorbent dosage, the pH of the solution, agitation speed and contact time were utilized as input parameters, while the removal percentage was applied as the output parameter. The range of variables used was summarized in the Table 2. The complete data normalized in the 0–1. Therefore, data (Xi) converted a normalized value (Xnormal) as follows:36,37| |
 | (2) |
Xmin and Xmax are minimum and maximum actual experimental data. The input signals are modified by interconnection weight known as a weight factor (Wij), which represents the interconnection of ith node of the first layer to jth node of the second layer. The sum of modified signals (total activation) is then modified by a sigmoid transfer function and output is collected at the output layer.38
 |
| | Fig. 1 Artificial neural network architecture | |
Table 2 Range of variables
| S. no. |
Variables |
Ranges |
| 1 |
Amount of adsorbent dose (g L−1) |
0.25–3 |
| 2 |
Initial concentration of Cr(VI) (mg L−1) |
10–100 |
| 3 |
pH |
2–8 |
| 4 |
Contact time (min) |
15–135 |
| 5 |
Agitation speed (rpm) |
100–800 |
| 6 |
Cr(VI) removal efficiency (%) |
0–100 |
The results of the various networks structure and training procedures were compared based on the mean squared error (MSE) and the coefficient of determination (R2) which can be defined as follows:39
| |
 | (3) |
| |
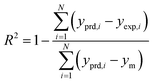 | (4) |
where
yprd,i was the predicted value of ANN model,
yexp,i was the experimental value,
N was the number of data and
ym was the average of the experimental value.
3. Results and discussion
3.1. Characterization of the adsorbent
To elucidate the components of QFW, the FT-IR spectroscopy was used and the spectrum is shown in Fig. 2. In the FT-IR studies of the QFW, the Si–O stretching vibrations were observed at 905.3 cm−1, 643.8 cm−1, 532.7 cm−1 and 464.5 cm−1 showing the presence of quartz. The appearance of ν(Si–O–Si) and δ(Si–O) bands also support the presence of quartz. A strong band at 3463 cm−1 indicates the possibility of the hydroxyl linkage. However, a broad band at 3463 cm−1 in the spectrum of soil suggests the possibility of water of hydration in the adsorbent. Feldspar an abundant group of rock morning minerals, which constitute 60% of the earth's crust. Chemically the feldspar is silicates of aluminum contain sodium, potassium, iron, calcium or barium or combinations of these elements. Feldspar is found in association with all rock types including granite, gneiss, basalt and other crystalline rocks. The peaks at 905.3 cm−1 is observed for albite. The peaks 1050–1055 cm−1 indicates the presence of microcline. The band at 3463 cm−1 indicates silanol OH groups, including 1610–1643 cm−1 which were due to CaO. Also the bands at 1389 cm−1 and 464 cm−1 assigned to carbonate. The FT-IR spectra showed the occurrence of wollastonite and provided a similar FT-IR pattern to that of natural wollastonite. The micrographs of the QFW samples are shown in Fig. 3. While the overall morphology of the sand sample shows smoother edges. Furthermore, smaller particulates can be observed on the QFW. Fig. 3 also shows that the sample has a considerable number of heterogeneous pores where there is a good possibility for metal ion to be adsorbed.
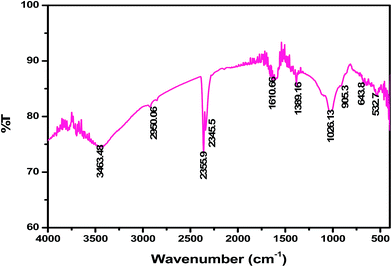 |
| | Fig. 2 FT-IR spectrum of QFW | |
 |
| | Fig. 3 SEM image of QFW | |
3.2. Effect of Cr(VI) ion concentration
Optimum concentrations are determined after experimental studies done under various metal concentrations ranging between 10 and 100 mg L−1. The adsorption efficiency decreased with increasing the concentration of Cr(VI). Following the saturation of the surface where the adsorption takes place to more metal ions can be adsorbed. The results obtained from the experimental studies are shown in Fig. 4.40–42
 |
| | Fig. 4 Effect of Cr(VI) ion concentration. | |
3.3. Effect of contact time
The influence of contact time on the adsorption capacity of QFW is depicted in Fig. 5, in which amount of adsorption of heavy metal is continuously increased with increased contact time durations from (15 to 150 min). That is probably due to the larger surface area of adsorbent at the beginning for the adsorption of Cr(VI). As the surface adsorption sites become exhausted the uptake rate is controlled by the rate at which the adsorbate is transported from the exterior to the interior sites of the adsorbent particles. This is mainly because of the fact that at the initial state of adsorption, vacant surface sites are available once equilibrium is attained; the remaining vacant sites are difficult to be occupied, probably caused by the repulsive forces between the molecules on the adsorbents the bulk phase.43–45
 |
| | Fig. 5 Effect of contact time. | |
3.4. Effect of agitation speed
The effect of agitation speed was investigated by a range from 100 to 800 rpm was shown in Fig. 6. The adsorption of Cr(VI) was low without agitation speed and at low agitation speed and increased as the agitation speed was increased to 500 rpm. However, beyond 500 rpm, the adsorption percentage reminds constant and the agitation speed of 500 rpm was selected in subsequent analysis. This effect can be attributed to the decrease in boundary layer thickness around the adsorbent particles being a result of increasing the degree of mixing.
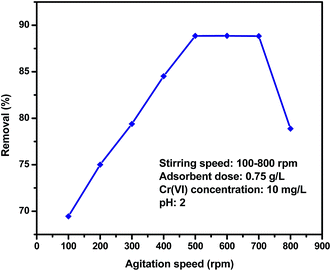 |
| | Fig. 6 Effect of agitation speed. | |
3.5. Effect of pH on Cr(VI) removal
The effect of pH on Cr(VI) removal was studied in the pH range of 2–8 and at 10 mg L−1 initial Cr(VI) concentration. As shown in Fig. 7 the percentage removal of Cr(VI) strongly depends on the solution pH. Adsorption is more favorable in acidic pH. The percentage removal decreased from 88.8% at pH = 2 to 66.08% at pH = 8. There are several forms of Cr(VI) ions existing in the aqueous solution, such as chromate (CrO42−), dichromate (Cr2O72−), and hydrogen chromate (HCrO4−). The relative amounts of these ions depend on the solution pH and total chromate concentration. In acidic pH, acid chromate ions (HCrO4−) are the dominant species than the chromate ions. The results indicate that the maximum uptake of Cr(VI) ions takes place at lower pH as shown in Fig. 7. At low pH, the adsorption was, therefore, facilitated by the electrostatic attraction between the protonated surface of the material and the negatively charged chromate ions in the solution.46,47 The possible mechanism is when the QFW adsorbent is treated with an aqueous solution of Cr(VI) ions in acidic media, the chloride anion (mobile dopant) in the riverbed sand surface is readily exchanged by dichromate or HCrO4− ions and thus the Cr(VI) was removed by exchange mechanism shown in Scheme 1.
 |
| | Fig. 7 Effect of pH on Cr(VI) removal. | |
 |
| | Scheme 1 | |
As the pH increase, the surface of the composite acquires a negative charge, a significantly high electrostatic repulsion exists between the negatively charged surface of riverbed sand and the anions, causing the decrease in Cr(VI) ions adsorption.
3.6. Effect of adsorbent dosage
The dependence of Cr(VI) ions onto QFW was conducted in various adsorbent dosages ranging from 0.25 to 3 g while keeping other parameters such as initial concentration, pH, agitation speed and contact time as constant. The selection of these doses was based on the preliminary adsorption test. The percent adsorption increased from about 65.14 to 88.8% as the amount of adsorbent increased from 0.25 to 0.75 g (Fig. 8) and thereafter further increase in dosage from 0.75 to 3 g percentage removal was very small. It is obvious that as adsorbent dosage increases, the number of available adsorption sites increases; this in turn increases the percentage removal of the metal ion. The reason for the decrease in the adsorption percentage to increase with adsorbent dosage is instauration of adsorption sites through adsorption process. Another possible reason may be the intraparticle interaction, for instance, aggregation, as a result of a high adsorbent dosage. Because of such aggregation, total surface area of adsorbent decreases and diffusion path length increases.48–50
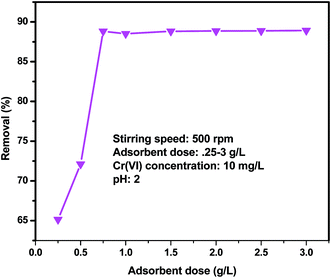 |
| | Fig. 8 Effect of dosage. | |
3.7. Adsorption isotherms
To optimize the design of the adsorption of the adsorbate, it is important to establish the most adsorptions, the surface properties and tendency of adsorbent toward each heavy metal ions. A number of isotherms have been developed to describe equilibrium relationships. In this study, Langmuir, Freundlich and Temkin and Dubinin–Radushkevich models were used to discuss the equilibrium characteristics of the adsorption process have been used.
3.7.1. Langmuir adsorption. Langmuir monolayer adsorption isotherm is very useful for predicting adsorption capacities and also interpreting into mass transfer relationship. The isotherm can be written as follows:51| |
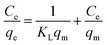 | (5) |
The constant KL (L g−1) is the Langmuir equilibrium constant, and the KL/aL gives the theoretical monolayer saturation capacity, Q0. These Langmuir parameters were obtained from the linear correlations between the values of Ce/qe and Ce. Generally, the Langmuir equation applies to the cases of adsorption on completely homogeneous surfaces where interactions between adsorbed molecules are negligible.52 In Langmuir model, the values of qm and KL can be calculated from the slope and intercept of linear plots of Ce/qe vs. Ce, and the results were listed in Table 3. The linear regression lines obtained have highly significant correlation coefficients (R2 = 0.976), indicating a good fit to the Langmuir equation. The type of the Langmuir isotherm can be predicted by a dimensionless constant separation factor “RL”, which is defined as RL = 1/(1 + KLC0). Where C0 (mg L−1) is the initial adsorbate concentration and KL (L mg−1) is the Langmuir constant. The parameter RL indicates the type of the isotherm accordingly:
Table 3 The Isotherm constants for Cr(VI) adsorption onto riverbed sand
| Isotherm models |
Parameters |
Results |
| Langmuir isotherm |
R2 |
0.976 |
| KL |
3.512 |
| qm (mg g−1) |
9.812 |
| RL |
0.0276 |
| Freundlich isotherm |
R2 |
0.926 |
| KF (L mg−1) |
1.5204 |
| n |
4.2016 |
| Tempkin isotherm |
R2 |
0.896 |
| Kt |
940.6 |
| b |
1.663 |
| D–R isotherm |
R2 |
0.756 |
| β |
0.03 |
| qm (mg g−1) |
9.048 |
| E (kJ mol−1) |
4.083 |
The calculated RL value is 0.0276 for different initial Cr(VI) concentration of 10 mg L−1, indicate that the adsorption of Cr(VI) by riverbed sand is favorable. The calculated separation factor value for Cr(VI) ions as a function of initial metal ion concentration is shown in Fig. 9.
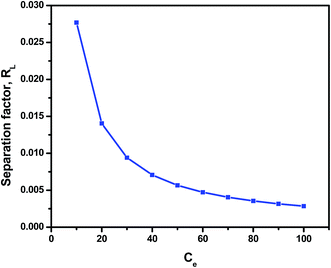 |
| | Fig. 9 The calculated separation factor value for Cr(VI) ions as a function of initial metal ion concentration. | |
3.7.2. Freundlich isotherm. The Freundlich expression53 is an empirical equation based on multilayer sorption to a heterogeneous surface and is expressed by the following equation:| |
 | (6) |
where qe and Ce are the amount of adsorbed adsorbate per unit weight of adsorbent and unadsorbed adsorbate concentration in solution at equilibrium, respectively. KF and 1/n are Freundlich constant characteristics of the system, which are determined from the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe vs. log
qe vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce. The Freundlich model is used to estimate the adsorption intensity of adsorbent towards the adsorbate. The values of KF and 1/n can be obtained from the slope and intercept of the linear plots of log(qe) vs. log(Ce), respectively, and the obtained values are shown in Table 3. KF show information about the bonding energy and the adsorption or distribution coefficient and represents the quantity of metal ion adsorbed onto adsorbent. 1/n show adsorption intensity of Cr(VI) ions onto the adsorbent (surface heterogeneity), its value gets closer to zero by rising heterogeneous of surface (1/n < 1 indicates normal Langmuir isotherm while 1/n above 1 indicate bi-mechanism and cooperative adsorption). It was generally accepted that under a constant temperature, the n values increased with decreasing adsorption energy, that the higher number show and support, the strong adsorption intensity. The n > 1 illustrate adsorb favorable adsorption and vice versa. The values of n is 4.2016 lie in the range of 1–10,54 reveals that adsorption is favorable, which are confirmed with the result of Langmuir model.
Ce. The Freundlich model is used to estimate the adsorption intensity of adsorbent towards the adsorbate. The values of KF and 1/n can be obtained from the slope and intercept of the linear plots of log(qe) vs. log(Ce), respectively, and the obtained values are shown in Table 3. KF show information about the bonding energy and the adsorption or distribution coefficient and represents the quantity of metal ion adsorbed onto adsorbent. 1/n show adsorption intensity of Cr(VI) ions onto the adsorbent (surface heterogeneity), its value gets closer to zero by rising heterogeneous of surface (1/n < 1 indicates normal Langmuir isotherm while 1/n above 1 indicate bi-mechanism and cooperative adsorption). It was generally accepted that under a constant temperature, the n values increased with decreasing adsorption energy, that the higher number show and support, the strong adsorption intensity. The n > 1 illustrate adsorb favorable adsorption and vice versa. The values of n is 4.2016 lie in the range of 1–10,54 reveals that adsorption is favorable, which are confirmed with the result of Langmuir model.
3.7.4. Temkin isotherm. This isotherm takes into account indirect adsorbate–adsorbent interactions of adsorbent surface. Temkin noted experimentally that the heat of adsorption more often decreases with increasing coverage. Temkin adsorption isotherm is expressed as:| |
qe = RT/b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kt + RT/b Kt + RT/b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce Ce
| (10) |
where, R is the gas constant, T is temperature in Kelvin, b is a constant related to the heat of adsorption and Kt is the equilibrium binding constant (L g−1) corresponding to maximum binding energy. The linear plot of qe vs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce shown for the adsorption system indicated the applicability of Temkin isotherm. The values of b and Kt were determined, respectively, from the slope and intercept of the plot (Table 3). Kt value at 303 was 940.6 L g−1, respectively; indicating considerable adsorbent–adsorbate interactions. The values of b were 1.663, indicating a small difference in heat of adsorption.
Ce shown for the adsorption system indicated the applicability of Temkin isotherm. The values of b and Kt were determined, respectively, from the slope and intercept of the plot (Table 3). Kt value at 303 was 940.6 L g−1, respectively; indicating considerable adsorbent–adsorbate interactions. The values of b were 1.663, indicating a small difference in heat of adsorption.
3.8. Adsorption kinetics
The rate and mechanism of adsorption depends upon various factors like physical and chemical properties of adsorbents as well as mass transfer process. In order to investigate the adsorption of Cr(VI) on the surface of QFW, different kinetic models are proposed to examine the controlling mechanism of adsorption process. In this study pseudo-second-order kinetic model and intra-particle-diffusion are investigated to find the best fitted model for the experimental data. The equation of kinetic models is expressed as follows:
3.8.1. Pseudo first-order equation. The pseudo first-order equation of Lagergren57 is given as follows:| |
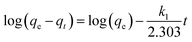 | (11) |
where qt and qe are the amounts of Cr(VI) adsorbed at time t and equilibrium (mg g−1), respectively, and k1 is the pseudo first-order rate constant for the adsorption process (min−1). The linear graph of ln(qe − qt) vs. t shows the applicability of first order kinetic (Table 4).
Table 4 Different kinetic model parameters
| Models |
Parameters |
| |
qe,exp (mg g−1) |
9.9684 |
| Pseudo-first order model |
R2 |
0.334 |
| k1 (min−1) |
0.0184 |
| qe,cal (mg g−1) |
1.0876 |
| Pseudo-second order model |
R2 |
0.960 |
| h (mg g−1 min−1) |
0.1863 |
| k2 (g mg−1 min−1) |
0.0408 |
| qe,cal (mg g−1) |
9.5367 |
| Intra-particle diffusion model |
R2 |
0.983 |
| Kid (mg g−1 min−0.5) |
0.210 |
| A (mg g−1) |
0.099 |
3.8.2. Pseudo second-order equation. This chemisorptions kinetic rate equation is expressed as follows:| |
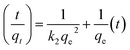 | (12) |
where k2 is the equilibrium rate constant of pseudo second order equation (g mg−1 min−1). The linearity of t/qt vs. t suggests the best fitted with pseudo-second order kinetic.58The results of kinetic parameters according to correlation coefficient (R2) (Table 4) the adsorption of Cr(VI) is best described by the pseudo-second order equation suggesting that the rate-limiting step may be the adsorption mechanism but not mass transport. Thus experimental results support the assumption behind the model that the rate limiting step in adsorption of heavy metal is chemisorptions involving valence forces through the sharing or exchange of electrons between adsorbent and metal ions.
3.8.3. Intra-particle equation. The intraparticle diffusion model is used to explain diffusion mechanism of adsorption process.59 The intraparticle diffusion model can be described as follows:where Kid is the intraparticle diffusion rate constant (mg g−1 h−0.5) and C is the intercept. The value of C relates to the thickness of the boundary layer. The larger C implies the greater effect of the boundary layer. According to eqn (13), if adsorption mechanism follows the intraparticle diffusion model, the plot of qt against t1/2 should show linear relationship. Slope Kid and intercept C will be obtained by linear fitting analysis. The value of rate constant of Morris–Weber transport, Kid, calculated from the slope of the linear plot of qt versus t1/2. The rate constant Kid = 0.210 h−0.5 was calculated from the slope of the straight line with a correlation factor of 0.983 (Table 4). When the adsorption mechanism follows the sole intraparticle diffusion process that impress the plot to cross origin. In the present study, the plot does not have nonzero intercept with multilinear behavior that proofs the contribution of two or more steps in the adsorption process. Since the first stage (external surface adsorption) is completed fast and is less apparent, only the second stage (intraparticle diffusion) and third stage (equilibrium) are demonstrated.
3.9. Comparison with other adsorbents
Various adsorbents for Cr(VI) removal, including activated carbon and clays were reported in literature.60–63 Cr(VI) adsorption capacity (value of qm derived from Langmuir equation) of various low cost adsorbents are summarized in Table 5.
Table 5 Comparison of adsorbents
| Adsorbent |
Metal ion |
Adsorption capacity (mg g−1) |
Concentration (mg L−1) |
Contact time |
Reference |
| Oak bark chars |
Cr(VI) |
3.031 |
100 |
48 h |
60 |
| Peanut shell |
Cr(VI) |
16.26 |
50 |
24 h |
61 |
| Activated carbon |
Cr(VI) |
73.89 |
200 |
|
62 |
| Ocimum Americanum L. seed pots |
Cr(VI) |
83.33 |
200 |
2 h |
63 |
| QFW |
Cr(VI) |
9.812 |
10 |
90 min |
Present study |
3.10. ANN optimization
Fig. 10 shows a BP algorithm with three-layer architecture (a single hidden layer) with a tangent sigmoid transfer function (tansig) at input and hidden layer and a linear transfer function (purelin) at output layer is used and run on using MATLAB R20011a software.64
 |
| | Fig. 10 Proposed ANN structure. | |
The network is tested with different number of neurons to find the optimal number of neurons at the hidden layer by observing the mean squared error.65–67 According to the results, MSE decreases with increasing hidden neuron sizes. MSE remains almost stable when the number of hidden neurons is greater than 20. With further increase in neuron numbers in hidden layer results a sharp increase in the MSE value. As it is well known, high number of hidden neurons can cause over fitting that means exact adaptation of the network to the specific noisy training data. Due to the fact that over fitting occurs when the difference between training error and test error rises with further increase of the number of hidden neuron, we set the optimal value of the number of hidden neurons as 15.
The LM training algorithm used was one of the fast training BP methods i.e., Levenberg–Marquardt algorithms. The LM algorithm is designed to approach second-order training speed without computing the Hessian matrix. This algorithm uses the approximation to the Hessian matrix as given in eqn (14).
| | |
Xk+1 = Xk − [JT − μI]−1JTe
| (14) |
The LM algorithm is appeared to be the fastest method for training moderate-sized feed forward neural networks (up to several hundred weights). It has better performance than the other methods for function approximation problems. Fig. 11 illustrated the training, validation and test mean squared error for the LM algorithm. The training was stopped after 12 epochs. A high degree of correlation between actual and predicted sorption efficiency (%) is observed as shown in Fig. 12. Coefficient of determination (R2) of 0.986 is obtained for training data set. When the network is well trained, testing of the network with testing data set is carried out. The prediction ability of the developed network model for responses of experimental data not forming part of the training set. During testing phase, output of the data is not presented to the network. A high degree of correlation (R2 = 0.986) between actual and predicted sorption percentage (%) is observed. In Fig. 13 the predicted data versus actual results for training, validation, test and all data are plotted. This figure shows the goodness of fit between all experimental data employed and the predicted results given by the ANN model.
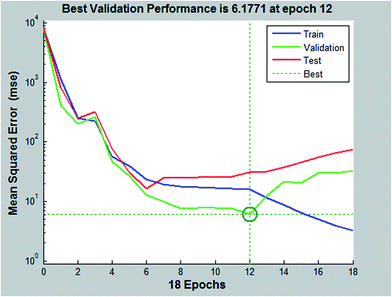 |
| | Fig. 11 ANN model training, validation and testing. | |
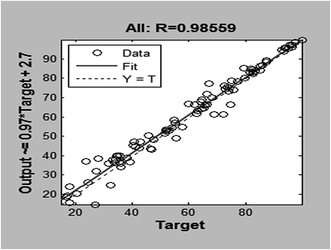 |
| | Fig. 12 Regression analysis for adsorption of Cr(VI). | |
 |
| | Fig. 13 Comparison between ANN simulated and experimental output data. | |
4. Conclusions
The present work demonstrates successful removal of Cr(VI) ions from the aqueous solutions using QFW with maximum removal efficiency (88.24%). One factor at a time experiments were achieved, and the effects of initial pH, adsorbent dosage (g L−1), contact time, agitation speed and initial concentration were investigated on the removable percentage (R%). The Cr(VI) adsorption by QFW was highly dependent on the initial pH and had a higher adsorption capacity at pH 2.0. Fitting with pseudo-second order kinetics indicates the chemisorption characteristics of Cr(VI) by QFW. The QFW follow the Langmuir adsorption isotherm with a calculated maximum adsorption capacity of 9.812 mg g−1. The traditional feed forward BP with the Levenberg–Marquardt training algorithm was taken into account for this purpose. As a result, the algorithm was found to be best with the lowest MSE (0.0056) and highest R2 (0.9855). Both the results obtained by ANN and with the full factor experimental design are compatible with each other. The proposed ANN modeling technique is simple to implement, cost-effective and requires less computational time.
References
- M. A. Behnajady and S. Bimeghdar, Chem. Eng. J., 2014, 239, 105 CrossRef CAS.
- F. G. Garcia, J. M. A. Merced, G. R. Morales, V. V. Guerrero, C. E. B. Diaz and B. Bilyeu, J. Ind. Eng. Chem., 2014, 20, 2477 CrossRef.
- C. Xu, B. Qiu, H. Gu, X. Yang, H. Wei, X. Huahg, Y. Wang, D. Rutman, D. Cao, S. Bhana, Z. Guo and S. Wei, ECS J. Solid State Sci. Technol., 2014, 3(3), m1 CrossRef.
- B. Qiu, C. Xu, D. Sun, H. Yi, J. Guo, X. Zhang, H. Qu, M. Guerrero, X. Wang, N. Noel, Z. Luo and S. Wei, ACS Sustainable Chem. Eng., 2014, 2(8), 2070 CrossRef CAS.
- Z. Yue, S. E. Bender and J. Wang, J. Hazard. Mater., 2009, 166, 74 CrossRef PubMed.
- P. Mitra, D. Sarkar, S. Chakrabarti and B. K. Dutta, Chem. Eng. J., 2011, 171, 54 CrossRef CAS.
- B. Deng and T. S. Alan, Environ. Sci. Technol., 1996, 30, 2484 CrossRef.
- Z. Ai, Y. Cheng, L. Zhang and J. Qiu, Environ. Sci. Technol., 2008, 42, 6955 CrossRef PubMed.
- B. Qiu, H. Gu, X. Yan, J. Guo, Y. Wang, D. Sun, Q. Wang, M. Khan, X. Zhang, B. L. Weeks, D. P. Young, Z. Guo and S. Wei, J. Mater. Chem. A, 2014, 2, 17454 CAS.
- B. Qiu, C. Xu, D. Sun, Q. Wang, H. Gu, X. Zhang, B. L. Weeks, J. Hopper, T. C. Ho, Z. Guo and S. Wei, Appl. Surf. Sci., 2015, 334, 7 CrossRef CAS.
- EPA, Technical Report: EPA/625/R-00/005, Washington, 2000 Search PubMed.
- J. Zhu, H. Gu, J. Guo, M. Chen, H. Wei, Z. Luo, H. A. Colorado, N. Yerra, D. Ding, T. C. Ho, N. Haldolaarachchige, J. Hopper, D. P. Young, Z. Guo and S. Wei, J. Mater. Chem. A, 2014, 2, 2256 CAS.
- T. A. Saleh and V. K. Gupta, J. Colloid Interface Sci., 2012, 371, 101–106 CrossRef CAS PubMed.
- S. N. Mukherjee, S. Kumar, A. K. Misra and F. Maohong, Chem. Eng. J., 2007, 129, 133 CrossRef CAS.
- A. Mittal, J. Mittal, A. Malviya, D. Kaur and V. K. Gupta, J. Colloid Interface Sci., 2010, 343, 463 CrossRef CAS PubMed.
- A. Mittal, J. Mittal, A. Malviya and V. K. Gupta, J. Colloid Interface Sci., 2009, 340, 16 CrossRef CAS PubMed.
- A. Mittal, D. Kaur, A. Malviya, J. Mittal and V. K. Gupta, J. Colloid Interface Sci., 2009, 337, 345 CrossRef CAS PubMed.
- A. K. Jain, V. K. Gupta, A. Bhatnagar and Suhas, Sep. Purif. Technol., 2003, 38(2), 463 CAS.
- H. B. Pirincci, MSc Thesis, Department of Chemical Engineering, Graduate School of Natural Applied Sciences of Firat University, Elazig, 2004.
- D. Sarala Thambavani and B. Kavitha, Int. J. Res., 2014, 1, 718 Search PubMed.
- D. Sarala Thambavani and B. Kavitha, Int. J. Eng. Sci. Res. Technol., 2014, 3, 906 CrossRef.
- J. S. J. van Deventer, S. P. Liebenberg, L. Lorenzen and C. Aldrich, Miner. Eng., 1995, 8, 1489 CrossRef CAS.
- K. Pramanik, J. Instit. Eng., 2004, 85, 31 CAS.
- A. Aleboyeh, M. B. Kasiri, M. E. Olya and H. Aleboyeh, Dyes Pigm., 2008, 77, 288 CrossRef CAS.
- S. Gob, E. Oliveros, S. H. Bossmann, A. M. Braun, R. Guardani and C. A. O. Nascimento, Chem. Eng. Process., 1999, 38, 373 CrossRef.
- S. Lek and J. F. Guegan, Ecol. Modell., 1999, 120, 65 CrossRef.
- S. Cinar, T. T. Onay and A. Erdincler, Adv. Environ. Res., 2004, 8, 477 CrossRef CAS.
- D. Salari, N. Daneshvar, F. Aghazadeh and A. R. Khataee, J. Hazard. Mater., 2005, 125, 205 CrossRef CAS PubMed.
- S. M. H. Asl, M. Ahmadi, M. Ghiasvand, A. Tardast and R. Katal, J. Ind. Eng. Chem., 2013, 19, 1044 CrossRef CAS.
- K. Yetilmezsoy and S. Demirel, J. Hazard. Mater., 2008, 153, 1288 CrossRef CAS PubMed.
- B. Das and N. K. Mondal, Univers. J. Environ. Res. Technol., 2011, 1, 515 CAS.
- F. Bergaya and M. Vayer, CEC of clays: Measurement by adsorption of a copper ethylenediamine complex, Appl. Clay Sci., 1997, 12, 275 CrossRef CAS.
- L. S. Clesceri, A. E. Greenberg and A. D. Eaton, Standard Methods for the Examination of Water and Wastewater, American Public Health Association, Washington, 1998, p. 1325 Search PubMed.
- B. Qiu, Y. Wang, D. Sun, Q. Wang, X. Zhang, B. L. Weeks, R. O. Connor, X. Huang, S. Wei and Z. Guo, J. Mater. Chem. A, 2015, 3(18), 9817 CAS.
- B. Qiu, J. Guo, X. Zhang, D. Sun, H. Gu, Q. Wang, H. Wang, X. Wang, X. Zhang, B. L. Weeks, Z. Guo and S. Wei, ACS Appl. Mater. Interfaces, 2014, 6, 19816 CAS.
- E. R. Rene, M. C. Veiga and C. Kennes, J. Chem. Technol. Biotechnol., 2009, 84, 941 CrossRef CAS.
- A. Elias, G. Ibarra-Berastegi, R. Arias and A. Barona, Bioprocess Biosyst. Eng., 2006, 29, 129 CrossRef CAS PubMed.
- K. Movagharnejad and M. Nikzad, Comput. Electron. Agr., 2007, 59, 78 CrossRef.
- M. Sadrzadeh, T. Mohammadi, J. Ivakpour and N. Kasiri, Chem. Eng. J., 2008, 144, 431 CrossRef CAS.
- M. Bhaumik, A. Maity, V. V. Srinivasu and M. S. Onyango, J. Hazard. Mater., 2011, 190, 381 CrossRef CAS PubMed.
- N. Ballav, A. Maity and S. B. Mishra, Chem. Eng. J., 2012, 198, 536 CrossRef.
- B. Qiu, C. Xu, D. Sun, H. Wei, X. Zhang, J. Guo, Q. Wang, D. Rutman, Z. Guo and S. Wei, RSC Adv., 2014, 4, 29855 RSC.
- L. DIlario, I. Francolini, A. Martinelli and A. Piozzi, Dyes Pigm., 2009, 80(3), 343 CrossRef CAS.
- S. Deng and R. Bai, Water Res., 2004, 38, 2424 CrossRef CAS PubMed.
- V. K. Gupta, S. Agarwal and T. A. Saleh, J. Hazard. Mater., 2011, 185, 17 CrossRef CAS PubMed.
- P. A. Kumar, M. Rayb and S. Chakraborty, J. Hazard. Mater., 2007, 143, 24 CrossRef CAS PubMed.
- R. Zhang, H. Ma and B. Wang, Ind. Eng. Chem. Res., 2010, 49, 9998 CrossRef CAS.
- M. Bhaumik, A. Maity, V. V. Srinivasu and M. S. Onyango, Chem. Eng. J., 2012, 181, 323 CrossRef.
- C. H. Yang, J. Colloid Interface Sci., 1998, 208, 379 CrossRef CAS PubMed.
- V. K. Gupta, R. Jain, A. Mittal, T. A. Saleh, A. Nayak, S. Agarwal and S. Sikarwar, Mater. Sci. Eng., C, 2012, 32, 12 CrossRef CAS PubMed.
- G. Q. Tan and D. Xiao, J. Hazard. Mater., 2009, 164, 1359 CrossRef CAS PubMed.
- M. Barkat, D. Nibou, S. Chearouche and A. Mellah, Chem. Eng. Process., 2009, 48, 38 CrossRef CAS.
- K. R. Hall, L. C. Eagleton, A. Acrivos and T. Vermeulen, I&EC Fundam., 1966, 5, 212 Search PubMed.
- Z. Chen, W. Ma and M. Han, J. Hazard. Mater., 2008, 155, 327 CrossRef CAS PubMed.
- M. M. Dubinin, E. D. Zaverina and L. V. Radushkevich, J. Phys. Chem., 1947, 21, 1351 CAS.
- S. Kundu and A. K. Gupta, Chem. Eng. J., 2006, 122(1–2), 93 CrossRef CAS.
- S. Lagergren, K. Sven. Vetenskapsakad. Handl., 1898, 24, 1 Search PubMed.
- Y. S. Ho, G. McKay, D. A. J. Wase and C. F. Foster, Adsorpt. Sci. Technol., 2000, 18, 639 CrossRef CAS.
- W. J. Weber and J. C. Morris, J. Sanit. Eng. Div., Am. Soc. Civ. Eng., 1963, 89, 31 Search PubMed.
- D. Mohan, S. Rajput, V. K. Sing, P. H. Steele and C. U. Pittiman Jr, J. Hazard. Mater., 2001, 188, 319 CrossRef PubMed.
- Z. A. Al-Othman, R. Ali and M. Naushad, Chem. Eng. J., 2012, 184, 238 CrossRef CAS.
- D. Duranoglu, A. W. Trochimczuk and U. Beker, Chem. Eng. J., 2012, 187, 193 CrossRef CAS.
- L. Levankumar, V. Muthukumaran and M. B. Gobinath, J. Hazard. Mater., 2009, 161, 709 CrossRef CAS PubMed.
- K. H. Chu, Eur. J. Miner. Process. Environ. Prot., 2003, 3, 119 Search PubMed.
- S. Gob, E. Oliveros, S. H. Bossmann, A. M. Braun and R. Guardani, Chem. Eng. Process., 1999, 38, 373 CrossRef.
- N. G. Turan, B. Mesci and O. Ozgonenel, Chem. Eng. J., 2011, 171, 1091 CrossRef CAS.
- N. G. Turan, B. Mesci and O. Ozgonenel, Chem. Eng. J., 2011, 173, 98 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. 


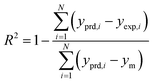
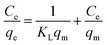

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe vs. log
qe vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce. The Freundlich model is used to estimate the adsorption intensity of adsorbent towards the adsorbate. The values of KF and 1/n can be obtained from the slope and intercept of the linear plots of log(qe) vs. log(Ce), respectively, and the obtained values are shown in Table 3. KF show information about the bonding energy and the adsorption or distribution coefficient and represents the quantity of metal ion adsorbed onto adsorbent. 1/n show adsorption intensity of Cr(VI) ions onto the adsorbent (surface heterogeneity), its value gets closer to zero by rising heterogeneous of surface (1/n < 1 indicates normal Langmuir isotherm while 1/n above 1 indicate bi-mechanism and cooperative adsorption). It was generally accepted that under a constant temperature, the n values increased with decreasing adsorption energy, that the higher number show and support, the strong adsorption intensity. The n > 1 illustrate adsorb favorable adsorption and vice versa. The values of n is 4.2016 lie in the range of 1–10,54 reveals that adsorption is favorable, which are confirmed with the result of Langmuir model.
Ce. The Freundlich model is used to estimate the adsorption intensity of adsorbent towards the adsorbate. The values of KF and 1/n can be obtained from the slope and intercept of the linear plots of log(qe) vs. log(Ce), respectively, and the obtained values are shown in Table 3. KF show information about the bonding energy and the adsorption or distribution coefficient and represents the quantity of metal ion adsorbed onto adsorbent. 1/n show adsorption intensity of Cr(VI) ions onto the adsorbent (surface heterogeneity), its value gets closer to zero by rising heterogeneous of surface (1/n < 1 indicates normal Langmuir isotherm while 1/n above 1 indicate bi-mechanism and cooperative adsorption). It was generally accepted that under a constant temperature, the n values increased with decreasing adsorption energy, that the higher number show and support, the strong adsorption intensity. The n > 1 illustrate adsorb favorable adsorption and vice versa. The values of n is 4.2016 lie in the range of 1–10,54 reveals that adsorption is favorable, which are confirmed with the result of Langmuir model.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = ln
qe = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qm − βε2
qm − βε2


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kt + RT/b
Kt + RT/b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce
Ce
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce shown for the adsorption system indicated the applicability of Temkin isotherm. The values of b and Kt were determined, respectively, from the slope and intercept of the plot (Table 3). Kt value at 303 was 940.6 L g−1, respectively; indicating considerable adsorbent–adsorbate interactions. The values of b were 1.663, indicating a small difference in heat of adsorption.
Ce shown for the adsorption system indicated the applicability of Temkin isotherm. The values of b and Kt were determined, respectively, from the slope and intercept of the plot (Table 3). Kt value at 303 was 940.6 L g−1, respectively; indicating considerable adsorbent–adsorbate interactions. The values of b were 1.663, indicating a small difference in heat of adsorption.