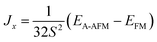First-principles study of the electronic and magnetic properties of the spin-ladder iron oxide Sr₃Fe₂O₅

Abstract

The electronic and magnetic properties of the novel spin-ladder iron oxide Sr₃Fe₂O₅, containing an unusual square-planar coordination around high-spin Fe²⁺ cations, were investigated using the generalized gradient approximation plus the Coulomb interaction correlation method. Our results demonstrated that the G-type antiferromagnetic configuration is the ground state, which is in excellent agreement with experimental neutron powder diffraction and Mössbauer spectroscopy measurements, as well as available theoretical results in the literature, albeit with slightly larger computed magnetic moments. Moreover, the outstanding discrepancy between the two-dimensional crystal structure and the three-dimensional electronic/magnetic properties was resolved via the special localization and orientation of electronic/spin charge in real space, i.e., the d_z² orbital ordering of the down-spin Fe 3d electron.

---

Introduction

The chemistry and physics of transition metal oxides have been full of surprises and intriguing structural, electronic and magnetic phenomena. One of the key ingredients of the origin of these effects is the availability of degenerate electronic orbitals. Whether such orbital degrees of freedom actually occur in a material depends on the nature of the atomic ions and the surrounding crystallographic structure, i.e., the coordination polyhedra. Thus, the ability to tune the coordination polyhedra of transition metal ions will offer an extra method of designing novel materials, which might possess fascinating properties and potential applications.

The coordination geometries of iron oxides have been exclusively restricted to three-dimensional polyhedra such as octahedra and tetrahedra. However, this restriction was recently circumvented by using calcium hydride as a powerful reductant at low temperatures,¹ as initiated and developed by Hayward et al., which provides an effective route for obtaining unprecedented coordination polyhedra in transition metal oxides.² By applying this new synthetic method to SrFeO₃, a new compound SrFeO₂, which displays an unusual square-planar coordination around Fe, has been obtained. It contains planar FeO₂ layers that comprise corner-sharing FeO₄ squares with high-spin Fe²⁺ ions separated by Sr²⁺ ions,^1,3 which are isostructural with the undoped high-T_c superconductor SrCuO₂. Compared with compounds with low dimensionality, SrFeO₂ exhibits interesting and apparently puzzling physical properties.¹ From the theoretical point of view, most of the available insight that originates from electronic structure calculations^4,5 indicates that the lone down-spin electron of the high-spin Fe²⁺ (d⁶) ion located in the square-planar coordinated structure occupies the d_z² orbital. This special electronic configuration indicates that SrFeO₂ is not subject to Jahn–Teller distortion when the temperature is lowered, and is associated with a three-dimensional antiferromagnetic spin order with a very high Néel temperature (T_N = 473 K).

The low-temperature reaction of the double-layered perovskite Sr₃Fe₂O₇ (space group I4/mmm) with CaH₂ gives rise to the stable novel spin-ladder iron oxide Sr₃Fe₂O₅.^6,7 Sr₃Fe₂O₅ adopts an I-centered orthorhombic space group (Immm) with a = 3.51485 Å, b = 3.95271 Å and c = 20.91251 Å,⁶ as shown in Fig. 1. It consists of double layers of corner-sharing planar FeO₂ interleaved by Sr²⁺ ions along the z direction, and exhibits a framework of ladders with two legs running along the [010] direction and rungs along the [001] direction. Neutron powder diffraction and Mössbauer spectroscopy measurements established the presence of long-range antiferromagnetic order, which is characterized by a magnetic propagation vector q = (1/2, 1/2, 0), and that the moments of iron of 2.76 μ_B are aligned parallel to the z direction.^6,7 In addition, first-principles density functional theory calculations employing the projected augmented wave method suggested that magnetic dipole–dipole interactions are essential for the three-dimensional magnetic ordering in Sr₃Fe₂O₅.⁸ Furthermore, identifying the fine details of the electronic structure and its tendency towards a magnetic configuration, as well as the strength of the coupling of the magnetic ions, is important for understanding the physical properties. Generally, it is well known that electronic and magnetic properties are very sensitive to coordination polyhedra. To the best of our knowledge, a clear picture of the role of the unusual square-planar coordination of Fe²⁺ ions in Sr₃Fe₂O₅ is lacking and deserves special attention. In an attempt to partly remedy this situation, we have investigated the electronic and magnetic properties of Sr₃Fe₂O₅ using full-potential density functional theory calculations. The implications of our work in relation to recent experiments are discussed in detail.

Fig. 1 The spin structure of Sr₃Fe₂O₅ below T_N. The large green and small red spheres represent Sr and O atoms, respectively. The arrows indicate the direction of the moment on the iron ions.

Approach

The band structure calculation was carried out within the framework of the generalized gradient approximation (GGA) + U method.^9–12 We used the highly accurate WIEN2k package,^13,14 which implements the linear augmented plane wave (LAPW) method with local orbitals.^15,16 In this method, the wavefunctions are expanded in spherical harmonics inside non-overlapping atomic spheres of a radius of R_MT and in plane waves in the interstitial region. We adopted the experimentally determined crystal structure with the space group Immm. In the calculation, we chose values of R_MT of 2.45, 1.95 and 1.73 Bohr for Sr, Fe and O, respectively. The Ewald cutoff radius was R_MTK_max = 7. The maximum value of l for the expansion of the wavefunctions in spherical harmonics inside the spheres was taken to be l_max = 10. The total number of k-points was 1000 in the whole Brillouin zone.¹⁷ To account for the strong electron correlation associated with the Fe 3d states, GGA + U calculations with an effective value of U_eff = 4.0 eV were performed; this value is similar to that in previous studies of Sr₃Fe₂O₅ (ref. 8) and SrFeO₂.^4,5,18 To test the sensitivity of our results to the on-site effective Coulomb repulsion, somewhat larger and smaller values of U_eff were also used for the Fe d electrons; our conclusion still holds, given that a sizable value of U_eff is present at the Fe²⁺ sites. The self-consistent calculations were considered to be converged only when the integrated charge difference per formula unit between input charge densities was less than 0.0001.

Results and discussion

In order to determine the magnetic ground state of Sr₃Fe₂O₅, three spin ordering configurations were studied, namely, a ferromagnetic arrangement, an A-type antiferromagnetic arrangement along the x direction, in which ferromagnetically ordered planes of Fe sites are antiferromagnetically coupled within each plane, and a G-type antiferromagnetic arrangement, in which antiferromagnetically ordered planes of Fe sites are antiferromagnetically coupled. The results of our calculations for these three magnetic configurations of the orthorhombic phase of Sr₃Fe₂O₅ are summarized in Table 1. The G-type antiferromagnetic state possesses the lowest energy, which is consistent with experimental determinations based on neutron powder diffraction,^6,7 irrespective of the calculation methods (GGA or GGA + U), and in fair agreement with previous theoretical reports.⁸ Concerning the magnetic ground state configuration, we determined the value of the superexchange parameters in terms of the classic Heisenberg spin Hamiltonian:

Table 1 Total energies and magnetic moments of the atomic sites calculated for the ferromagnetic, A-type antiferromagnetic and G-type antiferromagnetic configurations of Sr₃Fe₂O₅. The energies are given in units of eV per f.u. with respect to those of the ground state (G-type AFM). The magnetic moments are given in units of Bohr magnetrons (μ_B)

		FM	A-AFM	G-AFM
Total energy	GGA(U = 0.0 eV)	0.095 eV per a.u.	0.098 eV per a.u.	0.0 eV per a.u.
	GGA + U(U = 4.0 eV)	0.08718 eV per a.u.	0.03773 eV per a.u.	0.0 eV per a.u.

---

		Fe	O	Fe	O	Fe	O
Magnetic moment	GGA(U = 0.0 eV)	3.19	0.09–0.17	±3.36	±0.11–±0.19	±3.30	±0.10
	GGA + U(U = 4.0 eV)	3.57	0.08–0.12	±3.55	±0.07–±0.11	±3.54	±0.07

---

Here, J > 0 (J < 0) represents ferromagnetic (antiferromagnetic) interactions and S = 2 is the spin of 3d⁶ Fe²⁺ ions. On the basis of our calculations, we only considered the J_yz interaction within the yz planes and the J_x interaction between the yz planes along the x direction, respectively. The interaction between the perovskite building blocks was omitted, owing to the large distances.

According to the GGA + U(U_eff = 4.0 eV) results, we obtained values of J_yz = −1.57 meV and J_x = −3.10 meV. Note that both interactions are negative, which indicates antiferromagnetic interactions within the two-dimensional planes and between them, which confirms that the ground state is G-type antiferromagnetic. Owing to the two-dimensional character of the structure, however, one could expect that the strength of interplanar coupling should be small, exhibiting two-dimensional magnetic properties. Unexpectedly, it was found that the robust three-dimensional G-type antiferromagnetic state within the double layers of corner-sharing planar FeO₂ is the ground state as stated above, which is in apparent contrast to expectations. This suggests that the electronic configuration of Fe²⁺ within the planar coordination plays an important role in the magnetic properties of Sr₃Fe₂O₅.

The calculated magnetic moment at the Fe sites varies between 3.19 μ_B and 3.30 μ_B per Fe atom depending upon the magnetic configuration considered in our calculations at the GGA level. The calculated magnetic moment at the Fe sites was found to be slightly larger than the value of 2.76 μ_B measured in low-temperature neutron diffraction measurements,^6,7 whereas it is substantially smaller than the expected value. One of the reasons for the large decrease is that the effect of quantum magnetic fluctuations is inherently enhanced in the low-dimensional ladder, as was argued in ref. 6. Alternatively, the calculated magnetic moment at the iron sites might be reduced from the expected integer value of 4 μ_B, because the Fe d electrons exhibit hybridization interactions with the neighboring O ions. Owing to the hybridization interactions, we found that a magnetic moment of around 0.10 μ_B was induced at each O site, whereas the direction of the polarization depended on the magnetic configuration. The inclusion of an on-site Coulomb correlation on the Fe 3d electrons (U_eff = 4.0 eV) under the GGA + U formulation increases the computed magnetic moments. The remarkable increase in the theoretical value at the Fe sites is accompanied by a slight decrease in the computed value at the O sites. These observations are expected, because the GGA + U scheme tends to enhance the “localization” of Fe d states and then diminish the hybridization interactions between the Fe d electrons and the neighboring O ions.

Because the GGA + U method yielded a similar density of states and charge density to the GGA approach, the results discussed as follows are restricted to the GGA scheme unless otherwise indicated. Note that the ferromagnetic configuration (which is experimentally inaccessible) might provide useful references for understanding the G-type antiferromagnetic configuration that was confirmed. Fig. 2 shows the total and partial density of states corresponding to the Fe 3d electronic states of the ferromagnetic configuration. Majority and minority spins are shown above and below the vertical axis, respectively. The plots clearly demonstrate that there is a strong hybridization interaction between the Fe 3d states and the surrounding O 2p states. Moreover, one can observe that the Fe 3d spin-up states are completely occupied, whereas the spin-down states are partially occupied and cross the Fermi level. This reflects the large exchange splitting of the Fe 3d levels, which is responsible for the high-spin state of the Fe²⁺ ions and the computed magnetic moments. As a consequence, the GGA calculations for the ferromagnetic configuration converged to the metallic ground state with a high density of states at the Fermi level, which indicates the instability of this arrangement.

Fig. 2 Total (black solid line) and partial density of states of Fe (red dashed/dotted line) for the ferromagnetic configuration of Sr₃Fe₂O₅ obtained via GGA calculations.

However, when one introduces G-type antiferromagnetic ordering into the framework, the exchange interaction produces an exchange potential that effectively shifts the energy of the Fe 3d states to lower energy, giving rise to insulating behavior. The calculated band structures along the high-symmetry directions of the first Brillouin zone, as well as the total density of states, are presented in Fig. 3 and Fig. 4, respectively. It is evident that the antiferromagnetic coupling leads to a significant reduction in the bandwidth of the energy bands and a redistribution in spectral weight. A closer inspection of the representations of the site-projected density of states reveals that the Sr atoms have largely donated their valence electrons to the other constituents and have themselves entered into nearly pure ionic states (which is evident from the small number of states in the valence band and the larger number of states in the conduction band). Because the Fe and O states cover the same energy range with a similar pattern of the density of states curve, to some extent, there may be appreciable hybridization, that is, a significant degree of Fe–O covalent bonding character. More importantly, a thorough inspection of the density of states reveals that the electronic configuration is (d_z²)²(d_xzd_yz)²(d_xy)¹(d_x²−y²)¹ for the Fe²⁺ cations, where the minority-spin electron exclusively occupies the d_z² orbital, free from Jahn–Teller distortion. This scenario is in accordance with the experimental observations^6,7 and the existing theoretical results.^8,19 Taking the Coulomb correlation effects into account, although the band gap of Sr₃Fe₂O₅ for the G-type AFM configuration increases from 0.6 eV to 1.5 eV, the pattern of the density of states remains intact. In particular, the dispersion of the energy band along all the highly symmetrical directions of the Brillouin zone is moderate and isotropic, demonstrating strong three-dimensional behavior of the electronic properties, which is in sharp contrast with the two-dimensional crystallographic structure of Sr₃Fe₂O₅.

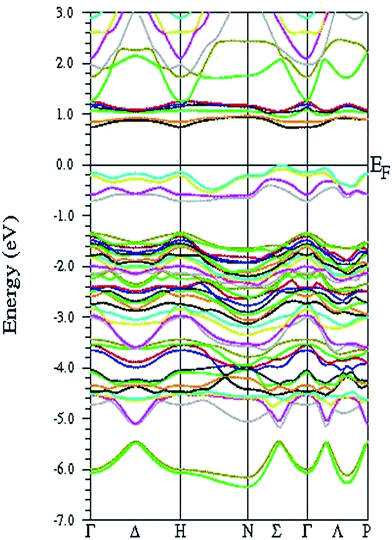Fig. 3 Band structure for G-type antiferromagnetic configuration of Sr₃Fe₂O₅ obtained via GGA calculations. The Fermi level, E_F, is set to 0 eV.

Fig. 4 Total density of states for the G-type antiferromagnetic configuration of Sr₃Fe₂O₅ obtained via GGA calculations.

Comparing the three-dimensional electronic/magnetic properties with the two-dimensional crystallographic structure, these features pose the interesting question of how this conundrum could be reconciled. Elucidating this paradox will no doubt lead to an improvement in our understanding of the diverse behavior of transition metal oxides, because of their versatile charge, spin and orbital degrees of freedom.

To reveal the mechanism behind the interesting and puzzling physical properties of Sr₃Fe₂O₅, we turned our attention to the spin density distribution of the G-type antiferromagnetic configuration of Sr₃Fe₂O₅ by plotting the local spin-up/down electron density for the energy window of 0.6 eV just below E_F, as illustrated in Fig. 5. The occupied majority/minority spin state of the sixth 3d electron is predominantly of d_z² orbital character, rather than the doubly degenerate d_xz and d_yz orbitals. Moreover, such localization in real space is accompanied by flat band levels in the Brillouin zone. Such a special electronic state originates from what is expected from the crystal field splitting of the D_4h point symmetry and molecular orbital energy,¹⁸ or the strong hybridization of the iron 3d_z² and 4s orbitals, as proposed by Takano et al.⁵ Hence, the three-dimensional G-type antiferromagnetic configuration could be explained on the basis of superexchange coupling and the special localization and orientation of electronic/spin charge in real space. On the one hand, according to the Goodenough–Kanamori–Anderson (GKA) rules,²⁰ it is well established that the spins of the Fe cations within the yz plane (Fig. 1) are aligned antiferromagnetically owing to linear Fe–O–Fe superexchange interactions. On the other hand, the obtained pattern of ferro-orbital order induces antiferromagnetic coupling along the x axis between the interplanes, which is in close accordance with the Kugel–Khomskii model.²¹ To sum up, we addressed the origin of the unusual and puzzling physical properties of Sr₃Fe₂O₅ and found that it might be associated with the d_z² orbital ordering of the minority-spin 3d electron. This accounts for the modest G-type antiferromagnetic configuration and in turn the corresponding three-dimensional electronic properties.

Fig. 5 Partial spin density of states for spin-up (top)/spin-down (bottom) Fe atoms in the G-type antiferromagnetic configuration of Sr₃Fe₂O₅ obtained via GGA calculations. Isosurface of d_z² orbital for spin-up (top)/spin-down (bottom) Fe d states centered at Fe sites in the G-type antiferromagnetic configuration of Sr₃Fe₂O₅ (inset).

Conclusions

In conclusion, we have investigated the electronic and magnetic properties of Sr₃Fe₂O₅, which is an unusual spin-ladder iron oxide with square-planar coordination around high-spin Fe²⁺. The obtained results demonstrated that the G-type antiferromagnetic configuration is the ground state, which is in excellent agreement with experimental neutron powder diffraction and Mössbauer spectroscopy measurements and existing theoretical reports, despite the slightly larger calculated magnetic moments. The paradox that the two-dimensional square lattice exhibits modest three-dimensional electronic and magnetic properties could be understood through the d_z² orbital ordering of the sixth minority 3d electron, on the basis of superexchange interactions and the ferro-orbital ordering pattern. The special localization and orientation of electronic/spin charge in real space is the key factor for understanding the structural stability and electronic and magnetic properties of the material.

Acknowledgements

This study was supported by the National Natural Science Foundation of China (Grant No. 21201148, 21303156, 21403185, and 21543006), Natural Science Foundation of Hebei province (Grant No. B2015203105), and Postdoctoral Science Foundation of China No. 2015M571277 and 2014M551048.

References

1. Y. Tsujimoto, C. Tassel, N. Hayashi, T. Watanabe, H. Kageyama, K. Yoshimura, M. Takano, M. Ceretti, C. Ritter and W. Paulus, Nature, 2007, 450, 1062.
2. (a) M. A. Hayward, M. A. Green, M. J. Rosseinsky and J. Sloan, J. Am. Chem. Soc., 1999, 121, 8843; (b) M. A. Hayward, E. J. Cussen, J. B. Claridge, M. Bieringer, M. J. Rosseinsky, C. J. Kiely, S. J. Blundell, I. M. Marshall and F. L. Pratt, Science, 2002, 295, 1882.
3. C. Tasssel, T. Watanabe, Y. Tsujimoto, N. Hayashi, A. Kitada, Y. Sumida, T. Yamamoto, H. Kageyama, M. Takano and K. Yoshimura, J. Am. Chem. Soc., 2008, 130, 3764.
4. H. J. Xiang, S.-H. Wei and M.-H. Whangbo, Phys. Rev. Lett., 2008, 100, 167207.
5. J. M. Pruneda, J. Íñiguez, E. Canadell, H. Kageyama and M. Takano, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 115101.
6. H. Kageyama, T. Watanabe, Y. Tsujimoto, A. Kitada, Y. Sumida, K. Kanamori, K. Yoshimura, N. Hayashi, S. Muranaka, M. Takano, M. Ceretti, W. Paulus, C. Retter and G. André, Angew. Chem., Int. Ed., 2008, 47, 5740.
7. T. Yamamoto, C. Tassel, Y. Kobayashi, T. Kawakami, T. Okada, T. Yagi, H. Yoshida, T. Kamatani, Y. Watanabe, T. Kikegawa, M. Takano, K. Yoshimura and H. Kageyama, J. Am. Chem. Soc., 2011, 133, 6036.
8. H.-J. Koo, H. Xiang, C. Lee and M.-H. Whangbo, Inorg. Chem., 2009, 48, 9051.
9. J. Perdew, S. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
10. A. Lichtenstein, V. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467.
11. V. Anisimov, F. Aryasetiawan and A. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767.
12. A. Petukhov, I. Mazin, L. Chioncel and A. Lichtenstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 153106.
13. K. Schwarz and P. Blaha, Comput. Mater. Sci., 2003, 28, 259.
14. P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k, An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, Vienna University of Technology, Austria, 2001, ISBN 3-9501031-1-2.
15. E. Sjöstedt, L. Nordström and D. J. Singh, Solid State Commun., 2000, 114, 15.
16. G. K. H. Madsen, P. Blaha, K. Schwarz, E. Sjöstedt and L. Nordström, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 195134.
17. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
18. R. Mavlanjan, N. Yao-zhuang and G. Cuang-hua, Inorg. Chem., 2013, 52, 12519.
19. T. Jia, H. Wu, X. Zhang, T. Liu, Z. Zeng and H. Lin, EPL, 2013, 102, 67004.
20. J. B. Goodenough, Magnetism and the Chemical Bond, Interscience-Wiley, New York, 1963;; J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87.
21. K. I. Kugel and D. I. Khomskii, Sov. Phys. Solid State, 1975, 17, 285.

---