The thermoelectric performance of anisotropic SnSe doped with Na

Abstract

Lead-free polycrystalline SnSe is a promising thermoelectric compound consisting of earth-abundant elements. However, the poor electrical transport property for low intrinsic defect concentration (3 × 10¹⁷ cm⁻³) limits the usage of the stoichiometric SnSe compound. In this work, Na₂Se as an acceptor was doped into SnSe in order to optimize the electrical transport properties, especially to increase the carrier concentration. As a result, the carrier concentrations increased and saturated at about 1.0 × 10¹⁹ cm⁻³ for Na_0.01Sn_0.99Se at 300 K, and a maximum power factor of 0.48 mW m⁻¹ K⁻² was obtained. A maximum zT value of 0.75 was obtained at 823 K for Na_0.01Sn_0.99Se along the direction perpendicular to the sintering pressure, which is 25% higher than that (0.6) of the undoped SnSe compound.

---

Introduction

Thermoelectric material is a kind of material that can convert heat to electricity directly, or vice versa. Devices made using thermoelectric materials have advantages of no moving parts, quiet operation, low environmental impact and high reliability. The performance of thermoelectric materials can be evaluated by the dimensionless figure of merit, zT = S²σT/κ where S, σ, κ, T are the Seebeck coefficient, the electrical conductivity, the thermal conductivity and the absolute temperature, respectively.¹ Continuous efforts have been invested into optimizing thermoelectric performance, for example, phonon engineering,^2,3 band engineering^4–6 and point defect engineering^7,8 etc. Binary bismuth and lead chalcogenides such as Bi₂Te₃, PbTe, and their solid solutions have been intensively studied with the above optimizing methods for thermoelectric applications.^9–11 However, for those thermoelectric materials, in spite of high zT values (>1) obtained, widespread application is restricted by toxic Pb and costly Te, which has led to SnSe obtaining more attention as a potential alternative.

Currently, SnSe crystal draws considerable attentions for its extremely high zT values (2.6 and 2.3 at 950 K along the b and c axes, respectively¹²). The extremely high zT values is mainly attributed to its ultralow lattice thermal conductivity for the distinctive anharmonic structure in SnSe.¹² SnSe has a layered orthorhombic crystal structure, resembling a distorted NaCl rock-salt structure (shown in Fig. 1). Along the b–c plane, two-atom-thick SnSe slabs creating a zig-zag accordion-like projection along the b axis spread within the plane of the slabs. Those two-atom-thick SnSe slabs were linked with weaker Sn–Se bonding along the a-axis direction, and contributed the easy cleavage along (l00) plane.¹³ The distinctive structure results in its outstanding anisotropy. For single crystal, weak bonding between Sn–Se in SnSe slabs leads to poor mechanical properties. And compared with polycrystalline, preparation technology of single crystal is complicated. These all contribute to the study of polycrystalline SnSe. The low intrinsic thermal conductivity values (0.3–0.8 W m⁻¹ K⁻²) and low intrinsic carrier concentration value (3 × 10¹⁷ cm⁻³) of undoped polycrystalline SnSe were reconfirmed at room temperature.¹⁴ One feasible solution toward the poor electrical transport property is increasing the carrier concentrations. Various candidates (Na, Ag, Sr, In, Pb and Tl) as dopants were attempted,¹⁵ but only Na and Ag seem to be able to dope and increase the carrier concentrations. In general, bipolar thermal transport is controlled by the minority carrier partial electrical conductivity and band gap for extrinsic cases.²² Na-doping in polycrystalline SnSe increases carrier concentrations but decreases the band gap. ​As a result, the band gap and the minority carrier partial electrical conductivity compensate each other for thermal conductivity, especially for bipolar conduction.

Fig. 1 (a) Crystal structure along the a axis: magenta, Sn atoms; green, Se atoms. (b) Structure along the b axis. (c) Structure along the c axis.

In this work, we synthesized a sequence of p-type Na_xSn_1−xSe (x = 0.0025–0.02) polycrystalline by melting and Spark Plasma Sintering (SPS) methods. And the orientation degree and the transport properties in different directions were investigated for the outstanding anisotropy of the single crystal SnSe. A maximum zT value of 0.75 was observed for Na_0.01Sn_0.99Se in perpendicular to the pressing direction at 823 K. In parallel to the pressing direction, a maximum zT value of 0.61 was obtained at 823 K.

Results and discussion

Fig. 2(a) shows the X-ray diffraction (XRD) patterns of Na_xSn_1−xSe (x = 0, 0.0025, 0.005, 0.0075, 0.01, 0.02) powders grounded from ingots. All diffraction peaks can be well indexed to the orthorhombic SnSe phase ((PDF#48-1224) low temperature phase, Cmcm), suggesting the formation of single phase SnSe-based solid solutions. No impurity phase is observed for all samples. The X-ray diffraction (XRD) patterns of the Na_xSn_1−xSe was refined by Rietveld full file fitting method, and the lattice parameter (a = 11.5147 Å, b = 4.159 Å, c = 4.451 Å) was calculated by using general structure analysis system (GSAS), which was in accordance with literature.¹⁵ Fig. 2(b) is the XRD patterns of the polycrystalline SnSe bulk in both perpendicular and parallel to the pressing direction. Different from the standard card (PDF#48-1224), the strongest peak in the direction parallel to pressing was observed in (400) peak not in (111) peak. However, in another measuring direction, the XRD with the strongest peak in (111) matches well with the standard card (PDF#48-1224). Those all suggest that the (400) peak in perpendicular to the pressing direction possesses some preferred orientation. The orientation degree of polycrystalline in (hkl) planes can be evaluated by orientation factor (termed as F) along the corresponding direction. The orientation factor of the c-planes (h00) was calculated with the Lotgering method by the following equations:¹⁶where P and P₀ are the ratios of the integrated intensities of all (h00) planes to those of all (hkl) planes for preferentially and randomly oriented samples, respectively. The orientation factor (F = 0.32) in parallel to the pressing direction is much higher than that (F = 0) in perpendicular to the pressing direction, which is coincide with the observed results (shown in Fig. 2(b)). This could be attributed to the cleavage in (h00) plane. Under the sintering pressure, the cleavage plane tends to the direction perpendicular to the pressing direction, which performs a highly oriented degree in parallel to the pressing direction, namely a stronger (400) peak in parallel to the pressing direction.

Fig. 2 (a) XRD patterns of Na_xSn_1−xSe (x = 0, 0.0025, 0.005, 0.0075, 0.01, 0.02) powders grounded from ingots. (b) XRD patterns of SnSe bulks sintered by SPS in both parallel and perpendicular to the pressing direction. (c) The sample cut direction for measurements along different directions. (d) A photograph of a bulk sample sintered by SPS. (e) Differential Scanning Calorimeter (DSC) for Na_0.01Sn_0.99Se. The exothermal (endothermal) peak is observed at 803 K.

Fig. 2(e) shows the DSC of the Na_0.01Sn_0.99Se compound. The exothermal (endothermal) peak of Na_0.01Sn_0.99Se is observed around 800 K, indicating the phase transition from the Pnma (D¹⁶_2h) phase to the Cmcm (D¹⁷_2h) phase. The temperature of phase transition matches well with the previous reports by Zhao et al.¹²

Fig. 3(a) shows the Hall carrier concentration of Na_xSn_1−xSe as function of Na content at 300 K. The measured Hall carrier concentration of the undoped SnSe is around 3 × 10¹⁷ cm⁻³ at 300 K, which is consistent with the prior report.¹⁵ With Na doping, the carrier concentration increases and saturates at about 1.0 × 10¹⁹ cm⁻³ for Na_0.01Sn_0.99Se. Fig. 3(b) shows UV-Vis-NIR spectrums results for all Na_xSn_1−xSe. The band gap of the undoped SnSe was determined to be 0.84 eV, which matches the past literature well.¹² With increasing Na, the band gap of the Na_xSn_1−xSe shows decreasing trends.

Fig. 3 (a) Hall carrier concentration as function of Na content at 300 K. (b) UV-Vis-NIR spectrums result for Na_xSn_1−xSe (x = 0, 0.0025, 0.005, 0.0075, 0.01, 0.02) with the measured band gap values shown in the inset, where α, S and energy are the absorption coefficient, scattering coefficients and photon energy, respectively.

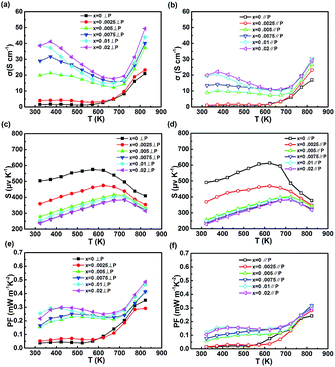
The electrical transport parameters of Na_xSn_1−xSe compounds in both parallel and perpendicular to the pressing direction are shown in Fig. 4. The electrical conductivity of undoped SnSe keeps a typical semiconducting behavior, which remains a low level below 573k, then rapidly increases with the temperature. It is noteworthy that the electrical conductivity of Na_0.0025Sn_0.9975Se shows a similar trend to that of SnSe, which is related to the low carrier concentration (shown in Fig. 3(a)). For the Na_xSn_1−xSe (x > 0.0025), the electrical conductivity decreases and turns to increase over 673 K with temperature indicating the thermal excitation of the intrinsic semiconducting carriers. The significant increase of the electrical conductivity is attributed to the improvement of the carrier concentrations. With Na doping, the carrier concentration increases from 3 × 10¹⁷ cm⁻³ to 1.0 × 10¹⁹ cm⁻³. A maximum electrical conductivity of 49.55 S cm⁻¹ is obtained for Na_0.01Sn_0.99Se at 823 K in perpendicular to the pressing direction.

Fig. 4 The electrical transport properties as a function of temperature for Na_xSn_1−xSe (x = 0, 0.0025, 0.005, 0.0075, 0.01, 0.02) measured along perpendicular and parallel to the sintering pressure. (a and b) The electrical conductivity. (c and d) The Seebeck coefficient. (e and f) The power factor.

At the same temperature, the electrical conductivity in perpendicular to pressing direction is higher than that in another measuring direction, (as shown in Fig. 3(b)). The difference in both measuring directions for electrical conductivity mainly comes from the outstanding anisotropy of the effective mass. Based on the Fermi surface shape, the effective mass possesses the highest value along a-axis direction (corresponding to perpendicular to the SnSe layers) meaning a higher effective mass in parallel to pressing direction.¹⁷ High effective band mass results in a low mobility. Because the mobility (μ = τe/m^∗_I) is inversely proportional to inertial mass when the carriers are predominantly scattered by phonons. And the scattering time τ decreases with m^∗_b. Simultaneously, overall density of states (DOS) effective mass (m^∗_d = N^2/3_Vm^∗_b) is proportional to effective band mass.⁵

All Seebeck coefficient is positive in the measured temperature range indicating p-type electrical transport property. For undoped SnSe, Seebeck coefficient starts to decrease over 573 K for the thermal excitation corresponding to the change in electrical conductivity. With increasing Na, the temperature of the maximum Seebeck coefficient demonstrates an increasing trend while the band gap gradually decreases. This mainly results from the elevation in carrier concentrations. Different from the electrical conductivity, the Seebeck coefficient of Na_xSn_1−xSe shows scarcely difference in both parallel and perpendicular to the pressing direction.

Fig. 3(e) and (f) show the power factor of Na_xSn_1−xSe as function of temperature in both parallel and perpendicular to the pressing direction. The maximum power factor of the undoped SnSe is 0.29 mW m⁻¹ K⁻². With Na doping, the maximum power factor of 0.48 mW m⁻¹ K⁻² is obtained for Na_0.02Sn_0.98Se at 823 K in the direction perpendicular to the sintering pressure, which is 39.58% higher than that for the SnSe. The power factor maximum in parallel to pressing direction is 0.32 mW m⁻¹ K⁻² which is 33.33% lower than that in another measuring direction. The outstanding anisotropy in power factor is observed.

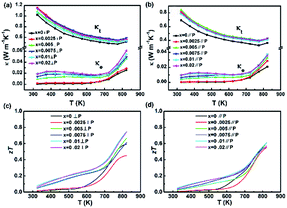
Fig. 5(a) and (b) show the temperature dependence of the thermal conductivity of all the samples in both perpendicular and parallel to the sintering pressure. The thermal conductivity of all samples decreases with temperature below 773 K due to the increased phonon-scattering. When the temperature is over 773 K, a turn happens to the thermal conductivity, which is related to the phase transition from Pnma space group to Cmcm space group around 800 K (as shown in Fig. 2(c)). Derived from the strong anharmonicity in bonding, low temperature Pnma phase SnSe possesses lower thermal conductivity values than high temperature Cmcm phase SnSe.¹⁸ The Pnma phase with a zig-zag geometry structure, like a retractable spring in (l00) plane, is called soft lattice. This “soft” structure slows down heat travelling well. Because the elastic net weaved with the weaker bonding between SnSe slabs does not transmit vibrations well and restricts the phonon transport.¹² Those above all give rise to low lattice thermal conductivity in ordered crystal structures.^19–21

Fig. 5 The thermal transport properties as a function of temperature for Na_xSn_1−xSe (x = 0, 0.0025, 0.005, 0.0075, 0.01, 0.02) measured along perpendicular and parallel to the sintering pressure. (a and b) The total thermal conductivity (κ_t) and electronic thermal conductivity (κ_e). (c and d) The zT.

At the same temperature, the thermal conductivity with different Na contents varies less than 15% among all compositions ranging from 0% to 2%. This results from that the improvement of thermal conductivity is mainly attributed to the phonon conduction component, not the electronic thermal conductivity. For Na_xSn_1−xSe (x > 0), the higher phonon conduction could be related to the fluctuation of soft lattice caused by the change in the strain field which mainly depends on bond polarity. The larger electronegativity difference between cations and anions is, the higher intensity of bond polarity is. The larger difference between Se and Na (the electronegativity of Na, Se and Sn are 0.93, 2.55 and 1.96) could rigidify the soft lattice, which results in a slight improvement in the phonon conduction.

In general, the significant improvement of the carrier concentration tends to contribute to the bipolar thermal conductivity. However, it is interesting that distinctive difference in thermal conductivity is not observed between SnSe and Na-doped SnSe at high temperature range. The barely difference in the trends of thermal conductivity could be attributed to the drop of gap band (E_g). For a single parabolic band and acoustic phonon scattering (λ = −1/2), bipolar thermal conductivity in semiconductors can be expressed as:²²

where k_B is the Boltzmann constant, e the free electron charge, ξ the reduce Fermi energy, F_x the Fermi integral of the order of x. Therefore ξ_n + ξ_p = −E_g/k_BT, where E_g is the band gap. In general, bipolar thermal transport is controlled by the minority carrier partial electrical conductivity for extrinsic cases.²² With increasing Na, the band gap of the Na_xSn_1−xSe shows a decreasing trend which weakens the effects of the carrier concentration on bipolar thermal conductivity. The thermal conductivity shows anisotropy in different measuring directions.

Fig. 5(c) and (d) show the temperature dependence of zT values for Na_xSn_1−xSe. The zT value of the undoped SnSe increases with temperature, and a maximum zT of 0.6 is obtained at 823 K, which is higher than the previous reports.^14,15 The maximum zT value of 0.75 is obtained for Na_0.01Sn_0.99Se at 823 K in perpendicular to the pressing direction. In parallel to the pressing direction, the maximum zT of 0.61 is obtained for Na_0.01Sn_0.99Se. The enhancement of zT for Na-doped SnSe is mainly attributed to the optimization of electrical transport performance.

Compared with Ag-doped SnSe,^15,26 the increase of zT values in both Na_xSn_1−xSe and Ag_xSn_1−xSe is attributed to the rise of electrical transport properties (shown in ESI†). It is worth noting that the extremum values of Na_xSn_1−xSe emerge at higher temperature than that of Ag_xSn_1−xSe in both resistivity and Seebeck coefficient. This could be derived from the effects of different dopants to different extents on band gap.

Experimental

The weighted elemental tin (Sn, 99.999%), selenium (Se, 99.999%), Na₂Se (99.99%) were loaded into graphite crucible, then loaded into quartz ampoules. The ampoules were evacuated to 7.5 × 10⁻⁵ Pa, sealed, and slowly heated up to 1253 K over 12 h, then kept that temperature for 24 h followed by water quench. The obtained ingots were annealed at 973 K for 7 days followed by another water quench. The annealed ingots were ground into powders with an agate mortar, the powders were loaded into graphite mould with 13 mm diameter and sintered in Spark Plasma Sintering (SPS) under 50 MPa pressure and 873 K for 5 min. The cylinders (Fig. 1(d)) were cut into Bar- and coin-shaped samples (Fig. 1(c)) along different directions for electrical and thermal transport measurements. The parallel (perpendicular) to pressing direction was defined as electrical and thermal properties test direction was parallel (perpendicular) to SPS pressing direction.

The phase composition was analyzed by powder X-ray diffraction (XRD) with X-ray diffract-meter (Cu Kα radiation λ = 0.154 nm, Bruker, German). The temperature dependence of electrical conductivity, Seebeck coefficient was tested by LSR-3 (Linseis) under static Helium atmosphere. The thermal conductivity was calculated from the relationship κ = ρC_pλ, the heat capacity value C_p was taken from Chen's work,¹⁵ which was calculated from a fitting equation given by Pashinkin et al.²³ and Yamaguchi et al.²⁴ The temperature dependence of thermal diffusivities λ was tested by the laser flash method (LFA-457, Netzsch) under flow argon atmosphere. Thermal analysis were carried out by Differential Scanning Calorimeter (DSC404-F3). The Hall coefficient was determined using the Physical Property Measurement System (PPMS-14, Quantum Design) under the magnetic field of −1 T to 1 T. The ultraviolet-visible-near infrared (UV-Vis-NIR) spectrum was obtained using a Cary 5000 spectrophotometer (Varian, USA) at 300 K. The density ρ of the SPS-sintered samples was measured by the Archimedes' method. The relative density of all the samples is over 97% of the theoretical value (6.18 g cm⁻³). The Hall mobility was calculated from the relationship: μ_H = σ/ne, where σ is electrical conductivity, n is carrier concentration and e is electron charge. The K_L was obtained using the Wiedemann–Franz law K_e = L₀σT, K_L = K − K_e. The L₀ is the Lorenz constant (L₀ = 1.50 × 10⁻⁸ V² K²) for non-degenerate.²⁵

Conclusions

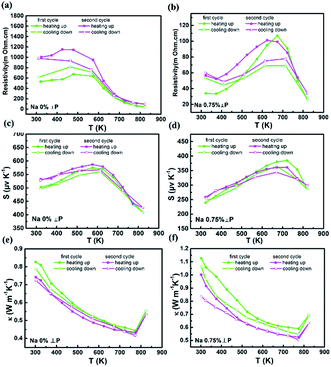
The polycrystalline Na-doped SnSe compounds were prepared by melting and Spark Plasma Sintering. Upon heating and cooling, compared with the hysteresis of Na-doped SnSe, the polycrystalline SnSe performs relatively stable reproducibility (Fig. 6). The Na_xSn_1−xSe alloys exhibit anisotropic thermoelectric performance. Na₂Se is an effective acceptor in SnSe compound. With Na doping, the carrier concentration increases from 3 × 10¹⁷ cm⁻³ to 1.0 × 10¹⁹ cm⁻³. The maximum zT value of 0.75 was obtained for Na_0.01Sn_0.99Se at 823 K, which is 25% higher than that (0.6) of the undoped SnSe compounds.

Fig. 6 Temperature dependence of (a and b) electrical conductivity, (c and d) Seebeck coefficient, (e and f) total thermal conductivity, for sample SnSe and Na_0.0075Sn_0.9925Se respectively with measurements from room temperature to 823 K (closed green circles squares), then back to room temperature (open green circles), then increased again to 823 K (closed pink squares), and then decreased to room temperature (open pink squares).

Notes and references

1. G. S. Nolas, J. Sharp and J. Goldsmid, Thermoelectrics: basic principles and new materials developments, Springer Science & Business Media, 2001.
2. H. Li, X. F. Tang, Q. J. Zhang and C. Uher, Appl. Phys. Lett., 2009, 94, 102114.
3. X. W. Wang, H. Lee, Y. C. Lan, G. H. Zhu, G. Joshi, D. Z. Wang, J. Yang, A. J. Muto, M. Y. Tang, J. Klatsky, S. Song, M. S. Dresselhaus, G. Chen and Z. F. Ren, Appl. Phys. Lett., 2008, 93, 193121.
4. Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. Jeffrey Snyder, Nature, 2011, 473, 66–69,  DOI:10.1038/nature09996.
5. Y. Pei, H. Wang and G. Snyder, Adv. Mater., 2012, 24, 6125–6135.
6. M. Zhou, Z. M. Gibbs, H. Wang, Y. Han, C. Xin, L. Li and G. J. Snyder, Phys. Chem. Chem. Phys., 2014, 16, 20741–20748.
7. L. Hu, T. Zhu, X. Liu and X. Zhao, Adv. Funct. Mater., 2014, 24(33), 5211–5218,  DOI:10.1002/adfm.201400474.
8. L.-P. Hu, T. Zhu, Y.-G. Wang, H.-H. Xie, Z.-J. Xu and X.-B. Zhao, NPG Asia Mater., 2014, 6(2), e88,  DOI:10.1038/am.2013.86.
9. J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, S. Y. Anek Charoenphakdee and G. Jeffrey Snyder, Science, 2008, 321(5888), 554–557,  DOI:10.1126/science.1159725.
10. J.-J. Shen, T.-J. Zhu, X.-B. Zhao, S.-N. Zhang, S.-H. Yang and Z.-Z. Yin, Energy Environ. Sci., 2010, 3, 1519.
11. A. L. Yanzhong Pei, S. Iwanaga and G. Jeffrey Snyder, Energy Environ. Sci., 2011, 4(6), 2085–2089,  10.1039/c0ee00456a.
12. L. D. Zhao, S. H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377.
13. M. Peters and L. McNeil, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 5893.
14. S. Sassi, C. Candolfi, J. B. Vaney, V. Ohorodniichuk, P. Masschelein, A. Dauscher and B. Lenoir, Appl. Phys. Lett., 2014, 104, 212105.
15. C.-L. Chen, H. Wang, Y.-Y. Chen, T. Day and G. J. Snyder, J. Mater. Chem. A, 2014, 2, 11171.
16. F. Lotgering, J. Inorg. Nucl. Chem., 1959, 9, 113–123.
17. K. Kutorasinski, B. Wiendlocha, S. Kaprzyk and J. Tobola, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 205201.
18. J. Carrete, N. Mingo and S. Curtarolo, Appl. Phys. Lett., 2014, 105, 101907.
19. D. Morelli, V. Jovovic and J. Heremans, Phys. Rev. Lett., 2008, 101, 035901.
20. M. D. Nielsen, V. Ozolins and J. P. Heremans, Energy Environ. Sci., 2013, 6, 570–578.
21. Y. Zhang, E. Skoug, J. Cain, V. Ozoliņš, D. Morelli and C. Wolverton, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 054306.
22. S. Wang, J. Yang, T. Toll, J. Yang, W. Zhang and X. Tang, Sci. Rep., 2015, 5, 10136.
23. A. Pashinkin, A. Malkova, V. Fedorov and M. Mikhailova, Inorg. Mater., 2006, 42, 593–595.
24. K. Yamaguchi, K. Kameda, Y. Takeda and K. Itagaki, Mater. Trans. JIM, 1994, 35, 118–124.
25. T. Caillat, A. Borshchevsky and J. P. Fleurial, J. Appl. Phys., 1996, 80, 4442–4449.
26. H. Q. Leng, M. Zhou, J. Zhao, Y. M. Han and L. F. Li, J. Electron. Mater., 2015, 45, 527–534.

---

Footnote

† Electronic supplementary information (ESI) available: (1) The calculated Hall mobility in this work as a function of Ag content (x) at 300 K. (2) The thermal stability of the polycrystalline materials. See DOI: 10.1039/c5ra19469e

---