Linking photoluminescence of α-Si₃N₄ to intrinsic point defects via band structure modelling

Abstract

Photoluminescence (PL) property data for reported α-Si₃N₄ to date are scattered and it is difficult to clarify the reason only through experimental study. In this paper, the relationship between photoluminescence and intrinsic point defects in α-Si₃N₄ has been established accordingly via band structure modelling based on density functional theory calculation. The results show that band structures of α-Si₃N₄ are significantly affected by the locations of defect levels, which are changed with various partial atomic structures around point defects. Formation energies are also calculated to determine the main types of intrinsic point defects in α-Si₃N₄ under different conditions (Si-rich or N-rich). The results suggest that multiple types of intrinsic point defects coexist in α-Si₃N₄, leading to various electronic transition modes. Furthermore, combined with the calculated results, the discrete photoluminescence data for α-Si₃N₄ are revealed by electronic transition modes under different conditions. The main visible luminescent peaks are attributed to the electron transitions of E_c → ≡Si˙ σ and ≡Si˙ σ → E_v for Si abundant α-Si₃N₄, while N₄⁺ → N₂⁰ for N plentiful α-Si₃N₄.

---

1. Introduction

Silicon nitride (Si₃N₄) is a wide band gap (∼5.0 eV) semiconductor material,^1,2 which has drawn much attention in the optoelectrical fields for its significant visible luminescence properties due to the wide defect levels.^3–5 There are four types of defects in intrinsic point defect Si₃N₄: N dangling bond (=N˙), Si dangling bond (≡Si˙), Si–Si and N–N bonds.^6–11 The =N˙ forms two defect levels in the band gap, namely N₂⁰ and N₄⁺, which are near the top of the valence band (VB) and the bottom of the conduction band (CB), respectively.^7,8 The ≡Si˙ forms one defect level at about the middle of the band gap according to previous works.^6–9 However, recent work shows the defect levels of ≡Si˙ can be either occupied or unoccupied in the band gap by L. E. Hintzsche.¹⁰ The Si–Si bond forms an occupied σ state close or on the top of VB and an empty σ* state close or on the bottom of CB, and the N–N bond gives rise to a filled state in the VB and an empty state in the CB.^6–9 Nevertheless, the majority of published studies on related defects have been primarily focused on nonstoichiometric amorphous SiN_x films or clusters rather than bulk crystals.^6–11

Density functional theory (DFT) offers an effective method to investigate physical properties for bulk crystals.^12,13 A lot of efforts based on DFT have been put on the mechanical, thermodynamic, optical and electronic properties for crystalline Si₃N₄.^14–20 Crystalline Si₃N₄ has two stable polymorphs at atmospheric environment, i.e. α-Si₃N₄ (trigonal, space group P31c) and β-Si₃N₄ (hexagonal, space group P6₃). α-Si₃N₄ is dynamically metastable phase under low temperature, and its periodic stacking structure of Si and N atoms is …ABCDABCD…, which is relatively complicated compared to …ABAB… for β-Si₃N₄.^17,18 Defect structures and electronic properties have been reported for intrinsic defects of β-Si₃N₄,^19,20 while little for α-Si₃N₄. Besides, the types of defects are mostly affected by the growth conditions.²¹ Herein, to make clear the main point defect types in α-Si₃N₄ under different conditions, the formation energies for α-Si₃N₄ with different types of intrinsic point defects under N-rich and Si-rich conditions are calculated in this work.

To date, the photoluminescence properties for crystalline α-Si₃N₄ are experimentally diverse due to the electron transition mechanisms still unclear.^22–25 For instance, the luminescence peak for α-Si₃N₄ at ∼600 nm (∼2.1 eV) could be explained by electron transition of N₄⁺ → N₂⁰ by F. Gao,²⁵ or E_c → ≡Si˙ by Y. Liu.²⁶ Some researchers concluded that the electron transition of E_c → ≡Si˙ or ≡Si˙ → E_v could form the emission peaks between 2.3 eV and 2.6 eV,^8,27 which is in conflict with the points that the ≡Si˙ → E_v produce the peaks at about 3.0 eV.^28,29 Moreover, the =N˙ would be grabbed by any surplus Si atom, in other words, the =N˙ do not coexist with the ≡Si˙.¹⁰ It is controversial to consider the =N˙ and ≡Si˙ simultaneously in the same system to explore the electron transition mechanism.^28,29 Therefore, lacking investigations of band structures for intrinsic point defects of α-Si₃N₄ is the main reason resulting in diverse explanations for electron transition mechanisms.

In this paper, we devotes to link photoluminescence properties of α-Si₃N₄ to intrinsic point defects via band structure modelling based on DFT calculation. The intrinsic point defects: Si vacancy (V_Si), N vacancy (V_N), N substitutional to Si (Si_N), Si substitutional to N (N_Si), Si interstitial (Si_i) and N interstitial (N_i) are systematically considered. Firstly, the geometry optimizations for α-Si₃N₄ with intrinsic point defects are carried out to study the partial atomic environments near the point defects. Secondly, the electronic properties are calculated with the hybrid Heyd–Scuseria–Ernzerhof (HSE06) functional^30,31 to illustrate the influences of different intrinsic point defects on the band structures in α-Si₃N₄. Thirdly, the formation energies are calculated to determine the main types of intrinsic point defects in α-Si₃N₄ under the N-rich and Si-rich conditions, respectively. Finally, combined with the calculated results, the electron transitions contributing to the photoluminescence peaks are discussed for Si abundant and N plentiful α-Si₃N₄.

2. Theoretical and computational methods

The calculations were performed using CASTEP package based on the plane wave pseudo potential approach.³² The optimized structures are obtained with the exchange-correlation functional was Perdew Burke Ernzerhof (PBE) of the generalized gradient approximation (GGA).³³ Then, the band structures and density of states were conducted by the HSE06 hybrid functional. To guarantee the calculation accuracy and efficiency, the 2 × 2 × 1 α-Si₃N₄ supercells with intrinsic point defects were calculated in this paper. A plane-wave cutoff energy of 400 eV and a k-point mesh of 3 × 3 × 5 were used. Reference configurations for the valence electrons were Si 3s 3p and N 2s 2p. The threshold for self-consistent field iterations was 1.0 × 10⁻⁵ eV per atom. The convergence tolerance parameters of optimized calculation were the energy of 2 × 10⁻⁵ eV per atom, the maximum force of 0.05 eV Å, the maximum inner stress of 0.1 GPa and the maximum displacement of 2 × 10⁻⁴ nm.

The lattice parameters and the density of states (DOS) of perfect α-Si₃N₄ supercells were calculated to validate the calculation schemes. The optimized lattice parameters are: a = b = 7.78 Å and c = 5.64 Å, and the calculated energy gap (E_g) by HSE06 hybrid functional is 5.37 eV, which are in good agreement with the experimental value.² Through analyzing the types of atoms and bond lengths, there are two types of Si atoms (Si₁ and Si₂) and four types of N atoms (N₁, N₂, N₃ and N₄) in α-Si₃N₄, as shown in Fig. 1. It is seen from Fig. 1 that the Si–N bond lengths of N₁ and N₂ are the same, respectively. The total and partial DOS of different atoms in perfect α-Si₃N₄ are plotted in Fig. 2, where the Fermi levels (E_F) are set at 0 eV as the dashed lines. It is observed clearly from Fig. 2 that the contributions to the total DOS of the Si₁ and Si₂ are almost the same, as well as the N₃ and N₄. Note that the peak on the top of VB for the total DOS is main composed with N pπ states and its width depends on the second-neighbor N–N (pσ) interactions.⁶ Different to the other types of N atoms, the tailing of the VB for the N₁ is significantly beyond the E_F resulting from the much larger pσ interactions for its planar configuration. The calculated DOS results are consistent with the previous calculations.^6,34 The above calculated results for perfect α-Si₃N₄ supercells confirm that our calculation schemes are reliable.

Fig. 1 Schematic diagram for different types of atoms in perfect α-Si₃N₄. The unit of bond length is Å.

Fig. 2 Total and partial density of states for different atoms in perfect α-Si₃N₄.

Considering there are two different Si atoms and four different N atoms in perfect α-Si₃N₄, six different vacant and six different substituted α-Si₃N₄ supercells are taken into account. Besides, there is a big interstice between the AB layer and CD layer in α-Si₃N₄,^17,18 so that two interstitial α-Si₃N₄ supercells are also considered. α-Si₃N₄ with vacant defects, one atom (Si or N) removed, are marked as V_Si1–Si₃N₄ and V_Si2–Si₃N₄ for Si vacancy, while V_N1–Si₃N₄, V_N2–Si₃N₄, V_N3–Si₃N₄ and V_N4–Si₃N₄ for N vacancy. α-Si₃N₄ with substitutional defects, one atom (Si or N) in the forms of a substitutional atom (Si_N or N_Si), are marked as Si_N1–Si₃N₄, Si_N2–Si₃N₄, Si_N3–Si₃N₄ and Si_N4–Si₃N₄ for Si substituting to N, while N_Si1–Si₃N₄ and N_Si2–Si₃N₄ for N substituting to Si. α-Si₃N₄ with interstitial defects, one atom (Si or N) occupying the interstice, are marked as Si_i–Si₃N₄ and N_i–Si₃N₄, respectively. After finishing geometry optimizations of all α-Si₃N₄ supercells with intrinsic point defects by the functional of GGA, the electronic properties are calculated with the HSE06 hybrid functional.

3. Results and discussion

3.1 Optimal crystal structures of α-Si₃N₄ with intrinsic point defects

Table 1 shows the lattice parameters and lengths of the new bonds for the optimal α-Si₃N₄ supercells with different intrinsic point defects. The variations of lattice parameters for α-Si₃N₄ with intrinsic point defects come from the changes of the partial atomic environments near the point defects. The partial atomic structures near the investigated point defects in α-Si₃N₄ are presented in Fig. 3. For α-Si₃N₄ with Si vacant defect (shown in Fig. 3(a) and (b)), the distances become larger between each two N atoms compared with that of ∼2.80 Å in perfect α-Si₃N₄, and no new bond is formed around the Si vacancy, leaving four unsaturated N dangling bonds (=N˙). For α-Si₃N₄ with N vacant defect, the three nearest Si atoms are not equivalent,¹⁶ with slightly shortening the distances of them (the distance of two nearest Si atoms is 2.96 Å in perfect α-Si₃N₄), to form two Si–Si bonds in the V_N1–Si₃N₄ and V_N2–Si₃N₄ (shown in Fig. 3(c) and (d)), one Si–Si bond in the V_N3–Si₃N₄ and V_N4–Si₃N₄ (shown in Fig. 3(e) and (f)), respectively. For α-Si₃N₄ with Si substituting to N defect (shown in Fig. 3(g)–(j)), the substitutional Si atom forms three Si–Si bonds with its ambient Si atoms, and the extra electron of the substitutional Si atom forms one Si dangling bond (≡Si˙).¹⁹ It could be observed that the lengths of the three Si–Si bonds are the same in the Si_N1–Si₃N₄ and Si_N2–Si₃N₄ (shown in Fig. 3(g) and (h)) while different in the Si_N3–Si₃N₄ and Si_N4–Si₃N₄ (shown in Fig. 3(i) and (j)), attributed to different coordination environments of different types of N atoms, as shown in Fig. 1. For α-Si₃N₄ with N substituting to Si defect, the substitutional N atom forms three N–N bonds with its adjacent N atoms and leaves an unsaturated matrix N atom to form one N dangling bond (shown in Fig. 3(k) and (l)). For α-Si₃N₄ with Si interstitial defect (shown in Fig. 3(m)), the interstitial Si atom forms two strong Si–Si bond and three weak Si–N bonds with the matrix atoms.²⁰ For α-Si₃N₄ with interstitial N defect, the unsaturated interstitial N atom forms one N–N bond and one new Si–N bond with the matrix Si and N atoms (shown in Fig. 3(n)). Compared with the optimized partial structures of all defective models, the V_Si1–Si₃N₄ and V_Si2–Si₃N₄, as well as the V_N3–Si₃N₄ and V_N4–Si₃N₄, the Si_N3–Si₃N₄ and Si_N4–Si₃N₄, as well as the N_Si1–Si₃N₄ and N_Si2–Si₃N₄ are almost the same. The main types of defects in α-Si₃N₄ with different intrinsic point defects are clearly illustrated by the partial atomic structures, whereas the electronic properties associated with the defects are discussed in the next section.

Table 1 Optimal lattice parameters and lengths of new bonds for α-Si₃N₄ with intrinsic point defects

Point defect	Cell parameter (Å)			Length of new bond (Å)
	a	b	c	Si–N	Si–Si	N–N
a The numbers in the parentheses show the number of bonds with same length.
VSi1	7.83	7.83	5.63
VSi2	7.84	7.78	5.63
VN1	7.75	7.78	5.63		2.70
					2.76
VN2	7.75	7.78	5.64		2.58
					2.70
VN3	7.79	7.76	5.65		2.56
VN4	7.76	7.78	5.65		2.58
SiN1	7.86	7.86	5.62		2.16(3)^a
SiN2	7.82	7.82	5.43		2.21(3)^a
SiN3	7.79	7.82	5.66		2.15
					2.19
					2.21
SiN4	7.85	7.84	5.67		2.10
					2.11
					2.12
NSi1	7.78	7.74	5.65			1.41
						1.45(2)^a
NSi2	7.77	7.79	5.65			1.42
						1.45(2)^a
Sii	7.79	7.80	5.64	2.10	2.32
				2.21	2.56
				2.36
Ni	7.79	7.81	5.65	1.81		1.59

---

Fig. 3 Optimal partial atomic structures for α-Si₃N₄ with intrinsic point defects: (a) V_Si1, (b) V_Si2, (c) V_N1, (d) V_N2, (e) V_N3, (f) V_N4, (g) Si_N1, (h) Si_N2, (i) Si_N3, (j) Si_N4, (k) N_Si1, (l) N_Si2, (m) Si_i, (n) N_i. The unit of distance between the two atoms is Å.

3.2 Band structures of α-Si₃N₄ with intrinsic point defects

The calculated band structures and partial density of states (PDOS) of the atoms adjacent to the investigated point defects for all defective α-Si₃N₄ are plotted in Fig. 4, where the Fermi levels (E_F) are set at 0 eV as the red dashed lines. It is clear that the band structures and PDOS of the V_Si1–Si₃N₄ and V_Si2–Si₃N₄ (shown in Fig. 4(a) and (b)), the V_N3–Si₃N₄ and V_N4–Si₃N₄ (shown in Fig. 4(e) and (f)), the Si_N3–Si₃N₄ and Si_N4–Si₃N₄ (shown in Fig. 4(i) and (j)), as well as the N_Si1–Si₃N₄ and N_Si2–Si₃N₄ (shown in Fig. 4(k) and (l)) are similar, respectively. Compared with the E_g = 5.37 eV for perfect α-Si₃N₄, the maximum energy gaps for all intrinsic defective α-Si₃N₄ become smaller owing to the emergence of defect levels in the band gaps. The E_v and E_c stand for the energies of the top of VB and the bottom of CB, respectively. The energies of N 2s and 2p states appear in the E_v and just below the E_c in the V_Si1–Si₃N₄ and V_Si2–Si₃N₄, respectively, which are in good agreement with the results of Robertson's research,^6,7 indicating that N₂⁰ and N₄⁺ are the main defects in α-Si₃N₄ with Si vacant defect. For α-Si₃N₄ with N vacant defect, the defect levels located in the E_v and below the E_c are related to the Si–Si bonding σ states and antibonding σ* states,^6–9 and the else two defect levels in the band gaps are the Si dangling bonds occupied (N₃≡Si˙ σ) and unoccupied (N₃≡Si˙ σ*) states.¹⁰ Particularly, for the V_N1–Si₃N₄ (see Fig. 4(c)), owing to the lower energy of the Si–Si σ compared with the pσ state, the defect level of the Si–Si σ state is certainly lower than the E_v. Besides, for the V_N2–Si₃N₄ (see Fig. 4(d)), because the short distances between the three Si atoms adjacent to the N vacancy, the unsaturated Si dangling bond are not entirely separated from the Si–Si bonds, causing the overlapping of the N₃≡Si˙ σ* and Si–Si σ* states. The distortion of the local Si environment and the Si–Si bond length could influence the location and composition of the electronic states of Si defect in the band gap.¹⁰ Unlike the long lengths of Si–Si bonds in α-Si₃N₄ with N vacancy defect, the Si–Si bonds are particularly short and the three Si–Si bonds are closely around the unsaturated Si dangling band (Si₃≡Si˙) in α-Si₃N₄ with Si substituting to N defect, resulting in the difference in the locations and compositions of Si–Si bonds and Si₃≡Si˙. Thus, for α-Si₃N₄ with Si substituting to N defect, the defect levels close or in the E_v and the E_c are corresponding to the Si–Si σ and σ* states, respectively, and the levels near the E_F are the Si₃≡Si˙. As reported in Robertson's research, the N–N bond is mainly consisted of N 2p states and appearing in the VB or CB.⁶ So the defect levels in the E_v are the N–N states, and the two defect levels in the band gap are the N₂⁰ and N₄⁺ for α-Si₃N₄ with N substituting to Si defect. Similarly, for the N_i–Si₃N₄ (shown in Fig. 4(n)), the defect levels composed of N 2p states in the VB and CB are the N–N σ and σ* states, and the defect level near the E_F is the unsaturated N dangling bond state. For the Si_i–Si₃N₄ (shown in Fig. 5(m)), the defect levels are consisted with N 2p and Si 3s 3p states in the VB and close to the E_c, which are related to the new Si–N bonds,²⁰ and the defect level near the E_F is the unsaturated Si dangling bond.

Fig. 4 Band structures and PDOS for α-Si₃N₄ with intrinsic point defects: (a) V_Si1, (b) V_Si2, (c) V_N1, (d) V_N2, (e) V_N3, (f) V_N4, (g) Si_N1, (h) Si_N2, (i) Si_N3, (j) Si_N4, (k) N_Si1, (l) N_Si2, (m) Si_i, (n) N_i. For the PDOS, the solid black lines stand for Si 3s, red for Si 3p, blue for N 2s and green for N 2p.

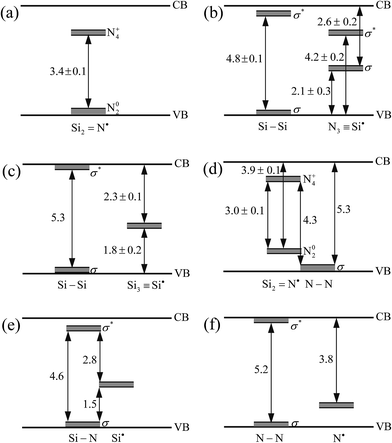Fig. 5 Defect levels and electron transition diagrams in α-Si₃N₄ with intrinsic point defects: (a) V_Si, (b) V_N, (c) Si_N, (d) N_Si, (e) Si_i and (f) N_i. The unit of energy gap is eV.

Considering the similar electronic properties for α-Si₃N₄ with similar intrinsic point defects, Fig. 5 summarizes the defect levels in the band gaps and electron transition diagrams for α-Si₃N₄ with six main point defects, which are the Si vacant defect (V_Si), N vacant defect (V_N), Si substituting to N defect (Si_N), N substituting to Si defect (N_Si), interstitial Si defect (Si_i) and interstitial N defect (N_i). The similar types of defect levels in the band gaps are different for the six main point defective models. For example, it is observed from Fig. 5(a) and (d) that the maximum energy gaps of the two N dangling bonds states are ∼3.4 eV in the V_Si–Si₃N₄, while ∼3.0 eV in the N_Si–Si₃N₄. The relative locations of the defect levels of the two Si–Si states integrally move up in the band gaps from the V_N–Si₃N₄ to Si_N–Si₃N₄, as shown in Fig. 5(b) and (c). For the defect levels of the unsaturated Si dangling bonds, there are two levels in the band gap for the V_N–Si₃N₄ (shown in Fig. 5(b)), while only one level located at about the E_F in the Si_N–Si₃N₄ and Si_i–Si₃N₄ (shown in Fig. 5(c) and (e)), respectively. The variations for the relative locations of similar defect levels come from different partial atomic environments.¹⁰ For instance, the nearby atoms of the unsaturated Si atoms are N atoms in the V_N–Si₃N₄, Si atoms in the Si_N–Si₃N₄, N and Si atoms in the Si_i-Si₃N₄, so that the locations of defect levels originated from the unsaturated Si dangling bands are different for α-Si₃N₄ with different intrinsic point defects. To further investigate the main defect types under different conditions, the formation energies of α-Si₃N₄ with different intrinsic point defects are discussed in the next section.

3.3 Formation energy of α-Si₃N₄ with intrinsic point defects

The stability of different intrinsic point defect α-Si₃N₄ can be determined by the value of formation energy (E_f(q)), which is obtained by the following formula:^20,21,35

E_f(q) = E_tot(q) − n_Siμ_Si − n_Nμ_N − qE_F

where E_f(q) stands for the total energy of the intrinsic defective α-Si₃N₄ supercell, n_Si and n_N for the numbers of Si and N atoms in the supercell, μ_Si and μ_N for the chemical potentials of Si and N atoms, q for the change state and E_F for the Fermi energy, respectively. Note that the E_f(q) is not fixed but depends on the growth condition, which can be changed from N-rich (μ_N = μ(N2)/2 and μ_Si = (μ(α-Si₃N₄)–4μ_N)/3) to Si-rich (μ_N = μ_bulk-Si and μ_N = (μ(α-Si₃N₄)–3μ_si)/4) conditions.²¹ Table 2 exhibits the formation energies for all α-Si₃N₄ supercells with intrinsic point defects under different growth conditions in the neutral charge state (q = 0). It can be clearly seen from Table 2 that E_f(q) is sensitive to the growing conditions. A low formation energy indicates a high equilibrium concentration of the corresponding intrinsic point defect, whereas a high energy implies that it does not occur spontaneously. Compared with the formation energies, under the Si-rich condition, the V_N–Si₃N₄, Si_N–Si₃N₄ and Si_i–Si₃N₄ are easily obtained, while under the N-rich condition, the N_Si–Si₃N₄, V_N–Si₃N₄, N_i–Si₃N₄ and V_Si–Si₃N₄ are easily formed, indicating multiple intrinsic point defects coexist in α-Si₃N₄ under different growth conditions. Moreover, the low formation energies of V_N–Si₃N₄ indicate that N vacant defect is easily formed whatever it is under the N-rich or Si-rich conditions, which confirms the view that the Si dangling bonds is the dominant defects in α-Si₃N₄.^20,36 Owing to the unsaturated N atom grabbed by any existing Si defect (Si–Si and ≡Si˙),¹⁰ the N substituting to Si defect and the interstitial N defect do not coexist with the N vacant defect. To make it easy to understand, we define the cases that the atomic ratio of Si and N in α-Si₃N₄ is more than 3 : 4 as Si₃N_4−x, which includes V_N–Si₃N₄, Si_N–Si₃N₄ and Si_i–Si₃N₄. The other cases of Si : N < 3 : 4 are defined as Si_3−xN₄, which are N_Si–Si₃N₄, N_i–Si₃N₄ and V_Si–Si₃N₄. It is clear that Si₃N_4−x can be easily formed under Si-rich condition, while Si_3−xN₄ can be prepared under N-rich condition.

Table 2 Formation energies (eV) for α-Si₃N₄ with intrinsic point defects under different conditions

Point defect	Si-rich	N-rich	Point defect	Si-rich	N-rich
VSi1	11.02	7.69	SiN2	4.61	10.47
VSi2	11.04	7.71	SiN3	5.25	11.12
VN1	3.36	5.89	SiN4	5.58	11.45
VN2	3.37	5.90	NSi1	11.60	5.76
VN3	3.00	5.52	NSi2	11.22	5.39
VN4	3.32	5.85	Sii	6.15	9.50
SiN1	4.88	10.75	Ni	8.23	5.74

---

3.4 Linking photoluminescence of α-Si₃N₄ to intrinsic point defects

The currently reported photoluminescence data for α-Si₃N₄ are plotted Fig. 6(a).^{22–24,37–42} It is observed that the PL data is quite scattered, and PL properties are analyzed using different electron transition modes. The reason now is clear because there are multiple intrinsic point defects for Si₃N_4−x and Si_3−xN₄, determined by different experiment processing methods, resulting in different electron transition in the band gap, and correspondingly a number of visible luminescence peaks. Some of the broaden peaks may be the integral of several single peak, which reflects certain electron transition mode. According to previous analysis, it is known that for Si₃N_4−x, the E_v and E_c may be composed of the occupied and empty states of Si–Si or Si–N bond, as exhibited in Fig. 5(b), (c) and (e), respectively. The defects levels in the band gap are related to the unsaturated Si dangling bonds (≡Si˙), which may be in different forms as N₃≡Si˙, Si₃≡Si˙ or the other unsaturated Si states. On the other hand, for Si_3−xN₄, the E_v and E_c may be composed of the N–N occupied and empty states as exhibited in Fig. 5(a), (d) and (f). The defect levels in the band gap are the unsaturated N dangling bonds (=N˙).

Fig. 6 (a) Photoluminescence data for α-Si₃N₄ in different literatures. (b) Wavelength ranges of the emission peaks for Si₃N_4−x (red bar) and Si_3−xN₄ (blue bars), respectively.

The wavelength ranges of the emission peaks are shown as the red and blue bars in Fig. 6(b) for Si₃N_4−x and Si_3−xN₄, respectively. Thus, it is clear that in the Si abundant α-Si₃N₄, the PL peaks at >440 nm (the corresponding energy gaps < 2.8 eV) are related to the electron transitions of ≡Si˙ σ → E_v, or E_c → ≡Si˙ σ. While in the N plentiful α-Si₃N₄, the PL peaks of 400–430 nm (2.8–3.0 eV) may be driven from the electron transitions of N₄⁺ → N₂⁰, and the peaks at <380 nm (>3.3 eV) relate to N₄⁺ → E_v in Si vacant α-Si₃N₄. For example, the main PL peaks located at >500 nm (ref. 37–39) may be derived from the electron transitions of ≡Si˙ σ → E_v or E_c → ≡Si˙ σ, however, the main peaks at 410–430 nm (ref. 23, 24 and 40–42) are related to the electron transitions of N₄⁺ → N₂⁰. The current investigation has successfully demonstrate the reason for the discreteness of the PL spectra for α-Si₃N₄.

4. Conclusions

Photoluminescence properties of α-Si₃N₄ have been connected to intrinsic point defects by band structure modelling using DFT calculations. The partial atomic structures, electronic properties and formation energies for α-Si₃N₄ with different intrinsic point defects are systematically investigated. The Si dangling bonds give rise to two defect levels (N₃≡Si˙ σ and σ*) in the band gap for the V_N–Si₃N₄, while only one defect level for the Si_N–Si₃N₄ and Si_i–Si₃N₄. The maximum energy gaps between N₂⁰ and N₄⁺ are different in the V_Si–Si₃N₄ and N_Si–Si₃N₄. The different locations of the similar defect levels are originated from the various partial atomic environments adjacent to the investigated point defects. Multiple types of intrinsic point defects would coexist in α-Si₃N₄ under different environments derived from formation energy calculation. The main visible luminescent peaks for α-Si₃N₄ are attributed to the electron transitions of E_c → ≡Si˙ σ and ≡Si˙ σ → E_v for Si₃N_4−x, while N₄⁺ → N₂⁰ for Si_3−xN₄. This work not only reveals the discrete photoluminescence data for α-Si₃N₄, but also provides theoretical foundations for electronic properties of Si₃N₄.

Acknowledgements

The project is supported by the National Natural Science Foundation of China (No. 51202171, No. 51472188, No. 51521001), the Specialized Research Fund for the Doctoral Program of Higher Education of China (No. 20120143120004) and the “111” project (No. B13035).

Notes and references

1. K. Ulman, R. Sathiyanarayanan, R. K. Pandey, K. V. R. M. Murali and S. Narasimhan, J. Appl. Phys., 2013, 113, 234102.
2. L. Zhang, H. Jin, W. Yang, Z. Xie, H. Miao and L. An, Appl. Phys. Lett., 2005, 86, 1908.
3. R. J. Xie and N. Hirosaki, Sci. Technol. Adv. Mater., 2007, 8, 588–600.
4. J. Cai, Y. L. Zhang, Z. Y. Lyu, J. Zhao, J. C. Shen, Q. Wu and Z. Hu, CrystEngComm, 2015, 17, 23–26.
5. B. Sain and D. Das, Phys. Chem. Chem. Phys., 2013, 15, 3881–3888.
6. J. Robertson, Philos. Mag. B, 1991, 63, 47–77.
7. J. Robertson, Mater. Res. Soc. Symp. Proc., 1993, 284, 65–76.
8. S. V. Deshpande, E. Gulari, S. W. Brown and S. C. Rand, J. Appl. Phys., 1995, 77, 6534–6541.
9. J. Robertson, W. L. Warren and J. Kanicki, J. Non-Cryst. Solids, 1995, 187, 297–300.
10. L. E. Hintzsche, C. M. Fang, M. Marsman, G. Jordan, M. W. P. E. Lamers, A. W. Weeber and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 155204.
11. P. A. Pundur, J. G. Shavalgin and V. A. Gritsenko, Phys. Status Solidi A, 1986, 94, K107–K112.
12. S. Baroni, S. De Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515.
13. J. Yu, P. Zhou and Q. Li, Phys. Chem. Chem. Phys., 2013, 15, 12040–12047.
14. D. Legut, U. D. Wdowik and P. Kurtyka, Mater. Chem. Phys., 2014, 147, 42–49.
15. G. Kresse, M. Marsman, L. E. Hintzsche and E. Flage-Larsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 045205.
16. V. A. Gritsenko, S. S. Nekrashevich, V. V. Vasilev and A. V. Shaposhnikov, Microelectron. Eng., 2009, 86, 1866–1869.
17. A. Kuwabara, K. Matsunaga and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 064104.
18. D. Hardie and K. H. Jack, Nature, 1957, 180, 332.
19. C. Di Valentin, G. Palma and G. Pacchioni, J. Phys. Chem. C, 2010, 115, 561–569.
20. M. E. Grillo, S. D. Elliott and C. Freysoldt, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 085208.
21. F. Oba, K. Tatsumi, I. Tanaka and H. Adachi, J. Am. Ceram. Soc., 2002, 85, 97–100.
22. Z. Wu, Z. Zhang, J. Yun, J. Yan and T. You, Phys. B Condens. Matter, 2013, 428, 10–13.
23. L. W. Lin and Y. H. He, CrystEngComm, 2012, 14, 3250–3256.
24. J. Huang, S. Zhang, Z. Huang, Y. Wen, M. Fang and Y. Liu, CrystEngComm, 2012, 14, 7301–7305.
25. F. Gao, W. Yang, Y. Fan and L. An, Nanotechnology, 2008, 19, 105602.
26. Y. Liu, Y. Zhou, W. Shi, L. Zhao, B. Sun and T. Ye, Mater. Lett., 2004, 58, 2397–2400.
27. G. Zou, B. Hu, K. Xiong, H. Li, C. Dong, J. Liang and Y. Qian, Appl. Phys. Lett., 2005, 86, 1901.
28. H. Du and A. Gao, Mater. Lett., 2012, 84, 31–33.
29. Y. Xu, C. Cao, Z. Chen, J. Li, F. Wang and H. Cai, J. Phys. Chem. B, 2006, 110, 3088–3092.
30. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
31. J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Ángyán, J. Chem. Phys., 2006, 124, 154709.
32. M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045.
33. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
34. Y. N. Xu and W. Y. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 17379.
35. Y. X. Han, C. L. Yang, M. S. Wang and X. G. Ma, RSC Adv., 2014, 4, 55452–55458.
36. J. Robertson and M. J. Powell, Appl. Phys. Lett., 1984, 44, 415–417.
37. M. Ahmad, J. Zhao, C. Pan and J. Zhu, J. Cryst. Growth, 2009, 311, 4486–4490.
38. G. Zou, B. Hu, K. Xiong, H. Li, C. Dong, J. Liang and Y. Qian, Appl. Phys. Lett., 2005, 86, 1901.
39. L. W. Yin, Y. Bando, Y. C. Zhu and Y. B. Li, Appl. Phys. Lett., 2003, 83, 3584.
40. Y. Xu, C. Cao, H. Du, J. Li and H. Zhu, Mater. Lett., 2007, 61, 3855–3858.
41. Y. Xu, C. Cao, Z. Chen, J. Li, F. Wang and H. Cai, J. Phys. Chem. B, 2006, 110, 3088–3092.
42. H. Du and A. Gao, Mater. Lett., 2012, 84, 31–33.

---