Magnetized property effect of a non-aqueous solvent upon complex formation between kryptofix 22DD with lanthanum(III) cation: experimental aspects and molecular dynamics simulation

Abstract

The complexation reaction between the La³⁺ cation and a macrocyclic ligand (kryptofix 22DD) in ordinary methanol (MeOH) and extraordinary methanol solvent (magnetized methanol) exposed to a magnetic field at different temperatures has been investigated using the conductometric method, in order to determine the effect of magnetic solvents on the thermodynamics of the complexation process between the metal cation and the ligand. The stoichiometry of the complex formed between the La³⁺ cation and the ligand is 1 : 1 [M : L] in both solvent systems. Comparison of the corresponding molar conductivity versus [L]_t/[M]_t for (kryptofix 22DD·La)³⁺ complex shows that the complex formed between the metal cation and kryptofix 22DD in the magnetized methanol is weaker compared to the ordinary methanol. The results of the density functional theory shows that addition of the metal ion to the ligand completely deforms the ligand from its planar shape and the orientation of two carbon chains attached to the ring changes in comparison with the free ligand. In addition, the molecular dynamics simulation can shed light on the influence of the magnetic field, from the molecular point of view, on the properties of solvents and is able to explain the variation of hydrogen bond and transport properties. These changes may be the reason for the interaction of the solvent and the solute as well as the stability constant of the complex formed between the La³⁺ cation and kryptofix 22DD in solution. As the strength of the magnetic field increases, the number of the hydrogen bonds formed between the methanol molecules increases and the methanol self-diffusion coefficient decreases. These changes restrict the movement of the molecules which results in increasing the viscosity of the methanol and therefore the stability constant of the (kryptofix 22DD·La)³⁺ complex decreases in magnetized methanol with respect to the ordinary methanol.

---

Introduction

The cryptand compounds, which are used in many fascinating areas of chemistry, biochemistry, and material science,^1–5 were first synthesized by Dietrich et al.⁶ They are macrobicyclic ligands that contain an internal cavity of about spherical shape well suited for the recognition of the spherical cations.⁷ Cryptands form very stable and selective complexes with a variety of metal cations.^7,8 Their alkali ion complexes possess stabilities several orders of magnitude higher than natural or synthetic macrocyclic ligands,³ a phenomenon which is called the “cryptate effect”.⁹

Lanthanides are widely distributed in low concentrations throughout the Earth's crust.¹⁰ La³⁺ cation with potentially high and variable coordination numbers and flexible coordination environments behaves as a hard acid with a strong affinity for a hard base containing neutral and negatively charged oxygen atoms.^11–15

In solutions, the metal ion, the macrocyclic ligand, and also the metal ion–macrocyclic ligand complex would be surrounded by the solvent molecules. Because of different physicochemical properties, each solvent can effect on the stability of metal ion complexes in different ways. Therefore, it is of great importance to study the effect of solvent on the complexation of metal ions with the macrocyclic ligands. One approach to achieve a detailed understanding of these interactions is to study the influence of magnetic field on the physicochemical properties of solvent and as a consequence on the formation of metal ion–macrocyclic complexes in solutions.

As the macrocyclic compounds are good models for the antibiotics and some of the other drugs treatment in biological systems,¹⁶ it is of great interest to investigate the effect of magnetic field upon complexation of such ligands with the metal ions. To our knowledge, the data about the effect of magnetic field upon formation of metal ion-macrocyclic complexes in non-aqueous solvents are very sparse. The first goal of the present study is to investigate how the magnetic field can influence on the physicochemical properties of a non-aqueous solvent passing through a magnetic field and as a result, the stability of the metal–ion complex at different temperatures.

The changes occurring in the structure of solvent under the effect of an external magnetic field are important in various applications such as chemical processes. It has been found that various aspects of the most common solvent (water) properties, including the size of the cluster,^17–19 hydrogen bonding,^20,21 electrical conductivity,²² dissolution rate into water,^23,24 van der Waals bonding between molecules,²⁵ and its melting point²¹ change when it is exposed to a magnetic field. Special attention has been devoted towards the structure of alloy clusters²⁶ as well as their growth.²⁷ Attempts to generate perpendicular magnetic anisotropy have been performed to check the shape anisotropy due to dipolar interactions, experimentally and theoretically. In addition, the use of a magnetic field is of considerable interest in a number of practical applications due to the self-diffusion coefficient alteration under a magnetic field. From molecular point of view, temperature influences on the properties of organic solvents in the presence of a magnetic field, the point that has not yet been under investigation.

Molecular dynamics (MD) simulations provide a powerful means of investigating the enhanced hydrogen bonding mechanism from an atomic viewpoint. Moreover, it is able to explore how surrounded ions by the solvent molecules may be retarded providing complex. In other words, solvent can effect on metal ion complex stability; as a result, achieving detailed insight on the influence of magnetic field on the physicochemical properties of solvent is of great importance. Temperature effect of external magnetic field on the properties of organic solvents has not yet been reported. Therefore, the temperature effect on external magnetic field change with the properties of methanol solvent is also under consideration to answer the above points in line with experimental results.

Experimental

Reagents and apparatus

La(NO₃)₃·6H₂O, 4,13-didecyl-1,7,10,16-tetraoxa-4,13-diazacyclooctadecane (kryptofix 22DD) and methanol with the highest purity were purchased from Merck (>99% purity) and were used without any further purification. The conductivity of methanol solvent was less than 3.0 × 10⁻⁷ S⁻¹ cm⁻¹ at 298.15 K. The conductance measurements were performed using a digital Jenway conductometer (model 4510), in a water bath thermostated at a constant temperature maintained within ±0.1 °C. The electrolytic conductance was measured using a dip-type conductivity cell consisting of two platinum electrodes to which an alternating potential was applied. A conductometric cell with a cell constant of 0.98 cm⁻¹ was used throughout the study.

The static magnetic field in a compact form, a unit called “AQUA CORRECT”, was used. The equipment has a coaxial static magnetic system of 6000 G field strength, and was imported from Germany (H.P.S Co.) [DN = 20, 3/4 in, flow 2 m³ h⁻¹] for the experiments. The equipment was connected from one end to the liquid pump and the other end to the pipelines of the solvent reservoir. The solvent had to flow through a coaxial static magnetic gap and came back to the solvent reservoir. Therefore, the solvent could pass through the magnetic field for many times in a closed cycle.

Procedure

The experimental procedure to obtain the stability constant of (kryptofix 22DD·La)³⁺ complex by conductometric method in both ordinary and magnetized methanol solutions were as follows: a solution of metal salt (1.0 × 10⁻⁴ M) was placed in a titration cell, thermostated at a given temperature, and the conductance of the solution was measured. The ligand solution (2.0 × 10⁻³ M) was transferred stepwise to the titration cell using a precalibrated microburette and the conductance of the solution was measured after each transfer at the desired temperature. Adding the ligand solution was continued until the total concentration of the kryptofix 22DD was approximately five times higher than that of the metal cation. The conductance of the solution was measured after each addition and the stability constant of the complex was obtained from variation of molar conductance as a function of [L]_t/[M]_t molar ratio plots using a GENPLOT computer program.²⁸ This procedure was exactly carried out for the magnetized methanol solvent. The magnetized solvent was immediately used after passing through the magnetic field for 2 min.

Simulation details

Density functional theory (DFT) is known to handle geometries and vibrational frequencies of different systems especially hydrogen bonded systems appropriately accurate.^29–31 DFT method at B3LYP functional coupled with 6-311++G(d,p) basis set was employed, by using GAUSSIAN 03 package,³² to find the structural parameters for the ground state of target solvent and no restrictions on symmetries were imposed on the initial structure of the solvent. A vibrational analysis was performed to ensure the absence of negative vibrational frequencies and authenticate the existence of a true minimum.^30,31 The geometrical parameters including bond lengths, bond angles, and dihedral angles, computed at B3LYP/6-311++G(d,p) level of theory as well as natural bond atomic charges were implemented in order to construct the initial configuration. In addition, for the description of the potential model, a classical force field approach has been used. The parametrized DREIDING force field applied to the MD simulations³³ has the following terms:where V_tot is the total interaction potential energy of the system. Harmonic potentials govern bond length, bond angle, and improper angle motion about nominal values, r_eq, θ_eq, and ϕ_eq and dihedral angles were modeled by Taylor cosine series. The results of DFT optimization, B3LYP/6-311++G(d,p) level of theory, were applied for r_eq, θ_eq, and ϕ_eq, and δ in standard form of molecular mechanics force field. The short range van der Waals interaction was expressed by the typical Lennard-Jones (12-6) function with the parameters for unlike atoms obtained using the Lorentz–Berthelot combining rule. Columbic interactions were modeled using fixed natural bond orbital analysis to compute partial charges on each atom center. Long-range electrostatic interactions were accounted by using Ewald procedure^34–38 within the isothermal–isobaric (NPT) ensemble at 3 temperature values, 298.15 K, 308.15 K, and 318.15 K. Moreover, columbic interactions were modeled using fixed partial charges on each atom center obtained by natural bond orbital, NBO, analysis and force constants including K_r, K_θ, K_χ, K_ϕ, besides the intermolecular Lennard-Jones (12-6) parameters, A and B, were taken from Mayo et al.³³ study. A cubic box containing 512 molecules with a period of 1 ns NPT (constant number of particles, constant pressure, and constant temperature) ensemble simulation was performed to adjust the simulation system achieving proper density at pressure of 1.01325 bar. The time step was set to be 1 fs and the equilibrium process was preset to 700 ps. After reaching equilibrium state, the system keeps running for 300 ps to collect the required data with the applied force field.

Neighborhood lists were updated every 10 time steps with a distance of 15 Å. Full electrostatic evaluations were calculated. The coupling methods for pressure and temperature were applied by Nose–Hoover thermostat–barostat every 1.0 and 0.1 ps, respectively.^36,37 Using Verlet leapfrog scheme,³⁸ the positions and velocities of particles were calculated.

The external magnetic field aligned along the Z direction at different temperatures may shed light on the thermodynamic, transport, and structural properties of the solvent using MD computation. All MD simulations were conducted using DL_POLY version 2.17 simulation package.^39,40 Notice that all mentioned details of simulation were applied in the case that the complex is present; mole fraction of the complex is 0.002 and the effect of temperature and magnetic field was studied. In this case, the cut off distance was set to 16 Å.

In this study, a static and constant magnetic field parallel to the Z-direction of the simulation box was applied. According to the Lorentz force, the output of the magnetic field depends on the velocity of solvent flow, magnetic force, number of particles with positive or negative charges in solvent, and the angle between particle velocity and applied magnetic field, which is always upright.

An accurate practical means for the analysis of the structure is provided by pair correlation function, g(r), defined as:

with r is the atomic separation and ρ the number density; r_i and r_j are the atomic positions. Atom–atom pair correlation functions made available from the histogram of trajectories were applied to estimate the spreading profile and thus the structural relation between the solvent atoms. In addition, the coordination numbers were computed by the aid of the RDF. The coordination number of the solvation is deduced from the solvent–solute pair correlation functions. The integral over the pair correlation function reveals the number of neighbors as function of their distancehere ρ represents the number density of the selected atom species. Integration over the entire first peak leads to a consistent number of nearest neighbors.

Besides, the molecular mobility was investigated by mean-square displacement.

MSD = 〈|r_j(t) − r_j(0)|〉² (4)

Results and discussion

Conductance studies

The changes of molar conductivity (Λ_m) versus the ligand to the metal cation mole ratio, ([L]_t/[M]_t), for complexation of kryptofix 22DD with La³⁺ cation in ordinary and magnetized methanol solvents were studied at different temperatures. The resulting molar conductivity versus [L]_t/[M]_t in these two conditions are shown in Fig. 1 and 2. As it is evident in these figures, addition of kryptofix 22DD to La³⁺ cation solution results in an increase in molar conductivity which indicates that the (kryptofix 22DD·La)³⁺ complex is in considerable amount than the free solvated La³⁺ cation. This result may be explained on the basis of the solvation sphere. It seems that La³⁺ cation is solvated to a high extent in this organic solvent. Upon complexation of the metal cation with kryptofix 22DD, the ligand molecule replaces the solvation sheath around the metal ion and the resulting complex becomes less bulky; therefore, the molar conductivity increases by ligand addition to the cation solution.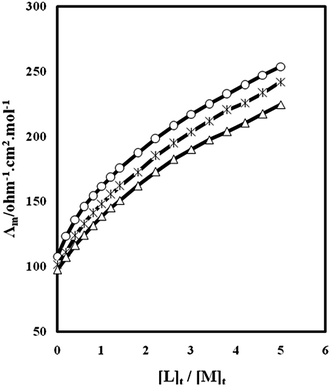

Fig. 1 Molar conductance–mole ratio plots for (kryptofix 22DD·La)³⁺ complex in methanol solution at different temperatures: 25 °C (open circle), 35 °C (asterisk), 45 °C (open triangle).

Fig. 2 Molar conductance–mole ratio plots for (kryptofix 22DD·La)³⁺ complex in methanol which is exposed to the magnetic field for two minutes at different temperatures: 25 °C (open circle), 35 °C (asterisk), 45 °C (open triangle).

As is shown in Fig. 1, the slope of the corresponding molar conductivity versus [L]_t/[M]_t changes at the point where the ligand to cation mole ratio is about one which is an evidence for formation of a relatively stable 1 : 1 [M : L] complex between kryptofix 22DD and La³⁺ cation in ordinary methanol solvent. On the other hand, the plot of corresponding molar conductivity versus [L]_t/[M]_t does not show any considerable change in slope emphasizing the formation of relatively weak 1 : 1 [M : L] complex in the magnetized methanol solvent (see Fig. 2).

In order to make the 1 : 1 [M : L] complex model more clear, the fitting and the experimental curves for the (kryptofix 22DD·La)³⁺ complex in magnetized methanol solvent at 298.15 K is shown in Fig. 3. As it is clearly evident in this Figure, there is an accurate acceptable agreement between experimental and least square regression.

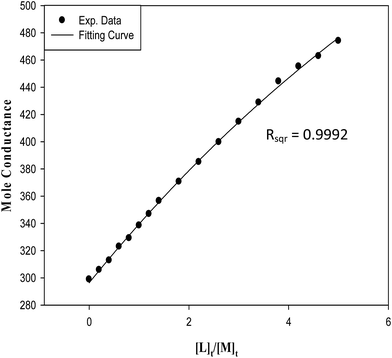Fig. 3 The experimental data and fitting curve for (kryptofix 22DD·La)³⁺ complex in magnetic methanolic solution at 298.15 K.

To gather accurate information about the conformational change of kryptofix 22DD upon complexation with lanthanum(III) cation, the molecular structures of the uncomplexed ligand and its 1 : 1 La³⁺ complex were computed with quantum calculations. The structure of the free ligand was optimized at B3LYP/Lanl2dz level of theory. The optimized structure of the ligand was then applied to find out the initial structure of its 1 : 1 lanthanum(III) complex (at the same level of theory). The optimized structures of the uncomplexed ligand (i.e. kryptofix 22DD) and its 1 : 1 complex with La³⁺ cation (i.e. kryptofix 22DD·La)³⁺ are presented in Fig. 4. In order to study the effect of solvent upon complexation, we compared the order of stability of the complexes formed between kryptofix 22DD and La³⁺ cation in the gas phase which were obtained based on binding energies with the order of stability of the complexes formed between kryptofix 22DD and La³⁺ cation in the presence of methanol. Fig. 4A and B shows the optimized structures of free ligand and its complex with La³⁺ cation in the gas phase. It is obvious from Fig. 4A that the ligand forms a more or less planar but interestingly, in the optimized structure of the 1 : 1 (kryptofix 22DD·La)³⁺ complex (Fig. 4B), lanthanum(III) ion is well incorporated inside the twisted macrocyclic ligand and coordinated to six donating atoms of the ligand, including four oxygen atoms and two nitrogen. It is fascinating to note that when the metal ion is added to the ligand, the ligand was twisted and completely deformed from its planar shape. Moreover, the orientation of two carbon chains attached to the ring changes in comparison with the free ligand. The optimized structures of free ligand and its complex with La³⁺ in the presence of methanol were also studied. For the calculations in the presence of methanol as a solvent, the Polarizable Continuum Model (PCM) was chosen. In this model, the cavity is created via a series of overlapping spheres. The PCM was applied within the B3LYP/LanL2DZ level to predict the solvent effects on the structures and interaction energy of kryptofix 22DD ligand and [kryptofix 22DD·La]³⁺. The results show there is no major changes occurred in the structures of free ligand and its complex in compression to the gas phase calculation. For this reason, the structures of free ligand and its complex are not shown in the presence of methanol. Moreover, the effect of solvent on the binding energy of complex was investigated. The pair wise binding energy ΔE between kryptofix 22DD ligand and La³⁺ is estimated as the difference between the energy of the complex [kryptofix 22DD·La]³⁺ and the energies of isolated partners:

ΔE = E_{[kryptofix 22DD·La]³⁺} − (E_La³⁺ + E_{kryptofix 22DD})

Fig. 4 Optimized structures of free kryptofix 22DD (A) and its 1 : 1 complex with La³⁺ cation (B).

The binding energy for the [kryptofix 22DD·La]³⁺ complex were obtained −53.1 and −481.2 kcal mol⁻¹ in the gas phase and in the presence of methanol, respectively. These results show that the stable complex is formed in the presence of methanol as a solvent.

Now, the question is how the magnetic field impacts on the solvent and how this magnetized solvent can change the thermodynamic of the complexation process between the kryptofix 22DD and La³⁺ cation. Chang and Weng¹⁷ have investigated the effects of the magnetic field on the hydrogen-bonded structure of water and they found that the number of the hydrogen bonds increases when it is exposed to a magnetic field. Since water molecules have two donors and two acceptor sites, liquid water forms a continuous network of hydrogen bonds. The presence of spatial network of hydrogen bonds is the main property of the liquid water.⁴¹ Furthermore, some researchers have carried out a series of studies to know if there is any relationship between the hydrogen bonding and temperature of water.^42,43 It has been recognized that the hydrogen bonding becomes weaker with increasing the thermal motion of the atoms involved.⁴⁴ Consequently, the water structure breaks down as the temperature increases. It has been suggested that the effects of a magnetic field on water hydrogen bonds are similar with the effects of decreasing the temperature.⁴⁵ The theory of cluster models points out that the average size of water cluster decreases with increasing temperature.^46,47 Normally, the viscosity and also the dielectric constant of liquid water decreases as the temperature increases.^48,49 From the other side of view, methanol is a polar solvent and its molecules are able to constitute hydrogen bonds through their hydrogen and oxygen atoms; therefore, it is expected a similar behavior is observed for this organic solvent as water. It has been shown that the hydrogen bond network in methanol molecules increases as the temperature decreases.⁵⁰ In addition, the viscosity and the dielectric constant of the liquid methanol increase as the temperature decreases.^49,51

The values of the stability constant (log K_f) of (kryptofix 22DD·La)³⁺ complex are given in Table 1. It can be seen that by applying magnetic field, the stability of the (kryptofix 22DD·La)³⁺ complex decreases at all studied temperatures. Similar results have been observed by the authors in the previous study which further corroborate the results reported in Table 1.⁵² This result may be attributed to the higher dielectric constant and possibly changing the donor number of the magnetized methanol solvent than that of the ordinary methanol. The higher dielectric constant and change in the donicity of the magnetized solvent with respect to the ordinary methanol may lessen the electrostatic interactions between the ligand and La³⁺ cation. As a result, the complex formation between kryptofix and La³⁺ cation weakens by imposing magnetic field on the solvent. Furthermore, it seems that the higher viscosity of the magnetized methanol solvent, leads to a decrease in the rate of the complexation reaction in this extraordinary solvent compared to the ordinary methanol solvent.

Table 1 log K_f values of (kryptofix 22DD·La)³⁺ complex in the methanol solution and magnetic methanolic solution at different temperatures

Medium	log Kf ± SD^a
(kryptofix 22DD·La)^3+	25 °C	35 °C	45 °C
a SD = standard deviation.b In the absence of the magnetic field.c In the presence of the magnetic field.
Pure MeOH^b	3.50 ± 0.04	3.39 ± 0.03	3.36 ± 0.02
Pure MeOH^c	2.76 ± 0.07	2.50 ± 0.10	2.80 ± 0.09

---

In order to shed light on this suggestion, MD was handled and the results are given in the following paragraphs.

Molecular dynamics studies

As mentioned before, the formation of hydrogen bonding between the methanol solvent molecules enhances due to the external magnetic field and its temperature effect is one of the substantial questions that are under study in the present research work. Fig. 5 compares the variation of hydrogen bond, O–H distance, in the present solvent at three different temperatures in the presence and absence of magnetic field. As an evident from this figure, external magnetic field has a direct effect on the structure of the solvent; in other words, the molecules are more ordered and stable. To evaluate the average number of hydrogen bonds, the present study adopts the geometric criterion⁵³ that a hydrogen bond will be formed if the distance between the oxygen and hydrogen atoms of a pair of methanol molecules is less than the first minimum of the O–H radial distribution function, 2.52 Å. This procedure has been applied on water molecules by Levitt et al.⁵⁴ The simulation results presented in Fig. 5 indicate that applying magnetic field intensifies the strength of hydrogen bond. Besides, as the temperature increases from 298.15 K to 318.15 K, the average variation of O–H bond length increases. The slight increase in the O–H bond length with increasing the temperature demonstrates the magnetic field enhances the networking ability and the temperature has an opposite effect. Moreover, near connection between H and O atoms of the methanol molecules implies that the cluster size increases under a magnetic field, and hence more compact in the structure of methanol molecules is observed. The results of this study show that the number of hydrogen bonds between the methanol molecules increases which are consistent with the findings reported before²⁰ and it has been suggested that the enhancement of the hydrogen bond strength under an external magnetic field is caused by the increasing the electron delocalization of the hydrogen bonded molecules. Furthermore, the effect of the magnetic field in increasing the number of hydrogen bonds is consistent with the weakening van der Waals bonding force between the solvent molecules under a magnetic field²⁵ and the suppression of thermal motions because of the tighter hydrogen bonding induced by the Lorentz forces.²¹

Fig. 5 Comparison of the target solvent H–O distance in the presence and absence of magnetic field at different temperatures.

Commonly, radial distribution function (RDF) examines the structure of a liquid; in the case of methanol, gO–H and gO–O are considered to investigate the structural dependence on the external magnetic field. The other correlations as C–C, C–H, and H–H show insignificant revolution with magnetic field that are not shown. In other words, the correlations due to hydrogen bond enjoy considerable variations that are under study here. The structural differences of pure liquid with and without the application of an external magnetic field are depicted for gO–H in Fig. 6, at T = 298.15, 308.15, and 318.15 K. The first peak occurs at 2.575 Å, at the absence of the magnetic field and at T = 298.15 K, which corresponds to the oxygen–hydrogen distance between the two hydrogen-bonding methanol molecules, which reduces to 2.525 Å, at T = 298.15 K and the presence of the magnetic field. It should be noted that this distance is greater than an O–H bond length obtained by DFT computation (0.961 Å), i.e., the aforementioned distance does not correspond to the O–H bond length. The tetrahedral structure of the near neighbors is related to the second peak of O–H RDF belonging to two molecules both hydrogen bonded to a third methanol.

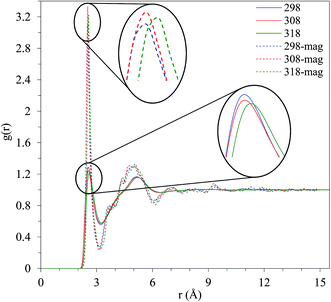Fig. 6 Comparison of g(r) O–H in the presence and absence of the magnetic field at different temperatures.

In order to shed light on the compactness of methanol molecules because of magnetic field, O–O RDF, the distribution of the oxygen atoms of the methanol molecules, at T = 298.15 K, 308.15 K, and 318.15 K was also considered, Fig. 7. Surprisingly, the distance between two methanol molecules in the absence and presence of the magnetic field is unchanged (3.475 Å) and the intensity of the peak just only increases sharply. However, the height of the second peak shows a slight change indicating the distance between the two oxygen atoms of two next-nearest neighbors is not influenced by the magnetic field. From the other side of view, the average tetrahedral hydrogen bonding length may not be affected by external magnetic field. The increased height of the first and second valleys under external magnetic field demonstrates that more molecules exist between methanol shells. The slight increase in the height of the first valley indicates that more molecules are located between the shells. However, magnetic field reforms the structure of the liquid methanol, forces more methanol molecules between the shells, and enhances the connectivity between molecules to progress the stability of the solvent–solvent network. Consequently, a small increase in the number of hydrogen bonds is apparent under an external magnetic field. According to the results presented in Fig. 7, the methanol molecules tend to form more stable connections with other molecules in all directions.

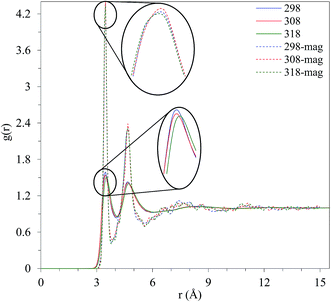Fig. 7 Comparison of g(r) O–O in the presence and absence of the magnetic field at different temperatures.

In summary, the results presented in Fig. 6 and 7 demonstrate that the magnetic field enhances the binding between the methanol molecules and stabilize the structure of the liquid methanol.

In this study, we also investigated the self-diffusion coefficients of the solvent molecules under a magnetic field. Study of the transport properties of a liquid is an important topic, both in fundamental sciences and also in its applications. The mobility of methanol molecules is indicated by the value of mean-square displacement (MSD), which depends on the temperature, pressure, structure, and so on. The value of the self-diffusion coefficients can be obtained from the Einstein relation based on MSD function. The present results show that a static magnetic field enhances the stability of methanol molecules and hence influences their mobility. Calculating the self-diffusion coefficient of the molecules provides a clearer understanding of their change in mobility. Fig. 8 presents the profiles of MSD under various temperatures and magnetic strengths. It is noticeable that the self-diffusion coefficient reduces as the magnetic field is applied. The decreasing self-diffusion coefficient by applying magnetic field points to the mobility decrease of methanol molecules. If the molecule mobility changes, the physical properties such as viscosity, thermal conductivity, and their melting point also change. Although the decrease of the self-diffusion coefficient caused by the magnetic field is not large, it indicates a change in the properties of the liquid. In general, based on the above finding, it seems that the changes of structure of the methanol solvent under the influence of the magnetic field are probably effective in changing the (kryptofix 22DD·Y)³⁺ complex stabilization in solution.

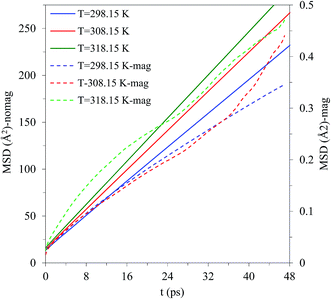Fig. 8 Comparison of the mean-square displacement of the solvent in the presence and absence of the magnetic field at different temperatures.

Now it is the point to emphasize on the second target of this computation. The goal is to investigate the effect of magnetic field on the complex stabilization since a molecular knowledge about the solvent and magnetic field is present. For this aim, a system containing the complex and solvent was simulated. The results of atomic RDF between the solvent, hydrogen atom connected to oxygen atom of complex represented by H(O), and the complex, N atom, at the presence of magnetic field and its absence are presented in Fig. 9. As the figure demonstrates, the complex interaction with the solvent increases at a distance about 3 Å with magnetic field without any substantial variation of distance between solvent and complex. Interestingly, the complex structure does not witness change showing that the complex is stable at the presence of magnetic field. However, the observation was quantified by computing coordination number where at different temperatures is compared between the system at the presence of magnetic field and its absence in Table 2. As the table tabulates, the previous statement is confirmed by coordination number values.

Fig. 9 Comparison of g(r) N⋯H(O) in the presence and absence of the magnetic field at different temperatures. The inset is g(r) in the absence of magnetic field at three studied temperatures.

Table 2 Coordination number (CN) value for methanol at present and absence of magnetic field as well as the complex at different temperatures

CN value		298.15 K	308.15 K	318.15 K
Pure methanol	Magnetic field off	0.89	0.86	0.84
	Magnetic field on	1.26	1.25	1.25
Solution	Magnetic field off	0.88	0.86	0.83
	Magnetic field on	1.23	1.22	1.27

---

Based on Table 2, it can be understood that coordination number (CN) of methanol at the presence of magnetic field enhances that is in good agreement with the decreasing temperature. However, the complex presence leads to a very slight decrease of coordination number. Additionally, the intermolecular interaction between the complex and the solvent may lessen the magnetic field effect on the solvent; as a result, the CN is less than its corresponding value for the pure methanol and the presence of magnetic field. In other words, the strong interaction between complex and solvent at magnetic field causes retard of complex provide.

Conclusions

Actually, in the host–guest recognition processes, the solvent plays a critical role in the local structure optimization and complex stabilization; thus, the stability of the metal ion complexes is known to vary drastically according to the chemical and physical properties of the solvent in which the complexation reactions occur. In the present work, we investigated the effect of methanol solvent properties on complexation reaction of the kryptofix 22DD with La³⁺ cation. The values of the stability constant of (kryptofix 22DD·La)³⁺ complex in both ordinary and magnetized methanol solvent were determined by electrical conductance measurements. The results show that the stability constants of the complex at different temperatures in magnetized methanol solution are lower than those obtained in the case of ordinary methanol. It seems that the changes of structure, viscosity, and the dielectric constant of the studied organic solvent under the influence of magnetic field are probably effective in changing the (kryptofix 22DD·La)³⁺ complex stabilization.

In addition, molecular dynamics simulation was applied to examine the effect of a static magnetic field on the liquid methanol at a various temperatures of 298.15, 308.15, and 318.15 K. It has been shown that an external magnetic field influences the number of hydrogen bonds, its strength, the structure of the liquid methanol, as well as its molecular mobility. The increasing number of the hydrogen bonds, due to the external magnetic field, indicates the formation of larger methanol molecule clusters. The magnetic field induces a tighter bonding between the methanol molecules and improves the stability of this liquid. Under the effect of the magnetic field, the structure of the liquid changes and more molecules are forced between the methanol shells decreasing the stability of the complex.

These molecules connect the shells and hence create a more stable methanol–methanol network. The transport properties of the molecules, as indicated by MSD, are of considerable interest in many applications. The current simulation results have shown that the molecular mobility reduces when a magnetic field is applied to the methanol solvent and, hence, resulting in a reduction in the self-diffusion coefficient of this organic solvent. In other words, the magnetic field constrains the movement of the methanol molecules, and hence changes both the thermal conduction and the viscosity in the liquid state. This change is in a good agreement with decreasing the stability constant of the (kryptofix 22DD·La)³⁺ complex in magnetized methanol compared to the ordinary methanol solvent.

Acknowledgements

The authors wish to acknowledge the financial supports (No. 18232) of this work by Ferdowsi University of Mashhad, Mashhad, Iran.

References

1. R. Z. Gnann, R. I. Wagner, K. O. Christe, R. Bau, G. A. Olah and W. W. Wilson, J. Am. Chem. Soc., 1997, 119, 112–115.
2. P. Ghosh, P. K. Bharadwaj, J. Roy and S. Ghosh, J. Am. Chem. Soc., 1997, 119, 11903–11909.
3. P. Chang and J. S. Shih, Anal. Chim. Acta, 1999, 380, 55–62.
4. R. Cacciapaglia, L. Mandolini and V. V. A. Castelli, J. Org. Chem., 1997, 62, 3089–3092.
5. M. J. Wagner, A. S. Ichimura, R. H. Huang, R. C. Phillips and J. L. Dye, J. Phys. Chem. B, 2000, 104, 1078–1087.
6. B. Dietrich, J. M. Lehn and J. P. Sauvage, Tetrahedron Lett., 1969, 10, 2885–2888.
7. J. M. Lehn, Pure Appl. Chem., 1978, 50, 871–892.
8. R. M. Izatt, K. Pawlak, J. S. Bradshaw and R. L. Bruening, Chem. Rev., 1991, 91, 1721–2085.
9. J. M. Lehn and J. P. Sauvage, J. Am. Chem. Soc., 1975, 97, 6700–6707.
10. R. E. Kirk and D. F. Othmer, Encyclopedia of Chemical Technology, Wiley, 1982, vol. 19, p. 836.
11. C.-B. Liu, C.-Y. Sun, L.-P. Jin and S.-Z. Lu, New J. Chem., 2004, 28, 1019–1026.
12. C.-B. Liu, M.-X. Yu, X.-J. Zheng, L.-P. Jin, S. Gao and S.-Z. Lu, Inorg. Chim. Acta, 2005, 358, 2687–2696.
13. X.-J. Zheng, L.-P. Jin and S. Gao, Inorg. Chem., 2004, 43, 1600–1602.
14. M. Watanabe, T. Nankawa, T. Yamada, T. Kimura, K. Namiki, M. Murata, H. Nishihara and S. Tachimori, Inorg. Chem., 2003, 42, 6977–6979.
15. V. Patroniak, P. N. W. Baxter, J.-M. Lehn, Z. Hnatejko and M. Kubicki, Eur. J. Inorg. Chem., 2004, 2379–2384.
16. R. G. Cooks and T. L. Kruger, J. Am. Chem. Soc., 1977, 99, 1279–1281.
17. K. T. Chang and C. I. Weng, J. Appl. Phys., 2006, 100, 043917.
18. S.-H. Lee, M. Takeda and K. Nishigaki, Jpn. J. Appl. Phys., Part 1, 2003, 42, 1828–1833.
19. M. Iwasaka and S. Ueno, J. Appl. Phys., 1998, 83, 6459–6461.
20. H. Hosoda, H. Mori, N. Sogoshi, A. Nagasawa and S. Nakabayashi, J. Phys. Chem. A, 2004, 108, 1461–1464.
21. H. Inaba, T. Saitou, K.-I. Tozaki and H. Hayashi, J. Appl. Phys., 2004, 96, 6127–6132.
22. S. Hakobyan and S. Ayrapetyan, Biofizika, 2005, 50, 265–270.
23. T. Itoi and A. Inoue, Mater. Trans., 2000, 41, 1256–1262.
24. A. Sugiyama, S. Morisaki and R. Aogaki, Mater. Trans., 2000, 41, 1019–1025.
25. R. V. Krems, Phys. Rev. Lett., 2004, 93, 013201–013204.
26. M. Einax, W. Dieterich and P. Maass, Rev. Mod. Phys., 2013, 85, 921–939.
27. M. Einax, S. Heinrichs, P. Maass, A. Majhofer and W. Dieterich, J. Phys.: Condens. Matter, 2007, 19, 086227.
28. http://www.genplot.com/RUMP/index.htm.
29. Y. Yang, T. A. Pakkanen and R. L. Rowley, Int. J. Thermophys., 2000, 21, 703–717.
30. X. Li, M. D. Sevilla and L. Sanche, J. Am. Chem. Soc., 2003, 125, 8916–8920.
31. A. Dkhissi, L. Houben, J. Smets, L. Adamowicz and G. Maes, J. Phys. Chem. A, 2000, 104, 9785–9792.
32. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, A. Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C.02.
33. S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909.
34. M. Kohagen, M. Brehm, J. Thar, W. Zhao, F. Müller-Plathe and B. Kirchner, J. Phys. Chem. B, 2010, 115, 693–702.
35. O. Guvench, S. N. Greene, G. Kamath, J. W. Brady, R. M. Venable, R. W. Pastor and A. D. Mackerell, J. Comput. Chem., 2008, 29, 2543–2564.
36. L. Weng, C. Chen, J. Zuo and W. Li, J. Phys. Chem. A, 2011, 115, 4729–4737.
37. C. Chen, W. Z. Li, Y. C. Song and J. Yang, J. Mol. Liq., 2009, 146, 23–28.
38. M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford University Press, 1989.
39. W. Smith and T. R. Forester, J. Mol. Graphics, 1996, 14, 136–141.
40. T. Forester and W. Smith, The DL_POLY_2 Reference Manual, Daresbury Laboratory, Daresbury, 2000.
41. N. A. Chumaevskii and M. N. Rodnikova, J. Mol. Liq., 2003, 106, 167–177.
42. R. Li, Z. Jiang, H. Yang and Y. Guan, J. Mol. Liq., 2006, 126, 14–18.
43. J. Urquidi, C. H. Cho, S. Singh and G. W. Robinson, J. Mol. Struct., 1999, 485, 363–371.
44. G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, 1997.
45. R. Cai, H. Yang, J. He and W. Zhu, J. Mol. Struct., 2009, 938, 15–19.
46. M. Starzak and M. Mathlouthi, Food Chem., 2003, 82, 3–22.
47. A. T. Hagler, H. A. Scheraga and G. Némethy, J. Phys. Chem., 1972, 76, 3229–3243.
48. F. Franks, Water: a comprehensive treatise, Plenum Press, New York, 1972.
49. M. Mohsen-Nia, H. Amiri and B. Jazi, J. Solution Chem., 2010, 39, 701–708.
50. S. L. Wallen, B. J. Palmer, B. C. Garrett and C. R. Yonker, J. Phys. Chem., 1996, 100, 3959–3964.
51. A. M. Katti, N. E. Tarfulea, C. J. Hopper and K. R. Kmiotek, J. Chem. Eng. Data, 2008, 53, 2865–2872.
52. M. Gholizadeh, G. H. Rounaghi, I. Razavipanah and M. R. Salavati, J. Iran. Chem. Soc., 2014, 11, 947–952.
53. I. Benjamin, J. Chem. Phys., 1992, 97, 1432–1445.
54. M. Levitt, M. Hirshberg, R. Sharon, K. E. Laidig and V. Daggett, J. Phys. Chem. B, 1997, 101, 5051–5061.

---