Modeling the relationship between melting point of a metal nanowire and its cap surface curvature†
Y.
Jiang
a and
K.
Zhang
*bc
aCentre for Advanced Macromolecular Design, School of Chemical Engineering, University of New South Wales UNSW, Kensington, NSW 2052, Australia
bKey Laboratory of Microgravity (National Microgravity Laboratory), Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
cNational Engineering Research Central for Rare Earth Materials, General Research Institute for Non-Ferrous Metals, GRIREM Advanced Co. Ltd., Beijing 100088, China. E-mail: zhangkunone@gmail.com
First published on 10th April 2015
Abstract
It is of practical importance to predict the melting point of metal nanowires in a confined environment. Based on molecular dynamics (MD) simulations, a universal model unravelling the relationship between the melting point of a metal nanowire in nanoconfinement and its cap surface curvature has been developed for the first time. The results have demonstrated that both the interaction strength between the nanowire and the nanoconfinement and the diameter of nanoconfinement dramatically affect the melting point of the embedded nanowire. These phenomena can be further expressed in a mathematical formula directly describing the curvature-dependent melting point. It is also found that the melting feature of the metal nanowire under weak interaction is quite different from that under strong interaction. Furthermore, the melting point of the free cluster can also be predicted using this model. Our findings have provided a direct way to analyze the melting point via the observed morphology of the metal nanoparticle.
Introduction
Metal nanoparticles, including free or substrate-supported clusters and nanowires in nanoconfinement, are currently used or have potential applications in catalytic, optical, magnetic, electronic, and alternative energy fields due to particular lower-dimensional advantages and the nanoscale structures.1,2 Especially, as for a nanowire in nanoconfinement, the nanoconfinement such as carbon nanotubes, not only acts as natural protection for the embedded nanowires against oxidation,3 but also gives the embedded nanowires more desirable properties, which makes them more stable and durable for these applications.4 For example, a melting point shift caused by the nanoconfinement tends to be a critical issue in practice because it may alter the features of the solid-state particle. In terms of the free or substrate-supported cluster, it has been well recognized that the melting temperature has a depressive tendency which yields the same linear or approximately linear equation with the reciprocal of the cluster diameter:5–8
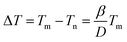
| (1) |
Meanwhile, Jackson and McKenna investigated the glass transition shift of organic liquids confined in pores, which has stimulated more and more people to research the phase transition that happens in porous media.13 The fundamental interest in this realm is to understand the influence that the nanoconfinement brings to the phase transition, from phenomena to mechanism.14 The melting point shift becomes particularly essential for the fabrication of nanomaterials in porous templates, which may be of great significance for catalysts, semiconductor devices, nonmagnetic recording media, fuel cells etc.15–18 According to existing experimental evidence on embedded metals in porous media, an enormous amount of work refers to the observation that the melting temperature depression is also inversely proportional to the pore size.19,20 In addition, for embedded nanowires, it is also found that the melting behavior is controlled not only by the particle size but also by the particle/matrix interfaces.21 The melting point depression of embedded nanowires, ΔT, as elucidated by the Gibbs–Thomson equation, an accepted thermodynamic model, is given by:22,23
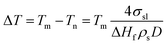
| (2) |
In our studies, MD simulations on the embedded metal nanowire in nanoconfinement have been carried out in a wide range of interaction strength and confinement size to investigate the relationship between Tm and the nanoconfinement and to answer whether the negative ΔT is possible. As existed in bulk metal material,26 another universal model accounting for the relation between the melting point and the surface curvature of the embedded metal nanowires has been proposed for the sake of the physical analysis and the manipulation on the melting point of the embedded nanowires. The melting mechanisms at different interaction strengths have also been illustrated in detail to provide insight into the interaction between the metal atoms and the nanoconfinement.
Details of methods
Herein, Fe nanowire has been chosen as the embedded particle, and porous systems such as carbon nanotubes and nanoscale pores have been abstracted into a tubular confinement with variable diameter and interaction strength.The second-moment approximation of the tight-binding (TB-SMA) potential was employed to describe the Fe–Fe interactions.27 The TB-SMA potential parameters for Fe–Fe were presented elsewhere.28 A Lennard-Jones 9/3 potential was used to describe the interaction between the Fe atoms and the confinement:
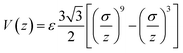
| (3) |
The parameter σ was kept constant at 0.2 nm, and the depth of potential well ε, which dominates the confinement-metal interaction strength ranges from 0.1 to 0.8 eV to adjust the surface curvature of the embedded particle.
The structure evolution of Fe
N
in the melting process was studied by constant temperature MD using the Berendsen method and an integration time step of 3 fs.29 The initial structures for the melting process were obtained by relaxing and annealing the randomly embedded nanowire at 500 K to reach equilibration. In the melting process, the initial structures were heated from 800 K to 1600 K with a temperature ramp of 10 K and 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MD steps at each constant temperature point.
000 MD steps at each constant temperature point.
In addition, it has been tested that when the length-to-diameter ratio of the embedded particle is larger than 2.5, the melting point of the particle becomes independent on its length (Fig. S1†). Therefore, the length-to-diameter ratio of all the samples in this study was set to be 3. The simulated melting point of bulk iron was obtained by extrapolating the cluster melting point to infinitely large size. The bulk Fe melting point we obtained is lower than the reported value. The difference between the simulated value and the experimental one may be caused by the inclusion of free cluster surfaces in the simulations or inaccuracies in the force field.30 This difference, which is attributed to the calculation methods we employed, does not affect the conclusions reported here because the current research mainly focuses on the melting point shift law of the embedded nanowires.
Results and discussion
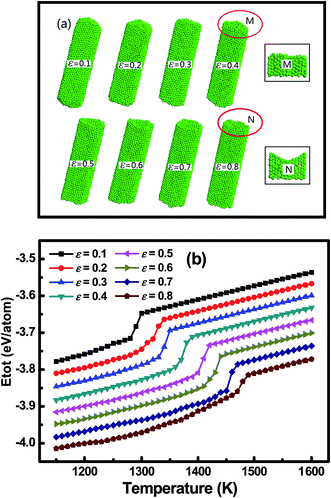
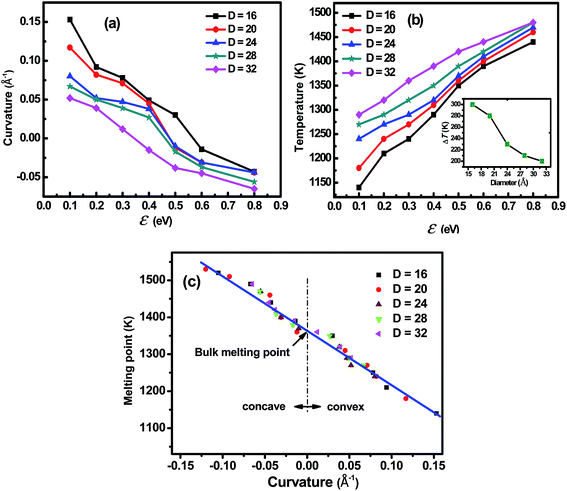
The main focus of the current work is to explore what influence the nanoconfinement exerts on the melting point of the embedded metal nanowires. Fig. 1a shows the morphology of Fe4800 nanowires in tubular nanoconfinements. The diameter of the confinement was set to be 32 Å. With the increase of confinement-metal interaction by increasing the potential parameter ε from 0.1 eV to 0.8 eV, the surface curvature of the Fe4800 gradually decreased and the morphology exhibited three typical cases ranging from convex to concave (Fig. S2†). This indicated a valid effect of potential parameter on the surface curvature, which changed the accuracy of the above mentioned Gibbs–Thomson equation where the embedded particle was generally considered to be a crystal with convex surface in the confinement. As for the corresponding energy curves in Fig. 1b, where the saltation point in each total energy curve was identified as the melting point at the given interaction strength. It is evident that the melting point increases with the enhanced interaction when Fe4800 was embedded in the confinement with the constant diameter; so that the potential parameter ε should not be ignored in the Gibbs–Thomson equation. Furthermore, it was clearly seen that for the nanowires embedded in the nanoscale confinement, the melting point could be higher, lower than or even equal to the bulk value (1370 K), which depended on the interaction strength between the confinement and the embedded particle. Therefore, the negative ΔT is possible when the interaction between the particle and the confinement is strong enough, which is also in agreement with the previous work reported by K. K. Nanda et al.31As reported by Hu and his coworkers,32–34 the size and geometry have a significant effect on the melting point of the nanoparticles with the appearing of a quasi-liquid phase. Actually, the nanoconfinement can affect the dimension of the embedded particles and at the same time it also introduces a size-dependent effect to the particles.35 As the size of the particle decreases towards atomic scale, the melting point will also shift with the particle size changing. Fig. 2a and b show the results of our investigation of the size effect on the surface curvature and the melting point, respectively. To ensure a proper length-to-diameter ratio, the Fe nanowires were built with diameters of 16, 20, 24, 28 and 32 Å, consisting of 400, 900, 1800, 3100, 4800 atoms, respectively. Results demonstrated that the melting points of the embedded Fe nanowires tended to increase, while the surface curvature had a decreasing tendency as the diameter increase. These phenomena provided more proof that the diameter had great effects on the phase transition process. The inset in Fig. 2b also shows the melting point difference ΔT between the maximum potential parameter ε = 0.8 eV and the minimum potential parameter ε = 0.1 eV as a function of the diameter. The decreasing tendency of ΔT against diameter indicated that the size effect was receding with the increasing diameter. According to the results in Fig. 1, the effect of interaction strength ε should be added in the relationship defined by eqn (2) besides the diameter D. Herein, considering that the surface curvature, similar to the melting point, is the combined results of the interaction strength ε and the diameter D. It is evident that the melting point is strongly correlated to the surface curvature which can be easily measured under the electron microscopy. We employed the surface curvature k as a single parameter to replace the parameters ε and D in the melting point variation equation, which can be described by the following expression:
| Tn = (1 − αk)Tm | (4) |
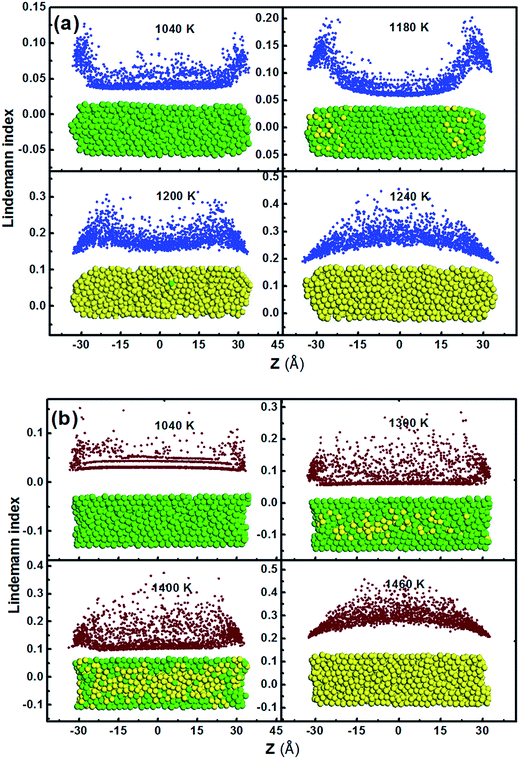
In order to further investigate the influence of surface curvature on melting mechanisms, the Lindemann index8 at each time step was calculated. Fig. 3 shows the Lindemann indices of the embedded Fe1800 at ε = 0.1 eV and 0.8 eV and the morphology of the embedded nanowires at the corresponding temperature. As shown in Fig. 3a, at ε = 0.1 eV the particle represents a convex surface and the surface atoms seem to diffuse more easily than the inner ones at T = 1040 K due to their poor coordination and weaker constraints. This leads to the formation of liquid-like capes when the temperature ramps to 1180 K and then the whole particle melts quickly at a melting point of 1200 K. This melting pattern is defined as cape-induced melting. In contrast to the melting model under weak interaction, the confinement exerts a strong constraint on the embedded particle at ε = 0.8 eV (in Fig. 3b). The surface curvature is negative. The atoms close to the confinement are less mobile than those at ε = 0.1 eV because they are almost fixed by the strong interaction between the confinement and the Fe atoms. Therefore, when the lowest point of the concave surface starts melting at 1300 K, the phase transformation occurs along the length in the inner layer where the constraint from the confinement is weaker than the outer layers. With the temperature rising, the melting of embedded particle slowly defuses from the inside out and completes at 1460 K. And this melting pattern is identified as the inner-diffusing melting. Therefore, with the increase of the interaction strength, the melting mechanism of embedded nanowires gradually evolves from the cape-induced melting to the inner-diffusing melting, which cannot be reduced into a single pattern as reported in previous work.19
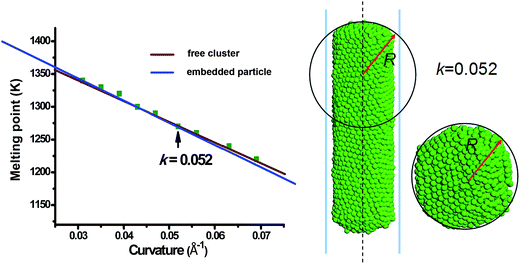
It has been confirmed that the melting point of free cluster follow the expression in eqn (1). Interestingly, eqn (1) can also be summarized into eqn (4) by replacing 1/D with k. This indicates that the melting point of the free clusters also follows the universal relation described in eqn (4). Further MD simulations have been conducted to obtain the melting points of the free clusters between N = 400 and N = 7000, and the results yield the established relationship as well (in Fig. 4). On the aspect of relation, eqn (1) and (4) are the same in nature. Therefore, it can be generalized that the surface curvature is of universal significance to the prediction of the cluster melting temperature.
Conclusion
Systematic analyses have shed light on the curvature-dependent melting point of metal nanowires in nanoconfinement. We have summarized this relationship into a linear model between the surface curvature k and the melting point Tn of the embedded metal nanowire: Tn = (1 − αk)Tm, where α is a material constant and Tm is the corresponding melting point of the metal in bulk. This equation is important to predict, measure, and even control the melting point of a metal nanoparticle in experiments and applications. The model elucidates that the melting point of metal nanowires embedded in nanoscale porous media would be lower or higher than or equal to their bulk counterparts. Based on our simulations, the melting mechanism of the embedded nanowires can be sorted into cap-induced melting and inner-diffusing melting with variation of the interaction strength. As an extension, this model is also applicable for the prediction of the melting point of the free metal cluster. Our findings would pave way to the application of the metal nanowires confined in porous media at different temperature ranges.Acknowledgements
The authors would like to acknowledge the support by the National Natural Science Foundation of China (Grant nos 51401028). We also thank Shanghai Supercomputer Center for computational support.References
- W. Liu, T.-Z. Yang, G. Chu, J.-S. Luo and Y.-J. Tang, Trans. Nonferrous Met. Soc. China, 2007, 17, 1347 CrossRef CAS.
- C. Q. Sun, Prog. Solid State Chem., 2007, 35, 1 CrossRef CAS.
- P. R. Couchman and W. A. Jesser, Nature, 1977, 269, 481 CrossRef CAS.
- R. Shi, J. Shao, X. Zhu and X. Lu, J. Phys. Chem. C, 2011, 115, 2961 CAS.
- L. Gråbaek, J. Bohr, E. Johnson, A. Johansen, L. Sarholt-Kristensen and H. H. Andersen, Phys. Rev. Lett., 1990, 64, 934 CrossRef PubMed.
- W. Y. Choi, J. W. Kang and H. J. Hwang, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 193405 CrossRef.
- W. Qi, Y. Li, S. Xiong and S.-T. Lee, Small, 2010, 6, 1996 CrossRef CAS PubMed.
- F. Ding, A. Rosén, S. Curtarolo and K. Bolton, Appl. Phys. Lett., 2006, 88, 133110 CrossRef.
- M. Zhang, M. Y. Efremov, F. Schiettekatte, E. A. Olson, A. T. Kwan, S. L. Lai, T. Wisleder, J. E. Greene and L. H. Allen, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 10548 CrossRef CAS.
- M. Dippel, A. Maier, V. Gimple, H. Wider, W. E. Evenson, R. L. Rasera and G. Schatz, Phys. Rev. Lett., 2001, 87, 095505 CrossRef CAS PubMed.
- K. F. Peters, Y.-W. Chung and J. B. Cohen, Appl. Phys. Lett., 1997, 71, 2391 CrossRef CAS.
- K. F. Peters, J. B. Cohen and Y.-W. Chung, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 13430 CrossRef CAS.
- C. L. Jackson and G. B. McKenna, J. Non-Cryst. Solids, 1991, 131–133(1), 221 CrossRef CAS.
- C. Alba-Simionesco, B. Coasne, G. Dosseh, G. Dudziak, K. E. Gubbins, R. Radhakrishnan and M. Sliwinska-Bartkowiak, J. Phys.: Condens. Matter, 2006, 18, R15 CrossRef CAS PubMed.
- W. D. Zhang, Y. Wen, S. Min Liu, W. C. Tjiu, G. Qin Xu and L. Ming Gan, Carbon, 2002, 40, 1981 CrossRef CAS.
- S. Arcidiacono, J. H. Walther, D. Poulikakos, D. Passerone and P. Koumoutsakos, Phys. Rev. Lett., 2005, 94, 105502 CrossRef CAS PubMed.
- Y. Kondo and K. Takayanagi, Science, 2000, 289, 606 CrossRef CAS PubMed.
- A. Titov, P. Zapol, P. Král, D.-J. Liu, H. Iddir, K. Baishya and L. A. Curtiss, J. Phys. Chem. C, 2009, 113, 21629 CAS.
- J. Shao, C. Yang, X. Zhu and X. Lu, J. Phys. Chem. C, 2010, 114, 2896 CAS.
- J. H. Strange, M. Rahman and E. G. Smith, Phys. Rev. Lett., 1993, 71, 3589 CrossRef CAS PubMed.
- K. Lu and Z. H. Jin, Curr. Opin. Solid State Mater. Sci., 2001, 5, 39 CrossRef CAS.
- M. Perez, Scr. Mater., 2005, 52, 709 CrossRef CAS.
- J. B. W. Webber, J. C. Dore, J. H. Strange, R. Anderson and B. Tohidi, J. Phys.: Condens. Matter, 2007, 19, 415117 CrossRef.
- K. Kaneko, A. Watanabe, T. Iiyama, R. Radhakrishan and K. E. Gubbins, J. Phys. Chem. B, 1999, 103, 7061 CrossRef CAS.
- Q. Jiang, Z. Zhang and J. C. Li, Chem. Phys. Lett., 2000, 322, 549 CrossRef CAS.
- R. Kofman, P. Cheyssac, A. Aouaj, Y. Lereah, G. Deutscher, T. Ben-David, J. M. Penisson and A. Bourret, Surf. Sci., 1994, 303, 231 CrossRef CAS.
- H. Lei, J. Phys.: Condens. Matter, 2001, 13, 3023 CrossRef CAS.
- J. Stanek, G. Marest, H. Jaffrezic and H. Binczycka, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 8414 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684 CrossRef CAS.
- H. Duan, F. Ding, A. Rosén, A. R. Harutyunyan, S. Curtarolo and K. Bolton, Chem. Phys., 2007, 333, 57 CrossRef CAS.
- K. K. Nanda, S. N. Sahu and S. N. Behera, Phys. Rev. A, 2002, 66, 013208 CrossRef.
- H. A. Alarifi, M. Atis, C. Ozdogan, A. Hu, M. Yavuz and Y. Zhou, J. Phys. Chem. C, 2013, 117, 12289 CAS.
- E. Marzbanrad, A. Hu, B. Zhao and Y. Zhou, J. Phys. Chem. C, 2013, 117, 16665 CAS.
- H. A. Alarifi, M. Atis, C. Özdoğan, A. Hu, M. Yavuz and Y. Zhou, Mater. Trans., 2013, 54, 884 CrossRef CAS.
- Y. Shibuta, Chem. Phys. Lett., 2012, 532, 84 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: See DOI: 10.1039/c5ra01203a |
| This journal is © The Royal Society of Chemistry 2016 |