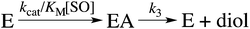Open Access Article
Open Access ArticleConformational diversity and enantioconvergence in potato epoxide hydrolase 1†
P.
Bauer
a,
Å. Janfalk
Carlsson
b,
B. A.
Amrein
a,
D.
Dobritzsch
*b,
M.
Widersten
*b and
S. C. L.
Kamerlin
*a
aScience for Life Laboratory, Department of Cell and Molecular Biology, Uppsala University, BMC Box 596, S-751 24 Uppsala, Sweden. E-mail: kamerlin@icm.uu.se
bDepartment of Chemistry-BMC, Uppsala University, BMC Box 576, S-751 23 Uppsala, Sweden. E-mail: doreen.dobritzsch@kemi.uu.se; mikael.widersten@kemi.uu.se
First published on 31st March 2016
Abstract
Potato epoxide hydrolase 1 (StEH1) is a biocatalytically important enzyme that exhibits rich enantio- and regioselectivity in the hydrolysis of chiral epoxide substrates. In particular, StEH1 has been demonstrated to enantioconvergently hydrolyze racemic mixes of styrene oxide (SO) to yield (R)-1-phenylethanediol. This work combines computational, crystallographic and biochemical analyses to understand both the origins of the enantioconvergent behavior of the wild-type enzyme, as well as shifts in activities and substrate binding preferences in an engineered StEH1 variant, R-C1B1, which contains four active site substitutions (W106L, L109Y, V141K and I155V). Our calculations are able to reproduce both the enantio- and regioselectivities of StEH1, and demonstrate a clear link between different substrate binding modes and the corresponding selectivity, with the preferred binding modes being shifted between the wild-type enzyme and the R-C1B1 variant. Additionally, we demonstrate that the observed changes in selectivity and the corresponding enantioconvergent behavior are due to a combination of steric and electrostatic effects that modulate both the accessibility of the different carbon atoms to the nucleophilic side chain of D105, as well as the interactions between the substrate and protein amino acid side chains and active site water molecules. Being able to computationally predict such subtle effects for different substrate enantiomers, as well as to understand their origin and how they are affected by mutations, is an important advance towards the computational design of improved biocatalysts for enantioselective synthesis.
Introduction
Epoxide hydrolases are a biocatalytically important class of enzymes, as they catalyse the transformation of chiral epoxides to the corresponding vicinal diols. This makes them particularly attractive as catalysts for the production of enantiopure fine chemicals and pharmaceuticals.1In vivo, these enzymes show widely distributed functions, with their precise roles depending on their organism of origin. In broad terms, their primary biological involvement is in detoxification pathways (through the breakdown of toxic epoxides), secondary metabolism, and in cellular signaling.2 Furthermore, due to their biocatalytic importance, epoxide hydrolases have been the subject of extensive biochemical, structural and computational studies,1–17 and, for example, limonene epoxide hydrolase has been recently used as a model system for the computational design of enantioselective enzymes.16Among the epoxide hydrolases, Solanum tuberosum epoxide hydrolase 1 (StEH1) has been a system of particular interest to both theory and experiment,3–6,10,12,13,17 and a generalized mechanism for the reaction catalysed by this enzyme is shown in Fig. 1, based on proposals put forward in the literature.4,10 The reaction occurs in three sequential steps: (I) nucleophilic attack by D105 on one of the two epoxide ring carbons of the bound substrate (labelled here as C-1 and C-2) to give rise to a covalent alkylenzyme intermediate; (II) hydrolysis of this intermediate through nucleophilic attack by a structurally conserved active-site water molecule, activated by a general base (H300) to form a tetrahedral intermediate, and, finally, (III) decay of the tetrahedral intermediate to the product, which is subsequently released from the enzyme. Features of this mechanism (in particular the use of an amino acid side chain as a nucleophile to yield an alkyl- or acylenzyme intermediate) are common to all α,β-hydrolases.18 The two active-site tyrosines, however, are typical for epoxide hydrolases and their role is to facilitate formation of an anionic intermediate resulting from opening of the epoxide ring, by stabilizing increasing charge localization on the epoxide ring oxygen as the C–O bond is broken during the reaction.5 In addition, we recently demonstrated that two additional residues close to the active site, E35 and H104, play important roles in this enzyme's catalytic activity, with the protonated form of H104 being essential for maintaining charge balance in the otherwise negatively charged StEH1 active site and E35 acting as a “backup” for the bona fide general base H30017 (Fig. 2).
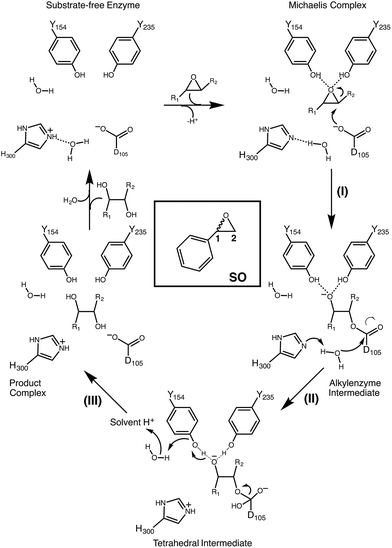 | ||
| Fig. 1 Schematic overview of a generalized mechanism for the reaction catalysed by potato epoxide hydrolase 1 (StEH1). Highlighted in particular here are (I) the alkylation step, involving nucleophilic attack of the side chain of D105 on one of the carbon atoms of the bound epoxide; (II) hydrolysis of the resulting alkylenzyme intermediate by an active site water molecule to yield a tetrahedral intermediate, and (III) breakdown of the tetrahedral intermediate, leading to release of the product diol from the active site. The structure of styrene oxide (SO) is also highlighted in the inlay box. This figure is adapted from ref. 17. | ||
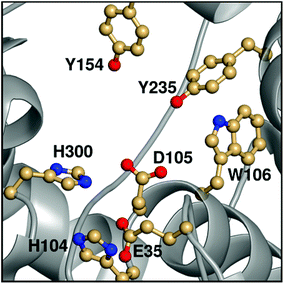 | ||
| Fig. 2 An overview of key active site residues in the unequilibrated substrate-free form of wild-type StEH1 based on a 1.95 Å-resolution crystal structure of the enzyme6 (PDB ID: 2CJP). | ||
Our previous computational work focused primarily on the large and bulky substrate trans-stilbene oxide (TSO),17 which is a symmetric substrate that almost fully fills the StEH1 active site. This removed the computational complications associated with the presence of multiple potential binding modes for the substrate, and allowed us to identify the importance of E35 and H104 as well as to pinpoint the key features contributing towards the selectivity of these enzymes. However, the most interesting aspect of StEH1 is its activity towards smaller substrates such as styrene oxide (SO, Fig. 1), where the enzyme displays enantioconvergent behaviour (Fig. 3), producing optically pure products as a result of changes in both enantio- and regioselectivity.3,12,13 In the present work, we have combined computational and crystallographic studies to pinpoint the origin of this enantioconvergent behaviour in wild-type StEH1 in terms of different substrate binding modes and reaction microsteps, as well as the effect of mutations in an engineered enzyme variant.13 Our empirical valence bond (EVB) calculations reproduce the enantio- and regioselectivity of this enzyme, and also demonstrate the link between substrate binding mode and selectivity, which is altered in the engineered variant. Computational prediction and rationalization of these differences provides an important prerequisite for the future design of engineered StEH1 variants with tailored catalytic properties.
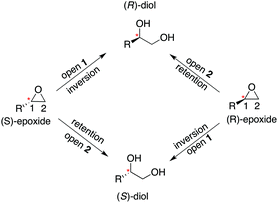 | ||
| Fig. 3 A schematic overview of the enantioconvergent hydrolysis of different enantiomers of an epoxide substrate to give the same product diol. In the present case, StEH1-catalyzed styrene oxide hydrolysis proceeds primarily through attack at C-1 for the (S)-enantiomer, and C-2 for the (R)-enantiomer), in contrast to the non-enzymatic hydroxide-catalyzed hydrolysis, where hydroxide addition at each of the two carbon atoms occurs with almost equal rates.19 | ||
Methodology
Theoretical background and simulation setup
Despite elegant recent studies,7,8,14–16,20,21 modelling enantioselective enzymes poses a significant challenge to theory due to the need for computational methods that are sufficiently accurate to capture the small differences in energy that often distinguish between different enantiomers. In addition, the presence of multiple potential binding modes for smaller substrates creates a demand for extensive conformational sampling to obtain convergent free energies, which requires an approach that captures a reasonable balance between accuracy and computational speed. Following from our previous work, our methodology of choice has been the Empirical Valence Bond (EVB) approach for calculating the relevant energies of the reaction. A detailed review of and theoretical background for this approach can be found in e.g.ref. 22–24. In brief, the EVB is an empirical VB/MM approach that uses a valence bond description of the n different reacting states during a reaction to model chemical reactivity. The total energy of the system is then calculated by first constructing a 2 × 2 Hamiltonian matrix of the different diabatic states, and then diagonalising this matrix to obtain the actual adiabatic ground state energy. The off-diagonal elements of this matrix describe the coupling between the different diabatic states. These off-diagonal parameters, as well as the gas-phase shift (α, which describes the relative energy of the two diabatic parabolas) are obtained by fitting to the energetics of a reference state, which can be either the background uncatalyzed reaction in aqueous solution or the wild-type enzyme against a set of enzyme variants, to either experimental data or high-level quantum chemical calculations. Due to the phase-independence of the coupling term,25,26 once these parameters have been obtained, the same unchanged parameters can then be used to describe the reaction in different electrostatic environments (e.g. in the protein). Finally, the chemical reaction is described by using free energy perturbation to map between the different valence bond states, using a defined number of umbrella sampling windows to allow for overlapping energy profiles.22The simulation protocol used in the present study is very similar to our previous work on the StEH1-catalyzed hydrolysis of trans-stilbene oxide,17 and the bond, angle and torsion parameters as well as a large number of the non-bonded potentials used to describe that reaction have been reused for the present study. The only terms that needed re-parameterization compared to our previous study were related to the exchange of the phenyl ring of the trans-stilbene to styrene oxide, and a full overview of the EVB parameters used in the present study are presented in the ESI.† All new parameters were obtained using MacroModel 9.1 (2001, Schrödinger LLC),27 with partial charges being calculated using the same HF/6-31G* RESP procedure28 used in our previous work,17 and the remainder of the system was described using the OPLS-AA force field29 as implemented into the Q simulation package v. 5.10,30 which was used for all molecular dynamics and EVB simulations.
Our simulations were performed on the hydrolysis of styrene oxide by the wild-type form of StEH1, as well as an engineered variant, R-C1B1, which shows altered regioselectivity in epoxide hydrolysis.13 Our starting structure for the simulations of wild-type StEH1 were taken from the Protein Data Bank,31 PDB ID: 2CJP.6 We provide here also a new crystal structure of the R-C1B1 variant (PDB ID: 4UFN), which was crystallized as described below, and which formed a starting point for all calculations on this variant. In the case of our previous work on TSO,17 this substrate is sufficiently large to almost fill the active site, and therefore substrate positioning did not pose a significant challenge to the simulations. In the present case, as styrene oxide (SO) is a much smaller substrate, it can occupy one of two productive binding positions: Mode 1, in which the phenyl ring of SO forms stacking interactions with the imidazole ring of H300, and Mode 2 in which the phenyl ring rather interacts with the indole of W106 (Fig. 4), forming either a π-stacking or an edge-on interaction with this side chain (depending on substrate enantiomer) during our equilibration runs. Therefore, to distinguish between these two possibilities, each enantiomer of styrene oxide was manually placed into the active site, in each of two different binding conformations. These were selected in such a way as to optimize interactions between the substrate and the oxyanion hole formed by the two Tyr hydroxyl groups (Fig. 2), in order to identify the most structurally stable Michaelis complex as a starting point for our simulations (based on maximal retention of hydrogen-bonding interactions with the active site tyrosines). Finally, as in our previous study,17 crystallographic water molecules within 16 Å from the reacting centre (D105) were retained for our simulations, and we completed our solvation sphere by solvating the system in a 20 Å sphere of TIP3P water molecules32 subject to surface-constrained all-atom solvent (SCAAS) boundary conditions30,33 and centred on the D105 Cδ carbon. All water molecules overlapping with heavy atoms from the protein or ligand were removed to avoid clashes in our simulations. Protein atoms outside this explicit sphere were kept restrained to their crystallographic coordinates during all calculation steps, while atoms within 3 Å of this boundary were being restrained using a harmonic restraint of 10 kcal mol−1 Å−2 following the standard procedure used in our previous studies (see e.g.ref. 17 and 34). Following this procedure, the final systems contained approximately 2000 free solute atoms and 160 free solvent molecules (varying slightly depending on the precise system). Additionally, on the order of 1200 atoms were constrained by the boundary conditions, out of a total of about 5600 atoms.
The system was then equilibrated by performing molecular dynamics simulations on the Michaelis complex at 1 K using a strong restraint of 200 kcal mol−1 Å−2 on all protein heavy atoms, in order to remove initial clashes in the system and also to optimize hydrogen positions. This was followed by gradual heating of the system to 300 K over the course of 90 ps of simulation time, in order to equilibrate the water molecules around the protein (while still applying the strong restraint to all protein heavy atoms). After this equilibration, the system was cooled down again to 5 K before dropping the restraints on the protein heavy atoms and heating the whole system to 300 K over the course of a final 150 ps of preparatory simulation time. After the initial heating and cooling, the only restraint remaining in our systems was a weak (0.5 kcal mol−1 Å−2) position restraint on the substrate and hydrolytic water molecule, in order to keep them close to their starting positions. Finally, once the system had been reheated to 300 K with the weaker restraint, we ran a final 40 ns of dynamics at 300 K, using the same weak restraint, in order to allow the system to fully equilibrate (see Fig. S1 and S2† for associated RMSD plots for each system). The endpoints of this equilibration run were used to generate starting points for ten independent EVB calculations, which were each initialized by performing a further 200 ps of simulation on the final 40 ns equilibrated structure using different starting velocities, generated from a Maxwell distribution by assigning different random seeds to each simulation.
Subsequently, we performed EVB simulations of the hydrolysis of both (R)-SO and (S)-SO, considering both potential binding modes described above, as well as ring opening via attack at either C-1 or C-2. As with our previous work, the reaction was modelled as a two-step process,17 using the valence bond descriptions shown in Fig. 5. As the starting point for our EVB simulations was the StEH1 Michaelis complex, only one equilibration step was needed, and the final checkpoint files from the EVB simulations on the first reaction step (corresponding to the alkylenzyme intermediate) were used to provide initial coordinates for the subsequent hydrolysis step. For each system, our protein EVB calculations were calibrated against the corresponding background reaction in aqueous solution, using the same fragment-capping scheme as employed for our previous calculations on the StEH1-catalyzed hydrolysis of TSO.17 Specifically, our model reactions for the first and second steps of the enzyme-catalyzed reaction were propionate attack on styrene oxide, and imidazole-catalysed hydrolysis of the product state of the first reaction step respectively. Due to the lack of experimental data for the catalytic breakdown of SO by nucleophilic attack of propionate, for comparative purposes, we emulated the procedure employed by Lau et al.35 to analyse the same reaction for trans-methyl styrene oxide, employing the B3LYP functional36–38 and COSMO solvent model,39 with energies of stationary points calculated using the 6-311+G** basis set. This also allows us to directly compare our results to previous quantum chemical studies of enzyme-catalysed epoxide ring opening.7,8,14,17 All quantum chemical calculations were performed using Gaussian09 Rev. C01,40 and were performed on the different conformations of styrene oxide, using the lowest energy conformer as our reference state in aqueous solution (as this will be closest to the global minimum for the reactant state). The subsequent hydrolysis step was parameterized by extrapolation from experimental data following the procedure used in our previous work (see the ESI† of this work and of ref. 17 and references cited therein). The simulation protocol used for our background reaction in aqueous solution was identical to that used for the corresponding enzymatic reactions, with the exception of the fact that the positional restraint on the reacting atoms was increased from 0.5 to 1 kcal mol−1 Å−2 in order to maintain system stability (in aqueous solution, this restraint was applied to all solute atoms). The energetics used for the fitting of the reference reaction for each reaction step are shown in Table S1.†
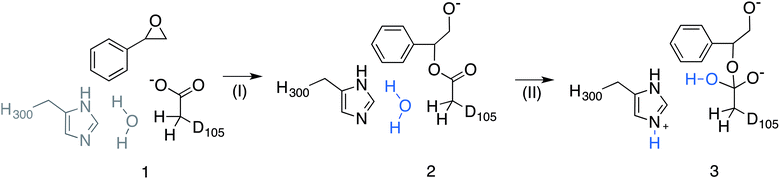 | ||
| Fig. 5 Overview of the valence bond states used to describe the StEH1 catalysed hydrolysis of styrene oxide (SO). Shown here are (1) the Michaelis complex, (2) the alkylenzyme intermediate and (3) the tetrahedral intermediate corresponding to (I) the alkylation and (II) hydrolysis steps of this reaction respectively. Note that the imidazole side chain and hydrolytic water molecule were not included in the reference EVB calculation of Step I. Additionally, the hydrolytic water molecule in step II has been highlighted in blue to follow the movement of protons. This figure has been adapted from ref. 17. | ||
Finally, each individual EVB simulation was 10.2 ns in length, with the EVB free energy calculations distributed over 51 equally spaced mapping windows using constant linear interpolation between relevant reacting states (Fig. 5). Ten replicates were performed for each system. All molecular dynamics and EVB simulations were performed using a 1 fs time step, to a total simulation time of 3.616 μs for all protein simulations, and a further 1.328 μs of simulations of the background reaction in aqueous solution.
Crystal structure of the R-C1B1 variant
The enzyme variant R-C1B1 was originally isolated from a laboratory evolution for StEH1 variants displaying enrichment of the (R)-enantiomer of the diol product from the enzyme-catalysed hydrolysis of racemic (2,3-epoxypropyl)benzene (EPB).41 This variant has accumulated four active-site mutations, specifically W106L, L109Y, V141K and I155V. In addition to the altered regioselectivity in the hydrolysis of EPB, this variant also exhibits a change in the regioselectivity during hydrolysis of (R)-SO13 and was therefore included in this study.Wild-type StEH1 and the R-C1B1 variant were expressed in Escherichia coli XL1-Blue (Stratagene Corp.), and purified by Ni(II)-IMAC and size exclusion chromatography as described previously.4 Protein concentrations were determined through measuring UV absorption at 280 nm, using an extinction coefficient (ε) based on the value for wild-type StEH1,4 corrected by:
| εvariant = εWT + (Trp × 5500)+(Tyr × 1490)+(Cys × 125) | (1) |
The R-C1B1 variant of StEH1 was crystallized by hanging drop vapour diffusion against a 1 ml reservoir at 20 °C. The 3 μl drop was prepared by mixing 2 μl protein solution (5 mg ml−1 in 30 mM Tris-HCl, pH 7.4) with 1 μl reservoir solution containing 18% (w/v) PEG 5000-monomethyl ether, 0.1 M Tris-HCL, pH 8.0, and 5% (v/v) dioxane.
Crystals of R-C1B1 were flash-frozen in liquid nitrogen without additional cryo-protection. Crystallographic data were collected at 100 K at beamline I04 of the Diamond Light Source (Didcot, UK). Data were indexed and integrated on site with XDS42–46 and scaled with SCALA from the CCP4 suite of programs.46,47 The crystals belong to space group P212121 and contain two identical polypeptide chains per asymmetric unit. Data collection statistics are given in Table 1.
| Data collection | |
|---|---|
| a Values given in parentheses are for the highest resolution shell. | |
| Wavelength (Å) | 0.9763 |
| Space group | P212121 |
| Cell dimensions a, b, c (Å) | 56.0, 99.1, 123.5 |
| Resolution (Å) | 99.14–2.00 (2.05–2.00) |
| R merge | 0.125 (0.571) |
| Mean I/σI | 9.0 (2.6) |
| Completeness (%) | 99.9 (100) |
| Multiplicity | 5.7 (5.8) |
| Wilson B-factor (Å2) | 20.0 |
| Refinement | |
| Resolution (Å) | 77.3–2.00 |
| No. reflections | 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 563 563 |
| No. refl. test set (in %) | 2292 (4.9) |
| R work/Rfree (%) | 17.1/21.1 |
| No. atoms/average B-factors (Å2) | |
| Protein | 5158/25.64 |
| Water molecules | 642/34.3 |
| Dioxane | 12/37.8 |
| r.m.s. deviations | |
| Bond lengths (Å) | 0.009 |
| Bond angles (°) | 1.30 |
The structure of the R-C1B1 variant was solved by molecular replacement with PHASER28 and wild-type StEH1 as a search model (PDB ID: 2CJP6). Manual model building was performed with COOT48 and alternated with restrained refinement in REFMAC5.49 A set of ∼5% randomly selected reflections were used for monitoring Rfree. Water molecules were added in COOT.
The final model contains residues 2–321 for both the A and B chain, respectively, and 642 water molecules. A dioxane molecule from the crystallization solution is bound to the active site of both R-C1B1 molecules present in the asymmetric unit. The model has good stereochemistry, with >98% of the residues found in the most favourable and 0.3% in the disallowed region of the Ramachandran plot, respectively. The refinement statistics are given in Table 1. The crystallographic data and structure of the StEH1 R-C1B1 variant have been deposited in the Protein Data Bank with the accession code 4UFN. This crystal structure provided the starting point for all subsequent simulations of the activity of the R-C1B1 variant presented in this work, following exactly the same procedures as used for wild-type StEH1.
Enzyme kinetics
The steady state parameters for StEH1 catalysed SO hydrolysis have been reported earlier.50 Pre-steady state kinetics were followed under pseudo first order, multiple-turnover conditions. Build-up of steady-state levels of the alkylenzyme intermediates formed in the catalysed hydrolysis of either SO enantiomer were followed by monitoring the decrease in intrinsic Trp fluorescence of the enzyme as described previously.50 The apparent rates (Fig. S3A†), kobs, were determined by fitting a single exponential function with a floating endpoint:F = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kobst) + C exp(−kobst) + C | (2) |
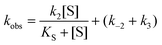 | (3) |
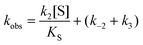 | (4) |
In cases when kobs displayed hyperbolic substrate concentration dependence, as in the hydrolysis of (S)-SO, k2 and KS were determined after fitting eqn (3) to the observed rates. k−2 and k3 were calculated from the determined value of their sum (at [S] = 0) applying the derived expression for kcat (numerator in eqn (5)).
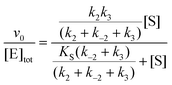 | (5) |
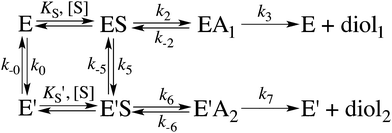
When substrate saturation was not achieved, as with (R)-SO, k2/KS was determined by fitting eqn (4) to the kobs data. Numberings of rate constants are according to Scheme 1.
Since the amplitude of fluorescence quenching is expected to be proportional to the concentration of accumulated alkylenzyme, at the steady state (EASS), the relationship in eqn (6) should be valid (f being a proportionality factor including e.g. the quantum yield of emission).
| ΔFmax ∝ [EAss]f | (6) |
The maximum amplitude (ΔFmax) of the recorded fluorescence quenching was determined from fitting eqn (7) to the recorded amplitudes (Fig. S3B†) (A in eqn (2)) under steady state conditions:
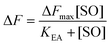 | (7) |
Here, KEA is the (apparent) dissociation constant of the alkylenzyme, and is defined as k3/(kcat/KM), by applying Scheme 2.51 Hence, the stabilization of EA can be estimated from the values of KEA. Furthermore, if applying the steady-state rate law (eqn (5)) the relationship between substrate binding, rate constants and KEA can be analysed further, i.e. KEA can be expressed by eqn (8):
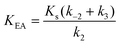 | (8) |
Results and discussion
Wild-type StEH1
The kinetics for the StEH1 catalysed ring opening of SO has been studied in detail in the present and our previous work13,50, and the regioselectivity of the wild-type enzyme has been studied by Monterde et al.3 The corresponding non-enzymatic hydrolysis of styrene oxide has also been studied in detail in e.g.ref. 19 and 52. This work in particular demonstrated that in the case of the hydroxide-catalyzed hydrolysis of styrene oxide, which is the best analogy for the enzymatic reaction shown in Fig. 1, 18OH attacks the two carbon atoms of styrene oxide at almost equal rates.19A summary of the relevant experimental data for the enzymatic reaction is presented in Table 2 and in the ESI.† In the case of (R)-SO, it was not possible to obtain saturating substrate conditions during the pre-steady state kinetic measurements (Fig. S3A†), and therefore the individual rate parameters could not be obtained. As a result of this, only a lower limit is available for the rate of the alkylation step, and we have to rely on kcat values for reliable comparison of our computational data in this case. Note that kcat does not necessarily correspond to a chemical step, but does provide an upper limit for the overall activation barrier for the process. Despite this lack of substrate saturation, a careful kinetic analysis of SO-catalysed StEH1 hydrolysis strongly suggested that the enantiopreference for (S)-SO is likely to be due to differences in the rate of alkylenzyme formation, with an enantioselectivity value [E = (kScat/KSM)/(kRcat/KRM)] of 70.50 In addition, the enzyme shows very clear enantiomer-dependent regioselectivity for nucleophilic attack by the D105 side chain, with the ring opening of the (S)-enantiomer proceeding with 99% attack at the benzylic carbon (C-1), and the (R)-enantiomer with 89% attack at the unsubstituted carbon (C-2). This results in the enantioconvergent behaviour illustrated in Fig. 3. We were, however, able to alter this regiopreference in a variant of StEH1, R-C1B1,13 which is an engineered form of the enzyme containing the W106L, L109Y, V141K and I155V active site replacements. R-C1B1 maintained a strong preference for ring opening at C-1 in the case of the (S)-enantiomer, but had lost the regioselectivity with the (R)-enantiomer.
| StEH1 (wt) | (R)-SO | (S)-SO |
|---|---|---|
| a K EA is the apparent dissociation constant of the alkylenzyme intermediate, as derived in the Methodology section for at detailed description of its derivation. b Data from ref. 50. c a.u., Arbitrary units. d k −2 and k3 are calculated from the determined values of k2, (k−2 + k3) and kcat. | ||
| K EA (M) | (5.8 ± 2) × 10−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
(4.1 ± 0.9) × 10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| K M (M) | (3.4 ± 1) × 10−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
(1.2 ± 0.2) × 10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
| K S (M) | — | (1.4 ± 0.6) × 10−3 |
| ΔFmax (a.u.)c | 0.63 ± 0.2 | 0.84 ± 0.08 |
| k 2 (s−1) | — | 210 ± 40 |
| k −2 + k3 (s−1) | 36 ± 5 | 48 ± 8 |
| k 3 (s−1) | — | 10 ± 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
| k −2 (s−1) | — | 38 ± 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
| k cat (s−1) | 3.3 ± 0.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
8.4 ± 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
| k 2/KS (s−1 × M−1) | (1.5 ± 0.5) × 104 | (1.8 ± 0.5) × 105 |
| k cat/KM (s−1 × M−1) | (9.9 ± 0.3) × 102![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
(6.8 ± 0.6) × 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
The origin of the difference in regioselectivity for the two different enantiomers is unclear from the experimental data, although we have previously proposed that the data strongly suggest different substrate-binding modes in the StEH1 active site.50 To test this hypothesis, we considered nucleophilic attack of D105 at both carbons and enantiomers of SO, with the substrate bound in either Mode 1 or Mode 2 (see the Methodology section and Fig. 4 for a definition of the substrate positions). An overview of the equilibrated Michaelis complexes for each enantiomer, in each substrate position, is shown in Fig. 6. It can be seen that already at the Michaelis complex, the most stable binding mode in the StEH1 active site is different for each enantiomer. That is, the (R)-enantiomer forms a more stable Michaelis complex when the phenyl ring of the substrate interacts with the indole of W106 (Mode 2) through an edge-on interaction, whereas the (S)-enantiomer forms a more stable complex when the phenyl ring of the substrate stacks with the imidazole ring of H300 (Mode 1). In contrast, while the (S)-enantiomer can be bound in Mode 2, the (R)-enantiomer is highly unstable when bound in Mode 1, and falls out of the binding pocket, as indicated by the increasing values for the substrate RMSD and the unstable coordination of the epoxide oxygen by the active site tyrosine residues seen in Fig. S4–S7 and Table S2.†
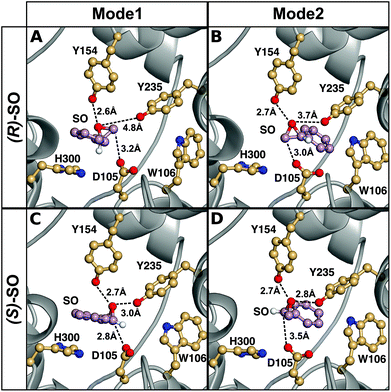 | ||
| Fig. 6 A comparison of representative structures of the Michaelis complexes obtained after molecular dynamics equilibration of wild-type StEH1 in complex with (A, B) (R)- and (C, D) (S)-SO, with the substrate placed in the active site in (A, C) Mode 1 and (B, D) Mode 2 respectively. The figure highlights the distance between the epoxide oxygen and the hydroxyl oxygens of Y154 and Y235, as well as the distance between the side chain of D105 for the preferred epoxide carbon for each enantiomer (C-1 for (S)-SO and C-2 for (R)-SO). The C-1 hydrogen has also been included in this figure to illustrate the stereochemistry. For discussion of the associated activation and reaction free energies of the different binding modes see the main text, and for structures of the corresponding transition states and intermediates for the first reaction step (formation of the alkyl-enzyme intermediate), see Fig. S8–S11.† | ||
This discrimination between the different binding modes ties in with the fact that efficient catalysis of a nucleophilic addition to either carbon of styrene oxide requires a 3-point substrate attachment to the enzyme that provides strong interactions of the benzylic carbon with the enzyme nucleophile, the styrene oxygen with the enzyme electrophile, and the phenyl ring with a hydrophobic protein patch. It can be seen that (R)-SO, which shows a low reactivity for nucleophile addition to the benzylic carbon (C-1), appears to be most conformationally stable in a binding conformation which places the primary styrene oxide carbon (C-2) close to the nucleophile carboxylate, and the ring oxygen close to the enzyme electrophile. Therefore, clearly, substrate positioning can in fact play a major role in determining the differences in regioselectivity for the two enantiomers. In addition, we would also like to note here that while the substrate could be kept in place in each binding mode by using stronger positional restraints, it was crucial to minimize any restraints in our simulations, in order to be able to directly compare the two conformations to each other without artificially biasing the system towards a given conformer. The differences in stability of the Michaelis complexes are also reflected in the differences in the energies of the alkylation step for each enantiomer (Table 3, for representative structures of the first transition state and the alkylenzyme intermediate, see Fig. S8 and S9†). That is, in the case of the (R)-enantiomer, nucleophilic attack at C-1/Mode 1 is 4.8 kcal mol−1 higher in energy than nucleophilic attack at C-1/Mode 2, with a corresponding (and smaller) 1.6 kcal mol−1 difference in energy for C-2 attack on the two different substrate binding modes. This conformational preference is reversed in the case of the (S)-enantiomer, where nucleophilic attack at carbon C-1 is 3.3 kcal mol−1 lower in energy for Mode 1 than Mode 2, with an (again smaller) difference of 1.4 kcal mol−1 between the two conformers in the case of ring opening through nucleophilic attack at carbon C-2. Additionally, for both binding modes, there is a strong regiopreference for ring opening through attack at C-1 for the (S)-enantiomer, and a smaller but still significant preference for ring opening through attack at C-2 for the (R)-enantiomer. This shows that already at the first alkylation step, we are able to obtain not just discrimination between the two binding modes for each enantiomer, but also the correct regioselectivity for nucleophilic attack at each enantiomer.
| System | (R)-SO, Mode 1 | (R)-SO, Mode 2 | (S)-SO, Mode 1 | (S)-SO, Mode 2 | |||||
|---|---|---|---|---|---|---|---|---|---|
| C-1 | C-2 | C-1 | C-2 | C-1 | C-2 | C-1 | C-2 | ||
| a For details of the alkylation and hydrolysis steps, see Fig. 1 and 5. All energies are given in kcal mol−1, and are averages and standard deviations over 10 independent trajectories. The energies of the alkylation and hydrolysis steps were calculated as two separate steps and therefore the energetics shown here for the hydrolysis step are independent of those shown for the alkylation step and do not take into account the energetics of the previous intermediate. For the corresponding energetics of the uncatalyzed reaction in aqueous solution see Table S1, and for a full reaction profile for the preferred mode of each enantiomer see Fig. 7. | |||||||||
| Wild-type StEH1 | |||||||||
| Alkylation | ΔG‡ | 24.3 ± 1.3 | 19.1 ± 0.7 | 19.5 ± 0.4 | 17.5 ± 0.5 | 11.7 ± 0.2 | 15.8 ± 0.4 | 15.0 ± 0.6 | 17.2 ± 1.2 |
| ΔG0 | 9.0 ± 1.3 | −7.1 ± 0.7 | 7.1 ± 0.4 | −8.2 ± 0.5 | −12.3 ± 0.4 | −10.4 ± 0.5 | −4.8 ± 1.7 | −1.4 ± 3.1 | |
| Hydrolysis | ΔG‡ | 14.9 ± 1.7 | 12.8 ± 1.3 | 12.6 ± 0.6 | 11.9 ± 1.7 | 19.3 ± 0.7 | 13.6 ± 1.2 | 15.1 ± 0.9 | 12.2 ± 1.7 |
| ΔG0 | 8.7 ± 1.9 | 6.0 ± 1.3 | 4.9 ± 0.9 | 4.5 ± 1.5 | 13.3 ± 0.8 | 8.0 ± 1.5 | 8.1 ± 1.2 | 6.5 ± 2.0 | |
| R-C1B1 variant | |||||||||
| Alkylation | ΔG‡ | 20.3 ± 0.5 | 16.3 ± 0.4 | 27.3 ± 0.7 | 23.0 ± 1.1 | 15.6 ± 1.0 | 19.8 ± 0.5 | 17.6 ± 1.5 | 19.7 ± 0.9 |
| ΔG0 | 8.1 ± 1.1 | −8.0 ± 1.5 | 18.4 ± 1.0 | 0.7 ± 1.1 | −9.2 ± 0.9 | −6.3 ± 0.6 | −3.8 ± 1.5 | −7.1 ± 1.2 | |
| Hydrolysis | ΔG‡ | 9.0 ± 1.1 | 9.0 ± 1.1 | 8.1 ± 0.5 | 10.8 ± 1.0 | 15.0 ± 0.7 | 9.8 ± 1.2 | 12.8 ± 1.4 | 10.9 ± 1.5 |
| ΔG0 | −0.1 ± 0.5 | −0.7 ± 1.7 | −1.9 ± 1.0 | 2.3 ± 1.5 | 8.1 ± 1.2 | 3.5 ± 1.3 | 4.8 ± 1.7 | 5.2 ± 1.7 | |
The only limitation of the calculations for this reaction step is the large exothermicity of the alkylation step, even considering the release in ring strain associated with breaking the carbon oxygen bond in the epoxide ring. That is, a comparison of k2 and k−2 in Table 2 suggests an exothermicity of ∼−1 kcal mol−1 for this step, and our calculated values are clearly much larger (this problem has also been observed in cluster calculations of the reactivity of other epoxide substrates for this enzyme7,8). This is most likely due to challenges associated with correctly calibrating the free energy of the background reaction in solution based on quantum chemical calculations, as a result of the problems posed when modeling nucleophilic attack by anionic nucleophiles using density functional theory and/or implicit solvent models (see discussion in e.g.ref. 53 and references cited therein, as well as previous quantum chemical studies, which also obtained artificially large exothermicities for this reaction7,8). However, as the EVB simulations are calibrated relative to a common reference state, any potential error here remains constant in all our simulations allowing us to nevertheless compare the relative energies of different enantiomers and binding modes to each other in a meaningful way.
An overview of the energetics of both reaction steps as well as the full calculated free energy profile for both alkylation and hydrolysis steps for the preferred conformation of each enantiomer is shown in Fig. 7 and the corresponding energetics are shown in Tables 3 and4. In our previous study, we suggested that in the case of the much larger substrate TSO, the regioselectivity of the reaction is determined in the second reaction step (hydrolysis of the alkylenzyme intermediate).17 In the present case, involving a smaller epoxide substrate, it appears that not only the preferred binding mode but also the rate-limiting step of the reaction is enantiomer dependent. That is, in the case of the (R)-enantiomer, which overall reacts more slowly than the (S)-enantiomer (Table 2 and ref. 13 and 50), the rate-limiting step for the preferred active site conformation (Mode 2) is already the alkylation step, with the subsequent hydrolysis step being either very similar in energy (Mode 2, attack at C-1) or up to 7 kcal mol−1 lower in energy depending on which carbon is being attacked by the nucleophile.
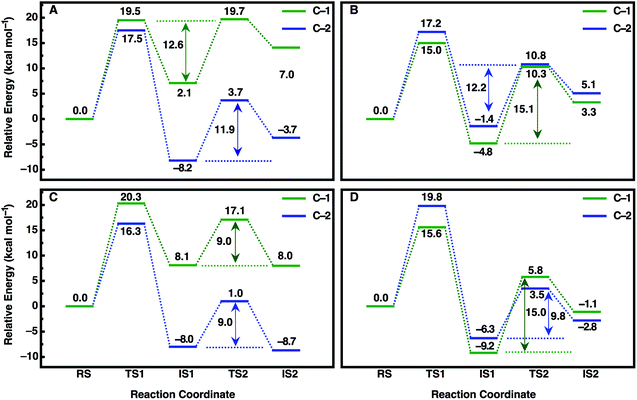 | ||
| Fig. 7 Calculated free energy profiles (kcal mol−1) for the hydrolysis of (A, C) (R)- and (B, D) (S)-SO by (A, B) wild-type StEH1 and (C, D) the R-C1B1 variant in the binding mode with the lowest activation free energies for each enantiomer respectively (for the corresponding activation free energies see Table 3). RS, TS1, IS1, TS2 and IS2 indicate the Michaelis complex (RS), the transition state for the alkylation step (TS1), the resulting alkylenzyme intermediate (IS1), the transition state for the hydrolysis step (TS2) and the tetrahedral intermediate (IS2). For details of the overall reaction mechanism see Fig. 1. All values above or below each reacting state show the calculated free energy relative to the Michaelis complex, and the values next to each arrow show the calculated activation free energy of the hydrolysis step relative to the energy of the alkylenzyme intermediate. | ||
| System | (R)-SO C-1 | (R)-SO C-2 | Experiment (R-SO) | (S)-SO C-1 | (S)-SO C-2 | Experiment (S-SO) | |
|---|---|---|---|---|---|---|---|
| a Shown here are the energetics for both the alkylation and hydrolysis steps. The preferred binding mode is Mode 2 (Fig. 4) for both enantiomers for the wild-type enzyme and Mode 1 for both enantiomers of the R-C1B1 variant. All calculated energies are given in kcal mol−1, and are averages and standard deviations over 10 independent trajectories. Experimental activation free energies are derived from this work and from data in ref. 13 and 50, and the experimental data are summarized in Table 2. The experimental data also suggests that the hydrolysis of (S)-SO proceeds exclusively through attack at C-1 for both the wild-type enzyme and the R-C1B1 variant. In contrast, the hydrolysis of (R)-SO proceeds exclusively through attack at C-2 for the wild-type enzyme, whereas ring opening can occur following attack at either carbon atom in the R-C1B1 variant (see ref. 13). The energies of the alkylation and hydrolysis steps were calculated as two separate steps and therefore the energetics shown here for the hydrolysis step are independent of those shown for the alkylation step and do not take into account the energetics of the previous intermediate. For the corresponding energetics of the uncatalyzed reaction in aqueous solution see Table S1, and for a full reaction profile for the preferred mode of each enantiomer see Fig. 7. | |||||||
| WT | Alkylation | 19.5 ± 0.4 | 17.5 ± 0.5 | 17.0 (kcat) | 15.0 ± 0.6 | 17.2 ± 1.2 | 14.5 (k2) |
| Hydrolysis | 12.6 ± 0.6 | 11.9 ± 1.7 | 15.1 ± 0.9 | 12.2 ± 1.7 | 16.3 (k3) | ||
| 16.5 (kcat) | |||||||
| R-C1B1 | Alkylation | 20.3 ± 0.5 | 16.3 ± 0.4 | 17.0 (kcat) | 15.6 ± 1.0 | 19.7 ± 0.9 | 16.6 (kcat) |
| Hydrolysis | 9.0 ± 1.1 | 9.0 ± 1.1 | 15.0 ± 0.7 | 10.9 ± 1.5 | |||
In contrast, in the case of the (S)-enantiomer, the alkylation step is relatively fast for both binding modes of the substrate (as deduced from the calculated activation barriers shown in Table 3); however, in the case of the apparently energetically preferred binding mode, Mode 1, we obtain both extreme stabilization of the alkylenzyme intermediate in the first reaction step, and a much higher calculated activation free energy (ΔG‡ = 19.4 kcal mol−1) for the subsequent hydrolysis step. Thus, despite this binding mode of styrene oxide being energetically favourable in the first reaction step, the high activation barrier to the subsequent hydrolysis step blocks further reaction following nucleophile attack at C-1 in this binding mode. We note here also that while attack at C-2 has a calculated activation barrier of only 15.8 kcal mol−1 for Mode 1, the 1000-fold difference in reactivity between the two carbon atoms will preclude reactivity at C-2 once the substrate is bound to the enzyme in this mode. In contrast, even though the alkylation step is higher in energy for attack at C-1 for Mode 2, the hydrolysis step is far more energetically favourable with a lower-energy rate-limiting step than that for hydrolysis of the alkylenzyme intermediate through the Mode 1 conformation, and, as with (R)-SO (Mode 2, Fig. 7), the alkylation and hydrolysis steps have very similar energetics following nucleophilic attack at C-1. Thus, even for trajectories that react following binding of SO in Mode 1, the system will be blocked at the alkylenzyme intermediate, fall back to the Michaelis complex due to the comparably low stabilization of the alkylenzyme intermediate seen in the experiments (see Table 2), and preferentially react through Mode 2 (note also that based on the experimental values shown in Table 2, it can be seen that binding effects are minimal for this system and that the selectivity is determined through the chemical rather than the binding step).
Overall, a comparison of our calculated and experimental values (Fig. 7 and Table 4) shows that while we slightly underestimate the energetics of the reaction of (S)-SO and slightly overestimate the energetics of the reaction of (R)-SO, our calculated values are still qualitatively correct, and within 1 kcal mol−1 of the experimental value in both cases. Therefore, we are able to computationally reproduce both the enantio- and regioselectivity and thus the enantioconvergence of the StEH1 catalysed hydrolysis of styrene oxide. From Fig. 6, as well as Fig. S8 and S9,† it is very easy to see the origin of the regiopreference of the enzyme towards the different carbon atoms of each enantiomer, as the enantiomers are positioned differently in the StEH1 active site. This is not just in terms of differences between Mode 1 and Mode 2, but also in terms of differences between the two enantiomers in the same binding mode. This will, in turn, affect how accessible each carbon atom is to the side chain of D105, as reflected in the corresponding energetics of attack at each carbon. Additionally, from Fig. 7, it can be seen that for each enantiomer, the alkylenzyme intermediate formed following nucleophilic attack at the “preferred” carbon atom is lower in energy than that following nucleophilic attack at the “non-preferred” carbon atom. Therefore, part of the regioselectivity comes from how well StEH1 can stabilize the alkylenzyme intermediate for each enantiomer, which will in turn affect the corresponding activation barrier for each reaction through a Hammond effect.
In order to also pinpoint the corresponding origin of the enantioselectivity of StEH1, we compared the electrostatic contribution of not only the different amino acid side chains of the protein, but also the electrostatic contribution coming from each of the explicit water molecules in our simulation system, to the overall calculated activation free energy for the formation of the alkylenzyme intermediate (i.e. the alkylation step) for each enantiomer. These values, which are shown in Fig. 8, were extracted from the corresponding EVB trajectories using the linear response approximation (LRA) as in our previous work, and are each averages over 10 trajectories. Here, we have compared the lowest energy pathways for each enantiomer, which correspond to C-2 attack for (R)-SO and C-1 attack for (S)-SO. Interestingly, Fig. 8 shows that there are not only differences in the interactions of individual amino acids with each enantiomer, but also significant differences in electrostatic contributions from the water molecules to the calculated activation free energies. Thus, the origin of the observed enantio- and regioselectivity is a combination of electrostatic and steric effects, in that subtle changes in preferred binding mode for each enantiomer not only affect the accessibility of each carbon atom of the epoxide ring to the nucleophile, but also the water penetration in the active site and protein–substrate interactions during the subsequent chemical reactions.
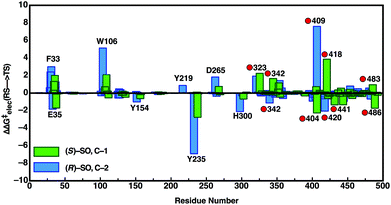 | ||
| Fig. 8 Overview of the electrostatic contributions of each individual residue and water molecule in our simulation systems to the overall calculated activation energy (ΔΔG‡elec) for formation of the alkylenzyme intermediate (energy of TS1 in Fig. 7), during the hydrolysis of (R)- and (S)-SO by wild-type StEH1, following nucleophilic attack at C-1 for (S)-SO (green bars) and C-2 for (R)-SO (blue bars). Shown here are the preferred Mode 2 conformations for both substrates, and the red circles on the annotations denote water molecules. All energies are in kcal mol−1, and were extracted from the EVB trajectories using the linear response approximation, as in our previous works.17,34 | ||
Being able to correctly computationally predict the resulting impact of such changes on both enantio- and regioselectivity is significant to subsequent enzyme design effort, and highlights the importance of considering the actual energetics of different putative binding modes, as well as the different binding steps, as different binding modes can lead to a change-in rate-limiting step rendering the apparently more stable conformation unfavourable along the reaction trajectory (as was the case here with (S)-SO when bound in Mode 1). Finally, note also that the determined (apparent) dissociation constants for the respective alkylenzymes with (R)-SO and (S)-SO supports the different calculated stabilities of the alkylenzymes. The value of KSEA is approximately 8-fold lower than that for the alkylenzyme with (R)-SO (Table 2). The reason for this difference can be traced back to the rates of formation and decay. Since the values of the sums of decay rates (k−2 + k3) are similar with either enantiomer (Table 2), differences in KEA are due to different rates of formation (k2/KS). It is not possible to deconvolute the relative influence from stabilization of ES (KS) or the alkylation rates (k2) but as proposed by the simulations, a combination of effects can be in play. The barrier for alkylation of the enzyme with (S)-SO is lower than with the (R)-enantiomer, leading to a higher rate, and the binding of (R)-SO in the active site appears to be less stable, leading to a higher value of KRS.
R-C1B1 variant of StEH1
To evaluate the impact of the amino acid exchanges on the active site architecture we determined the structure of the R-C1B1 variant. It crystallized under similar conditions, in the same space group and with the same unit cell dimensions as wild-type StEH1, containing two monomers per asymmetric unit. Their pairwise superimposition with wild-type StEH1 (PDB ID: 2CJP) gives an RMSD of 0.2–0.46 Å, with the largest deviations observed for residues 93–96 of a solvent-exposed loop (Fig. 9). This is most likely caused by the unintentional, random mutagenesis of P94 to leucine in the course of the iterative saturation mutagenesis-driven directed evolution. In the B monomer of R-C1B1, the helix preceding this loop terminates one residue earlier, leading to a conformational change and slight repositioning of this loop, possibly as a consequence of the increased backbone conformational freedom of a leucine compared to a proline. Due to its distance from the active site (∼25 Å) it is not expected to influence any catalytic parameters of StEH1.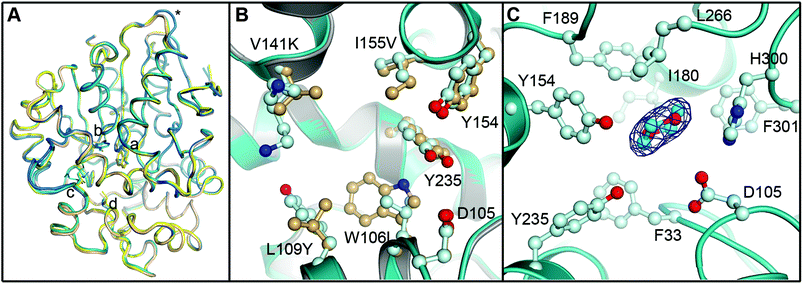 | ||
| Fig. 9 Crystal structure of the R-C1B1 variant of StEH1. Shown here are: (A) superimposed Cα-traces of the two subunits of wild-type StEH1 (PDB-ID: 2CJP) and the R-C1B1 variant (PDB-ID: 4UFN) present in the asymmetric unit of the respective crystals, coloured yellow and wheat for the wild-type enzyme, and teal and marine for the variant. The locations of amino acid exchanges are marked by a (W106L), b (L109Y), c (V141K), d (I155V), and * (P94L). (B) A zoom-in on the superimposed active sites of wild-type StEH1 (grey cartoon) and R-C1B1 (blue cartoon), showing the side chains of the two lid tyrosines, the catalytic D105 as well as the sites of amino acid exchanges, with carbon atoms in gold for wild-type StEH1 and in light blue for the variant. (C) The dioxane binding site observed in R-C1B1. All side chains within or near van der Waals distance of the ligand are shown, coloured as in B. The carbon atoms of the dioxane are coloured in cyan. The final electron density observed for the dioxane is contoured at Sigma levels of 1.0 for the 2FoFc map (blue mesh), and 3.0 (green) and −3.0 (red) for the FoFc map. Note that no sufficiently high density peaks are observed around the ligand in the latter. | ||
The R-C1B1 variant contains four (engineered) single point replacements, W106L, L109Y, V141K and I155V. Besides the side chain replacement itself, none of them causes any larger additional changes in active site architecture (see Fig. 9 for a side-by-side comparison of the two structures). The main difference to wild-type StEH1 is the formation of a hydrogen bond between the side chain of N241 and the hydroxyl group of Y109, which replaces the corresponding interaction of N241 with a water molecule that was previously placed at the position now occupied by the Y109 hydroxyl group. As a consequence the Y109 side chain is oriented away from the binding site, increasing its volume. In addition, the hydroxyl group position of the lid tyrosine Y235 differs by 1.2 Å between wild type StEH1 and R-C1B1, which may be the consequence of either the deletion of a methyl group by the I155V exchange or of the structural relaxation of the protein caused by the replacement of the bulky W106 by the considerably smaller leucine, or both. V141 is located at the entrance to the active site. Its replacement by the larger lysine could potentially affect active site accessibility. However, as the weakness or lack of electron density for all atoms beyond Cα indicates high mobility of the side chain it is also likely that K141 can adopt conformations that do not interfere with substrate entry to the active site.
The crystal structure of R-C1B1 has a dioxane molecule originating from the crystallization solution bound in the active site (Fig. 9). The side chains of the lid tyrosines, the catalytic D105, H300 involved in the activation of the catalytic water, as well as of F33, I180, F189, L266, and F301, are all placed within or just outside van der Waals distance to the ligand. This binding site coincides with that of the SO phenyl ring (Mode 1) as well as that of valpromide bound in the crystal structure of wild-type StEH1. Dioxane binding does not cause any significant conformational changes of residues constituting the binding site, although the above described minor change in Y235 ring orientation and positioning may occur to avoid too short contacts with this ligand.
The biggest change, however, in the context of our predictions for wild-type StEH1, is the removal of W106, which appears to be important for stabilizing SO in its preferred Mode 2 conformation. In order to examine whether such changes in active site shape would also affect the preferred reactive mode for SO binding in the R-C1B1 variant, we repeated the protocol used for wild-type StEH1 and performed EVB calculations of all reaction steps, enantiomers, binding modes and ring-opening positions involved in the hydrolysis of SO by R-C1B1 variant. Our results can be found in Tables 3 and 4 and in Fig. 7. We demonstrated in a recent work13 that while the regioselectivity of (S)-SO is unperturbed by these mutations, the shift in regioselectivity with (R)-SO is lost such that attack at C-1 and C-2 are equally possible. While we do not observe this change in regioselectivity in the R-C1B1 variant, with our calculations maintaining a C-2 preference for (R)-SO and a C-1 preference for (S)-SO, we do see that the side chain exchanges introduced in the R-C1B1 variant, and, in particular, the replacement of W106 with a smaller leucine changes the apparent preferred conformation for SO-hydrolysis for each enantiomer. That is, in the case of (R)-SO, we observe a complete reversal in the preferred binding mode, with the substrate now preferentially reacting through Mode 1, in which the phenyl ring forms a stacking interaction with the H300 side chain. However, and in contrast to the wild-type enzyme, in the case of (S)-SO, reaction through both Modes 1 and 2 are now energetically accessible to the substrate, with a substantially lower activation barrier to the hydrolysis step after forming an alkylenzyme intermediate from Mode 1 after removing W106, and therefore with Mode 1 now being the binding mode with the lowest overall activation free energy (for representative structures of the first transition state and the corresponding alkyl-enzyme intermediate for each enantiomer, see Fig. S10 and S11†). In addition, as shown in Tables 3 and 4, we are able to once again reproduce the (S)-preference of the enzyme, as with wild-type StEH1.
This shows the role of conformational diversity in facilitating differential selectivity towards different substrate enantiomers, and that this conformational diversity can be controlled through selective engineering of the enzyme. This is significant because it highlights the importance of shape complementarity, even for systems where the experimental data suggest that the contribution from binding effects are negligible. It also shows, however, that this can change along evolutionary trajectories, even though it is masked by the overall larger changes in kinetics. Our calculations highlight the power of theory to not only rationalize changes in and the origins of both enantio- and regioselectivity in terms of binding conformation and energetic contributions from different reaction steps, but also to tease out preferred binding modes and how these are affected upon mutation. This, in turn, provides a crucial pre-screening tool for computational engineering effort, as long as the activation energies of each binding conformation and the key microsteps of the reaction are considered in the calculations.
Conclusions
The present work has provided a detailed computational and structural analysis of the enantio- and regioselective hydrolysis of styrene oxide by StEH1, reproducing the enantioconvergent behaviour of the wild-type enzyme as well as the enantioselectivities of both the wild-type enzyme and the engineered R-C1B1 variant. In contrast to our previous computational study,17 styrene oxide is a small substrate that can occupy multiple binding modes in the active site, leading to different side chain interactions depending on both binding mode and enantiomer (see Fig. 4 and 6). Our study demonstrates that this conformational diversity is the origin of the observed enantioconvergent behaviour of the wild-type enzyme (and of modifications to this behaviour in the engineered variant), as different enantiomers can take on different preferred binding modes. This, in turn, leads to changes in both shape and electrostatic complementarity, based on how the substrate interacts with active site residues and the corresponding changes in electrostatic stabilization of the oxyanion intermediate, which drives the observed changes in selectivity. Additionally, we demonstrate that the actual differences in energy at the step that determines the selectivity can be much larger than that predicted from experiment, as the experimental measurements consider an average over different conformations and binding modes.There has recently been great interest in using epoxide hydrolases as model systems for artificial design of chirally controlled biocatalysts.1,13,16 We demonstrate here that the EVB approach is a powerful tool with which to tease out changes in both enantio- and regioselectivity even in such challenging systems involving the binding of a comparatively small substrate to a large active site, as well as an effective approach with which to decompose the contributions of different reaction steps to the overall observed selectivity. In doing so, we believe our work provides a template for subsequent protein engineering efforts on these biocatalytically important systems.
Acknowledgements
The European Research Council provided financial support under the European Community's Seventh Framework Programme (FP7/2007-2013)/ERC Grant Agreement 306474. The authors also acknowledge funding and support from the Swedish Research Council Grant 621-2011-6055 (to MW), Carl Tryggers Foundation (CTS13:104, DD), and a Sven and Lilly Lawski scholarship for doctoral studies to PB. Support from COST Action 1303 “Systems Biocatalysis” is also gratefully acknowledged. We are very grateful for the allocation of computational resources from the Swedish National Infrastructure for Computing (SNIC, Grant Number SNIC2014-11-2). All calculations have been performed on the Akka and Abisko clusters at the HPC2N centre in Umeå. Finally, the authors would like to thank the Diamond Light Source and the European Synchrotron Radiation Facility for beamtime (proposals mx11171, mx1639), and the staff of beamlines I02, I04 (DLS), and ID23-2 (ESRF) for assistance with crystal testing and data collection. Access was supported in part by the EU FP7 infrastructure grant BIOSTRUCT-X (contract nr: 283570).References
- A. Archelas and R. Furstoss, Curr. Opin. Chem. Biol., 2001, 5, 112–119 CrossRef CAS PubMed.
- C. Morisseau and B. D. Hammock, Annu. Rev. Pharmacol. Toxicol., 2004, 45, 311–333 CrossRef PubMed.
- M. I. Monterde, H. Lombard, A. Archelas, A. Cronin, A. Arand and R. Furstoss, Tetrahedron: Asymmetry, 2004, 15, 2801–2805 CrossRef CAS.
- L. T. Elfström and M. Widersten, Biochem. J., 2005, 390, 633–640 CrossRef PubMed.
- L. T. Elfström and M. Widersten, Biochemistry, 2006, 45, 205–212 CrossRef PubMed.
- S. L. Mowbray, T. L. Elfström, K. M. Ahlgren, C. E. Andersson and M. Widersten, Protein Sci., 2006, 15, 1628–1637 CrossRef CAS PubMed.
- K. H. Hopmann and F. Himo, Chemistry, 2006, 6, 6898–6909 CrossRef PubMed.
- K. H. Hopmann and F. Himo, J. Phys. Chem. B, 2006, 110, 21299–21310 CrossRef CAS PubMed.
- A. Thomaeus, J. Carlsson, J. Åqvist and M. Widersten, Biochemistry, 2007, 46, 2466–2479 CrossRef CAS PubMed.
- A. Thomaeus, A. Naworyta, S. L. Mowbray and M. Widersten, Protein Sci., 2008, 17, 1275–1284 CrossRef CAS PubMed.
- M. T. Reetz, M. Bocola, L.-W. Wang, J. Sanchis, A. Cronin, M. Arand, J. Zou, A. Archelas, A.-L. Bottalla, A. Naworyta and S. L. Mowbray, J. Am. Chem. Soc., 2009, 131, 7734–7343 Search PubMed.
- D. Lindberg, M. de la Fuente Revenga and M. Widersten, Biochemistry, 2010, 49, 2297–2304 CrossRef CAS PubMed.
- Å. Janfalk Carlsson, P. Bauer, H. Ma and M. Widersten, Biochemistry, 2012, 51, 7627–7637 CrossRef PubMed.
- R. Lonsdale, S. Hoyle, D. T. Grey, L. Ridder and A. J. Mulholland, Biochemistry, 2012, 51, 1774–1786 CrossRef CAS PubMed.
- M. E. S. Lind and F. Himo, Angew. Chem., Int. Ed., 2013, 52, 4563–4567 CrossRef CAS PubMed.
- H. J. Wijma, R. J. Floor, S. Bjelic, S. J. Marrink, D. Baker and D. B. Janssen, Angew. Chem., Int. Ed., 2015, 54, 3726–3730 CrossRef CAS PubMed.
- B. A. Amrein, P. Bauer, F. Duarte, Å. Janfalk Carlsson, A. Naworyta, S. L. Mowbray, M. Widersten and S. C. L. Kamerlin, ACS Catal., 2015, 5, 5702–5713 CrossRef CAS PubMed.
- P. Heikinheimo, A. Goldman, C. Jeffries and D. L. Ollis, Structure, 1999, 7, R141–R146 CrossRef CAS PubMed.
- J. J. Blumenstein, V. C. Ukachukwu, R. S. Mohan and D. L. Whalen, J. Org. Chem., 1993, 58, 924–932 CrossRef CAS.
- M. P. Frushicheva and A. Warshel, ChemBioChem, 2012, 13, 215–223 CrossRef CAS PubMed.
- P. Schopf and A. Warshel, Proteins, 2014, 82, 1387–1399 CrossRef CAS PubMed.
- A. Warshel, Computer Modeling of Chemical Reactions in Enzymes and Solutions, Wiley, New York, 1991 Search PubMed.
- S. C. L. Kamerlin and A. Warshel, WIREs Comput. Mol. Sci., 2011, 1, 30–45 CrossRef CAS.
- A. Shurki, E. Derat, A. Barrozo and S. C. L. Kamerlin, Chem. Soc. Rev., 2015, 44, 1037–1052 RSC.
- G. Hong, E. Rosta and A. Warshel, J. Phys. Chem. B, 2006, 110, 19570–19574 CrossRef CAS PubMed.
- E. Rosta and A. Warshel, J. Chem. Theory Comput., 2012, 8, 3574–3585 CrossRef CAS PubMed.
- Schrödinger Release 2013-3: MacroModel version 9.1, Schrödinger LLC, New York, 2013 Search PubMed.
- P. Cieplak, W. D. Cornell, C. Bayly and P. A. Kollman, J. Comput. Chem., 1995, 16, 1357–1377 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. J. Tiado-Rives, J. Am. Chem. Soc., 1996, 118, 1125–11236 CrossRef.
- J. Marelius, K. Kolmodin, I. Feierberg and J. Åqvist, J. Mol. Graphics Modell., 1998, 16, 213–225 CrossRef CAS PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- G. King and A. Warshel, J. Chem. Phys., 1989, 91, 3647–3661 CrossRef CAS.
- J. Aqvist and S. C. L. Kamerlin, Biochemistry, 2015, 54, 546–556 CrossRef PubMed.
- E. Y. Lau, Z. E. Newby and T. C. Bruice, J. Am. Chem. Soc., 2001, 123, 3350–3357 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Paar, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- G. W. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, M. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, M. J. T. Gaussian 09 Rev. C01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- A. Gurell and M. Widersten, ChemBioChem, 2010, 11, 1422–1429 CrossRef CAS PubMed.
- W. Kabsch, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66, 125–132 CrossRef CAS PubMed.
- R. W. Grosse-Kunstleve, N. K. Sauter, N. W. Moriarty and P. D. Adams, J. Appl. Crystallogr., 2002, 35, 126–136 CrossRef CAS.
- M. D. Winn, C. C. Ballard, K. D. Cowtan, E. J. Dodson, P. Emsley, P. R. Evans, R. M. Keegan, E. B. Krissinel, A. G. W. Leslie, A. McCoy, S. J. McNicholas, G. N. Murshudov, N. S. Pannu, E. A. Potterton, H. R. Powell, R. J. Read, A. Vagin and K. S. Wilson, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2011, D67, 235–242 CrossRef PubMed.
- G. Winter and K. E. McAuley, Methods, 2011, 55, 81–93 CrossRef CAS PubMed.
- P. Evans, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2006, 62, 72–82 CrossRef PubMed.
- Collaborative Computational Project, 4, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1994, 50, 760–763 CrossRef PubMed.
- P. Emsley, B. Lohkamp, W. G. Scott and K. Cowtan, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66, 486–501 CrossRef CAS PubMed.
- G. N. Murshudov, P. Skubak, A. A. Lebedev, N. S. Pannu, R. A. Steiner, R. A. Nicholls, M. D. Winn, F. Long and A. A. Vagin, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2011, 67, 355–367 CrossRef CAS PubMed.
- D. Lindberg, S. Ahmad and M. Widersten, Arch. Biochem. Biophys., 2010, 495, 165–173 CrossRef CAS PubMed.
- A. Fersht, Structure and Mechanism in Protein Science, W. H. Freeman, USA, 1999 Search PubMed.
- B. Lin and D. L. Whalen, J. Org. Chem., 1994, 59, 1638–1641 CrossRef CAS.
- F. Duarte, T. Geng, G. Marloie, A. O. Al Hussain, N. H. Williams and S. C. L. Kamerlin, J. Org. Chem., 2014, 79, 2816–2828 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Further details on calibration of our simulations, QM data and RMSD plots from the MD simulations, further experimental data, and all EVB parameters used to model styrene oxide hydrolysis in this study. See DOI: 10.1039/c6ob00060f |
| This journal is © The Royal Society of Chemistry 2016 |