Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Increased duplex stabilization in porphyrin-LNA zipper arrays with structure dependent exciton coupling†
Daniel G.
Singleton
a,
Rohanah
Hussain
b,
Giuliano
Siligardi
b,
Pawan
Kumar
c,
Patrick J.
Hrdlicka
c,
Nina
Berova
d and
Eugen
Stulz
*a
aSchool of Chemistry and Institute for Life Sciences, University of Southampton, Highfield, Southampton, SO17 1BJ, UK. E-mail: est@soton.ac.uk; Web: http://www.southampton.ac.uk/chemistry/about/staff/est.page?
bDiamond Light Source, Harwell Science and Innovation Campus, Didcot, Oxfordshire OX11 0DE, UK
cDepartment of Chemistry, University of Idaho, Moscow, ID 83844, USA
dDepartment of Chemistry, Columbia University, 3000 Broadway, New York, NY 10027, USA
First published on 22nd September 2015
Abstract
Porphyrins were attached to LNA uridine building blocks via rigid 5-acetylene or more flexible propargyl-amide linkers and incorporated into DNA strands. The systems show a greatly increased thermodynamic stability when using as little as three porphyrins in a zipper arrangement. Thermodynamic analysis reveals clustering of the strands into more ordered duplexes with both greater negative ΔΔS and ΔΔH values, and less ordered duplexes with small positive ΔΔS differences, depending on the combination of linkers used. The exciton coupling between the porphyrins is dependent on the flanking DNA sequence in the single stranded form, and on the nature of the linker between the nucleobase and the porphyrin in the double stranded form; it is, however, also strongly influenced by intermolecular interactions. This system is suitable for the formation of stable helical chromophore arrays with sequence and structure dependent exciton coupling.
Introduction
DNA has become very attractive as a supramolecular scaffold in nano-biotechnology,1–7 because it offers the possibility to add functionality exceeding its role in biological contexts.8 Chemical modification of nucleotides at either the nucleobase or sugar moiety with aromatic compounds or metal complexes,9–13 or replacement of the nucleobase14–16 or the nucleoside altogether,17,18 allows for attachment of a huge variety of functional substituents,19 in particular for energy or electron transfer20–23 or sensing applications.24,25 In this way, helical chromophore arrays were generated to create photonic wires or mimic the antenna effect of the photosynthetic system, either through standard DNA synthesis or via enzymatic DNA extension.Building blocks consisting of porphyrins covalently attached to nucleotides26–28 offer great versatility due to their tuneable electrochemical and optical properties. Methods for attachment include modification of the nucleobases,29–35 ribofuranose residues,35–43 phosphate backbone44–47 and using acyclic linkers.18,48–51 This led to assemblies in which porphyrin residues were positioned as 3′- or 5′-molecular caps,39,48,50,52,53 and used instead of a nucleobase in the middle of the helix18,49,51 or as a label in the minor37,42,43,47 and major30–35 grooves. The systems have been used to detect structural switching using chiroptical methods,39,46,54,55 realize viral DNA sensing using micro-electrochemistry,56 and form reversible photonic wires through hybridization.33 Porphyrins have been shown to be particularly useful substituents for DNA based bio-nanotechnology, allowing the formation of DNA tubes57 or acting as lipophilic anchors for insertion of nanopores58,59 and electronic systems into lipid bilayers.60
Incorporation of multiple porphyrins can lead to substantial thermodynamic destabilization of the duplex when only one strand is modified;30 this can be compensated by arranging the porphyrins in interstrand zippers, resulting in the formation of very stable duplexes.31,33 Here we investigated the use of porphyrin-LNA (LNA = locked nucleic acid, LNA-P) as building blocks due to its potential ability to further stabilize the DNA duplex.61
The advantage of using C5-functionalization of pyrimidine bases is that the substituents can precisely be oriented into the major groove of the DNA.30,62 In this respect, the LNA modifier is identical to the 2′-deoxyuridines (dU) normally used for modifying DNA. This has been shown for other systems using C5-modified LNA,63–65 and generally contrasts the attachment of substituents on the 2′-position of the ribose which positions them into the minor groove.62 Here we show that the LNA modification indeed has a positive effect on duplex stability despite the very large and hydrophobic porphyrin substituents, and that the excitonic coupling between the chromophores can be modulated by selecting different linkers to the substituent.
Results and discussion
Synthesis of the LNA building blocks
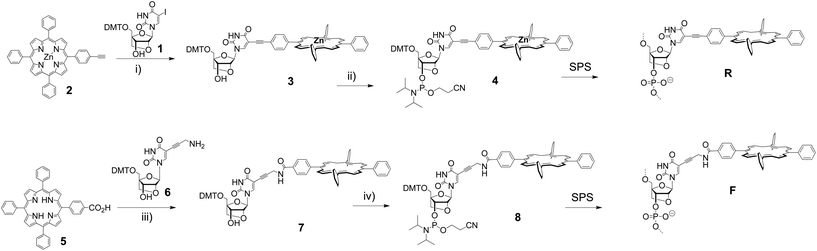
We have synthesized two porphyrin-LNA building blocks, where the porphyrin is attached either via a short rigid acetylene linker (4), or via a more flexible propargyl-amide linker (8); the synthetic route is outlined in Scheme 1. The 5-iodo-LNA-U building block 1 was obtained by methods previously reported.65 Attachment of acetylene porphyrin 230 was realized using Sonogashira coupling to give 3 in 91% yield. The carboxylate porphyrin 531 was coupled to the propargyl-amine-LNA-U 663 using EDC/HOBt mediated peptide coupling giving access to 7 in 68% yield. The building blocks were transformed into their phosphoramidite counterparts and used directly for solid phase synthesis of the oligodeoxynucleotide (ODN) strands (see ESI† for details of the synthesis and Table 1 for sequences). Incorporation of 4 gave the R-series, whereas 8 gave the F-series denoting rigid and flexible linker, respectively, and the unmodified ODN sequence is denoted as U-series. The coupling of the modified building blocks generally was highly efficient according to the trityl monitoring using an extended 6 min coupling protocol; the isolated yields after HPLC purification were between 23% and 70% according to UV-measurements (see ESI†). The central zinc metal in 4, which is inserted to prevent copper metallation during the Sonogashira coupling, is lost during SPS due to the acidic conditions in DMT removal, thus both modifiers R and F in the DNA are obtained as free base porphyrins. The strands were analysed by UV-vis and CD spectroscopy, and by thermal denaturation experiments to obtain insight into both thermodynamic and optical aspects of the LNA arrays.| ODN duplex | T m/°C [ΔTm] | ΔH/kJ mol−1 [ΔΔH] | −T298ΔS/kJ mol−1 [Δ(−T298ΔS)] | ΔG298/kJ mol−1 [ΔΔG298] | |
|---|---|---|---|---|---|
| a Data obtained by thermal denaturing using UV monitoring. b Data obtained by thermal denaturing using CD monitoring; ΔTm is calculated relative to the base value obtained by the same method. The Tm values were obtained from the first derivative of the melting curves at 260 nm (0.1 °C min−1, no hysteresis was observed; 2.5 μM DNA, 50 mM phosphate buffer, 100 mM NaCl, 1 mM Na2EDTA, pH 7.0). | |||||
| a | U1 5′-GTG ATA TGC | 37.6 | −279 ± 0.2 | 233 | −46.4 |
| U2 3′-CAC TAT ACG | 39.7b | −285 ± 12b | 239b | −45.9b | |
| b | R1 5′-GTG A![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) A TGC A TGC |
32.5 [−5.1] | −261 ± 1 [+18] | 220 [−13] | −40.7 [+5.7] |
| U2 3′-CAC TAT ACG | |||||
| c | U1 5′-GTG ATA TGC | 33.0 [−4.6] | −281 ± 0.6 [−2] | 239 [+6] | −41.9 [+4.5] |
R2 3′-CAC ![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) AT ACG AT ACG |
34.5b [−5.2] | −283 ± 6b [+2] | 241 [+2] | −42.1b [+4.3] | |
| d | U1 5′-GTG ATA TGC | 31.4 [−6.2] | −255 ± 0.7 [+24] | 215 [−18] | −40.3 [+6.1] |
R3 3′-CAC TA![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) ACG ACG |
|||||
| e | U1 5′-GTG ATA TGC | 27.7 [−9.9] | −254 ± 0.5 [+25] | 217 [−16] | −36.6 [+9.8] |
R4 3′-CAC ![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) A A![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) ACG ACG |
|||||
| f | F1 5′-GTG A![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) A TGC A TGC |
36.7 [−0.9] | −356 ± 0.2 [−77] | 308 [+75] | −47.7 [−1.3] |
| U2 3′-CAC TAT ACG | |||||
| g | U1 5′-GTG ATA TGC | 35.7 [−1.9] | −257 ± 0.3 [+22] | 214 [−19] | −42.6 [+3.8] |
F2 3′-CAC ![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) AT ACG AT ACG |
|||||
| h | U1 5′-GTG ATA TGC | 35.4 [−2.2] | −333 ± 0.1 [−54] | 287 [+54] | −45.9 [+0.5] |
F3 3′-CAC TA![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) ACG ACG |
|||||
| i | U1 5′-GTG ATA TGC | 29.9 [−7.7] | −203 ± 0.7 [+76] | 165 [−68] | −37.5 [+8.9] |
F4 3′-CAC ![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) A A![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) ACG ACG |
28.9b [−10.8] | −222 ± 7b [+63] | 186b [−53] | −35.7b [+10.7] | |
| j | R1 5′-GTG A![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) A TGC A TGC |
35.6 [−2.0] | −357 ± 0.8 [−78] | 310 [+77] | −47.2 [−0.8] |
R2 3′-CAC ![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) AT ACG AT ACG |
|||||
| k | R1 5′-GTG A![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) A TGC A TGC |
35.5 [−2.1] | −368 ± 0.2 [−89] | 321 [+88] | −46.9 [−0.5] |
R3 3′-CAC TA![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) ACG ACG |
|||||
| l | R1 5′-GTG A![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) A TGC A TGC |
39.7 [+2.1] | −362 ± 0.2 [−83] | 312 [+79] | −50.4 [−4.0] |
R4 3′-CAC ![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) A A![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) ACG ACG |
|||||
| m | F1 5′-GTG A![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) A TGC A TGC |
36.8 [−0.8] | −344 ± 0.2 [−65] | 297 [+64] | −46.7 [−0.3] |
F2 3′-CAC ![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) AT ACG AT ACG |
|||||
| n | F1 5′-GTG A![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) A TGC A TGC |
35.9 [−1.7] | −256 ± 0.3 [+23] | 213 [−20] | −42.5 [+3.9] |
F3 3′-CAC TA![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) ACG ACG |
|||||
| o | F1 5′-GTG A![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) A TGC A TGC |
40.9 [+3.3] | −274 ± 0.2 [+5] | 226 [−7] | −48.3 [−1.9] |
F4 3′-CAC ![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) A A![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) ACG ACG |
|||||
| p | R1 5′-GTG A![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) A TGC A TGC |
37.7 [+0.1] | −344 ± 0.2 [−65] | 295 [+62] | −48.5 [−2.1] |
F2 3′-CAC ![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) AT ACG AT ACG |
|||||
| q | R1 5′-GTG A![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) A TGC A TGC |
37.8 [+0.2] | −270 ± 0.2 [+9] | 225 [−8] | −45.5 [+0.9] |
F3 3′-CAC TA![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) ACG ACG |
38.2b [−1.5] | −348 ± 4b [−63] | 300b [+61] | −47.8b [+1.4] | |
| r | R1 5′-GTG A![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) A TGC A TGC |
41.3 [+3.7] | −349 ± 0.1 [−70] | 297 [+70] | −52.0 [−5.6] |
F4 3′-CAC ![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) A A![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) ACG ACG |
|||||
| s | F1 5′-GTG A![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) A TGC A TGC |
38.0 [+0.4] | −280 ± 0.5 [−1] | 234 [+1] | −46.3 [+0.1] |
R2 3′-CAC ![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) AT ACG AT ACG |
|||||
| t | F1 5′-GTG A![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) A TGC A TGC |
40.5 [+2.9] | −269 ± 0.4 [+10] | 221 [−12] | −47.8 [−1.4] |
R3 3′-CAC TA![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) ACG ACG |
|||||
| u | F1 5′-GTG A![[F with combining low line]](https://www.rsc.org/images/entities/b_char_0046_0332.gif) A TGC A TGC |
42.6 [+5.0] | −287 ± 0.4 [−8] | 237 [−4] | −50.3 [−3.9] |
R4 3′-CAC ![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) A A![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif) ACG ACG |
|||||
DNA duplexes were designed to feature either one porphyrin at a central position (Table 1, entries b, c, d, f, g, h), two porphyrins on one of the strands (entries e, i), interstrand zipper arrays with two porphyrins (entries j, k, m, n, p, q, s, t), or three porphyrins (entries l, o, r, u).
Thermodynamic stability
The DNA duplexes, which have the LNA-porphyrin building block incorporated in only one strand, generally show a decrease in thermal stability (b–i). This is more pronounced for the rigid acetylene linker (R-series) than for the propargyl-amide linker (F-series). Clearly, the attachment of the porphyrin outweighs the stabilizing effect of the LNA skeleton, which is in the range of +4.0–+6.5 °C in this sequence context.65 Note that we define “sequence context” as placing the porphyrins at different positions within the given DNA sequence, resulting in variation of the porphyrin environment with respect to the neighbouring DNA sequence. The attachment of two porphyrins in complementary strands using the same linker (j, k, m, n) equally does not show duplex stabilization. However, forming a two-porphyrin array with different linkers on the complementary strands (p, q, s, t) leads to a compensation of the destabilizing effect, and the duplex F1·R3 actually displays a stabilization of ΔTm = +2.9 °C, and with it revealing sensitivity of the system with respect to the linker moiety used. Introduction of three porphyrin-functionalized LNA monomers into DNA duplexes (l, o, r, u) results in substantial thermodynamic stabilization, as revealed by the higher ΔTm and lower ΔΔG values; a more detailed discussion on the entropic and enthalpic contributions is given further below.Detailed analysis of the Tm-values shows that the influence in the zipper-systems is not a simple sum of the modifications. To illustrate, R1·U2 and U1·R2 show ΔTm = −5.1 °C and ΔTm = −4.6 °C, respectively, whereas the duplex R1·R2 shows ΔTm = −2.0 °C. The same is the case for R1·R3, and this effect is even more pronounced in R1·R4. In contrast, the stabilizing effect is less pronounced when both strands are modified by the flexible linker (Table 1, m–o), suggesting that flexibility is detrimental for array stability. This means that placement of the R monomers in zipper arrangements counteracts the inherent destabilizing properties of the R monomers more efficiently than is the case with the F monomers; in other words, ΔΔTm is larger for R than for F when comparing U·X to X·X. That being said, porphyrin zippers that entail F monomers, and especially mixtures of F and R monomers, are the most stable in absolute terms. F1·R4 shows the highest stabilization effect with a ΔTm = +5.0 °C. This increase of 1.7 °C per porphyrin is decisively larger than that seen with the dU-P system (0.3–0.5 °C),31,33 suggesting that array formation between porphyrin units is more stabilising in LNA-P based systems.
In the closely related dU-zipper system, which contains six porphyrins per modified strand, the order of stabilisation was found to be U·F > F·F > U·R > R·F > R·R.31 In the LNA-system, the order is F·R > F·F > R·R > U·F > U·R. This suggests that (i) the less restricted dU-P is better tolerated by an unmodified complementary strand, and in both dU-P and LNA-P the flexible linker is beneficial; (ii) a certain degree of flexibility is necessary in order to form stable zipper arrays; (iii) the preorganised LNA modifier forms a duplex in which the mixed porphyrin array forms a better stack whereas dU adjusts better to flexible linker. It was suggested previously through molecular modelling that the mixed porphyrin system forms a more evenly distributed porphyrin arrangement in the major groove of the duplex.31 This, however, applies only to the zipper-arrangement; the thermodynamic analysis of all combinations is more complex as discussed further below. An influence of the linker length in F cannot be ruled out to act in combination with the increased flexibility.
Overall, hydrophobic interactions exert a positive effect with increasing number of porphyrins, and the system is very sensitive to the nature of the linker and sequence context of the modification. The melting temperatures were, in a few cases, also determined using CD-melting (Table 1) and are in good agreement with the UV-melting temperatures. The overall duplex structure continues to exhibit the B-form helical conformation where the melting is reflected by a global change of the molecule, and is not affected by secondary structures or intermolecular interactions induced by the porphyrin (see below).
The melting curves were fitted to provide thermodynamic parameters (see Table 1 and ESI†). The differences in enthalpy and entropy, as expressed in ΔΔH and ΔΔS, are illustrative of the influence of the modification compared to the unmodified DNA duplex. Plotting ΔΔS vs. ΔΔH shows a linear correlation with an intercept very close to the origin (red line in Fig. 1a); the intercept of −5.8 J mol−1 and slope of 3.15 K agrees well with the reported values for a series of LNA strands (intercept 9.5 J mol−1, slope 2.95 K).66
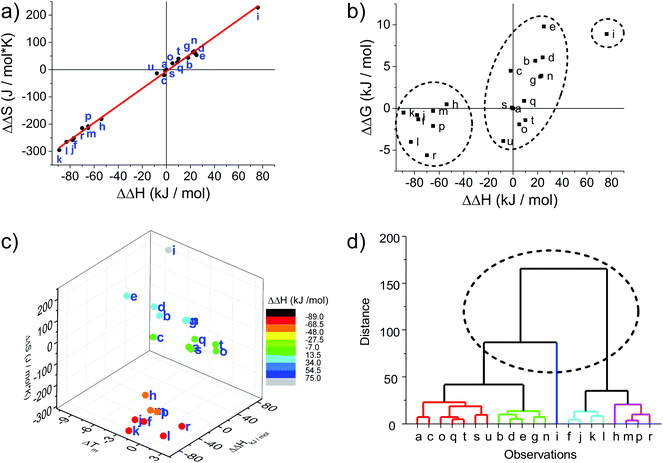 | ||
| Fig. 1 Thermodynamic plots of the porphyrin-LNA duplexes. Data are taken from Table 1. (a) Enthalpy–entropy compensation with linear regression [ΔΔS = −5.88 + (3.15 K)ΔΔH; R2 = 0.996]. (b) Correlation between ΔΔH and ΔΔG298 demonstrating that there is a linear correlation between ΔΔG and ΔΔH.66 (c) Enthalpy–entropy-change in ΔTm correlation showing further clustering when compared to net change of entropy. (d) Hierarchical analysis using the euclidean distance carried out by OriginLab software presenting five clusters of duplex samples. The dashed circle indicates the classification of the three groups identified in (a), (b) and (c); the main groups can be further divided into five major subgroups. | ||
From a global point of view, the plots of thermodynamic parameters ΔΔS vs. ΔΔH revealed one isolated and two main groups of duplex architecture systems (Fig. 1a). The group comprising the f, h, j, k, l, m, p and r duplex systems with both greater negative ΔΔS and ΔΔH values should be considered to be more ordered compared to the reference duplex “a” relative to which the ΔΔS and ΔΔH values were calculated. The second group comprising the remaining duplex systems (except “i”) with small positive ΔΔS differences can be viewed as less ordered than “a”. The duplex “i” (U1·F4) clearly falls outside the clustering, indicating that the use of two flexible F monomers on one DNA strand is enthalpically very unfavourable. The systems U·F, R·R and R·F fall mainly into the first group, and the systems U·R, F·F and F·R can be predominantly found in the second clustering.
The enthalpy–entropy compensation has been discussed for LNA, and since the plot of ΔΔG298vs. ΔΔH shows a positive correlation rather than random scattering (Fig. 1b) it suggests that the compensation is not due to experimental error, and that the porphyrin-LNA building blocks can stabilize the duplex by either preorganization or improved stacking, but not both simultaneously.66
From the ΔΔG298 and ΔΔH plot (Fig. 1b), it can be deduced that the duplex architecture of the first group is energetically more favourable than that of the reference duplex “a”, whereas for the second group the difference is smaller and towards less stable duplex formation than “a” with “i” forming the least stable duplex. The 3D plot of Tm, ΔΔH and ΔΔS is a better way of representing the thermodynamic parameters (Fig. 1c) and shows the trends of the three groups in a more accurate and complete way. The cluster analysis as shown in Fig. 1d is consistent with the broad classification of the duplex architectures as revealed in Fig. 1a–c. In fact, the systems can be represented in five major subgroups with the systems {a, c, o, q, s, t, u} with mainly F·R zippers; {b, d, e, g, n} with mainly U·R duplexes; {i}; {f, j, k, l} with mainly R·R zippers; and {h, m, p, r} with mainly R·F zippers. Outliers are present in each of the groups.
The destabilizing characteristics of R-modified ODNs (R·U or U·R) are of an enthalpic nature (ΔΔH > 0 kJ mol−1), consistent with structural perturbation by the porphyrin in the major groove. The underlying structural reasons for the destabilizing properties of the monomer F (F·U or U·F) appear to be much more sequence/position-dependent since highly unfavourable entropic contributions are observed in some cases (see Δ(−T298ΔS) for F1·U2), while strongly unfavourable enthalpic contributions are seen in others (see ΔΔH for U1·F2). In the zipper arrays, R stabilizes the duplexes through enthalpic contributions, in agreement with the formation of π–π stacks (ΔΔH ≪ 0 kJ mol−1 for R·R). The more flexible F in the F·F arrays stabilizes DNA duplexes through favourable enthalpic contributions in some constructs (−1 zipper constructs) and entropic contribution in others (+1 zipper construct). Finally, the R·F hetero-arrays are either stabilized due to strong enthalpic contributions (e.g., R1·F2), or through minor differences in enthalpy/entropy contributions (F1·R3).
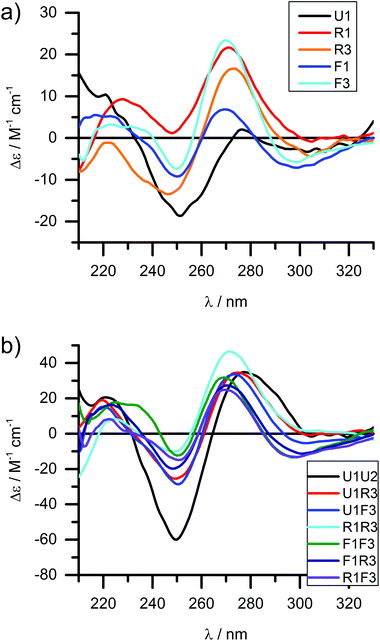
Circular dichroism of free-base LNA strands
Circular dichroism (CD) spectroscopy is a very versatile tool in assessing structural aspects through electronic interactions,67 and both the DNA and the porphyrin parts of the spectrum are indicative of the impact of the modifications on structure. Single-stranded LNA-modified ODNs show a signature reminiscent of a DNA·RNA hybrid duplex structure68,69 with varying effects that are depending on the sequence context; Fig. 2a displays representative examples for both building blocks (see ESI† for full analysis). This effect is not pronounced in the double stranded ODNs where all systems largely display the structural characteristics consistent of a B-type DNA duplex (Fig. 2b), although the +275 nm band is shifted to lower value, and the Δε values are reduced, indicating reduced helicity in the modified systems. The interpretation of the porphyrin region of the CD spectra is more complex as it shows large variance with respect to the nature of the modifier, sequences and hybridization state (see Fig. 3 for examples and ESI† for full spectral analysis). In the single-modified porphyrin strands (R1–R3, F1–F3), the signatures are more complex than would be anticipated, as either a single positive or single negative Cotton effect should be expected. The bisignate or multisignate structure and the similarity between the single stranded forms (Fig. 3a and b) and double stranded forms (Fig. 3c and d) indicates that several chromophores are involved in inter-molecular and/or in intra-strand interactions. We have previously shown by SAXS31 and EPR spectroscopy70 that porphyrin-DNA tends to associate in solution, and it was estimated that a minimum of six porphyrins interact through a combination of intra- and intermolecular interactions, having an average centre-to-centre distance of 6.5–8.9 Å.70 Here, this is also demonstrated by recording the CD spectra of selected systems in various salt concentrations (0 M, 0.1 M and 1.0 M NaCl), where a low salt concentration should suppress intermolecular interactions (Fig. 3e). The spectra clearly change upon increasing salt concentration; however, even in pure water the intermolecular interactions persist owing to the high hydrophobicity of the porphyrins. For example the multiple CD bands in the Soret region of U1·F3, which are more clearly seen in the presence of NaCl, point out that inter-duplex interactions are a result of the stacking and is more pronounced for the flexible linker. Similar multiple CD bands due to porphyrin–porphyrin stacking in inter-duplex aggregates have been described by Berova et al.53 The phenomenon of intermolecular interactions can also be seen with pyrenes,71,72 perylenes73,74 or other porphyrin constructs.35,75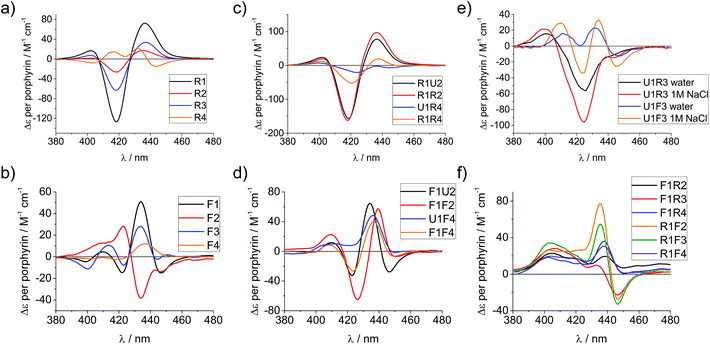 | ||
| Fig. 3 CD spectra of porphyrin-LNA strands of selected examples showing the porphyrin region of the spectra. (a) and (b) spectra of single strands with LNA-1 or LNA-2 modification, respectively. (c) and (d) spectra for selected duplexes where the same modifier has been used in both strands. (e) Comparison of stands U1·R3/F3 in pure water or in 1 M NaCl (50 mM phosphate buffer) solution. (f) Mixed LNA duplexes where the complementary strands have been modified with different modifiers. Δε values are given per porphyrin (normalized to the number of porphyrins present). Conditions as in Fig. 2. | ||
Particularly interesting are the strands R4 and F4 containing two porphyrins, which do show differences going from ssODN to dsODN forms, since a combination of intra- and intermolecular interactions determines the shape of the overall CD profile. The differences between the single and double stranded forms demonstrate the sensitivity of CD spectroscopy, which allows to distinguish between the intramolecular 1,3-porphyrin interactions and the intermolecular stacking. Comparing the R with the F series confirms that the added flexibility of the linker induces different orientations of the porphyrins, giving a better overlap of the π-systems which is seen in the larger bisignate bands of the spectra.
Similar trends can be seen in the zipper arrays R·R and F·F. Both the R- and the F-series show similar CD spectra (Fig. 3c and d), indicating that the porphyrins adopt a similar chiral twist. In the F-series, the porphyrins clearly act as circular oscillators since due to the restricted rotation around the bond between the porphyrin and the functionalized phenyl group both Soret components Bx and By are given equal weight.76 This results into complex CD bands consisting of multiple exciton couplet contributions; the porphyrins seem to be closer aligned due to the added flexibility of the linker. Exceptions are the systems R1·R4 and F1·F4, where the CD signals do not appear as a superposition of the +1 or −1 interstrand zipper-arrangements. We speculate that the sterical demand of the porphyrins distorts the array formation. Mixed arrays R·F and F·R have more distorted CD signatures as can be seen from Fig. 3f. The arrays R1·F2 and R1·F3 show similar signatures in the spectra and their porphyrin arrangement seems comparable; the same holds for the arrays R1·F4 and F1·R4. These arrays also have ΔTm values in a similar range (Table 1). Whilst it is not possible to deduce the structure of the arrangement from the CD spectra, the overall picture does confirm that the type of linker (acetylene vs. propargyl-amide) as well as the sequence context strongly influences the intramolecular interactions and leads to a different orientation of the porphyrins in the major groove of the DNA.31 Particularly the use of mixed linker systems seems advantageous in terms of forming more evenly distributed porphyrin stacks.
Circular dichroism of zinc metallated LNA strands
We have shown previously that the porphyrins can be metallated easily with zinc, cobalt or copper when attached to DNA.31,40 This works equally well in the case of LNA, though we have only explored zinc in this respect and made R4-Zn and F4-Zn, respectively. The CD spectra of arrays containing the Zn-LNA and either U1, R1 or F1 as a complementary strand show that the exciton coupling signatures are quite similar in duplexes containing either R4-Zn or F4-Zn (Fig. 4) and are distinctively different to their non-metallated counterparts (apart U1·R4 and U1·R4-Zn). Zn porphyrins that are attached via rigid linker clearly interact more prominently with each other in R4-Zn. They therefore exhibit a characteristic CD spectrum as in U1·R4-Zn. In comparison with U1·R4, the Zn analogue possesses not only added planarity and symmetry, but is also more hydrophilic due to axially coordinated water, and should therefore be less prone to aggregation in the presence of NaCl. In R1·R4-Zn three rigid porphyrins are available for interaction, but the CD profile seems to exclude the middle rigid porphyrin from interaction, as indicated by the similarity with U1·R4-Zn, but this is difficult to predict without a precise 3D model. The same is observed for F1·R4-Zn. Therefore, all the three CD profiles appear very similar, showing pair-wise porphyrin–porphyrin interactions which is independent on the array composition, and the systems give very similar Δε values per porphyrin for all duplexes. Clearly, the increased flexibility of the F-type porphyrin is beneficial for exciton coupling interactions, though the CD spectra look similar to the ones obtained for the R-series. However, the F-series is far more sensitive to changes in the system with changing Δε values per porphyrin for the three different duplexes. Here the differences to the non-metallated counterparts are more striking and indicate very different interactions.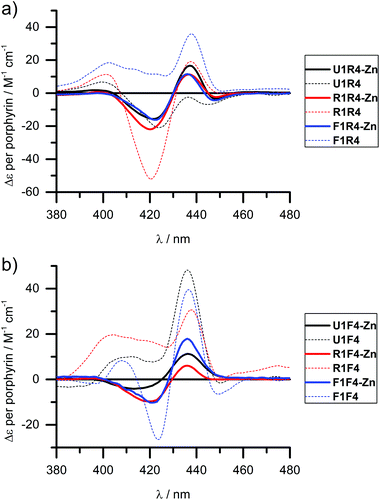 | ||
| Fig. 4 CD spectra of zinc metallated porphyrin arrays, containing either (a) R4-Zn or (b) F4-Zn, in comparison with the non-metallated duplexes. Δε values are given per porphyrin (normalized to the number of porphyrins present). Conditions as in Fig. 2. | ||
Conclusions
Porphyrins are building blocks for DNA based bio-nanotechnology with a wide range of applications, such as electron or energy transfer moieties and lipid anchors. The stability of DNA arrays containing multiple porphyrins is strongly influenced by the probe architecture, in particular single-strand modification vs. zipper arrangement. Here we have evaluated a porphyrin substituted LNA building block which inherently should give a more stable DNA duplex upon hybridization. We have shown that more stable arrays are formed when using three porphyrin-functionalized LNA monomers, compared to arrays based on the natural 2′-deoxyuridine derived building blocks, which is very promising for the formation of stable higher-ordered systems. Both thermodynamic data and CD spectra are complex and show a large dependency on the nature of the linker to the porphyrin and on the architecture of the porphyrin array. General trends indicate that: (i) modifying one DNA strands leads to either less ordered (acetylene linker) or more ordered (propargyl-amide linker) duplexes; (ii) the use of a rigid acetylene linker in a homo-porphyrin zipper-array leads to more ordered structures; (iii) the flexible linker induces less ordered structures in both homo- and hetero-porphyrinic zipper arrays, (iv) mixed zipper arrays are most stable and exceed the stability of the analogous dU-systems; (v) excitonic coupling between the porphyrins is strongly influenced by the nature of the linker and the sequence context but correlates well with the thermodynamic analysis; (vi) the flexible (and longer) linker allows for a better inter-strand interaction and formation of porphyrin-DNA clusters leading to more complex CD signatures. The detailed structure of the DNA and of the porphyrin arrangements in the modified region are not accessible yet, but clearly is affected by the parameters mentioned; the data therefore are valuable to gain insight into relative stability and electronic interactions in such systems.Author contributions
The manuscript was written through contributions of all authors.Acknowledgements
This work was supported by the BBSRC through a Doctoral Training Account (BBSRC-DTA) to DGS, and the University of Southampton. We thank Diamond Light Source for access to beamline B23 (SM5872, SM6703, SM6705) that contributed to the results presented here. Data and fit functions for UV and CD melting analysis can be found at DOI: 10.5258/SOTON/381422.Notes and references
- E. Stulz, Chem. – Eur. J., 2012, 18, 4456–4469 CrossRef CAS PubMed.
- C. Song, Z. G. Wang and B. Q. Ding, Small, 2013, 9, 2382–2392 CrossRef CAS PubMed.
- R. Chhabra, J. Sharma, Y. Liu, S. Rinker and H. Yan, Adv. Drug Delivery Rev., 2010, 62, 617–625 CrossRef CAS PubMed.
- C. Lin, Y. Liu and H. Yan, Biochemistry, 2009, 48, 1663–1674 CrossRef CAS PubMed.
- N. C. Seeman, Nature, 2003, 421, 427–431 CrossRef PubMed.
- J. Bath and A. J. Turberfield, Nat. Nanotechnol., 2007, 2, 275–284 CrossRef CAS PubMed.
- E. Stulz, G. Clever, M. Shionoya and C. Mao, Chem. Soc. Rev., 2011, 40, 5633–5635 RSC.
- R. Schreiber, J. Do, E. M. Roller, T. Zhang, V. J. Schuller, P. C. Nickels, J. Feldmann and T. Liedl, Nat. Nanotechnol., 2014, 9, 74–78 CrossRef CAS PubMed.
- A. Griffith, T. J. Bandy, M. Light and E. Stulz, Chem. Commun., 2013, 49, 731–733 RSC.
- J. R. Burns, J. Zekonyte, G. Siligardi, R. Hussain and E. Stulz, Molecules, 2011, 16, 4912–4922 CrossRef CAS PubMed.
- V. L. Malinovskii, D. Wenger and R. Häner, Chem. Soc. Rev., 2010, 39, 410–422 RSC.
- P. Ensslen and H. A. Wagenknecht, Dalton Trans., 2015, 44, 6715–6718 RSC.
- D. Lindegaard, A. S. Madsen, I. V. Astakhova, A. D. Malakhov, B. R. Babu, V. A. Korshun and J. Wengel, Bioorg. Med. Chem., 2008, 16, 94–99 CrossRef CAS PubMed.
- E. T. Kool, Acc. Chem. Res., 2002, 35, 936–943 CrossRef CAS PubMed.
- J. Chelliserrykattil, H. Lu, A. H. F. Lee and E. T. Kool, ChemBioChem, 2008, 9, 2976–2980 CrossRef CAS PubMed.
- D. A. Malyshev, K. Dhami, T. Lavergne, T. J. Chen, N. Dai, J. M. Foster, I. R. Correa and F. E. Romesberg, Nature, 2014, 509, 385–388 CrossRef CAS PubMed.
- F. Menacher and H. A. Wagenknecht, Eur. J. Org. Chem., 2011, 4564–4570 CrossRef CAS.
- M. Vybornyi, A. L. Nussbaumer, S. M. Langenegger and R. Häner, Bioconjugate Chem., 2014, 25, 1785–1793 CrossRef CAS PubMed.
- T. J. Bandy, A. Brewer, J. R. Burns, G. Marth, T. Nguyen and E. Stulz, Chem. Soc. Rev., 2011, 40, 138–148 RSC.
- M. M. Rubner, C. Holzhauser, P. R. Bohlander and H. A. Wagenknecht, Chem. – Eur. J., 2012, 18, 1299–1302 CrossRef CAS PubMed.
- M. Probst, S. M. Langenegger and R. Häner, Chem. Commun., 2014, 50, 159–161 RSC.
- P. Roethlisberger, F. Wojciechowski and C. J. Leumann, Chem. – Eur. J., 2013, 19, 11518–11521 CrossRef CAS PubMed.
- Y. N. Teo and E. T. Kool, Chem. Rev., 2012, 112, 4221–4245 CrossRef CAS PubMed.
- D. Dziuba, R. Pohl and M. Hocek, Chem. Commun., 2015, 51, 4880–4882 RSC.
- E. Palecek, J. Tkac, M. Bartosik, T. Bertok, V. Ostatna and J. Palecek, Chem. Rev., 2015, 115, 2045–2108 CrossRef CAS PubMed.
- I. Bouamaied, L. A. Fendt, M. Wiesner, D. Häussinger, N. Amiot, S. Thöni and E. Stulz, Pure Appl. Chem., 2006, 78, 2003–2014 CrossRef CAS.
- I. Bouamaied and E. Stulz, Chimia, 2005, 59, 101–104 CrossRef CAS.
- I. Bouamaied and E. Stulz, Synlett, 2004, 1579–1583 CAS.
- I. Bouamaied, L. A. Fendt, D. Häussinger, M. Wiesner, S. Thöni, N. Amiot and E. Stulz, Nucleosides, Nucleotides Nucleic Acids, 2007, 26, 1533–1538 CAS.
- L. A. Fendt, I. Bouamaied, S. Thöni, N. Amiot and E. Stulz, J. Am. Chem. Soc., 2007, 129, 15319–15329 CrossRef CAS PubMed.
- A. Brewer, G. Siligardi, C. Neylon and E. Stulz, Org. Biomol. Chem., 2011, 9, 777–782 CAS.
- I. Bouamaied, T. Nguyen, T. Rühl and E. Stulz, Org. Biomol. Chem., 2008, 6, 3888–3891 CAS.
- T. Nguyen, A. Brewer and E. Stulz, Angew. Chem., Int. Ed., 2009, 48, 1974–1977 CrossRef CAS PubMed.
- M. Endo, M. Fujitsuka and T. Majima, Tetrahedron, 2008, 64, 1839–1846 CrossRef CAS.
- A. W. I. Stephenson, A. C. Partridge and V. V. Filichev, Chem. – Eur. J., 2011, 17, 6227–6238 CrossRef CAS PubMed.
- H. Morales-Rojas and E. T. Kool, Org. Lett., 2002, 4, 4377–4380 CrossRef CAS PubMed.
- S. Sitaula and S. M. Reed, Bioorg. Med. Chem. Lett., 2008, 18, 850–855 CrossRef CAS PubMed.
- M. Balaz, A. E. Holmes, M. Benedetti, G. Proni and N. Berova, Bioorg. Med. Chem., 2005, 13, 2413–2421 CrossRef CAS PubMed.
- M. Balaz, K. Bitsch-Jensen, A. Mammana, G. A. Ellestad, K. Nakanishi and N. Berova, Pure Appl. Chem., 2007, 79, 801–809 CrossRef CAS.
- A. Mammana, T. Asakawa, K. Bitsch-Jensen, A. Wolfe, S. Chaturantabut, Y. Otani, X. X. Li, Z. M. Li, K. Nakanishi, M. Balaz, G. A. Ellestad and N. Berova, Bioorg. Med. Chem., 2008, 16, 6544–6551 CrossRef CAS PubMed.
- M. Balaz, A. E. Holmes, M. Benedetti, P. C. Rodriguez, N. Berova, K. Nakanishi and G. Proni, J. Am. Chem. Soc., 2005, 127, 4172–4173 CrossRef CAS PubMed.
- A. W. I. Stephenson, N. Bomholt, A. C. Partridge and V. V. Filichev, ChemBioChem, 2010, 11, 1833–1839 CrossRef CAS PubMed.
- C. Wellner and H. A. Wagenknecht, Org. Lett., 2014, 16, 1692–1695 CrossRef CAS PubMed.
- M. Balaz, B. C. Li, S. Jockusch, G. A. Ellestad and N. Berova, Angew. Chem., Int. Ed., 2006, 45, 3530–3533 CrossRef CAS PubMed.
- M. Balaz, J. D. Steinkruger, G. A. Ellestad and N. Berova, Org. Lett., 2005, 7, 5613–5616 CrossRef CAS PubMed.
- M. Balaz, B. C. Li, J. D. Steinkruger, G. A. Ellestad, K. Nakanishi and N. Berova, Org. Biomol. Chem., 2006, 4, 1865–1867 CAS.
- M. Endo, M. Fujitsuka and T. Majima, J. Org. Chem., 2008, 73, 1106–1112 CrossRef CAS PubMed.
- A. Onoda, M. Igarashi, S. Naganawa, K. Sasaki, S. Ariyasu and T. Yamamura, Bull. Chem. Soc. Jpn., 2009, 82, 1280–1286 CrossRef CAS.
- K. Berlin, R. K. Jain, M. D. Simon and C. Richert, J. Org. Chem., 1998, 63, 1527–1535 CrossRef CAS.
- T. Le Doan, D. Praseuth, L. Perrouault, M. Chassignol, N. T. Thuong and C. Helene, Bioconjugate Chem., 1990, 1, 108–113 CrossRef CAS PubMed.
- T. Murashima, K. Hayata, Y. Saiki, J. Matsui, D. Miyoshi, T. Yamada, T. Miyazawa and N. Sugimoto, Tetrahedron Lett., 2007, 48, 8514–8517 CrossRef CAS.
- H. D. Li, O. S. Fedorova, W. R. Trumble, T. R. Fletcher and L. Czuchajowski, Bioconjugate Chem., 1997, 8, 49–56 CrossRef CAS PubMed.
- A. Mammana, G. Pescitelli, T. Asakawa, S. Jockusch, A. G. Petrovic, R. R. Monaco, R. Purrello, N. J. Turro, K. Nakanishi, G. A. Ellestad, M. Balaz and N. Berova, Chem. – Eur. J., 2009, 15, 11853–11866 CrossRef CAS PubMed.
- N. Berova, L. D. Bari and G. Pescitelli, Chem. Soc. Rev., 2007, 36, 914–931 RSC.
- M. Balaz, M. De Napoli, A. E. Holmes, A. Mammana, K. Nakanishi, N. Berova and R. Purrello, Angew. Chem., Int. Ed., 2005, 44, 4006–4009 CrossRef CAS PubMed.
- I. Grabowska, D. G. Singleton, A. Stachyra, A. Gora-Sochacka, A. Sirko, W. Zagorski-Ostoja, H. Radecka, E. Stulz and J. Radecki, Chem. Commun., 2014, 50, 4196–4199 RSC.
- M. Endo, N. C. Seeman and T. Majima, Angew. Chem., Int. Ed., 2005, 44, 6074–6077 CrossRef CAS PubMed.
- J. R. Burns, E. Stulz and S. Howorka, Nano Lett., 2013, 13, 2351–2356 CrossRef CAS PubMed.
- J. R. Burns, K. Gopfrich, J. W. Wood, V. V. Thacker, E. Stulz, U. F. Keyser and S. Howorka, Angew. Chem., Int. Ed., 2013, 52, 12069–12072 CrossRef CAS PubMed.
- J. G. Woller, J. K. Hannestad and B. Albinsson, J. Am. Chem. Soc., 2013, 135, 2759–2768 CrossRef CAS PubMed.
- H. Kaur, B. R. Babu and S. Maiti, Chem. Rev., 2007, 107, 4672–4697 CrossRef CAS PubMed.
- R. Varghese and H. A. Wagenknecht, Chem. Commun., 2009, 2615–2624 RSC.
- D. C. Guenther, P. Kumar, B. A. Anderson and P. J. Hrdlicka, Chem. Commun., 2014, 50, 9007–9009 RSC.
- M. E. Østergaard, P. Kumar, B. Baral, D. C. Guenther, B. A. Anderson, F. M. Ytreberg, L. Deobald, A. J. Paszczynski, P. K. Sharma and P. J. Hrdlicka, Chem. – Eur. J., 2011, 17, 3157–3165 CrossRef PubMed.
- P. Kumar, M. E. Østergaard, B. Baral, B. A. Anderson, D. C. Guenther, M. Kaura, D. J. Raible, P. K. Sharma and P. J. Hrdlicka, J. Org. Chem., 2014, 79, 5047–5061 CrossRef CAS PubMed.
- P. M. McTigue, R. J. Peterson and J. D. Kahn, Biochemistry, 2004, 43, 5388–5405 CrossRef CAS PubMed.
- R. Hussain, T. Javorfi and G. Siligardi, J. Synchrotron Rad., 2012, 19, 132–135 CrossRef PubMed.
- K. Datta, N. P. Johnson and P. H. von Hippel, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 17980–17985 CrossRef CAS PubMed.
- O. Romainczyk, B. Endeward, T. F. Prisner and J. W. Engels, Mol. BioSyst., 2011, 7, 1050–1052 RSC.
- T. Nguyen, P. Hakansson, R. Edge, D. Collison, B. A. Goodman, J. R. Burns and E. Stulz, New J. Chem., 2014, 38, 5254–5259 RSC.
- O. Doluca, J. M. Withers, T. S. Loo, P. J. B. Edwards, C. Gonzalez and V. V. Filichev, Org. Biomol. Chem., 2015, 13, 3742–3748 CAS.
- I. J. Lee and B. H. Kim, Chem. Commun., 2012, 48, 2074–2076 RSC.
- C. Wagner and H. A. Wagenknecht, Org. Lett., 2006, 8, 4191–4194 CrossRef CAS PubMed.
- D. Baumstark and H. A. Wagenknecht, Angew. Chem., Int. Ed., 2008, 47, 2612–2614 CrossRef CAS PubMed.
- G. Sargsyan and M. Balaz, Org. Biomol. Chem., 2012, 10, 5533–5540 CAS.
- G. Pescitelli, S. Gabriel, Y. K. Wang, J. Fleischhauer, R. W. Woody and N. Berova, J. Am. Chem. Soc., 2003, 125, 7613–7628 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic procedures for the building blocks and DNA strands, full spectroscopic analysis of the ssDNA and duplex systems. See DOI: 10.1039/c5ob01681a |
| This journal is © The Royal Society of Chemistry 2016 |