 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
FRET enhancement close to gold nanoparticles positioned in DNA origami constructs†
Nesrine
Aissaoui
a,
Kasper
Moth-Poulsen
 a,
Mikael
Käll
b,
Peter
Johansson
c,
L. Marcus
Wilhelmsson
a and
Bo
Albinsson
a,
Mikael
Käll
b,
Peter
Johansson
c,
L. Marcus
Wilhelmsson
a and
Bo
Albinsson
 *a
*a
aDepartment of Chemistry and Chemical Engineering, Chalmers University of Technology, Gothenburg, Sweden. E-mail: balb@chalmers.se
bDepartment of Applied Physics, Chalmers University of Technology, Gothenburg, Sweden
cSchool of Science and Technology, Örebro University, Örebro, Sweden
First published on 5th December 2016
Abstract
Here we investigate the energy transfer rates of a Förster resonance energy transfer (FRET) pair positioned in close proximity to a 5 nm gold nanoparticle (AuNP) on a DNA origami construct. We study the distance dependence of the FRET rate by varying the location of the donor molecule, D, relative to the AuNP while maintaining a fixed location of the acceptor molecule, A. The presence of the AuNP induces an alteration in the spontaneous emission of the donor (including radiative and non-radiative rates) which is strongly dependent on the distance between the donor and AuNP surface. Simultaneously, the energy transfer rates are enhanced at shorter D–A (and D–AuNP) distances. Overall, in addition to the direct influence of the acceptor and AuNP on the donor decay there is also a significant increase in decay rate not explained by the sum of the two interactions. This leads to enhanced energy transfer between donor and acceptor in the presence of a 5 nm AuNP. We also demonstrate that the transfer rate in the three “particle” geometry (D + A + AuNP) depends approximately linearly on the transfer rate in the donor–AuNP system, suggesting the possibility to control FRET process with electric field induced by 5 nm AuNPs close to the donor fluorophore. It is concluded that DNA origami is a very versatile platform for studying interactions between molecules and plasmonic nanoparticles in general and FRET enhancement in particular.
Introduction
Förster resonance energy transfer (FRET) is based on a well-defined distance-dependent dipole–dipole interaction within a donor–acceptor pair. FRET involves non-radiative energy transfer between an electronically excited donor, D, and a ground state acceptor molecule, A.1 The concept has been used in numerous studies as a spectroscopic ruler to measure the distance between donor and acceptor at the nanometer length scale,2–4 and, thus, has become a useful tool to study structure and dynamics of biomacromolecules.5,6 Moreover, FRET is the dominant energy transfer mechanism in photosynthesis and other light harvesting systems,7–10 in some photovoltaics,11 and in biosensing.12 The dipole–dipole interaction in a FRET system depends on the optical properties of the coupled donor and acceptor pair, on the distance separating them, R, and on the relative orientation of their transition dipole moments.13In the presence of metallic nanoparticles, the effect of the localized surface plasmons (LSP) in modifying FRET efficiencies has been investigated in both experimental14–17 and theoretical18–20 studies. Contradictory results about LSP enhanced FRET efficiency have been shown to depend on the spectral and geometrical properties such as size and shape of the metallic nanoparticle (MNP),17,21 or position and orientation of the fluorophore relative to the MNP.15,17,22 Other studies have shown that the spontaneous emission rate of the luminescent entity, including radiative and non-radiative rates, can be altered by the effect of LSP.23–25 Ever since the pioneering works of Purcell and Drexhage,26,27 different nanophotonic geometries have been developed to study how the Förster energy transfer is modified by the optical environment using microcavities,28–30 nanoantennas,31 metallic films,32,33 microresonators,34,35 or photonic crystals.36 Many of these studies have argued that the FRET rate might be entirely controlled by the localized surface plasmons.28,30,31,33–35 However, disparity in the observed results can be related to the lack of control of a multitude of experimental parameters such as donor–acceptor distance, cross-talk between neighboring FRET pairs, donor–acceptor transition dipole moment orientation, spatial configuration, etc.22
To better understand the LSP-coupled FRET mechanism and determine the conditions for enhancement of the FRET process, it is critical to control the spatial organization of the metallic nanoparticles relative to the donor–acceptor FRET pair. DNA origami has been demonstrated to be a versatile platform for positioning plasmonic nanostructures and fluorophore molecules with nanometer precision.37–42 In this way, DNA origami nanostructures have been used to investigate (i) distance-dependence of energy transfer between FRET pairs,43,44 (ii) fluorophores or quantum dots quenched by metal nanoparticles,41,42,45–48 (iii) SERS effects,40,49 and (iv) the controlled assembly of plasmonic nanostructures for (bio)nanophotonic applications.50
In this study, a rectangular DNA origami construct has been used to systematically investigate the distance-dependent interactions induced by the local field of a 5 nm gold nanoparticle (AuNP) in close proximity to a FRET pair consisting of Alexa Fluor 568 as donor and Atto 647N as acceptor. The distances were varied by changing the position of the donor while maintaining fixed locations of the acceptor and AuNP (see Fig. 1a for schematic drawing). We first verified that nanoparticles and fluorophores were situated on the expected sites on the origami through estimates of the FRET efficiencies in absence of AuNP and characterized the surface morphology using atomic force microscopy (AFM). Secondly we investigated the distance dependent donor–AuNP interactions. Finally, we studied the complete system containing a donor–acceptor couple in the vicinity of the AuNP by time-resolved and steady-state fluorescence. In order to describe the interaction between the donor and acceptor in presence or absence of the 5 nm AuNP, we considered a simple additive model (see Fig. 2). In this model we hypothesize that the excited donor is quenched by a combination of energy transfer to the acceptor and to the AuNP. Our interest is to understand if the presence of AuNP induces an enhanced energy transfer, i.e. if there is a larger degree of donor quenching than accounted for by the individual energy transfer rates to the acceptor and AuNP. The origin of the observed energy transfer enhancement is discussed in terms of changes in the donor decay rates.
Results and discussion
Positioning of dyes and gold nanoparticles using DNA origami
Assembly of donor–acceptor FRET pairs at predefined locations with nanometer spatial resolution, determined by the distance between the DNA staple strands, was realized using a previously reported rectangular origami construct (100 × 70 nm).51 Specific DNA strands were modified with the fluorophores Alexa Fluor 568 as donor (D) and Atto 647N as acceptor (A) (see ESI, section 2,† for DNA strands sequences details), and mixed with the non-modified staple strands and the M13mp18-viral single stranded scaffold.51 Attachment of 5 nm gold nanoparticles (AuNP) was obtained by extending three staples (capture strands) by 15 nucleotides, complementary to the single strands used to functionalize the AuNP (see Fig. S1†). The use of three capture strands increases the binding strength between the AuNP and the DNA origami and reduces the conformational freedom.41 Details of the AuNP modification and conjugation to the DNA origami are given in the Experimental section. The conjugation of AuNP to the DNA origami was performed according to published procedures with some modifications.52–54Fig. 1a is a schematic illustration of the DNA origami design showing the locations of the modified strands with donor and acceptor fluorophores and AuNP at opposite sides of the DNA origami. The design, using both sides of the DNA origami, is chosen to prevent the dyes from direct contact with the AuNP, thereby avoiding strong fluorescence quenching effects.55 The successful formation of AuNP–DNA origami conjugates was clearly observed through AFM imaging (Fig. 1b), showing the rectangular DNA origami structure with the AuNP at the predefined location. Cross section profile indicates the approximate diameter of AuNP ∼ 5 nm and DNA origami dimensions (2 nm is the expected thickness of the DNA origami and 70 nm is the lateral distance).In this study, the system is designed such that the donor and acceptor are located at different distances to each other, and at the same time in the vicinity of a single 5 nm AuNP. In these three-“particle” geometries (D + A + AuNP), the locations of the acceptor and the AuNP are fixed with a distance of A–AuNP = 8.5 ± 0.3 nm between the acceptor and gold nanoparticle surface while the donor–acceptor distance is varied. All possible combinations of D, A, and AuNP were prepared in order to separately investigate the effects of the acceptor, the AuNP and the combination of acceptor and AuNP on the excited donor (Fig. 3).
From the design, distances between the dye molecules and between the dyes and the AuNP surface could be estimated and are given in Table 1. In the estimated distances, uncertainties are calculated by considering a random conformational orientation of the linker attaching the fluorophores to the DNA strands (see ESI, section 3†).
| Sample | R (nm) | τ (ns) | f |
k
T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e (ns−1) e (ns−1) |
|---|---|---|---|---|
| a Estimated distances from the donor to either the acceptor or the surface of the AuNP. Uncertainties are estimated from the design (see ESI, section 3). b Average fluorescence lifetimes from tri-exponential fits. Errors are estimated from inspecting the reduced chi-square values’ sensitivity to the fitted lifetimes (see Experimental section). c Fraction unquenched donor lifetime from tri-exponential fits, see Experimental section. d Fraction unquenched fixed to 0.10 (10%), see Experimental section. e Rate constants are calculated as kT(DX) = 1/τDX − 1/τD where X is A, Au or A + Au as appropriate. f Enhanced energy transfer due to presence of the AuNP: kenh = kT(DA–Au) − (kT(DA) + kT(D–Au)). | ||||
| D1 | 3.4 ± 0.05 | |||
| D1–Au | 9.1 ± 0.3 | 2.1 ± 0.1 | 0.10d | 0.18 ± 0.02 |
| D1A | 4 ± 1.8 | 0.52 ± 0.07 | 0.10 ± 0.03 | 1.6 ± 0.3 |
| D1A–Au | 0.34 ± 0.05 | 0.03 ± 0.01 | 2.6 ± 0.4 | |
| enhf | 0.8 ± 0.5 | |||
| D2 | 3.6 ± 0.05 | |||
| D2–Au | 10.2 ± 0.3 | 2.5 ± 0.1 | 0.10d | 0.12 ± 0.02 |
| D2A | 7.7 ± 1.7 | 2.9 ± 0.1 | 0.0 ± 0.01 | 0.07 ± 0.01 |
| D2A–Au | 1.4 ± 0.08 | 0.12 ± 0.04 | 0.44 ± 0.04 | |
| enhf | 0.25 ± 0.05 | |||
| D3 | 3.7 ± 0.05 | |||
| D3–Au | 11.5 ± 0.5 | 1.9 ± 0.1 | 0.10d | 0.26 ± 0.03 |
| D3A | 7.7 ± 1.7 | 2.0 ± 0.2 | 0.10d | 0.23 ± 0.05 |
| D3A–Au | 1.3 ± 0.08 | 0.12 ± 0.06 | 0.50 ± 0.05 | |
| enhf | 0.01 ± 0.07 | |||
| D4 | 3.4 ± 0.05 | |||
| D4–Au | 15.5 ± 0.7 | 3.3 ± 0.1 | 0.0 | 0.01 ± 0.01 |
| D4A | 13 ± 2 | 3.3 ± 0.1 | 0.0 | 0.01 ± 0.01 |
| D4A–Au | 3.1 ± 0.1 | 0.0 | 0.03 ± 0.01 | |
| enhf | 0.01 ± 0.02 | |||
Normalized emission and absorption spectra of the donor and acceptor together with the absorption spectrum of 5 nm AuNP are shown in Fig. 4. The characteristic Förster distance for energy transfer between the donor and acceptor, R0 = 6.4 nm, is calculated from the spectral overlap including a donor fluorescence quantum yield of 0.69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 56 (see Experimental section, eqn (2)).
56 (see Experimental section, eqn (2)).
Fig. 4b shows an example of steady-state emission spectra of the donor–acceptor FRET pair D2A that have an intermediate D–A distance of 7.7 ± 1.7 nm. The donor has a maximum emission at 601 nm and the acceptor a maximum emission at 665 nm. For the example shown in Fig. 4b, energy transfer is signaled by significant decrease in donor emission and increase of acceptor emission. Steady-state emission spectra and fluorescence decays for all combinations of D, A, and AuNP are shown in Fig. 5.
 | ||
| Fig. 5 (a) Steady-state fluorescence spectra normalized to the DNA absorption at 260 nm, (b) donor fluorescence decays monitored at 603 nm of DNA origamis labelled with single fluorophores (donor at specific position D1, D2, D3, and D4), and donor–acceptor FRET pairs at the different distances (D1A, D2A, D3A, and D4A) with or without AuNPs. The black lines are numerical fits convoluted by the instrument response function (IRF, gray line). The different combinations: D, D–Au, DA, and DA–Au in (a) and (b) are shown with green, red, blue, and orange lines, respectively. Estimated distances between donor and AuNP surface and between donor–acceptor FRET pairs are collected in Table 1. Details of distances calculations and normalization of steady-state emission spectra are described in ESI sections 3 and 7,† respectively. | ||
For samples with only a single donor modification, the lifetimes were, as expected, obtained by fitting to a single exponential model. It should be noted that identical lifetimes were obtained for the donor attached at different locations on the DNA origami (see ESI, Fig. S6†) and were also very close to the value reported for Alexa Fluor 568 in buffer solution τD ∼ 3.6 ns,56 indicating that the DNA origami itself does not affect the average lifetime of the attached fluorophore and that no aggregates are formed under the experimental preparation.57 A tri-exponential fitting was used for all but the least quenched samples containing the acceptor and/or AuNP. One of the exponential components was fixed to the lifetime of the unquenched donor and its fraction describes the amount of incompletely labelled structures (e.g. an origami lacking the acceptor chromophore). The other two (shorter) lifetimes describe the distribution of transfer rates as a consequence of the conformational flexibility of the construct. Average quenched lifetimes were based on the amplitude weighted average of these two lifetimes (see the Experimental section).
The fluorescence decays of the samples with donor and acceptor (without AuNP) could be compared to the donor only samples to estimate the rate of energy transfer as explained in the Experimental section. These rate constants are collected in Table 1 and show the expected strong distance dependence. In addition, the steady state emission spectra qualitatively show the same trend with higher degree of donor quenching and acceptor sensitization at shorter distance (Fig. 5a). In order to verify the origami design, we experimentally estimate the donor–acceptor distances (R) through the measured energy transfer rates and the Förster equation (eqn (5) in the Experimental section):
 | (1) |
 | ||
| Fig. 6 Donor–acceptor distances calculated from lifetime measurements (○) and compared to the design (●). Uncertainties in distances are estimated from the design (see ESI, section 3† for details about the distance calculation) and estimated errors in the fluorescence lifetimes are discussed in the experimental section. | ||
Donor–AuNP energy transfer
In order to ensure maximum assembly yield and at the same time prevent unspecific quenching due to high amount of AuNPs dispersed in solution, molar ratios between 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (AuNP
1 (AuNP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA origami) have been tested (see ESI section 5†). In this experiment the donor D1 was kept at a fixed distance to the AuNP surface (∼9 nm). Fluorescence lifetime measurements indicated similar donor lifetime quenching when a stoichiometric molar ratio (1
DNA origami) have been tested (see ESI section 5†). In this experiment the donor D1 was kept at a fixed distance to the AuNP surface (∼9 nm). Fluorescence lifetime measurements indicated similar donor lifetime quenching when a stoichiometric molar ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) between AuNP and DNA origami was used or in the presence of a slight excess of AuNPs (up to 2
1) between AuNP and DNA origami was used or in the presence of a slight excess of AuNPs (up to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of AuNP
1 molar ratio of AuNP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA origami). To ensure sufficient yield of the DNA origami–AuNPs conjugate and at the same time avoid unspecific quenching of the dyes, all subsequent measurements were performed with a molar ratio of AuNP
DNA origami). To ensure sufficient yield of the DNA origami–AuNPs conjugate and at the same time avoid unspecific quenching of the dyes, all subsequent measurements were performed with a molar ratio of AuNP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA origami = 2
DNA origami = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
The absorbance of the 5 nm AuNP overlaps with the donor emission but less significantly with the acceptor (Fig. 4a). This is expected to lead to a pronounced coupling between donor and AuNP, while weaker interactions are expected with the acceptor. This was also observed experimentally (ESI, Fig. S5†) by comparing the decrease in fluorescence intensity of donor and acceptor dyes at approximately the same distance from the AuNP ∼ 9 nm.
Once the origami is prepared and the nanoparticles and fluorophores are verified to be situated on the expected sites on the DNA origami, the effects of the AuNP on the energy transfer mechanism can be investigated. First, energy transfer from the various donors to the AuNP was investigated followed by studying the complete system comprising the pair of donor and acceptor dyes in presence of the AuNP. In all these measurements the energy transfer rates of the different donor–acceptor or donor–AuNP constructs were obtained from time resolved fluorescence and were also compared to the corresponding changes in steady-state fluorescence intensities (Fig. 5). Rate constants for energy transfer are collected in Table 1 and calculated as described in the Experimental section.
In this study, the donors are designed to be located at distances between 9 and 15 nm from the AuNP. From Table 1, a significant quenching of the donor fluorescence by the AuNP is observed for the shortest distance (D1–Au) and tapering off with increasing distance. This is the expected general distance dependence and in Fig. 7 the experimental rate constants are displayed in a double logarithmic plot and fitted to straight lines. The optimized slope of the donor–AuNP distance dependence is −5.7 which is fairly close to the value (−6) expected from the FRET model for energy transfer. In addition, from the intercept of Fig. 7, an estimate of the characteristic transfer distance, d0 = 9.2 nm, is obtained for the interaction between Alexa Fluor 568 and the 5 nm gold nanoparticle. Very similar results (d0 = 9.3 nm) are obtained if a fit with fixed slope, n = 6, is used. Here, by considering the 5 nm AuNP to be a molecular acceptor, the d0-value (R0-value) could be estimated from the 1/R6 distance dependence characteristic of the FRET model. The characteristic transfer distance obtained from the spectral overlap was estimated to be R0 = 12.5 nm (eqn (6) in Experimental section) which is quite different from the d0 = 9.3 nm found for the fit with fixed slope n = 6. However, since the Förster model assumes point dipoles situated in the center of the chromophores, for the AuNP with 5 nm diameter, the actual distance between the donor and the AuNP surface is close to the value found experimentally also with the Förster model. By considering the NSET model for energy transfer to small AuNPs,58 a line with slope = −4 in Fig. 7 fits the experimental data slightly worse but considering the quite large uncertainties it cannot be excluded. If a fit with fixed slope, n = 4, is used, very similar characteristic distance (d0 = 8.4 nm) is obtained. This value could be compared to the corresponding value estimated by the simple NSET model (eqn (7) in Experimental section) giving d0 = 8.3 nm. In summary, in spite of the quite large relative errors in the estimated rates at long distances, both the FRET and NSET models can be applied to estimate the characteristic transfer distance d0 for energy transfer between the molecular donor and the 5 nm AuNP. It is reassuring that both models yield quite similar characteristic distances and that these distances agree with the respective theoretical estimates.
 | ||
| Fig. 7 Double logarithmic plot of the distance dependence for energy transfer between donor and AuNP. RD–Au is the estimated donor to AuNP surface distance and linear fits to the generalized Förster equation (eqn (5) in Experimental section) are shown for an optimized slope of n = 6.5 (solid), for the Förster model with n = 6 (dashed), and for the NSET model with n = 4 (dot-dashed). The corresponding characteristic distances are estimated from the intercepts to be d0 = 9.2, 9.3, and 8.4 nm, respectively. | ||
It should be noted from Fig. 7 and the values of Table 1, that the sample D3–Au with slightly larger nanoparticle–dye separation than D2–Au shows larger energy transfer rate. This is unexpected but could be related to static quenching of a fraction of the D3 dyes on the DNA origami. In fact, we observe a lower fluorescence quantum yield (cf.Table 2) while the lifetime of the D3 dye is similar to the other positions. In addition, fluorescence anisotropy measurements (not shown) show that the D1, D2 and D4 dyes are freely rotating (anisotropy close to zero) while the D3 dye has more restricted rotational mobility (anisotropy of 0.08). Although not a full explanation, this observation might in turn indicate partial stacking of the D3 fluorophore with the DNA bases (usually guanine) which indeed many times lead to static quenching of dyes.59–61 Restricted mobility might also lead to changes in transfer rates due to both distance and orientational factors related to this unexpected behavior.
| Sample | Φ f (D)a | Φ f (D–Au)a | k enh(rad)b/ns−1 | k enh/ns−1 |
|---|---|---|---|---|
a Estimated from the steady emission spectra in Fig. 5a and relative to the fluorescence quantum yield of Alexa Fluor 568 (Φf = 0.69).56
b Rate constant for the increased radiative rate of the donor calculated as: 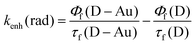 .
c Negative values are due to cancelation errors and should be regarded as negligible contributions. .
c Negative values are due to cancelation errors and should be regarded as negligible contributions.
|
||||
| AD1–Au | 0.67 | 0.57 | 0.08 | 0.84 |
| AD2–Au | 0.62 | 0.38 | −0.02c | 0.25 |
| AD3–Au | 0.45 | 0.27 | 0.02 | 0.01 |
| AD4–Au | 0.69 | 0.58 | −0.03c | 0.01 |
Donor–acceptor energy transfer in presence of AuNP
In the three “particle” complete systems with donor, acceptor and AuNP we expect that both the acceptor and AuNP contribute to the donor quenching. One important question is if, in addition to the sum of these two energy transfer channels, there is also an indirect enhancement of the energy transfer caused by the presence of the AuNP. In Table 1, for each donor entry the experimentally determined rate constants for energy transfer are complemented by the difference between the rate for the “complete” DA–Au system and the sum of the DA and D–Au systems. This difference is denoted enh for enhanced energy transfer caused by the presence of the AuNP. If the individual measurements of the donor quenching in the DA and D–Au samples add up to the quenching measured for the complete DA–Au (i.e. if kT(DA–Au) = kT(DA) + kT(D–Au)) we don't have any enhancement of the energy transfer. On the other hand, if the rate constant for the complete DA–Au sample is larger than the sum, the difference could be attributed to an enhancement of energy transfer (kenh = kT(DA–Au)) − (kT(DA) + kT(D–Au)). For the shortest donor–acceptor distance there is a substantial difference in the enhanced total energy transfer rate. This enhancement decreases rapidly in absolute terms with increasing donor–acceptor distance and becomes negligible for the largest separation. For the intermediate donor–acceptor distances (D2A–Au and D3A–Au) the enhancement is still significant. This shows that the donor quenching in these three “particle” systems is not merely the sum of the pairwise interactions between donor/acceptor and donor/AuNP.FRET rate enhancement in the presence of gold nanoparticle
The presence of the gold nanoparticle clearly has a significant influence on the rate of energy transfer between the donor and acceptor. There are two ways that the presence of the AuNP influences the excited donor, either through increased intrinsic decay rate of the donor or enhanced energy transfer to the acceptor. From measurements of the change in lifetimes and steady-state emission intensities for the donor and donor–AuNP samples we could directly estimate the change in the donor radiative rate constant (kenh(rad), Table 2). This change signals how the AuNP directly influences the donor and can be compared to our observed enhanced energy transfer rate, kenh. Note that kenh and kenh(rad) are indeed two separate quantities. kenh is the increase in FRET rate due to the presence of the gold nanoparticle, kenh = kFRET − k(0)FRET where superscript (0) refers to the situation without the AuNP, (i.e. kFRET = kT(DA–Au) − kT(D–Au) and k(0)FRET = kT(DA) in terms of the experimental quantities defined above), while kenh(rad) is the increase in the rate of radiative decay involving energy transfer from the donor to the far field when the Au particle is present, kenh(rad) = krad − k(0)rad. While separate, these two enhancements are at the same time related in that they refer to the same geometric arrangement of the donor molecule and the Au particle, and therefore can be expected to vary in a similar way as the donor–AuNP distance changes. For the different distances the radiative rate enhancement is close to negligible. The enhancement effect is therefore attributed to be dominated by increased non-radiative (FRET) decay rate. For the D1A–Au sample with the shortest donor–acceptor (and donor–AuNP) distance there is a significant enhancement of the energy transfer and this is paralleled by a slightly increased radiative decay rate. The FRET rate enhancement is about ten times larger than the increased radiative rate for this shortest distance. For the longer distances the observed enhancements are much smaller and the radiative effects seem to be negligible. However, the FRET enhancements for the intermediate distance in D2A–Au are still measurable.For the longest distances the effect is marginal in absolute terms and the inherent uncertainties in the rate constants makes a quantitative comparison between radiative and FRET effects difficult. It could be noted that the total enhancement in relative terms, i.e. relative to the total decay rate in the DA–Au constructs, is fairly constant, about 30–50% for all distances (excluding D3). However, as stated above, given the weakness of the effect at the largest distance it is difficult to justify a mechanistic discussion at this point. We are planning to expand this study to bind dimeric AuNP constructs (nanogaps) and to include larger gold nanoparticles on the DNA origami to investigate if the enhancement effects could be extended to larger distances.
A different illustration of the enhanced energy transfer in presence of AuNP at different donor–acceptor (and donor–AuNP) distances is shown in Fig. 8a. Similarly to the radiative changes, the highest non-radiative changes of the donor are observed at the shortest distances to the AuNP (Table 2). These results reflect the influence of the 5 nm AuNP to influence the FRET process as has been shown for other nanophotonic structures,25,62 and indicate that alteration of donor rates is strongly distance dependent.23,24,63
Moreover, as has been argued in recent papers,30,31,64 a linear relationship (Fig. 8b) between the FRET rate in DA–Au and the energy transfer rate in D–Au systems indicates the possibility to control FRET rates through the modification of the electromagnetic field induced by the 5 nm AuNP in close proximity to the donor fluorophore. These studies indicated that the FRET can be controlled by the photonic environment. There is in the literature an ongoing debate about the role played by the local photon density of states (LDOS) in FRET, claiming linear28,30,31,61 as well as non-linear33 relations between the LDOS and the FRET rate. Here it should be pointed out that while the rate of spontaneous emission is proportional to the photon LDOS at the emission frequency of an excited molecule, the FRET rate depends on the response, at the emission frequency, of a wide spectrum of photon modes. This is because the FRET process acting at very short donor–acceptor distances involves photons of a large range of wavelengths. Hence, as discussed for example in ref. 33, spontaneous emission rates and FRET rates need not be linked to each other. However, in a lot of cases involving metal nanoparticles, enhancements of the photon mode density can occur over a wide range of frequency and lead to both increased rates of spontaneous emission and FRET, as this study, as well as those of ref. 30 and 31, indicate.
Experimental section
Materials
M13mp18 scaffolds were purchased from Bionordika (Sweden), unmodified staple strands from DNA Technology (Denmark), and fluorescently modified staple strands purified by HPLC were purchased from ATDBio (UK). Tris base, acetic acid, EDTA, 2 mM, magnesium acetate, boric acid, NaCl, bis(p-sulfonatophenyl) phenylphosphane dihydrate dipotassium salt (BSPP), tris(2-carboxyethyl)phosphine hydrochloride (TCEP), and 5 nm gold nanoparticles were purchased from Sigma-Aldrich (Sweden). Water used for all experiments was ultrapure water (Milli-Q, Millipore, Sweden). Amicon ultra-0.5 centrifugal filter units (100 kDa) were purchased from Millipore (Germany), and G25 micro-spin columns from Healthcare (UK).DNA origami structure
The rectangular DNA origami are folded as described in Rothemund's original rectangular design.51 The structures are formed using a single stranded M13mp18 scaffold strand at a concentration of 10 nM with 40–70 times excess of unmodified staple strands, or fluorescently modified staple strands (Alexa Fluor 568 and ATTO 647N). The self-assembly of DNA origami is performed in 1× TAE-Mg2+ buffer (Tris base, 40 mM; acetic acid, 20 mM; EDTA, 2 mM; and magnesium acetate, 12.5 mM; pH 8.0) by thermal annealing and slow cooling from 85 °C to 5 °C over 4 hours in a thermocycler. At the end, the assembled origami is washed three times with 1× TAE-Mg2+ buffer using Amicon filters units (100 kDa MWCO) at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm speed for 30 min each time.
000 rpm speed for 30 min each time.
Three capture strands are extended from their ends with 15-base-long sticky ends to hybridize the complementary DNA functionalized AuNP.41,53,65 In all origami–AuNP conjugated samples, the same 3 capture strands (r-3t14f, r-5t14e, and r-5t14f with the sequence TGACCAATTGACCGATT at the 5′ end) are used to attach the AuNP.
DNA origami samples labelled with donor and/or acceptor dyes (Alexa Fluor 568 and Atto 647N, respectively) were obtained by using the modified staple strand r-5t14e with Atto 647N, and different DNA staple strands labelled with Alexa Fluor 568, for different donor locations, i.e., D1, D2, D3, and D4 for r-5t16e, r-5t10f, r-5t14f, and r-5t16f, respectively.
Functionalization of the gold nanoparticles
5 nm gold nanoparticles were purchased from Sigma Aldrich (Sweden). The procedure of modification used in this study is based on common protocols reported in the literature.37,65–67(i) AuNP were stabilized through replacement of citrate on the surface with bis(p-sulfonatopheny) phenylphosphane dihydrate dipotassium salt (BSPP) by adding 3 mg per 10 mL AuNP. After overnight incubation, the AuNPs were concentrated by adding slowly 370 mg of NaCl under stirring until the color changed from deep burgundy to light purple. The supernatant was carefully removed after centrifugation for 1 h at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm. AuNPs were then resuspended in 200 μl of BSPP (3 mg in 10 ml ultrapure water), and 200 μl of methanol were added, the supernatant is removed after centrifugation (1 h at 15
000 rpm. AuNPs were then resuspended in 200 μl of BSPP (3 mg in 10 ml ultrapure water), and 200 μl of methanol were added, the supernatant is removed after centrifugation (1 h at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm). Finally, AuNPs were resuspended into 200 μL BSPP solution. The concentration of the 5 nm AuNPs was estimated from the absorption at 520 nm.
000 rpm). Finally, AuNPs were resuspended into 200 μL BSPP solution. The concentration of the 5 nm AuNPs was estimated from the absorption at 520 nm.
(ii) The disulfide bond in the thiol-modified oligonucleotides was reduced by adding 20 mM tris(2-carboxyethyl)phosphine hydrochloride (TCEP) solution in water to DNA solution using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 vol/vol ratio and incubating at room temperature for 1 h. The unreacted TCEP was removed using G25 micro-spin columns (Healthcare, UK).
1 vol/vol ratio and incubating at room temperature for 1 h. The unreacted TCEP was removed using G25 micro-spin columns (Healthcare, UK).
(iii) Monothiol-modified oligonucleotides and phosphinated AuNPs were incubated at a DNA to Au molar ratio of more than 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in 0.5× TBE buffer (89 mM Tris base, 89 mM boric acid, 2 mM EDTA, pH 8.0) containing 50 mM NaCl for at least over night at room temperature.
1 in 0.5× TBE buffer (89 mM Tris base, 89 mM boric acid, 2 mM EDTA, pH 8.0) containing 50 mM NaCl for at least over night at room temperature.
AuNP–DNA conjugates were washed 3 times by centrifugation (45 min at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm each time) using 0.5× TBE buffer to remove the extra free oligonucleotides. The concentration of these AuNP–DNA conjugates was estimated from the absorption at ∼520 nm using a nanodrop UV-vis spectrophotometer (Thermo scientific, Sweden). Freshly prepared, fully covered AuNPs did not precipitate in 1× TAE-Mg2+ buffer which is preferable for the formation of DNA origami.
000 rpm each time) using 0.5× TBE buffer to remove the extra free oligonucleotides. The concentration of these AuNP–DNA conjugates was estimated from the absorption at ∼520 nm using a nanodrop UV-vis spectrophotometer (Thermo scientific, Sweden). Freshly prepared, fully covered AuNPs did not precipitate in 1× TAE-Mg2+ buffer which is preferable for the formation of DNA origami.
Gold nanoparticles binding
Preformed DNA origami structures were mixed with DNA-functionalized AuNPs using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio of the DNA nanostructures to gold nanoparticles. The mixture was cooled from 40 °C to 22 °C over night.53,66
2 molar ratio of the DNA nanostructures to gold nanoparticles. The mixture was cooled from 40 °C to 22 °C over night.53,66
AFM characterization of origami nanostructures
10 μL of 1 nM DNA origami solution was deposited on a freshly cleaved mica surface for 5 min. The sample was then rinsed with water and gently dried under nitrogen gas flow. Images were recorded under tapping mode in air, using a Dimension ICON scanning probe microscope (Bruker, Massachusetts, USA) with NP-S oxide-sharpened silicon nitride tip (NT-MDT, Sweden). The AFM image showed in this paper is flattened raw data.Steady state absorption and fluorescence measurements
Steady state absorption and fluorescence measurements were performed using a Varian Cary 5000 UV-vis spectrophotometer and a SPEX fluorolog 3 fluorimeter, respectively. The samples were placed in a 50 μL quartz cell with 3 mm path length. The fluorescence spectra for FRET were collected over a broad range of excitation and emission wavelengths, i.e., excitation spectra (λex = 400–655 nm, λem = 665) and emission spectra (λex = 575 nm, λem = 585–800 nm). For quantitative evaluation, the steady-state spectra were normalized to the DNA absorbance at 260 nm (ESI, section 7†). The effect of AuNPs absorption on DNA absorbance was also eliminated according to the method by Jennings et al.68 (ESI, section 7†). It should be noted that the correction factor of the emitted light passing through the sample at λex = 575 nm due to the inner-filter effect, which is function of the sample absorbance and the cuvette geometry,69 was calculated. The calculated errors are negligible (lower than 0.1%) because of the low measured absorbance values (<0.03) at λex = 575 nm.Time-resolved fluorescence
Fluorescence lifetimes were determined using time correlated single photon counting. The samples were excited using a 560 nm pulsed laser diode (PicoQuant GMBA). The photons were collected by a thermoelectrically cooled microchannel plate photomultiplier tube (MCP-PMT R3809U-50; Hamamatsu) and fed into a multichannel analyzer with a minimum of 1024 channels. 2500 counts were recorded in the top channel. The fluorescence decay curves, measured at 603 nm, were fitted to single or multi-exponential expressions through iterative re-convolution with the IRF using the program FluoFit Pro v.4 (PicoQuant GMBA).Fluorescence lifetime analysis
For donor–acceptor labeled DNA samples non-exponential decays are often observed. The reasons for this could be multifold but the most likely candidates are (1) the flexibility of the dye conjugation yielding a distribution in distances and (2) incomplete dye labelling. In the former case for a well behaved donor–acceptor couple with transfer rates given by the Förster equation, a distribution of rates as a consequence of the distribution in distances could sometimes be fitted. In this way distribution of distances in double stranded DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 and small DNA nanoconstructs71 have been estimated through analysis of time-resolved fluorescence. For incomplete labeling with samples having a (small) fraction of molecules lacking the acceptor a bi-exponential decay is expected where one of the lifetimes is identical to the reference lifetime for the donor only construct and the other, shorter lifetime, is the one related to the energy transfer rate. In reality both of these sources for deviation from single exponential decay operate in parallel and are often very difficult to separate. In our origami constructs we observe non-exponential decays for all double (DA and D–AuNP) and triple (DA–AuNP) modified samples except for the least quenched ones. Attempts to fit to distribution of distances, including a fraction incompletely labelled, worked in a few cases but not for the whole set of distances. We therefore decided to fit all the fluorescence decays (Fig. 5b) for the doubly and triply modified samples with a tri-exponential model with one of the lifetimes fixed to the unquenched donor lifetime (∼3.6 ns). The remaining two lifetimes are used to describe the distribution of transfer rates due to the conformational flexibility of the construct. The average lifetimes in Table 1 are calculated from the amplitude weighted average of the two shortest lifetimes describing the energy transfer. The amplitude of the fixed unquenched lifetime is a measure of the amount of incomplete labelling and is expected to be quite small. For the less quenched samples with large donor–acceptor (AuNP) distances there is sometimes an ambiguity between the fixed lifetime and the distribution of lifetimes and we decided to fix the fraction of the unquenched decay to 0.10 (10%) in a few cases. Quality of the fits was judged by inspecting the residuals and reduced chi-squares (χr2) values. Error estimates were made through varying the fitting parameters and establishing χr2 – surfaces (e.g. parameters are considered correct if the χr2 value is below 1.3). Naturally, in a 3-exponential fit there are many sets of parameters that yield similarly good fits. It turned out, however, that many reasonable statistically significant fits yielded very similar average quenched lifetime so the relative uncertainty in this important variable was quite low (see Table 1).
70 and small DNA nanoconstructs71 have been estimated through analysis of time-resolved fluorescence. For incomplete labeling with samples having a (small) fraction of molecules lacking the acceptor a bi-exponential decay is expected where one of the lifetimes is identical to the reference lifetime for the donor only construct and the other, shorter lifetime, is the one related to the energy transfer rate. In reality both of these sources for deviation from single exponential decay operate in parallel and are often very difficult to separate. In our origami constructs we observe non-exponential decays for all double (DA and D–AuNP) and triple (DA–AuNP) modified samples except for the least quenched ones. Attempts to fit to distribution of distances, including a fraction incompletely labelled, worked in a few cases but not for the whole set of distances. We therefore decided to fit all the fluorescence decays (Fig. 5b) for the doubly and triply modified samples with a tri-exponential model with one of the lifetimes fixed to the unquenched donor lifetime (∼3.6 ns). The remaining two lifetimes are used to describe the distribution of transfer rates due to the conformational flexibility of the construct. The average lifetimes in Table 1 are calculated from the amplitude weighted average of the two shortest lifetimes describing the energy transfer. The amplitude of the fixed unquenched lifetime is a measure of the amount of incomplete labelling and is expected to be quite small. For the less quenched samples with large donor–acceptor (AuNP) distances there is sometimes an ambiguity between the fixed lifetime and the distribution of lifetimes and we decided to fix the fraction of the unquenched decay to 0.10 (10%) in a few cases. Quality of the fits was judged by inspecting the residuals and reduced chi-squares (χr2) values. Error estimates were made through varying the fitting parameters and establishing χr2 – surfaces (e.g. parameters are considered correct if the χr2 value is below 1.3). Naturally, in a 3-exponential fit there are many sets of parameters that yield similarly good fits. It turned out, however, that many reasonable statistically significant fits yielded very similar average quenched lifetime so the relative uncertainty in this important variable was quite low (see Table 1).
Finally, the rate constants in Table 1 were calculated from the average lifetimes according to:
 | (2) |
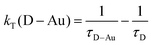 | (3) |
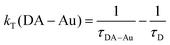 | (4) |
Distance dependence of the energy transfer
For discussing the distance dependence of the energy transfer a generalized Förster equation is used: | (5) |
| R0 = 0.211(κ2n−4ΦDJ(λ))1/6 (in Å) | (6) |
Singlet energy transfer is well described between molecules at sufficiently large separation by the Förster equation. For transfer between molecules (or quantum dots) and AuNPs a number of models have been discussed in the literature giving both similar and weaker distance dependence as the Förster equation. In the NSET model introduced by Strouse and co-workers68 a 1/d4 distance dependence (n = 4) is expected for small AuNPs and the characteristic distance is given by the simple equation
 | (7) |
Conclusions
By combining the ability of DNA origami to control distance and spatial configuration with nanometer precision with the optical plasmonic effect of metallic nanostructures, we were able to create a promising platform that could be considered an analytical tool to study interactions between dyes and plasmonic nanostructures at the single molecule level. In this study, the designed origami constructs showed moderate enhancement of the FRET rates between donor and acceptor dyes in presence of a 5 nm AuNP. To investigate the mechanism of FRET enhancement, we looked at a simple additive model. For that we considered that the excited donor, in addition to be quenched by a combination of energy transfer to the acceptor (FRET process) and to the AuNP, is experiencing an enhanced energy transfer rate in presence of the AuNP. This enhancement is mainly explained by an increased non-radiative contribution to the transfer rate, thus increasing the action radius of the FRET process. Our results further showed that the alteration of the donor decay rates is strongly distance dependent, both for the radiative and non-radiative decays of the donor in the presence of AuNP, allowing enhancement of FRET at short donor–acceptor (and donor–AuNP) distances.Acknowledgements
The authors acknowledge financial support from the Swedish Research Council (VR) and the Chalmers Area of Advance in Nanoscience and Nanotechnology. We thank Johnas Eklöf for his contribution in AFM imaging. Kasper Moth-Poulsen acknowledges funding from the European research council, ERC.Notes and references
- R. Roy, S. Hohng and T. Ha, Nat. Methods, 2008, 5, 507–516 CrossRef CAS PubMed.
- L. Stryer and R. P. Haugland, Proc. Natl. Acad. Sci. U. S. A., 1967, 58, 719–726 CrossRef CAS.
- A. Iqbal, L. Wang, K. C. Thompson, D. M. J. Lilley and D. G. Norman, Biochemistry, 2008, 47, 7857–7862 CrossRef CAS PubMed.
- S. Weiss, Science, 1999, 283, 1676–1683 CrossRef CAS PubMed.
- B. Schuler, E. A. Lipman and W. A. Eaton, Nature, 2002, 419, 743–747 CrossRef CAS PubMed.
- K. Börjesson, S. Preus, A. H. El-Sagheer, T. Brown, B. Albinsson and L. M. Wilhelmsson, J. Am. Chem. Soc., 2009, 131, 4288–4293 CrossRef PubMed.
- S. Akimoto, T. Shinoda, M. Chen, S. Allakhverdiev and T. Tomo, Photosynth. Res., 2015, 125, 115–122 CrossRef CAS PubMed.
- J. G. Woller, J. K. Hannestad and B. Albinsson, J. Am. Chem. Soc., 2013, 135, 2759–2768 CrossRef CAS PubMed.
- J. K. Hannestad, P. Sandin and B. Albinsson, J. Am. Chem. Soc., 2008, 130, 15889–15895 CrossRef CAS PubMed.
- K. Börjesson, J. Tumpane, T. Ljungdahl, L. M. Wilhelmsson, B. Nordén, T. Brown, J. Mårtensson and B. Albinsson, J. Am. Chem. Soc., 2009, 131, 2831–2839 CrossRef PubMed.
- K. Borjesson, D. Dzebo, B. Albinsson and K. Moth-Poulsen, J. Mater. Chem. A, 2013, 1, 8521–8524 Search PubMed.
- I. L. Medintz, A. R. Clapp, H. Mattoussi, E. R. Goldman, B. Fisher and J. M. Mauro, Nat. Mater., 2003, 2, 630–638 CrossRef CAS PubMed.
- J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Springer, New York, 2006 Search PubMed.
- M. Lunz, V. A. Gerard, Y. K. Gun'ko, V. Lesnyak, N. Gaponik, A. S. Susha, A. L. Rogach and A. L. Bradley, Nano Lett., 2011, 11, 3341–3345 CrossRef CAS PubMed.
- X. Zhang, C. A. Marocico, M. Lunz, V. A. Gerard, Y. K. Gun'ko, V. Lesnyak, N. Gaponik, A. S. Susha, A. L. Rogach and A. L. Bradley, ACS Nano, 2014, 8, 1273–1283 CrossRef CAS PubMed.
- M. Lunz, X. Zhang, V. A. Gerard, Y. K. Gun'ko, V. Lesnyak, N. Gaponik, A. S. Susha, A. L. Rogach and A. L. Bradley, J. Phys. Chem. C, 2012, 116, 26529–26534 CAS.
- J. Zhang, Y. Fu, M. H. Chowdhury and J. R. Lakowicz, J. Phys. Chem. C, 2007, 111, 11784–11792 CAS.
- J. I. Gersten and A. Nitzan, Chem. Phys. Lett., 1984, 104, 31–37 CrossRef CAS.
- X. M. Hua, J. I. Gersten and A. Nitzan, J. Chem. Phys., 1985, 83, 3650–3659 CrossRef CAS.
- A. O. Govorov, J. Lee and N. A. Kotov, Phys. Rev. B: Condens. Matter, 2007, 76, 125308 CrossRef.
- J. Zhang, Y. Fu and J. R. Lakowicz, J. Phys. Chem. C, 2007, 111, 50–56 CAS.
- J. A. Gonzaga-Galeana and J. R. Zurita-Sánchez, J. Chem. Phys., 2013, 139(24), 244302 CrossRef PubMed.
- R. Ruppin, J. Chem. Phys., 1982, 76, 1681–1684 CrossRef CAS.
- M. Thomas, J.-J. Greffet, R. Carminati and J. R. Arias-Gonzalez, Appl. Phys. Lett., 2004, 85, 3863–3865 CrossRef CAS.
- K.-S. Kim, J.-H. Kim, H. Kim, F. Laquai, E. Arifin, J.-K. Lee, S. I. Yoo and B.-H. Sohn, ACS Nano, 2012, 6, 5051–5059 CrossRef CAS PubMed.
- E. M. Purcell, H. C. Torrey and R. V. Pound, Phys. Rev., 1946, 69, 37–38 CrossRef CAS.
- K. H. Drexhage, J. Lumin., 1970, 1–2, 693–701 CrossRef.
- P. Andrew and W. L. Barnes, Science, 2000, 290, 785–788 CrossRef CAS PubMed.
- C. E. Finlayson, D. S. Ginger and N. C. Greenham, Chem. Phys. Lett., 2001, 338, 83–87 CrossRef CAS.
- P. Ghenuche, J. de Torres, S. B. Moparthi, V. Grigoriev and J. Wenger, Nano Lett., 2014, 14, 4707–4714 CrossRef CAS PubMed.
- P. Ghenuche, M. Mivelle, J. de Torres, S. B. Moparthi, H. Rigneault, N. F. Van Hulst, M. F. García-Parajó and J. Wenger, Nano Lett., 2015, 15, 6193–6201 CrossRef CAS PubMed.
- P. Andrew and W. L. Barnes, Science, 2004, 306, 1002–1005 CrossRef CAS PubMed.
- C. Blum, N. Zijlstra, A. Lagendijk, M. Wubs, A. P. Mosk, V. Subramaniam and W. L. Vos, Phys. Rev. Lett., 2012, 109, 203601 CrossRef PubMed.
- F. Schleifenbaum, A. M. Kern, A. Konrad and A. J. Meixner, Phys. Chem. Chem. Phys., 2014, 16, 12812–12817 RSC.
- A. Konrad, M. Metzger, A. M. Kern, M. Brecht and A. J. Meixner, Nanoscale, 2015, 7, 10204–10209 RSC.
- Z. Yang, X. Zhou, X. Huang, J. Zhou, G. Yang, Q. Xie, L. Sun and B. Li, Opt. Lett., 2008, 33, 1963–1965 CrossRef CAS PubMed.
- A. Kuzyk, R. Schreiber, Z. Fan, G. Pardatscher, E.-M. Roller, A. Hogele, F. C. Simmel, A. O. Govorov and T. Liedl, Nature, 2012, 483, 311–314 CrossRef CAS PubMed.
- V. V. Thacker, L. O. Herrmann, D. O. Sigle, T. Zhang, T. Liedl, J. J. Baumberg and U. F. Keyser, Nat. Commun., 2014, 5, 3448 Search PubMed.
- G. P. Acuna, F. M. Möller, P. Holzmeister, S. Beater, B. Lalkens and P. Tinnefeld, Science, 2012, 338, 506–510 CrossRef CAS PubMed.
- P. Kühler, E.-M. Roller, R. Schreiber, T. Liedl, T. Lohmüller and J. Feldmann, Nano Lett., 2014, 14, 2914–2919 CrossRef PubMed.
- S. Pal, Z. Deng, B. Ding, H. Yan and Y. Liu, Angew. Chem., Int. Ed., 2010, 49, 2700–2704 CrossRef CAS PubMed.
- S. Pal, P. Dutta, H. Wang, Z. Deng, S. Zou, H. Yan and Y. Liu, J. Phys. Chem. C, 2013, 117, 12735–12744 CAS.
- I. H. Stein, V. Schüller, P. Böhm, P. Tinnefeld and T. Liedl, ChemPhysChem, 2011, 12, 689–695 CrossRef CAS PubMed.
- B. Saccà, Y. Ishitsuka, R. Meyer, A. Sprengel, E.-C. Schöneweiß, G. U. Nienhaus and C. M. Niemeyer, Angew. Chem., Int. Ed., 2015, 54, 3592–3597 CrossRef PubMed.
- A. Samanta, Y. Zhou, S. Zou, H. Yan and Y. Liu, Nano Lett., 2014, 14, 5052–5057 CrossRef CAS PubMed.
- G. P. Acuna, M. Bucher, I. H. Stein, C. Steinhauer, A. Kuzyk, P. Holzmeister, R. Schreiber, A. Moroz, F. D. Stefani, T. Liedl, F. C. Simmel and P. Tinnefeld, ACS Nano, 2012, 6, 3189–3195 CrossRef CAS PubMed.
- S. H. Ko, K. Du and J. A. Liddle, Angew. Chem., Int. Ed., 2013, 52, 1193–1197 CrossRef CAS PubMed.
- J. V. Pellegrotti, G. P. Acuna, A. Puchkova, P. Holzmeister, A. Gietl, B. Lalkens, F. D. Stefani and P. Tinnefeld, Nano Lett., 2014, 14, 2831–2836 CrossRef CAS PubMed.
- T. Zhang, N. Gao, S. Li, M. J. Lang and Q.-H. Xu, J. Phys. Chem. Lett., 2015, 6, 2043–2049 CrossRef CAS PubMed.
- D. Wang, S. L. Capehart, S. Pal, M. Liu, L. Zhang, P. J. Schuck, Y. Liu, H. Yan, M. B. Francis and J. J. De Yoreo, ACS Nano, 2014, 8, 7896–7904 CrossRef CAS PubMed.
- P. W. K. Rothemund, Nature, 2006, 440, 297–302 CrossRef CAS PubMed.
- C. Steinhauer, R. Jungmann, T. L. Sobey, F. C. Simmel and P. Tinnefeld, Angew. Chem., Int. Ed., 2009, 48, 8870–8873 CrossRef CAS PubMed.
- G. Dai, X. Lu, Z. Chen, C. Meng, W. Ni and Q. Wang, ACS Appl. Mater. Interfaces, 2014, 6, 5388–5392 CAS.
- X. Lan, Z. Chen, G. Dai, X. Lu, W. Ni and Q. Wang, J. Am. Chem. Soc., 2013, 135, 11441–11444 CrossRef CAS PubMed.
- S. L. Capehart, M. P. Coyle, J. E. Glasgow and M. B. Francis, J. Am. Chem. Soc., 2013, 135, 3011–3016 CrossRef CAS PubMed.
- C. Dwyer, A. Rallapalli, M. Mottaghi and S. Wang, in Nanophotonic Information Physics, ed. M. Naruse, Springer, Tokyo, 2014, pp. 41–65 Search PubMed.
- M. P. Singh, T. L. Jennings and G. F. Strouse, J. Phys. Chem. B, 2009, 113, 552–558 CrossRef CAS PubMed.
- C. S. Yun, A. Javier, T. Jennings, M. Fisher, S. Hira, S. Peterson, B. Hopkins, N. O. Reich and G. F. Strouse, J. Am. Chem. Soc., 2005, 127, 3115–3119 CrossRef CAS PubMed.
- C. A. M. Seidel, A. Schulz and M. H. M. Sauer, J. Phys. Chem., 1996, 100, 5541–5553 CrossRef CAS.
- K. Pan, E. Boulais, L. Yang and M. Bathe, Nucleic Acids Res., 2014, 42, 2159–2170 CrossRef CAS PubMed.
- M. Torimura, S. Kurata, K. Yamada, T. Yokomaku, Y. Kamagata, T. Kanagawa and R. Kurane, Anal. Sci., 2001, 17, 155–160 CrossRef CAS PubMed.
- L. Zhao, T. Ming, L. Shao, H. Chen and J. Wang, J. Phys. Chem. C, 2012, 116, 8287–8296 CAS.
- E. Dulkeith, M. Ringler, T. A. Klar, J. Feldmann, A. Muñoz Javier and W. J. Parak, Nano Lett., 2005, 5, 585–589 CrossRef CAS PubMed.
- J. de Torres, P. Ghenuche, S. B. Moparthi, V. Grigoriev and J. Wenger, ChemPhysChem, 2015, 16, 782–788 CrossRef CAS PubMed.
- B. Ding, Z. Deng, H. Yan, S. Cabrini, R. N. Zuckermann and J. Bokor, J. Am. Chem. Soc., 2010, 132, 3248–3249 CrossRef CAS PubMed.
- A. Udomprasert, M. N. Bongiovanni, R. Sha, W. B. Sherman, T. Wang, P. S. Arora, J. W. Canary, S. L. Gras and N. C. Seeman, Nat. Nanotechnol., 2014, 9, 537–541 CrossRef CAS PubMed.
- X. Shen, C. Song, J. Wang, D. Shi, Z. Wang, N. Liu and B. Ding, J. Am. Chem. Soc., 2012, 134, 146–149 CrossRef CAS PubMed.
- T. L. Jennings, M. P. Singh and G. F. Strouse, J. Am. Chem. Soc., 2006, 128, 5462–5467 CrossRef CAS PubMed.
- M. Kubista, R. Sjoback, S. Eriksson and B. Albinsson, Analyst, 1994, 119, 417–419 RSC.
- R. A. Hochstrasser, S.-M. Chen and D. P. Millar, Biophys. Chem., 1992, 45, 133–141 CrossRef CAS PubMed.
- P. Sandin, P. Lincoln and B. Albinsson, J. Phys. Chem. C, 2008, 112, 13089–13094 CAS.
- S. Preus, a|e - UV-Vis-IR Spectral Software, Fluor Tools, http://www.fluortools.com (accessed June 2016) Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6nr04852h |
| This journal is © The Royal Society of Chemistry 2017 |





