An experimental and theoretical investigation of the anisotropic branching in gold nanocrosses

Abstract

In this work, copper (Cu) species were used as reducing reagents in the colloidal preparation of novel cross-shaped gold (Au) nanostructures in oleylamine. The reduction rate can be controlled through an appropriate choice of Cu species to obtain Au nanocrosses of varying sizes. It was found that the presence of Cu species during the nucleation stage is crucial to the formation of a branched morphology. Further analysis revealed that the four primary branches of the Au nanocrosses grow along the <110> and <001> directions, and that secondary branched growth occurs along the <111> direction. First-principles calculations and phase-field models were used to rationalize the observed preferential branching and understand the morphological evolution of the nanocrosses. These unique cross-like Au nanostructures exhibit strong NIR absorption and remarkable plasmonic properties that make them promising materials for optical and biomedical applications.

---

1. Introduction

The presence of nanometer-sized gold (Au) particles in centuries-old Roman dichroic glass cups and medieval stained glass windows indicates that Au nanostructures have been produced since ancient times. However, it was only in the mid-19th century when the preparation of Au nanostructures in solution was first documented.¹ The work was conducted by Michael Faraday, who was able to produce spherical-shaped Au nanocrystals by reducing gold chloride with phosphorus in water. In recent years, continuing developments in colloidal nanocrystal synthesis have enabled the preparation of Au nanostructures with a wide array of morphologies.^2–9 Among the most often synthesized morphologies are the faceted geometries, such as cubes, octahedra and dodecahedra, and the one-dimensional structures, such as rods and wires. An emerging class of nanostructure morphology is the branched architecture, which includes shapes such as urchins,^10,11 stars^12–15 and multipods.^16–19 Previous studies have shown that metal nanostructures with branched morphological features exhibit enhanced properties that can be exploited in the areas of catalysis, plasmonics and biomedicine.²⁰ For this reason, the creation of branched metal nanostructures has become an area of great interest in nanotechnology.

Our group was the first to report on the colloidal synthesis of branched Au nanostructures with a unique cross-like morphology (i.e., Au nanocrosses), which have attracted considerable attention in the last few years owing to their remarkable optical and plasmonic properties.^21,22 Because of their huge potential in a range of optical and biomedical applications, we find it important to explore new synthetic routes to Au nanocrosses and investigate the formation and growth mechanisms of these anisotropically branched nanostructures. In this paper, we present vital information on the basis of both experimental results and theoretical calculations, which have provided us with a profound understanding of the morphological evolution of Au nanocrosses. Experimentally, highly crystalline Au nanocrosses were prepared in solution with the cooperative use of oleylamine and copper-based reducing agents. The reduction rate can be controlled through an appropriate choice of copper (Cu) species to obtain Au nanocrosses of varying sizes. The Au nanocrosses possess four primary branches that extend along the <110> and <001> directions, as well as secondary branches that grow along the <111> direction. The primary branching behavior was rationalized by first-principles simulations through studying the influence of Cu incorporation and oleylamine adsorption on different Au surfaces. Meanwhile, phase-field models were established to understand not only the primary branching but also the secondary branching observed. The Au nanocrosses were found to display intense photon absorption in the near-infrared region (NIR) that is tunable with size. Their strong NIR absorption allows their use in biomedical applications, where the use of NIR light is beneficial to achieve deeper penetration into tissues. Moreover, quantification of their precise optical response revealed high plasmon quality factors, indicating the suitability of these novel cross-shaped Au nanostructures for optical-related applications.

2. Experimental methods

Materials

Copper(I) chloride (CuCl, 99%) and gold(III) chloride (AuCl₃, 99.99+%) were purchased from Sigma-Aldrich. Oleylamine (technical grade) was purchased from Sigma-Aldrich. Hexane and ethanol (analytical grade) were obtained from Riverbank Chemicals. All chemicals were used without further purification. All the experimental manipulations were carried out under an argon flow in a Schlenk line.

Synthesis of Au nanocrosses using Cu nanostructures and Cu⁺ as reductants (Method 1)

In a typical synthesis, 2.0 mmol of CuCl was rapidly dissolved in 5 mL of oleylamine upon heating to 100 °C. After degassing under reduced pressure for 30 min, the pale yellow solution was heated to 200 °C and maintained at this temperature for 10 min. The resulting reddish brown mixture was then allowed to cool to 50 °C, after which a solution of 0.3 mmol of AuCl₃ in 5 mL of oleylamine was injected. The reaction mixture was maintained at this temperature for 1 h, during which the color of the mixture turned blue. After centrifugation to remove unreacted Cu nanostructures, the blue supernatant was heated to 100 °C and maintained at this temperature for 30 min. The dark brown solid that was formed (i.e., Au nanocrosses) was washed three times using the solvent mixture of ethanol/hexane, and dispersed in hexane for further use.

Synthesis of Au nanocrosses using purified Cu nanowires as reductants (Method 2)

Typically, 2.0 mmol of CuCl was rapidly dissolved in 5 mL of oleylamine upon heating to 100 °C. After degassing under reduced pressure for 30 min, the pale yellow solution was heated to 200 °C and maintained at this temperature for 30 min. The resulting Cu nanowires were isolated through centrifugation and purified using the solvent mixture of ethanol/hexane, and then later dispersed into 5 mL of oleylamine containing 0.3 mmol of AuCl₃. The solution was then mixed with 5 mL of oleylamine at 50 °C, and maintained at this temperature for 1 h. After centrifugation to remove the remaining Cu nanowires, the blue supernatant was heated to 100 °C and maintained at this temperature for 30 min. The as-obtained Au nanocrosses (dark brown solid) were washed three times using the solvent mixture of ethanol/hexane, and dispersed in hexane for further use.

Synthesis of Au nanocrosses using Cu⁺ as a reductant (Method 3)

Typically, 2.0 mmol of CuCl was rapidly dissolved in 5 mL of oleylamine by heating to 100 °C. After degassing under reduced pressure for 30 min, the solution was cooled to 50 °C and this was followed by the addition of a solution of 0.3 mmol of AuCl₃ in 5 mL of oleylamine. The pale yellow solution immediately turned blue, and was maintained at 50 °C for 1 h. It was then heated to 100 °C and further reacted for 30 min at this temperature. The as-obtained Au nanocrosses (dark brown solid) were washed three times using the solvent mixture of ethanol/hexane, and dispersed in hexane for further use.

Overgrowth of Au nanostructures onto 12 nm Au seeds

For preparing Au seeds, 0.05 mmol of AuCl₃ was first dissolved in 5 mL of oleylamine at room temperature. After degassing under reduced pressure for 15 min, the resulting solution was heated to 100 °C and maintained at this temperature for 30 min. The obtained 12 nm Au nanocrystals (dark red solid) were isolated, purified and then re-dispersed in 2.5 mL of oleylamine for further use as seeds to grow larger Au nanostructures. In a separate flask, 2.0 mmol of CuCl was rapidly dissolved in 5 mL of oleylamine by heating to 100 °C. The pale yellow solution was degassed for 30 min and then cooled to 50 °C. To this solution, the dark red oleylamine solution of the pre-synthesized Au seeds (2.5 mL) was added. This was immediately followed by addition of 0.3 mmol of AuCl₃ in 2.5 mL of oleylamine. The reaction temperature was maintained at 50 °C for 1 h, after which the solution was heated to 100 °C and reacted for 30 min. The obtained Au nanostructures were purified three times using the solvent mixture of ethanol/hexane, and dispersed in hexane for further use.

Characterization

Transmission electron microscopy (TEM) images were examined with a JEOL 1010 transmission electron microscope and a JEOL 2010 high-resolution TEM (HRTEM), operated at 100 and 200 kV, respectively. The powder X-ray diffraction (XRD) patterns were recorded on a Bruker D8 GADDS diffractometer using Cu_Kα radiation (λ = 1.5418 Å). The molar ratios of Cu/Au of Au nanocrosses were determined by using a Perkin-Elmer Optima 3000 inductively coupled plasma-atomic emission spectrometer (ICP-AES). The UV-Vis-NIR absorption spectra of the branched Au nanostructures were recorded using a Shimadzu UV-1800 spectrophotometer. The surface plasmons of a Au nanocross (synthesized using Method 1) were mapped using a monochromated FEI Titan TEM operating at 80 kV equipped with a Gatan Tridiem ER EELS detector.

3D tomography reconstruction

The 3D tomography analysis of Au nanocrosses was performed on a JEOL 2100 (200 kV) scanning transmission electron microscope (STEM), which is equipped with a High-Angle Annular Dark-Field (HAADF) detector and a single-tilt tomography holder. Multiple HAADF-STEM images of a Au nanocross for STEM tomography were collected in a tilt range of −65° to +65°, with 2° tilt steps from −40° to +40° and 1° tilt intervals for the other high angles. The image acquisition, tracking and focus were carried out automatically by using JEOL Recorder software. The magnification was 200 000 times, corresponding to a pixel size of 0.875 nm. The obtained tilt series data were aligned and reconstructed by a weighted back-projection method using Inspect3D, and their 3D volume was visualized by surface rendering using Amira 4.1. In this process, smaller Au nanoparticles (5–15 nm) were used as markers for image tracking and alignment during reconstruction.

First-principles simulations of the influence of Cu incorporation on the branched growth of Au nanocrosses

In the first-principles calculations,^23–27 the stability of a Au or a Cu atom on the Au (001), (110), and (111) surfaces was investigated using 2 × 2, 2 × 3 and 3 × 3 supercells, respectively. A vacuum space of 30 Å above the Au surface in the supercells was used. When a Cu atom is deposited on a Au surface, and subsequently a Au atom replaces the Cu atom on the Au surface, the substitution/formation energy is estimated from E_f = E_{(Au surface+1 Au atom)} − E_{(Au surface+1 Cu atom)} − μ_(Au) + μ_(Cu),^28,29 where E_{(Au surface+1 Au atom)} and E_{(Au surface+1 Cu atom)} are the total energies of the Au surface deposited with 1 Au atom and 1 Cu atom, respectively. The μ_(Au) and μ_(Cu) are the chemical potentials of Au and Cu, respectively.

First-principles simulations of the influence of surface-adsorbed ligands on the branched growth of Au nanocrosses

In the first-principles calculations,^23–27 the stability of the adsorbate on the Au (001), (110), and (111) surfaces was investigated using 3 × 3, 2 × 3, and 3 × 3 supercells, respectively. The vacuum space of 30 Å above the Au surface in the supercells was used. The calculated binding energy of the adsorbate on a Au surface is E_b = E_{(Au+Adsorbate)} − E_(Au) − E_(Adsorbate), where E_(Au) and E_(Adsorbate) are the energies of the Au surface and the adsorbate, respectively. E_{(Au+Adsorbate)} is the total energy of the adsorbate-attached Au surface.

Phase-field model for simulating the branched growth of Au nanocrosses

To understand the kinetics for the growth of the Au nanocrosses, we modeled the growth process using a phase-field model formulated by Karma and Plapp.³⁰ A discrete Fourier transform method³¹ was used to solve the governing equations of the phase-field model for both the primary and secondary growth of the Au nanocrosses.

3. Results and discussion

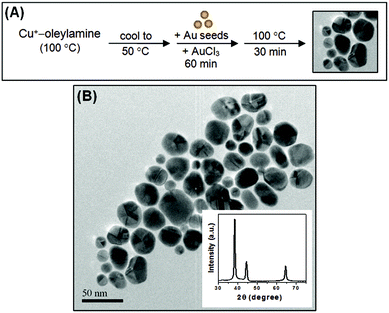
Colloidal Au nanostructures are typically prepared through reduction of Au precursors, such as HAuCl₄ and AuCl₃, by chemical reducing agents in the presence of capping ligands (or surface stabilizers). In many cases, the appropriate choice of capping ligands is critical for the formation of the desired Au nanostructure morphology. In creating branched architectures, capping ligands can mediate in branch formation through selective stabilization of certain crystallographic facets.³² While preparing our Au nanocrosses, the reduction of the Au precursor is facilitated with the use of Cu species as reducing agents and oleylamine as the shape-directing capping ligand. Interestingly, we find that our Cu-based reducing agents also play a key role in determining the final morphology of the Au nanostructures. As Cu and Au belong to the same group, Cu can be easily incorporated into the Au lattice and can significantly influence the growth of the Au nanostructures.

A schematic depiction of our synthetic protocol is displayed in Fig. 1A and we refer to this procedure as Method 1. First, a mixture of CuCl and oleylamine was heated to 100 °C, at which a pale yellow solution was observed due to the formation of a Cu⁺–oleylamine complex. When further heated at 200 °C for 10 min, the color of the reaction mixture turned reddish brown, which is indicative of the formation of Cu nanostructures. The presence of Cu nanostructures at this stage of the reaction is confirmed by the X-ray diffraction (XRD) pattern shown in Fig. S1 (in the ESI†), where the diffraction signals seen at 2θ = 43.5°, 50.7°, and 74.4° can be indexed to the (111), (200) and (220) crystal planes of face-centered cubic Cu (JCPDS #03-1018). The transmission electron microscopy (TEM) image in Fig. 1B reveals that the resulting Cu nanostructures exist in a variety of shapes (i.e., wires, rods, cubes etc.). In our previous work on colloidal Cu nanostructures, we have found that heating the Cu⁺–oleylamine complex at 200 °C for a sufficient length of time (i.e., ≥30 min) results in disproportionation of Cu⁺ (2Cu⁺ → Cu⁰ + Cu²⁺) to produce high-quality Cu nanowires.³³ Because our present procedure involves heating at 200 °C for only 10 min, a fraction of Cu⁺ remained undisproportionated, and this accounts for the smaller Cu nanostructures that are observed along with the expected nanowires. The reaction mixture, which at this point consists of three different Cu species (i.e., Cu nanostructures, Cu²⁺ and Cu⁺) due to partial disproportionation of Cu⁺, was then allowed to cool to 50 °C. After cooling, an oleylamine solution of AuCl₃ was added and the resulting mixture was incubated at 50 °C for 1 h. During this period, the reddish brown mixture turned blue, which denotes the consumption of Cu nanostructures and the generation of more Cu²⁺. From the potentials of half-cells, Cu⁰ − e⁻ → Cu⁺, ϕ = −0.521 V and Cu⁰ − 2e⁻ → Cu²⁺, ϕ = −0.337 V, one can see that Cu⁰ can easily reduce Au³⁺ to Au⁰ (Au³⁺ + 3e⁻ → Au⁰, ϕ = 1.498 V) to form Cu⁺ and Cu²⁺. Furthermore, it is also possible for Cu⁺ to reduce Au³⁺ to Au⁰, considering the potential of the half-cell, Cu⁺ − e⁻ → Cu²⁺, ϕ = −0.153 V. Thus, Au³⁺ was reduced by both the Cu nanostructures and Cu⁺ to produce the initial Au seeds and Cu²⁺. This was followed by centrifugation to remove any unreacted Cu nanostructures. The blue supernatant was then heated to 100 °C for 30 min to allow for growth of the Au seeds. Finally, a dark brown mixture that contains the oleylamine-capped Au nanocrosses was obtained.

Fig. 1 Synthesis of Au nanocrosses in oleylamine via reduction of AuCl₃ by Cu-based reducing agents: a mixture of Cu nanostructures and Cu⁺. (A) Schematic depiction of the synthetic protocol. (B) TEM image of the pre-formed Cu nanostructures. (C) TEM image of the as-obtained Au nanocrosses. (D and E) TEM image of a representative Au nanocross with (D) the D_2h symmetry and (E) the C_2v symmetry.

Fig. 1C shows a low-magnification TEM image of the as-obtained Au nanocrosses. The four-branched cross-like structure is clearly seen in the TEM images of individual nanocrosses in Fig. 1D and E. Two typical morphologies are observed, one with the D_2h symmetry (Fig. 1D and S2A in the ESI†) and the other with the C_2v symmetry (Fig. 1E and S2B in the ESI†). Analysis of their high-resolution TEM (HRTEM) images reveals that the nanocrosses have either single or double twins in their centers (Fig. S2 in the ESI†). In the case of the singly-twinned nanocross, the lattice direction changes after the twin boundary. For the doubly-twinned nanocross, the lattice direction remains the same before and after the twin boundaries. Further analysis indicates that the Au nanocrosses possess two longer branches that extend along the <110> direction and two shorter branches that extend along the <001> direction (depicted in Fig. 1D and E). The XRD pattern in the inset of Fig. S2B (in the ESI†) shows diffraction peaks that can be indexed according to the standard diffraction pattern of face-centered cubic Au (JCPDS #04-0784). While not very evident in the XRD pattern, ICP measurement revealed that there is a small percentage of Cu (∼0.5 mol%) in the as-synthesized Au nanocrosses.

To confirm that both Cu and Cu⁺ are able to reduce the Au precursor to produce Au nanocrosses, we tried using these Cu species independently. Fig. 2A shows a schematic representation of the procedure used when only Cu nanostructures are employed as reducing agents, which we will refer to as Method 2. In this case, the Cu⁺–oleylamine complex was heated at 200 °C for a longer time (30 min) to ensure complete disproportionation of Cu⁺ to Cu and Cu²⁺. As shown in the TEM image in Fig. 2B, the complete disproportionation of Cu⁺ in oleylamine yielded highly monodisperse Cu nanowires. These Cu nanowires were isolated through centrifugation, purified and re-dispersed in an oleylamine solution containing AuCl₃. The reddish brown mixture was then heated to 50 °C, and was incubated at this temperature for 1 h. At this stage, Au³⁺ was reduced gradually on the surface of the Cu nanowires to form small anisotropic Au seeds together with Cu²⁺. The generation of Cu²⁺ was indicated by the change of the solution color to blue. It is worth noting that the color transition from reddish brown to blue occurred at a slower rate than when Method 1 was used, suggesting that the reduction of Au³⁺ is faster when Cu⁺ is also present as a reductant. The as-reacted Cu nanowires and the newly formed Au seeds are seen in the TEM image displayed in Fig. 2C. It can be observed from this figure that the diameter of the Cu nanowires was greatly decreased as it gets oxidized to Cu²⁺. After centrifugation to remove the remaining Cu nanowires, the anisotropic Au seeds (Fig. 2D) remained in the supernatant, which was further heated at 100 °C to allow for seeded growth. The Au seeds grew bigger and started their branched growth after heating for 10 min at 100 °C (Fig. S3 in the ESI†). Au nanocrosses (Fig. 2E) were eventually observed when the reaction was allowed to proceed for another 20 min. These results indicate that Cu nanostructures alone can reduce Au³⁺ to Au in the presence of oleylamine to generate Au nanocrosses. Interestingly, the Au nanocrosses obtained with this method are larger than those produced when a combination of Cu nanostructures and Cu⁺ was employed as the reductant (Method 1).

Fig. 2 Synthesis of Au nanocrosses in oleylamine via reduction of AuCl₃ by purified Cu nanowires. (A) Schematic depiction of the synthetic protocol. (B) TEM image of Cu nanowires prepared by disproportionation of Cu⁺ in oleylamine at 200 °C for 30 min. (C) TEM image of Cu nanowires that remained after reacting with AuCl₃ at 50 °C for 1 h. The smaller particles seen are the newly formed Au seeds. (D) TEM image of the anisotropic Au seeds that were separated from the unreacted Cu nanowires by centrifugation. (E) TEM image of Au nanocrosses prepared by heating the pre-formed anisotropic Au seeds at 100 °C for 30 min.

Fig. 3A shows a schematic illustration of the procedure employed when Cu⁺ is used as the sole reducing agent (i.e., Method 3). CuCl was first heated in oleylamine at 100 °C to form the Cu⁺–oleylamine complex. The next step differs from Methods 1 and 2 as the resulting pale yellow solution was not heated to 200 °C so as to avoid the disproportionation of Cu⁺. As discussed above, the disproportionation of Cu⁺ will generate Cu nanostructures, which we do not want to be present in the reaction mixture. Thus, instead of heating to 200 °C, the Cu⁺–oleylamine solution was allowed to cool to 50 °C. After cooling, an oleylamine solution of AuCl₃ was added and the resulting mixture was incubated at 50 °C for 1 h. It was noted that shortly after the addition of AuCl₃, the pale yellow solution immediately turned blue, which is in contrast with the gradual change in color that was observed when Methods 1 and 2 were employed. This tells us that Cu⁺ was able to reduce Au³⁺ more quickly than Cu nanostructures to yield Au and Cu²⁺. The resulting mixture was then heated to 100 °C for 30 min to allow for growth of the Au nanostructures. Fig. 3B shows the TEM images of the final product. As one can see, Au nanocrosses were also obtained through Method 3, where Cu⁺ was used solely as the reductant. However, as compared to the nanocrosses obtained through the first two methods, the nanocrosses produced by Method 3 are much smaller.

Fig. 3 Synthesis of Au nanocrosses in oleylamine via reduction of AuCl₃ by Cu⁺. (A) Schematic depiction of the synthetic protocol. (B) TEM images of the as-obtained Au nanocrosses. The inset shows a TEM image of two Au nanocrosses.

In terms of size, the Au nanocrosses produced using the three different synthetic protocols can be ranked as follows: Method 2 (350 ± 40 nm) > Method 1 (230 ± 25 nm) > Method 3 (100 ± 15 nm). The difference in size can be attributed to the difference in the observed reduction rate, which follows the order: Method 3 > Method 1 > Method 2. This means that the reduction of Au³⁺, and thus the nucleation of Au seeds, is fastest when Cu⁺ is used as the sole reductant (Method 3). Because both Cu⁺ and Au³⁺ are dissolved in oleylamine, the reduction reaction proceeds instantly upon mixing at 50 °C, and this leads to fast nucleation of a large number of Au seeds, which grow into small Au nanocrosses. On the other hand, when Cu nanostructures are used as reductants (Method 2), fewer Au seeds are formed as the reduction of Au³⁺ proceeds gradually on the surface of the Cu nanostructures, and this eventually gives larger Au nanocrosses. When both Cu⁺ and Cu nanostructures are present as reducing agents (Method 1), the reduction reaction proceeds at a faster rate than when only Cu nanostructures are used (Method 2), but more slowly than when Cu⁺ is used alone (Method 3). In this case, Au nanocrosses of an intermediate size are obtained. Thus, the appropriate choice of Cu species (Cu⁺, Cu nanostructures or their combination) can be used to manipulate the reduction rate and can lead to size-controllable synthesis of Au nanocrosses.

The absorption spectra of the branched Au nanostructures prepared using Methods 1–3 are shown in Fig. 4A. The localized surface plasmon resonance (LSPR) bands at both short (500–600 nm) and long (800–1200 nm) wavelengths, which are attributable to the unique cross-like morphology, can be clearly distinguished. The band at the visible range arises from the transverse dipolar resonance of the branches while the intense broad band at the NIR spectral window is attributed to the longitudinal resonance, similar to the longitudinal mode observed in Au nanorods. Due to the smaller size of the Au nanocrosses obtained using Method 3, the longitudinal resonance seen in the NIR region falls at a shorter wavelength compared with those observed for the larger nanocrosses obtained by Methods 1 and 2. This tells us that by simply changing the size of the Au nanocrosses, we are able to tune their NIR absorption. The strong NIR absorption displayed by these nanocrosses renders them useful in applications where the use of NIR light is necessary, such as in photothermal therapy and in biomedical imaging and detection.

Fig. 4 (A) Absorption spectra of the Au nanocrosses obtained using Methods 1–3. (B–D) Plasmon modes, experimentally visualized with monochromated EELS, where (B) maps the low-energy modes at 1.1 and 1.6 eV, while (C) maps the modes at 1.9 and 2.1 eV. (D) Monochromated EELS taken in STEM mode, by placing a 1 nm electron probe at locations 1–5 indicated in the panel (C). All five spectra were normalized at the ‘zero-loss peak’ maximum, after which a pre-measured background was subtracted. The spectral peaks represent the plasmon modes, around which the colour-coded, grey 0.2 eV energy windows were placed for the EFTEM experiments, giving the maps in (B) and (C).

To understand the shape–property relationship of these Au nanocrosses, we used the monochromated electron energy-loss (EELS) mapping technique that we have developed previously²² to visualize the spatial distribution of plasmon antinodes on the nanocross. Fig. 4B and C show the scanning TEM (STEM) dark field image of a representative Au nanocross, overlaid with monochromated energy-filtered TEM (EFTEM) maps of the plasmon modes arising from the cross. In STEM mode, by placing a 1 nm electron probe at locations 1–5 indicated in Fig. 4C, we successfully obtained the corresponding monochromated EELS spectra as shown in Fig. 4D. In comparison with the absorption spectra in Fig. 4A, the plasmon bands revealed by the EELS spectra are sharper; furthermore, even the dark mode (∼650 nm), which is invisible in the absorption measurement, can be mapped. With the sharp plasmon bands, the quality factors of each plasmon mode were calculated and the results are shown in the inset between Fig. 4B and C. The high quality factors (Q) strongly indicate that our cross-like Au nanostructures can be promising materials for optical-related applications, especially for those that require large local-field enhancements, such as in surface-enhanced Raman scattering (SERS).

The potential utility of Au nanocrosses in many important applications has led us to investigate their formation and growth mechanisms. ICP measurements showed that there is a small percentage of Cu (∼0.5 mol%) in the Au nanocrosses prepared using the three synthetic protocols described above. This tells us that Cu has been incorporated during the formation of the Au nanocrosses and is possibly involved in the generation of the cross-like morphology. Note that for Methods 1–3, Cu and/or Cu⁺ was able to reduce Au³⁺ at 50 °C. However, we find that when the Cu-based reductants are not present in the reaction mixture, Au³⁺ can also be reduced by oleylamine but only at temperatures ≥100 °C. Moreover, without Cu or Cu⁺, only unbranched Au nanostructures are produced, indicating that Cu incorporation is crucial to branching. Fig. S4 (in the ESI†) shows the TEM image of the 12 nm Au nanostructures that were obtained when AuCl₃ was heated in oleylamine at 100 °C for 30 min in the absence of Cu species. These unbranched Au nanostructures seem nearly spherical but a closer look at their HRTEM image (inset of Fig. S4 in the ESI†) reveals that they actually exhibit a multiply-twinned decahedral structure. For fcc metals like Au, the formation of decahedral nanocrystals with multiple cyclic twins is not unusual particularly in small sizes.^20,34 Previous studies have shown that these multiply-twinned nanocrystals can evolve into larger nanostructures with interesting morphologies.^35,36 To further investigate the role of Cu species in the branched growth of Au nanocrosses, we have tried to synthesize Au nanocrosses through reduction of Au³⁺ by Cu⁺ in the presence of our pre-synthesized multiply-twinned decahedral Au seeds. The synthetic protocol, which can be described as a modified version of Method 3, is schematically depicted in Fig. 5A. In this seeded growth approach, the pre-synthesized multiply-twinned 12 nm Au seeds were added together with AuCl₃ to the Cu⁺–oleylamine complex at 50 °C. The reaction mixture was incubated at this temperature for 1 h, and was then heated at 100 °C for 30 min to allow for nanocrystal growth. Instead of nanocrosses, the Au nanostructures obtained from this protocol are unbranched multiply-twinned polyhedra with the size ranging from 15 to 50 nm, as shown in the TEM image in Fig. 5B. This indicates that the Au atoms that were produced by the reduction of Au³⁺ by Cu⁺ are deposited onto the surface of the existing decahedral Au seeds, and this growth behavior leads to larger polyhedral Au nanostructures. Because branching was not observed, it is believed that Cu incorporation must occur during the nucleation of Au seeds to lead to branched architectures.

Fig. 5 An attempt to use multiply-twinned Au nanocrystals as seeds for synthesizing Au nanocrosses. (A) Schematic depiction of the synthetic protocol. (B) TEM image and XRD pattern (inset) of the as-obtained unbranched Au nanostructures.

On the basis of the above experimental results, it can be concluded that apart from serving as reductants for Au³⁺, Cu species also play a role in the formation of cross-shaped Au nanostructures when present during the nucleation of Au seeds. The presence of Cu species during the nucleation stage initially produces anisotropic Cu-doped Au seeds, as illustrated in Fig. 2. Subsequently, the preferential anisotropic growth of these Cu-doped Au seeds along both <110> and <001> directions leads to Cu-incorporated Au nanocrosses (depicted in Fig. 1D and E and 6A). Note that the anisotropic growth along <110> and <001> corresponds to the preferred growth of 1D Cu nanostructures along <110> in the absence of Au and the preferred growth of 1D Au nanostructures along <001> in the absence of Cu, respectively. Thus, the preferential growth along these two directions could be seen as the driving force for the formation of the cross-like morphology. Also noteworthy is that the nanocrosses are observed to exhibit secondary branching along the <111> direction, as highlighted in Fig. 6A. The secondary branches are not seen during the early stage of growth (Fig. S3 in the ESI†) but become evident when the nanocrosses are grown for a longer time. Interestingly, the secondary branches grow perpendicular to the primary branches and are predominantly on the two longer branches. The primary and secondary branching seen in our Au nanocrosses was investigated through theoretical calculations, and the results are discussed below.

Fig. 6 (A) Surface-rendered view of an individual Au nanocross reconstructed by HAADF-STEM tomography. The nanocross is labeled with two primary branched growth directions along <110> and <001> together with the secondary branched growth direction along <111> ([111] and [11-1]). The inset shows the corresponding HAADF-STEM image. (B, C) Phase-field models for simulating the growth of the primary branches of a doubly-twinned Au nanocross with the D_2h symmetry when using (B) ε₁ = 0.04, ε₂ = 0.04 and f = 0.0002 and (C) ε₁ = 0.04, ε₂ = 0.08 and f = 0.0002. (D, E) Phase-field models for simulating the growth of the secondary branches of a nanocross when using ε₁ = 0.04, ε₂ = 0.08 and f = 0.0002 with (D) symmetric and (E) asymmetric nucleation. In all the simulation results, blue corresponds to the medium (ξ = 0) and red corresponds to the Au nanocrosses (ξ = 1).

The preferential growth of Au nanocrosses observed here is expected to depend on the ways in which Cu atoms are incorporated onto the Au surfaces. This argument was further rationalized by first-principles simulations. First-principles calculations were performed to study the influence of Cu incorporation and oleylamine adsorption on the branched growth of Au nanocrosses by employing the density functional theory (DFT)²³ and Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA)²⁶ with the use of the projector augmented wave (PAW) scheme^24,27 as incorporated in the Vienna ab initio simulation package (VASP).²⁵

We first investigated the stability of the Au (001), (110) and (111) surfaces with and without surface deposition of Cu. Without the involvement of Cu, the calculated surface energies are 4.98, 8.87 and 10.51 eV nm⁻² for the Au (111), (001) and (110) surfaces, respectively. Hence, the surface energy for the Au (111) surface is much lower than the energies for the Au (001) and (110) surfaces. This causes the dominant formation of the Au (111) surface to greatly lower the surface energy of Au nanostructures, which is consistent with the commonly observed growth of Au nanoparticles with the preferentially exposed (111) surfaces. With the involvement of Cu, the calculated substitution energies are −0.211, −0.255 and −0.256 eV for a Au atom replacing a Cu atom at the Au (001), (110) and (111) surfaces, respectively.^28,29 The negative formation energies indicate that Cu atoms on the Au surface can be much easily replaced by Au atoms.²⁶ Since the substitution energies for the Cu-deposited Au (111) and (110) are very close and much lower than that for the Cu-deposited Au (001), it is expected that the Au (111) and (110) surfaces would grow faster than the Au (001) surface.

The simulation supports that the involvement of Cu can facilitate the favored growth of Au (110), which grows slower for pure Au whose surface energy follows the order of Au (110) > (001) > (111). However, this is still in contrast to the experimental observation in the growth of the Au nanocrosses, whose growth rate for the Au surfaces follows a trend of Au (110) > (001) > (111). To resolve this difficulty, we hypothesize that the growth of Au (111) is hindered by the strong surface adsorption of oleylamine, leading to the anisotropic growth along <001> and <110> as observed experimentally. To prove this hypothesis, we further performed first-principles simulations to study the influence of surface-adsorbed ligands on the branched growth of Au nanocrosses. We investigated the stability of the adsorbate on the (001), (110), and (111) surfaces of Au. In our experiments, oleylamine with the formula C₁₈H₃₇N is used as the adsorbate on the Au surface, where the N atom of the amine has a lone electron pair that is bound to the Au surface via a long-distance interaction.³⁷ A model molecule, NH₃ was chosen to simplify the simulation of the binding energies. The calculated binding energies are −1.429, −0.868 and −0.797 eV for the Au (111), (001) and (110) surfaces, respectively. The negative binding energies of the adsorbate on the Au surfaces indicate that the molecule is stably adsorbed on these surfaces. It is seen that there is an increase in the binding energy with the surface from (111), (001) to (110), as a result, the stability of the system follows a trend of (111) > (001) > (110). Since the binding energies on the Au (001) and (110) surfaces are close, both the Au (110) and (001) surfaces are expected to grow more easily than the Au (111) surface. Hence, it can be said that the strong adsorption of oleylamine on the Au (111) surface hinders its growth. In addition, the calculated binding distance (Au–N) on the Au (111) surface is 2.133 Å, which is much shorter than that on the other two surfaces (2.183 Å for (001) and 2.228 Å for (110)), further supporting that the Au (111) surface is difficult to grow in the presence of oleylamine. Finally, since the binding energy for Au (110) is lower than that for Au (001), the nanocrosses grow longer along <110> than <001>, as observed experimentally.

In addition to first-principles simulations, we have also established phase-field models for simulating the branched growth of Au nanocrosses. Gold nanostructures with fascinating morphologies have been of great interest in recent years,³⁸ and the formation and evolution of such nanostructures are often studied using diffusion-limited aggregation (DLA) and cluster–cluster aggregation (CCA) models.^39–41 It is commonly believed that these various nanostructures are formed by the competition between the growth rate and the diffusion rate. Since the mass transport at moving interfaces controls these nanostructures, it is important to track the evolution dynamics of the interfaces. The phase-field method is an efficient tool in describing the interface evolution in complex morphologies wherein a diffused interface is defined using order parameters such as composition, density and orientation fields. In the present work, we use the phase-field model formulated by Karma and Plapp³⁰ to simulate the kinetics of the growth of the Au nanocrosses. In this model, the evolution equations are written in terms of the order parameter ξ and the concentration field c. The order parameter ξ = 0 refers to the growth medium while ξ = 1 refers to the Au nanostructure. The concentration field c is defined in terms of the concentration of the Au atoms g in the solution as c = Ω(g − g_eq), where Ω is the surface area of the Au nanostructure and g_eq is the equilibrium concentration of the Au adatoms on the surface. The evolution equations for ξ and c are

and
where D is the diffusion coefficient, f is the flux of the Au adatoms arriving at the surface, γ is a dimensionless system constant, t is the growth time variable, t_h is the characteristic time of attachment of the adatoms to the surface, and t_s is the mean life time of the Au adatoms on the surface, which is much larger than t_h. [scr F, script letter F] is the free energy that is given as

Here K²(∇ξ)² is the gradient energy that is dependent on the gradient of the order parameter (non-zero at the interface) for describing interfacial energy. In this term, we introduce the anisotropy by using two cosine terms in K² = k²{1 + ε₁ cos(4θ) + ε₂ cos(2θ)} to model the morphology of a Au nanocross. The term k² corresponds to the average interface energy, and ε₁ and ε₂ are the strengths of the anisotropy to accommodate the 4- and 2-fold symmetries of Au nanocrosses, respectively. The morphologies of the nanocrosses are primarily controlled by two model parameters: the flux of Au atoms f and the diffusion coefficient D. The terms −1/π cos(π[ξ − ξ₀]) + γc{ξ + 1/π sin(π[ξ − ξ₀])} correspond to the bulk thermodynamic energy. This free energy with the combination of sine and cosine terms has minima at ξ − ξ₀ = +1 and −1, independent of c, where −1 represents the solution with reagents and +1 represents the Au nanocrosses.

The discrete Fourier transform method³¹ is used to solve this phase-field model for the formation of Au nanocrosses. We solve for ξ(x,y,t) under periodic boundary conditions in the x and y directions and use the phase-field units for length and time measurements, i.e., K² = 1 and t_h = 1. The equations are discretized in both space and time, and we use Δx = Δy = 1 and Δt = 0.01. The parameters used are t_s = 10⁶, γ = 10 and g_eq = g(x,y,0) = 0.5. Starting with a cylindrical nucleus with a radius of 1 unit, the simulations are carried out at different values of flux f. All the results shown here are for a system size of 512 × 512 units. In the phase-field model, the flux term f defines the rate at which the dissolved Au atoms attach to the surface of the nanocross. Hence, it influences the rate of growth of the branches. Clearly, the flux controls the width of the branches: the branches widen as the flux is increased. In the experiments, the flux of the Au atoms arriving at the nanocross surface is controlled by the reaction rate, the concentration of reagents and the reaction temperature. Hence the flux term f used in the present model is related to the above mentioned factors. By controlling these factors, we are able to tune the growth flux, which in turn controls the morphology of the nanocrosses.

In our experiments, the presence of Cu is observed to result in an anisotropically branched morphology. Hence, it is deduced that the formation of such fascinating nanostructures arises from the fact that the presence of Cu atoms gives rise to the anisotropy in the surface energy of Au, which is supported by our first-principles calculations. In the phase field method, such surface energy anisotropy is described by using the terms ε₁ and ε₂, allowing the growth of certain orientations to be more energetically favorable than others, leading to the cross pattern. These parameters were systematically changed to reproduce the morphology of various Au nanocrosses. With the above understanding, we present our simulation results. We first simulated the formation of a doubly-twinned Au nanocross with the D_2h symmetry that is shown in Fig. 6A. Using ε₁ = 0.04, ε₂ = 0.04 and f = 0.0002, the simulated morphology of the Au nanocross has four branches with an equal length (Fig. 6B). To introduce growth anisotropy, we choose different values for ε₁and ε₂. For example, when using ε₁ = 0.04, ε₂ = 0.08 and f = 0.0002, the resulting morphology shows that the branches are no longer of the same length with one pair being shorter than the other (Fig. 6C). This is consistent with our experimental observation that the longer pair of branches is more energetically favourable to grow along <110> as compared to the shorter pair of branches along <001>. Meanwhile, to understand the formation of the singly-twinned Au nanocross with the C_2v symmetry (Fig. 7A), we utilize the mirror symmetry to simulate the single twin in the nanocross. The obtained structure is shown in Fig. 7B, with ε₁ = 0.04, ε₂ = 0.08 and f = 0.0002. It is seen that good agreement between the experimental and simulation results is achieved.

Fig. 7 (A) TEM image of a singly-twinned Au nanocross with the C_2v symmetry and (B) the corresponding simulation structure using ε₁ = 0.04, ε₂ = 0.08 and f = 0.0002. Blue corresponds to the medium (ξ = 0) and red corresponds to the Au nanocross (ξ = 1).

Experimentally, we observed that an increase in the reaction time results in secondary branching; where the growth of the secondary branches is perpendicular to the primary branches and is predominantly on the longer branches. However, in the present model, as the longer branch is more energetically favored to grow, any perturbation parallel to the longer branch will grow at the cost of growth along the shorter branch and this is in direct contrast with the experimental results. We hypothesize that such a formation of secondary branched structures is controlled by nucleation rather than growth. To confirm our hypothesis, we introduced new nuclei on the longer arms and observed their evolution after the nanocross grows to a certain size. The results are shown in Fig. 6D and E. It is seen that the nuclei, when placed either symmetrically or randomly along the longer branches, grow into secondary branches. In Fig. 6D, the branches grow symmetrically on either side due to the symmetrical introduction of nuclei, whereas in Fig. 6E, the branches grow asymmetrically due to the random introduction of nuclei. Thus, it is the subsequent nucleation on the Au nanocrosses that results in secondary branching. Clearly, the longer the arms are the larger the surface is available for nucleation; hence, the secondary branches are mostly formed on the longer arms. Overall, our simulation results reproduced the typical morphologies of the Au nanostructures observed in the experiments, confirming that the surface energy anisotropy and the growth flux are the controlling factors for the formation and morphological evolution of the Au nanocrosses.

4. Conclusions

In summary, we have synthesized Au nanostructures with a unique cross-like architecture through chemical reduction of AuCl₃ using Cu-based reductants in the presence of oleylamine. The appropriate choice of Cu species (Cu⁺, Cu nanostructures or their combination) can be used to manipulate the reduction rate, and this leads to size-controllable synthesis of Au nanocrosses. By controlling the size, the strong NIR absorption of these nanocrosses can be conveniently tuned. Investigation of the formation mechanism revealed that Cu is incorporated during the nucleation of the Au seeds and plays a vital role in the generation of the cross-like morphology. With the use of first-principles simulations, we were able to provide a theoretical understanding of the observed anisotropic branching behavior by studying the influence of Cu incorporation and oleylamine adsorption on different Au surfaces. Moreover, we have shown that the phase-field models used here can successfully explain several interesting features of the growth and evolution of the Au nanocrosses. By considering the surface energy anisotropy and the growth flux as important parameters, we were able to reproduce the typical morphologies of Au nanocrosses observed in the experiments. The results and information presented in this paper could help in the understanding of the branching behavior of other novel nanostructured materials.

Acknowledgements

This work was supported by the Institute of Materials Research & Engineering, the Institute of High Performance Computing, and the A*STAR Computational Resource Centre through the use of its high performance computing facilities.

Notes and references

1. M. Faraday, Philos. Trans. R. Soc. London, 1857, 147, 145–181.
2. B. Nikoobakht and M. A. El-Sayed, Chem. Mater., 2003, 15, 1957–1962.
3. F. Kim, S. Connor, H. Song, T. Kuykendall and P. Yang, Angew. Chem., Int. Ed., 2004, 43, 3673–3677.
4. T. K. Sau and C. J. Murphy, J. Am. Chem. Soc., 2004, 126, 8648–8649.
5. M. Grzelczak, J. Pérez-Juste, P. Mulvaney and L. M. Liz-Marzán, Chem. Soc. Rev., 2008, 37, 1783–1791.
6. J. Xiao and L. Qi, Nanoscale, 2011, 3, 1383–1396.
7. J. Zhang, M. R. Langille, M. L. Personick, K. Zhang, S. Li and C. A. Mirkin, J. Am. Chem. Soc., 2010, 132, 14012–14014.
8. J. W. Hong, S.-U. Lee, Y. W. Lee and S. W. Han, J. Am. Chem. Soc., 2012, 134, 4565–4568.
9. R. Long, S. Zhou, B. J. Wiley and Y. Xiong, Chem. Soc. Rev., 2014, 43, 6288–6310.
10. O. M. Bakr, B. H. Wunsch and F. Stellacci, Chem. Mater., 2006, 18, 3297–3301.
11. L.-C. Cheng, J.-H. Huang, H. M. Chen, T.-C. Lai, K.-Y. Yang, R.-S. Liu, M. Hsiao, C.-H. Chen, L.-J. Her and D. P. Tsai, J. Mater. Chem., 2012, 22, 2244–2253.
12. C. G. Khoury and T. Vo-Dinh, J. Phys. Chem. C, 2008, 112, 18849–18859.
13. P. S. Kumar, I. Pastoriza-Santos, B. Rodriguez-Gonzalez, F. J. G. de Abajo and L. M. Liz-Marzan, Nanotechnology, 2008, 19, 015606.
14. H.-L. Wu, C.-H. Chen and M. H. Huang, Chem. Mater., 2008, 21, 110–114.
15. S. Barbosa, A. Agrawal, L. Rodríguez-Lorenzo, I. Pastoriza-Santos, R. A. Alvarez-Puebla, A. Kornowski, H. Weller and L. M. Liz-Marzán, Langmuir, 2010, 26, 14943–14950.
16. D. Y. Kim, T. Yu, E. C. Cho, Y. Ma, O. O. Park and Y. Xia, Angew. Chem., Int. Ed., 2011, 50, 6328–6331.
17. C. J. DeSantis, A. A. Peverly, D. G. Peters and S. E. Skrabalak, Nano Lett., 2011, 11, 2164–2168.
18. Z. Li, W. Li, P. H. C. Camargo and Y. Xia, Angew. Chem., Int. Ed., 2008, 47, 9653–9656.
19. L. Ma, C. Wang, B. Y. Xia, K. Mao, J. He, X. Wu, Y. Xiong and X. W. Lou, Angew. Chem., Int. Ed., 2015, 54, 5666–5671.
20. E. Ye, M. D. Regulacio, S.-Y. Zhang, X. J. Loh and M.-Y. Han, Chem. Soc. Rev., 2015, 44, 6001–6017.
21. E. Ye, K. Y. Win, H. R. Tan, M. Lin, C. P. Teng, A. Mlayah and M.-Y. Han, J. Am. Chem. Soc., 2011, 133, 8506–8509.
22. M. Bosman, E. Ye, S. F. Tan, C. A. Nijhuis, J. K. W. Yang, R. Marty, A. Mlayah, A. Arbouet, C. Girard and M.-Y. Han, Sci. Rep., 2013, 3, 1312.
23. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
24. P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953–17979.
25. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
27. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter, 1999, 59, 1758–1775.
28. W. Zhu, X. Qiu, V. Iancu, X.-Q. Chen, H. Pan, W. Wang, N. M. Dimitrijevic, T. Rajh, H. M. Meyer III, M. P. Paranthaman, G. M. Stocks, H. H. Weitering, B. Gu, G. Eres and Z. Zhang, Phys. Rev. Lett., 2009, 103, 226401.
29. H. Pan, Y.-W. Zhang, V. Shenoy and H. Gao, Appl. Phys. Lett., 2010, 96, 192510.
30. A. Karma and M. Plapp, Phys. Rev. Lett., 1998, 81, 4444–4447.
31. M. Frigo and S. G. Johnson, http://www.fftw.org.
32. J. Xie, J. Y. Lee and D. I. Wang, Chem. Mater., 2007, 19, 2823–2830.
33. E. Ye, S. Y. Zhang, S. Liu and M. Y. Han, Chem. – Eur. J., 2011, 17, 3074–3077.
34. J. L. Elechiguerra, J. Reyes-Gasga and M. J. Yacaman, J. Mater. Chem., 2006, 16, 3906–3919.
35. A. R. Tao, S. Habas and P. Yang, Small, 2008, 4, 310–325.
36. H. Zhang, X. Xia, W. Li, J. Zeng, Y. Dai, D. Yang and Y. Xia, Angew. Chem., Int. Ed., 2010, 49, 5296–5300.
37. N. A. Lambropoulos, J. R. Reimers and N. S. Hush, J. Chem. Phys., 2002, 116, 10277–10286.
38. M.-C. Daniel and D. Astruc, Chem. Rev., 2004, 104, 293–346.
39. T. A. Witten and L. M. Sander, Phys. Rev. Lett., 1981, 47, 1400–1403.
40. P. Meakin, Phys. Rev. Lett., 1983, 51, 1119.
41. T. A. Witten and L. M. Sander, Phys. Rev. B: Condens. Matter, 1983, 27, 5686–5697.

---

Footnote

† Electronic supplementary information (ESI) available: XRD patterns and TEM images. See DOI: 10.1039/c5nr07182h

---