A high performance, visible to mid-infrared photodetector based on graphene nanoribbons passivated with HfO₂

Abstract

Graphene has drawn tremendous attention as a promising candidate for electronic and optoelectronic applications owing to its extraordinary properties, such as broadband absorption and ultrahigh mobility. Nevertheless, the absence of a bandgap makes graphene unfavorable for digital electronic or photonic applications. Although patterning graphene into nanostructures with the quantum confinement effect is able to open a bandgap, devices based on these graphene nanostructures generally suffer from low carrier mobility and scattering losses. In this paper, we demonstrated that encapsulation of an atomic layer deposited high-quality HfO₂ film will greatly enhance the carrier mobility and decrease the scattering losses of graphene nanoribbons, because this high-k dielectric layer weakens carrier coulombic interactions. In addition, a photodetector based on HfO₂ layer capped graphene nanoribbons can cover broadband wavelengths from visible to mid-infrared at room temperature, exhibiting ∼10 times higher responsivity than the one without a HfO₂ layer in the visible regime and ∼8 times higher responsivity in the mid-infrared regime. The method employed here could be potentially used as a general approach to improve the performance of graphene nanostructures for electronic and optoelectronic applications.

---

Introduction

Graphene, a two-dimensional allotrope of honeycomb carbon atoms, has been considered as an attractive building block for electronic and optoelectronic applications,^1–6 such as novel photodetectors with ultrafast speed^7–9 and broadband operation wavelengths ranging from visible to terahertz.^10–12 Such broadband absorption emerged from the unique conic band structure and linear energy dispersion of massless Dirac fermions.^13–15 Nevertheless, this zero bandgap characteristic of the monolayer graphene introduces some limitations that render its applications. First, the low absorption (∼2.3%) of monolayer graphene via interband transitions is still a critical challenge.¹⁶ Second, the zero bandgap leads to a short photogenerated carrier lifetime at the picosecond level, which causes fast electron–hole recombinations.^17,18 As a result, the photoresponse of the pristine graphene photodetectors is quite weak nowadays.

Several approaches have been used to enhance the photoresponse of graphene photodetectors. For example, graphene quantum dot (GQD) arrays were successfully employed to create a bandgap of around 100 meV to improve the responsivity of pure graphene photodetectors through bandgap and defect engineering.¹⁹ Although a broadband photodetector with a responsivity of up to 8.6 A W⁻¹ was achieved in the visible range, it still remains as a challenge to obtain room temperature operation of graphene photodetectors with a relatively fast response speed in a broadband range due to the random scattering losses. Alternatively, graphene nanoribbons (GNRs)^20–22 have been demonstrated to have a bandgap opening by utilizing the quantum confinement effect,^23–25 which has been realized through unzipping of carbon nanotubes,²⁶ lithographic patterning^23–25 and other chemical approaches.^27,28 However, disordered edges, impurities and phonon scattering of the GNR reduce the carrier mobility and increase the carrier scattering losses, which limit the device performance.²⁹ Previously, graphene photodetectors based on ∼240 nm wide GNRs were reported with a low photoresponse in the mid-infrared regime, because graphene nanoribbons with this width cannot open a sufficient bandgap, even though the light–graphene interaction is enhanced by graphene plasmons.³⁰ On the contrary, ultra-narrow GNRs with widths of ∼2–5 nm were used for graphene photodetectors for achieving a considerable bandgap.²⁶ However, the performance of the device is significantly limited by the low mobility of GNR as induced by the tremendous carrier scattering losses from defects and GNR edges with such a narrow width. Therefore, it is critical to design appropriate GNR structures to obtain a suitable bandgap for broadband operation, while still maintaining its high mobility in order to achieve high photodetection performance.

In this paper, we demonstrated a graphene field-effect transistor (FET) made of 10 nm wide GNRs encapsulated by an ultrathin high-k HfO₂ layer, where the obtained GNR FET shows a semiconductor behaviour with an ON/OFF ratio of 7 ± 1. The GNR photodetector shows a high responsivity across a broadband wavelength range from visible to mid-infrared, i.e. 1.75 A W⁻¹ in the visible, 1.5 A W⁻¹ in the near-infrared and 0.18 A W⁻¹ in the mid-infrared, at room temperature with a source–drain voltage as low as 10 mV. In addition, the photoresponse speed of our GNR photodetector, fabricated by electron-beam lithography (EBL) and reactive-ion etching (RIE), is relatively faster than the devices obtained by chemical methods.^19,22,31 This promising performance is due to the proper design of the GNR width for broadband operation, and the increment of carrier mobility due to the reduction of carrier scattering losses in GNR via high-k HfO₂ passivation.^32–34 Our work reveals the importance of the dielectric environment for graphene nanostructures and it provides insights to optimize graphene-based photodetectors and transistors for optoelectronic and electronic applications.

Results and discussion

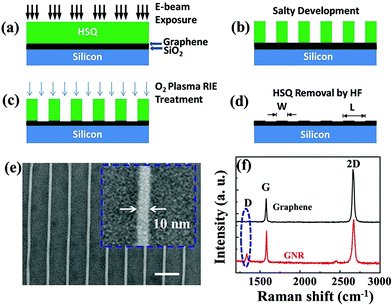
Monolayer graphene was fabricated by mechanical exfoliation of highly-ordered pyrolytic graphite (HOPG) on SiO₂/Si wafer and identified by optical microscopy and Raman spectroscopy.³⁵ We first fabricated the graphene FET devices using standard photolithography, followed by an e-beam evaporation of Ti/Au electrodes (20 nm/80 nm). The fabrication processes of GNR FET devices are shown in Fig. 1(a)–(d), where a monolayer graphene was patterned into nanoribbons by using electron beam lithography (EBL) and reactive-ion etching (RIE) oxygen plasma treatment. First, a negative e-beam resist, hydrogen silsesquioxane (HSQ), with a thickness of ∼30 nm was spin-coated onto the substrate. After the electron-beam exposure, the sample was then developed by using a NaOH/NaCl salty solution,³⁶ and the corresponding scanning electron micrograph (SEM) of the 10 nm wide HSQ resist mask is shown in Fig. 1(e). Here, we did not obtain SEM images of GNR directly because the high energy electron beams will change the doping level of graphene so as to affect the GNR photodetector's performance. The doping effect has been reported previously.^37–40 With this HSQ etching mask, patterns were transferred onto the underlying graphene monolayer via RIE oxygen plasma treatment. HSQ was then removed by immersing the sample in a hydrofluoric acid solution (HF ∼2%) for 30 seconds. Furthermore, the Raman spectrum of GNR presents a clear D-peak at ∼1350 cm⁻¹ in Fig. 1(f), indicating that the EBL process induced defects, impurities and edge scattering in the GNR.

Fig. 1 Electron beam lithography (EBL) processes and characterization of graphene nanoribbons (GNR). (a)–(d) Schematic illustration on the process to fabricate GNR using EBL and reactive-ion etching (RIE) oxygen plasma treatment. (e) Scanning electron micrograph (SEM) of the hydrogen silsesquioxane (HSQ) resist mask prior to the RIE oxygen plasma treatment. The scale bar is 100 nm. The inset presents a close-up SEM image of the 10 nm wide HSQ resist mask. (f) Raman spectra of the exfoliated monolayer graphene and GNR.

Field-effect transistor (FET) devices were fabricated for both unpatterned graphene and 10 nm wide GNRs. V_DS, I_DS and V_G denote the source–drain bias voltage, current, and bottom gate voltage, respectively. The devices have a pair of metal pads (Ti/Au) as source/drain metal contacts, a heavily p-doped Si as the backgate, and 285 nm thick SiO₂ as the gate dielectric. Moreover, Fig. S2† and Fig. 2 show the comparison of electrical characterization of the unpatterned graphene and GNR-based FETs at room temperature, where both measured I_DS–V_DS curves in Fig. S2(a)† and 2(a) are linear over a wide range of gate voltages. Such a linear dependence indicates that the Ti/Au electrodes have a good ohmic contact. By comparing Fig. S2(b)† and 2(b), GNR-based FET exhibits a semiconducting transport behaviour with an ON/OFF ratio of ∼7 ± 1, where the ON/OFF ratio was measured at V_G − V_D = −80 V, and V_D denotes the neutral point.

Fig. 2 Electrical characterization of the GNR-based field-effect transistor (FET) at room temperature. (a) I_DS–V_DS curves recorded at different gate voltages. (b) Dependence of the resistance on the gate voltage recorded at V_DS = 10 mV, indicating a semiconducting behaviour curve.

The GNR FET is shown to behave like a semiconducting material with an adequate bandgap to operate in the mid-infrared regime at room temperature, and the relationship between the GNR width and its bandgap can be expressed as:²⁴

where W₀ indicates the renormalization of geometrical charging energy by virtual charge fluctuations and it has a typical value of ∼40 nm.²⁴e is the electron charge and W is the actual width of GNR. For instance, the 10 nm wide GNR possesses a bandgap of ∼100 meV for our obtained samples.

On the other hand, the mobility of the GNR device is reduced significantly compared to the unpatterned graphene devices, and the carrier mobility μ can be calculated by:

where L and M denote the channel length, and the total width of the FET respectively. d denotes the thickness of the SiO₂ layer (285 nm in our devices). One should note that the actual width of GNR FET with graphene nanoribbons is M/10 according to the ribbon ratio (i.e. 10%) as shown in Fig. 1(e). ε₀ and ε_r represent the dielectric constant of vacuum and SiO₂ (ε_r = 3.9), respectively. Based on eqn (2), the mobility of GNR FET is ∼100 cm² V⁻¹ s⁻¹, which is ∼25 times smaller than the pristine graphene FETs fabricated in our experiment. The relatively low mobility of GNR is caused by carrier scattering with impurities, defects, and surface roughness.⁴¹ Although a built-in electrical field can be used to separate photo-excited carriers in optoelectronic devices,³¹ the low mobility (∼100 cm² V⁻¹ s⁻¹) restrains its potential applications.

The carrier mobility could be enhanced by passivating a layer of high-k dielectric material, such as HfO₂, on top of GNR, the detailed sample schematic structure is shown in Fig. 3(a), and this approach of using high-k dielectrics was previously employed in MoS₂ ^31,32 and graphene devices.^33,34 The source and drain electrodes are exposed by selectively etching with a HF solution after the photolithography process. The use of this high-k dielectric material (HfO₂) is that it can change the dielectric environment of GNR so as to reduce the carrier scattering from impurities, defects, and surface roughness through dielectric screening. The HfO₂ layer is grown by using the atomic layer deposition (ALD) method, where an atomic force microscope (AFM) was then used to characterize the surface profile of the ALD grown HfO₂ film, and the line-scan profile shows a thickness of 1.8 nm in Fig. 3(a) for 20 ALD process cycles. The thickness of the HfO₂ film can be well controlled based on the number of ALD process cycles. Moreover, the high crystallization quality of the HfO₂ layer was confirmed by the X-ray photoelectron spectroscopy (XPS) measurements in Fig. S1.†

Fig. 3 Schematic and characterization results of GNR-based FET deposited with HfO₂ films. (a) Height profile of the HfO₂ film as measured by using an atomic force microscope (AFM). The HfO₂ film was grown using the atomic layer deposition (ALD) method with 20 cycles. (b) I_DS–V_DS curves of different HfO₂ coated GNR-based FETs recorded at V_DS = 10 mV. (c) I_DS–V_G curves of HfO₂ coated GNR array based FET recorded at V_DS = 10 mV. (d) Mobility of GNR-based FET with a different thickness of HfO₂ layer. (e) Coulomb potential corresponding to two different dielectric environments, i.e. ε_g > ε_e and ε_g < ε_e. ε_h denotes the dielectric constant of HfO₂.

The electrical transport characterization was then carried out for both the GNR-based FETs with and without an HfO₂ film under the same conditions. The I_DS–V_DS curves, as shown in Fig. 3(b), are linear and symmetric at the small bias voltages. All devices with the deposited HfO₂ show a larger source–drain current than the one without HfO₂, which is because of the mobility enhancement of GNR due to dielectric screening. In order to demonstrate the mechanism of the dielectric environment effect on carrier scattering as caused by the charged impurity, we compared the results on mobility by using two kinds of dielectric materials capped on GNR as shown in Fig. 3(e). For the first scenario, the capping material has a higher dielectric constant than GNR, i.e. ε_e > ε_g. ε_e refers to the dielectric constant of HfO₂ in our case and ε_g refers to the dielectric constant of graphene. For the second scenario, the capping material is a low-k material with ε_e < ε_g, e.g. ε_e = 1. Due to the mismatch of the dielectric constant between GNR and the capping material, image charges are induced in the capping dielectric materials.³² To be more specific, the induced array of image charges are located at z_n = na, where a is the thickness of GNR and n = ±1, ±2, … The n-th point charge has a magnitude of eγ^|n| and γ = (ε_e − ε_g)/(ε_e + ε_g). Then, we could calculate the net electric potential seen by the electron due to these image charges as:⁴²

where ε₀ is the vacuum permittivity.

Fig. 3(e) shows the schematic diagram Coulomb potential contours, from which we can conclude that the Coulomb potential is enhanced in the low-k case, while it is strongly damped in the high-k case. In addition, the GNR FET with the 1.8 nm thick HfO₂ layer shows a larger mobility value, where the mobility decreases with the increment of HfO₂ layer thickness calculated from Fig. 3(c) as shown in Fig. 3(d). This phenomenon is consistent with eqn (3) and it can be explained by the increment of defects and surface roughness induced scattering with thicker ALD HfO₂ layers.⁴² Here, we would like to mention that we could not carry out experiments with the thickness of the HfO₂ layer being below 1.8 nm since the ALD fabricated film is not uniform with less than 20 ALD cycles. Further improvements are also possible when using other materials with a thinner layer and better uniformity, such as ALD grown Al₂O₃ ^43,44 or monolayer h-BN.⁴⁵

We analyzed the optoelectronic properties of bare and HfO₂ capped GNR photodetectors and their time-dependent photoresponse, with the excitation laser wavelengths of 632 nm, 1.47 μm and 10 μm, respectively. A parabolic mirror with a micromechanical stage was used to focus laser spots onto the sample and the estimated power intensity is ∼2.5 W cm⁻². The time-dependent photocurrent responses at different wavelengths are shown in Fig. 4(a)–(c). It is shown that, in a broadband range from visible, to near-infrared, and mid-infrared, the photocurrent of HfO₂ capped GNR photodetectors is about ∼8–10 times higher than the one without HfO₂ capping, corresponding to a responsivity of 1.75 A W⁻¹, 1.5 A W⁻¹, and 0.18 A W⁻¹, respectively, with a small source–drain bias voltage of only 10 mV. This high responsivity achieved in our devices can be attributed to the enhancement of mobility through dielectric screening. The response time is still at the second level as shown in Fig. 4(a)–(d), which is limited by the long trapping lifetime of carriers in the defect and edges states. However, the response speed demonstrated here is about one order of magnitude faster than the previous reports on a randomly distributed graphene quantum dot (GQD) photodetector¹⁹ which has complex deep surface and edge states and an electron trapping time of ∼30 seconds. The improvement was achieved by the e-beam lithography fabrication method which is used to define the edge and surface states of graphene nanoribbons with low-level chemical processes involved, thus producing graphene nanoribbons with cleaner and less surface and edge defects. The usage of high-k HfO₂ as a passivated layer, apart from enhancing the carrier mobility, can also efficiently modify the edge and defect states of GNRs, leading to a faster response speed. Moreover, further improvements of the response speed are possible by using monolayer h-BN for dielectric engineering or optimizing the nanofabrication process to achieve well-defined edges and clean surfaces with less defects and residues.

Fig. 4 (a) Photodetection measurement of HfO₂ capped GNR-based FETs with visible, near-infrared and mid-infrared lasers. (a)–(c) Time-dependent photocurrent measurements on the GNR-based FETs under the laser illumination with the wavelength of 632 nm, 1.47 μm, and 10 μm, respectively. The power density for all the measurements was kept at 2.5 W cm⁻². (d) Photocurrent of 1.8 nm thick HfO₂ capped GNR FETs measured in one period of modulation with the 1.47 μm laser illumination (12 mW). (e) Power dependence of the photocurrent with 1.47 μm lasers, for every laser illumination we measured 3 different samples. (f) Photocurrent and decay time measurements of graphene with different thicknesses of HfO₂ film, corresponding to thicknesses as shown in Fig. 3(e), at least 3 different samples are measured with the same thickness of the HfO₂ film.

Fig. 4(e) presents the detailed photoresponse as a function of the laser power at the wavelength of 1.47 μm, and it is fitted by the relationship I_PC = CP^γ, where C is a constant and P is the illumination power. The value of γ is calculated to be ∼1.09 and this relatively high value of γ in GNR is attributed to the 1 − d transport characteristic of GNR and the relatively high mobility of our HfO₂ capped GNR devices. A further increment of the HfO₂ thickness will increase the response time slightly as shown in Fig. 4(f), which is due to the increased density of defect states and trapping states with the increasing thickness of the dielectric layer.⁴² We note that the HfO₂ capped GNR photodetector operated in the mid-infrared regime exhibits a longer photoresponse time compared to those in the visible and near-infrared regimes as shown in Fig. 4(a)–(c), the detailed mechanism for this slower decay time at the mid-infrared regime needs further investigations.

The photocurrent obtained by our HfO₂ capped graphene nanoribbons is higher than that by bare graphene nanoribbons³¹ and chemically etched GQDs,¹⁹ because the Coulomb interactions and carrier/defect scattering are strongly decreased through the passivation of a high-k dielectric layer and e-beam lithography fabrication of the GNRs. The design of graphene nanoribbons of an appropriate width is important for optoelectronic applications. For example, we measured the photodetector with 100 nm wide GNR, in which the photoresponse is only ∼5 mA W⁻¹ under illumination with a 10 μm laser as shown in Fig. S3.† On the other hand, the photoresponse in our work is higher than the one using ∼240 nm wide graphene nanoribbons, because the GNR width is not narrow enough to open a bandgap according to eqn (1), even though the absorption is enhanced by graphene plasmons.³⁰ In comparison, although the ultra-narrow (<5 nm) GNR was fabricated by unzipping of carbon nanotubes (CNT) exhibiting typical semiconductor behaviour,²⁶ the photoresponse is very weak due to the strong edge scattering losses, which increase as W⁻⁴ with W being the width of the nanoribbons.⁴¹ Furthermore, other newly proposed 2D materials with narrow bandgaps⁴⁶ combined with this dielectric engineering strategy are promising in the development of novel mid-infrared photodetectors.

Conclusions

In summary, we demonstrated a novel strategy to enhance the mobility of 10 nm wide GNR FETs by capping a high-k dielectric HfO₂ layer, which improves the mobility of the GNR FETs by ∼3 times, compared to the pure GNR devices. Such an improvement in mobility is attributed to the reduced carrier scattering in capped GNR. Furthermore, the optical characterization results of HfO₂ capped GNR photodetectors show that the response time will be ∼5 times faster and the responsivity was enhanced by ∼10 times in the visible and near-infrared regions, and ∼8 times in the mid-infrared region. We believe that our work paves a way towards high performance and flexible graphene-based optoelectronic devices, especially with the potential combination of large-area CVD growth of graphene and the CMOS technology.⁴⁷

Acknowledgements

This work was supported by (MOE2011-T2-2-147 and MOE2011-T3-1-005) the Ministry of Education, Singapore. Z. D. and J. K. W. Y. would like to acknowledge the funding support from the Agency for Science, Technology and Research (A*STAR) Young Investigatorship (grant number 0926030138), SERC (grant number 092154099), and the National Research Foundation (grant number NRF-CRP 8-2011-07). X. Y., Z. D. and Y. L. contributed equally to this work.

Notes and references

1. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
2. K. S. Novoselov, V. I. Falko, L. Colombo, P. R. Gellert, M. G. Schwab and K. Kim, Nature, 2012, 490, 192–200.
3. F. H. L. Koppens, T. Mueller, P. Avouris, A. C. Ferrari, M. S. Vitiello and M. Polini, Nat. Nanotechnol., 2014, 9, 780–793.
4. L. Shao, X. Wang, H. Xu, J. Wang, J.-B. Xu, L.-M. Peng and H.-Q. Lin, Adv. Opt. Mater., 2014, 2, 162–170.
5. B. J. Schultz, R. V. Dennis, V. Lee and S. Banerjee, Nanoscale, 2014, 6, 3444–3466.
6. W. Jie and J. Hao, Nanoscale, 2014, 6, 6346–6362.
7. K. J. Tielrooij, L. Piatkowski, M. Massicotte, A. Woessner, Q. Ma, Y. Lee, K. S. Myhro, C. N. Lau, P. Jarillo Herrero, N. F. van Hulst and F. H. L. Koppens, Nat. Nanotechnol., 2015, 10, 437–443.
8. T. Mueller, F. Xia and P. Avouris, Nat. Photonics, 2010, 4, 297–301.
9. T. J. Echtermeyer, P. S. Nene, M. Trushin, R. V. Gorbachev, A. L. Eiden, S. Milana, Z. Sun, J. Schliemann, E. Lidorikis, K. S. Novoselov and A. C. Ferrari, Nano Lett., 2014, 14, 3733–3742.
10. Q. Bao and K. P. Loh, ACS Nano, 2012, 6, 3677–3694.
11. Z. Sun and H. Chang, ACS Nano, 2014, 8, 4133–4256.
12. X. Cai, A. B. Sushkov, R. J. Suess, M. M. Jadidi, G. S. Jenkins, L. O. Nyakiti, R. L. Myers-Ward, S. Li, J. Yan, D. K. Gaskill, T. E. Murphy, H. D. Drew and M. S. Fuhrer, Nat. Nanotechnol., 2014, 9, 814–819.
13. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200.
14. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162.
15. J. Li, L. Niu, Z. Zheng and F. Yan, Adv. Mater., 2014, 26, 5239–5273.
16. R. R. Nair, P. Blake, A. N. Grigorenko, K. S. Novoselov, T. J. Booth, T. Stauber, N. M. R. Peres and A. K. Geim, Science, 2008, 320, 1308–1308.
17. P. A. George, J. Strait, J. Dawlaty, S. Shivaraman, M. Chandrashekhar, F. Rana and M. G. Spencer, Nano Lett., 2008, 8, 4248–4251.
18. K. J. Tielrooij, J. C. W. Song, S. A. Jensen, A. Centeno, A. Pesquera, A. Zurutuza Elorza, M. Bonn, L. S. Levitov and F. H. L. Koppens, Nat. Phys., 2013, 9, 248–252.
19. Y. Zhang, T. Liu, B. Meng, X. Li, G. Liang, X. Hu and Q. J. Wang, Nat. Commun., 2013, 4, 1811.
20. Y. F. Zhu, Q. Q. Dai, M. Zhao and Q. Jiang, Sci. Rep., 2013, 3, 1524.
21. V. Barone, O. Hod and G. E. Scuseria, Nano Lett., 2006, 6, 2748–2754.
22. B. Chitara, L. S. Panchakarla, S. B. Krupanidhi and C. N. R. Rao, Adv. Mater., 2011, 23, 5419–5424.
23. M. Y. Han, B. Özyilmaz, Y. Zhang and P. Kim, Phys. Rev. Lett., 2007, 98, 206805.
24. F. Sols, F. Guinea and A. H. C. Neto, Phys. Rev. Lett., 2007, 99, 166803.
25. X. Liang, Y.-S. Jung, S. Wu, A. Ismach, D. L. Olynick, S. Cabrini and J. Bokor, Nano Lett., 2010, 10, 2454–2460.
26. D. Wei, L. Xie, K. K. Lee, Z. Hu, S. Tan, W. Chen, C. H. Sow, K. Chen, Y. Liu and A. T. S. Wee, Nat. Commun., 2013, 4, 1374.
27. X. Li, X. Wang, L. Zhang, S. Lee and H. Dai, Science, 2008, 319, 1229–1232.
28. A. N. Abbas, G. Liu, A. Narita, M. Orosco, X. Feng, K. Müllen and C. Zhou, J. Am. Chem. Soc., 2014, 136, 7555–7558.
29. E. Ulrich Stützel, T. Dufaux, A. Sagar, S. Rauschenbach, K. Balasubramanian, M. Burghard and K. Kern, Appl. Phys. Lett., 2013, 102, 043106.
30. M. Freitag, T. Low, W. Zhu, H. Yan, F. Xia and P. Avouris, Nat. Commun., 2013, 4, 1951.
31. J. G. Son, M. Son, K.-J. Moon, B. H. Lee, J.-M. Myoung, M. S. Strano, M.-H. Ham and C. A. Ross, Adv. Mater., 2013, 25, 4723–4728.
32. Z.-Y. Ong and M. V. Fischetti, Phys. Rev. B: Condens. Matter, 2013, 88, 165316.
33. L. Liao, J. Bai, R. Cheng, Y.-C. Lin, S. Jiang, Y. Huang and X. Duan, Nano Lett., 2010, 10, 1917–1921.
34. F. Chen, J. Xia, D. K. Ferry and N. Tao, Nano Lett., 2009, 9, 2571–2574.
35. X. Yu, J. Tao, Y. Shen, G. Liang, T. Liu, Y. Zhang and Q. J. Wang, Nanoscale, 2014, 6, 9925–9929.
36. Z. Dong, M. Asbahi, J. Lin, D. Zhu, Y. M. Wang, K. Hippalgaonkar, H.-S. Chu, W. P. Goh, F. Wang, Z. Huang and J. K. W. Yang, Nano Lett., 2015, 15, 5976–5981.
37. I. Childres, L. A. Jauregui, M. Foxe, J. Tian, R. Jalilian, I. Jovanovic and Y. P. Chen, Appl. Phys. Lett., 2010, 97, 173109.
38. D. Teweldebrhan and A. A. Balandin, Appl. Phys. Lett., 2009, 94, 013101.
39. M. M. Ugeda, I. Brihuega, F. Hiebel, P. Mallet, J.-Y. Veuillen, J. M. Gómez-Rodríguez and F. Ynduráin, Phys. Rev. B: Condens. Matter, 2012, 85, 121402.
40. L. Tao, C. Qiu, F. Yu, H. Yang, M. Chen, G. Wang and L. Sun, J. Phys. Chem. C, 2013, 117, 10079–10085.
41. T. Fang, A. Konar, H. Xing and D. Jena, Phys. Rev. B: Condens. Matter, 2008, 78, 205403.
42. D. Jena and A. Konar, Phys. Rev. Lett., 2007, 98, 136805.
43. C. Goo Kang, S. Kyung Lee, T. Jin Yoo, W. Park, U. Jung, J. Ahn and B. Hun Lee, Appl. Phys. Lett., 2014, 104, 161902.
44. C. G. Kang, S. K. Lee, S. Choe, Y. G. Lee, C.-L. Lee and B. H. Lee, Opt. Express, 2013, 21, 23391–23400.
45. H. Zeng, C. Zhi, Z. Zhang, X. Wei, X. Wang, W. Guo, Y. Bando and D. Golberg, Nano Lett., 2010, 10, 5049–5055.
46. S. Zhang, Z. Yan, Y. Li, Z. Chen and H. Zeng, Angew. Chem., Int. Ed., 2015, 54, 3112–3115.
47. X. Zhang, J. Ning, X. Li, B. Wang, L. Hao, M. Liang, M. Jin and L. Zhi, Nanoscale, 2013, 5, 8363–8366.

---

Footnotes

† Electronic supplementary information (ESI) available: Method, characterization results, calculation of photoresponsivity, and calculation of photoconductive gain. See DOI: 10.1039/c5nr06869j

‡ Equal contribution.

---