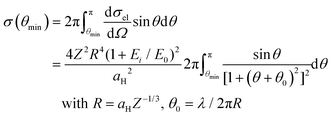Interactions between C and Cu atoms in single-layer graphene: direct observation and modelling

Abstract

Metal doping into the graphene lattice has been studied recently to develop novel nanoelectronic devices and to gain an understanding of the catalytic activities of metals in nanocarbon structures. Here we report the direct observation of interactions between Cu atoms and single-layer graphene by transmission electron microscopy. We document stable configurations of Cu atoms in the graphene sheet and unique transformations of graphene promoted by Cu atoms. First-principles calculations based on density functional theory reveal a reduction of energy barrier that caused rotation of C–C bonds near Cu atoms. We discuss two driving forces, electron irradiation and in situ heating, and conclude that the observed transformations were mainly promoted by electron irradiation. Our results suggest that individual Cu atoms can promote reconstruction of single-layer graphene.

---

Introduction

The interactions between metals and graphene have been studied extensively with the aim to control the local properties of graphene for its applications in electrocatalysts and nanoelectronic devices^1–3 and to create novel carbon nanostructures.^4–7 Theoreticians predicted that transition metal atoms in graphene vacancies have unique electronic and magnetic properties.^8–10 However, there are only a few experimental reports on such metal–graphene systems, due to the difficulty of direct observation of them. Researchers applied aberration-corrected transmission electron microscopy (TEM) and scanning TEM (STEM) to observe metal atoms in a graphene sheet, such as Fe dimers¹ and single atoms of Pt, Co and In¹¹ doped into graphene vacancies, as well as the etching of graphene mediated by metal atoms (Cr, Ti, Pd, Ni or Al).¹² These studies suggest that most metal atoms, except Au, promote the etching of graphene. Such destruction to graphene will result in a serious problem for its practical applications.

Here we report the structures and dynamics of Cu atoms embedded in single-layer graphene as observed by aberration-corrected TEM. We selected Cu because it has a similar electronic configuration to Au and is known to be the best catalyst for graphene growth;^13–15 hence, Cu will not etch graphene and is expected to catalyse the growth or modification of graphene structures. We directly observed unique morphological changes in Cu-doped graphene that have not been observed in other metals: reconstruction of graphene grains, various transformations promoted near Cu atoms, and formation and mending of nanopores. First-principles calculations based on density functional theory (DFT) were performed to explain the observed stability and dynamics as well as Cu-assisted transformations of graphene.

Results and discussion

Cu sites in graphene

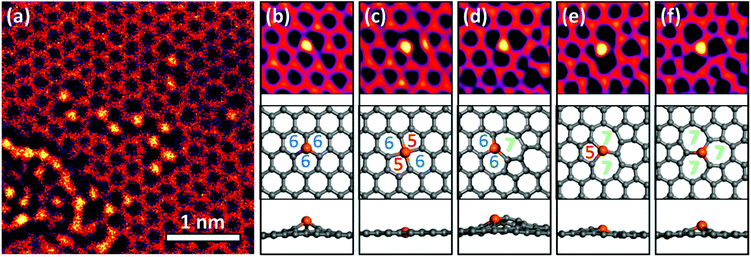
In the areas irradiated by a focused electron beam, some Cu atoms replaced carbon atoms in the graphene lattice. This substitution was observed more frequently in areas containing residual oxygen and hydrocarbon contaminations. These contaminations could be reduced by in situ annealing. Thus the density of Cu–C substitutions in graphene could be controlled by varying the electron beam current and the sample annealing temperature, which may be useful for its practical applications.

The TEM image in Fig. 1a shows more than 10 Cu atoms embedded in ∼4 × 4 nm² area of graphene. We took TEM images under overfocus conditions to highlight Cu atoms, and Cu atoms appeared 1.8 ± 0.2 times brighter than C atoms. Meanwhile, at underfocus (Scherzer focus) the contrasts are reversed and Cu atoms are more difficult to image. Multislice simulation for the present overfocus conditions yielded a Cu/C intensity ratio of 1.92 (further details of Cu identification are given in ESI Fig. S1–3†).

Fig. 1 Cu atoms embedded in graphene. (a) Unprocessed TEM image of Cu atoms (brighter spots) embedded in graphene. (b–f) Averaged and low-pass-filtered TEM images (top row) and the corresponding DFT models of Cu sites (top and side views, the second and third rows, respectively).

Most previous studies^1,8–11,16 focused on metal atoms in single or double vacancies (Fig. 1b and c), i.e., in the cases when metal atoms substituted for one or two carbon atoms in a pristine graphene lattice. In contrast, the Cu atoms in our experiments exhibited a more complex behaviour and were frequently observed at topological defects in graphene (Fig. 1d–f). We name the corresponding structures according to the number of atoms making up the carbon rings, including the central Cu atom. For example, the Cu atom shown in Fig. 1d makes two six-membered rings and one seven-membered ring with neighbouring C atoms, so we call this structure 667.

DFT calculations suggest that most Cu-related defects are non-planar, except for those containing four-coordinated Cu (Fig. 1c). Three-coordinated Cu atoms (Fig. 1b and d–f) protrude from the graphene surface because single vacancies are too small to accommodate them. The height is the smallest for the 577 structure shown in Fig. 1e, whereas in the 667 configuration several carbon atoms are displaced out of the graphene plane along with Cu. Malola et al.¹⁶ claimed that Au preferentially occupies double or larger vacancies to reduce the height; however, we observed no clear correlation between the height and stability (lifetime) of the observed structures. For example, the highly distorted 667 was more frequently observed and had a longer lifetime than the almost planar 577 structure. Krasheninnikov et al.⁹ found that metal atoms, including Cu and Au, form covalent bonds with the C atoms at the vacancies. The stability depends primarily on the strain around the Cu atoms and the bonding strength between Cu and C; hence, the height of a defect is not a decisive factor.

In addition, Cu atoms physically adsorbed on a pristine graphene surface have been rarely observed, because their diffusion barrier is more than 10 times lower than that of substitutional Cu atoms.¹⁷ The energy provided by heating and electron irradiation was sufficient to transform the Cu atoms embedded in graphene but was too large to observe the atoms adsorbed on its surface.

Reconstruction of graphene

Cu substitution resulted in a gradual reconstruction of graphene during the TEM observations. Fig. 2a was taken 13 min after Fig. 1a from the same sample area. A small misoriented region was created near Cu atoms. It contains pairs of five- and seven-membered rings at a 30° grain boundary (yellow in Fig. 2b). Such pairs are called Stone–Wales (SW) defects. Fig. 2c and d show TEM images taken before and after the reconstruction, taken from another area. Note the broadening of the corresponding fast Fourier transform (FFT) patterns (cf. insets of Fig. 2c and d), which reveals that the reconstruction resulted in an angular disorder due to the formation of 1–3 nm sized grains. We numbered the four grains shown in Fig. 2d as follows: grain #1 kept its original orientation, but became a bit distorted; #2 and #4 reconstructed and rotated by 18° and 23° from the original, respectively; and #3 rotated while preserving its original six-membered ring structure.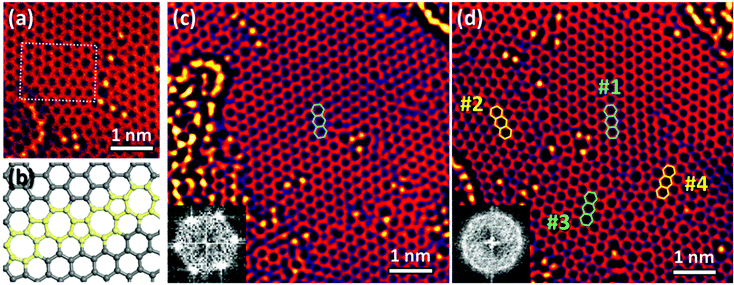

Fig. 2 Reconstruction of graphene. (a) TEM image taken after ∼13 min from the same area as that shown in Fig. 1a. (b) Model of the grain boundary marked by a white box in (a). Five- and seven-membered rings appear in yellow. (c) TEM image taken before the reconstruction. (d) TEM image taken 20 min after (c). Insets in (c) and (d) are FFT images.

Most grains were disrupted by the local strain induced by the contaminants, and reconstructed via repeated rotation of C–C bonds near Cu atoms to minimize the overall strain. In Fig. 2a, hydrocarbon contaminants on the left side of the image were partially graphitized by electron irradiation, distorting the underlying graphene lattice. Grain #2 was also covered by hydrocarbons (Fig. 2c); it reconstructed after their removal by electron irradiation, albeit with a different orientation.

ESI Movie S1† was taken 15–21 min after Fig. 2c, which shows a different type of reconstruction, namely a grain rotation. In contrast to the former reconstruction, the grains kept the original graphene structure during the reconstruction. Grain #3 retained its orientation until a small pore was mended by Cu atoms, and gradually rotated by about 17° owing to the strain from contaminants on the left and defects on the right side (see ESI Fig. S4†). During this process, many SW defects moved via C–C bond rotation and helped fit grain #3 to its neighbours.

Lehtinen et al.¹⁸ found that aggregated interstitials in graphene, which have a strong local curvature in graphene, are energetically more favourable than isolated ones. The same was true of Cu atoms and SW defects: SW defects were reported to distort graphene,^19,20 and Cu atoms in our experiment tended to combine with them rather than remain isolated. Cu atoms can also distort graphene, thereby promoting both generation of defects and their healing via C–C bond rotation. Such repeated distortion and reconstruction, promoted by Cu atoms and electron irradiation, gradually changed the graphene structure.

Transformations promoted by Cu atoms

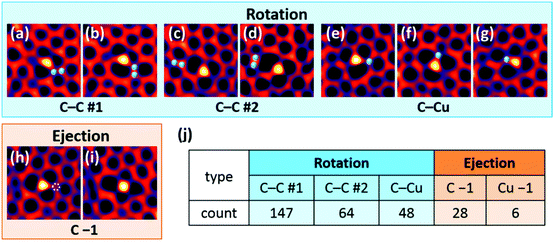
We analysed the dynamics and stability of 56 single Cu atoms to further elaborate the graphene transformations mentioned above. Fig. 3 shows the four typical transformation types: (a and b) and (c and d) are C–C bond rotations #1 and #2. They differ by the fact that in #1, one of the rotating C atoms is attached to a Cu atom, while in #2, the rotating pair is separated from Cu. The third transformation is the rotation of a C–Cu bond (e–g), and the fourth is ejection of one C atom (h and i). Selected images were converted into an animation which includes all transformation types (see ESI Movie S2 and Fig. S5†).

Fig. 3 TEM images of the structures before and after each transformation: (a, b) rotation of the C–C bond attached to a Cu atom, (c, d) rotation of the C–C bond near a Cu atom, (e–g) rotation of the C–Cu bond, and (h, i) ejection of the C atom next to Cu. Rotated C atoms are highlighted as light blue balls. (j) Observation frequency for each transformation (arb. units).

The majority of the observed transformations were C–C rotations near the Cu atoms. C–C rotation #1 was most common and occurred reversibly, while C–C rotation #2 was less frequent (Fig. 3j). We can explain this preference by the number of bonds that break and recombine during each transformation. Two strong C–C bonds break in process #2, whereas #1 involves one C–C bond and one weak C–Cu bond. The binding energies of substitutional C and Cu atoms in graphene were calculated to be 15.7 and 3.9 eV, respectively. Because each C and Cu atom is bonded with three neighbouring C atoms, the energy difference between one C–C bond and one C–Cu bond, or between rotations #2 and #1, is estimated to be ∼4 eV. This scenario explains the relative frequencies of C–C rotations #1 and #2, but not those of the other transformations: it predicts that C–C #1 and C–Cu rotation should be equally frequent, as they both involve one C–C and one C–Cu bond. Meanwhile the C–C #1 process was 3 times more common in our observations. Furthermore, C ejections were rather common, despite their expected high energy barrier, whereas very few Cu ejections were observed. We will discuss this inconsistency later.

We performed first-principles calculations based on DFT, to evaluate the activation energy barrier and the total energy change for each transformation. Our DFT calculations of the energy barrier do explain why the C–C rotations are promoted by Cu atoms. They agree with the analysed observation frequency (Fig. 3j) and stability (lifetime) of each structure and the binding energy estimates mentioned above, although they are simplified models and do not take into account the defect-related lattice distortions in the large area.

Fig. 4a and b show the C–C rotation that converts four six-membered rings into two SW defects. Replacing one C atom with a Cu atom in these figures results in the 666, 667, 567 and 577 defects as shown in Fig. 4d–g, respectively (see ESI Fig. S6† for other Cu configurations). Fig. 4c shows the energy diagram of C–C bond rotation without a Cu atom. The total energy increased by 5.06 eV when a SW defect was created. The top of the barrier corresponds to the transition state with two broken C–C bonds; it is 9.36 eV above the pristine graphene and 4.30 eV above the SW defect level. These values are consistent with a previous report.²¹ As discussed below, the 9.36 eV energy can be easily supplied by a typical TEM operated at 200–300 kV, but not at 80 kV.

Fig. 4 Energy required for the bond rotations. (a, b) Atomic models of C–C bond rotation without Cu atoms. Orange frames outline the cells used in DFT calculations, which contain 96 atoms. (c) Energy diagram of the transformation between (a) and (b). (d–g) Atomic models of Cu sites in graphene. If the two carbon atoms highlighted by yellow ellipses are rotated, the model of Cu atoms embedded in SW defects (e–g) will become a pristine structure (d). (h) Energy diagrams of transformations between (d) and (e), (f) or (g). Insets show models of transition states.

We also calculated C–C bond rotation with Cu atoms (Fig. 4d–f), and found that the energy barrier of C–C rotations was significantly reduced from that in pristine graphene (Fig. 4h). The C–C rotation #1 was most frequently observed, because the energy barrier was reduced to 3.18 eV, and the energy required to return to the 666 structure in Fig. 4d was only 0.84 eV. This reduction came from the low C–Cu binding energy and from the partial passivation of carbon dangling bonds by Cu (see the inset of Fig. 4h).

The stability of each structure depends on the energy barrier height rather than the total energy difference. For example, although the SW defect is 5.06 eV less stable than pristine graphene, once it is created, the energy barrier of 4.30 eV prevents its relaxation from the SW defect to pristine graphene. The 577 structure (Fig. 4g) has a lower total energy than the 667 structure (Fig. 4e); however, there is no transition state between the 577 structure and the 666 structure (Fig. 4d), as shown in Fig. 4h; therefore, it will soon transform into 666 (the pristine structure without SW defects). The Cu atom at the vertex of the pentagon induces a large stress in graphene and therefore is less stable than in the other configurations, despite the low total energy of its optimized structure.

This factor appears in our experimental observations as the defect lifetime. Defects involving five-membered rings, such as 577 and 568, had approximately half the lifetime of the 667 or 677 structures (see ESI Table S1†). The 577 structure can also be regarded as a transition state of diffusion of the Cu atom. The Cu atom in the 666 structure will exchange positions with the neighbouring C atom by the 180° C–Cu rotation. The corresponding energy barrier is 2.32 eV (energy difference between the 577 and 666 states), which is similar to the value of 2.2 eV for Au atom diffusion in graphene.²²

Driving force of the transformations

In this section, we discuss two driving forces: in situ heating and electron irradiation. C–C bond rotations occurred within 5 min in our experiment, which had a temporal resolution of 1 s. We estimated the energy required to rotate the C–C bond to be 3.2 eV, which is sufficient to cause SW defect formation by C–C rotation #1 and relaxation by C–C rotation #2, as shown in Fig. 4h. We then calculated the time required for the next rotation via thermal activation:²³ the C–C bond rotation takes ∼10¹⁵ s at 300 °C, with an attempt frequency of 5 × 10¹² s⁻¹ given by the G-mode vibration of graphene.²⁴ This calculation suggests that most transformations could not be induced by thermal activation (except for the relaxation of SW defects via C–C rotation #1), and were promoted by electron irradiation. This conclusion is supported by our observations that the graphene structure remained unchanged in weakly irradiated sample areas.

When an electron is elastically scattered at an angle θ by an atom, it transfers an energy E_t to it;²⁵E_t increases with θ and decreases with the atomic mass number (12 and 63.5 for C and Cu, respectively). We used an accelerating voltage of 80 kV because the corresponding E_t value is lower than the sputtering threshold energy (∼22 eV (ref. 26 and 27)), which reduces the knock-on damage. However, this low beam energy can still induce transformations in Cu-doped graphene, with carbon atoms being more susceptible owing to their low atomic number. The maximum transfer energies E_max (E_t at θ = 180°) are 15.74 eV for C and 2.97 eV for Cu.

The energy transfer model can help explain why C–C bond rotation and C atom ejection were more frequently observed than C–Cu bond rotation and Cu ejection. The energy transferred to Cu atoms cannot exceed 2.97 eV; hence, the observed transformations arose mainly via excitation of C atoms. Electron irradiation less affected Cu atoms; thus, Cu atoms were less mobile than C atoms. Although the binding energy of a Cu atom in a single vacancy is 4–5 times smaller than that of a C atom, Cu atom ejections from the graphene lattice were rarely observed in our TEM experiments. The ejected C and Cu atoms likely moved too fast to be observed by TEM and were trapped by other vacancies or contaminants in graphene. Cu atoms are expected to be more mobile near contaminants or nanoparticles than in a perfect graphene lattice.

For all the transformations described above, the energy transferred from electron beams should be greater than the energy barrier E_b. The scattering cross section σ for an energy transfer E_t ≥ E_b is given by^23,25

where θ_min is the minimum scattering angle given by the equation E_t = E_max sin²(θ/2), dσ_el/dΩ is the differential elastic cross section, a_H is the Bohr radius (5.29 × 10⁻¹¹ m), Z is the atomic number (6 for C and 29 for Cu), and E₀ is the electron rest energy (0.511 MeV). Thus, taking E_b = 3.2 eV for the C–C rotation (which leads to θ_min = 54° for carbon), we obtain σ = 2.9 × 10⁻⁶ Å. The defect lifetime t is inversely proportional to the product of σ and the electron beam current density j (t = 1/σj).

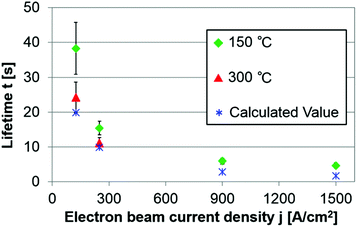
Fig. 5 shows the averaged lifetimes, including all types of structures and transformations, at different current densities (respective lifetime values of typical structures are shown in ESI Table S1†). The green and blue symbols respectively show the experimental values measured at 150 °C and the calculated values, assuming that the energy transferred to C is 7.26 eV (the maximum value for C–C bond rotation near a Cu atom). Although the experimental lifetimes are slightly longer than the calculated ones, their orders of magnitude are the same and both lifetimes are inversely proportional to current density j. For j = 125 A cm⁻² at 150 °C, transformations occurred within a few seconds in defective areas, whereas stable structures such as 667, 666, 677 and 5656 in a relatively clean graphene often survived for more than 2 min. We conclude that Cu atoms promote C–C rotation when they are surrounded by many defects, but not when reconstruction of graphene is complete.

Fig. 5 Lifetime under electron irradiation. The observed lifetimes at 150 and 300 °C were averaged and plotted as a function of the electron beam current density. Blue symbols indicate the calculated values assuming that E_t = 7.26 eV for C.

As shown in Fig. 5, the effect of temperature on the lifetime t became significant at lower current density j, albeit it was smaller than the electron irradiation effect. In contrast to the energy transferred from the electron beam, the thermal activation energy affects C and Cu equally; hence, increasing the temperature reduced the lifetime of every Cu–graphene configuration. Gan et al.²⁸ measured the diffusion rates of Pt and Au atoms at different temperatures and calculated the diffusion barriers. However, Malola et al.¹⁶ pointed out that these results may not be accurate because of the strong irradiation effect. Further observations are necessary for a quantitative discussion of the temperature effect, especially at low electron beam densities (≤125 A cm⁻²).

Cu atoms and nanoparticles started to evaporate at much lower temperature than the melting temperature of 1085 °C of bulk Cu. Electron irradiation also promoted the aggregation and evaporation of Cu; however, Cu nanoparticles were evaporated only by heating. We took a low-magnification TEM image (ESI Fig. S1c†) and then turned off the beam. About half of the nanoparticles disappeared after 11 h of heating at 300 °C. Cu atoms embedded in the graphene lattice were more stable than the particles physically adsorbed on the graphene surface. The ejection frequency of Cu atoms from the graphene lattice did not increase at 300 °C compared to that at 150 °C. However, above 300 °C, Cu evaporated very rapidly, before promoting Cu substitutions. Such a heating should be avoided while manufacturing Cu-doped graphene devices.

Uniqueness of Cu compared with other transition metals

Many metals, including Cr, Ti, Pd, Ni and Al, were experimentally reported to etch graphene,¹² and a similar activity was theoretically predicted for Fe and Co.²⁹ Cu atoms, however, promoted graphene reconstruction rather than etching in our experiment. Even when small pores were created by irradiation, Cu atoms covered their edges to prevent expansion of the pores and mended them by trapping the C atoms floating around (e.g. ESI Fig. S4b†). We have not observed such effects for Pt under similar experimental conditions.³⁰ Double-vacancy transformation processes were observed in graphene without Cu atoms (ESI Movie S3 and Fig. S7†); however, they occurred at an angstrom rather than a nanometre scale.

We believe that this unique ability of Cu originates from its electronic configuration specific to noble metals. The binding energy of Cu at the single and double vacancies was calculated to be 3.90 and 5.26 eV, respectively, whereas those of the other transition metals are 6–8 eV.^8,9 While diffusing, these metal atoms bind to C atoms and remove them from the graphene lattice. This effect should be much smaller for Cu, Ag, Au (binding energy 2–5 eV) and Zn atoms (binding energy 1–3 eV).^8,9

Furthermore, we also calculated the energy difference ΔE between Fe, Cr, and Ni substitutional atoms at SW defects and those at single vacancies without SW defects (models and results are shown in ESI Fig. S6†). We found that their ΔE are ∼1 eV higher than those for the Cu atoms in the same models; hence, compared to Fe, Cr, and Ni, Cu atoms are more stable near SW defects and thereby promote C–C bond rotations and unique reconstructions.

Conclusions

We directly observed atomic-scale transformations of Cu-doped graphene using aberration-corrected TEM. Our observations suggest that Cu atoms tend to combine with SW defects and preferentially replace C atoms in defective graphene areas. They also modify graphene by promoting C–C bond rotation, formation and mending of nanopores, and rotation of grains mediated by contaminants and lattice defects. Cu atoms and SW defects form grain boundaries between the reconstructed and original grains. All these transformations were assisted by electron irradiation, which affected C atoms much more than Cu atoms because of the higher energy transferred to them from the electron beam. Thermal effects need a further study, and our results reveal that Cu atoms are stable in graphene sheets up to 300 °C. We combined experiment with DFT calculations to investigate the stability of Cu atoms embedded in graphene and the activation energy barriers for the experimentally observed transformations. Our results reveal that individual Cu atoms can catalyse the reconstruction of carbon nanostructures.

Methods

Sample preparation

Single-layer graphene on a Cu foil was transferred onto in situ heating chips (E-chips for Aduro™, Protochips) using the previously reported poly(methyl methacrylate) support method.³⁰ To avoid metallic impurities, we etched the Cu foil with a metal-free (NH₄)₂S₂O₈ (ammonium persulfate) solution. Heating in a vacuum of 0.6–1 × 10⁻⁵ Pa at high temperatures above 400 °C created clean graphene patches about 200 × 200 nm² in size. Cu was then deposited using an ion beam etching system (PECS, Gatan). When observed at room temperature just after deposition, Cu had not formed crystals; it was dispersed with oxygen and hydrocarbons. A recent study suggested that partial oxidation of Cu suppresses nucleation, and a large graphene sheet with a single domain can be synthesized.³¹ In fact, oxidized Cu nanoparticles promoted the etching of graphene, whereas pure Cu nanoparticles did not. Therefore, we heated the sample at 150–300 °C to remove oxygen, and Cu atoms formed nanoparticles (the corresponding size distributions are shown in ESI Fig. S1†). Cu nanoparticles gradually evaporated at 300 °C and rapidly disappeared at ∼500 °C. Si contamination was possible because we used quartz-tube furnaces and silicon nitride in situ heating chips, yet we believe that Si was a minor impurity and most of the observed atoms were Cu. Indeed all nanoparticles around the observation areas and a few dispersed atoms were identified as Cu by using STEM combined with electron energy loss spectroscopy (EELS, Fig. S2†).

TEM imaging experiments

Aberration-corrected TEM (JEM-ARM200F, JEOL) was used for in situ observations. The microscope was operated at a relatively low voltage of 80 kV to reduce the knock-on damage to the graphene sheets. The sample temperature during observation was kept at 150 and 300 °C by using an in situ heating holder (Aduro™, Protochips). Most results are reported for 150 °C, unless mentioned otherwise, but the frequency of each transformation type and lifetimes of each structure were measured at both temperatures. TEM movies were acquired at a speed of 0.5–2 frames per s. All the TEM images shown in Fig. 1–3, except Fig. 1a, are snapshots from the TEM movies that are processed as follows: frames were shifted to compensate for thermal drift, and then averaged and low-pass filtered to improve the signal-to-noise ratio (Fig. 1a and 2a are unfiltered images).

First-principles calculations

We performed first-principles calculations based on DFT using the PHASE/0 code.³² The generalized gradient approximation³³ and ultrasoft pseudopotential³⁴ were employed. The spin polarization was considered. The cut-off energies of the plane-wave basis set and charge density were taken at 25 and 255 Ry, respectively. Each defect was introduced into a graphene supercell of periodicity (96 atoms). The lateral size of the unit cell was measured using the optimized lattice constant of graphene, 2.476 Å, which is 0.6% larger than the experimental lattice constant. The graphene sheet was isolated by a vacuum layer of 10 Å thickness (we used 12 Å-thick cells with ∼2 Å distortion height). A Monkhorst and Pack mesh of 3 × 3 × 1 size was used for k-sampling.³⁵ The atomic positions were optimized until the residual force became smaller than 5.0 × 10⁻⁴ hartree per bohr. To evaluate energy barriers, a climbing image nudged elastic band method with eight images was employed.³⁶

Acknowledgements

We thank Dr E. Okunishi from JEOL Ltd for his help with STEM-EELS, Dr Y.-C. Lin from AIST for his advice on sample preparation, and Dr K. Iakoubovskii from NIMS for discussions. A part of this work was supported by the ‘Nanotechnology Platform Project’ sponsored by the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan, and a Grant-in-Aid for Japan Society for the Promotion of Science (JSPS) Fellows.

Notes and references

1. Z. He, K. He, A. W. Robertson, A. I. Kirkland, D. Kim, J. Ihm, E. Yoon, G.-D. Lee and J. H. Warner, Nano Lett., 2014, 14, 3766–3772.
2. E. Yoo, T. Okata, T. Akita, M. Kohyama, J. Nakamura and I. Honma, Nano Lett., 2009, 9, 2255–2259.
3. K. Pi, K. M. McCreary, W. Bao, W. Han, Y. F. Chiang, Y. Li, S.-W. Tsai, C. N. Lau and R. K. Kawakami, Phys. Rev. B: Condens. Matter, 2009, 80, 075406.
4. X. Li, W. Cai, L. Colombo and R. S. Ruoff, Nano Lett., 2009, 9, 4268–4272.
5. S. Saadi, F. Abild-Pedersen, S. Helveg, J. Sehested, B. Hinnemann, C. C. Appel and J. K. Nørskov, J. Phys. Chem. C, 2010, 114, 11221–11227.
6. P. Han, K. Akagi, F. F. Canova, H. Mutoh, S. Shiraki, K. Iwaya, P. S. Weiss, N. Asao and T. Hitosugi, ACS Nano, 2014, 8, 9181–9187.
7. J.-Y. Raty, F. Gygi and G. Galli, Phys. Rev. Lett., 2005, 95, 096103.
8. E. J. G. Santos, A. Ayuela and D. Sánchez-Portal, New J. Phys., 2010, 12, 053012.
9. A. V. Krasheninnikov, P. O. Lehtinen, A. S. Foster, P. Pyykkö and R. M. Nieminen, Phys. Rev. Lett., 2009, 102, 126807.
10. Z. Ning, Z. Chen, X. Du, R. Ran, W. Dong and C. Chen, J. Supercond. Novel Magn., 2013, 27, 115–120.
11. H. Wang, Q. Wang, Y. Cheng, K. Li, Y. Yao, Q. Zhang, C. Dong, P. Wang, U. Schwingenschlögl, W. Yang and X. X. Zhang, Nano Lett., 2012, 12, 141–144.
12. Q. Ramasse, R. Zan, U. Bangert, D. W. Boukhvalov, Y.-W. Son and K. S. Novoselov, ACS Nano, 2012, 6, 4063–4071.
13. X. Li, W. Cai, J. An, S. Kim, J. Nah, D. Yang, R. Piner, A. Velamakanni, I. Jung, E. Tutuc, S. K. Banerjee, L. Colombo and R. S. Ruoff, Science, 2009, 324, 1312–1314.
14. Q. Yu, L. A. Jauregui, W. Wu, R. Colby, J. Tian, Z. Su, H. Cao, Z. Liu, D. Pandey, D. Wei, T. F. Chung, P. Peng, N. P. Guisinger, E. A. Stach, J. Bao, S.-S. Pei and Y. P. Chen, Nat. Mater., 2011, 10, 443–449.
15. C. Mattevi, H. Kim and M. Chhowalla, J. Mater. Chem., 2011, 21, 3324–3334.
16. S. Malola, H. Häkkinen and P. Koskinen, Appl. Phys. Lett., 2009, 94, 043106.
17. O. V. Yazyev and A. Pasquarello, Phys. Rev. B: Condens. Matter, 2010, 82, 045407.
18. O. Lehtinen, N. Vats, G. Algara-siller, P. Knyrim and U. Kaiser, Nano Lett., 2015, 15, 235–241.
19. J. H. Warner, E. R. Margine, M. Mukai, A. W. Robertson, F. Giustino and A. I. Kirkland, Science, 2012, 337, 209–212.
20. J. Ma, D. Alfè, A. Michaelides and E. Wang, Phys. Rev. B: Condens. Matter, 2009, 80, 033407.
21. L. Li, S. Reich and J. Robertson, Phys. Rev. B: Condens. Matter, 2005, 72, 184109.
22. W. Zhang, L. Sun, Z. Xu, A. V. Krasheninnikov, P. Huai, Z. Zhu and F. Banhart, Phys. Rev. B: Condens. Matter, 2010, 81, 125425.
23. J. Lee, W. Zhou, S. J. Pennycook, J.-C. Idrobo and S. T. Pantelides, Nat. Commun., 2013, 4, 1650.
24. P. Koskinen, S. Malola and H. Häkkinen, Phys. Rev. Lett., 2008, 101, 115502.
25. L. Reimer and H. Kohl, Transmission Electron Microscopy, Springer, USA, 2008.
26. A. V. Krasheninnikov, F. Banhart, J. X. Li, A. S. Foster and R. M. Nieminen, Phys. Rev. B: Condens. Matter, 2005, 72, 125428.
27. A. Zobelli, A. Gloter, C. P. Ewels, G. Seifert and C. Colliex, Phys. Rev. B: Condens. Matter, 2007, 75, 245402.
28. Y. Gan, L. Sun and F. Banhart, Small, 2008, 4, 587–591.
29. D. W. Boukhvalov and M. I. Katsnelson, Appl. Phys. Lett., 2009, 95, 023109.
30. E. Kano, M. Takeguchi, J. Fujita and A. Hashimoto, Carbon, 2014, 80, 382–386.
31. Y. Hao, M. S. Bharathi, L. Wang, Y. Liu, H. Chen, S. Nie, X. Wang, H. Chou, C. Tan, B. Fallahazad, H. Ramanarayan, C. W. Magnuson, E. Tutuc, B. I. Yakobson, K. F. McCarty, Y.-W. Zhang, P. Kim, J. Hone, L. Colombo and R. S. Ruoff, Science, 2013, 342, 720–723.
32. https://azuma.nims.go.jp/ .
33. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
34. D. Vanderbilt, Phys. Rev. B: Condens. Matter, 1990, 41, 7892–7895.
35. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5191.
36. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.

---

Footnote

† Electronic supplementary information (ESI) available: Three TEM movies, additional TEM data corresponding to movies, calculated models, and lifetime results. See DOI: 10.1039/c5nr05913e

---