TiC2: a new two-dimensional sheet beyond MXenes†
Tianshan
Zhao
ab,
Shunhong
Zhang
ab,
Yaguang
Guo
ab and
Qian
Wang
*ab
aCenter for Applied Physics and Technology, College of Engineering, Peking University, Beijing 100871, China
bIFSA Collaborative Innovation Center, and Key Laboratory of High Energy Density Physics Simulation, Ministry of Education, Beijing 100871, China. E-mail: qianwang2@pku.edu.cn
First published on 15th October 2015
Abstract
MXenes are attracting attention due to their rich chemistry and intriguing properties. Here a new type of metal–carbon-based sheet composed of transition metal centers and C2 dimers rather than individual C atom is designed. Taking the Ti system as a test case, density functional theory calculations combined with a thermodynamic analysis uncover the thermal and dynamic stability of the sheet, as well as a metallic band structure, anisotropic Young's modulus and Poisson's ratio, a high heat capacity, and a large Debye stiffness. Moreover, the TiC2 sheet has an excellent Li storage capacity with a small migration barrier, a lower mass density compared with standard MXenes, and better chemical stability as compared to the MXene Ti2C sheet. When Ti is replaced with other transition metal centers, diverse new MC2 sheets containing C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C dimers can be formed, the properties of which merit further investigation.
C dimers can be formed, the properties of which merit further investigation.
Introduction
Carbon, due to its unique flexibility to manipulate its four valence electrons in a very flexible way, forms diverse allotropes ranging from the well-known graphite and diamond to more recent C60 fullerenes, nanotubes, nanochains, and to the newly discovered two-dimensional (2D) carbon like graphene,1 graphyne,2 graphdiyne,2 and penta-graphene.3 The unusual mechanical, electronic, optical, catalytic, and transport properties of these 2D carbon systems and their numerous technological applications have led to considerable interest in the study of other C-based 2D materials. One such example is the hotly pursued MXene type Mn+1Cn layers,4–7 a group of 2D early transition metal (TM) carbides derived from chemical exfoliation of the MAX phases, where the concentration of the transition metal atoms (including Sc, Ti, V, Cr, Zr, Zb, Mo, Hf and Ta) exceeds that of carbon, and carbon is atomically bonded to the metal atoms. Because of their rich structural chemistry and good electronic conductivity, MXenes are promising candidates for applications in sensors, electronic devices, catalysts, conductive reinforcement additives to polymers, and electrochemical energy storage or conversion materials.8,9 However, the main disadvantage of MXenes is that the metal atoms are highly exposed on the surfaces. In addition, the surface functionalization is needed for applications in many cases.8,10 Thus, it is necessary to go beyond the morphology of MXenes to design a new type of metal carbide sheet where the metal atoms are less than carbon and carbon is bonded molecularly rather than atomically with the metal atoms. Such kind of sheets can not only reduce their mass density and exposed metal sites with improved chemical stability, but also have different properties due to the change of the binding mode.In fact, the C2 dimer is the basic structural unit in the growth of many carbon structures such as fullerenes, nanotubes, graphene, and graphyne,2,11–14 and even emerges on the reconstructed diamond surface.15 C2 is also the building unit of diverse carbon compounds such as metallocarbohedrenes (Met-Cars) MmCn,16,17 metal–alkynide complexes,18 alkynide complexes,19 organic materials,20 and some binary or ternary metal carbides (LiAgC2, KAgC2, CsAgC2 and NaPdC2).21,22 The first member of the Met-Cars family, Ti8C12, was discovered in 1992 by the Castleman group,16 then the other members, M8C12 with M = Sc, Zr, Hf, V, Nb, Ta, Cr, Mo, and Fe, were also synthesized23,24 and joined in the family soon afterward. The common structural feature of these Met-Cars is that the six C2 dimers are connected by eight TM atoms, forming cage-like structures. In addition, the C2 molecule is a well-known pseudo-oxygen unit with an electron affinity (EA) of 3.4 eV which is nearly three times as large as that of a carbon atom. It has been demonstrated that the C2 dimers play a key role in stability during the growth of Met-Cars where the clusters containing C2 dimers are energetically more favorable than the structures containing only individual carbon atoms or trimers.25 More interestingly, the C2 dimers are also found to exist in both low and high carbon steels.26,27
Despite the versatility of the C2 dimer in forming diverse structures, there has been no report to date on a 2D crystal that consists of transition metal atoms and C2 dimers. In MXenes4,8 and other theoretically predicted metal carbide sheets,28 the carbon atoms bind to the metal atoms individually. Here we present a comprehensive theoretical study of a 2D sheet composed of transition metal centers and C2 dimers by taking the Ti system as an example. The calculated results reveal that the TiC2 sheet is not only stable dynamically and thermally, but also it is metallic with outstanding Li storage capacity beyond existing MXene Ti2C layers. Like MXene Ti2C, the Ti in TiC2 could also be replaced with other transition metal elements, thus giving rise to a new type of 2D metal carbides MC2 with exceptional properties.
Computational methods
Atomic structure optimizations and electronic structure calculations are carried out using density functional theory (DFT) as implemented in the Vienna Ab initio Simulation Package (VASP).27 The projector augmented wave (PAW) method29 and Perdew–Burke–Ernzerhof (PBE) exchange correlation functional within generalized gradient approximation (GGA)30 are used. The 2s1, 2s22p2 and 3d34s1 atomic orbitals are treated as valence states for Li, C, and Ti, respectively. Plane waves with a kinetic energy cutoff of 500 eV are used to expand the valence electron wave functions. For all structural relaxations the convergence criteria for total energy and Hellmann–Feynman force are set to be 10−4 eV and 10−2 eV Å−1, respectively. A unit cell with a vacuum space of 20 Å in a direction perpendicular to the nanosheet is used in order to avoid virtual interactions. The first Brillouin zone is sampled by a 7 × 7 × 1 k-point grid within the Monkhorst–Pack scheme.31 To check the dynamic stability, we use density functional perturbation theory (DFPT) to calculate the force constants. The Phonopy code32 is used to calculate the vibrational spectra. Ab initio molecular dynamics (AIMD) simulations are also performed to assess the thermal stability of the TiC2 sheet. Canonical (NVT) ensemble is adopted using the Nosé heat bath method.33 Bader charge analysis34 is carried out to study the charge distribution and transfer quantitatively. By using the nudged elastic band (NEB) method,35 we calculate the diffusion energy barrier and the minimum energy pathway of Li diffusion on the TiC2 sheet.Results and discussion
Geometry and stability
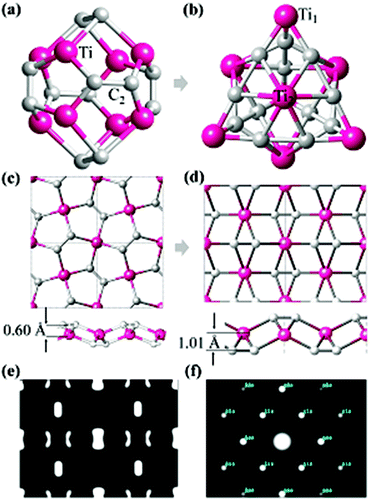
The most well-known carbon–metal nanostructure containing C2 units is the Ti8C12 Met-Car that was initially suggested to have Th symmetry where 20 atoms form a nearly regular pentagonal dodecahedron,16,17 as shown in Fig. 1a. However, the Ti8C12 all-pentagon cage structure was later found to be unstable and transformed to a C3v-like structure17 (Fig. 1b). Rohmer et al.36 analyzed all the possible structures of the Ti8C12 cluster, and found that the 8 Ti atoms forms a pseudocubic framework, each C2 unit could be oriented along one or other diagonal of the underlying face of the pseudocubic framework, independent of other dicarbon fragments. Following such an idea, we use a planar triangular Ti lattice like the first layer of (0001) surface of hcp bulk Ti, and build a 2D Ti–C sheet by depositing the C2 dimers on the surface with different positions and orientations, yielding three candidate structures with a chemical formula TiC2, as shown in Fig. S1.† It is interesting to note that the most stable configuration (Fig. 1d) has the same geometry as optimized from penta-graphene like structure (Fig. 1c). Different from MXenes,4,9,10,37 in the stable TiC2 sheet, Ti atoms are sandwiched between the top and bottom C2 layers, leading to a quasi-2D sheet with no exposed Ti atoms on the surfaces. Another difference between TiC2 and the MXene layers is that in MXenes, the carbon atoms are atomically bonded to its neighboring TM atoms with the C–C distance in the range of 2.80 to 3.35 Å,4,9,11,38 while the C–C distance in TiC2 is only 1.33 Å, showing a double bond character,39 and implying that the carbon atoms exist in the form of a C2 dimer. In addition, unlike the MXenes that have hexagonal symmetry,4 TiC2 has a rectangular lattice with the optimized lattice parameters of a = 4.96 Å and b = 3.59 Å. The C–C bond in TiC2 is also stronger than that in the dodecahedral Ti8C12 cage where the C–C bond length is 1.40 Å,16 and is comparable to that in the C3v-like structure (1.34 Å).17 Note that in bulk metal carbides the C–C bond can vary from conventional single bonds to typical triple bonds.39To study the possible reasons why the structures in Fig. 1a and c are less stable than those in Fig. 1b and d, respectively, we have carefully checked their bonding features and found that in the Th cage structure, all C2 dimers bind with the Ti atoms in an end-on configuration (EOC),40 while in the C3v-like structure41 besides the EOC binding for some Ti atoms (labeled as Ti1 in Fig. 1b), the C2 dimers also bind with Ti in a side-on configuration (SOC) (labeled such Ti atoms as Ti2). Similarly, the pentagon based sheet (Fig. 1c) only contains the EOC binding mode, while the three-atomic-layer sheet (Fig. 1d) has both the EOC and SOC binding modes. The corresponding Ti–C bond length in the EOC and SOC modes is 2.05 Å and 2.20 Å, respectively, close to that of 2.10 Å in the Ti2C MXene monolayer.42 In fact, it has been demonstrated experimentally and theoretically that the SOC binding mode is more energetically favorable over the EOC mode in the Met-Car structures.17,36,43–45 Therefore, containing the SOC binding mode is the possible reason why the C3v-like structure is more stable than the pentagonal dodecahedron as is also the case with the TiC2 sheet which adopted the configuration containing the SOC mode. The simulated Scanning Tunneling Microscopy (STM) (using the constant height model46 with a height of 0.9 Å and a negative bias of 0.05 V) and Transmission Electron Microscopy (TEM)47,48 (base on the so-called independent atom model which is also called the procrystal model49) images of the optimized TiC2 sheet are given in Fig. 1e and f for convenience in comparison with the experimental results in future.
The thermodynamic stability of the 2D TiC2 structure was studied by carrying out additional calculations with many other possible structural isomers. For instance, two energetically low-lying isomers are given in Fig. S2a and S2b,† which are also composed of C2 units and Ti atoms with square and rectangular lattices, respectively. The former one contains both the EOC and SOC binding modes, while the latter has the EOC mode only. The optimized structures are given in Fig. S2c and S2d.† Total energy calculations show that these two structures are respectively 0.75 and 0.78 eV per formula unit (f. u.) higher in energy than the structure given in Fig. 1d. The underlying reason is that the binding mode is different in these three configurations. In Fig. S2d,† the binding between the Ti and C2 units is EOC only, while in Fig. S2c,† although the SOC binding mode also exists, the two neighboring C2 units are perpendicular to each other, which also differ from the parallel alignment of the C2 units in Fig. 1d. Thus, the resulting stresses make the two structures energetically unfavorable as compared to the one shown in Fig. 1d. We also compare the thermodynamic stability of the TiC2 sheet with some previously identified Ti–C compounds with other stoichiometry. Detailed discussion can be found in the ESI.†
We now focus on the energetically most stable structure of the TiC2 sheet. The phonon frequencies and phonon density of states (DOS) are calculated with high accuracy to examine its dynamical stability. The calculated results are summarized in Fig. 2, which show that the TiC2 sheet is dynamically stable as no imaginary frequencies exist in the entire Brillouin zone. The vibrational modes below 350 cm−1 including the three acoustic bands and three optical bands are mainly contributed by Ti due to its larger atomic mass.50 The two highest optical modes are separated from others by a large phonon gap of around 800 cm−1. Comparing the peaks of phonon PDOS with the phonon bands, the following features are identified: the z direction displacement pattern of the Ti atoms (Tiz) contributes to the z direction acoustic branch (ZA), the y direction displacement pattern (Tiy) constitutes the transverse acoustic branch (TA), and the longitudinal acoustic (LA) branch is formed by the displacement of Ti along the x direction (Tix). The Cy and Cz vibrations make main contributions to the optical bands between 350 cm−1 and 650 cm−1. The stretching mode of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds (Cx) corresponds to the two highest optical branches. The highest optical mode reaches up to 1600 cm−1, which is comparable to that of the C
C bonds (Cx) corresponds to the two highest optical branches. The highest optical mode reaches up to 1600 cm−1, which is comparable to that of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds in recently reported carbon structures,3,51 but it is higher than that of the Ti8C12 cluster (1360 cm−1)52 due to the different bond orders.
C bonds in recently reported carbon structures,3,51 but it is higher than that of the Ti8C12 cluster (1360 cm−1)52 due to the different bond orders.
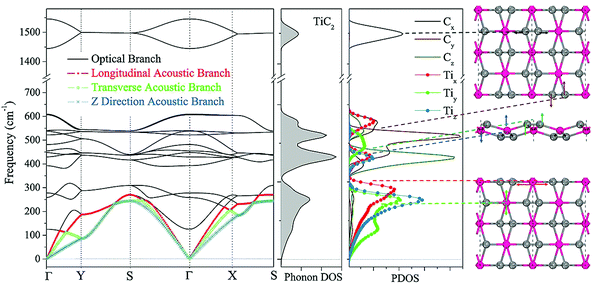 | ||
| Fig. 2 Phonon dispersion, and total and partial phonon DOS of the TiC2 sheet. Some characteristic vibrational modes are indicated in the rightmost column. | ||
To study the thermal stability of the TiC2 sheet at finite temperature, we perform AIMD simulations at 350 K using a relatively large (4 × 4) supercell as a small unit cell may easily result in false instability. The time step is set as 1 femtosecond (fs). After 5 picoseconds of simulation, no structural distortion or reconstruction is found, and the average total potential energy remains nearly constant as shown in Fig. S5,† confirming that TiC2 is thermally stable at room temperature. The thermal stability of TiC2 provides the possibility of its future synthesis and application under ambient conditions.
Thermodynamic properties
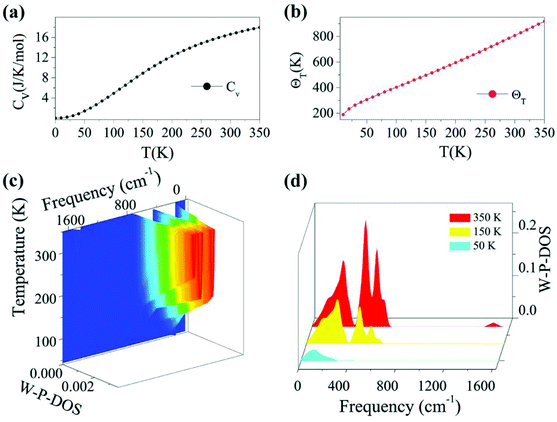
Based on the calculated phonon spectrum, a series of thermodynamic properties can be derived. Here we concentrate on studies of the heat capacity and Debye temperature of the TiC2 sheet. The calculated phonon heat capacity with respect to temperature is plotted in Fig. 3a. The heat capacity can also be expressed using the phonon DOS.53 The Debye temperature ΘD = hνD/kB is determined by fitting the calculated CV–T curve using the Debye model. The fitted Debye temperature ΘD (T) is given in Fig. 3b, which shows that the ΘD(T) is as high as 850 K at room temperature. Since the vibrational frequency is proportional to the square root of the stiffness within the harmonic approximation, ΘD can be used as a measurement of the “stiffness” of solids.53 Therefore, from Fig. 3b we see that the TiC2 sheet can display large Debye stiffness due to its high Debye temperature, resulting from covalent C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds.
C bonds.
As the phonons are subjected to Bose–Einstein distribution, the weighted phonon DOS g(ν)W(hν/kBT) describes the contribution of vibrational modes with a certain frequency to the heat capacity. The frequency and temperature dependence of the weighted phonon DOS is plotted in Fig. 3c. We find that at 50 K, only about 2.5% or even less weighting factor W (hv/kBT) exists in the frequency region over 400 cm−1, indicating that only low-frequency states contribute to the heat capacity at low temperature. This is evidenced by Fig. 3d showing the variation of the weighted phonon DOS with respect to frequency at different temperatures. Since the heat capacity defined by the Debye model is proportional to the cross section of frequency-phonon DOS at a given temperature, a larger amount of heat is required to increase the temperature by one Kelvin when the cross section is larger. Because TiC2 has more vibrational states than graphite and diamond53 in the low frequency region, TiC2 exhibits larger heat capacity under 350 K.
Mechanical properties
To further investigate how lattice distortions affect the structural stability of TiC2, we first calculate the elastic constants to examine its mechanical stability. The elastic constants are calculated to be: C11 = 140.58 N m−1, C22 = 70.52 N m−1, C12 = 25.10 N m−1, and C44 = 16.19 N m−1. Obviously, they satisfy the Born criteria,54,55 namely, C11, C22, C44 > 0 and C11C22 − C122 > 0, suggesting that the TiC2 sheet is mechanically stable. Based on the obtained elastic constants,56 the Young's modulus E(θ) and Poisson's ratio ν(θ) along an arbitrary in-plane direction θ (θ is the angle relative to the x direction) are calculated using the formula:57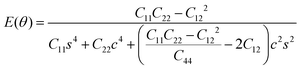 | (1) |
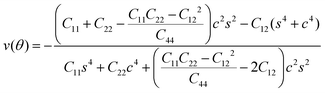 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and s = sin
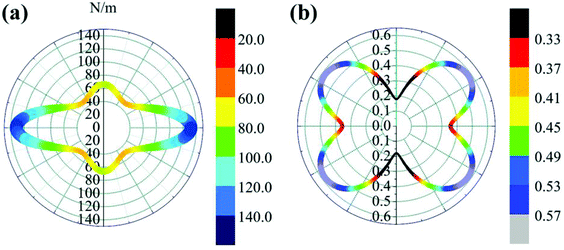
θ and s = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. The results are plotted in Fig. 4. The deviations of E(θ) and ν(θ) from the perfect circles indicate the elastic anisotropy of the TiC2 sheet, which results from the fact that all the C
θ. The results are plotted in Fig. 4. The deviations of E(θ) and ν(θ) from the perfect circles indicate the elastic anisotropy of the TiC2 sheet, which results from the fact that all the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C units are aligned parallel in the x direction. The Young's modulus in the x and y directions are found to be Ex = 131.17 N m−1 and Ey = 66.04 N m−1, respectively. Ex is close to that of MXene Ti2C (130 N m−1).42 In the y direction, the Ti atoms bind to the C2 units through the interaction between Ti-3d and π orbitals of the C–C dimer. Because this interaction is weaker than the C
C units are aligned parallel in the x direction. The Young's modulus in the x and y directions are found to be Ex = 131.17 N m−1 and Ey = 66.04 N m−1, respectively. Ex is close to that of MXene Ti2C (130 N m−1).42 In the y direction, the Ti atoms bind to the C2 units through the interaction between Ti-3d and π orbitals of the C–C dimer. Because this interaction is weaker than the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, it results in a small value of Ey, being only half of Ex. Poisson's ratio is also a fundamental parameter describing the mechanical behavior of a material. For a perfectly incompressible and isotropic material, the Poisson's ratio is exactly equal to 0.5.58 However, Fig. 4b shows that for the anisotropic TiC2 sheet, the Poisson's ratio reaches 0.59 in some directions, which is much larger than that of MXene Ti2C (0.23). For comparison, the main results of the elastic constants, Young's modulus, and Poisson's ratio of TiC2 and other 2D layers are listed in Table 1.56,58–60
C bond, it results in a small value of Ey, being only half of Ex. Poisson's ratio is also a fundamental parameter describing the mechanical behavior of a material. For a perfectly incompressible and isotropic material, the Poisson's ratio is exactly equal to 0.5.58 However, Fig. 4b shows that for the anisotropic TiC2 sheet, the Poisson's ratio reaches 0.59 in some directions, which is much larger than that of MXene Ti2C (0.23). For comparison, the main results of the elastic constants, Young's modulus, and Poisson's ratio of TiC2 and other 2D layers are listed in Table 1.56,58–60
Electronic properties
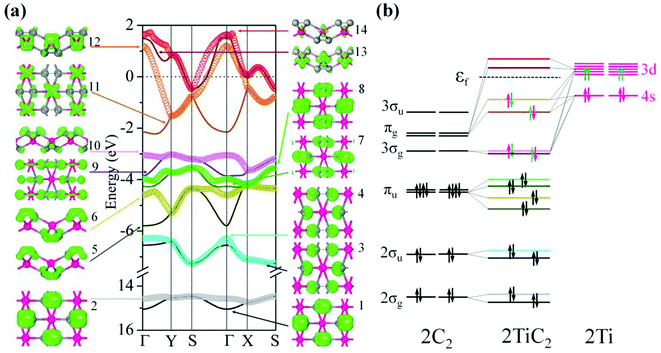
To study the electronic properties we calculate the electronic band structure of the TiC2 sheet. The results are plotted in Fig. 5a. TiC2 is found to be metallic as the partially occupied bands, namely the bands numbered as 12, 13, and 14, cross the Fermi level in the Brillouin zone. The metallicity is further confirmed by using the more accurate HSE06 functional.61,62 Orbital analysis suggests that the bands near the Fermi level are dominated by the Ti-3d orbitals, while the C-2s and 2p orbitals also make small contributions to the observed metallicity through hybridization with the Ti-3d states. We further calculate the band-decomposed charge densities and plot them in Fig. 5a as well. By carefully examining the charge distribution of each band, we clarify the interactions between the frontier orbitals of the C2 units and the Ti atoms, as illustrated in Fig. 5b. The ground state electronic configuration of an isolated C2 dimer is (1σg)2(1σu)2(2σg)2(2σu)2(1πu)4 with the higher states (3σg)(1πg)(3σu) unoccupied. The Ti atoms form a slightly distorted triangular sublattice, akin to that in the recently predicted TiB2.63 The Ti-3d orbitals split into e1(dxy, dxx−yy),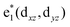 , and a*(dzz) in a triangular crystal field. For comparison, we plot the energy bands formed by the sublattices of the C2 units and the Ti atoms in Fig. S6,† respectively.
, and a*(dzz) in a triangular crystal field. For comparison, we plot the energy bands formed by the sublattices of the C2 units and the Ti atoms in Fig. S6,† respectively.
In Fig. 5a, 1st to 8th energy bands with energy ranging from −15 to −3.5 eV correspond to the 2σg (bonding), 2σu (anti-bonding), and πu (bonding) states of the C2 units, and lie deep under the Fermi level because their energies are much lower than that of the Ti-3d states. The C2-3σg and πg states hybridize with the Ti-3d and 4s states, forming the three fully occupied bands (the 9th, 10th, and 11th bands) and three partially occupied bands (the 12th, 13th, and 14th bands). The bands with energy higher than 2.0 eV are unoccupied and hence are not given in the band structure. To visualize the charge distribution, we plot the band-decomposed charge density isosurfaces for each individual band of the band structure in Fig. 5a, which clearly show the main contribution to the charge density of each band. For instance, the band-decomposed charge densities of the 9th and 10th bands mainly aggregate in the proximity of C2, indicating that the C2-3σg orbitals are filled by the electrons of Ti donors in this 2D crystal. This is qualitatively consistent with our Bader charge analysis, which indicates that each Ti atom transfers about 1.5 electrons to each C2 unit. The bands near the Fermi level are dominated by the Ti-3d states, and consequently the corresponding band-decomposed charge accumulates around the Ti atoms. The band-decomposed charge densities of the 11th and 12th bands clearly show the characteristics of Ti-3dxy and 3dxz orbitals, respectively, while both the 13th and 14th bands have the feature of Ti-3dzz orbitals, indicating that the metallicity of TiC2 originates from the electrons in Ti-3dxz and 3dzz orbitals. Interestingly, we note that the orbital interactions in TiC2 are similar to those in bulk UC2.39 However, Ti-3d and 4s orbitals have much lower energy as compared to U-6d, which enables them to have a stronger interaction with the frontier orbitals of C2 units, leading to the stable 2D sheet.
We further discuss the influence of the occupation of C2 orbitals on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond length. It has been demonstrated that in C2 containing metal carbide systems, the more the C2-πu bonding orbital is occupied, or the less the C2-πg antibonding orbital is filled, the shorter is the C
C bond length. It has been demonstrated that in C2 containing metal carbide systems, the more the C2-πu bonding orbital is occupied, or the less the C2-πg antibonding orbital is filled, the shorter is the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond length.39 The ground state of the isolated C2 has an equilibrium C–C distance of 1.31 Å. The reason that the C–C bond length (1.33 Å) in TiC2 is slightly longer than that of an isolated C2 dimer is because the C2-πg orbital is partially occupied.
C bond length.39 The ground state of the isolated C2 has an equilibrium C–C distance of 1.31 Å. The reason that the C–C bond length (1.33 Å) in TiC2 is slightly longer than that of an isolated C2 dimer is because the C2-πg orbital is partially occupied.
Potential applications of TiC2 as an anode material in lithium ion battery
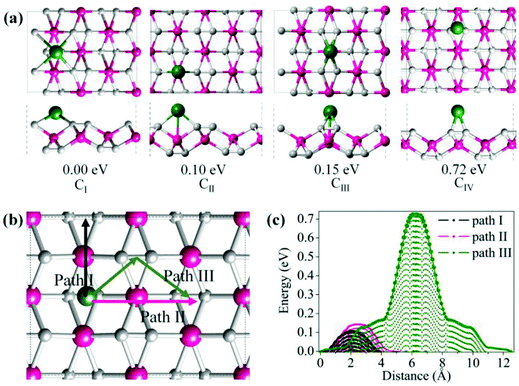
The metallicity of TiC2 provides an intrinsic advantage in electrical conductivity as compared to semiconducting or insulating transition-metal oxides and TMD layers. Therefore, it may find applications as electrodes. In fact, recently MXenes have been widely studied both theoretically and experimentally as promising anode materials for Li ion batteries (LIBs).64,65 Considering that TiC2 possesses higher carbon content as compared to the MXene Ti2C, we expect that this sheet can have a better Li storage capacity. In the following, we systematically explore the possibility of TiC2 as a LIB anode material by looking at the adsorption and diffusion behaviors of Li atoms on this sheet, and derive the relative electrochemical properties of the Li adsorbed TiC2.To determine the preferable adsorption site of Li on the TiC2 sheet, we use a 2 × 2 supercell and deposit one Li atom on different sites, corresponding to a stoichiometry of Ti8C16Li. Four typical adsorption configurations with high structural symmetry, labeled as CI, CII, CIII and CIV, are considered, as shown in Fig. 6a, where CI is the hollow site of the four neighboring carbon dimers, CII is the on-top site of Ti that is in between the two neighboring C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C units lying along a line, CIII is the on-top site of Ti that is in between the two parallel C
C units lying along a line, CIII is the on-top site of Ti that is in between the two parallel C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C units lying in two neighboring lines, and CIV is the bridge site of the C
C units lying in two neighboring lines, and CIV is the bridge site of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C units. Full geometry optimizations and total energy calculations are performed to identify their relative stability. CI is found to be the lowest energy configuration with energy by 0.10, 0.15 and 0.72 eV respectively lower than that of CII, CIII and CIV, suggesting that the Li atom prefers to occupy the hollow site of the carbon dimers on the TiC2 sheet.
C units. Full geometry optimizations and total energy calculations are performed to identify their relative stability. CI is found to be the lowest energy configuration with energy by 0.10, 0.15 and 0.72 eV respectively lower than that of CII, CIII and CIV, suggesting that the Li atom prefers to occupy the hollow site of the carbon dimers on the TiC2 sheet.
To evaluate the potential application of the TiC2 sheet as an anode material for LIB, we investigate the possible diffusion paths of the Li atom on this sheet and their corresponding energy barriers. We consider three trial diffusion paths that connect the two neighboring most preferable Li adsorption sites with high structural symmetry, as indicated in Fig. 6b. Pathway I is found to have the lowest diffusion barrier of 0.11 eV and the shortest diffusion length of 4.38 Å. The magnitude of energy barrier is even smaller than half of those of titanium carbide MXenes (see Table 2)10,64 implying a good conductivity of the Li ions on the TiC2 sheet, which is an important parameter for a LIB electrode material. When Li ions diffuse along path II (perpendicular to path I), the energy barrier is 0.16 eV. This is only 0.05 eV higher than that of path I. While the energy barrier is 0.76 eV when Li ions diffuse along path III, which is much larger than that of path I or path II. The variation of energy barrier with respect to the migration distance of Li on this sheet is plotted in Fig. 6c. Thus, it is clear that both path I and II are the possible routes for Li ion diffusion, which is beneficial for an electrode material.
| Materials | Specific capacity (mA h g−1) | Diffusion barrier (eV) | OCV (V) | ||
|---|---|---|---|---|---|
| Theo. | Expt. | Theo. | Expt. | ||
| TiC2 | 622 | — | 0.11 | — | 0.96 |
| Ti2C | 44010 | — | 0.27 | — | 0.44 |
| Nb2C | 25310 | — | — | — | 0.52 |
| V2C | 41910 | — | — | — | 0.47 |
| Ti3C2 | 32066 | — | 0.07 | — | 0.62 |
| f-Ti3C2 | 44964 | 410 | 0.28 | — | — |
| Graphite | 372 | 372 | 0.467 | — | 0.2 |
| TiO2 | 20068,69 | 200 | — | 0.35–0.6570 | 1.8 |
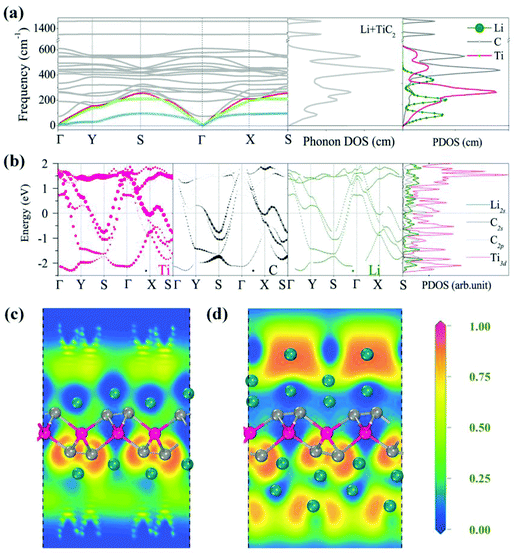
After investigating the adsorption site and the migration path, we studied the adsorption of Li with high concentration. It has been demonstrated that the weight percentage of Li can reach 9% on the surfaces of the functionalized MXenes and multi-layer Li adsorption has been achieved, which significantly enhances the Li storage capacity.64,65 For the TiC2 sheet, we first increase the concentration of Li from the stoichiometry of Ti8C16Li to Ti2C4Li. The preferable adsorption site of Li is again determined to be the hollow site by following the same procedure mentioned above. Based on Bader charge analysis, we find that each adsorbed Li atom transfers 0.86 electrons to the TiC2 sheet. We then calculate the phonon spectrum to examine the effect of Li adsorption on the dynamic stability of the TiC2 sheet at such a relatively high Li adsorption concentration. The calculated results are plotted in Fig. 7a, which shows that all the vibrational modes are real in the Brillouin zone, indicating that the adsorption of the Li atom does not disturb the dynamic stability of the TiC2 sheet. The total and partial phonon DOS are then plotted in Fig. 7a as well, showing that the vibrations of the adsorbed Li atoms mainly contribute to the acoustic modes at the low frequency region.
To study the effect of high Li concentration on the electronic structure, we calculated the electronic band structure of the Ti2C4Li sheet and compared it with that of the pristine TiC2 sheet. We noted that the number of energy bands crossing the Fermi level increases upon Li adsorption, as shown in Fig. 7b, and the interaction between Li and Ti orbitals in the vicinity of the Fermi level is weak due to the repulsive interactions between the Ti and Li ions.
We further increased the concentration of Li by depositing a single layer of Li atoms on both the sides of the TiC2 sheet, leading to a stoichiometry of TiC2Li2 (corresponding to a weight percentage of Li of 16.2%). The electrons over the Li layer form negatively charged cloud, the same is the case with MXenes.65 This is visualized by the calculated electron localization functions (ELF) (Fig. 7c). The average adsorption energy for each Li ion in this situation is 0.96 eV. We then introduce one more layer of Li atoms on both sides of the lithiated TiC2 sheet, corresponding to a chemical ratio of TiC2Li4. The interaction between the two Li layers is visible from the calculated ELF shown in Fig. 7d, indicating that the second Li layer is able to bind with the lithiated TiC2 sheet, as the negatively charged environment is favorable to the adsorption of the second Li layer. Here we see that the TiC2 sheet has a high Li storage capacity, this is very different from the MXene Ti2C sheet which needs surface functionalization for ion intercalation batteries.65
In the following, we calculate the average open circuit voltage (OCV) and the theoretical Li storage capacity, which are important electrochemical properties of an electrode material. OCV can be directly derived in a rather simple way:66
| OCV ≈ [E(TiC2) + xE(Li) − E(TiC2Lix)]/x | (3) |
Conclusions
In conclusion, stimulated by the special role of the C2 dimer in the synthesis of many carbon-based materials as well as its special properties compared to the individual C atoms, we have explored a new type of 2D transition metal carbide by taking the TiC2 sheet as an example, which is composed of Ti centers and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C dimers. Using the state-of-the-art theoretical calculations, we demonstrated that this sheet is not only dynamically, mechanically and thermally stable, but also exhibits exceptional properties including a metallic band structure, anisotropic elasticity, a large heat capacity and Debye stiffness. Due to its unique atomic configuration, the pristine TiC2 sheet has an outstanding Li storage capacity with a smaller migration energy barrier as compared with regular MXenes. In addition, compared to MXene Ti2C sheets, TiC2 has less exposed metal sites on the surfaces showing better chemical stability and lower mass density (only 60% of the Ti2C sheet). In short, as a new member of the 2D metal carbide family, the studied TiC2 sheet is unique as it contains C
C dimers. Using the state-of-the-art theoretical calculations, we demonstrated that this sheet is not only dynamically, mechanically and thermally stable, but also exhibits exceptional properties including a metallic band structure, anisotropic elasticity, a large heat capacity and Debye stiffness. Due to its unique atomic configuration, the pristine TiC2 sheet has an outstanding Li storage capacity with a smaller migration energy barrier as compared with regular MXenes. In addition, compared to MXene Ti2C sheets, TiC2 has less exposed metal sites on the surfaces showing better chemical stability and lower mass density (only 60% of the Ti2C sheet). In short, as a new member of the 2D metal carbide family, the studied TiC2 sheet is unique as it contains C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C dimers instead of individual C atoms, and displays novel properties beyond MXenes.
C dimers instead of individual C atoms, and displays novel properties beyond MXenes.
Acknowledgements
This work is partially supported by grants from the National Natural Science Foundation of China (NSFC-11174014 and NSFC-51471004), the National Grand Fundamental Research 973 Program of China (Grant No. 2012CB921404), and the Doctoral Program of Higher Education of China (20130001110033). The calculations were carried out in Shanghai supercomputer center.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- Y. Li, L. Xu, H. Liu and Y. Li, Chem. Soc. Rev., 2014, 43, 2576–2582 Search PubMed.
- S. Zhang, J. Zhou, Q. Wang, X. Chen, Y. Kawazoe and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2372–2377 CrossRef CAS PubMed.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS PubMed.
- M. Naguib and Y. Gogotsi, Acc. Chem. Res., 2015, 48, 128–135 CrossRef CAS PubMed.
- J.-C. Lei, X. Zhang and Z. Zhou, Front. Phys., 2015, 10, 276–286 CrossRef.
- M. Kurtoglu, M. Naguib, Y. Gogotsi and M. W. Barsoum, MRS Commun., 2012, 2, 133–137 CrossRef CAS.
- M. Khazaei, M. Arai, T. Sasaki, C.-Y. Chung, N. S. Venkataramanan, M. Estili, Y. Sakka and Y. Kawazoe, Adv. Funct. Mater., 2013, 23, 2185–2192 CrossRef CAS.
- M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992–1005 CrossRef CAS PubMed.
- C. Eames and M. S. Islam, J. Am. Chem. Soc., 2014, 136, 16270–16276 CrossRef CAS PubMed.
- F. Calvo, S. Diaz-Tendero and M. A. Lebeault, Phys. Chem. Chem. Phys., 2009, 11, 6345–6352 RSC.
- Q. Wang, M.-F. Ng, S.-W. Yang, Y. Yang and Y. Chen, ACS Nano, 2010, 4, 939–946 CrossRef CAS PubMed.
- M. Sternberg, P. Zapol and L. A. Curtiss, Phys. Rev. B: Condens. Matter, 2003, 68, 205330 CrossRef.
- L. Xu, Y. Jin, Z. Wu, Q. Yuan, Z. Jiang, Y. Ma and W. Huang, J. Phys. Chem. C, 2013, 117, 2952–2958 CAS.
- K. Bobrov, A. J. Mayne and G. Dujardin, Nature, 2001, 413, 616–619 CrossRef CAS PubMed.
- B. C. Guo, K. P. Kerns and A. W. Castleman, Science, 1992, 255, 1411–1413 CAS.
- M.-M. Rohmer, M. Bénard and J.-M. Poblet, Chem. Rev., 2000, 100, 495–542 CrossRef CAS PubMed.
- N. J. Long and C. K. Williams, Angew. Chem., Int. Ed., 2003, 42, 2586–2617 CrossRef CAS PubMed.
- V. W.-W. Yam, Acc. Chem. Res., 2002, 35, 555–563 CrossRef CAS PubMed.
- T. P. Vaid, J. Am. Chem. Soc., 2011, 133, 15838–15841 CrossRef CAS PubMed.
- R. Buschbeck, P. J. Low and H. Lang, Coord. Chem. Rev., 2011, 255, 241–272 CrossRef CAS.
- A. L. Ivanovskii, A. A. Sofronov and Y. N. Makurin, Theor. Exp. Chem., 1999, 35, 270–274 CrossRef CAS.
- B. C. Guo, S. Wei, J. Purnell, S. Buzza and A. W. Castleman, Science, 1992, 256, 515–516 CAS.
- S. Wei, B. C. Guo, J. Purnell, S. Buzza and A. W. Castleman, Science, 1992, 256, 818–820 CAS.
- J.-O. Joswig and M. Springborg, J. Chem. Phys., 2008, 129, 134311 CrossRef PubMed.
- A. T. Paxton and C. Elsässer, Phys. Rev. B: Condens. Matter, 2013, 87, 224110 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186 CrossRef CAS.
- Z. Zhang, X. Liu, B. I. Yakobson and W. Guo, J. Am. Chem. Soc., 2012, 134, 19326–19329 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter, 2008, 78, 134106 CrossRef.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- G. Mills and H. Jónsson, Phys. Rev. Lett., 1994, 72, 1124–1127 CrossRef CAS PubMed.
- M.-M. Rohmer, M. Benard, C. Henriet, C. Bo and J.-M. Poblet, J. Chem. Soc., Chem. Commun., 1993, 1182–1185 RSC.
- X. Zhang, Z. Ma, X. Zhao, Q. Tang and Z. Zhou, J. Mater. Chem. A, 2015, 3, 4960–4966 CAS.
- M. Naguib, O. Mashtalir, J. Carle, V. Presser, J. Lu, L. Hultman, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2012, 6, 1322–1331 CrossRef CAS PubMed.
- J. Li and R. Hoffmann, Chem. Mater., 1989, 1, 83–101 CrossRef CAS.
- R. Sumathi and M. Hendrickx, Chem. Phys. Lett., 1998, 287, 496–502 CrossRef CAS.
- C. Berkdemir, A. W. Castleman and J. O. Sofo, Phys. Chem. Chem. Phys., 2012, 14, 9642–9653 RSC.
- S. Wang, J.-X. Li, Y.-L. Du and C. Cui, Comput. Mater. Sci., 2014, 83, 290–293 CrossRef CAS.
- M. A. Sobhy, A. W. Castleman and J. O. Sofo, J. Chem. Phys., 2005, 123, 154106 CrossRef CAS PubMed.
- J. I. Martinez, A. Castro, A. Rubio and J. A. Alonso, J. Chem. Phys., 2006, 125, 074311 CrossRef CAS PubMed.
- G. K. Gueorguiev and J. M. Pacheco, Phys. Rev. Lett., 2002, 88, 115504 CrossRef CAS PubMed.
- J. Tersoff and D. R. Hamann, Phys. Rev. B: Condens. Matter, 1985, 31, 805–813 CrossRef CAS.
- S. Mogck, B. J. Kooi, J. T. M. De Hosson and M. W. Finnis, Phys. Rev. B: Condens. Matter, 2004, 70, 245427 CrossRef.
- J. C. Meyer, S. Kurasch, H. J. Park, V. Skakalova, D. Künzel, A. Groß, A. Chuvilin, G. Algara-Siller, S. Roth, T. Iwasaki, U. Starke, J. H. Smet and U. Kaiser, Nat. Mater., 2011, 10, 209–215 CrossRef CAS PubMed.
- L. Wu, Y. Zhu, T. Vogt, H. Su, J. W. Davenport and J. Tafto, Phys. Rev. B: Condens. Matter, 2004, 69, 064501 CrossRef.
- W. Li and N. Mingo, Phys. Rev. B: Condens. Matter, 2014, 90, 094302 CrossRef.
- S. Zhang, Q. Wang, X. Chen and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 18809–18813 CrossRef CAS PubMed.
- P. Liu, J. A. Rodriguez, H. Hou and J. T. Muckerman, J. Chem. Phys., 2003, 118, 7737–7740 CrossRef CAS.
- T. Tohei, A. Kuwabara, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter, 2006, 73, 064304 CrossRef.
- K. Huang and M. Born, Dynamical Theory of Crystal Lattices, Clarendon, Oxford, 1954 Search PubMed.
- J. Wang, S. Yip, S. R. Phillpot and D. Wolf, Phys. Rev. Lett., 1993, 71, 4182–4185 CrossRef CAS PubMed.
- K. H. Michel and B. Verberck, Phys. Rev. B: Condens. Matter, 2009, 80, 224301 CrossRef.
- E. Cadelano, P. L. Palla, S. Giordano and L. Colombo, Phys. Rev. B: Condens. Matter, 2010, 82, 235414 CrossRef.
- G. N. Greaves, A. L. Greer, R. S. Lakes and T. Rouxel, Nat. Mater., 2011, 10, 823–837 CrossRef CAS PubMed.
- R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter, 2012, 85, 125428 CrossRef.
- R. C. Cooper, C. Lee, C. A. Marianetti, X. Wei, J. Hone and J. W. Kysar, Phys. Rev. B: Condens. Matter, 2013, 87, 035423 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- L. Z. Zhang, Z. F. Wang, S. X. Du, H. J. Gao and F. Liu, Phys. Rev. B: Condens. Matter, 2014, 90, 161402 CrossRef CAS.
- Y. Xie, M. Naguib, V. N. Mochalin, M. W. Barsoum, Y. Gogotsi, X. Yu, K.-W. Nam, X.-Q. Yang, A. I. Kolesnikov and P. R. C. Kent, J. Am. Chem. Soc., 2014, 136, 6385–6394 CrossRef CAS PubMed.
- Y. Xie, Y. Dall'Agnese, M. Naguib, Y. Gogotsi, M. W. Barsoum, H. L. Zhuang and P. R. C. Kent, ACS Nano, 2014, 8, 9606–9615 CrossRef CAS PubMed.
- Q. Tang, Z. Zhou and P. Shen, J. Am. Chem. Soc., 2012, 134, 16909–16916 CrossRef CAS PubMed.
- K. Persson, V. A. Sethuraman, L. J. Hardwick, Y. Hinuma, Y. S. Meng, A. van der Ven, V. Srinivasan, R. Kostecki and G. Ceder, J. Phys. Chem. Lett., 2010, 1, 1176–1180 CrossRef CAS.
- M. V. Koudriachova, N. M. Harrison and S. W. de Leeuw, Solid State Ionics, 2002, 152–153, 189–194 CrossRef CAS.
- M. V. Koudriachova, N. M. Harrison and S. W. de Leeuw, Solid State Ionics, 2003, 157, 35–38 CrossRef CAS.
- C. H. Sun, X. H. Yang, J. S. Chen, Z. Li, X. W. Lou, C. Li, S. C. Smith, G. Q. Lu and H. G. Yang, Chem. Commun., 2010, 46, 6129–6131 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5nr04472c |
| This journal is © The Royal Society of Chemistry 2016 |