Effective magnetic coupling with strong spin frustration in (Ph₃MeP⁺)(C₆₀˙⁻) and reversible C₆₀˙⁻ dimerization in (Ph₃MeP⁺)(C₆₀˙⁻)·C₆H₅CN. Effect of solvent on structure and properties

Abstract

Solvent free and solvent containing salts of the C₆₀˙⁻ radical anions with the triphenylmethylphosphonium cations, (Ph₃MeP⁺)(C₆₀˙⁻) (1) and (Ph₃MeP⁺)(C₆₀˙⁻)·C₆H₅CN (2), have been obtained. The salts show different structures and physical properties. Complex 1 has double chains from C₆₀˙⁻ with triangular fullerene arrangement and short interfullerene center-to-center distances of 10.079(1)–10.103(1) Å. No dimerization is observed in 1 preserving unpaired spins down to 1.9 K and providing magnetic moment of 1.68 μ_B at 300 K. Weiss temperature of Θ = −60 K indicates a strong antiferromagnetic coupling of spins. In spite of that, no magnetic ordering is observed down to 1.9 K showing that 1 has strong frustration of spins (f = Θ/T_N > 30) due to triangular fullerene lattice. Compound 2 additionally contains the C₆H₅CN solvent molecules and has a layered structure with fullerene hexagons accommodating the Ph₃MeP⁺ cations and C₆H₅CN solvent molecules in the center. Interfullerene center-to-center distances vary in the fullerene layers in the 9.921(2)–10.066(2) Å range. Fullerenes dimerize reversibly in pairs with a shortest interfullerene center-to-center distance of 9.921(2) Å below 220 K to form diamagnetic singly-bonded (C₆₀⁻)₂ dimers.

---

Introduction

Radical anion compounds of fullerene C₆₀ show promising magnetic and conducting properties.^1–7 The fullerene salt with tetrakis(dimethylamino)ethylene, TDAE·C₆₀, shows ferromagnetic properties with T_c = 16 K,¹ whereas fullerene salts with alkali metals (M⁺)(C₆₀⁻), where M = K, Rb and Cs obtained by doping C₆₀ in a gaseous phase, are metallic polymers with a one-dimensional chain structure.^2,3 Fullerene compounds can also be obtained as crystals by direct synthesis in solution to form compounds with quasi-one- and two-dimensional metallic conductivity (Na⁺)_x(THF)_yC₆₀ (x ∼ 0.4, y ∼ 2.2),⁴ (K⁺)(THF)₅(C₆₀˙⁻)·2THF⁵ and (MDABCO⁺)(C₆₀˙⁻)·TPC (where MDABCO⁺ is the N-methyldiazabicyclooctanium cation and TPC is triptycene).^6,7 The C₆₀˙⁻ radical anions should be closely packed in a crystal to show strong magnetic coupling of spins or metallic conductivity. At the same time they have strong tendency to dimerize forming singly-bonded (C₆₀⁻)₂ dimers in the 140–250 K range when short van der Waals C⋯C contacts are present between them.^8–14 Since unpaired electrons are paired at the formation of the interfullerene C–C bonds in the dimers, the compounds transfer to the diamagnetic state and cannot show high conductivity. Generally, ionic fullerene compounds with closely packed C₆₀˙⁻ manifest dimerization,^8–14 whereas such structures with monomeric C₆₀˙⁻ radical anions are rare.^1,6,7,15,16 Most probably, bulky cations or neutral molecules separate fullerenes and prohibit them from approaching each other to dimerize. Namely the cations and neutral molecules with appropriate shapes and sizes are required to provide promising physical properties of ionic fullerene compounds.^1,6,7,15,16 Fullerenes can also be dimerized¹⁷ or polymerized^2,3 by the [2+2] cycloaddition reaction. In this case, the additional electron is preserved on the singly occupied molecular orbital (SOMO) of C₆₀ and the compound can either be metallic^2,3 or show strong magnetic coupling of spins.¹⁷ However, there are only several examples of such doubly bonded (C₆₀⁻)₂ dimers and (C₆₀⁻)_n polymers.

In this work we obtained two new fullerene salts (Ph₃MeP⁺)(C₆₀˙⁻) (1) as solvent free and (Ph₃MeP⁺)(C₆₀˙⁻)·C₆H₅CN (2) as solvent containing phases and found that the additional solvent molecule can affect essentially the packing of fullerenes in a crystal and results in different physical properties of the salts. Solvent free 1 preserves monomeric C₆₀˙⁻ radical anions down to 1.9 K and shows spin ladder behavior with effective antiferromagnetic coupling of spins and strong frustration of spins in the triangular fullerene lattice. Salt 2 has a layered structure in which the C₆₀˙⁻ pairs with a short interfullerene center-to-center distance can be outlined. As a result, dimerization of C₆₀˙⁻ is realized in 2 to form singly-bonded (C₆₀⁻)₂ dimers and the reversible transition of the salt to the diamagnetic state.

Results and discussion

1. Synthesis

(Ph₃MeP⁺)(C₆₀˙⁻) (1) and (Ph₃MeP⁺)(C₆₀˙⁻)·C₆H₅CN (2) were obtained by different synthetic procedures. For the preparation of 1, deep blue salt of vanadyl(IV) phthalocyanine, V^IVOPc, with the Ph₃MeP⁺ cations, was generated in o-dichlorobenzene. First, V^IVOPc was reduced by sodium fluorenone ketyl in the presence of the excess of Ph₃MePBr. Then (Ph₃MeP⁺){V^IVOPc(3−)˙⁻} was filtered into the flask containing the equimolar amount of fullerene C₆₀. Fullerene oxidized the V^IVOPc(3−)˙⁻ radical anions forming a violet solution of (Ph₃MeP⁺)(C₆₀˙⁻), whereas neutral V^IVOPc, which is insoluble in pure o-dichlorobenzene, quantitatively precipitated from the solution. The crystals of 1 were obtained by slow mixing of the obtained o-dichlorobenzene solution of the salt with hexane during 1 month. When C₆₀ was reduced by fluorenone ketyl in C₆H₄Cl₂ in the presence of Ph₃MeP⁺, insoluble precipitates were formed (most plausibly, salt 1), which was dissolved by adding C₆H₅CN. The crystallization with hexane gave 2, which additionally contained the C₆H₅CN solvent molecules.

2. Optical properties

Both salts exhibit similar IR and UV-visible-NIR spectra which show the presence of the Ph₃MeP⁺ anions, the C₆₀˙⁻ radical anions and C₆H₅CN solvent molecules (for salt 2) (see ESI,† Table S1 and Fig. S1). The positions of the F_1u(4) C₆₀ mode at 1391 (1) and 1390 cm⁻¹ (2) correspond to the formation of −1 charged C₆₀ since this mode is shifted from 1429 cm⁻¹ (neutral state) to 1390–1396 cm⁻¹ in radical anion salts with −1 charged C₆₀.^8,18–20 Absorption bands in the UV-visible-NIR spectra of the salts at 932 and 1082 nm (1) and 933 and 1087 nm (2) are also characteristic of C₆₀˙⁻.^8,18–20 The broad low-energy band in the spectrum of 2 at about 1660 nm (0.74 eV, Fig. 1) can be attributed most probably to a charge transfer (CT) band at photoinduced electron transfer between C₆₀˙⁻ in closely packed fullerene pairs. Such band is not observed in the spectrum of 1. The CT bands are generally observed in the spectra of the radical anion salts of fullerenes at λ < 2000 nm (>0.62 eV).⁷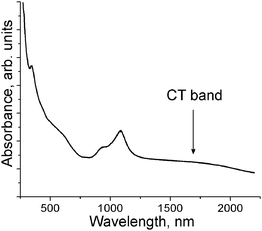

Fig. 1 Spectrum of 2 in the UV-visible-NIR range measured at room temperature in the KBr pellet prepared under anaerobic conditions.

3. Crystal structures

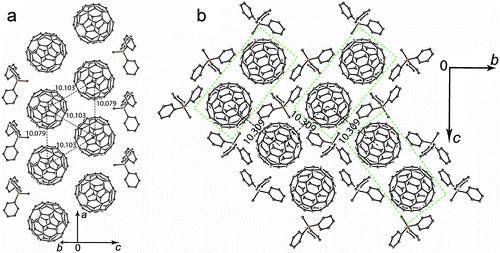
The crystal structure of 1 was determined at 100 K. The C₆₀˙⁻ radical anions are monomeric at 100 K. They are close to the ordered state since the second orientation of fullerene has only 0.093(3) occupancy (Fig. 2 shows only one major occupied orientation). The C₆₀˙⁻ radical anions in the crystal structure of 1 form double chains along the a axis with short interfullerene center-to-center (ctc) distances equal to 10.079(1) Å in the chains and 10.103(1) Å between the chains (Fig. 2a). As a result, the fullerene triangles have nearly equal side lengths of 10.103(1) Å, 10.103(1) Å and 10.079(1) Å. Double fullerene chains are nearly isolated from each other, and the shortest ctc distance with fullerenes from the neighboring double chains is 10.309(1) Å (Fig. 2b). These distances are essentially longer than the van der Waals (vdW) diameter of C₆₀ of 10.18 Å and no vdW C⋯C contacts are formed in this case. The C₆₀˙⁻ radical anions are not dimerized in 1 most probably due to the fact that the methyl substituent of Ph₃MeP⁺ penetrates into the cavity between C₆₀˙⁻ to prevent the dimerization despite the short interfullerene ctc distance (min. 10.079(1) Å). Thus, the main structural motif of 1 is double chains from monomeric C₆₀˙⁻ containing nearly equilateral fullerene triangles.

Fig. 2 Crystal structure of (Ph₃MeP⁺)(C₆₀˙⁻) (1): (a) view of the double chains containing triangles from C₆₀˙⁻; (b) view along the a axis and the double C₆₀˙⁻ chains. Figures show the ctc distances between fullerenes. Rectangles of green dashed lines outline double C₆₀˙⁻ chains. Only one major orientation is shown for C₆₀˙⁻.

To understand the nature of interactions between monomeric C₆₀˙⁻ radical anions in 1, the molecular orbital and intermolecular overlap integrals (s's) were calculated by applying the semiempirical method (AM1 Hamiltonian). Only one fullerene is crystallographically unique but it is disordered between two orientations at 100 K. To carry out the calculations we used the data for major orientation of fullerene, which has the 0.907(3) occupancy. In total, each fullerene has five fullerene neighbors with three types of ctc distances. One and two fullerene neighbors with the 10.079(1) Å and 10.103(1) Å ctc distances, respectively (Fig. 2a), are located in the double fullerene chains (overlap integrals s1 and s2, respectively). Two other fullerene neighbors with the 10.309(1) Å ctc distance are located in the neighboring double chains (Fig. 2b, overlap integral s3). The biggest overlap integral is s2 = 1.79 × 10⁻³, whereas the s1 value is smaller being 1.19 × 10⁻³ in spite of the fact that the ctc distance between fullerenes is shorter for the s1 overlap integral. Most probably that is due to better overlapping of π-orbitals between fullerenes with the 10.103(1) Å ctc distance. The lowest value of the overlap integral (0.58 × 10⁻³) is observed for fullerenes with the longest interfullerene ctc distance. On the whole, the overlap integrals between C₆₀˙⁻ in the layers of 1 are essentially smaller than those in the previously studied layered metallic compound (MDABCO⁺)·(C₆₀˙⁻)·TPC (1.91–2.57 × 10⁻³).⁶ It is also seen that the interactions between C₆₀˙⁻ in 1 are essentially more anisotropic than those in the metal.

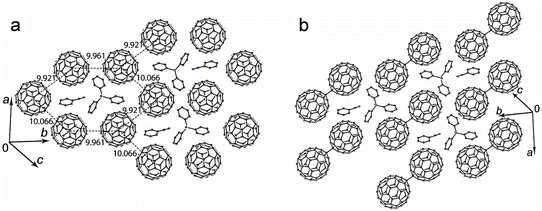
The C₆H₅CN solvated salt 2 shows a different structural motif. The C₆₀˙⁻ radical anions are monomeric at 250 K and disordered between two orientations. The crystal structure can be better described as layers formed by the fullerene hexagons in which each C₆₀˙⁻ has three fullerene neighbors with three slightly different interfullerene ctc distances of 9.921(2) Å, 9.961(2) Å and 10.066(2) Å. The Ph₃MeP⁺ cations and C₆H₅CN solvent molecules are located in the centers of the fullerene hexagon with the nitrile group of C₆H₅CN directed to the methyl substituents of the Ph₃MeP⁺ cations (Fig. 3a). It should be noted that C₆H₄Cl₂ cannot be incorporated instead of C₆H₅CN in 2. As a result, the reaction in pure C₆H₄Cl₂ provided solvent-free 1 with different crystal structure. It is interesting that the composition, packing pattern and crystal structure are destined by the small difference of solvent molecule, most probably the size. Each fullerene layer in 2 is shifted relatively to the adjacent fullerene layers in such a way that the center of fullerene hexagon is shifted relatively to the adjacent fullerene layers by 9.961(2) Å along the b axis. The shortest ctc distance between C₆₀˙⁻ from the adjacent fullerene layers of 10.152(2) Å is slightly longer than that within the layers.

Fig. 3 Crystal structure of the monomeric (a) and dimeric (b) phases of (Ph₃MeP⁺)(C₆₀˙⁻)·C₆H₅CN (2) at 250 and 120 K, respectively. Figures show the ctc distances between fullerenes. Only one major orientation is shown for C₆₀˙⁻ and (C₆₀⁻)₂ dimers.

The formation of closely packed C₆₀˙⁻ pairs with multiple short vdW C⋯C contacts between them in the monomeric phase of 2 most probably results in the appearance of a charge transfer band associated with electron transfer between C₆₀˙⁻ (Fig. 1), whereas such band is not found in the spectrum of 1 due to longer interfullerene ctc distances.

Upon cooling down to 120 K, the C₆₀˙⁻ radical anions form singly bonded (C₆₀⁻)₂ dimers in 2 (Fig. 3b). These dimers are bound by a single intercage C–C bond of 1.689(10) Å length and has 9.277(4) Å ctc distance (for the dimers in major orientation). Such parameters are characteristic for singly bonded (C₆₀⁻)₂ dimers.^8–14 The dimerization of fullerenes is realized in the pairs with the shortest ctc distance of 9.921(2) Å. No sterical hindrances were found there against the dimerization in this direction (Fig. 3a).

4. Magnetic properties

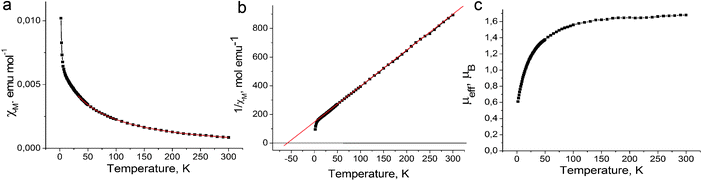
The magnetic properties of both salts were studied by the SQUID (1) and EPR (1 and 2) techniques. The effective magnetic moment of 1 of 1.68 μ_B at 300 K (Fig. 4c) corresponds to the contribution of one S = 1/2 spin per formula unit (the calculated value for the system of one non-interacting S = 1/2 spin is 1.73 μ_B). The magnetic moment is nearly temperature independent at a high temperature and begins to decrease below 150 K. The magnetic behavior of 1 can be described well by the Curie–Weiss law in the 50–300 K range with a negative Weiss temperature of −60 K (Fig. 4a and b) showing strong antiferromagnetic coupling of spins. Nevertheless, antiferromagnetic ordering is not observed in 1 down to 1.9 K. Such behavior can be explained by strong frustration of spins in nearly equilateral fullerene triangles. The estimation provides the frustration index in 1 of f = Θ/T_N > 30. Therefore, salt 1 can be classified as a strongly frustrated system.²¹ Up to now only several strongly antiferromagnetically interacting spin frustrated systems based on fullerenes have been obtained such as (MQ⁺)(C₆₀˙⁻)·TPC (f > 14.2) (where MQ⁺ is the N-methylquinucledinium cation and TPC is triptycene)⁷ and f.c.c. Cs₃C₆₀ salt (f = 48).²² These salts are interesting for the development of the quantum spin liquid state which can be realized at very low temperatures.^23,24

Fig. 4 Magnetic properties of (Ph₃MeP⁺)(C₆₀˙⁻) (1). Temperature dependences of (a) molar magnetic susceptibility and fitting of the data by the Curie–Weiss law with a Weiss temperature of −60 K (red curve); (b) resiprocal molar magnetic susceptibility and linear fitting of the data with a Weiss temperature of −60 K (red line); and (c) effective magnetic moment.

The EPR spectrum of 1 contains one Lorentzian line in the 4–300 K range. The EPR signal with g = 1.9995 and linewidth (ΔH) of 4.32 mT at 300 K (Fig. 5c, inset) is characteristic for the C₆₀˙⁻ radical anions.^{19,20,25–28} The temperature dependences of the g-factor and ΔH can be explained by strong magnetic coupling of spins in 1. For example, the g-factor is strongly temperature dependent and shifts to smaller values when the temperature decreases down to 4 K (Fig. 5a). The signal is broadened with a decrease in the temperature from 300 K down to about 200 K, and only below this temperature noticeable narrowing of the EPR signal is observed. The signal is broadened again below 20 K (Fig. 5b). The broadening of the EPR signal can be explained by a noticeable magnetic coupling of spins manifested even at room temperature. A similar behavior is even observed for the anionic fullerene systems with a strong magnetic coupling of spins, for example, C₆₀˙⁻ salts with DMF solvated transition metal cations (M = Fe²⁺, Co²⁺, Ni²⁺).²⁹ The integral intensity of the EPR signal in 1 increases with the decrease in the temperature from 293 down to 4 K indicating that no long range magnetic ordering of spins is realized in spite of strong antiferromagnetic coupling of spins (Fig. 5c).

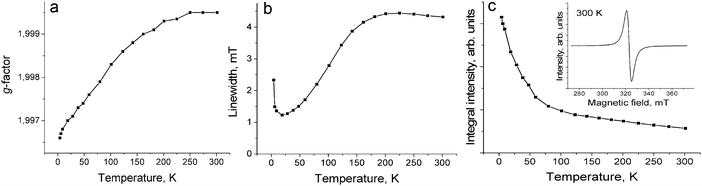Fig. 5 Temperature dependence of the g-factor (a), linewidth (b) and integral intensity (c) of the EPR signal from polycrystalline 1 in the 4–300 K range.

The EPR spectrum of 2 also shows a single Lorentzian line with g = 1.9996 and ΔH = 4.2 mT at 295 K. The integral intensity of the signal decreases strongly below 220 K in accordance with the formation of diamagnetic singly bonded (C₆₀⁻)₂ dimers (see ESI,† Fig. S2). This transition is completely reversible. A similar behavior is demonstrated by many anionic closely packed fullerene compounds in which the reversible dimerization of the C₆₀˙⁻ radical anions is observed.^8–14

Conclusion

We prepared solvent-free and solvent-containing phases of the C₆₀˙⁻ salt with the Ph₃MeP⁺ cations (1 and 2). Salt 1 involves isolated double chains with nearly equilateral fullerene triangles. Salt 2 has a layered structure in which the C₆₀˙⁻ radical anions are located in the fullerene hexagons with three fullerene neighbors for each C₆₀˙⁻. However, the formation of closely packed C₆₀˙⁻ pairs in 2 with a short interfullerene ctc distance of 9.921(2) Å results in their reversible dimerization and the formation of diamagnetic singly bonded (C₆₀⁻)₂ dimers. The arrangement of the C₆₀˙⁻ spins in 1 is similar to those in the spin ladder compounds,³⁰ and this salt manifests strong magnetic coupling of spins. The magnetic coupling of spins in 1 with Weiss temperature of −60 K is intermediate between those for (MQ⁺)(C₆₀˙⁻)·TPC (Θ = −27 K) with longer ctc distances of 10.124–10.177 Å at 250 K⁷ and (MDABCO⁺)(C₆₀˙⁻) (Θ = −118 K) with 3D fullerene packing and shorter ctc distances of 9.912–10.050 Å (six neighbors).¹⁶ However, a rather strong magnetic coupling does not provide long range magnetic ordering down to 1.9 K. This is explained by strong spin frustration in the triangular fullerene lattice. This compound is interesting for the development of a quantum spin liquid state.^23,24

Experimental

Materials

C₆₀ of 99.9% purity was used from MTR Ltd. without further purification. Ph₃MePBr (98%) and V^IVOPc (85%) were purchased from Aldrich and Acros, respectively. Sodium fluorenone ketyl was obtained as described.³¹ The solvents were purified in an argon atmosphere and degassed. o-Dichlorobenzene (C₆H₄Cl₂) was distilled over CaH₂ under reduced pressure, benzonitrile was distilled over Na under reduced pressure, and hexane was distilled over Na/benzophenone. All manipulations for the syntheses of 1 and 2 were carried out in a MBraun 150B-G glove box with a controlled argon atmosphere and the content of H₂O and O₂ less than 1 ppm. The solvents and crystals were stored in the glove box. The polycrystalline samples of 1 and 2 were placed in 2 mm quartz tubes under anaerobic conditions for EPR and SQUID measurements and sealed under 10⁻⁵ torr pressure. KBr pellets for IR- and UV-visible-NIR measurements were prepared in the glove box.

General

The UV-visible-NIR spectra were recorded in KBr pellets on a Perkin Elmer Lambda 1050 spectrometer in the 250–2500 nm range. The FT-IR spectra were obtained in KBr pellets with a Perkin-Elmer Spectrum 400 spectrometer (400–7800 cm⁻¹). The EPR spectra were recorded for polycrystalline samples of 1 and 2 with a JEOL JES-TE 200 X-band ESR spectrometer equipped with a JEOL ES-CT470 cryostat working between room and liquid helium temperatures. A Quantum Design MPMS-XL SQUID magnetometer was used to measure the static magnetic susceptibility of 1 at 100 mT magnetic field under cooling and heating conditions in the 300–1.9 K range. A sample holder contribution and core temperature independent diamagnetic susceptibility (χ_d) were subtracted from the experimental values. The χ_d values were estimated by the extrapolation of the data in the high-temperature range by fitting the data with the following expression: χ_M = C/(T−Θ) + χ_d, where C is the Curie constant and Θ is the Weiss temperature. The effective magnetic moment (μ_eff) was calculated with the following formula: μ_eff = (8·χ_M·T)^1/2.

Synthesis

The crystals of 1 and 2 were obtained by the diffusion technique. The reaction mixture was filtered into a 1.8 cm-diameter, 50 mL glass tube with a ground glass plug, and then 30 mL of hexane was layered over the solution. The slow mixing of the solutions resulted in the precipitation of crystals over 1 month. The solvent was then decanted from the crystals, and these were washed with hexane. The compositions of the obtained salts were determined from X-ray diffraction analysis on a single crystal. Several crystals from one synthesis were found to consist of a single crystalline phase. Due to high air sensitivity of 1 and 2, elemental analysis could not be used to determine the composition because the salts reacted with oxygen in the air before the quantitative oxidation procedure could be performed.

The salt (Ph₃MeP⁺)(C₆₀˙⁻) (1) was obtained by the following procedure. The reduction of vanadyl(IV) phthalocyanine (V^IVOPc, 24.4 mg, 0.042 mmol) in 16 ml of C₆H₄Cl₂ with sodium fluorenone ketyl (14 mg, 0.069 mmol) in the presence of the excess of Ph₃MePBr (30 mg, 0.084 mmol) during 4 hours at 100 °C yielded the deep blue (Ph₃MeP⁺){V^IVOPc(3−)˙⁻} salt. The solution was filtered into the flask containing equimolar amount of C₆₀ (30 mg, 0.042 mmol). Fullerene oxidized the V^IVOPc(3−)˙⁻ radical anions forming a violet solution of (Ph₃MeP⁺)(C₆₀˙⁻), whereas insoluble neutral V^IVOPc quantitatively precipitated from the solution. The solution was filtered from V^IVOPc into the tube for diffusion. The crystals of 1 were obtained as black parallelepipeds in 72% yield.

The salt (Ph₃MeP⁺)(C₆₀˙⁻)·C₆H₅CN (2) was obtained via the reduction of C₆₀ (30 mg, 0.042 mmol) using the excess of sodium fluorenone ketyl (14 mg, 0.069 mmol) in the presence of the excess of Ph₃MePBr (30 mg, 0.084 mmol) in 15 ml of o-dichlorobenzene. The reduction was performed overnight at 90 °C. After the reaction, the precipitates were formed in the solution and 3.5 ml of benzonitrile was added into the mixture to dissolve the insoluble material with stirring for two hours at 90 °C. The resulting violet-red solution was cooled down to room temperature and filtered into a tube for diffusion. Thin red plates were obtained in 65% yield.

X-ray crystal structure determination

Crystal data of 1 at 100(2) K: C₅₀₄H₂₈₈N₁₆Na₈O₄₈, M_r = 997.90 g mol⁻¹, black parallelepiped, orthorhombic, P2₁2₁2₁, a = 10.0792(2) Å, b = 15.6628(3) Å, c = 26.4166(5) Å, V = 4170.35(14) ų, Z = 4, d_calc = 1.589 g cm⁻³, μ = 0.128 mm⁻¹, F(000) = 2028, 2θ_max = 58.458°, reflections measured 32 109, unique reflections 9507, reflections with I > 2σ(I) = 8177, parameters refined 905, restraints 8616, R₁ = 0.0571, wR₂ = 0.1423, G.O.F. = 1.136, CCDC 1431772.

Crystal data of 2 at 250(2) K: C₈₆H₂₃NP, M_r = 1101.02 g mol⁻¹, brown plate, triclinic, P1̄, a = 12.725(3) Å, b = 13.759(2) Å, c = 15.056(2) Å, α = 100.102(15), β = 112.513(18), γ = 90.150(15)°, V = 2390.4(8) ų, Z = 2, d_calc = 1.530 g cm⁻³, μ = 0.120 mm⁻¹, F(000) = 1122, max. 2θ_max = 62.520°, reflections measured 24306, unique reflections 13294, reflections with I > 2σ(I) = 3839, parameters refined 1334, restraints 810, R₁ = 0.0803, wR₂ = 0.2443, G.O.F. = 0.961, CCDC 1431776.

Crystal data of 2 at 120(2) K: C₈₆H₂₃NP, M_r = 1101.02 g mol⁻¹, brown plate, triclinic, P1̄, a = 12.5760(18) Å, b = 13.8505(17) Å, c = 15.035(2) Å, α = 101.006(11), β = 113.801(13), γ = 90.849(11)°, V = 2339.8(6)ų, Z = 2, d_calc = 1.563 g cm⁻³, μ = 0.122 mm⁻¹, F(000) = 1122, max. 2θ_max = 659.516°, reflections measured 23 224, unique reflections 11 111, reflections with I > 2σ(I) = 4848, parameters refined 800, restraints 1263, R₁ = 0.0720, wR₂ = 0.1667, G.O.F. = 0.977, CCDC 1431773.

The X-ray diffraction data for the crystals of 1 were collected on a Bruker Smart Apex II CCD diffractometer with graphite monochromated MoK_α radiation using a Japan Thermal Engineering Co. cooling system DX-CS190LD. Raw data reduction to F² was carried out using Bruker SAINT.³² The X-ray diffraction data for 2 were collected on an Oxford diffraction “Gemini-R” CCD diffractometer with graphite monochromated MoK_α radiation using an Oxford Instrument Cryojet system. Raw data reduction to F² was carried out using CrysAlisPro, Oxford Diffraction Ltd. The structures were solved by a direct method and refined by the full-matrix least-squares method against F² using SHELX 2013.³³ Non-hydrogen atoms were refined in the anisotropic approximation. The positions of hydrogen atoms were estimated geometrically. To keep the fullerene geometry close to the ideal one in the disordered groups, the bond length restraints were applied along with the next-neighbor distances, using the SADI SHELXL instruction. To keep the anisotropic thermal parameters of the fullerene atoms within reasonable limits the displacement components were restrained using ISOR and DELU SHELXL instructions. This results in a great number of restraints used for the refinement of the crystal structures of 1 and 2.

Disorder in the crystal structures of 1 and 2

The C₆₀˙⁻ radical anions are disordered in 1 between two orientations with the 0.907(3)/0.093(3) occupancies. Monomeric C₆₀˙⁻ radical anions are disordered in 2 at 250 K between two orientations with the 0.853(4)/0.147(4) occupancies. The singly-bonded (C₆₀⁻)₂ dimers are disordered in 2 at 120 K between two orientations with the 0.540(3)/0.460(3) occupancies.

Acknowledgements

The work was supported by the Russian Science Foundation (project No. 14-13-00028) and by JSPS KAKENHI Grant Numbers 23225005 and 26288035.

References

1. P. W. Stephens, D. Cox, J. W. Lauher, L. Mihaly, J. B. Wiley, P.-M. Allemand, A. Hirsch, K. Holczer, Q. Li, J. D. Thompson and F. Wudl, Nature, 1992, 355, 331.
2. P. W. Stephens, G. Bortel, G. Faigel, M. Tegze, A. Jánossy, S. Pekker, G. Oszlanyi and L. Forró, Nature, 1994, 370, 636.
3. F. Bommeli, L. Degiorgi, D. Wachter, Ö. Legeza, A. Jánossy, G. Oszlanyi, O. Chauvet and L. Forro, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 14794.
4. H. Kobayashi, H. Tomita, H. Moriyama, A. Kobayashi and T. Watanabe, J. Am. Chem. Soc., 1994, 116, 3153.
5. A. Kromer, U. Wedig, E. Roduner, M. Jansen and K. Yu. Amsharov, Angew. Chem., Int. Ed., 2013, 52, 12610.
6. D. V. Konarev, S. S. Khasanov, A. Otsuka, M. Maesato, G. Saito and R. N. Lyubovskaya, Angew. Chem., Int. Ed., 2010, 49, 4829.
7. D. V. Konarev, S. S. Khasanov, A. Otsuka, M. Maesato, M. Uruichi, K. Yakushi, A. Shevchun, H. Yamochi, G. Saito and R. N. Lyubovskaya, Chem. – Eur. J., 2014, 20, 7268.
8. D. V. Konarev, S. S. Khasanov, G. Saito, A. Otsuka, Y. Yoshida and R. N. Lyubovskaya, J. Am. Chem. Soc., 2003, 125, 10074.
9. D. V. Konarev, S. S. Khasanov, G. Saito, A. Otsuka and R. N. Lyubovskaya, J. Mater. Chem., 2007, 17, 4171.
10. D. V. Konarev, S. S. Khasanov and R. N. Lyubovskaya, Russ. Chem. Bull., 2007, 56, 371.
11. E. A. Schupak, D. M. Lyubov, E. V. Baranov, G. K. Fukin, O. N. Suvorova and A. A. Trifonov, Organometallics, 2010, 29, 6141.
12. N. V. Kozhemyakina, K. Yu. Amsharov, J. Nuss and M. Jansen, Chem. – Eur. J., 2011, 17, 1798.
13. D. V. Konarev, L. V. Zorina, S. S. Khasanov and R. N. Lyubovskaya, Dalton Trans., 2012, 41, 9170.
14. D. V. Konarev, S. S. Khasanov, A. Otsuka, H. Yamochi, G. Saito and R. N. Lyubovskaya, Inorg. Chem., 2012, 51, 3420.
15. D. V. Konarev, A. V. Kuzmin, S. S. Khasanov, A. Otsuka, H. Yamochi, G. Saito and R. N. Lyubovskaya, New J. Chem., 2013, 37, 2521.
16. D. V. Konarev, S. S. Khasanov, A. Otsuka, H. Yamochi, G. Saito and R. N. Lyubovskaya, Chem. – Asian J., 2014, 9, 1629.
17. D. V. Konarev, S. S. Khasanov, A. Otsuka, G. Saito, H. Yamochi and R. N. Lyubovskaya, New J. Chem., 2011, 35, 1829.
18. V. N. Semkin, N. G. Spitsina, S. Krol and A. Graja, Chem. Phys. Lett., 1996, 256, 616.
19. C. A. Reed and R. D. Bolskar, Chem. Rev., 2000, 100, 1075.
20. D. V. Konarev and R. N. Lyubovskaya, Russ. Chem. Rev., 2012, 81, 336.
21. J. L. Manson, E. Ressouche and J. S. Miller, Inorg. Chem., 2000, 39, 1135.
22. A. Y. Ganin, Y. Takabayashi, P. Jeglič, D. Arčon, A. Potocnik, P. J. Baker, Y. Ohishi, M. T. McDonald, M. D. Tzirakis, A. McLennan, G. R. Darling, M. Takata, M. J. Rosseinsky and K. Prassides, Nature, 2010, 466, 221.
23. Y. Shimizu, K. Miyagawa, K. Kanoda, M. Maesato and G. Saito, Phys. Rev. Lett., 2003, 91, 107001.
24. S. Yamashita, T. Yamamoto, Y. Nakazawa, M. Tamura and R. Kato, Nat. Commun., 2011, 2, 275.
25. P. M. Allemand, G. Srdanov, A. Koch, K. Khemani, F. Wudl, Y. Rubin, F. Diederich, M. M. Alvarez, S. J. Anz and R. L. Whetten, J. Am. Chem. Soc., 1991, 113, 2780.
26. A. Pènicaud, A. Peréz-Benítez, R. Gleason V., E. Muñoz P. and R. Escudero, J. Am. Chem. Soc., 1993, 115, 10392.
27. D. V. Konarev, A. Yu. Kovalevsky, S. S. Khasanov, G. Saito, A. Otsuka and R. N. Lyubovskaya, Eur. J. Inorg. Chem., 2005, 4822.
28. B. Gotschy and G. Völkel, Appl. Magn. Reson., 1996, 11, 229.
29. D. V. Konarev and R. N. Lyubobskaya, Russ. Chem. Bull., 2008, 57, 1944.
30. C. Rovira, Struct. Bonding, 2001, 100, 163.
31. D. V. Konarev, S. S. Khasanov, E. I. Yudanova and R. N. Lyubovskaya, Eur. J. Inorg. Chem., 2011, 816.
32. Bruker Analytical X-ray Systems, Madison, Wisconsin, U.S.A, 1999.
33. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112.

---

Footnote

† Electronic supplementary information (ESI) available: The IR spectra of starting compounds and salts 1 and 2. CCDC 1431772, 1431773 and 1431776. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5nj02886h

---