Heat of formation distributions of components involved in bi-component cocrystals and simple binary eutectic mixtures

Abstract

A computationally inexpensive screening tool was formulated allowing for rational pre-selection of components as the most promising candidates for synthesis of two-component cocrystals. The proposed procedure relies on the scoring function quantifying dissimilarity of 2D histograms, which describe distributions of heat of formation resulting from two counterparts of database consisting of 1599 cocrystals and 492 cases of pairs immiscible in the solid state. It has been observed that higher probability of cocrystal formation is to be expected if components differ by heat of formation (Hf) values and at least one of components is hydrophilic. This observation was also validated based on an additional 1590 cocrystals not included in the training set. On the contrary, the high probability of simple eutectic systems is expected for cases of high similarities and positive values of Hf. Based on the formulated scoring function, the regions of observed highest probability of cocrystallization can be identified. Although the proposed phenomenological approach cannot provide absolute prediction of cocrystal formation, it does offers practical and simple guidance for rationalizing the selection of potential components for real practical purposes.

---

Introduction

The synthesis of new solid-state materials via cocrystallization has attracted attention not only due to many practical applications^1–3 but also for more fundamental research.^4,5 The emergent character of such systems, leading to new physicochemical properties, is especially welcomed in the pharmaceutical industry.^4–6 Multicomponent cocrystals involving active pharmaceutical ingredients (API)^7,8 have been successfully applied for increasing solubility^9–11 and other pharmacokinetic properties such as bioavailability.^12–14 Also dose response modulation,^13,15 stability,^16–19 hygroscopicity²⁰ and prolonged life shelf²¹ are worth mentioning. Furthermore, cocrystals have been explored in high-energetic material industry since they offer tunable power and safety of explosive compounds.^22–24 Cocrystal screening for agrochemically active substances has also been the subject of increasing interests.^25,26 Properties of optical and semiconducting materials have likewise been improved with the aid of cocrystallization.^27,28

According to one of the most useful definitions,^29,30 a cocrystal is a homogeneous crystalline solid containing stoichiometric amounts of discrete neutral molecular species that are solids under ambient conditions. It is also worth mentioning that cocrystals are supposed to be more beneficial than salts especially in the cases with absence of ionizable functional groups. Additionally, the number of neutral components of potential use included in International Food Additive Database or Codex General Standard for Food Additives³¹ far more exceeds the number of available counterions.

In this context, it is quite understandable that a great diversity of experimental techniques has been developed for cocrystal synthesis starting from direct mechanochemical approach,^32–34 sonification,³⁵ solvent evaporation^36,37 including microfluidic method,³⁸ many variations of slurry methods³⁹ or melting techniques.⁴⁰ It is also worth mentioning that droplet evaporation and sample orientation^41,42 can also offer some advantages of cocrystal screening.⁴³ However, the selection of potential cocrystal formers is not obvious especially for pharmaceutically acceptable heteromolecular complexes.

Thus, it is essential to develop theoretical strategies for identifying the most promising candidates for cocrystallization before the actual synthesis. This was especially emphasized by formulating a practically sensible screening paradigm,⁴ emphasizing the necessity for a computationally inexpensive pre-screening tool that allows for rational selection of chemical species as the most promising candidates for cocrystal synthesis. For this purpose many theoretical approaches have been formulated. Especially, those ignoring the crystal lattice details seem to be valuable in this context, allowing for broad and relatively inexpensive scans of cocrystallization landscapes. For example, the electrostatic potential surface of the molecule was used for identification of the most likely contacts between components.⁴⁴ Nowadays, the mixing enthalpy of supercooled coformers with a given stoichiometry was used for screening of API cocrystallization.⁴⁵ Besides, the Hansen solubility parameters^46–48 were also applied as they take advantage of only the knowledge of the chemical structure of interacting components. The concept of supramolecular phenomena^49,50 has been also proven as valuable guide for practical application of crystal engineering principles⁵¹ revealing major driving forces toward molecular compound formation.⁵² For example, a synthon design approach demonstrated preference of heterosynthons over a homosynthons.^53,54 Prediction of hydrogen-bonding propensities based on Cambridge Structural Database (CSD)⁵⁵ statistics was proven to be very effective.^56,57 Alternatively the semiquantitative model for predicting of cocrystallization chance was formulated⁵⁸ in terms of statistical analysis of molecular descriptors distributions. The detailed analysis of known cocrystals, led to identification of shape and polarity similarities between components involved in structures deposited in the CSD.

Such methodology, relying on finding statistically significant patterns adopted by a particular set of structures, was the background of this paper. However, instead of focusing exclusively on cocrystals the attention was extended also on simple binary eutectic mixtures as negative cases of intermolecular complexation. Such a complementary approach can provide more details on similarities between formers of either systems. The application of structure-to-property approach often adopted in chemoinformatics requires the definition of the scoring function. This element, which the previous studies lacked, is addressed in this paper and the discriminating factors between either of the system types are quantified in order to guide the selection of the most promising candidates for screening of cocrystals or simple eutectics.

Methods

The database comprising positive and negative cases of cocrystallization was constructed after an extensive literature search. In the first step the list of binary mixtures was built based on patterns documented on binary phase diagrams. Such data offer full characteristics of thermodynamic properties of solid–liquid phenomena and allow for identification of eutectics points. In the case of simple eutectic or monotectic mixtures, lack of reaction in the solid state is expected and consequently formation of two separate solids of either of components is observed. If a reaction between components occurs, its consequence is also clearly evidenced by patterns on binary phase diagrams. The list of pairs of monomers showing immiscibility in the solid state defined the negative part of the database (further denoted as (−)). It contains 492 pairs involving 280 chemical compounds. These species were enumerated in supporting materials as Table S1 (ESI†).

The positive counterpart of the database (further denoted as (+)) was built by addition of cocrystals found in the Cambridge Structural Database (CSD)⁵⁵ for solved structures and also from other sources providing binary phase diagrams. Organometallic compounds were excluded along with solvates, hydrates, clathrates, ions or polymers. The positive part of the database comprises 1636 pairs and the final list of considered compounds reached 1001 constituents. They show great diversity of physicochemical properties, starting from non-polar species such as aromatic hydrocarbons, and ending on highly polar carboxylic acids, amides or alcohols.

All molecules were optimized using a PM7 semiempirical model⁵⁹ using implicit COSMO model⁶⁰ in water solution. These computations were performed with an aid of Mopac2012 program.⁶¹ Based on obtained geometries single-point computations were completed for getting various molecular descriptors. The full list of molecular descriptors derived from MOPAC2012,⁶¹ NBO^62,63(G09⁶⁴) or AIMALL⁶⁵ outputs is provided in supplementary materials (Table S2, ESI†).

The obtained distributions were analyzed in terms of normalized 2D histograms for which contour maps were plotted using SigmaPlot (ver.12.3). It is worth mentioning that for making the description independent from the numbering of components the number of pairs was doubled with reversed order of constituents. Since all distributions usually failed in fulfilling the requirement of normality, the Spearman's nonparametric correlation coefficient was used as a measure of correlations. It is based on the ranking of values rather than mean and standard deviation as offered by the often used Pearson correlation coefficient.

For quantifying the difference between patterns provided by 2D histograms, characterizing either of the counterpart of the database, the root mean square deviation was computed and similarity parameter was computed according to the following formula: s = 100%/(1 + rmsd), for each of molecular descriptor distributions. Based on similarity values, the molecular indices were classified according to their potential of discriminating two-component cocrystals from simple binary eutectic mixtures.

Results and discussion

The majority of the 71 molecular descriptors (defined in Table S2 of ESI†) have very similar distributions for both of the counterparts of the database and cannot be used for distinguishing of cocrystals from simple eutectics. However, there are 12 descriptors showing similarity lower than 90% and three parameters with likeness below 85%. The statistical characteristics of these distributions were provided in supporting materials (for details see Table S3 and Fig. S1, ESI†). Among these descriptors the highest value of rmsd was observed for the heat of formation (Hf). The resulting contour maps are presented in Fig. 1. It appears that distributions of Hf for two counterparts of the database offer a quite straightforward selection rule. In Fig. 1 all values are provided in the normalized form but actual data are within the range from −500 to + 150 kcal mol⁻¹. The change of the sign of Hf corresponds to normalized value of Hf_N = 0.77. It is expected that those components which have positive values of Hf are often found as constituents of eutectic mixtures in contrast to solid solutions. Of course this is not the only rule since one can find some percentage of compounds, which are unable to cocrystallize despite low values of heat of formation and vice versa, cocrystallizing despite positive Hf values.

Fig. 1 The distributions of normalized values of heat of formation (Hf) characterizing compounds involved in cocrystallization (left) and not-forming the molecular complex in the solid state (right).

However, the Spearman rank correlation coefficient for pairs involved in the simple eutectic mixtures is as high as σ₍₋₎ = 0.533 (P < 0.05), while for pairs of cocrystals it equals σ₍₊₎ = −0.258 (P < 0.05). It is interesting to notice the opposite sign of correlation coefficient in the latter case. For binary eutectic mixtures a quite moderate and positive trend suggests that similarity in terms of heat of formation is one of the most important factors contributing to immiscibility in the solid state. As presented in Fig. 1. there is quite a small range of Hf for the most often occurring pairs involved in binary eutectics. To the contrary, negative sign of Spearman rank correlation coefficient for cocrystals indicates rather the dissimilarity of cocrystal formers as a driving factor for cocrystallization. This statistical observation is further illustrated by patterns of the most frequently appearing pairs of cocrystals. On 2D histograms one can find a maximum located almost in the same place as for binary eutectics, characterizing hydrophobic nature of one of co-formers, while the value for the other component is off-diagonal and corresponds to a more hydrophilic character. Also, there are many cases of cocrystals for which both reagents have negative values of Hf. However, it is rather typical for such kind of systems in which the heat of formation values are different for both constituents. Thus, it seems that one of direct indicators of the possibility of cocrystallization is a sufficiently high affinity toward polar solution of at least one of compounds.

The second molecular descriptor being able to discriminate cocrystals from simple eutectics is the energy of the highest occupied molecular orbital, ε_HOMO. In Fig. 2 there are presented contour maps portraying such distributions for both sets of analyzed binary mixtures. All molecules considered here are characterized by ε_HOMO between −12.43 and −7.98 eV. Again, quite distinct patterns are observed for two counterparts of the database. Although the correlation between HOMO energies of compounds involved in simple eutectics is quite low, σ₍₋₎ = 0.289 (P < 0.05), there is a strong peak on the 2D histogram suggesting that there is a preferred range of ε_HOMO value close to −9.1 eV (ε_HOMO,N = 0.75). It is quite rare to see immiscibility in the solid phase associated with strong differences between both components expressed in terms of ε_HOMO. In the cases of interacting monomers involved in cocrystals the correlation between compounds is even weaker, σ₍₊₎ = −0.153 (P < 0.05), and the 2D pattern is quite complex. This indicates a great diversity of molecules exhibiting high affinity for intermolecular interactions. Since ε_HOMO quantifies the ability of electron donation and acting as a donor, it is quite expected that an opposite trend should occur in the cases of intermolecular compounds. However, generally it seems that ε_HOMO has a lower potential of distinguishing cocrystals from simple eutectics compared to Hf. Besides, there are also other molecular descriptors, which exhibit some abilities in predicting the chance of cocrystallization or simple eutectic formation. However, they are either correlated each to other or have similarities of corresponding 2D histograms higher than 85%. Illustrative plots of distributions of these alternative indices are provided in supporting material as Fig. S2 and S3 (ESI†). Furthermore, the application of two different descriptors on abscissa and ordinate was also considered. The use of ε_HOMO and M/H results in rmds = 0.183 and similarity s = 84.5%. Alternatively, selection of Hf and ε_HOMO provides rmds = 0.181 and similarity s = 84.7%. These plots are provided in supporting materials as Fig. S4 and S5 (ESI†). However, none of these combinations of molecular descriptors provides a better explanation of differences between both counterparts of the database than Hf. Hence, there is no gain in extending the number of parameters on 2D histograms, and heat of formation in aqueous solution as a single parameter description, can serve as quite an effective measure of components affinities.

Fig. 2 The distributions of HOMO energies (ε_HOMO) characterizing compounds involved in cocrystallization (left) and not-forming the molecular complex in the solid state (right).

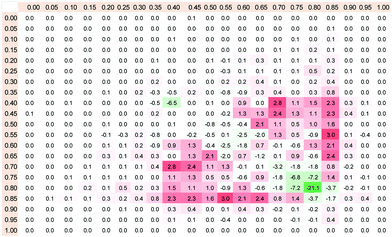
The distributions of the heat of formation for both analyzed counterparts of the database can be used for formulation of the rule for pre-selection of candidates for cocrystallization. Regions of dissimilarities between 2D histograms prepared for positive and negative cases of cocrystallization were examined just by calculating the difference between distributions presented in Fig. 1. This leads to the matrix presented in Fig. 3., which defines the scoring function. Each square, representing a region of Hf with 5% × 5% resolution, comprises a Δp number which defines the relative probability of pairs occurrence within given range of Hf values. The graded intensities of the red color indicate an increasing chance for cocrystallization and the more intense the green color, the more probable is the formation of simple eutectics by a given pair of components. The scoring function provided in Fig. 3 can be used for selection of compounds with the highest chance for either molecular complex formation or immiscibility in the solid state. The applicability of the proposed rule is demonstrated in Fig. 4, where the percentage of pairs selected from the whole database is plotted against Δp. Changes of this criterion impose restrictions on components properties (Hf in this case) and can help in selecting compounds with a high chance of cocrystallization or simple binary eutectic mixture formation. The black line represents positive cases of cocrystallization, while grey color was used for denoting the negative counterpart of the database. In the cases of cocrystals it is expected to find regions for which not only the chance of success is maximized but also, concurrently the probability of failure is minimized. Let's represent the percentage of selected structures with respect to the whole database (total number of pairs in training set is equal to 492 + 1636 = 2128). Obviously, if no restrictions are imposed on pairs, the chance of randomly picking the cocrystal is equal to 1636/2128 = 76.9% and simultaneous chance of failure is 492/2128 = 23.1%. After application of the scoring function one can expect to find regions with as high as possible number of cocrystals and as low as practically available number of binary simple eutectics. As it is documented in Fig. 4, the application of the exclusion criterion, Δp, significantly affects the number of considered compounds and application of a too restrictive norm can exclude too many potential pairs. In general this is not very limiting since one can consider many other potential cocrystals.³¹ Considering cocrystal screening, one can assume that Δp ≥ 0.15% and in consequence the number of positive cases fulfilling this requirement drops down to 1018 cases. Correspondingly, the number of simple eutectic systems found in the same range of Hf values is reduced to only 83. Thus, the chance of failure was reduced from 23.1% down to 3.9%. This is considered as the uncertainty of the proposed pre-selection rule for screening of cocrystals. Thus, selecting pairs of co-formers, which adopt values of heat of formation in the range fulfilling requirement of Δp ≥ 0.15%, leads to quite an acceptable ratio of success with reasonably low chance of failure. Of course one can increase the Δp criterion, but the gain in reducing the number of simple eutectics will not be worth the exclusion of too many potential cocrystallizing pairs.

Fig. 3 The scoring function representing probability differences (Δp) between 2D distributions of heat of formation for pairs of compounds involved in cocrystals with respect to simple binary eutectics. The squares of arbitrary 5% × 5% resolution were coloured in red for regions with higher probability of forming cocrystals while green colour denotes regions with increased probability of simple eutectics. The range of normalised values of Hf is denoted in the top row and first left column.

Fig. 4 The percentage of structures selected from the database as a function of the relative probability of cocrystallization (Δp) after application of the scoring function defined in Fig. 3. Provided number of structures correspond to Δp = 0.15.

It is interesting to see how the proposed selection rule will perform in selection of compounds not included in the training set. For this purpose there were selected such cocrystals deposited in the CSD that were not used in the definition of the scoring function. The following four categories were used, namely all available aromatic carboxylic acids (ArCOOH), aliphatic carboxylic acids (AlCOOH), aromatic amides (ArCONH₂) and also 400 other systems randomly selected from all known 7688 binary cocrystals deposited in the CSD. The resulting distributions were presented in Fig. 5. First of all, the contour maps exhibit essentially the same patterns as observed for compounds constituting the training set. The percentage of structures predicted by the rule utilizing Hf is in average 62%. Although the (ArCONH₂) set seems to be the worst among all others considered, it is also the smallest pool. Bearing in mind that the proposed pre-selection rule is very simple, the acceptable chance of success is surprisingly effective. It is also worth underlining that from a practical point of view the elimination of many positive cases from the analysis is not very limiting, since there is still a sufficient amount of possible pairs³¹ for which the screening can be performed with high efficiency.

Fig. 5 The applications of selection rules for picking of components in regions of the highest probability of cocrystallization based on scoring function defined in Fig. 3.

Conclusions

The binary solid mixtures, both in the form of simple eutectics or molecular compounds found in cocrystals, are important for many practical applications. The synthesis of such systems as a target in many industrial applications is typically preceded by screening of suitable constituents based on different criterions, for example expected physicochemical properties, toxicity, stability, availability, or simple price. Such selection rules are expected to fulfill a practically sensible screening paradigm outlined by Blagden et al.⁴ Here, after analyzing many cases of miscible and immiscible pairs of compounds in the solid state, a computationally inexpensive pre-selection tool allowing for rational choice of potential formers was formulated based on distributions of heat of formation. The proposed procedure relies on the scoring function defined using quite an extended training set of both types of systems. The main idea behind the rule for discriminating components involved in cocrystals from those found in simple binary eutectics comes from observed distinct patterns appearing on corresponding heat of formation distributions. Interestingly, among 71 arbitrary defined parameters this very simple and intuitive molecular descriptor has been found as the most promising index for distinguishing between the two types of analyzed systems. It has been observed that higher probability of cocrystal formation is to be expected if at least one of components has high hydrophilicity expressed in terms of Hf in aqueous media (modeled by COSMO approach). Since the Spearman rank correlation in the case of cocrystals is quite low and negative σ₍₊₎ = −0.258, the second component is expected to be different and possess lower affinity in water solution. On the contrary, the high probability of simple eutectic systems is expected for cases of high similarities of Hf and preferentially of positive values. This is also underlined by values of Spearman rank correlation, which in the case of simple eutectic mixtures is as high as σ₍₋₎ = 0.533.

Based on the formulated scoring function the regions of observed highest probability of cocrystallization can be identified. The procedure proposed here has several advantages. First of all, it allows for direct and practical applications in the presented form, which will be documented in a forthcoming paper. The heat of formation computed on cheap quantum chemistry level can be easily estimated for a variety of even sizable chemical systems without sophisticated computational resources. Besides, the procedure is flexible and new molecular descriptors of probably even better discriminating potential can be used in a similar manner as the heat of formation in this case, which is also worth further exploration. Furthermore, the extension of the database will eventually lead to better tuning of the scoring function, which seems to be a natural extension of this study on structure-to-property relationships revealed through diversities/similarities of components. Such a strategy is commonly applied in chemoinformatics and might be helpful as the initial step before actual experiments. Since the collected database comprised 1636 cocrystals and 492 binary eutectic systems it seems to be quite representative. Interestingly, the extension of the number of cocrystals up to 3226 cases not included in the training set does not change the observed patterns of Hf distributions. Although the proposed model-based approach cannot provide absolute prediction of cocrystals or simple eutectic mixtures, it is of practical importance since it offers guidance for rationalizing the selection of potential cocrystal formers for real purposes.

Notes and references

1. C. B. Aakeröy, N. R. Champness and C. Janiak, CrystEngComm, 2010, 12, 22.
2. S. L. Childs and M. J. Zaworotko, Cryst. Growth Des., 2009, 9, 4208–4211.
3. E. R. T. Tiekink, J. Vittal and M. Zaworotko, Organic Crystal Engineering: Frontiers in Crystal Engineering, 2010.
4. N. Blagden, S. J. Coles and D. J. Berry, CrystEngComm, 2014, 16, 5753.
5. H. G. Brittain, J. Pharm. Sci., 2013, 102, 311–317.
6. N. J. Babu and A. Nangia, Cryst. Growth Des., 2011, 11, 2662–2679.
7. N. Qiao, M. Li, W. Schlindwein, N. Malek, A. Davies and G. Trappitt, Int. J. Pharm., 2011, 419, 1–11.
8. C. C. Sun, Expert Opin. Drug Delivery, 2013, 10, 201–213.
9. S. B. Murdande, M. J. Pikal, R. M. Shanker and R. H. Bogner, J. Pharm. Sci., 2011, 100, 4349–4356.
10. B. C. Hancock and M. Parks, Pharm. Res., 2000, 17, 397–404.
11. H. D. Williams, N. L. Trevaskis, S. A. Charman, R. M. Shanker, W. N. Charman, C. W. Pouton and C. J. H. Porter, Pharmacol. Rev., 2013, 65, 315–499.
12. J.-R. Wang, C. Zhou, X. Yu and X. Mei, Chem. Commun., 2014, 50, 855–858.
13. D. P. McNamara, S. L. Childs, J. Giordano, A. Iarriccio, J. Cassidy, M. S. Shet, R. Mannion, E. O’Donnell and A. Park, Pharm. Res., 2006, 23, 1888–1897.
14. M. L. Cheney, N. Shan, E. R. Healey, M. Hanna, L. Wojtas, M. J. Zaworotko, V. Sava, S. Song and J. R. Sanchez-Ramos, Cryst. Growth Des., 2010, 10, 394–405.
15. D. R. Weyna, M. L. Cheney, N. Shan, M. Hanna, M. J. Zaworotko, V. Sava, S. Song and J. R. Sanchez-Ramos, Mol. Pharmaceutics, 2012, 9, 2094–2102.
16. S. Karki, T. Friščić, L. Fabián, P. R. Laity, G. M. Day and W. Jones, Adv. Mater., 2009, 21, 3905–3909.
17. C. M. Reddy, S. Basavoju and G. R. Desiraju, Chem. Commun., 2005, 2439–2441.
18. N. J. Babu, P. Sanphui and A. Nangia, Chem.–Asian J., 2012, 7, 2274–2285.
19. A. V. Trask, W. D. S. Motherwell and W. Jones, Int. J. Pharm., 2006, 320, 114–123.
20. M. Viertelhaus, R. Hilfiker, F. Blatter and M. Neuburger, Cryst. Growth Des., 2009, 9, 2220–2228.
21. A. V. Yadav, A. S. Shete, A. P. Dabke, P. V. Kulkarni and S. S. Sakhare, Indian J. Pharm. Sci., 2009, 71, 359–370.
22. C. Guo, H. Zhang, X. Wang, J. Xu, Y. Liu, X. Liu, H. Huang and J. Sun, J. Mol. Struct., 2013, 1048, 267–273.
23. C. Zhang, X. Xue, Y. Cao, J. Zhou, A. Zhang, H. Li, Y. Zhou, R. Xu and T. Gao, CrystEngComm, 2014, 16, 5905–5916.
24. D. I. A. Millar, H. E. Maynard-Casely, D. R. Allan, A. S. Cumming, A. R. Lennie, A. J. Mackay, I. D. H. Oswald, C. C. Tang and C. R. Pulham, CrystEngComm, 2012, 14, 3742.
25. D. Braga, L. Chelazzi, F. Grepioni, S. Nanna, K. Rubini, M. Curzi, S. Giaffreda, H. E. Saxell, M. Bratz and T. Chiodo, Cryst. Growth Des., 2014, 14, 1430–1437.
26. E. Nauha, A. Ojala, M. Nissinen and H. Saxell, CrystEngComm, 2011, 13, 4956.
27. R. Sekiya and R. Kuroda, Chem. Commun., 2011, 47, 10097–10099.
28. A. N. Sokolov, T. Friscić and L. R. MacGillivray, J. Am. Chem. Soc., 2006, 128, 2806–2807.
29. C. B. Aakeröy and D. J. Salmon, CrystEngComm, 2005, 7, 439.
30. A. D. Bond, CrystEngComm, 2007, 9, 833–834.
31. A. T. M. Serajuddin, Adv. Drug Delivery Rev., 2007, 59, 603–616.
32. N. Shan, F. Toda and W. Jones, Chem. Commun., 2002, 2372–2373.
33. A. V. Trask and W. Jones, Top. Curr. Chem., 2005, 254, 41–70.
34. D. R. Weyna, T. Shattock, P. Vishweshwar and M. J. Zaworotko, Cryst. Growth Des., 2009, 9, 1106–1123.
35. T. Friščić, S. L. Childs, S. A. A. Rizvi and W. Jones, CrystEngComm, 2009, 11, 418.
36. E. Gagnière, D. Mangin, F. Puel, A. Rivoire, O. Monnier, E. Garcia and J. P. Klein, J. Cryst. Growth, 2009, 311, 2689–2695.
37. P. Vishweshwar, J. A. McMahon, J. A. Bis and M. J. Zaworotko, J. Pharm. Sci., 2006, 95, 499–516.
38. S. Goyal, M. R. Thorson, G. G. Z. Zhang, Y. Gong and P. J. A. Kenis, Cryst. Growth Des., 2012, 12, 6023–6034.
39. S. Karki, T. Friščić, W. Jones and W. D. S. Motherwell, Mol. Pharmaceutics, 2007, 4, 347–354.
40. E. Lu, N. Rodríguez-Hornedo and R. Suryanarayanan, CrystEngComm, 2008, 10, 665.
41. M. Przybyłek, P. Cysewski, M. Pawelec, D. Ziółkowska and M. Kobierski, J. Mol. Model., 2015, 21, 49.
42. P. Cysewski, M. Przybyłek, T. Miernik, M. Kobierski and D. Ziółkowska, Struct. Chem., 2015, 26, 705–712.
43. M. Kobierski, P. Cysewski, M. Przybyłek and D. Ziółkowska, 2015,  DOI:10.1016/j.jcrysgro.2015.10.015.
44. P. G. Karamertzanis, A. V. Kazantsev, N. Issa, G. W. A. Welch, C. S. Adjiman, C. C. Pantelides and S. L. Price, J. Chem. Theory Comput., 2009, 5, 1432–1448.
45. C. Loschen and A. Klamt, J. Pharm. Pharmacol., 2015, 67, 803–811.
46. M. A. Mohammad, A. Alhalaweh and S. P. Velaga, Int. J. Pharm., 2011, 407, 63–71.
47. J. E. Code, A. J. Holder and J. D. Eick, QSAR Comb. Sci., 2008, 27, 841–849.
48. J. Gupta, C. Nunes, S. Vyas and S. Jonnalagadda, J. Phys. Chem. B, 2011, 115, 2014–2023.
49. D. P. Elder, J. E. Patterson and R. Holm, J. Pharm. Pharmacol., 2015, 67, 757–772.
50. A. W. Newman and S. R. Byrn, Drug Discovery Today, 2003, 8, 898–905.
51. G. He, C. Jacob, L. Guo, P. S. Chow and R. B. H. Tan, J. Phys. Chem. B, 2008, 112, 9890–9895.
52. L.-Z. W. Zhanting Li, Hydrogen Bonded Supramolecular Structures, Springer, 2015.
53. A. Delori, P. T. A. Galek, E. Pidcock and W. Jones, Chem.–Eur. J., 2012, 18, 6835–6846.
54. T. K. Adalder, R. Sankolli and P. Dastidar, Cryst. Growth Des., 2012, 12, 2533–2542.
55. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388.
56. M. W. Hosseini, Coord. Chem. Rev., 2003, 240, 157–166.
57. J.-M. Lehn and J.-M. Lehn, Chem. Soc. Rev., 2007, 36, 151–160.
58. L. Fábián, Cryst. Growth Des., 2009, 9, 1436–1443.
59. J. J. P. Stewart, J. Mol. Model., 2013, 19, 1–32.
60. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799.
61. (a) MOPAC2012, James J. P. Stewart, Stewart Computational Chemistry, Version 15.089W; (b) J. D. C. Maia, G. A. U. Carvalho, C. P. Mangueira, S. R. Santana, L. A. F. Cabral and G. B. Rocha, J. Chem. Theory Comput., 2012, 8, 3072–3081.
62. E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42.
63. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
64. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09, Gaussian, Inc., Wallingford, CT, 2009.
65. T. A. Keith, AIMAll (Version 15.05.18), TK Gristmill Software, Overl. Park KS, USA, 2015, 2015.

---

Footnote

† Electronic supplementary information (ESI) available: List of content of the negative counterpart of the database, definition of molecular descriptors and additional contour maps. See DOI: 10.1039/c5nj02013a

---