Statistics, damned statistics and nanoscience – using data science to meet the challenge of nanomaterial complexity
Baichuan
Sun
,
Michael
Fernandez
and
Amanda S.
Barnard
*
CSIRO Virtual Nanoscience Laboratory, Parkville, VIC 3052, Australia. E-mail: amanda.barnard@csiro.au; Tel: +61 3 9662 7356
First published on 2nd February 2016
Abstract
For many years dealing with the complexity of nanoscale materials, the polydispersivity of individual samples, and the persistent imperfection of individual nanostructures has been secondary to our search for novel properties and promising applications. For our science to translate into technology, however, we will inevitably need to deal with the issue of structural diversity and integrate this feature into the next generation of more realistic structure/property predictions. This is challenging in the field of nanoscience where atomic level precision is typically inaccessible (experimentally), but properties can depend on structural variations at the atomic scale. Fortunately there exists a range of reliable statistical methods that are entirely applicable to nanoscale materials; ideal for navigating and analysing enormous amount of information required to accurately describe realistic samples. Combined with advances in automation and information technology the field of data science can assist us in dealing with our big data, characterising our uncertainties, and more rapidly identifying useful structure/property relationships. Taking greater advantage of data-driven methods involves thinking differently about our research, but applied appropriately these methods can accelerate the discovery of nanomaterials that are optimised to make the transition from science to technology.
Scientists have been generating big data for decades; in many cases without even realising it. Unfortunately, in our search for the “one perfect result”, much of our data has not been fully utilised. Once the “one perfect result” has been published, the remaining data is subsequently undervalued; archived and ignored. Nanoscience, emerging around the time when synthesis and characterization methods simultaneously improved in terms of the selectivity and specificity, is a perfect example. Over the past two decades it has been well established that many fundamental thermochemical, mechanical, electronic, optical and magnetic properties of nanomaterials have a strong dependence on size,1–7 shape,8–12 the solid phase,13–15 and the surface chemistry.16 These dependencies are referred to as structure/property relationships,17,18 and they underpin the design, development and performance of almost all new emerging technologies. This includes new medical platforms,19 electronic devices,20 fuel cells,21–23 and coatings.24 Tuning the properties to improve performance,25,26 is what nanotechnology is all about, but this can only be achieved by controlling the structure of the nanomaterial, typically by employing variations in the temperature,27–31 chemical environment,32–34 exposure to external electromagnetic fields,35,36 substrates,37,38 the density of defects39 and growth kinetics (time).40–44
Although experimental studies aim to identify and quantify structure/property relationships with specific applications in mind, many of the challenges are independent of the final objectives and are shared by all. The inability to control one structural or processing parameter independently often masks the particular physicochemical features that are most important, and makes the connection from properties to performance difficult to address. Experimental methods cannot, at this stage, access atomic level precision, and struggle to make definitive associations between a desirable functional property and a realistically controllable structural feature. This is undoubtedly why they are called structure/property relationships, and not structure/property rules, but should not been viewed as a significant impediment. One area in which imperfection has not hindered the transition from nanoscience to nanotechnology is in the field of electronics. For many applications it is not essential to exercise precise control, provided the impact of a given imperfection is small, as their combined effect is usually additive not a multiplier, and the imperfections of individual structural elements contribute to a narrow distribution.45 The key is to design with some uncertainty in the structure/property relationships from the outset.
Theoretical and computational methods have also been used to investigate the structure/property relationships of nanomaterials by many groups around the world. In general, this problem is ideally suited to theory and simulation, since it is possible to control the structure with atomic level precision. It is also possible to generate structure/property relationships specific to particular thermochemical environments, which is invaluable in assessing the meta-stability of equilibrium or kinetically grown nanoparticles transplanted into highly non-equilibrium storage, operational or natural environments. However, the vast majority of structure/property predictions in materials and nanoscience involve simulations of single, individual (isolated) nanostructures. Knowledge of single-particle properties is very important, as they provide insights into the stability of each structure (subject to a set of conditions), as well as helping to identify novel structures to target for particular applications. However, the reason for this single-particle approach is usually pragmatic, not scientific. Modelling in nanoscience was born of more mature areas such as solid state physics, where materials are continuous, and therefore well described by irreducible subunits; or chemistry, where samples can be purified and all subunits (molecules) are the same. Unfortunately, neither of these assumptions holds for nanomaterials.
By virtue of the finite size and low dimensionality, nanoparticles have no translational symmetry, and so cannot be described by a standard irreducible (periodic) subunit; we need to model the whole nanostructure to understand its properties. Nanomaterials cannot be purified, and polydispersivity persists at the atomic level irrespective of how carefully they are grown, fabricated or processed. Idealised samples with perfect monodispersivity are commercially unrealistic. It will simply be too expensive to ensure all structures are atomically identical. However, when we calculate the properties of a single “representative” structure, the (computational) measurement uncertainty may be vanishingly small, but the statistical uncertainty goes to infinity. This effectively makes the prediction technologically obsolete.
It is possible to restrict the dispersivity of samples on a commercially relevant scale, but this comes with an additional cost to the manufacturing process every time another restriction is introduced. To predict which restrictions will be worthwhile we need to model entire ensembles of structures, accounting for a much larger amount of the structural configuration space. Structure/property relationships should not be a series of delta functions; they are distributions, just as the structure of experimental samples of nanoparticles is made up of mixtures and distributions of sizes, shapes and defects.
What is data science?
Undoubtedly one of the biggest things to happen in the physical sciences in recent years is the recognition that the quantity and complexity of materials data is accelerating, and we need new ways of analysing, visualising, and interrogating this deluge of information. The emergence of materials informatics to answer this call (following the famous announcement of the US Materials Genome Initiative (MGI) by US President Barak Obama in June 201146) heralds a new era in research. The MGI was born of the desire to overcome trial-and-error and the lack of systematic data in materials research, by leveraging large-scale collaborations between statisticians, materials and computer scientists, and spearheading the development of novel scalable approaches to discover, manufacture, and deploy advanced materials more rapidly, and at a lower cost.47The MGI is not the only initiative of this type, as it is essentially a large scale exercise in data science. As indicated above, the success of this (and similar) venture(s) is contingent on collaborations between three bastions of science: Computer Science to develop the communication and visualisation technologies; Mathematics and Statistics to interrogate and interpret the information; and Scientific Domains such as physics and chemistry to provide the context, insights and explanations.
Each of these disciplines add unique value, and at the interface between them different types of research is conducted, as illustrated in Fig. 1. At the interface between the physical science domains and mathematical modelling we have the traditional “normal science” undertaken using theoretical, computational or experimental methods. The combination of science domain knowledge and computer science has given us high-throughput methods, using automated (robotic) systems. And finally, collaborations between mathematical and computer sciences developed informatics, which can be applied autonomously to any domain.
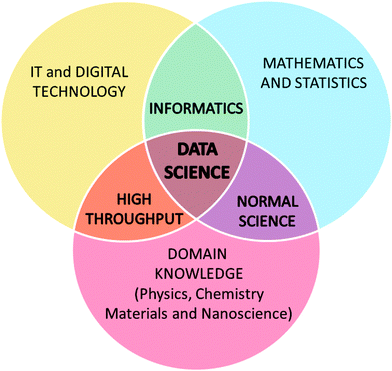 | ||
| Fig. 1 The convergence of traditional scientific and technical disciplines, and the relationship to data science. | ||
At the nexus we have data science, where the combination of knowledge and experience is greater than the sum of the parts. Beyond the challenges associated with generating, hosting, standardizing and interpreting results, data science is essentially a new field research. It is the rightful home of our scientific “big data”, as expertise from each discipline is needed to effectively generate, analyse and utilise it.
Big data challenges for the science of small things
Nanomaterials, in particular, represent the greatest challenge for data science, since characterising the structural configuration space alone involves “big data”, even before we include the impact of the synthesis, processing or storage environment, and the rich variety of functional properties. We can meet this challenge, but in so doing we must be ready to change the way we think about research in the field.“Some” vs. “All”
For most of history, scientists have worked with relatively small data sets, because the tools for collecting, organising, storing, and analysing information were poor. An enormous amount of time was taken in planning research and, based on intuition and assumptions, working out what information could be omitted from the outset. This was achieved through sampling, so that (within a certain margin of error) we could infer the properties of a total sample of material or nanoparticles based on a small sub-set of “representative” structures. When pre-selecting these “representative” sub-sets it was also necessary to know how it would be used in the future (so that data that we did not plan to use could be ignored), so the data that was collected was often useless in other contexts. Winnowing the required information down to the barest minimum made science practical, but one wonders how many discoveries were never made because we judged the outcomes before doing the work.Fortunately the technological environment has changed, and dealing with massive amounts of data is now far less limiting. If we collect all the data (“N = all”, to use the terminology of statistics) many of our technical and scientific problems disappear. We do not need to know beforehand what we plan to use it for. We do not need to know which structures are “representative” from the outset. If some of the structures are chemically unrealistic or physically unstable, they will naturally be identified as statistical outliers in the data set. In some cases “N = all” may still be infeasible, but with the advent of high-throughput simulation of nanomaterials (expedited by the perpetual investment in high performance computing that we have enjoyed in recent years, and are likely to continue to enjoy for years to come) it is feasible to capture vastly more of a phenomenon than a simple sub-set. In particular, the ability to couple this with electronic structure methods provide an unprecedented capability to identify and characterise structure/property relationships with a level of accuracy that is essential for making reliable predictions (and explanations) for the vast majority of high performance applications.
“Clean” vs. “Messy”
However, if we are to circumvent the careful planning of small curated sub-sets of data there is a trade-off to be made. When we increase the scale by orders of magnitude, we will have to tolerate some messiness. Size-dependent trends, for example, will no longer be smooth linear (or non-linear) relations. There will be noise, and there will be uncertainty. The obsession with accuracy and precision is in some ways an artefact of an information-constrained environment, and while the value of accuracy and precision should not be understated, tapping vastly more data means that we can now allow some inaccuracies to slip in (provided the data set is not completely incorrect).In return we benefit from the insights that a massive body of data provides. By reproducing the polydispersivity and structural complexity characteristic of experimental samples we gain the ability to quantify our uncertainties with statistical significance. We gain error bars, which are traditionally omitted from computational studies (much to the chagrin of experimentalists), and we gain insights into the variance in structure/property relationships, which is essential for the design of future products. We can predict quality factors, and therefore classify our materials.
“Causation” vs. “Correlation”
The final challenge to our way of thinking, is the move away from always trying to understand the deeper reasons behind how the world works, and focus on extracting knowledge from the correspondence of phenomena. “Normal science”, based exclusively on domain knowledge (articulated by mathematical and statistical models, as highlighted in Fig. 1), seeks the underlying causes that govern structure/property relationships: why does a specific structure give rise to a particular property. Data science seeks the overarching associations that manifest as structure/property relationships: how does a specific structure give rise to a particular property. The difference is subtle, but overarching associations can be identified much more quickly than underlying reasons, and finding one does not prohibit us from seeking the other.This distinction, and the positive impact correlations can have in driving research is evidenced by the success of the field of bioinformatics. Bioinformatics has become an important part of many areas of biology, facilitating the extraction of useful results in big data sets and elucidating evolutionary aspects of molecular biology. In the field of genomics, it aids in sequencing and annotating of genomes, and the development of ontologies to interrogate biological data. Most importantly, it enables us to more rapidly make reliable decisions in bio-medical research, and more accurately quantify the probable risks. Bioinformatics has not replaced biology or medicine, but provides another useful tool in their kit – just as nanoinformatics will provide a new tool in ours.
Statistical nanoscience
The power of probability distributions
One of the most simple things we can do when confronted with a large, messy data set of nanostructures is to take an average. We feel justified in doing this because this is effectively what is measured in conventional laboratory experiments; an average over all of the structures present in the sample, and an error bar accounting for the statistical and measurement uncertainty.48 However, taking averages can be more useful than merely condensing a messy list of results to a single convenient value. Firstly, the simple numerical average (dividing the sum of the results by the number of results) is only truly applicable when each and every structure contributes the same amount to the ensemble average (has an equal weighting). This corresponds to a frequency distribution, which is entirely valid if we have on the order of Avogadro's number of structures in the data set or legitimately have gathered N = all in each case. However, if we are using a smaller, more manageable data set (N < all) it is entirely likely that some structures will be more important than others, and a different distribution will be more suitable.In many cases the structure and properties of nanoparticles exhibit a normal distribution (or some variant there of) and, provided the data set spans the range of the configuration space, it is a simple matter to weight each individual data point accordingly and divide by the canonical partition function.49 The properties of structures with a higher probability of observation will contribute more to the expectation value of the sample, and the properties of outliers will hardly contribute at all. Alternatively, there are cases where a thermodynamic (Boltzmann) distribution is more appropriate, so that the properties of structures that are more thermodynamically stable contribute more to the average, and the properties of unstable or meta-stable structures are suppressed.50,51 Different statistical distributions can be applied as needed, easily compared, rapidly explored and conveniently chosen to correspond with the outcomes of specific experimental conditions or industrial processes.49 This includes applications in more mature areas in the nanoelectronics industry.
Another advantage of paying mind to how we average over our large, messy sets of results is that we can use the distributions to define the variance and ultimately the scattering (or bandwidth) of the properties. In addition to understanding how different synthesis techniques or purification processes may tune the (peak value of) specific properties, we can also begin to predict how the same techniques or processes impact the property dispersion. The expectation value and the variance (the property, and the property dispersion) can be combined to deliver a type of quality factor (Q-factor) that facilitates the classification of nanomaterials and informs materials design by predicting how different experimental strategies can impact performance.52,53 Carefully tuning a property to a specific peak value (improved selectivity) is useless if the dispersion increases and a range of alternative values are equally likely (loss of sensitivity).
Structure searching, sampling and reduction methods
Averaging is a convenient way to avoid dealing with the complexity of large data sets, but statistics also offer some powerful ways to characterise the polydispersivity and heterogeneity of nanoparticle ensembles, and to identify the truly relevant structures among the billions of possibilities. Different dimension reduction techniques are routinely applied to find patterns in high complexity data sets across different research fields from pharmaceutical to earth sciences.54,55 For example, k-means clustering and principal component analysis (PCA) are techniques for unsupervised pattern recognition commonly used to identify intrinsic patterns in material science data.56 Clustering methods assign materials that share similar features to individual groups, while PCA transforms the data into a new coordinate system (the so called principal components, PCs) using an orthogonal linear transformation where the axes are oriented to account for maximal variation in the data set.Alternatively, archetypal analysis (AA)57 is a relatively new matrix factorisation method that results in easy interpretable components similar to PCs but with added flexibility over clustering.58 Cutler and Breiman first introduced archetypal analysis in 1994 to study air pollution and the shape of human heads, but it can be used to identify any individual structure with a convex combinations of features that optimally approximate the features of the entire data set, yielding a set of archetypes or “pure materials” on the convex hull.59 AA has been applied in the identification of extreme practices in bench-marking and market research; signal enhancement and feature extraction of IR image sequences;60,61 extracting features from different high-dimensional data sets; identifying extreme and representative human genotypes within the population;62 analysis of gene expression data63 and most recently to the identification of archetypal nanoparticles.64
Data mining and analytics
The unprecedent speed and volume at which nanomaterials are being currently investigated, both experimentally and in silico, clearly outpaces our existing capacity to store, analyse, visualise and ultimately interpret results; a problem that is discussed further in the next section. In this “big data” scenario, “normal science” (defined above) is unequipped to manage the diversity of large and complex datasets, which are better handled by modern data mining and informatics techniques. Combining virtual high-throughput data and “big data” analytics sheds new insights on the structure/property relationships of more experimentally realistic samples of nanomaterials, and can accelerate ground-breaking innovations.Data mining techniques are based on structural similarity, which in the case of nanoparticles can be detected by different types of structural descriptors from simple geometrical features to more sophisticate topological, electronic, and quantum chemical features. Once a large set of structures are collected these descriptors can be used to investigate structure/property relationships in quantitative terms. Data mining methods can extract useful information using abstract structural representations from graph information theory, or computational predictive tools can be developed such as quantitative structure/property relationships (QSPR) models.65
In particular, structure/property relationships that are impacted by variability in particle size, shape, surface structure and chemistry (etc.) can be computed using machine learning techniques such as linear multiple regression (MLR),66 decision tree (DTree)67 and k-nearest-neighbour (kNN),68 as well as more sophisticated nonlinear techniques such as artificial neural networks (ANNs)69 and support vector machines (SVM).70 Models are trained using structural features from a sub-set of the data, while the remaining fraction of the data set is used to test the predictability of the models. Powerful machine learning algorithms, such as ANNs69 and SVMs,70 can produce accurate QSPR predictive tools,72 whilst simpler QSPR models implementing MLR and DTree can reveal simple correlations and “rules-of-thumbs” that can guide rational nanomaterials design.65
In addition to this, genetic algorithms (GAs) are a different type of stochastic optimisation method inspired by evolutionary principles.71 Each GA solution explores different regions in parameter space, in such a way that many possible solutions are investigated simultaneously. When our nanostructures are too complicated, and functional properties could depend on too many structural features, GAs reduce the complexity of the QSPR models by identifying which features are the most influential, and which are contributing to the noise.65
High-throughput automation
So how do we gather our big data in the first place? Traditional experimental testing and validation of nanomaterials can be time-consuming and plagued with inaccuracy due to human errors, and so considerable effort is being directed toward the development of high-throughput screening (HTS) methods,73 consisting of robotics, mechanical controllers, sensitive detectors and data processing software (among other things). Robotic systems, once restricted to pharmaceutical companies, are now being used to simultaneously synthesise and characterised large arrays of hundreds to thousands of subtlety unique samples. These systems offer advantages in terms of increased speed and accuracy, reduced sample volumes, and an increase in the sheer number of samples that can be tested, in addition to working around the clock without human intervention. Automation is essential to the collection of big experimental data sets, but these systems can be expensive.Large-scale computational screening nanostructures is also gaining momentum, as evidenced by recent work on metal–organic frameworks (MOFs);74 a promising nanoporous material for natural gas storage usage. From 102 metal and organic molecule “building blocks” Wilmer, et al.75 generated 137![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 953 hypothetical MOFs, with constraints of single type metal atom and functional group, and no more than two kinds of organic links within each MOF unit cell. Each structure can be defined by the characteristic volumetric/gravimetric surface area, pore volume, void fraction, dominant pore diameter, and functional group types, and were correlated with the functional properties such as methane uptake.75 This study provided valuable guidance for MOFs development for natural gas storage, and could be rapidly expanded if more metallic centres or organic linkers were included. Much like automated experiments, mathematical algorithms can systematically generate even more unique, hypothetical structures suitable for computational structure/property predictions.
953 hypothetical MOFs, with constraints of single type metal atom and functional group, and no more than two kinds of organic links within each MOF unit cell. Each structure can be defined by the characteristic volumetric/gravimetric surface area, pore volume, void fraction, dominant pore diameter, and functional group types, and were correlated with the functional properties such as methane uptake.75 This study provided valuable guidance for MOFs development for natural gas storage, and could be rapidly expanded if more metallic centres or organic linkers were included. Much like automated experiments, mathematical algorithms can systematically generate even more unique, hypothetical structures suitable for computational structure/property predictions.
Technical limitations
However, regardless of the source, as big data is generated the physical hardware limitations inevitably become a bottleneck for high performance data analysis. Co-location of big data sets is the first technical challenge, and in many cases large data sets must be split up and distributed among different storage spaces (in clusters). Transfer of data back and forth to facilitate unified analyses is inconvenient, and frequently limited by input/output (I/O) performance. These issues first arise in the early stages of data collection, when (typically) unstructured data must be curated to populate a relational database; organised into tables which can be analysed using standardised methods such as the Structured Query Language (SQL) or a suitable alternative.Currently this issue is circumvented by sending processing and analysis programs to each data storage node to work independently on a portion of the whole data, rather than sending all of the data to a single computational node. Upon completion the computational results are collected, co-located and summarised on the master node, and the big data remains distributed. MapReduce, inspired by functional programming, is a popular example, and is well supported by the open-source framework Apache Hadoop. Though Hadoop itself is written in Java, complementary mapper and reducer programs can be developed in other languages including C++ or Python. A package is also available for Mathematica to interface with Hadoop Distributed File System (HDFS).76 However, the MapReduce programming model is designed for batch processing and can hold back the response to analytical questions. Some of these limitations are overcame by in-memory processing in Spark, the open-source cluster computing framework from the Apache Software Foundation, that allows real-time, responsive applications. Even if the challenge of nanomaterial complexity increases faster than the physical limits of data storage media, the development of new algorithms can help to overcome any technical barriers to innovation.
Open access; open minds
One persistent challenge, however, is ensuring the longevity of data sets and data storage. To enhance global collaboration, avoid unnecessary repetition of work, and enable open-access to publicly funded research results, there is increasing demand for long-term storage of scientific data. Some cloud-based scientific data storage facilities are already available, such as the CSIRO Data Access Portal,77 the NoMaD Repository,78 and the Materials Project.79 Taking greater advantage of cloud-based computing resources provided, for example, by Amazon EC2/RDS/EMR, is one strategy that could also free researchers (or any people who are interested in the data) from the limitations of their local computer's capacity. In addition to this, more data would be generated and accumulated using the cloud-based computing environments, and reduce the carbon footprint of computational research.Concluding remarks
The application of data-driven science in the fields of nanoscience and nanotechnology represents a new research direction that is at the heart of the innovation ecosystem of the future. Data science does not replace “normal science”; it complements it. It is not a competitive approach; it is a collaborative one. Big data is not just a matter of creating somewhat larger samples; it is about harnessing as much of the existing data as possible about what is being studied. It is about identifying and understanding correlations that are impossible to discern from a limited set of pre-determined (often idealised) structures; about dealing with complexity and extracting more value from the research we have already invested in. This is ideal for cases where structure/property relationships are unknown, or poorly understood, as data science does not require a deep understanding of the structure or properties at the outset. By adding data science to our scientific toolkit, we will be able to more rapidly identify areas where deep understanding (the realm of normal science) can have real impact; but we will be able to go even further. We will be able to predict the quality of properties, in addition to quantity; the sensitivity (bandwidth) in addition to the selectivity (peak position). Perhaps most importantly, we will regain opportunities for serendipitous discovery, as we do not need to restrict our science before we even begin.References
- C. T. Campbell, S. C. Parker and D. E. Starr, Science, 2002, 298, 811–814 CrossRef CAS PubMed.
- S. Kan, T. Mokari, E. Rothenberg and U. Banin, Nat. Mater., 2003, 2, 155–158 CrossRef CAS PubMed.
- J. V. Lauritsen, J. Kibsgaard, S. Helveg, H. Topsøe, B. S. Clausen, E. Lægsgaard and F. Besenbacher, Nat. Nanotechnol., 2007, 2, 53–58 CrossRef CAS PubMed.
- W. Jiang, B. Y. S. Kim, J. T. Rutka and W. C. W. Chan, Nat. Nanotechnol., 2008, 3, 145–150 CrossRef CAS PubMed.
- S. Zhang, J. Li, G. Lykotrafitis, G. Bao and S. Suresh, Adv. Mater., 2009, 21, 419–424 CrossRef CAS PubMed.
- M. Barisik, S. Atalay, A. Beskok and S. Qian, J. Phys. Chem. C, 2014, 118, 1836–1842 CAS.
- Y. Cheng, H. Su, T. Koop, E. Mikhailov and U. Pöschl, Nat. Commun., 2015, 6, 5923 CrossRef CAS PubMed.
- K. L. Kelly, E. Coronado, L. L. Zhao and G. C. Schatz, J. Phys. Chem. B, 2003, 107, 668–677 CrossRef CAS.
- C. L. Nehl and J. H. Hafner, J. Mater. Chem., 2008, 18, 2415–2419 RSC.
- H. Yu and S. L. Brock, ACS Nano, 2008, 2, 1563–1570 CrossRef CAS PubMed.
- S. Mostafa, F. Behafarid, J. R. Croy, L. K. Ono, L. Li, J. C. Yang, A. I. Frenkel and B. Roldan Cuenya, J. Am. Chem. Soc., 2010, 132, 15714–15719 CrossRef CAS PubMed.
- M. Gerigk, P. Ehrenreich, M. R. Wagner, I. Wimmer, J. S. Reparaz, C. M. Sotomayor Torres, L. Schmidt-Mende and S. Polarz, Nanoscale, 2015, 7, 16969–16982 RSC.
- A. Navrotsky, Geochem. Trans., 2003, 4, 34–37 CrossRef.
- C. Magne, F. Dufour, F. Labat, G. Lancel, O. Durupthy, S. Cassaignon and Th. Pauporté, J. Photochem. Photobiol., A, 2012, 232, 22–31 CrossRef CAS.
- P. O. Andersson, C. Lejon, B. Ekstrand-Hammarström, C. Akfur, L. Ahlinder, A. Bucht and L. Österlund, Small, 2011, 7, 514–523 CrossRef CAS PubMed.
- M.-C. Daniel and D. Astruc, Chem. Rev., 2004, 104, 293–346 CrossRef CAS PubMed.
- J. Jancar, J. F. Douglas, F. W. Starr, S. K. Kumar, P. Cassagnau, A. J. Lesser, S. S. Sternstein and M. J. Buehler, Polymer, 2010, 51, 3321–3343 CrossRef CAS.
- R. J. Moon, A. Martini, J. Nairn, J. Simonsen and J. Youngblood, Chem. Soc. Rev., 2011, 40, 3941–3994 RSC.
- D. Ho, C.-H. K. Wang and E. K.-H. Chow, Sci. Adv., 2015, 1, e1500439 Search PubMed.
- K. S. Novoselov, V. I. Fal'ko, L. Colombo, P. R. Gellert, M. G. Schwab and K. Kim, Nature, 2012, 490, 192–200 CrossRef CAS PubMed.
- Z. Liu, X. Y. Ling, X. Su and J. Y. Lee, J. Phys. Chem. B, 2004, 108, 8234–8240 CrossRef CAS.
- R. R. Adzic, J. Zhang, K. Sasaki, M. B. Vukmirovic, M. Shao, J. X. Wang, A. U. Nilekar, M. Mavrikakis, J. A. Valerio and F. Uribe, Top. Catal., 2007, 46, 249–262 CrossRef CAS.
- E. F. Holby, W. Sheng, Y. Shao-Horn and D. Morgan, Energy Environ. Sci., 2009, 2, 865–871 CAS.
- P. Ragesh, V. A. Ganesh, S. V. Nair and A. S. Nair, J. Mater. Chem. A, 2014, 2, 14773–14797 CAS.
- A. G. Kolhatkar, A. C. Jamison, D. Litvinov, R. C. Willson and T. R. Lee, Int. J. Mol. Sci., 2013, 14, 15977–16009 CrossRef PubMed.
- H. Zhang, Z. Zheng, C. Ma, J. Zheng, N. Zhang, Y. Li and B. H. Chen, ChemCatChem, 2015, 7, 245–249 CrossRef CAS.
- A. S. Barnard, N. Young, A. I. Kirkland, M. A. van Huis and H. Xu, ACS Nano, 2009, 3, 1431–1436 CrossRef CAS PubMed.
- A. L. Gonzalez, C. Noguez and A. S. Barnard, J. Phys. Chem. C, 2012, 116, 14170–14175 CAS.
- A. S. Barnard, H. Konishi and H. Xu, Catal. Sci. Technol., 2011, 1, 1440–1488 CAS.
- A. S. Barnard and L. Y. Chang, ACS Catal., 2011, 1, 76–81 CrossRef CAS.
- A. S. Barnard, Catal. Sci. Technol., 2012, 2, 1485–1492 CAS.
- A. S. Barnard and H. Xu, ACS Nano, 2008, 2, 2237–2242 CrossRef CAS PubMed.
- A. S. Barnard, Energy Environ. Sci., 2011, 4, 439–443 CAS.
- A. S. Barnard, Cryst. Growth Des., 2013, 13, 5433–5441 CAS.
- R. Jin, Y. W. Cao, C. A. Mirkin, K. L. Kelly, G. C. Schatz and J. G. Zheng, Science, 2001, 294, 1901–1903 CrossRef CAS PubMed.
- G. P. Lee, Y. Shi, E. Lavoie, T. Daeneke, P. Reineck, U. B. Cappel, D. M. Huang and U. Bach, ACS Nano, 2013, 7, 5911–5921 CrossRef CAS PubMed.
- Y. Sun and Y. Xia, Science, 2002, 298, 2176–2179 CrossRef CAS PubMed.
- S. Y. Bae, H. W. Seo, H. C. Choi, J. Park and J. Park, J. Phys. Chem. B, 2004, 108, 12318–12326 CrossRef CAS.
- D. Wang and C. M. Lieber, Nat. Mater., 2003, 2, 355–356 CrossRef CAS PubMed.
- X. Peng, L. Manna, W. Yang, J. Wickham, E. Scher, A. Kadavanich and A. P. Alivisatos, Nature, 2000, 404, 59–61 CrossRef CAS PubMed.
- A. R. Tao, S. Habas and P. Yang, Small, 2008, 4, 310–325 CrossRef CAS.
- A. S. Barnard and Y. Chen, J. Mater. Chem., 2011, 21, 12239–12245 RSC.
- A. J. Biacchi and R. E. Schaak, ACS Nano, 2011, 5, 8089–8099 CrossRef CAS PubMed.
- A. S. Barnard, Acc. Chem. Res., 2012, 45, 1688–1697 CrossRef CAS PubMed.
- Microelectronics to Nanoelectronics: Materials, Devices & Manufacturability, ed. A. B. Kaul, CRC Press, 2012 Search PubMed.
- http://https://www.whitehouse.gov/mgi .
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- A. S. Barnard, Nanoscale, 2014, 8, 9983–9990 RSC.
- A. S. Barnard and H. F. Wilson, J. Phys. Chem. C, 2015, 119, 7969–7977 CAS.
- A. S. Barnard, J. Mater. Chem. A, 2015, 3, 60–64 CAS.
- H. Barron and A. S. Barnard, Catal. Sci. Technol., 2015, 5, 2848–2855 CAS.
- L. Lai and A. S. Barnard, J. Phys. Chem. C, 2014, 118, 30209–30215 CAS.
- H. Q. Shi, R. J. Rees, M. C. Per and A. S. Barnard, Nanoscale, 2015, 7, 1864–1871 RSC.
- R. Potyrailo, K. Rajan, K. Stoewe, I. Takeuchi, B. Chisholm and H. Lam, ACS Comb. Sci., 2011, 20, 579–633 CrossRef PubMed.
- R. F. Murphy, Nat. Chem. Biol., 2011, 7, 327–330 CrossRef CAS PubMed.
- M. Fernandez, N. R. Trefiak and T. K. Woo, J. Phys. Chem. C, 2003, 7, 14095–14105 Search PubMed.
- A. Cutler and L. Breiman, Technometrics, 1994, 36, 338–347 CrossRef.
- M. Mørup and L. K. Hansen, Neurocomputing, 2012, 80, 54–63 CrossRef.
- E. Stone and A. Cutler, Phys. D, 1996, 90, 209–224 CrossRef.
- S. Marinetti, L. Finesso and E. Marsilio, Infrared Phys. Technol., 2007, 49, 272–276 Search PubMed.
- G. C. Porzio, G. Ragozini and D. Vistocco, Appl. Stoch. Models Bus. Ind., 2008, 24, 419–437 CrossRef.
- P. Huggins, L. Pachter and B. Sturmfels, Bull. Math. Biol., 2007, 69, 2723–2735 CrossRef CAS PubMed.
- J. C. Thøgersen, M. Mørup, S. Damkiær, S. Molin and L. Jelsbak, BMC Bioinf., 2013, 4, 279 CrossRef PubMed.
- M. Fernandez and A. S. Barnard, ACS Nano, 2015, 9, 11980–11992 CrossRef CAS PubMed.
- M. Fernandez, T. K. Woo, C. E. Wilmer and R. Q. Snurr, J. Phys. Chem. C, 2013, 117, 7681–7689 CAS.
- A. Edwards, An introduction to linear regression and correlation, W. H. Freeman & Co., San Francisco, 1997 Search PubMed.
- J. R. Quinlan, C4.5: Programs for Machine Learning, Morgan Kaufmann Publishers, San Mateo, 1993 Search PubMed.
- D. W. Aha D. Kibler and M. K. Albert, Mach. Learn., 1991, 6, 37–66 Search PubMed.
- C. Bishop, Neural networks for pattern recognition, Oxford University Press, USA, 1995 Search PubMed.
- C. Cortes and V. Vapnik, Mach. Learn., 1995, 20, 273–297 Search PubMed.
- H. Holland, Adaption in natural and artificial systems, The University of Michigan Press, Ann Arbor, 1975 Search PubMed.
- M. Fernandez, H. Shi and A. S. Barnard, J. Chem. Inf. Model., 2015, 55, 2500–2506 CrossRef CAS PubMed.
- J. Inglese, R. L. Johnson, A. Simeonov, M. Xia, W. Zheng, C. P. Austin and D. S. Auld, Nat. Chem. Biol., 2007, 3, 466–479 CrossRef CAS PubMed.
- H. Li, M. Eddaoudi, M. O'Keeffe and O. M. Yaghi, Nature, 1999, 402, 276–279 CrossRef CAS.
- C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Nat. Chem., 2012, 4, 83–89 CrossRef CAS PubMed.
- http://https://github.com/shadanan/HadoopLink .
- http://https://data.csiro.au .
- http://nomad-repository.eu .
- http://https://www.materialsproject.org .
| This journal is © The Royal Society of Chemistry 2016 |
