 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanical meta-materials
Amir A.
Zadpoor
Additive Manufacturing Laboratory, Department of Biomechanical Engineering, Faculty of Mechanical, Maritime, and Materials Engineering, Delft University of Technology (TU Delft), Mekelweg 2, Delft 2628 CD, The Netherlands. E-mail: a.a.zadpoor@tudelft.nl; Fax: +31-15-2784717; Tel: +31-15-2781021
First published on 14th April 2016
Abstract
The emerging concept of mechanical meta-materials has received increasing attention during the last few years partially due to the advances in additive manufacturing techniques that have enabled fabricating materials with arbitrarily complex micro/nano-architectures. The rationally designed micro/nano-architecture of mechanical meta-materials gives rise to unprecedented or rare mechanical properties that could be exploited to create advanced materials with novel functionalities. This paper presents an overview of the recent developments in the area of mechanical meta-materials. Extremal materials that are extremely stiff in certain modes of deformation, while extremely soft in other modes of deformation are discussed first. Penta-mode, dilational, and other auxetic meta-materials are all discussed within the context of extremal materials. Negative meta-materials are presented next with special focus on materials with negative compressibility and negative stiffness. Ultra-property meta-materials are the topic of the following section that covers ultra-light, ultra-stiff, and ultra-tough materials. Finally, the emerging areas of research in mechanical meta-materials including active, adaptive, programmable, and origami-based mechanical meta-materials are reviewed. This paper concludes with some suggestions for future research.
1. Introduction
The mechanical properties of natural materials span a specific, limited range. A clear example is Poisson's ratio. Poisson's ratio of most engineered and natural materials known to date is positive with some notable exceptions.1 Moreover, the mechanical and physical properties of most natural materials are related to each other. For example, the elastic modulus and density (and thus porosity) of specific classes of materials including most cellular materials are related to each other through a power law.2 These constraints limit the design space and practical applications of natural materials. It is therefore desirable to develop materials that could exhibit an arbitrarily chosen set of mechanical and physical properties. Mechanical meta-materials aspire to do just that.Meta-materials are often made of purposefully designed micro-architectures that give rise to the desired set of mechanical properties. Since the mechanical properties of meta-materials are dependent on their micro/nano-scale structure, the design of meta-materials reduces the rational design of the micro/nano-scale structure that gives rise to the desired mechanical properties. In the spectrum from pure natural materials that possess intrinsic mechanical properties to large-scale structures that are characterized by highly design-specific structural properties, meta-materials are somewhere in between. When zooming in to look at their micro/nano-scale behavior, meta-materials behave more like structures. However, the overall homogenized behavior of meta-materials resembles that of materials. The homogenized macro-scale properties are, of course, highly dependent on the micro/nano-scale structure that could be designed such that the resulting meta-materials exhibit an unusual, rare, or unprecedented range of physical and mechanical properties.
Meta-materials were initially used in the context of optics and electromagnetism.3–7 That is why the term meta-material is sometimes understood as a specific term referring to optical and electromagnet meta-materials. The concept of “mechanical meta-materials” has emerged during the last few years and is relatively less explored. Specific classes of mechanical meta-materials were already known since a few decades ago. For example, the concept of auxetic materials (materials with a negative Poisson's ratio) has been known to scientists for a few decades and specific examples of such materials have been observed, built, tested, and reported.1 Many other classes of meta-materials with an unusual set of mechanical properties have been recently identified through a systematic study of the possible range of mechanical properties that could be obtained through geometrical design of micro/nano-architectures.
In this paper, we will particularly focus on meta-materials with a rare or unprecedented range of elastic mechanical properties including both the linear elastic behavior described by the elasticity tensor and the nonlinear behavior observed in the large deformation range. In what follows, we will explore the different categories of mechanical meta-materials including extremal materials, negative materials (i.e. materials with negative moduli), and some emerging classes of meta-materials including the active/programmable meta-materials and meta-materials based on the ancient Japanese art of paper folding (i.e. origami). We will conclude by suggesting some likely directions for future research.
2. Extremal materials
Extremal materials were introduced by Milton and Cherkaev in 19958 and are defined as materials that are extremely stiff in certain modes of deformation, while extremely compliant in other modes. The eigenvalues of the elasticity tensor determine the behavior of extremal materials under any given mode of deformation and are either very large (i.e. approach infinity) or are very small (i.e. approach zero). A very small eigenvalue indicates that the material is very compliant when subjected to deformation in the direction (i.e. eigenvector) corresponding to that particular eigenvalue. Extremal materials can therefore be categorized based on their number of very small eigenvalues of the elasticity tensor. If an extremal meta-material has only one very small eigenvalue, it is called unimode. If it has two, three, four, or five very small eigenvalues, it is called bimode, trimode, quadramode, or penta-mode, respectively.8 Milton and Cherkaev8 showed that specific combinations of two phases – one very complaint and the other very stiff – could be used to fabricate extremal materials. The extremal materials could then be combined to fabricate materials with any given elasticity tensor that satisfies the usual thermodynamics admissibility criteria (i.e. materials with positive definite elasticity tensors).8 This is an important result, because in addition to composite materials that could combine very compliant and very stiff materials, one could simply use 3D printing techniques to achieve any material with positive definite elasticity tensors simply by combining void space (i.e. very complaint material) with a stiff 3D-printed material (e.g. metals and metallic alloys). Two specific categories of extremal materials, namely penta-mode meta-materials and dilational materials, have received particular attention in the literature and will be discussed below.2.1. Penta-mode meta-materials
Penta-mode meta-materials have five very small eigenvalues, meaning that they are very compliant in five out of six principal directions. This translates to a very large bulk modulus, B, as compared to their shear modulus, G. Very large values of the bulk modulus mean that the volume of penta-mode meta-materials does not change as a result of deformation, which is the same as saying that the Poisson ratio of meta-materials is 0.5. Very small values of the shear modulus mean that ideal penta-mode meta-materials will immediately flow away, a behavior which is similar to fluids and has earned penta-mode meta-materials the name ‘meta-fluids’.9A specific design of penta-mode meta-materials was proposed by Milton and Cherkaev in 1995,8 in which beams with a specific type of variable cross-section, i.e. two conical beams attached to each other at their bases, were arranged in a diamond-type lattice structure (Fig. 1). This type of penta-mode lattice structure was not realized until 2012 when Wegener and co-workers used 3D printing techniques to fabricate and test approximations of the penta-mode meta-materials from polymers.9 The 3D printed meta-materials at the micro-9 or macro-scale10 are all approximations of the ideal penta-mode meta-materials, because the apex of the cone has a finite diameter in actual realizations of penta-mode meta-materials as opposed to the zero diameter in the ideal penta-mode. Generalizations of penta-mode meta-materials to anisotropic cases11,12 and to Bravais lattice structures other than diamond13 have also been reported.
 | ||
| Fig. 1 A specific design of penta-mode meta-materials proposed by Milton and Cherkaev8 was first realized in 20129 (Reprinted from ref. 9 with the permission of AIP Publishing) (a) and the first metallic penta-mode meta-material based on the same design and manufactured at Additive Manufacturing Laboratory of TU Delft using selective laser melting (Medical Delta © de Beeldredacteur) (b). | ||
A specific point about lattice structures based on penta-mode meta-materials is that any stress flowing through the lattice structure has to be transferred through the apex of the cones.14 Increasing the diameter of the cone therefore has a minimal influence in terms of increasing the stiffness of the lattice structure, while significantly influencing the mass density of the lattice structure. The mass density of penta-mode meta-materials could therefore be decoupled from their stiffness. This is different from most porous materials and lattice structures where there is a power law relationship (the so-called Ashby plot15) between the mass density and the elastic modulus of the structure.
The specific properties of penta-mode meta-materials make them attractive for several applications. For example, they could be used for steering elastodynamic waves in specific directions so as to achieve the equivalent of optical cloaking for acoustic waves.9,10 The fact that the elastic modulus and mass density (or porosity) of penta-mode meta-materials can be changed independently from each other makes them useful for extending the design space when designing porous tissue engineering scaffolds where the pore size and porosity have consequences in terms of cell attachment, cell nutrition/oxygenation, and rate of tissue regeneration.16,17 Moreover, by combining penta-mode meta-materials within the same lattice structure, one could make lattice structures with any positive definite elasticity tensor.8 This makes penta-mode meta-materials a general framework within which meta-materials can be designed and (additively) manufactured. This is particularly useful for realizing materials with complex distribution of mechanical properties. The complex distribution of the mechanical properties may have resulted, for example, from application of topology optimization algorithms.
It is important to realize that the penta-mode structure proposed by Milton and Cherkaev8 is not the only type of penta-mode meta-material. A completely different example of penta-mode materials is a gel that can be easily deformed in any given direction but strongly resists changes in volume under hydrostatic pressure.18 Other examples include granular materials.19
2.2. Dilational and other auxetic meta-materials
The relationship between the bulk modulus, B, shear modulus, G, and Poisson' ratio, ν, of isotropic materials can be written as follows:20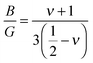 | (1) |
Various structures are proposed for creating dilational meta-materials. Milton has recently reviewed dilational structures and has offered some new examples of dilational meta-materials.21 The earlier designs of dilational materials were based on sliding surfaces,22 while later models18–20,23–26 used various other constructions of which one is presented in Fig. 2. Cabras and Brun19 enumerated a number of compressible materials whose shape is difficult to change including certain molecular structures27–29 and re-entrant foams.30,31
 | ||
| Fig. 2 A three-dimensional dilational elastic meta-material realized at macroscopic (a) and microscopic (b and c) scales using various additive manufacturing techniques (Reprinted from ref. 20). | ||
Materials with negative Poisson's ratio are broader than only dilational materials. Indeed, any material with a negative Poisson ratio is called an auxetic material. The term ‘auxetic’ originates from the Greek word ‘auxeis’ that means ‘to increase and grow’.19 According to Cabras and Brun,19 this term was first used by Evans32,33 to describe materials that expand in the direction perpendicular to the tensile loading direction. Auxetic materials are perhaps the most widely studied meta-materials, see e.g.ref. 34–41. An excellent review paper has been recently published that covers the different aspects of auxetic materials and their properties.1 Auxetic materials in general and dilational materials in particular have improved resistance against damage, as a result of their capability to distribute stress over a larger part of the material.19 Cabras and Brun19 summarized the useful properties of auxetic materials such as improved indentation resistance and better acoustic/vibration properties and discussed the areas where auxetic materials are applied including an “efficient membrane filter with variable permeability, fasteners, shape memory materials and acoustic dampers”.
3. Negative meta-materials
Negative meta-materials are meta-materials with negative moduli such as the negative bulk modulus or negative elastic modulus. Exhibiting negative moduli is a whole new level of anomaly in the mechanical behavior of meta-materials compared to what we have seen up to now. That is because we have so far assumed that the elasticity tensor should be positive definite, which means that both the bulk modulus and the shear modulus should be positive. This condition has been considered the necessary condition for an elasticity tensor to be thermodynamically admissible for many years by most researchers studying continuum mechanics. The thermodynamic argument behind this condition is that negative compressibility or negative stiffness results in unstable materials. Materials with negative compressibility or negative stiffness have been, nevertheless, observed under various experimental conditions. Such materials could have many applications, if their stability can be ensured. Lakes and Wojciechowski42 argued that even though an unconstrained material with negative moduli may not be stable, a constrained material with negative moduli can very well be stable. They argued that the elasticity tensor of constrained materials does not need to be positively definite in order to be stable, as the requirements for the stability and uniqueness of the solution are strong ellipticities in the case of constrained materials.42 Strong ellipticity imposes the following less stringent conditions for stability:42| −∞ < E < ∞ or −4G/3 < K < ∞ | (2) |
The negative properties of materials include negative thermal expansion that has been identified in many oxides44,45 and cellular solids46 but are not discussed here, because this paper mostly focuses on the pure mechanical behavior of meta-materials.
3.1. Negative compressibility
The most general definition of compressibility distinguishes between three types of compressibilities, namely line, area, and volume compressibility. Line, area, and volume compressibilities are, respectively, defined as the change in the length, the area, and the volume of a material under hydrostatic pressure. Negative compressibility basically means that a material expands in response to hydrostatic pressure. Depending on the number of dimensions along which the expansion occurs, the material may have a negative length, area, or volume compressibility. The thermodynamic arguments mentioned above regarding the negative compressibility mostly refer to the volume compressibility. Length and area compressibility may be admissible even within the conventional context of thermodynamic restrictions.Crystals with negative line and area compressibility have been identified47 including recent discovery of negative linear compressibility in methanol monohydrate, which is a relatively simple molecular crystal and shows negative linear compressibility along with negative and anisotropic thermal expansion.48
In addition to crystals, a number of other systems exhibit negative compressibility that could be categorized into four major categories.49 In the first category of these materials, the geometry of cellular structures is the cause of negative compressibility.50,51 For example, hexagonal honeycombs show negative linear compressibility in 2D,50 while lattice structures made from an elongated hexagonal dodecahedron are 3D geometries that exhibit negative Poisson's ratio and negative compressibility.51 Tetragonal beam structures also show negative linear compressibility.47 The second category of meta-materials with negative compressibility owes this property to the combination of two materials with different mechanical properties. An example of such an engineered material has been presented by Gatt and Grima.43 The same researchers proposed a truss-type structure composed of multiple materials.52 The proposed structure shows negative linear compressibility and in some cases even negative area and volumetric compressibilities. The negative compressibility of the third category of such materials is caused by specific constraints.42,53 Finally, bulk materials that could potentially exhibit negative compressibility have recently received attention.54,55 Particular types of (bi-stable) potential functions could cause negative compressibility in such materials. The important point about this last category of materials is that negative compressibility is a property of the bulk material and not the way the geometry of the material is organized. The research on this type of material has been so far largely theoretical.
Studies that report negative volumetric compressibility are relatively rare. Most instances of negative volumetric compressibility mentioned above are reported in theoretical or computational studies. In an interesting study where negative volumetric compressibility was clearly observed, open-cell foams were pre-strained under hydrostatic pressure (Fig. 3).56 Beyond ≈20% strain, the specimens expanded as the hydrostatic pressure increased, clearly showing negative volumetric compressibility.56
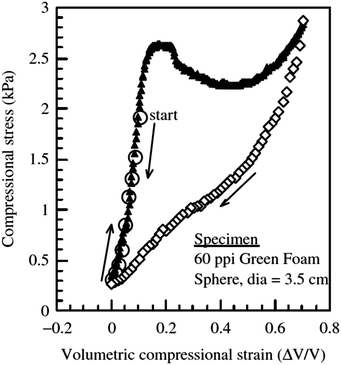 | ||
| Fig. 3 Negative incremental compressibility observed in foams mechanically tested under hydrostatic pressure56 (Reprinted from B. Moore, T. Jaglinski, D. Stone and R. Lakes, Negative incremental bulk modulus in foams, Philos. Mag. Lett., 2006, 86, 651–659 by permission of Taylor & Francis Ltd, http://www.tandfonline.com, http://www.informaworld.com). | ||
Several applications have been proposed for materials with negative compressibility49,54,57–59 including protection of sensors and other sensitive instruments in deep ocean applications when compression needs to be avoided,57,58 study of muscles,59 and micro-electro-mechanical systems.49
3.2. Negative stiffness
Materials with positive stiffness deform in the direction of applied force and form a restoring force that tries to restore the original shape of the deformed material, thereby resisting deformation. Materials with negative stiffness, on the other hand, deform in a direction opposite to the direction of the applied force and form an assisting force, thereby assisting the deformation. Negative stiffness materials therefore experience larger deformations as compared to positive stiffness materials, when subjected to comparable loading conditions. That is the reason materials with negative stiffness are assumed to be unstable unless they are constrained. Materials with negative stiffness can, however, be combined with or embedded within positive stiffness materials or be otherwise constrained for stabilization. In a number of studies,60–63 Lakes and co-workers have shown that combinations of materials with positive and negative stiffness offer extraordinary properties such as extremely high damping coefficients.Perhaps the simplest system that could show negative stiffness is a planar beam buckled under compression.64,65 A force applied laterally could reduce the lateral deflection of the buckled beam and even restore the original non-buckled shape of the beam. Increasing the lateral force further will cause the beam to deflect in the opposite direction. There are exactly three states where maintaining the position of the beams requires no lateral force: both buckled states of the beam in two possible directions and the original straight position of the beam. There is, however, a fundamental difference between the buckled states of the beam on the one hand and the original position of the beam on the other hand. The first two positions are the stable equilibriums of the system, meaning that slight perturbations around these positions create forces that restore the equilibrium. The original position is, however, unstable, meaning that a slight perturbation will cause the system to move further and further away from this equilibrium. If the lateral force is replaced by a constraint, one can see that the beam immediately snaps through to a new shape, once the constraint is removed. This snap-through behavior is the hallmark of negative stiffness systems.65 The behavior described above can be explained in terms of the potential energy of the deflected beam. If the potential energy of the deflected beam is plotted as a function of the applied lateral force,64 it shows three extremum points corresponding to the three above-mentioned states of the buckled beam.66 The first derivative of the potential function with respect to lateral displacement is zero in all of these extremum points. The second derivative of the potential function with respect to displacement, which equals the stiffness of the system is, however, different for the stable and non-stable equilibrium points of the system. While the second derivative is positive for both buckled states of the beam, it is negative for the original non-buckled position. The buckled positions of the beam, thus, correspond to the local minima of the potential function, while the original non-buckled position corresponds to a local maximum of the potential function.
In addition to systems with buckled states that are known to exhibit negative stiffness, other materials with negative stiffness have been reported in the literature. Many of the materials that exhibit negative stiffness are associated with some types of bi-stable (having two stable states) and snap-through behaviors. For example, materials that undergo volume-change phase transformation such as barium titanate67 or ferroelastic materials such as vanadium dioxide62 could show the negative stiffness behavior primarily due to their energy storing capability. In addition, new types of negative stiffness behavior, e.g. “discontinuous buckling”,68 continue to be discovered in systems that comprise buckled elements.
One of the most important applications of negative stiffness materials is achieving high damping and high stiffness at the same time. The commonly used engineering materials with high stiffness usually do not have high damping ratios, while engineering materials with high damping ratios are generally compliant. It is therefore very challenging to achieve both properties at the same time. One solution would be to make composites of both types of materials to achieve both properties to some extent. For example, polymeric materials with a high damping ratio may be reinforced with stiff inclusions that increase the stiffness of the composite. The problem is that the stiffness and damping coefficients of these composites will be somewhere between those of their constituting materials. The solution proposed by Lakes and co-workers60–62 was to embed negative stiffness materials as inclusions in a positive stiffness matrix. Since negative stiffness materials are unstable on their own, their inclusion in a positive stiffness matrix ensures their stability. Indeed, it has been shown that the presence of a sufficiently stiff matrix could stabilize a composite containing negative stiffness inclusions.69 On the other hand, the resulting composite is shown to achieve very high damping coefficients and stiffness values that by far exceed those of the constituting materials.60–62 Materials that simultaneously have high damping coefficients and high stiffness could be used for applications such as vibration isolation.
Another somewhat related application is the use of meta-materials for transformation acoustic applications such as acoustic cloaking that we discussed also in the context of penta-mode meta-materials (see Section 2.1). Meta-materials with negative stiffness together with other categories of meta-materials that show anisotropic and negative effective mass tensors are shown to offer clear advantages for acoustic cloaking and other transformation acoustic applications.70,71
Materials with extremely high stiffness values can be made with a particular arrangement of negative stiffness and positive stiffness elements.65,72 If a negative stiffness material with the stiffness k− were used in series with a positive stiffness material with the stiffness k+, the equivalent stiffness of the construction would be 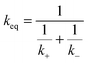 . When the absolute values of the positive and negative stiffness materials approach the same value, the equivalent stiffness of the combined system approaches infinity that in practice means extremely high stiffness values. However, the series construction of negative and positive stiffness materials is unstable and needs to be stabilized for practical applications.65 Kochmann and Milton have recently presented some mathematically rigorous bounds for the elastic moduli of the composites that incorporate negative stiffness constituents. Those boundaries need to be respected in order to make sure that the composites are stable.73
. When the absolute values of the positive and negative stiffness materials approach the same value, the equivalent stiffness of the combined system approaches infinity that in practice means extremely high stiffness values. However, the series construction of negative and positive stiffness materials is unstable and needs to be stabilized for practical applications.65 Kochmann and Milton have recently presented some mathematically rigorous bounds for the elastic moduli of the composites that incorporate negative stiffness constituents. Those boundaries need to be respected in order to make sure that the composites are stable.73
Many more applications of negative stiffness materials could be found in the literature including vehicle vibration protection systems,74,75 seismic protection of structures,76 and rail-road vibration isolation.77
4. Ultra-property meta-materials
An ideal material for many structural applications would simultaneously possess two or more of the following properties: high stiffness, high strength, high toughness, and low mass density. Due to their conflicting nature, it is difficult or impossible to combine some of the above-mentioned properties in most engineering materials used for structural applications today. For example, it is well known that there is a conflict between toughness and strength.78 Biological materials such as nacre can achieve high stiffness, high strength, and high toughness all at the same time due to their hierarchical and “staggered microstructure”.78,79 Learning from nature, many researchers have been recently trying to develop meta-materials with rationally designed architectures that give rise to ultra-stiff, ultra-strong, ultra-tough, and ultra-light meta-materials.Ashby plots (Fig. 4) are useful tools that could be used for comparing the properties of different materials with each other and for choosing/designing the right material for any given application. For example, the elastic modulus of materials could be plotted vs. mass density or strength could be plotted vs. toughness. Ashby plots allow for easy comparison of different (categories of) materials and for putting the properties of ultra-property meta-materials in perspective. Some examples of ultra-property meta-materials recently reported in the literature are presented here for demonstration. More examples can be found in the literature.
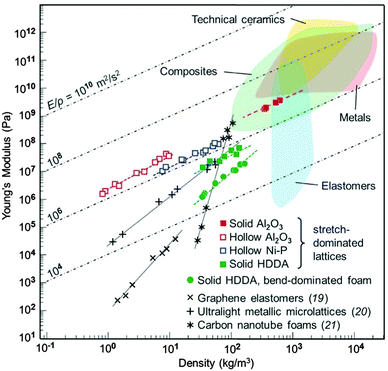 | ||
| Fig. 4 Different designs of ultra-light ultra-stiff meta-materials based on various types of repeating unit cells. Ashby plots are used to compare the mechanical properties of the meta-materials based on different designs and materials with each other and with other categories of materials82 (from X. Zheng, H. Lee, T. H. Weisgraber, M. Shusteff, J. DeOtte, E. B. Duoss, et al., Ultralight, ultrastiff mechanical metamaterials, Science, 2014, 344, 1373–1377. Reprinted with permission from AAAS). | ||
Meza et al. recently demonstrated ultra-strong and ultra-light meta-materials made from ceramics using two-photo lithography, atomic layer deposition, and oxygen plasma etching at the nano-scale.80 Despite being made from a brittle material, i.e. alumina, the nano-lattices exhibited recoverable deformation even when the meta-materials were compressed beyond 50% strain.80 The specific architecture of the lattices and the thickness to the radius ratio of the hollow tubes that made the nano-lattices were found to govern the mechanical behavior of those meta-materials.80
Jang et al. reported very high strength values up to 1.75 GPa in a related study that used rationally designed meta-materials for achieving ultra high values of mechanical properties.81 The integrity of meta-materials was preserved after undergoing multiple loading cycles.
Finally, Zheng et al. reported meta-materials with “a nearly constant stiffness per unit mass density”82 (Fig. 4). The stiffness of most materials rapidly decreases as the mass density approaches smaller values. The micro-lattices presented in the study by Zhang et al.82 showed an almost constant stiffness per unit mass density even when the mass density was reduced by three orders of magnitude (Fig. 4).82 This is a remarkable combination of high stiffness and low density that has been rarely observed elsewhere.
5. Emerging areas
Previous sections covered the various categories of mechanical meta-materials with a clear focus on their elastic behavior in general and elasticity tensor in particular. In this section, we will present a number of emerging paradigms in design, manufacturing, and analysis of mechanical meta-materials that have received a lot of attention recently and were not covered in the previous sections.5.1. Active, adaptive, and programmable meta-materials
Three recurrent themes in active, adaptive, and programmable meta-materials are the use of soft materials, large deformations, and instability. Various designs of mechanical meta-materials have been proposed using clever combinations of the three above-mentioned concepts with rationally designed geometries that could, for example, harness the instability of soft materials in the nonlinear deformation range so as to achieve unprecedented or rarely seen properties and functionalities.Extending the considered range of deformations to the large deformation range is a distinct feature of this type of study. This is a necessity and opportunity once soft materials are used for design and manufacturing of mechanical meta-materials. The first natural question to ask is ‘what kind of material property can be realized in the nonlinear range of deformation?’ Although no clear answer similar to what was presented for the elastic range8 can be given for the nonlinear range, general approaches based on topology optimization have been presented for designing materials that demonstrate prescribed properties in the finite deformation range.83
Active and programmable mechanical meta-materials are concepts that have primarily emerged from research on the instability regimens of soft and patterned materials. Extreme levels of programmability based on blocks that could perform mathematical operations such as spatial differentiation, integration, and convolution have been achieved in electromagnetic meta-materials.84 Although the same level of programmability is yet to be shown for mechanical meta-materials, the idea of active and programmable meta-materials has spread to the mechanical meta-materials community too. Cellular solids made from soft materials and confined laterally are found to show some level of programmability in their mechanical behavior as well as multi-stability and “giant hysteresis”.85
Switching, activating, adapting, or regulating the mechanical behavior of meta-materials and their associated functionalities are the main purposes of another category of meta-materials. Prescribing and controlling the instability modes of meta-materials is the most widely used strategy for achieving those purposes. Two- and three-dimensional cellular soft solids are often used for regulating the instability behavior of materials86–89 (Fig. 5), because the geometry of the pores and their sizes could be used not only for changing the instability thresholds but also for regulating the instability types and patterns sometimes fully independent of the mechanical properties of the bulk material from which they are made.90 Various instability patterns and the way they break the applicable symmetries lead to distinct mechanical properties and functionalities. If one could, for example, control the instability modes of a (multi-stable) meta-material or at least prescribe it through the rational design of the cellular structure, one could control the functionality of the meta-material and activate specific modes of instability when required. That is the main idea behind the design of active/adaptive meta-materials which is often supplemented with other novel approaches such as coupled gyroscopes on a lattice91 or utilizing the so-called “soft modes” that function as possible building blocks for smart soft actuators.92
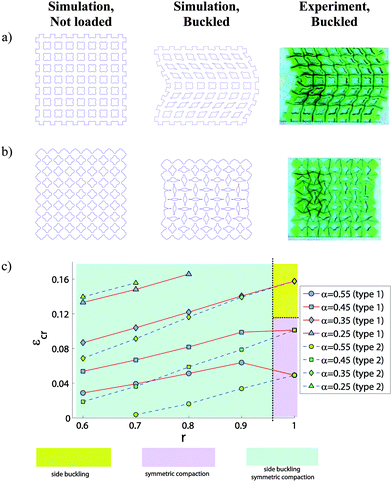 | ||
| Fig. 5 Some design of cellular soft matter shows instability thresholds and instability patterns that could be fully controlled by geometry regardless of the mechanical properties of the bulk materials from which they are made.90 In this specific design, the instability patterns may be side-buckling (a) or compaction (b) depending on the shape of the pores. An instability map could be used to relate various geometrical parameters to the instability patterns (c) (Reprinted from ref. 90). | ||
5.2. Origami-based meta-materials
The ancient Japanese art of paper folding has recently emerged as a new design and manufacturing paradigm that could be used for different applications including self-folding robots,93 medical stents,94 active and deployable structures,95 and mechanical meta-materials.96 In these applications, the concept of “paper” is extended to include various types of initially flat materials that could be folded or activated to self-fold to a desired (three-dimensional) shape. Depending on the design of the crease and folding patterns, the resulting folded three-dimensional structure will have different geometries, mechanical properties, and functionalities. A sub-category of origami structures, called rigid origami, has so far received the most attention. In rigid origami, the folding lines could be considered as kinematic joints. Therefore, the process of folding a particular “paper” to the desired origami shape reduces to a kinematic process with a number of constraints. The different parts of the paper joined by the kinematic joints are assumed to remain undeformed as a result of the applied folds. Pure origami always starts from a square sheet of paper and is supposed to complete without any in cuts in the paper or any use of glue. However, many practical applications of the origami concept relax those constraints. A closely related concept called kirigami allows for cuts to be made to the paper.Miura-ori origami is perhaps the most widely studied type of origami structures (Fig. 6). Mechanical meta-materials created based on (some variants of) the Miura-folded origami have been, for example, shown to exhibit negative (in-plane) Poisson's ratios.96–98 Some variants of the Miura-ori origami have been used for developing reprogrammable mechanical meta-materials.99 Another study has shown that specific designs of Miura-ori origami tubes could be used for obtaining stiff and reconfigurable mechanical meta-materials.100 Origami-like structures have shown to demonstrate some other features of mechanical meta-materials such as bi-stability101 and multi-stability.102 Overall, combining the features of origami structures such as low weight, design flexibility, and alternative manufacturing possibilities with the anomalous properties shown by mechanical meta-materials is a promising area of research that is expected to deliver new categories of meta-materials and novel features not seen in other types of mechanical meta-materials.
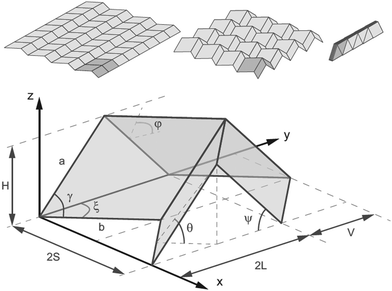 | ||
| Fig. 6 The geometrical design of Miura-ori origami structures. Several geometrical parameters determine the shape of the folds (Reprinted from ref. 98). | ||
6. Future directions
The emerging areas discussed in the previous section present a roadmap for the future directions of research on mechanical meta-materials for years to come. In particular, extending the study of the mechanical behavior of mechanical meta-materials to the nonlinear range of deformations and to soft meta-materials is expected to receive more attention during the next years. There seems to be a general consensus in the community that there are many possible designs of soft nonlinear meta-materials that have not been discovered yet and could present opportunities for researchers.The advances in 3D printing and additive manufacturing techniques have also provided research opportunities that may be explored by many researchers in the coming years. Many of the designs of meta-materials discussed in the previous sections were only studied theoretically or computationally. The widespread availability of advanced 3D printing and additive manufacturing machines and services should enable researchers to realize the previously proposed theoretical concepts and experimentally observe the mechanical behavior of the resulting meta-materials. Of particular importance are multi-material 3D printing techniques that could start new paradigms in the design of mechanical meta-materials. For example, the spatial distribution of materials with different mechanical properties could be combined with rationally designed micro-architecture when designing mechanical meta-materials. 3D printing of soft materials is another emerging area that could further enrich the possibilities for design and manufacturing of active, adaptable, and programmable meta-materials.
In addition to 3D printing, other design and production paradigms such as origami and kirigami need to be further explored. A number of very innovative designs of mechanical meta-materials based on those concepts have been already proposed and more novel concepts are expected to result from further research in those directions.
Another aspect that has not received much attention is the fatigue behavior of mechanical meta-materials. The vast majority of previous studies have focused on the static, quasi-static or specific types of dynamic behaviors of mechanical meta-materials. However, actual use of mechanical meta-materials for structural applications requires a thorough study of their fatigue behavior, which is proposed as a possible avenue for future research.
Overall, the years ahead are expected to be exciting years for research on mechanical meta-materials given the widespread availability of advanced design techniques such as topology optimization and the ever increasing possibilities offered by a wide range of rapidly evolving additive manufacturing techniques.
References
- G. N. Greaves, A. Greer, R. Lakes and T. Rouxel, Poisson's ratio and modern materials, Nat. Mater., 2011, 10, 823–837 CrossRef CAS PubMed.
- L. J. Gibson and M. F. Ashby, Cellular solids: structure and properties, Cambridge University Press, 1997 Search PubMed.
- H. Chen, C. Chan and P. Sheng, Transformation optics and metamaterials, Nat. Mater., 2010, 9, 387–396 CrossRef CAS PubMed.
- H.-T. Chen, J. F. O'Hara, A. K. Azad, A. J. Taylor, R. D. Averitt and D. B. Shrekenhamer, et al., Experimental demonstration of frequency-agile terahertz metamaterials, Nat. Photonics, 2008, 2, 295–298 CrossRef CAS.
- C. M. Soukoulis and M. Wegener, Optical metamaterials—more bulky and less lossy, Science, 2010, 330, 1633–1634 CrossRef CAS PubMed.
- J. Valentine, S. Zhang, T. Zentgraf, E. Ulin-Avila, D. A. Genov and G. Bartal, et al., Three-dimensional optical metamaterial with a negative refractive index, Nature, 2008, 455, 376–379 CrossRef CAS PubMed.
- Y. Zhao, M. Belkin and A. Alù, Twisted optical metamaterials for planarized ultrathin broadband circular polarizers, Nat. Commun., 2012, 3, 870 CrossRef CAS PubMed.
- G. W. Milton and A. V. Cherkaev, Which elasticity tensors are realizable?, J. Eng. Mater. Technol., 1995, 117, 483–493 CrossRef.
- M. Kadic, T. Bückmann, N. Stenger, M. Thiel and M. Wegener, On the practicability of pentamode mechanical metamaterials, Appl. Phys. Lett., 2012, 100, 191901 CrossRef.
- R. Schittny, T. Bückmann, M. Kadic and M. Wegener, Elastic measurements on macroscopic three-dimensional pentamode metamaterials, Appl. Phys. Lett., 2013, 103, 231905 CrossRef.
- M. Kadic, T. Bückmann, R. Schittny and M. Wegener, On anisotropic versions of three-dimensional pentamode metamaterials, New J. Phys., 2013, 15, 023029 CrossRef.
- C. N. Layman, C. J. Naify, T. P. Martin, D. C. Calvo and G. J. Orris, Highly anisotropic elements for acoustic pentamode applications, Phys. Rev. Lett., 2013, 111, 024302 CrossRef PubMed.
- G. F. Méjica and A. D. Lantada, Comparative study of potential pentamodal metamaterials inspired by Bravais lattices, Smart Mater. Struct., 2013, 22, 115013 CrossRef.
- M. Kadic, T. Bückmann, R. Schittny, P. Gumbsch and M. Wegener, Pentamode metamaterials with independently tailored bulk modulus and mass density, Phys. Rev. Appl., 2014, 2, 054007 CrossRef.
- M. F. Ashby and D. Cebon, Materials selection in mechanical design, J. Phys. IV, 1993, 3, C7-1–C7-9 Search PubMed.
- C. M. Murphy, M. G. Haugh and F. J. O'Brien, The effect of mean pore size on cell attachment, proliferation and migration in collagen–glycosaminoglycan scaffolds for bone tissue engineering, Biomaterials, 2010, 31, 461–466 CrossRef CAS PubMed.
- A. A. Zadpoor, Bone tissue regeneration: the role of scaffold geometry, Biomater. Sci., 2015, 3, 231–245 RSC.
- G. W. Milton, Complete characterization of the macroscopic deformations of periodic unimode metamaterials of rigid bars and pivots, J. Mech. Phys. Solids, 2013, 61, 1543–1560 CrossRef.
- L. Cabras and M. Brun, Auxetic two-dimensional lattices with Poisson's ratio arbitrarily close to—1, Proc. R. Soc. A, 2014, 20140538 CrossRef.
- T. Bückmann, R. Schittny, M. Thiel, M. Kadic, G. W. Milton and M. Wegener, On three-dimensional dilational elastic metamaterials, New J. Phys., 2014, 16, 033032 CrossRef.
- G. W. Milton, New examples of three-dimensional dilational materials, Phys. Status Solidi B, 2015, 252, 1426–1430 CrossRef CAS.
- G. W. Milton, Composite materials with Poisson's ratios close to—1, J. Mech. Phys. Solids, 1992, 40, 1105–1137 CrossRef.
- L. Cabras, M. Brun, A class of auxetic three-dimensional lattices, 2015, arXiv preprint arXiv:150604919.
- H. Mitschke, G. Schröder-Turk, K. Mecke, P. Fowler and S. Guest, Symmetry detection of auxetic behaviour in 2D frameworks, EPL, 2013, 102, 66005 CrossRef CAS.
- H. Mitschke, J. Schwerdtfeger, F. Schury, M. Stingl, C. Körner and R. F. Singer, et al., Finding auxetic frameworks in periodic tessellations, Adv. Mater., 2011, 23, 2669–2674 CrossRef CAS PubMed.
- D. Prall and R. Lakes, Properties of a chiral honeycomb with a Poisson's ratio of—1, Int. J. Mech. Sci., 1997, 39, 305–314 CrossRef.
- R. H. Baughman, J. M. Shacklette, A. A. Zakhidov and S. Stafström, Negative Poisson's ratios as a common feature of cubic metals, Nature, 1998, 392, 362–365 CrossRef CAS.
- L. J. Hall, V. R. Coluci, D. S. Galvão, M. E. Kozlov, M. Zhang and S. O. Dantas, et al., Sign change of Poisson's ratio for carbon nanotube sheets, Science, 2008, 320, 504–507 CrossRef CAS PubMed.
- A. Yeganeh-Haeri, D. J. Weidner and J. B. Parise, Elasticity of α-cristobalite: a silicon dioxide with a negative Poisson's ratio, Science, 1992, 257, 650–652 CAS.
- E. Friis, R. Lakes and J. Park, Negative Poisson's ratio polymeric and metallic foams, J. Mater. Sci., 1988, 23, 4406–4414 CrossRef CAS.
- R. Lakes, Foam structures with a negative Poisson's ratio, Science, 1987, 235, 1038–1040 CAS.
- K. Evans, M. Nkansah and I. Hutchinson, Molecular network design, Nature, 1991, 353, 124 CrossRef CAS.
- K. E. Evans, Auxetic polymers: a new range of materials, Endeavour, 1991, 15, 170–174 CrossRef CAS.
- S. Babaee, J. Shim, J. C. Weaver, E. R. Chen, N. Patel and K. Bertoldi, 3D Soft metamaterials with negative Poisson's ratio, Adv. Mater., 2013, 25, 5044–5049 CrossRef CAS PubMed.
- K. Bertoldi, P. M. Reis, S. Willshaw and T. Mullin, Negative Poisson's ratio behavior induced by an elastic instability, Adv. Mater., 2010, 22, 361–366 CrossRef CAS PubMed.
- S. Czarnecki and P. Wawruch, The emergence of auxetic material as a result of optimal isotropic design, Phys. Status Solidi B, 2015, 252, 1620–1630 CrossRef CAS.
- R. Gatt, L. Mizzi, J. I. Azzopardi, K. M. Azzopardi, D. Attard and A. Casha, et al., Hierarchical Auxetic Mechanical Metamaterials, Sci. Rep., 2015, 5 CAS.
- A. Pozniak, J. Smardzewski and K. Wojciechowski, Computer simulations of auxetic foams in two dimensions, Smart Mater. Struct., 2013, 22, 084009 CrossRef.
- S. Shan, S. H. Kang, Z. Zhao, L. Fang and K. Bertoldi, Design of planar isotropic negative Poisson's ratio structures, Extreme Mech. Lett., 2015, 4, 96–102 CrossRef.
- I. Shufrin, E. Pasternak and A. V. Dyskin, Negative Poisson's ratio in hollow sphere materials, Int. J. Solids Struct., 2015, 54, 192–214 CrossRef.
- M. Taylor, L. Francesconi, M. Gerendás, A. Shanian, C. Carson and K. Bertoldi, Low Porosity Metallic Periodic Structures with Negative Poisson's Ratio, Adv. Mater., 2014, 26, 2365–2370 CrossRef CAS PubMed.
- R. Lakes and K. Wojciechowski, Negative compressibility, negative Poisson's ratio, and stability, Phys. Status Solidi B, 2008, 245, 545–551 CrossRef CAS.
- R. Gatt and J. N. Grima, Negative compressibility, Phys. Status Solidi RRL, 2008, 2, 236–238 CrossRef CAS.
- G. Barrera, J. Bruno, T. Barron and N. Allan, Negative thermal expansion, J. Phys.: Condens. Matter, 2005, 17, R217 CrossRef CAS.
- A. W. Sleight, Negative thermal expansion, MRS Proceedings: Cambridge Univ Press, 2002. p. DD10. 6.
- R. Lakes, Cellular solids with tunable positive or negative thermal expansion of unbounded magnitude, Appl. Phys. Lett., 2007, 90, 221905 CrossRef.
- D. Barnes, W. Miller, K. E. Evans and A. Marmier, Modelling negative linear compressibility in tetragonal beam structures, Mech. Mater., 2012, 46, 123–128 CrossRef.
- A. D. Fortes, E. Suard and K. S. Knight, Negative linear compressibility and massive anisotropic thermal expansion in methanol monohydrate, Science, 2011, 331, 742–746 CrossRef CAS PubMed.
- J. N. Grima and R. Caruana-Gauci, Mechanical metamaterials: materials that push back, Nat. Mater., 2012, 11, 565–566 CrossRef CAS PubMed.
- J. N. Grima, D. Attard, R. Caruana-Gauci and R. Gatt, Negative linear compressibility of hexagonal honeycombs and related systems, Scr. Mater., 2011, 65, 565–568 CrossRef CAS.
- J. N. Grima, R. Caruana-Gauci, D. Attard and R. Gatt, Three-dimensional cellular structures with negative Poisson's ratio and negative compressibility properties, Proc. R. Soc. A, 2012, 3121–3138 CrossRef.
- J. N. Grima, D. Attard and R. Gatt, Truss-type systems exhibiting negative compressibility, Phys. Status Solidi B, 2008, 245, 2405–2414 CrossRef CAS.
- T. S. Maruszewski and K. W. Wojciechowski, Anomalous deformation of constrained auxetic square, Rev. Adv. Mater. Sci., 2010, 23, 169–174 Search PubMed.
- M. Chen and E. Karpov, Bistability and thermal coupling in elastic metamaterials with negative compressibility, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 033201 CrossRef CAS PubMed.
- Z. G. Nicolaou and A. E. Motter, Mechanical metamaterials with negative compressibility transitions, Nat. Mater., 2012, 11, 608–613 CrossRef CAS PubMed.
- B. Moore, T. Jaglinski, D. Stone and R. Lakes, Negative incremental bulk modulus in foams, Philos. Mag. Lett., 2006, 86, 651–659 CrossRef CAS.
- R. H. Baughman, S. Stafström, C. Cui and S. O. Dantas, Materials with negative compressibilities in one or more dimensions, Science, 1998, 279, 1522–1524 CrossRef CAS PubMed.
- A. B. Cairns, J. Catafesta, C. Levelut, J. Rouquette, A. Van Der Lee and L. Peters, et al., Giant negative linear compressibility in zinc dicyanoaurate, Nat. Mater., 2013, 12, 212–216 CrossRef CAS PubMed.
- M. Caruel, J.-M. Allain and L. Truskinovsky, Muscle as a metamaterial operating near a critical point, Phys. Rev. Lett., 2013, 110, 248103 CrossRef CAS PubMed.
- R. Lakes, Extreme damping in composite materials with a negative stiffness phase, Phys. Rev. Lett., 2001, 86, 2897 CrossRef CAS PubMed.
- R. Lakes, Extreme damping in compliant composites with a negative-stiffness phase, Philos. Mag. Lett., 2001, 81, 95–100 CrossRef CAS.
- R. Lakes, T. Lee, A. Bersie and Y. Wang, Extreme damping in composite materials with negative-stiffness inclusions, Nature, 2001, 410, 565–567 CrossRef CAS PubMed.
- Y. Wang and R. Lakes, Composites with inclusions of negative bulk modulus: extreme damping and negative Poisson's ratio, J. Compos. Mater., 2005, 39, 1645–1657 CrossRef CAS.
- T. Klatt and M. R. Haberman, A nonlinear negative stiffness metamaterial unit cell and small-on-large multiscale material model, J. Appl. Phys., 2013, 114, 033503 CrossRef.
- Y. Wang and R. Lakes, Extreme stiffness systems due to negative stiffness elements, Am. J. Phys., 2004, 72, 40–50 CrossRef.
- M. T. A. Saif, On a tunable bistable MEMS-theory and experiment, J. Microelectromech. Syst., 2000, 9, 157–170 CrossRef.
- T. Jaglinski, D. Kochmann, D. Stone and R. Lakes, Composite materials with viscoelastic stiffness greater than diamond, Science, 2007, 315, 620–622 CrossRef CAS PubMed.
- C. Coulais, J. T. Overvelde, L. A. Lubbers, K. Bertoldi and M. vanHecke, Discontinuous Buckling of Wide Beams and Metabeams, Phys. Rev. Lett., 2014, 115, 044301 CrossRef PubMed.
- W. Drugan, Elastic composite materials having a negative stiffness phase can be stable, Phys. Rev. Lett., 2007, 98, 055502 CrossRef CAS PubMed.
- T. Bückmann, M. Kadic, R. Schittny and M. Wegener, Mechanical metamaterials with anisotropic and negative effective mass-density tensor made from one constituent material, Phys. Status Solidi B, 2015, 252, 1671–1674 CrossRef.
- G. W. Milton, New metamaterials with macroscopic behavior outside that of continuum elastodynamics, New J. Phys., 2007, 9, 359 CrossRef.
- R. Lakes and W. Drugan, Dramatically stiffer elastic composite materials due to a negative stiffness phase?, J. Mech. Phys. Solids, 2002, 50, 979–1009 CrossRef.
- D. M. Kochmann and G. W. Milton, Rigorous bounds on the effective moduli of composites and inhomogeneous bodies with negative-stiffness phases, J. Mech. Phys. Solids, 2014, 71, 46–63 CrossRef.
- T. D. Le and K. K. Ahn, A vibration isolation system in low frequency excitation region using negative stiffness structure for vehicle seat, J. Sound Vib., 2011, 330, 6311–6335 CrossRef.
- C.-M. Lee, V. Goverdovskiy and A. Temnikov, Design of springs with “negative” stiffness to improve vehicle driver vibration isolation, J. Sound Vib., 2007, 302, 865–874 CrossRef.
- A. A. Sarlis, D. T. R. Pasala, M. Constantinou, A. Reinhorn, S. Nagarajaiah and D. Taylor, Negative stiffness device for seismic protection of structures, J. Struct. Eng., 2012, 139, 1124–1133 CrossRef.
- C.-M. Lee and V. Goverdovskiy, A multi-stage high-speed railroad vibration isolation system with “negative” stiffness, J. Sound Vib., 2012, 331, 914–921 CrossRef.
- R. O. Ritchie, The conflicts between strength and toughness, Nat. Mater., 2011, 10, 817–822 CrossRef CAS PubMed.
- F. Barthelat and R. Rabiei, Toughness amplification in natural composites, J. Mech. Phys. Solids, 2011, 59, 829–840 CrossRef.
- L. R. Meza, S. Das and J. R. Greer, Strong, lightweight, and recoverable three-dimensional ceramic nanolattices, Science, 2014, 345, 1322–1326 CrossRef CAS PubMed.
- D. Jang, L. R. Meza, F. Greer and J. R. Greer, Fabrication and deformation of three-dimensional hollow ceramic nanostructures, Nat. Mater., 2013, 12, 893–898 CrossRef CAS PubMed.
- X. Zheng, H. Lee, T. H. Weisgraber, M. Shusteff, J. DeOtte and E. B. Duoss, et al., Ultralight, ultrastiff mechanical metamaterials, Science, 2014, 344, 1373–1377 CrossRef CAS PubMed.
- F. Wang, O. Sigmund and J. S. Jensen, Design of materials with prescribed nonlinear properties, J. Mech. Phys. Solids, 2014, 69, 156–174 CrossRef.
- A. Silva, F. Monticone, G. Castaldi, V. Galdi, A. Alù and N. Engheta, Performing mathematical operations with metamaterials, Science, 2014, 343, 160–163 CrossRef CAS PubMed.
- B. Florijn, C. Coulais and M. van Hecke, Programmable mechanical metamaterials, Phys. Rev. Lett., 2014, 113, 175503 CrossRef PubMed.
- S. H. Kang, S. Shan, W. L. Noorduin, M. Khan, J. Aizenberg and K. Bertoldi, Buckling-Induced Reversible Symmetry Breaking and Amplification of Chirality Using Supported Cellular Structures, Adv. Mater., 2013, 25, 3380–3385 CrossRef CAS PubMed.
- A. Lazarus and P. M. Reis, Soft actuation of structured cylinders through auxetic behavior, Adv. Eng. Mater., 2015, 17, 815–820 CrossRef.
- J. Paulose, A. S. Meeussen and V. Vitelli, Selective buckling via states of self-stress in topological metamaterials, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7639–7644 CrossRef CAS PubMed.
- J. Shim, S. Shan, A. Košmrlj, S. H. Kang, E. R. Chen and J. C. Weaver, et al., Harnessing instabilities for design of soft reconfigurable auxetic/chiral materials, Soft Matter, 2013, 9, 8198–8202 RSC.
- S. Janbaz, H. Weinans and A. A. Zadpoor, Geometry-based control of instability patterns in cellular soft matter, RSC Adv., 2016, 6, 20431–20436 RSC.
- L. M. Nash, D. Kleckner, V. Vitelli, A. M. Turner and W. Irvine, Topological mechanics of gyroscopic metamaterials, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 14495–14500 CrossRef CAS PubMed.
- J. Paulose, B. G. G. Chen and V. Vitelli, Topological modes bound to dislocations in mechanical metamaterials, Nat. Phys., 2015 Search PubMed , in press.
- S. Felton, M. Tolley, E. Demaine, D. Rus and R. Wood, A method for building self-folding machines, Science, 2014, 345, 644–646 CrossRef CAS PubMed.
- K. Kuribayashi, K. Tsuchiya, Z. You, D. Tomus, M. Umemoto and T. Ito, et al., Self-deployable origami stent grafts as a biomedical application of Ni-rich TiNi shape memory alloy foil, Mater. Sci. Eng., A, 2006, 419, 131–137 CrossRef.
- E. A. Peraza-Hernandez, D. J. Hartl, R. J. Malak Jr and D. C. Lagoudas, Origami-inspired active structures: a synthesis and review, Smart Mater. Struct., 2014, 23, 094001 CrossRef.
- C. Lv, D. Krishnaraju, G. Konjevod, H. Yu and H. Jiang, Origami based mechanical metamaterials, Sci. Rep., 2014, 4, 5979 CAS.
- M. Eidini and G. H. Paulino, Unraveling metamaterial properties in zigzag-base folded sheets, Sci. Adv., 2015, 1, e1500224 Search PubMed.
- M. Schenk and S. D. Guest, Geometry of Miura-folded metamaterials, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3276–3281 CrossRef CAS PubMed.
- J. L. Silverberg, A. A. Evans, L. McLeod, R. C. Hayward, T. Hull and C. D. Santangelo, et al., Using origami design principles to fold reprogrammable mechanical metamaterials, Science, 2014, 345, 647–650 CrossRef CAS PubMed.
- E. T. Filipov, T. Tachi and G. H. Paulino, Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 12321–12326 CrossRef CAS PubMed.
- J. L. Silverberg, J.-H. Na, A. A. Evans, B. Liu, T. C. Hull and C. D. Santangelo, et al., Origami structures with a critical transition to bistability arising from hidden degrees of freedom, Nat. Mater., 2015, 14, 389–393 CrossRef CAS PubMed.
- S. Waitukaitis, R. Menaut, B. G.-g. Chen and M. van Hecke, Origami multistability: from single vertices to metasheets, Phys. Rev. Lett., 2015, 114, 055503 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2016 |

