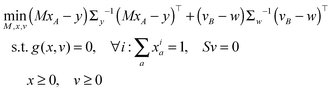Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Simultaneous tracing of carbon and nitrogen isotopes in human cells†
Roland
Nilsson
*ab and
Mohit
Jain
*c
aUnit of Computational Medicine, Department of Medicine, Karolinska Institutet, Karolinska University Hospital, SE-17176 Stockholm, Sweden. E-mail: roland.nilsson@ki.se
bCenter for Molecular Medicine, Karolinska Institutet, Karolinska University Hospital, SE-17176 Stockholm, Sweden
cDepartments of Medicine and Pharmacology, University of California, San Diego, USA. E-mail: mjain@ucsd.edu
First published on 13th April 2016
Abstract
Stable isotope tracing is a powerful method for interrogating metabolic enzyme activities across the metabolic network of living cells. However, most studies of mammalian cells have used 13C-labeled tracers only and focused on reactions in central carbon metabolism. Cellular metabolism, however, involves other biologically important elements, including nitrogen, hydrogen, oxygen, phosphate and sulfur. Tracing stable isotopes of such elements may help shed light on poorly understood metabolic pathways. Here, we demonstrate the use of high-resolution mass spectrometry to simultaneously trace carbon and nitrogen metabolism in human cells cultured with 13C- and 15N-labeled glucose and glutamine. To facilitate interpretation of the complex isotopomer data generated, we extend current methods for metabolic flux analysis to handle multivariate mass isotopomer distributions (MMIDs). We find that observed MMIDs are broadly consistent with known biochemical pathways. Whereas measured 13C MIDs were informative for central carbon metabolism, 15N isotopes provided evidence for nitrogen-carrying reactions in amino acid and nucleotide metabolism. This computational and experimental methodology expands the scope of metabolic flux analysis beyond carbon metabolism, and may prove important to understanding metabolic phenotypes in health and disease.
Introduction
Stable isotope tracing is a well-established method for measuring intracellular metabolic enzyme activities across the metabolic network of living cells.1 In this technique, cells are cultured with nutrients labeled with stable isotopes, and the resulting isotopic patterns in cellular metabolites are measured by mass spectrometry or NMR. While software for quantifying isotopic distributions is well established,2,3 a wide variety of methods are used for interpreting the resulting isotope data to draw conclusions about metabolism, ranging from manual inspection and qualitative reasoning to sophisticated model-based computational techniques for quantitative metabolic flux analysis.4 While qualitative tracing methods have been important in biochemistry to systematically map metabolic pathways, quantitative methods for flux analysis have largely been employed in lower organisms5 and plants,6 where precise information about central metabolism is important to optimize product yields or crops. More recently, stable isotope tracing has been applied to study the metabolism of mammalian cells grown in batch cultures,7–11 aiming to systematically understand human metabolism and identify enzymes or pathways that are affected in human diseases.To date, the vast majority of studies have employed a single labeling strategy, typically using 13C-labeled substrates and focusing on central carbon metabolism, usually including glycolysis, the pentose phosphate pathway, and the tricarboxylic acid (TCA) cycle.7 Using other stable isotopes, including 15N, 2H, 18O, and 34S, could yield information about additional metabolic activities in a given experiment, or even allow for study of pathways not amenable to carbon labeling. For instance, metabolic flux analysis using deuterium 2H has proven useful to monitor redox reactions.12 Similarly, tracing nitrogen using 15N may provide valuable information on amino acid and nucleotide metabolism; oxygen tracers 18O could be used to monitor phosphates (PO4) in energy metabolism; and sulfur isotopes (34S) can inform on metabolism of cysteine, methionine and related sulfur-containing compounds.13
Here, we use a combination of 13C- and 15N-labeled tracers to interrogate carbon and nitrogen metabolism of human cells within a single experiment. Using high resolution mass spectrometry we can resolve and quantify pairwise combinations of 13C and 15N mass isotopomers, resulting in multivariate mass isotopomer distributions (MMIDs) that reflect the simultaneous cellular metabolism of these chemical elements. To systematically handle MMID data, we describe a generalization of the Elementary Metabolite Unit (EMU) framework14 that extends metabolic flux analysis to multiple elements. We discuss features of carbon and nitrogen metabolism observable in human cells with this method.
Materials and methods
Cell culture and metabolite extraction
Human HeLa cells were cultured in 6-well culture dishes using RPMI-1640 medium (Life Technologies) with 11 mM glucose, of which 70% was U-13C-glucose (Cambridge Isotope Laboratories) and 2 mM glutamine, of which 70% was U-13C,15N-glutamine (Cambridge Isotope Laboratories), and supplemented with 5% dialyzed FBS (Hyclone). Cell extracts were analyzed after 24 and 72 hour culture periods. HeLa cells were plated at a density that resulted in ∼85% confluency (∼1 × 106 cells per well) at the end of the culture period, and to maintain a doubling time of ∼30 hours throughout the culture period. At the completion of the culture period, spent medium was removed, cells rapidly washed with phosphate buffered saline to remove residual medium, and metabolites extracted using 1 mL of 100% HPLC grade methanol pre-cooled at −80 °C. Cellular material was scraped in the cold methanol, collected and vortexed for 1 minute. Cellular material was centrifuged at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RPM × 10 min at 4 °C and the organic supernatant containing extracted metabolites was collected and maintained at −80 °C until analysis. Separate wells with identical plating were used for confirmation of final cell counts. Three independent biological replicates were used for all cell culture experiments.
000 RPM × 10 min at 4 °C and the organic supernatant containing extracted metabolites was collected and maintained at −80 °C until analysis. Separate wells with identical plating were used for confirmation of final cell counts. Three independent biological replicates were used for all cell culture experiments.
Mass spectrometry and mass isotopomer distributions
Metabolites were assayed as previously described15 using liquid chromatography coupled to high resolution mass spectrometry (LC-MS). Liquid chromatographic separation was achieved using hydrophilic interaction chromatography (HILIC) employing an Atlantis HILIC column (150 × 2.1 mm; Waters, Milford, MA) or Luna NH2 column (5 μm, 150 × 2 mm; Phenomenex) with both positive and negative electrospray ionization (ESI). LC was coupled to a high resolution Q Exactive Quadrupole-Orbitrap mass spectrometer (ThermoFisher) operating at 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 resolution, scanning a mass range of 50–1000 m/z. Metabolites were identified by retention time and m/z from pure standards.15 Observed m/z accuracy was maintained at <5 ppm. Chromatographic peaks areas were obtained by manual integration using in-house software. Peaks corresponding to mass isotopomers were manually inspected to verify identical chromatrographic peak shapes, and false isotopes were excluded. Mass isotopomer distributions were calculated for each sample by normalizing values to the total peak area for all mass isotopomers of each metabolite.
000 resolution, scanning a mass range of 50–1000 m/z. Metabolites were identified by retention time and m/z from pure standards.15 Observed m/z accuracy was maintained at <5 ppm. Chromatographic peaks areas were obtained by manual integration using in-house software. Peaks corresponding to mass isotopomers were manually inspected to verify identical chromatrographic peak shapes, and false isotopes were excluded. Mass isotopomer distributions were calculated for each sample by normalizing values to the total peak area for all mass isotopomers of each metabolite.
Uptake/release measurements
Absolute concentrations of glutamine, glutamate and lactate in fresh (0 h) and spent (72 h) culture medium were measured using a commercial YSI 2900 bioanalyzer.15 Net rates consumption or release of glutamine, glutamate and lactate per cell were calculated by normalizing to cell proliferation, as previously described,15 assuming constant fluxes over time. Rates of acetate, alanine, asparate, citrulline, and biomass components (protein, RNA, glycogen, and glutathione) were estimated from literature values (S3 Dataset) for the purpose of bounding the model fluxes, assuming 10% error.Metabolic network model
The metabolic network model used in this work is fully described in the ESI.† Reaction stoichiometry were obtained from a previously published model of human cellular metabolism.16 Atom maps were obtained from KEGG17 and were manually curated. Molecular symmetry for fumarate, succinate and urea was handled using EMU equivalence classes, as previously described.14Multivariate mass isotopomer distributions
To represent the isotopic labeling state of multiple chemical elements, we introduce multivariate mass isotopomer distributions (MMIDs). Denote the elements by e = 1,…, E, and consider a metabolite i having nie atoms of element e. Then any possible multivariate mass isotopomer of this metabolite can be represented by an E-dimensional vector a taking values in the array Gi = {0,…, ni1} × ⋯ × {0,…, niE}, representing all possible combinations of mass isotopomers for each element. An MMID of metabolite i is then a probability (frequency) distribution xia over this array, satisfying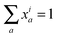 and xia ≥ 0 for all a ∈ Gi. For example, if considering 13C and 15N isotopes, then the MMID of glutamine (C5H10O3N2) is a probability distribution over Gi = {0,1,2,3,4,5} × {0,1,2}, as in Fig. 1D. Note that it is not sufficient to consider the sets of atoms for each element separately as 1-dimensional MIDs: this would be correct only if the isotopomers of each element are independent, so that the full MMID is a product distribution.
and xia ≥ 0 for all a ∈ Gi. For example, if considering 13C and 15N isotopes, then the MMID of glutamine (C5H10O3N2) is a probability distribution over Gi = {0,1,2,3,4,5} × {0,1,2}, as in Fig. 1D. Note that it is not sufficient to consider the sets of atoms for each element separately as 1-dimensional MIDs: this would be correct only if the isotopomers of each element are independent, so that the full MMID is a product distribution.
To relate MMIDs to fluxes in metabolic networks, we generalize of the Elementary Metabolite Unit (EMU) framework14 to multiple elements. We define a multiple-element EMU (MEMU) of a given metabolite as a list of subsets of atoms, one for each element, not necessarily contiguous in the molecular structure. Again, the mass isotopomers of an MEMU are elements of an E-dimensional array, and the MMID of an MEMU is a probability distribution on this array. Cleavage or unimolecular reactions are viewed simply as a transfer of an MEMU, which means their MMIDs must be equal. For a condensation reaction forming MEMU i from MEMUs j and k, the product MMID xi is a now multidimensional convolution of the MMIDs xj, xk of the substrates: for each a ∈ Gi,
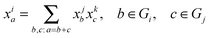 | (1) |
Given the MEMU decomposition, for each product MEMU, if reactions with fluxes v1,…, vN transfer MEMUs with MMIDs x1,…xN to the same product MEMU, then at steady-state, the product's MMID x0 is a linear combination
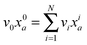 | (2) |
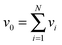 is the total flux “through” the product. The only difference between (2) and the 1-dimensional case14 is that the MMID xa is no longer a vector but an E-dimensional array (for carbon–nitrogen data, E = 2, so xa is a matrix), and convolutions must be calculated according to eqn (1). While time-dependent equations for isotopic nonstationary data can similarly be derived, as previously described,18 we here consider the steady-state case.
is the total flux “through” the product. The only difference between (2) and the 1-dimensional case14 is that the MMID xa is no longer a vector but an E-dimensional array (for carbon–nitrogen data, E = 2, so xa is a matrix), and convolutions must be calculated according to eqn (1). While time-dependent equations for isotopic nonstationary data can similarly be derived, as previously described,18 we here consider the steady-state case.
Metabolic flux analysis
The vector of metabolic fluxes v was estimated by fitting the MEMU network model to measured MMID data using a previously described nonlinear optimization method,19 as follows. Let x denote the “flattened” vector collecting all mass isotopomer fractions of all MMIDs, and write g(x,v) = 0 to represent the collection of all eqn (1) and (2) for all MEMUs, relating fluxes v to all MMIDs in the system. For metabolites present in both mitochondria and cytosol, the observed MMIDs y was modeled as a linear mixture MxA = y, where A is an index vector for the corresponding model MMIDs and M is a mixing matrix. We consider both M, x and v as free variables, and estimate them by solving the constrained optimization problemwhere B is an index vector for the measured fluxes w, and S is the stoichiometry matrix (needed here because cofactor balances are not implied by the MEMU balance equations). Note that, while the objective is linear in x, the constraints g(x,v) = 0 are nonlinear due to eqn (1). Assuming independent errors, the covariance matrices Σy and Σw were chosen to be diagonal. Since all possible mass isotopomers do not occur practise, many MI fractions were close to or identical to zero, resulting in near-zero standard deviations
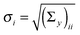 on the diagonal. To avoid a singular covariance matrix, we therefore enforced a minimum bound σi > 0.01.
on the diagonal. To avoid a singular covariance matrix, we therefore enforced a minimum bound σi > 0.01.
Optimization was done using CONOPT v.3.15 (ARKI Consulting & Development A/S) controlled via the GAMS modeling language (GAMS Software GmbH). A separate optimization problem was generated for each biological replicate in order to inspect the resulting variation in flux estimates. To check for occurrence of local minima, each problem was solved 100 times starting from randomly chosen initial points. Since most flux solutions were close together with nearly identical objective values, the centroid of these 100 solutions was taken as the final estimate.
Results
Measuring multivariate MIDs in intracellular metabolites
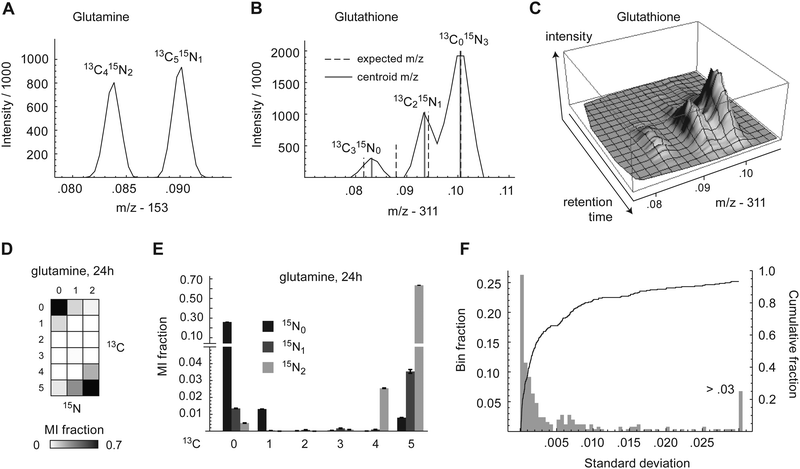
To investigate the metabolism of carbon and nitrogen in human HeLa cells, cells were labeled with 70% U-13C-glucose and 70% U-13C,15N-glutamine and cell extracts were taken at 24 h and 72 h time points. The fraction of 70% labeled tracer was chosen to yield information-rich isotopomer patterns, as fully labeled substrates tend to produce less informative data.20 The mass shift due to incorporation of a single 13C atom in a downstream metabolite is ∼1.003 μ, while that due to 15N is ∼0.997 μ. Hence, isotopomers due to 13C or 15N incorporation differ by ∼0.006 μ, which is readily detectable in small metabolites using high resolution mass spectrometers, operating at >70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mass resolution. In principle, it is therefore possible to distinguish any pairwise combination of 13C and 15N mass isotopomers; we refer to these combinations as multivariate mass isotopomers (MMIs). Cellular metabolites were analyzed by LC-MS which fully resolved isotopic peaks from adjacent carbon and nitrogen MMIs (m/z difference = 0.006) in metabolites having m/z of approximately <250. An example of separation of carbon/nitrogen MMIs in glutamine is shown in Fig. 1A. For larger metabolites, adjacent MMIs were not completely baseline resolved, as shown for glutathione (Fig. 1B), but centroiding of m/z spectra still yielded intensity estimates for peak resolved peaks, which appeared to be stable during chromatography (Fig. 1C), indicating that MMIs can still be measured.
000 mass resolution. In principle, it is therefore possible to distinguish any pairwise combination of 13C and 15N mass isotopomers; we refer to these combinations as multivariate mass isotopomers (MMIs). Cellular metabolites were analyzed by LC-MS which fully resolved isotopic peaks from adjacent carbon and nitrogen MMIs (m/z difference = 0.006) in metabolites having m/z of approximately <250. An example of separation of carbon/nitrogen MMIs in glutamine is shown in Fig. 1A. For larger metabolites, adjacent MMIs were not completely baseline resolved, as shown for glutathione (Fig. 1B), but centroiding of m/z spectra still yielded intensity estimates for peak resolved peaks, which appeared to be stable during chromatography (Fig. 1C), indicating that MMIs can still be measured.
A total of 38 metabolites with high quality peaks were identified using pure standards, of which 25 contained at least one nitrogen atom. For each of these metabolites, we calculated the fractional abundance of all possible carbon–nitrogen MMIs, resulting in 2-dimensional MMI distributions (MMIDs). As an example, the MMID for glutamine is shown in Fig. 1D and E. Measured MMIDs ranged in complexity from glycine (3 × 2 = 6 MMIs) to ADP (11 × 6 = 66 MMIs), for a total of 616 carbon–nitrogen MMIs monitored (S3 Dataset), compared to 258 when considering 13C isotopes only. Of these 616 MMIs, 328 were below sensitivity thresholds in all samples, indicating that they are not synthesized by cells in these conditions. Nonzero mass isotopomers were highly reproducible over biological replicates (independent cell cultures), with standard deviation less than 0.01 in more than 90% of cases (Fig. 1F). However, low-abundance mass isotopomers were often systematically underestimated, probably reflecting loss of signal near threshold levels (Fig. S1, ESI†). With a few exceptions discussed below, MMIDs were similar between the 24 h and 72 h time points, indicating that in most pathways monitored, metabolic and isotopic steady-state was reached already at 24 h (Fig. S2, ESI†). In the remainder of analyses, we consider the metabolic state at the 24 h time point.
Network model and fit to data
The resulting MMID dataset is quite complex, reflecting a variety of activities in the metabolic network, and is difficult to analyze manually. To aid in systematic interpretation, we constructed a model of metabolism covering the major interrogated pathways, including glycolysis, the pentose phosphate shunt, and the TCA cycle, as well as metabolism of nonessential amino acids, nucleotide and glutathione biosynthesis, and a simplified biomass synthesis reaction. This model consists of 125 reactions and 51 uptake or release fluxes, includes cofactor balancing, and covers 121 metabolites compartmentalized into mitochondria and cytosol. The atom map for carbons and nitrogens comprised 1403 atom-to-atom mappings in total. The eight essential amino acids measured (his, ile, leu, lys, met, thr, trp, val) are not synthesized in human cells and contained no label from glucose or glutamine as expected, and were omitted from the model. Also, the MMID glucose-6-phosphate (g6p) was poorly measured and was omitted as well. The full model description is given in ESI.†To relate carbon–nitrogen MMIDs to metabolic fluxes in this model, we developed an extension of the Elementary Metabolite Unit (EMU) mathematical framework14 that describes MMIDs as a function of the metabolic flux state and the metabolic tracers (see Methods for details). Briefly, a multi-element EMU (MEMU) of a given metabolite is a list of subsets of atoms, one for each element. These MEMUs allows representing reactions that cleave metabolites into smaller fragments, or condense metabolites into larger ones: for example, glycine can be derived from the MEMU consisting of carbons 1,2 and nitrogen 4 of serine. From the atom mappings for all reactions in the metabolic network model, we can generate the minimal set of MEMUs whose MMIDs must be calculated to relate the observed MMIDs to metabolic fluxes. For the present model, this analysis resulted in 575 two-dimensional carbon–nitrogen MEMUs, for a total of 3317 MMIs.
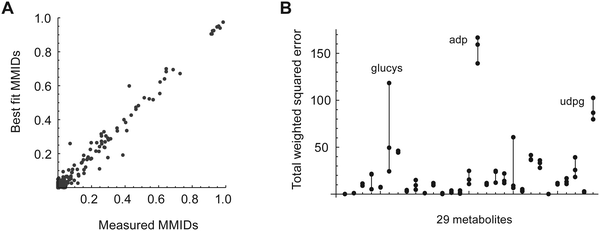
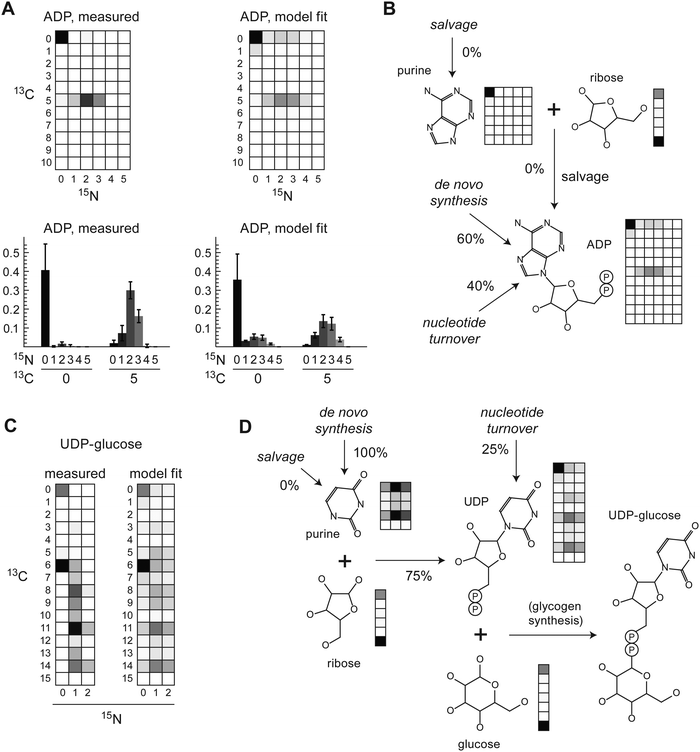
Metabolic fluxes were estimated by fitting this MEMU model to the measured MMID and metabolite uptake/release data. Of the 29 measured metabolites used to fit the model, 12 were present in both the cytosol and mitochondria compartments; these were modeled using linear mixtures, whose coefficients were estimated from data (see Methods for details). A separate model fit was performed for each biological replicate (n = 3) and for each time point. In most cases, fitted MMIDs were highly similar between replicates (Fig. S3, ESI†). While most measured MMIDs agreed well with model estimates (Fig. 2A), we obtained rather large errors for glutamyl-cysteine, ADP and UDP-glucose (Fig. 2B), leading to higher total squared error (598–663 across replicates) than allowed by the chi-square criterion (95% χ2 quantile = 401). This likely reflects inaccurate or biased estimates of these MMIDs and/or lack of metabolic steady state for nucleotide metabolism. For this reason, quantitative estimates of metabolic fluxes in this model should be considered uncertain; however, it is still possible to gain insight into metabolism by analyzing those MMIDs that fit the model.
Amino acid metabolism
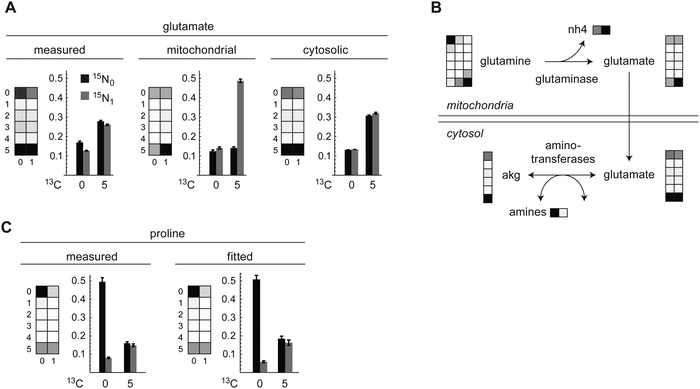
The carbon-only MID of glutamate was consistent with synthesis from consumed glutamine via glutaminase, with partial recycling from alpha-ketoglutarate (Fig. 3A). The full carbon–nitrogen MMID of glutamate, however, exhibited markedly less of the 13C515N1 mass isotopomer than would be expected if synthesized solely from glutamine (Fig. 3A and 1F). This suggested that the glutamate MMID mostly reflects cytosolic glutamate, which should contain less 13C515N1 due to influx of 12N from other amino acids via reversible transamination reactions (Fig. 3B). The MMID of proline indicated that approximately 55% of this intracellular amino acid is synthesized from cytosolic glutamate (Fig. 3C), with the remainder originating from uptake from medium or an unlabeled precursor. Of the remaining amino acids that can be synthesized by HeLa cells,21 the MMID for alanine was consistent with synthesis from pyruvate, and nearly all aspartate was derived from oxaloacetate, while asparagine, serine, and glycine were not synthesized from glucose or glutamine (Fig. S3, ESI†).The carbon skeleton of arginine was not synthesized, consistent with arginine being essential for HeLa cells.21 In addition, both nitrogens in arginine were unlabeled, consistent with the lack of an active urea cycle in these cells.22 Disposal of excess nitrogen according to the model was mainly in the form of ammonium and glutamate (alanine synthesis could not be estimated accurately). Ornithine, an important precursor of polyamines required by proliferating cells, was unlabeled, indicating that it is synthesized from arginine, not from glutamate. Taken together, these results indicate that carbon–nitrogen MMIDs can provide additional information on amino acid metabolism compared to carbon labeling alone.
Nucleotides
Since de novo synthesis of nucleotides requires nitrogen, we anticipated that carbon–nitrogen MMIDs may be valuable for studying nucleotide metabolism as well. Due to low LC-MS peak intensities, estimated MMIDs for nucleotides were not accurate enough to allow for quantitative flux analysis, as seen in large squared errors for these metabolites (Fig. 2B). Nevertheless, the measured MMID of adenosine disphosphate (ADP) was broadly consistent with the known pathway of de novo purine synthesis (Fig. 4A and B). Incorporation of a labeled ribose moiety was evident from the 13C5 carbon mass isotopomer alone. Importantly, carbon–nitrogen MMIs provided evidence of de novo synthesis of the purine ring, during which labeled nitrogen is incorporated from glutamine and glutamine-derived aspartate, while the carbons of the purine ring derive from unlabeled glycine, serine and CO2. It was evident that purine nucleobase salvage did not occur in these cells, which would appear as a 13C515N0 isotopomer, which was not observed (Fig. 4A). About 40% of the purine pool remained unlabeled (13C015N0), suggesting that only 60% of purines were de novo synthesized at the 24 h time point, with the remainder obtained from a pre-existing unlabeled purine pool, possibly including turnover of RNA (Fig. 4B).For pyrimidines, UDP-glucose was the only pyrimidine-containing compound definitively identified from this experiment (Fig. 4C). While we could not resolve all carbon–nitrogen MMIs in this large molecule (m/z = 565), some MMIs could be identified without risk of confounding. The abundant 13C615N0 MMI indicated incorporation of labeled glucose (13C6) into pre-existing unlabeled UDP, which may reflect ongoing glycogen synthesis. The presence of various 15N1 and 15N2 mass isotopomers indicated synthesis of the pyrimidine ring from aspartate, glutamine and CO2. The model estimated 75% of pyrimides to be de novo synthesized at 24 h (Fig. 4D). As with purines, there was no evidence of salvage of pyrimidine nucleobases, since 13C515N0 or 13C1115N0 MMIs were not observed (Fig. 4C); this was expected since the medium did not contain these metabolites. In summary, the carbon–nitrogen MMIDs of nucleotides were in good agreement with the known metabolic network structure, and provided evidence of de novo nucleotide synthesis and turnover.
Discussion
Our results indicate that simultaneous tracing of isotopes in multiple elements such as 13C and 15N is experimentally and computationally feasible, and allows for a more detailed analysis of the metabolic network than with 13C labeling alone. In particular, amino acid metabolism and nucleotide synthesis are clearly observable with this approach. Although this information might also be obtained using additional 13C tracers in parallel labeling experiments, as reported by others,23 multiplexing tracers may generate more information per experiment, and provides independent, direct evidence for nitrogen metabolism. Our computational framework also allows handling other isotopes of interest, such as 2H, 18O or 24S, in a uniform, systematic manner. The multivariate methods presented herein is a straightforward generalization of the EMU methodology. In our experience, the increase in mass isotopomer variables is not prohibitively large: for the model used herein, we obtained a total of 3317 MMI variables using carbon–nitrogen EMUs, compared to 1971 when treating carbon only. Also, introducing additional elements tends to result in more and smaller EMU subnetworks, which reduces the computational complexity of solving EMU balance equations. Methods based on the cumomer framework24 can be easily extended along the same lines.While our computational method can simultaneously track isotopes in any number of elements, a practical limitation is that low-abundance metabolites become more difficult to measure as the metabolite pool is divided into a large number of isotopomers. For example, if one would consider the isotopes of 13C, 2H, 15N, and 18O simultaneously, even a simple metabolite such as serine (C3H7O3N) has a MMID with dimensions 4 × 8 × 3 × 2 (192 isotopomers total). Therefore, multiple isotopes will likely be most effective when studying compounds that generate strong LC-MS peaks. In addition, mass resolution limits what isotopes can be confidently resolved, particularly in larger metabolites such as UDP-glucose. Moreover, natural 34S1 isotopomers are present at +1.996 Da above the base isotopomer with ∼4% relative abundance, and may be confounded with 15N2 mass isotopomers at +1.994 Da. In our data, only glutamylcysteine (C8H13N2O5S) and reduced glutathione (C10H16N3O6S) could theoretically generate both 15N2 and 34S1 mass isotopomers, and in these cases 15N2 was not present, but this caveat remains important. In our study, a mass resolution of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 was sufficient for all but the largest metabolites. Higher resolution mass analyzers could theoretically allow using multiple isotopes to generate more rich data. The MMID approach could also be useful with other analytical methods, in particular the recently introduced high resolution GC-Orbitrap instruments. Future work could also explore combining the MMID methodology with data-dependent tandem mass spectrometry to determine positional isotope incorporation from MMIDs of metabolite fragments (MEMUs).
000 was sufficient for all but the largest metabolites. Higher resolution mass analyzers could theoretically allow using multiple isotopes to generate more rich data. The MMID approach could also be useful with other analytical methods, in particular the recently introduced high resolution GC-Orbitrap instruments. Future work could also explore combining the MMID methodology with data-dependent tandem mass spectrometry to determine positional isotope incorporation from MMIDs of metabolite fragments (MEMUs).
The use of multiple isotopes markedly increases the number of measured mass isotopomers, which provides additional information, but also reveals discrepancies that may go unnoticed when fitting carbon isotopomers only. While more measurements is of course desirable, it also places high demands on an accurate model of cellular metabolism, rendering model fitting more difficult; this was previously seen in a large study19 of E. coli metabolism, consisting of 162 measured mass isotopomers (carbon only) from 13 metabolites. Our analysis required fitting 462 carbon–nitrogen mass isotopomers from 29 metabolites, and although our model agreed reasonably well with data, we were unable to reach a statistically acceptable fit, particularly for nucleotides. Partly, this may be due to model errors, such as neglected reactions, substrate channeling, and metabolite pools that have not completely reached steady state. Also, our model includes balancing of cofactors like NAD and NADP, which imposes additional constraints rarely included in metabolic flux analyses. However, it is also evident that the error model underlying the standard χ2 model fit criterion (zero bias, normal distributed residuals) is not fully appropriate for orbitrap mass spectrometers, as low abundance mass isotopomers were systematically underestimated (Fig. S1, ESI†). Future work should explore alternative error models for such data in order to take full advantage of the rich isotopomer patterns observable with high resolution mass spectrometry instruments.
In addition to establishing a framework for isotope tracing with multiple elements, this study also revealed a number of interesting metabolic features of the HeLa cell line. These cells synthesized only a few amino acids, namely glutamate, aspartate, alanine and proline under standard culture conditions, while the remaining are presumably obtained from the growth medium. Interestingly, the amino acids synthesized generally appear to have important roles in central metabolism independent of protein synthesis: glutamate is a key amine group donor in various amino transferases; aspartate is involved in the malate–aspartate shuttle, which is known to be active in a variety of cultured cells;25 and alanine has been suggested to act as an ammonia scavenger.26 Why proline is synthesized to a large extent despite being present in the medium is not clear, although it has been hypothesized to act as a redox carrier in mitochondria.27 In addition, while some cell lines have been reported to be dependent on serine synthesis from glucose,28 we find little evidence of serine synthesis in HeLa cells. Indeed, a recent report indicated that serine synthesis varies dramatically between cell types.29 The regulation of specific amino acid synthesis pathways by amino acid availability is still not well understood,30 and we anticipate that our method may be useful for studying these processes. Our analysis was also informative for studying nucleotide metabolism, and suggested compartmentalization of glutamate not evident from carbon isotopomers alone. Extending these studies to additional cell types, both normal and transformed, will be of importance for better understanding of cellular metabolism.
Conclusions
Simultaneous tracing of carbon and nitrogen in mammalian cells is feasible with modern high-resolution mass spectrometers, and computational methods for steady-state metabolic flux analysis can be extended to handle the resulting data. Nitrogen isotopomers are informative for areas of amino acid and nucleotide metabolism that are rarely addressed using 13C tracers. Although further work is needed to fully understand the statistical properties of full-scan high resolution mass spectrometry data, multivariate mass isotopomers obtained from dual substrate labeling provides rich information that can help advance our understanding of systems metabolism.Acknowledgements
This work was supported by grants from Vetenskapsrådet Medicine (B0305901), the Strategic Programme in Cancer Research at Karolinska Institutet, Stiftelsen för Strategisk Forskning (ICA10-0023) to RN; as well as grants from the National Institutes of Health (K08HL107451), Sidney Kimmel Foundation, and V Foundation to MJ.References
- U. Sauer, Metabolic networks in motion: 13C-based flux analysis, Mol. Syst. Biol., 2006, 2, 62 CrossRef PubMed.
- X. Huang, et al. X13CMS: global tracking of isotopic labels in untargeted metabolomics, Anal. Chem., 2014, 86, 1632–1639 CrossRef CAS PubMed.
- J. Capellades, et al. GeoRge: A Computational Tool to Detect the Presence of Stable Isotope Labeling in LC/MS-Based Untargeted Metabolomics, Anal. Chem., 2016, 88, 621–628 CrossRef PubMed.
- J. M. Buescher, et al. A roadmap for interpreting 13C metabolite labeling patterns from cells, Curr. Opin. Biotechnol., 2015, 34, 189–201 CrossRef CAS PubMed.
- W. Wiechert, 13C Metabolic Flux Analysis, Metab. Eng., 2001, 3, 195–206 CrossRef CAS PubMed.
- I. G. L. Libourel and Y. Shachar-Hill, Metabolic flux analysis in plants: from intelligent design to rational engineering, Annu. Rev. Plant Biol., 2008, 59, 625–650 CrossRef CAS PubMed.
- J. Niklas, K. Schneider and E. Heinzle, Metabolic flux analysis in eukaryotes, Curr. Opin. Biotechnol., 2010, 21, 63–69 CrossRef CAS PubMed.
- H. Yoo, M. R. Antoniewicz, G. Stephanopoulos and J. K. Kelleher, Quantifying reductive carboxylation flux of glutamine to lipid in a brown adipocyte cell line, J. Biol. Chem., 2008, 283, 20621–20627 CrossRef CAS PubMed.
- C. Metallo, P. Gameiro, E. Bell and K. Mattaini, Reductive glutamine metabolism by IDH1 mediates lipogenesis under hypoxia, Nature, 2011, 481, 380–384 Search PubMed.
- J. Fan, et al. Quantitative flux analysis reveals folate-dependent NADPH production, Nature, 2014, 510, 298–302 CrossRef CAS PubMed.
- J. Munger, et al. Systems-level metabolic flux profiling identifies fatty acid synthesis as a target for antiviral therapy, Nat. Biotechnol., 2008, 26, 1179–1186 CrossRef CAS PubMed.
- C. A. Lewis, et al. Tracing Compartmentalized NADPH Metabolism in the Cytosol and Mitochondria of Mammalian Cells, Mol. Cell, 2014, 55, 253–263 CrossRef CAS PubMed.
- J. O. Krömer, E. Heinzle, H. Schroder and C. Wittmann, Accumulation of homolanthionine and activation of a novel pathway for isoleucine biosynthesis in Corynebacterium glutamicum McbR deletion strains, J. Bacteriol., 2006, 188, 609–618 CrossRef PubMed.
- M. R. Antoniewicz, J. K. Kelleher and G. Stephanopoulos, Elementary metabolite units (EMU): a novel framework for modeling isotopic distributions, Metab. Eng., 2007, 9, 68–86 CrossRef CAS PubMed.
- M. Jain, et al. Metabolite Profiling Identifies a Key Role for Glycine in Rapid Cancer Cell Proliferation, Science, 2012, 336, 1040–1044 CrossRef CAS PubMed.
- N. C. Duarte, et al. Global reconstruction of the human metabolic network based on genomic and bibliomic data, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 1777–1782 CrossRef CAS PubMed.
- M. Arita, The metabolic world of Escherichia coli is not small, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 1543–1547 CrossRef CAS PubMed.
- J. D. Young, J. L. Walther, M. R. Antoniewicz, H. Yoo and G. Stephanopoulos, An Elementary Metabolite Unit (EMU) Based Method of Isotopically Nonstationary Flux Analysis, Biotechnol. Bioeng., 2008, 99, 686–699 CrossRef CAS PubMed.
- P. F. Suthers, et al. Metabolic flux elucidation for large-scale models using 13C labeled isotopes, Metab. Eng., 2007, 9, 387–405 CrossRef CAS PubMed.
- M. Möllney, W. Wiechert, D. Kownatzki and A. A. de Graaf, Bidirectional reaction steps in metabolic networks: IV. Optimal design of isotopomer labeling experiments, Biotechnol. Bioeng., 1999, 66, 86–103 CrossRef.
- B. Y. H. Eagle, The Specific Amino Acid Requirements of a Human Carcinoma Cell (Strain HeLa) in Tissue Culture, J. Exp. Med., 1955, 102, 37–48 CrossRef PubMed.
- E. H. Van Beers, et al. Intestinal carbamoyl phosphate synthase I in human and rat. Expression during development shows species differences and mosaic expression in duodenum of both species, J. Histochem. Cytochem., 1998, 46, 231–240 CrossRef CAS PubMed.
- R. W. Leighty and M. R. Antoniewicz, Parallel labeling experiments with [U-13C]glucose validate E. coli metabolic network model for 13C metabolic flux analysis, Metab. Eng., 2012, 14, 533–541 CrossRef CAS PubMed.
- W. Wiechert, M. Möllney, S. Petersen and A. A. de Graaf, A universal framework for 13C metabolic flux analysis, Metab. Eng., 2001, 3, 265–283 CrossRef CAS PubMed.
- W. V. V. Greenhouse and A. L. Lehninger, Occurrence of the Malate-Aspartate Shuttle in Various Tumor Types, Cancer Res., 1976, 36, 1392–1396 CAS.
- R. Leke, et al. Detoxification of ammonia in mouse cortical GABAergic cell cultures increases neuronal oxidative metabolism and reveals an emerging role for release of glucose-derived alanine, Neurotoxic. Res., 2011, 19, 496–510 CrossRef CAS PubMed.
- C. H. Hagedorn and J. M. Phang, Transfer of Reducing Equivalents into Mitochondria by the Interconversions of Proline and Delta1-pyrroline-5-carboxylate, Arch. Biochem. Biophys., 1983, 225, 95–101 CrossRef CAS PubMed.
- R. Possemato, et al. Functional genomics reveal that the serine synthesis pathway is essential in breast cancer, Nature, 2011, 476, 346–350 CrossRef CAS PubMed.
- G. M. DeNicola, et al. NRF2 regulates serine biosynthesis in non-small cell lung cancer, Nat. Genet., 2015, 47, 1475–1481 CrossRef CAS PubMed.
- A. Efeyan, W. C. Comb and D. M. Sabatini, Nutrient-sensing mechanisms and pathways, Nature, 2015, 517, 302–310 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6mb00009f |
| This journal is © The Royal Society of Chemistry 2016 |