Continuous micro-vortex-based nanoparticle manipulation via focused surface acoustic waves†
David J.
Collins
ac,
Zhichao
Ma
a,
Jongyoon
Han
bcd and
Ye
Ai
 *a
*a
aPillar of Engineering Product Development, Singapore University of Technology and Design, Singapore 487372, Singapore. E-mail: aiye@sutd.edu.sg; Tel: (+65) 6499 4553
bDepartment of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
cSingapore-MIT Alliance for Research and Technology (SMART) Centre, Singapore 138602, Singapore
dDepartment of Biological Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 16th November 2016
Abstract
Despite increasing demand in the manipulation of nanoscale objects for next generation biological and industrial processes, there is a lack of methods for reliable separation, concentration and purification of nanoscale objects. Acoustic methods have proven their utility in contactless manipulation of microscale objects mainly relying on the acoustic radiation effect, though the influence of acoustic streaming has typically prevented manipulation at smaller length scales. In this work, however, we explicitly take advantage of the strong acoustic streaming in the vicinity of a highly focused, high frequency surface acoustic wave (SAW) beam emanating from a series of focused 6 μm substrate wavelength interdigital transducers patterned on a piezoelectric lithium niobate substrate and actuated with a 633 MHz sinusoidal signal. This streaming field serves to focus fluid streamlines such that incoming particles interact with the acoustic field similarly regardless of their initial starting positions, and results in particle displacements that would not be possible with a travelling acoustic wave force alone. This streaming-induced manipulation of nanoscale particles is maximized with the formation of micro-vortices that extend the width of the microfluidic channel even with the imposition of a lateral flow, occurring when the streaming-induced flow velocities are an order of magnitude larger than the lateral one. We make use of this acoustic streaming to demonstrate the continuous and differential focusing of 100 nm, 300 nm and 500 nm particles.
1. Introduction
Manipulation of submicron particles, those smaller than 1000 nm in diameter, is vitally important to an increasing number of industrial and biomedical applications. The increased surface area of nanoparticles is vital to their use in reaction catalysis,1 batteries,2 fuel cells3 and petrochemical industry.4 In cancer diagnostics, submicron sized vesicles called exosomes are increasingly regarded as crucial diagnostic targets, since they often contain various molecular markers of their cell of origin, including DNA, RNA and proteins, that are correlated with the existence of cancer lesions and other pathophysiology that are not yet visible in standard imaging techniques.5 Despite this potential need for nanoscale particle manipulation, there is a dearth of effective methods for the manipulation and size-selective concentration of objects at this scale; conventional techniques such as nanopore filters or ultracentrifugation are lossy with poor material recovery rate, resulting in incomplete separation, or too low throughput and/or expensive for routine use.6The expanding field of microfluidics, where fluids are guided and manipulated in microscale channels, offers the ability to circumvent these constraints by applying forces closer to the scale of nanoparticles themselves. Previous work, however, has almost exclusively demonstrated the manipulation of only individual or small numbers of nanoparticles.7–9 Manipulation of particles and biological specimens has long been a goal of microfluidic systems, where sorting, separation, mixing and concentration of microscale particles has been routinely demonstrated.10 Manipulation of submicron particles, however, presents a challenge for the microfluidic paradigm, where force gradients on the order of the particles themselves are usually required for effective motion. Hydrodynamic,11–13 electrostatic14 and electrokinetic15 forces have been used for submicron separation and concentration, though their utility is strongly constrained by the physical features required to generate nanoscale shear and force gradients, often resulting in either poor separation efficiency or clogging risk. Optical methods have had the most success scaling forces down to the nanoscale, where optical beams can be readily focused and near-field interactions have been used to trap individual nanoparticles8,16–21 and nanowires.22 The strength of these optical forces, however, is not sufficient for high-throughput manipulation of nanoparticles, and as such is usually demonstrated in static fluids.
Acoustic actuation is capable of generating large forces on particles, though the traditional method of generating them in microfluidic systems, by affixing a typically <10 MHz frequency-matched transducer to a system with resonant-condition channels or membranes, generally creates acoustic wavelengths of >100 μm in a coupled fluid.23–26 This large wavelength typically limits their application to ∼10 μm order particles, where larger acoustic field gradients and smaller wavelengths would improve their capacity to manipulate nanoparticles. Relatively recently, an acoustic transducer technology, one based on the generation of surface acoustic waves (SAW), has been developed for microfluidic actuation.27–29 Actuating a series of interdigital transducers (IDTs) on a piezoelectric material at their resonant frequency generates substrate displacements that travel along the surface and efficiently couples acoustic energy into contacting fluids. A significant advantage of SAW for nanoparticle manipulation is the range of frequencies it typically operates in, ∼10–1000 MHz, corresponding to wavelengths from ∼4–400 μm,30,31 and has demonstrated good biocompatibility in a variety of applications.32–35 Moreover, because the force propagates within the fluid itself, the clogging and poor yields associated with physical separation methods such as nanopore filters are avoided. Similar to optical fields, recent work has shown that acoustic fields can be highly focused into microscale regions as well. Collins et al. demonstrated the use of a focused set of IDTs to produce narrow acoustic beams only ∼10–20 μm wide.36,37 Compared to optical forces, those arising from acoustic fields are more suitable for high throughput, real-world applications due to the substantial forces on cells and particles they can generate without the need for complex optical equipment.38
However, travelling surface acoustic waves (TSAW) and standing surface acoustic waves (SSAW) alone are not inherently suitable for continuous nanoparticle manipulation. Standing acoustic waves (including those arising from SSAW) are theoretically capable of acting on submicron particles,37,39–41 and indeed have demonstrated the manipulation of 500 nm particles in standing wave nodal positions.30,41–43 Antfolk et al. cleverly combined a standing wave field with a streaming field that focused particles at the nodal position, where acoustic streaming typically acts to disperse nanoparticles rather than concentrate them,40 though this required the imposition of fine-tuned phase control and a long focusing channel.42 Manipulation in an acoustic standing wave occurs due to an acoustic radiation force that serves to push particles from regions of high acoustic energy density to lower ones; in the case of objects more dense than the surrounding media this results in collection at force equilibrium positions,44,45 typically at standing wave nodes.32,46–48 The potential for highly efficient separation in a standing wave field combined with a continuous flow is diminished, however, by the small distance over which displacements can occur (up to ¼ of the acoustic wavelength), which for high frequency SAW (>100 MHz) may only be a few microns. Setting the field at an angle to flow direction can circumvent this limitation,41,49 though this occurs to the detriment of throughput. Acoustic standing wave methods moreover have not demonstrated the ability to manipulate object diameters on the typical scale of common biological entities such as exosomes and viruses (∼200 nm).50–52 Similarly, TSAW requires fluid wavelengths on the order of the particle size for anisotropic scattering to generate sufficient translations for size-selective manipulation,53–56 which for nanoparticles would require wavelengths that are neither practically realizable nor useable even in microchannels, given the strong acoustic attenuation in the fluid and along the substrate at frequencies of GHz order or more. At the sub-GHz TSAW frequencies applied to date, the smallest particle size that has been successfully separated is 2 μm, utilizing a 10 μm SAW wavelength (≈3.7 μm in water) at 385 MHz,36 but is still larger than the dimensions of many bacteria (∼1 μm).57 Further, acoustic streaming, resulting from the nonlinear amplitude attenuation of an acoustic wave as it propagates through a dispersive media such as water, usually acts to defocus particle streamlines via the generation of acoustic streaming that reorganizes the flow in the vicinity of the acoustic field.58,59 The principles and effects of acoustic streaming are discussed in the next section.
Accordingly, there is a dearth of practical methods for the manipulation of nanoparticles to fulfil the technological need in current and future industrial and diagnostic processes. In this work we demonstrate high-frequency, highly-focused SAW for a continuous, filter-free manipulation of microscale particles and nanoparticles. In contrast to previous TSAW work, we demonstrate the continuous focusing of submicron particles using focused TSAW well below the particle size/wavelength ratio at which a travelling wave alone can effectively result in particle motion. This is made possible by explicitly taking advantage of the strong streaming that occurs in the vicinity of the focused TSAW beam, which serves to amplify the effect of the acoustic radiation force resulting from the strong force-potential gradient between the beam centre and its periphery by recirculating particles through this region. This acoustic streaming based focusing is demonstrated using a focused 6 μm wavelength, 633 MHz focused SAW device.
2. System principles and design
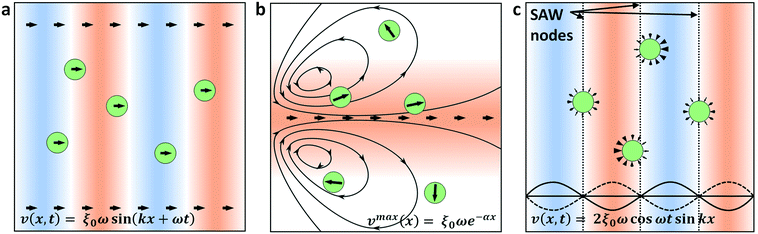
The acoustic radiation forces of interest for microfluidic particle manipulation are those arising from travelling waves and spatial gradients in a time-averaged force potential field, or in a periodic field arising from the intersection of two counter-propagating waves, this latter force is often termed the standing wave acoustic radiation force.47,60–62 These forces are typically applied independently in different systems, where either a TSAW or SSAW field is preferentially produced by the use of either one or two sets of IDTs, respectively. Despite the success of SAW systems in manipulating microscale objects, the acoustic manipulation of objects in the submicron regime has been limited by the physics of acoustic fields with microscale wavelengths, especially with regards to the relationship between the direct forces generated on the particles and those induced in the fluid through which the acoustic waves propagate, termed ‘acoustic streaming’.63 These acoustofluidic principles and their effects on particle trajectories are represented in Fig. 1. In the case of a travelling wave, the relationship between the generated force and particle size is strongly dependent on the ratio of the particle dimensions and the acoustic wavelength. For a particle radius R ≪ λ, the travelling wave force scales with the sixth power of the radius (FTW ∝ R6), is strongly nonlinear in the case where R ∼ λ, and scales with the interface area for R ≫ λ (FTW ∝ R2).53,64–70 While the scaling in the R ≪ λ regime is preferential for size-selective particle separation, the force magnitude in this case is too small to be practically useful; only when the particle diameter approaches that of the acoustic wavelength is the force substantial enough to generate significant particle translations, where the nature of the scattering of an acoustic wave off a particle interface transitions from isotropic (Rayleigh scattering regime) to anisotropic-dominant (Mie Regime).71,72 Several studies have shown the practical implications of this relationship, where a critical value of κ is required for effective particle translation (κ ≳ 1.3 for polystyrene in water), where κ = 2πR/λ.55,58,73,74 The minimum particle sizes that can be practically manipulated using the travelling wave force alone are thus limited by the acoustic wavelengths that can be generated; for typical 100–1000 MHz acoustic fields in water, the smallest particle diameters that can be manipulated are on the order of ∼1 μm. Further, even at the higher frequencies that might be used to generate particle translation, the effect of acoustic streaming becomes increasingly dominant for higher frequencies, where the attenuation per unit length in the fluid scales with ω2 and with ω1 along the substrate–fluid interface.75,76 This streaming works to the disadvantage of typical travelling wave translation systems, where a focused particle stream in a sheath flow is exposed to an acoustic force orthogonal to the fluid flow direction, and acts to defocus the output particle trajectories. Indeed, this effect has been utilized to continuously mix fluids to generate concentration gradients.77 Acoustic streaming is the result of the time-averaged body force generated in an amplitude-attenuating fluid volume as an acoustic wave travels within it, oriented in the direction of propagation.70 Though directional pumping is viable at limited pressure heads,75 the primary outcome of this propagation is rotational vortices arising from spatial variations in the body force. In the case of a finite-width SAW beam acting on an enclosed fluid volume, these vortices form at the edge of the SAW field.37,78,79Though other models of the body force arising from SAW have been successfully applied elsewhere,80–85 a model that properly incorporates attenuation in the fluid itself is required to simulate the behavior at higher frequencies. The coefficient of this attenuation scales with the square of the acoustic frequency, with attenuation lengths on the order of ∼10’s of μm for frequencies approaching 1 GHz. Given a substrate wave propagating along the x-direction, the time averaged acoustic body force at a given point (x, z) in a fluid subject to an attenuating plane wave that couples into it is given by37,86
FB = ρβ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) U1(x, U1(x,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) z)2, z)2, | (1) |
U1(x,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) z) = ξ0ωe−α(x−ztanθR)e−βzsecθR, z) = ξ0ωe−α(x−ztanθR)e−βzsecθR, | (2) |
The time-averaged acoustic radiation force component most significant for nanoparticle manipulation arises from spatial gradients in the time-averaged pressure and velocity fields in the fluid. Particles immersed in these fields preferentially migrate to discrete locations at minima in the force potential field, unlike the travelling wave force that is unbounded (albeit decaying) in the direction of acoustic propagation. Importantly for submicron particle manipulation, the acoustic radiation force scales with particle dimensions less strongly than the travelling wave force for R ≪ λ, with FR ∝ R3 instead of FTW ∝ R6, does not require wavelengths on the order of the particle sizes, and has flexibly demonstrated the effective manipulation of particles both on the order of the length scale of the acoustic force gradients32,87,88 and well below them.89,90 This force is most frequently applied in the form of an acoustic standing wave, in which particles most often preferentially migrate to nodal locations in a resonant channel or in a SSAW field. Less often utilized for particle manipulation, however, are the acoustic field gradients that arise at the edges of a travelling wave field, though examples exist in air and in water for particle patterning and manipulation in shaped fields,91 acoustic holograms92,93 or Bessel beams;90,94,95 these gradients are equally capable of generating particle forces as those in a periodic standing wave field (Fig. 1c). In typical SSAW transducer designs where the IDT aperture is significantly larger than the acoustic wavelength,34,47,73,84,96,97 this is a sensible design consideration, where the spatial gradient between adjoining nodal/antinodal positions is more predictable than the varying one at the periphery of the SAW beam.98 Focused transducer designs that utilize curved IDTs have been more recently applied, however, specifically to shape the acoustic beam within the desired dimensions and permit the generation of highly localized fields.36,37,56,83,99–102
In this work we utilize acoustic streaming combined with the acoustic radiation force to focus particles in a continuous flow for dimensions below the limit at which the travelling wave force alone cannot be used to manipulate particle trajectories. Fig. 2a shows an illustration of this principle in action, where an input of nanoscale particles is continually focused in the combined SAW/streaming field. Fig. 2b shows the principle of how acoustic streaming serves to enhance displacement by extending the time to which particles are exposed to the acoustic force potential gradients in the vicinity of an acoustic beam. Fluid streamlines are oriented at increasingly orthogonal orientations to the principle flow direction for increasing acoustic powers, leading to shallower angles at which the particles interact with the acoustic field and thus larger displacements relative to the streamlines from which they are originated. Fig. 2c and Video S1† demonstrate this principle in action, where 300 nm particles in an incoming particle suspension are firstly trapped in the vortices resulting from acoustic steaming in the vicinity of a focused, high frequency SAW beam (λSAW = 6 μm at 633 MHz) and are subsequently focused into the most distal streamlines. In this work we explore the limitations in utilizing forces arising from the travelling wave force alone and demonstrate the manipulation of nanoscale particles using focused TSAW, though in the absence of effective forces from travelling waves themselves.
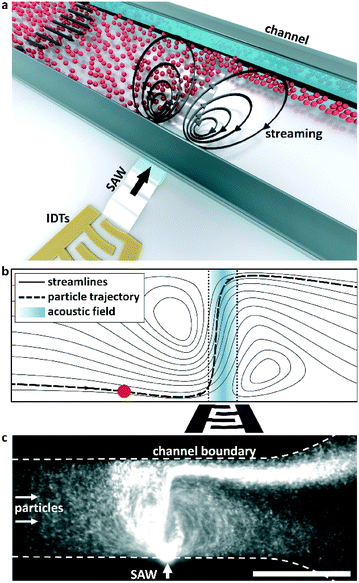 | ||
| Fig. 2 Principle of SAW based nanoparticle focusing. (a) Conceptual diagram: the combined streaming field and acoustic radiation forces resulting from the coupling of substrate vibrations produced by an IDT on a piezoelectric substrate results in focused particle displacements. (b) A particle (red) is displaced relative to the fluid streamlines by the acoustic radiation force as it passes through a focused SAW beam. The streaming serves to direct the particle laterally to the acoustic beam and maximize its exposure to the acoustic gradients in its periphery. (c) A continuous influx of 300 nm particles is focused in a low velocity flow, as shown in Video S1.† Scale bar is 100 μm. | ||
3. Methods
A SAW beam is produced when an AC signal is applied across a series of IDTs at their resonant frequency; the substrate displacement amplitudes are maximized when the displacements emanating from one set of IDT finger-pairs are reinforced by nearby ones. This frequency is given by f = c/λSAW, where λSAW is the minimum periodic length scale of the IDTs, equal to the width of one finger-pair in a conventional (two-finger) IDT design. While directional transducer designs have been widely utilized elsewhere,77,103–106 these typically require feature sizes ∼λSAW/8, a dimension non-trivial to fabricate for small wavelength SAW devices. Other surface-displacement vibration modes have been utilized elsewhere that do not require microscale electrode structures,107,108 though these are unable to generate the highly localized SAW displacements that are required for locally enhanced acoustic streaming.The SAW device is comprised of a focused IDT electrode structure patterned on a piezoelectric 128° rotated Y-cut X-propagation lithium niobate (LN, LiNbO3) substrate. IDTs are composed of a conductive 200 nm Al layer on top of an adhesion-promoting 7 nm Cr layer, with 300 nm SiO2 coating the entirety of the substrate to enhance channel bonding. The circularly focused 6 μm wavelength IDTs subtend an angle of 26°, with 42 finger pairs and a terminal aperture of 14 μm. The required 633 MHz AC signal was generated from a high frequency signal generator (Rigol DSG815, Beijing, China) and amplified using a broadband amplifier (Empower 1100, Inglewood, CA). Channels were formed using polydimethylsiloxane (PDMS) soft-lithography from a 12 μm high SU-8 pattern (SU-8 2025, MicroChem, Newton, MA) on a silicon wafer. PDMS channels were bonded to the piezoelectric substrate after components were exposed to an air plasma (Harrick Plasma PDC-32G, Ithaca, NY), with oxygen as the reactive component to yield hydroxyl-group termination on both surfaces. Fluorescent polystyrene particles (coefficient of variation ≈ 3%) were obtained from Magsphere, USA.
Numerical simulations with a 3D geometry were performed using a multiphysics finite element analysis tool (COMSOL v5.0) to model the fluid streamlines in the vicinity of the focused SAW beam, where the body force is simulated according to eqn (1) within a 12 μm wide band, using eqn (2) to model the displacement velocity in the fluid. The parameters α−1 ≈ 12.8λSAW and β−1 ≈ 3e6λSAW2 (the attenuation lengths at the substrate/fluid interface and in the fluid) were used to calculate the attenuation along the substrate–fluid interface and within the fluid itself,37,76 using the material values ρf = 998 kg m−3, cf = 1484 m s−1, ρs = 4628 kg m−3, cs = 3931 m s−1, and b ≈ 2 mP s (ref. 81, 109 and 110). Each voxel in these simulations is less than 1 μm3, an order of magnitude less than the beam width or channel height, to eliminate numerical error arising from mesh parameters.
4. Results and discussion
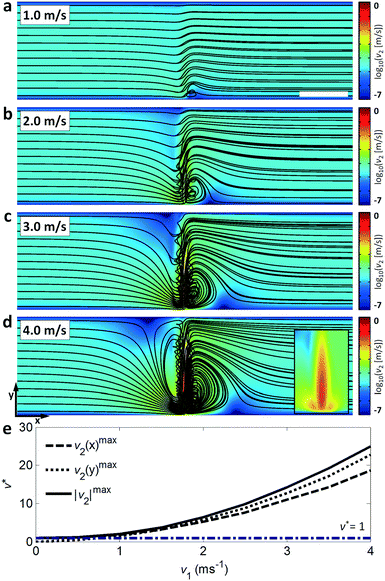
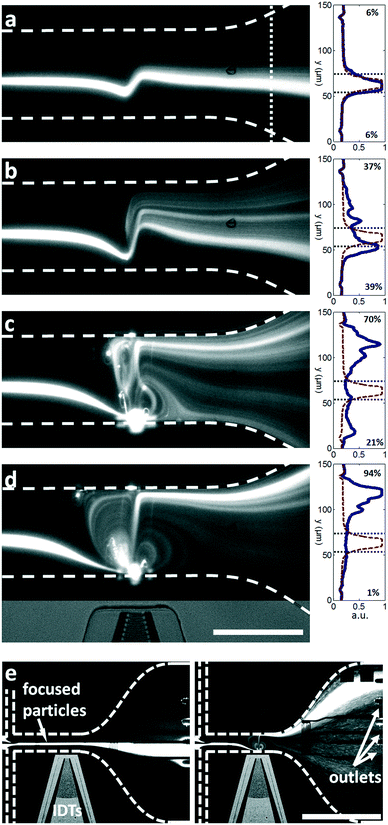
The travelling wave force arises from the directional scattering of a plane wave off a non-zero acoustic contrast interface, and is capable of generating appreciable particle displacements when the particle dimensions are on the order of the acoustic wavelength in the fluid. Fig. 3(a–c) shows the translation and concentration of 1 μm and 2 μm particles in a 160 μm wide, 20 μm high channel subject to a focused λSAW = 6 μm SAW. With a 2.25 μm fluid wavelength (λf = CfλSAW/Cs) in the case of λSAW = 6 μm, these particle sizes result in κ values of κ1μm ≈ 1.4 and κ2μm ≈ 2.8, at or above the critical value κc ≈ 1.3 at which the plane wave scattering transitions from an isotropic regime66 to the directional, backscattering dominant one.111 Interestingly, this force is roughly equivalent for both particle sizes (based on their similar displacements), despite their 8-fold difference in volume, due to the nonlinear force scaling when the particle dimension approaches the fluid wavelength.55 Video S2† shows the increased particle displacements for a focused λSAW = 6 μm beam for increasing applied powers, from 0.1 mW to 10 mW. However, this κc value is not attained for both particle sizes for larger acoustic wavelengths. Fig. 3(d–f) shows the same particle solution in a 400 μm wide, 40 μm high channel subject to a focused λSAW = 10 μm SAW. While the larger 2 μm particles are still displaced relative to their initial trajectories (with κ2μm ≈ 1.7), 1 μm particles (κ1μm ≈ 0.8) are not, emphasizing the critical nature of the κ parameter for travelling wave particle manipulation. In practice this characteristic makes the travelling wave force impractical to utilize for submicron particles, where particles smaller than ∼600 nm would require submicron electrode features that are impractical to reliably fabricate with conventional lift-off photolithography. Furthermore, Fig. 3(c and f) shows the effect of higher power levels on particle behaviour, where increasing streaming velocities lead to vortex-based trapping and non-uniform particle displacements due to acoustic streaming-based perturbations of the incoming flow profile, where trapped particles exit from the vicinity of vortex locations once their trapping capacities have been reached. The streaming effect is pronounced in this case compared to other travelling wave-based displacement work owing to the strongly focused nature of the transducers used, which maximize the acoustic force gradients in the vicinity of the focused beam.37 Though the effects of travelling wave force and acoustic streaming-based particle translation are mismatched for particle sizes where κ > κc, where the travelling waves tend to dominate particle trajectories, particle with sizes in the κ < κc regime are not affected by the former. If streaming-based effects can yield particle displacements in the absence of the travelling wave force, then particle focusing and translation can still occur for submicron particles.To evaluate the effects of streaming on suspended particle trajectories, we examine the nature of the developed streaming patterns when acoustic streaming is combined with the lateral flow. Previous work has utilized TSAW oriented perpendicular to a continuous flow without appreciable streaming-based effects, even where focused transducers are used.36,54,58,112 In these cases, however, streaming patterns are not readily apparent because the rate of lateral flow is substantially higher than that generated from the acoustic beam, where the power applied to generate sufficient travelling wave induced particle translation is insufficient to generate appreciable flow disturbances. Moreover, because the magnitude of the body force scales with the square of the applied frequency (as per eqn (1)), streaming is more likely to dominate as the acoustic attenuation length scale (β−1) in the fluid and along the substrate (α−1) approaches that of the channel dimensions, a condition not realized in with <200 MHz SAW that is typically employed for travelling wave work.58,74Fig. 4 examines the flow patterns that develop when this relationship is inverted (the streaming velocity magnitude is larger than that of the lateral velocity) and shows the simulated effect of increasing body forces for a simulated 6 μm wavelength, 633 MHz acoustic beam acting orthogonal to a 7 mm s−1 (mean) lateral flow in a 100 μm wide channel. To conform to the convention where the x-direction is the horizontal one (with respect to our figures), we define our coordinates here such that the SAW propagates along the y-direction and the fluid flow moves from left to right in the x-direction. The effects of these forces on fluid velocities and streamlines are shown here for the maximum velocity induced in the path of the acoustic beam from acoustic streaming (characterized by the time-averaged second-order streaming velocity v2) relative to the maximum lateral flow velocity (10.9 mm s−1), given by v* = vmax2/vf, where the streamlines are increasingly streaming-dominated for increasing applied powers. At relatively small substrate velocities (v* = 1.9, Fig. 4a) the body force acts to divert momentarily those fluid streamlines directly in the path of the beam, where vortices first occur on the channel side where the beam enters for increasing v*; the streaming induced flow is strongest here, where the beam is unattenuated (ξ = ξ0) relative to the opposing side of the channel (ξ = 0.27ξ0). For increased power levels the flow is increasingly diverted at more significant angles relative to the steady-state flow, with the appearance of a vortex on the opposite side of the channel (v* = 14, Fig. 4c). Finally, the streaming field comes to completely dominate streamline behaviour when v* ≫ 1, where effectively symmetric vortices emerge and the flow in the direct path of the acoustic beam is almost perpendicular to the fluid flow direction (Fig. 4d). Though previous work has demonstrated the generation of gradients using a focused acoustic beam,77 it is likely that fluid reorganization occurs primarily due to flow in the z-plane in a channel substantially higher (140 μm) than that used in this work (12 μm). Fig. 4e shows v* for increasing susbtrate velocities for the maximum velocity in the x and y directions as well as the absolute maximum. The v2 (y)max parameter is naturally at a minimum without the imposition of an acoustic beam, but makes the primary contribution to the absolute velocity magnitude at higher substrate velocities. Though the beam is directed along the y-direction, v2 (x)max nonetheless increases in line with v2 (y)max, where mass conservation requires the fast ingress of fluid toward the beam centreline to replace the fluid translated by the acoustic body force.
From the perspective of particle manipulation the streaming force in the v* ≫ 1 regime serves to force all fluid streamlines to enter the path of the beam in a highly localized region (near the channel wall at the beam source) so they experience near-identical acoustic radiation forces regardless of their entry point in the upstream channel, and generates flow nearly parallel to the acoustic beam that enhances the effect of the acoustic radiation force to displace these particles relative to the fluid streamlines. The interaction of a focused 300 nm particle stream in a continuous flow (0.45 μl min−1) is shown in Fig. 5. These results demonstrate the importance of the v* regime for consistent particle manipulation. For v* ≤ 1 the particles are largely unperturbed relative to the fluid streamlines (Fig. 5a), as demonstrated by the percentage of fluorescence intensity (with SAW, blue line) relative to the initial case (without SAW, red dashed line) displaced in either the +y or −y direction, shown in the distributions to the right of each image. These intensities are assayed at the x-location of the white dashed line in Fig. 5a. At intermediate power levels a substantial fraction of particles are displaced, but even in a focused particle stream this is still most likely to occur for particles near the channel boundaries where the acoustic radiation force is locally sufficient to dominate over fluid drag (Fig. 5b and c); particles in faster moving streamlines are displaced less by the acoustic field. Moreover, particle translation does not strictly occur in the direction of propagation, especially when particles flow into or are momentarily retained in streamlines on the outlet side of the focused beam, occurring when particles cross over the acoustic beam at locations closer to the SAW source. Here the same acoustic radiation force that results in +y displacement on the inlet side of the beam generates the opposite displacement, displacing particles into streamlines that exit in the −y direction. It is only in the v* ≫ 1 case that substantial streaming-induced particle redirection occurs; by tightly focusing the fluid streamlines and particles, they are all exposed to a roughly equivalent acoustic radiation force that results in 94% of measured fluorescence intensity being displaced relative to the initial state (Fig. 5d). Fig. 5e shows the macro-scale perspective, where this focused particle stream is redirected to different microchannel outlets.
Importantly, strong acoustic streaming (with v* ≫ 1) aligns fluid streamlines along the axis of the acoustic beam; without this effect the acoustic radiation forces alone do not lead to particle focusing. Substituting practically realisable acoustic energy densities into the equation describing the acoustic radiation force resulting from the force potential gradients on either side of a focused acoustic beam yields forces on the order of <10−11 N for submicron particles, with ∼10 μm beam widths and ∼1 m s−1 substrate velocities.67 This force is on the same order of magnitude as the counteracting viscous drag for these particles in ∼1–10 mm s−1 velocity flows in water. Realizing a sufficient acoustic radiation force to oppose fluid drag is a necessary condition for particle manipulation, though as the acoustic radiation force acts primarily orthogonally to the flow direction here, and at no position along the propagation direction is the acoustic radiation force greater than that of the average countervailing drag force resulting from lateral flow, this force alone is insufficient to result in particle focusing. It is by orienting the particle trajectory via acoustic streaming along the direction of beam propagation that particles are preferentially displaced into streamlines that exit the streaming region closer to the opposing channel wall.
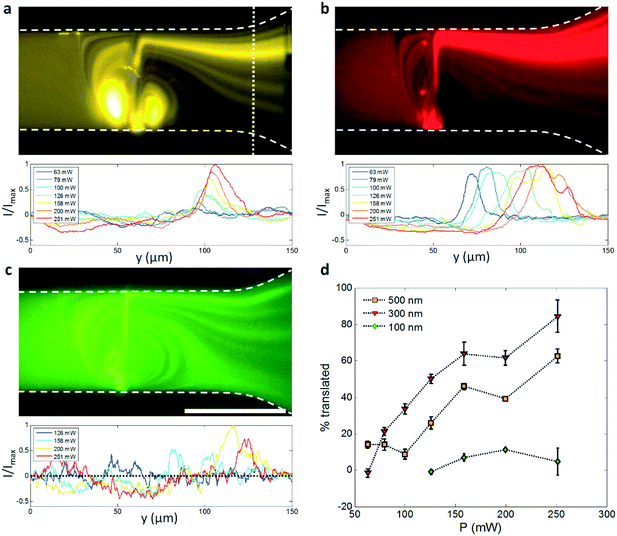
Fig. 6 demonstrates that this effect occurs for all fluid streamlines entering the acoustic streaming field, not just those that are pre-focused hydrodynamically. Here a continuous 500 nm, 300 nm and 100 nm particle suspension is concentrated into a focused particle stream in Fig. 6a–c, respectively. The coloration shown represents the natural fluorescence of these particles, namely orange, red, and green, without colour manipulation. This streaming-induced particle focusing is power dependent, where concentration is maximized with the formation of a vortex immediately upstream of the focused beam that results in the exposure of particles to similar acoustic gradients regardless of their initial starting location in the y-direction and results in a greater proportion of particles being displaced into more distal streamlines. Because the acoustic radiation force is size dependent, with FR ∝ R3, it seems intuitive that larger particle sizes result in larger deflections and thus better particle focusing for a given pressure amplitude. Indeed, this is the case for 300 nm vs. 100 nm particles, where the percentage of particles cleared from the lower half of the channel is 84 ± 9% vs. 5 ± 7% at 251 mW (Fig. 6d). Percentages are assessed by the proportion of fluorescence intensity reduction in the lower half of the channel relative to the base case (with particles but no SAW applied), where image intensity is measured by the area under the curve and where Fig. 6d shows the measured image intensity normalized by the base case. The reduced fluorescence intensity in the lower half of the channel is reflected in the increased intensity in the upper half. Values represent the average of five separate measurements taken 5 seconds after the application of SAW (to ensure particle focusing stability) at the white dashed line to the right of Fig. 6a. These experimental observations, where the smaller 100 nm particles cannot be effectively manipulated en-masse for the utilized channel height and beam width, are in line with previous work which shows that a critical particle size exists for a given combination of these parameters, where smaller channel heights and/or larger acoustic gradients are required for the acoustic radiation force to dominate over the x-direction streaming velocities that serve to disperse particles.37 This phenomenon arises from a straightforward balance between the acoustic radiation force and the viscous drag arising from acoustic streaming that opposes it; the dominance of viscous drag generally precludes particle manipulation by the acoustic radiation force.39,40
What is interesting, however, is that this size dependence with respect to concentration efficiency is not linear, even when acoustic radiation pressure is dominant, with 500 nm particles actually concentrating less completely than 300 nm ones for a given input power. Also notable is the differing relationship between the y-location of focused particle streams and applied power for 300 nm and 500 nm particles; whereas the y-location of the intensity peaks in Fig. 6a is roughly stable for the larger particles, it translates across the channel width for increasing applied powers in the case of the 300 nm ones. Both results can be explained by the increased acoustic radiation force imparted on these larger particles. Because of these larger radiation pressures, particles actually have the propensity to become trapped within the rotating vortices on either side of the focused beam in the same manner in which the larger 2 μm particles were trapped in Fig. 3; the accumulation of particles in this region alters fluid streamlines and their velocities, and creates a mass of particles that expands into and leaks across the focused SAW beam as it accumulates particles, including the region at the top of the channel closest to the channel wall where the displacement magnitude of the acoustic beam propagating at θR is somewhat reduced.53 The relatively stable location of the maximum intensity is also explained by the larger force imparted on the 300 nm particles, where the acoustic radiation force is given by:
| FR = 4πφR3kEac, | (3) |
While the combination of focused SAW and the resulting streaming has a defined effect on suspended particles, its activity is not limited to translation and focusing. Fig. 7 demonstrates two properties: that the translation activity genuinely occurs primarily as a result of acoustic interactions rather than a simple reorganization of the streamlines (which nevertheless occurs, especially evident in Fig. 7a), where particles in a hydrodynamically focused dye suspension are displaced and concentrated at particular locations within the outlet fluid, and that the strong streaming in the vicinity of the focused beam can also perform rapid mixing. Here, tight focusing of fluid streamlines in the vicinity of the focused beam – the streamlines from the 100 μm wide channel are all focused into a region only microns wide – results in diffusion in a manner analogous to the fluid folding action from microfluidic mixing herringbone structures,113,114 which minimize the distance over which diffusion occurs. Strikingly, while these structures require multiple periodic elements to accomplish appreciable mixing, we observe mixing indices of 0.61, 0.30 and 0.16 for the 63 mW, 126 mW and 251 mW applied powers (where 1 is no mixing and 0 is complete mixing) in Fig. 7 after only one mixing element, computed according to the same mixing index formulation as in previous SAW work.115 Destgeer et al. previously employed SAW for gradient generation in continuous flow, though the appearance of vortices, which both enhance diffusive mixing and permit the translation of fluid across the entire extend of the channel, were not present.77 See Video S3† for a side-by side comparison of the particle suspension from Fig. 7 (left images) in both fluorescence and brightfield imaging.
5. Conclusions
There is a dearth of microfluidic methods for manipulating nanoscale objects, especially when throughput is required. High frequency acoustic forces are uniquely suited to microfluidic applications, though have typically been utilized for manipulation of microscale objects or larger. For standing acoustic waves, the small wavelengths required to act on submicron particles result in particle translations relative to the field that are at most a quarter of the wavelength. Acoustic streaming, which tends to manifest more profoundly at higher frequencies, also typically acts to the detriment of acoustic-based focusing. Streaming occurs in both standing and travelling acoustic wave-dominant fields, though has the advantage of acting over multiple acoustic wavelengths in the case of a travelling wave field. Travelling waves, however, are incapable of generating substantial forces on submicron objects for sub GHz frequencies from the travelling force alone.Overcoming the limitations in utilizing the travelling wave or standing wave force alone, we have combined the acoustic forces resulting from the imposition of a stationary, high-gradient focused acoustic beam with a strong streaming field that serves to normalize the exposure of suspended objects to this field. As substrate-bound wavemodes are uniquely suited for generating highly localized acoustic beams, we demonstrate here a technique based on acoustic streaming enhanced SAW to robustly manipulate particles well below 1 μm in diameter. Methods based on this technique have the unique potential to concentrate and focus nanoscale objects in a continuous flow without the need for filters or submicron structures.
Acknowledgements
This work was supported by SUTD Startup Research Grant (SREP13053) and Singapore Ministry of Education Academic Research Fund Tier 2 (T2MOE1603) awarded to YA. D. J. C. gratefully acknowledges the support from SUTD-MIT Postdoctoral Fellowship.References
- M. Stratakis and H. Garcia, Chem. Rev., 2012, 112, 4469–4506 CrossRef CAS PubMed.
- B. Koo, H. Xiong, M. D. Slater, V. B. Prakapenka, M. Balasubramanian, P. Podsiadlo, C. S. Johnson, T. Rajh and E. V. Shevchenko, Nano Lett., 2012, 12, 2429–2435 CrossRef CAS PubMed.
- F. S. Majedi, M. M. Hasani-Sadrabadi, S. H. Emami, M. Taghipoor, E. Dashtimoghadam, A. Bertsch, H. Moaddel and P. Renaud, Chem. Commun., 2012, 48, 7744–7746 RSC.
- M. Hosseinpour, S. Fatemi and S. J. Ahmadi, Fuel, 2015, 159, 538–549 CrossRef CAS.
- R. Xu, D. W. Greening, A. Rai, H. Ji and R. J. Simpson, Methods, 2015, 87, 11–25 CrossRef CAS PubMed.
- B. J. Tauro, D. W. Greening, R. A. Mathias, H. Ji, S. Mathivanan, A. M. Scott and R. J. Simpson, Methods, 2012, 56, 293–304 CrossRef CAS PubMed.
- H. Zheng, U. M. Mirsaidov, L.-W. Wang and P. Matsudaira, Nano Lett., 2012, 12, 5644–5648 CrossRef CAS PubMed.
- A. A. Saleh and J. A. Dionne, Nano Lett., 2012, 12, 5581–5586 CrossRef CAS PubMed.
- M. Tanyeri and C. M. Schroeder, Nano Lett., 2013, 13, 2357–2364 CrossRef CAS PubMed.
- G. Destgeer and H. J. Sung, Lab Chip, 2015, 15, 2722–2738 RSC.
- M. Fouet, M.-A. Mader, S. Iraïn, Z. Yanha, A. Naillon, S. Cargou, A.-M. Gué and P. Joseph, Lab Chip, 2016, 16, 720–733 RSC.
- A. Mitra, F. Ignatovich and L. Novotny, J. Appl. Phys., 2012, 112, 014304 CrossRef PubMed.
- K. He, S. T. Retterer, B. R. Srijanto, J. C. Conrad and R. Krishnamoorti, ACS Nano, 2014, 8, 4221–4227 CrossRef CAS PubMed.
- K. K. Zeming, N. V. Thakor, Y. Zhang and C.-H. Chen, Lab Chip, 2016, 16, 75–85 RSC.
- A. Syed, L. Mangano, P. Mao, J. Han and Y.-A. Song, Lab Chip, 2014, 14, 4455–4460 RSC.
- A. H. Yang, S. D. Moore, B. S. Schmidt, M. Klug, M. Lipson and D. Erickson, Nature, 2009, 457, 71–75 CrossRef CAS PubMed.
- M. Ploschner, T. Cizmar, M. Mazilu, A. Di Falco and K. Dholakia, Nano Lett., 2012, 12, 1923–1927 CrossRef CAS PubMed.
- B. J. Roxworthy, K. D. Ko, A. Kumar, K. H. Fung, E. K. Chow, G. L. Liu, N. X. Fang and K. C. Toussaint Jr, Nano Lett., 2012, 12, 796–801 CrossRef CAS PubMed.
- O. M. Maragò, P. H. Jones, P. G. Gucciardi, G. Volpe and A. C. Ferrari, Nat. Nanotechnol., 2013, 8, 807–819 CrossRef PubMed.
- O. Brzobohatý, M. Šiler, J. Trojek, L. Chvátal, V. Karásek, A. Paták, Z. Pokorná, F. Mika and P. Zemánek, Sci. Rep., 2015, 5 Search PubMed.
- O. Brzobohatý, M. Šiler, J. Trojek, L. Chvátal, V. Karásek and P. Zemánek, Opt. Express, 2015, 23, 8179–8189 CrossRef PubMed.
- L. Zhang, X. Dou, C. Min, Y. Zhang, L. Du, Z. Xie, J. Shen, Y. Zeng and X. Yuan, Nanoscale, 2016, 8, 9756–9763 RSC.
- I. Leibacher, P. Reichert and J. Dual, Lab Chip, 2015, 15, 2896–2905 RSC.
- I. Leibacher, S. Schatzer and J. Dual, Lab Chip, 2014, 14, 463–470 RSC.
- G. Vuillermet, P.-Y. Gires, F. Casset and C. Poulain, Phys. Rev. Lett., 2016, 116, 184501 CrossRef PubMed.
- T. Laurell, F. Petersson and A. Nilsson, Chem. Soc. Rev., 2007, 36, 492–506 RSC.
- D. Beyssen, L. Le Brizoual, O. Elmazria and P. Alnot, Sens. Actuators, B, 2006, 118, 380–385 CrossRef CAS.
- A. Wixforth, Superlattices Microstruct., 2003, 33, 389–396 CrossRef CAS.
- H. Li, J. R. Friend and L. Y. Yeo, Biomed. Microdevices, 2007, 9, 647–656 CrossRef PubMed.
- R. J. Shilton, M. Travagliati, F. Beltram and M. Cecchini, Adv. Mater., 2014, 26, 4941–4946 CrossRef CAS PubMed.
- Z. Ma, J. Guo, Y. J. Liu and Y. Ai, Nanoscale, 2015, 7, 14047–14054 RSC.
- D. J. Collins, B. Morahan, J. Garcia-Bustos, C. Doerig, M. Plebanski and A. Neild, Nat. Commun., 2015, 6, 8686 CrossRef CAS PubMed.
- F. Guo, Z. Mao, Y. Chen, Z. Xie, J. P. Lata, P. Li, L. Ren, J. Liu, J. Yang and M. Dao, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 1522–1527 CrossRef CAS PubMed.
- F. Guo, P. Li, J. B. French, Z. Mao, H. Zhao, S. Li, N. Nama, J. R. Fick, S. J. Benkovic and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 43–48 CrossRef CAS PubMed.
- N. Sivanantha, C. Ma, D. J. Collins, M. Sesen, J. Brenker, R. L. Coppel, A. Neild and T. Alan, Appl. Phys. Lett., 2014, 105, 103704 CrossRef.
- D. J. Collins, A. Neild and Y. Ai, Lab Chip, 2016, 16, 471–479 RSC.
- D. J. Collins, Z. Ma and Y. Ai, Anal. Chem., 2016, 88, 5513–5522 CrossRef CAS PubMed.
- J. Nilsson, M. Evander, B. Hammarström and T. Laurell, Anal. Chim. Acta, 2009, 649, 141–157 CrossRef CAS PubMed.
- H. Bruus, Lab Chip, 2012, 12, 1578–1586 RSC.
- P. B. Muller, R. Barnkob, M. J. H. Jensen and H. Bruus, Lab Chip, 2012, 12, 4617–4627 RSC.
- D. J. Collins, T. Alan and A. Neild, Lab Chip, 2014, 14, 1595–1603 RSC.
- M. Antfolk, P. B. Muller, P. Augustsson, H. Bruus and T. Laurell, Lab Chip, 2014, 14, 2791–2799 RSC.
- H. Li, J. R. Friend and L. Y. Yeo, Phys. Rev. Lett., 2008, 101, 084502 CrossRef PubMed.
- P. Augustsson, J. T. Karlsen, H.-W. Su, H. Bruus and J. Voldman, Nat. Commun., 2016, 7 Search PubMed.
- J. W. Ng, D. J. Collins, C. Devendran, Y. Ai and A. Neild, Microfluid. Nanofluid., 2016, 20, 151 CrossRef.
- B. W. Drinkwater, Lab Chip, 2016, 16, 2360–2375 RSC.
- C. Devendran, N. R. Gunasekara, D. J. Collins and A. Neild, RSC Adv., 2016, 6, 5856–5864 RSC.
- R. D. O'Rorke, C. D. Wood, C. Wälti, S. D. Evans, A. G. Davies and J. E. Cunningham, J. Appl. Phys., 2012, 111, 094911 CrossRef.
- X. Ding, Z. Peng, S.-C. S. Lin, M. Geri, S. Li, P. Li, Y. Chen, M. Dao, S. Suresh and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 12992–12997 CrossRef CAS PubMed.
- M. Delbrück, J. Bacteriol., 1945, 50, 131 Search PubMed.
- W. Bernhard, Cancer Res., 1960, 20, 712–727 CAS.
- C. Mazzeo, J. A. Cañas, M. P. Zafra, A. R. Marco, M. Fernández-Nieto, V. Sanz, M. Mittelbrunn, M. Izquierdo, F. Baixaulli and J. Sastre, J. Allergy Clin. Immunol., 2015, 135, 1603–1613 CrossRef CAS PubMed.
- G. Destgeer, B. H. Ha, J. Park, J. H. Jung, A. Alazzam and H. J. Sung, Anal. Chem., 2015, 87, 4627–4632 CrossRef CAS PubMed.
- J. Behrens, S. Langelier, A. R. Rezk, G. Lindner, L. Y. Yeo and J. R. Friend, Lab Chip, 2015, 15, 43–46 RSC.
- V. Skowronek, R. W. Rambach, L. Schmid, K. Haase and T. Franke, Anal. Chem., 2013, 85, 9955–9959 CrossRef CAS PubMed.
- D. J. Collins, T. Alan and A. Neild, Appl. Phys. Lett., 2014, 105, 033509 Search PubMed.
- D. Issadore, H. J. Chung, J. Chung, G. Budin, R. Weissleder and H. Lee, Adv. Healthcare Mater., 2013, 2, 1224–1228 CrossRef CAS PubMed.
- G. Destgeer, B. H. Ha, J. H. Jung and H. J. Sung, Lab Chip, 2014, 14, 4665–4672 RSC.
- G. Destgeer, K. H. Lee, J. H. Jung, A. Alazzam and H. J. Sung, Lab Chip, 2013, 13, 4210–4216 RSC.
- P. Mishra, M. Hill and P. Glynne-Jones, Biomicrofluidics, 2014, 8, 034109 CrossRef PubMed.
- Y. Chen, S. Li, Y. Gu, P. Li, X. Ding, L. Wang, J. P. McCoy, S. J. Levine and T. J. Huang, Lab Chip, 2014, 14, 924–930 RSC.
- X. Ding, S.-C. S. Lin, M. I. Lapsley, S. Li, X. Guo, C. Y. Chan, I.-K. Chiang, L. Wang, J. P. McCoy and T. J. Huang, Lab Chip, 2012, 12, 4228–4231 RSC.
- A. Riaud, M. Baudoin, J.-L. Thomas and O. B. Matar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 013008 CrossRef PubMed.
- T. Hasegawa and K. Yosioka, J. Acoust. Soc. Am., 1975, 58, 581–585 CrossRef.
- T. Hasegawa and K. Yosioka, J. Acoust. Soc. Am., 1969, 46, 1139–1143 CrossRef.
- L. V. King, Proc. R. Soc. London, Ser. A, 1934, 147, 212–240 CrossRef.
- M. Settnes and H. Bruus, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 016327 CrossRef PubMed.
- B. T. Chu and R. E. Apfel, J. Acoust. Soc. Am., 1982, 72, 1673–1687 CrossRef.
- R. T. Beyer, J. Acoust. Soc. Am., 1978, 63, 1025–1030 CrossRef.
- J. A. Rooney and W. L. Nyborg, Am. J. Phys., 1972, 40, 1825–1830 CrossRef.
- I. Baydoun, D. Baresch, R. Pierrat and A. Derode, 2016, arXiv preprint arXiv:1607.06249.
- W. Kim and A. Majumdar, J. Appl. Phys., 2006, 99, 084306 CrossRef.
- G. Destgeer, H. Cho, B. H. Ha, J. H. Jung, J. Park and H. J. Sung, Lab Chip, 2016, 16, 660–667 RSC.
- Z. Ma, D. J. Collins and Y. Ai, Anal. Chem., 2016, 88, 5316–5323 CrossRef CAS PubMed.
- M. B. Dentry, J. R. Friend and L. Y. Yeo, Lab Chip, 2014, 14, 750–758 RSC.
- M. B. Dentry, L. Y. Yeo and J. R. Friend, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 013203 CrossRef PubMed.
- G. Destgeer, S. Im, B. H. Ha, J. H. Jung, M. A. Ansari and H. J. Sung, Appl. Phys. Lett., 2014, 104, 023506 Search PubMed.
- J. Reboud, Y. Bourquin, R. Wilson, G. S. Pall, M. Jiwaji, A. R. Pitt, A. Graham, A. P. Waters and J. M. Cooper, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15162–15167 CrossRef CAS PubMed.
- A. Sonato, M. Agostini, G. Ruffato, E. Gazzola, D. Liuni, G. Greco, M. Travagliati, M. Cecchini and F. Romanato, Lab Chip, 2016, 16, 1224–1233 RSC.
- D. J. Collins, O. Manor, A. Winkler, H. Schmidt, J. R. Friend and L. Y. Yeo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 056312 CrossRef PubMed.
- M. Alghane, B. Chen, Y. Fu, Y. Li, J. Luo and A. Walton, J. Micromech. Microeng., 2011, 21, 015005 CrossRef.
- S. Shiokawa, Y. Matsui and T. Ueda, Jpn. J. Appl. Phys., 1990, 29, 137 CrossRef.
- M. Darmawan and D. Byun, Microfluid. Nanofluid., 2015, 18, 1107–1114 CrossRef CAS.
- Y. Bourquin and J. M. Cooper, PLoS One, 2013, 8, e42686 CAS.
- A. Bernassau, P. Glynne-Jones, F. Gesellchen, M. Riehle, M. Hill and D. Cumming, Ultrasonics, 2014, 54, 268–274 CrossRef CAS PubMed.
- W. L. Nyborg, J. Acoust. Soc. Am., 1953, 25, 68–75 CrossRef.
- M. Caleap and B. W. Drinkwater, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 6226–6230 CrossRef CAS PubMed.
- A. Bernassau, P. MacPherson, J. Beeley, B. Drinkwater and D. Cumming, Biomed. Microdevices, 2013, 15, 289–297 CrossRef CAS PubMed.
- C. R. Courtney, C. E. Demore, H. Wu, A. Grinenko, P. D. Wilcox, S. Cochran and B. W. Drinkwater, Appl. Phys. Lett., 2014, 104, 154103 Search PubMed.
- C. R. Courtney, B. W. Drinkwater, C. E. Demore, S. Cochran, A. Grinenko and P. D. Wilcox, Appl. Phys. Lett., 2013, 102, 123508 CrossRef.
- C. E. Démoré, P. M. Dahl, Z. Yang, P. Glynne-Jones, A. Melzer, S. Cochran, M. P. MacDonald and G. C. Spalding, Phys. Rev. Lett., 2014, 112, 174302 CrossRef PubMed.
- K. Melde, A. G. Mark, T. Qiu and P. Fischer, Nature, 2016, 537, 518–522 CrossRef CAS PubMed.
- A. Marzo, S. A. Seah, B. W. Drinkwater, D. R. Sahoo, B. Long and S. Subramanian, Nat. Commun., 2015, 6 Search PubMed.
- D. Baresch, J.-L. Thomas and R. Marchiano, Phys. Rev. Lett., 2016, 116, 024301 CrossRef PubMed.
- A. Riaud, J.-L. Thomas, E. Charron, A. Bussonnière, O. B. Matar and M. Baudoin, Phys. Rev. Appl., 2015, 4, 034004 CrossRef.
- Y. Ai, C. K. Sanders and B. L. Marrone, Anal. Chem., 2013, 85, 9126–9134 CrossRef CAS PubMed.
- D. J. Collins, C. Devendran, Z. Ma, J. W. Ng, A. Neild and Y. Ai, Sci. Adv., 2016, 2, e1600089 Search PubMed.
- A. R. Rezk, O. Manor, J. R. Friend and L. Y. Yeo, Nat. Commun., 2012, 3, 1167 CrossRef PubMed.
- L. Ren, Y. Chen, P. Li, Z. Mao, P.-H. Huang, J. Rufo, F. Guo, L. Wang, J. P. McCoy and S. J. Levine, Lab Chip, 2015, 15, 3870–3879 RSC.
- A. A. Nawaz, Y. Chen, N. Nama, R. H. Nissly, L. Ren, A. Ozcelik, L. Wang, J. P. McCoy, S. J. Levine and T. J. Huang, Anal. Chem., 2015, 87, 12051–12058 CrossRef CAS PubMed.
- Y. Ai and B. L. Marrone, Microfluid. Nanofluid., 2012, 13, 715–722 CrossRef.
- D. J. Collins, T. Alan, K. Helmerson and A. Neild, Lab Chip, 2013, 13, 3225–3231 RSC.
- Y. Fu, J. Luo, X. Du, A. Flewitt, Y. Li, G. Markx, A. Walton and W. Milne, Sens. Actuators, B, 2010, 143, 606–619 CrossRef CAS.
- A. R. Rezk, A. Qi, J. R. Friend, W. H. Li and L. Y. Yeo, Lab Chip, 2012, 12, 773–779 RSC.
- L. Meng, Z. Deng, L. Niu, F. Li, F. Yan, J. Wu, F. Cai and H. Zheng, Theranostics, 2015, 5, 1203 CrossRef CAS PubMed.
- L. Alhasan, A. Qi, A. R. Rezk, L. Y. Yeo and P. P. Chan, Integr. Biol., 2016, 8, 12–20 RSC.
- A. R. Rezk, L. Y. Yeo and J. R. Friend, Langmuir, 2014, 30, 11243–11247 CrossRef CAS PubMed.
- G. Destgeer, B. H. Ha, J. Park and H. J. Sung, Anal. Chem., 2016, 88, 3976–3981 CrossRef CAS PubMed.
- X. He, H. Wei, J. Shi, J. Liu, S. Li, W. Chen and X. Mo, Opt. Commun., 2012, 285, 4120–4124 CrossRef CAS.
- G. S. Fanourgakis, J. Medina and R. Prosmiti, J. Phys. Chem. A, 2012, 116, 2564–2570 CrossRef CAS PubMed.
- W. H. Lin and A. Raptis, J. Acoust. Soc. Am., 1983, 73, 736–748 CrossRef.
- V. Skowronek, R. W. Rambach and T. Franke, Microfluid. Nanofluid., 2015, 1–7 Search PubMed.
- A. D. Stroock, S. K. Dertinger, A. Ajdari, I. Mezić, H. A. Stone and G. M. Whitesides, Science, 2002, 295, 647–651 CrossRef CAS PubMed.
- J. Marschewski, S. Jung, P. Ruch, N. Prasad, S. Mazzotti, B. Michel and D. Poulikakos, Lab Chip, 2015, 15, 1923–1933 RSC.
- R. J. Shilton, L. Y. Yeo and J. R. Friend, Sens. Actuators, B, 2011, 160, 1565–1572 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6lc01142j |
| This journal is © The Royal Society of Chemistry 2017 |