On-chip electromagnetic tweezers – 3-dimensional particle actuation using microwire crossbar arrays

Abstract

Emerging miniaturization technologies for biological and bioengineering applications require precise control over position and actuation of microparticles. While many of these applications call for high-throughput approaches, common tools for particle manipulation, such as magnetic or optical tweezers, suffer from low parallelizability. To address this issue, we introduce a chip-based platform that enables flexible three-dimensional control over individual magnetic microparticles. Our system relies on microwire crossbar arrays for simultaneous generation of magnetic and dielectric forces, which actuate the particles along highly localized traps. We demonstrate the precise spatiotemporal control of individual particles by tracing complex trajectories in three dimensions and investigate the forces that can be generated along different axes. Furthermore, we show that our approach for particle actuation can be parallelized by simultaneously controlling the position and movement of 16 particles in parallel.

---

Introduction

The ability to remotely manipulate microscopic objects is of major interest in various research applications. Consequently, the scientific community has seen a vivid activity in the development of methods for actuation and trapping of particles by defined force fields. Prominent examples include magnetic,¹ optical,^2,3 and acoustic tweezers.⁴

During the past thirty years, magnetic and optical tweezers have found a number of biophysical applications. In particular, the ability to generate and measure forces with high spatial resolution allows studies on the cellular,⁵ as well as the molecular level.^6–10 In this context, the complexity of many biological systems results in the need of high sample numbers to gather statistically reliable data. Recent examples show the feasibility of high-force actuation of molecules or cells,^11–14 yet, it is still difficult to operate tweezers in parallel.^6,8 While some degree of parallelization was shown, for instance, for magnetic¹⁵ and optical tweezers,¹⁶ the generation of large numbers of independent traps still remains a challenge.

A common approach to facilitate parallelization is the conversion of benchtop-scale experiments to chip-based tools. Driven by interest in miniaturization, chip-based particle actuation and its applications have been studied extensively during the past two decades.^17–20

Two of the most prominent methods used to manipulate particles on-chip are magnetophoresis and dielectrophoresis.^{18,19,21–23} Both methods rely on external fields that exert forces on a dipole. For most practical applications, this dipole is itself induced by the external field. Consequently, the application of forces is limited to objects with a susceptibility that differs significantly from that of the surrounding medium. Concerning magnetophoresis, this results in most biological matter being practically unaffected by the application of external magnetic fields. Hence, magnetic tags can be used very efficiently for sorting,^24–26 manipulation,^27,28 analysis,²⁹ and stimulation of cells.^30–32 In the case of dielectrophoresis, the differences in susceptibilities that are used to generate forces are usually intrinsic. The different susceptibilities of cells in different stages of the cell cycle, for instance, can be used to sort and synchronize cell populations.^33–35

A common approach to generate the fields needed for actuation in an on-chip setting is by using microstructured conductors.³⁶ These conductors can be soft-lithographically structured wires,³⁷ planar coils,³⁸ polyphasic conductors,³⁹ or meandering wires.⁴⁰ Theoretical aspects of the conductor geometry, as well as the force acting on an individual particle, have been presented by Ramadan et al.⁴¹ and Shevkoplyas et al.⁴²

A particularly versatile platform to generate localized magnetic fields on-chip is the microwire crossbar array. Lee et al. previously introduced their use for two-dimensional magnetic actuation and demonstrated control over groups of micro- and nanoparticles,⁴³ as well as biological cells.²⁷ More recently, we have used microscale crossbar arrays to split and merge groups of microparticles,⁴⁴ and steer individual microbeads.⁴⁵

Overall, however, many chip-based actuation platforms suffer from the ability to only actuate objects along one or two dimensions. Full three-dimensional control can usually only be achieved by implementing multiple layers of actuators, which comes at the cost of increased fabrication complexity. To circumvent this drawback, we present a chip-based actuation concept that uses a combination of attractive magnetophoretic and repellent dielectrophoretic forces (see Fig. 1).

Fig. 1 Schematic of three-dimensional particle actuation with microwire crossbar arrays. The wires are used to generate an attractive magnetic force, as well as a repulsive dielectrophoretic force. In combination, both of these forces can be used to generate stable traps in three-dimensional space.

Our actuation concept is able to control a particle's position with respect to all three dimensions of space while relying on standard planar microfabrication. This is achieved using combinations of attractive magnetophoretic and repellent dielectrophoretic force fields. We discuss simulated electric and magnetic fields that can be used for such a trap. We then apply these fields to the levitation of a single particle and measure its levitation height, which is dependent on the amplitudes of the DC and AC signals used to generate the magnetic and electric fields, respectively. Parallelization of the actuation concept is demonstrated by actuating 16 individual microbeads in parallel. In order to demonstrate full three-dimensional control, we present switching sequences that allow moving the levitating particle with respect to the x- and y-axes of the system and apply these sequences to complex three-dimensional trajectories. Finally, we evaluate the forces at play during the actuation by tracking the particle and back-calculating the force exerted on it.

Materials & methods

Chip fabrication

The microwire crossbar arrays were fabricated using state-of-the-art clean room technology. Briefly, a first set of 17 wires (wire width: 10 μm, wire spacing: 4 μm, metal stack: Ti/Al/Ti, 15/300/10 nm in thickness, respectively) was structured on an oxidized silicon substrate (purchased from Si-Mat Silicon Materials, Kaufering, Germany; oxidized in-house under wet conditions to obtain 1 μm of oxide) via optical lithography and a lift-off process (photoresist: LOR3B/NLOF2020, developer: MIF326; purchased from Micro-resist Technology, Berlin, Germany). Subsequently, an insulating stack of silicon dioxide/silicon nitride/silicon dioxide (100/50/100 nm in thickness, respectively) was deposited via plasma enhanced vapor deposition (Sentec Instrument GmbH, Berlin, Germany) and the second layer of wires was structured identical to the first one. In order to passivate the wires from the liquid during the experiments, a polyimide layer (PI-2610, HD Microsystems GmbH, Germany) was spin coated to a thickness of 1.4 μm (6000 rpm, 30 s). After passivation, the contact pads were opened via single layer resist lithography (AZ-5340, AZ Electronic Materials GmbH, Wiesbaden, Germany) and subsequent wet chemical etching in AZ-326 (metal ion free, MicroChemicals, Ulm, Germany). Resist residues were stripped using acetone. Finally, a glass ring was glued to the chip using poly(dimethylsiloxane) (Sylgard 184, Dow Corning Co., Midland, USA) to provide a liquid reservoir on top of the chip surface.

Experimental setup

During the particle actuation experiments, the chips were mounted in a custom-made socket. This socket connected the individual wires to the in-house built driving circuitry (see the ESI† for a more detailed description of the system). Using custom control software, each of the wires could be supplied with a DC signal for magnetic actuation. The AC signals used for the dielectrophoretic actuation were generated externally by a function generator and routed through the driving circuitry. All experiments described herein used an AC frequency of 2 MHz ensuring negative dielectrophoresis for the particles used in the experiments. Before application to a given wire, the signal was multiplied with an amplitude modulation factor as described below.

Simulations of the electric and magnetic fields

The electric fields were simulated using the finite element method (COMSOL Multiphysics®). The simulation considered a simplified 2-dimensional geometry. The chip was simulated as a rectangular domain of 200 μm in width, 100 μm in height and located at z = −50 μm. The material properties of this block were set to match the material properties of the polyimide used in the chip fabrication (ε_rel = 3.4, σ = 1.5 × 10¹⁷ Ωm). The medium on the chip was simulated by a rectangular domain of identical size located at z = 50 μm. For this domain, the material properties for water (ε_rel = 80, σ = 0.18 × 10⁶ Ωm) were used. In addition, four wires of a width of 10 μm and a height of 0.3 μm and a pitch of 14 μm were implemented symmetrically around the origin such that the top surfaces of the wires lie 1.4 μm beneath the polyimide/water interface. For the wires, the material properties of aluminum (ε_rel = 1, σ = 2.82 × 10⁻⁹ Ωm) were used. In order to calculate the electric field for a given input voltage, a quasi-static case was assumed. The potentials of the wires were set according to the maximum voltages reached during one cycle. The electric potential was obtained by solving LaPlace's equation (Δϕ = 0) with Dirichlet boundary conditions (ϕ = 0 for all external boundaries). The resulting electric field distributions were then converted to root-mean-square values by multiplication with .

The magnetic fields were simulated using analytical expressions for the magnetic field of a wire of rectangular cross-section as described before.⁴⁵ Briefly, Biot–Savart's law was integrated over the cross-section of the wire. Due to their low magnetic susceptibilities, the influence of all non-current carrying materials was neglected.

Particle actuation

For the particle actuation experiments, individual micrometer-sized beads were deployed into active magnetic traps. These traps were generated by supplying four wires with currents oriented such that the magnetic fields in the center of the wires overlap constructively. For particle deployment, the trap was operated at 50 mA per wire (see the ESI† for a more detailed description of current patterns). Subsequently, a microcapillary was loaded with a suspension of carboxyl functionalized particles (Dynabeads M-270 carboxylic acid, Life Technologies, Darmstadt, Germany; diluted 1 : 100 in deionized water) and paraffin oil. The capillary was brought into proximity of the active magnetic trap and a single particle was deployed by applying a gentle overpressure.⁴⁵ For the parallel actuation of multiple particles, several traps were activated and particles were individually deployed. The particles were then actuated using direct switching protocols as described in ref. 45 applied to all traps in parallel. In order to avoid overlap between neighboring traps, as well as unambiguities during actuation, only every third trap of the array in x- and y-directions was used.

The measurement of a single particle's levitation height was performed as follows. First, the current per wire was set to the desired value and amplitude modulated AC signals were applied to the four upper wires left and right of the particle's position. Subsequently, the particle's focal plane was determined with and without the AC signal using the microscope's z-stage. To obtain the absolute levitation height relative to the chip's surface, the radius of the particle was added to the difference of these values.

In order to actuate the levitating particle, the following protocols were used (see the ESI† for detailed schematics of the switching protocols). After trapping an individual particle as described above, a 3-dimensional trap was activated. To this end, four wires of the upper set were supplied with AC signals to fix the particle's x-position. Simultaneously, four wires of the lower set were supplied with DC currents to define the particle's y-position. In order to move the particle along the y-axis, only the DC configuration was modified. By changing the currents in the wires, the particle was moved to its target location in two steps. Similarly, in the case of switching along the x-axis, only the AC configuration was modified. Again, a two-step procedure was used to modify the particle's position with respect to the x-axis. A more detailed description of these procedures can be found in the ESI.†

Force calculation

In order to calculate the actuation forces in the focal plane, videos of the particle levitating in a square were recorded. Subsequently, the particle's position as a function of time was extracted from the video data as described before (see the ESI† for a short description of the data analysis).⁴⁵ This system can be described by an actuation force in the x/y-plane, F⃑_act,x/y, and the viscous drag force, F⃑_drag. The characteristic lag time for a sphere experiencing an actuation and a drag force is given as , where R is the particle's radius, ρ_p its density, and η the viscosity of the surrounding fluid.⁴⁶ For our system, τ evaluates to ≈0.4 μs. Given an interframe time of ≈20 ms, a constant equilibrium between the viscous drag force and the actuation force can be assumed. Hence the actuation force can be calculated using F⃑_act,x/y = −F⃑_drag,x/y = 6πηRv⃑_x/y, where η is the viscosity of the surrounding medium (1.002 × 10⁻³ Pa s for water at 20 °C), R is the hydrodynamic radius of the particle (1.35 μm for the particles used in the experiments) and v⃑_x/y is the particle's velocity in the x/y-plane. The latter can be approximated as the product of the particle displacement between two frames and the frame rate of the video data. The individual jumps along the x- or y-direction were separated and averaged over 70 jumps each (35 in the corresponding positive direction and 35 in the negative direction). Using the above given expression, the actuation force in the x/y-plane was calculated.

For the calculation of the magnetic force, the gradient of the squared magnetic field at a distance of 10 μm off the chip's surface was evaluated. The force on a magnetizable particle at low field strengths is then given as , where m⃑ is the particle's magnetic moment, B⃑ is the external magnetic flux density, V is the volume of the particle, Δχ represents the difference in the magnetic susceptibilities of the medium and the particle, and μ is the permeability of the surrounding medium. In our experiment, the particle was actuated in water. Due to the low susceptibility of water (χ_H2O = −9.035 × 10⁻⁶), we neglected the influence of the medium by using Δχ = χ_particle = 0.17 (taken from ref. 47) and μ = μ₀.

Results

Simulated electric and magnetic fields for 3D particle actuation

The actuation scheme presented in this paper makes use of the simultaneous application of repulsive dielectrophoretic and attractive magnetic forces to establish 3-dimensional control over a particle. To this end, AC and DC signals are applied simultaneously to the microwire crossbar array to generate the respective electric and magnetic fields. Fig. 2a shows a schematic of a subset of the array that is used to generate an AC electric field as indicated.

Fig. 2 Generation of electric and magnetic fields for 3-dimensional particle actuation. (a) and (b): Supplying two neighboring wires with an AC signal as indicated in (a) yields the electric field distribution shown in (b) (chip surface at z = 0, wire positions indicated by yellow rectangles; simulated at an AC input of 15 V). The negative gradient of the squared electric field creates a repellent force in the z-direction. However, the particle is repelled from the center position as well. (c) and (d): By distributing the signal over four wires as indicated in (c), the field distribution shown in (d) is obtained (chip surface at z = 0, wire positions indicated by yellow rectangles; simulated at an AC input of 15 V). In this case, a repellent force in the z-direction that simultaneously focuses the particle with respect to the x-axis is achieved. (e) Schematic of the DC currents applied to the lower set of wires to control the particle's y-position, as well as balance the repellent dielectrophoretic force. (f) Squared magnetic flux distribution in the y/z-plane simulated for the DC current configuration depicted in (e) (chip surface at z = 0, wire positions indicated by yellow rectangles; simulated at a DC input of 40 mA). The gradient of the squared magnetic flux creates an attractive force with respect to the z-axis, which balances the dielectrophoretic repulsion and fixes the particle's position with respect to the y-axis.

Fig. 2b shows a finite element simulation of the resulting field distribution in the x/z-plane. The chip's surface is located at z = 0 and the wires' positions are indicated by the yellow rectangles. As can be seen, the electric field is strongest at the chip's surface in between the two center wires (x = 0 μm). As intended this results in a dielectrophoretic force that repels the particle from the surface. At the same time, however, the gradient with respect to the x-axis will repel the particle from the center position, impeding a stable trap configuration.

In order to generate a field distribution that repels the particle from the chip's surface without destabilizing a potential trap, a more complex pattern, as shown in Fig. 2c, has to be used. Here, the AC signal is applied to four wires instead of two. Furthermore, to assure a force towards the center of the chip, the inner two wires' amplitude is modified by a factor of 0.75. The field distribution resulting from this configuration is shown in Fig. 2d. Similar to Fig. 2b, the field is strongest close to the chip's surface. Due to the additional use of the outer two wires, however, the negative gradient with respect to the x-direction points towards the center of the wires (x = 0). Consequently, the dielectrophoretic force resulting from this configuration can be used to repel a particle in the z-direction, while simultaneously fixing its position with respect to the x-axis. At a z-position of approximately 8–9 μm, a local minimum in field strength can be observed. This is due to the fact that two equipotential lines cross orthogonally at this point (see the ESI† for a more detailed explanation of this effect). As a result, the dielectrophoretic force above this position is attractive with respect to the chip.

As described above, using AC signals distributed over four wires allows the generation of a stable trap for the particle with respect to the x- and z-positions. In order to control the particle position in three dimensions, a second force field controlling its y-position, as well as balancing the repellent dielectrophoretic force, is needed. To this end, we make use of the lower set of wires to generate a magnetic field. Fig. 2e shows a schematic of the application of a DC current to four wires of the lower set. The corresponding field distribution in the y/z-plane is shown in Fig. 2f. A pronounced maximum in field strength can be seen around x = 0 in the proximity of the surface. Since the magnetic force is proportional to the gradient of the squared magnetic field, this will lead to a force attracting the particle towards the chip and fixing its position with respect to the y-axis. In combination with the dielectrophoretic force field described above, the particle's position with respect to all three axes of space is determined. The dielectrophoretic force field determines the particle's x-position, the magnetic force field determines the particle's y-position, and the ratio between the AC and the DC signals' amplitudes determines the particle's z-position.

Single particle levitation

The electric fields presented in the previous section yield dielectrophoretic forces that repel the particle from the chip's surface while simultaneously fixing its position with respect to the x-axis. In order to experimentally validate this behavior, a magnetic trap with four wires (as previously described^27,43–45) was used. Briefly, this type of trap was generated by supplying to pairs of neighboring wires with antiparallel DC currents of 10 mA such that the overall magnetic field in the center of the wires is strongest. After trapping an individual magnetic bead, an AC signal as described above was applied to the four upper wires next to the particle. Fig. 3a–d show an image sequence demonstrating the effect of different AC amplitudes. With the AC amplitude deactivated (Fig. 3a), the particle is trapped at the chip's surface. When increasing the AC amplitude to 6, 8, and 10 V (Fig. 3b–d, respectively), the particle slowly leaves the focal plane indicating a shift in the z-position (compare Video S1†). This shift is due to the higher electric field strength that results in stronger dielectrophoretic forces.

Fig. 3 Image sequence of a particle levitating at different AC amplitudes (compare Video S1†). (a) At an AC amplitude of 0 V, the particle is trapped at the chip's surface (scale bar amounts to 15 μm and applies to b–d as well). (b)–(d) At increasing AC amplitudes of 6, 8, and 10 V (respectively), the particle levitates out of the focal plane.

Using the microscope's z-stage, this shift was measured in dependence of the DC, as well as the AC amplitude. Fig. 4 shows measured levitation heights for DC amplitudes of 5, 10, and 15 mA at AC input amplitudes in the range of 4–20 V (n = 20). The plot shows that, at constant AC input amplitudes, higher DC amplitudes result in lower levitation heights. This is due to the DC amplitude increasing the magnetic field strength and thus the attractive effect of the magnetic force on the particle. However, at higher AC amplitudes, the influence of the DC amplitude decreases and the values tend towards a maximum levitation height of approximately 10 μm. In this regime, the effect of the dielectrophoretic force dominates and thus the attractive component of the magnetic force becomes negligible. The maximum levitation height illustrated by the plot corresponds to the local minimum in field strength visible in Fig. 2d. As the dielectrophoretic force attracts the particle to regions of low field strength, the particle will only be repelled to this position. At higher z-positions, the dielectrophoretic force acts attractive with respect to the chip's surface.

Fig. 4 Levitation height in dependence of the DC and AC amplitudes (n = 20). At lower AC input amplitudes, the amplitude of the DC signal has a strong influence on the levitation height. However, at high AC amplitudes, the measured values tend towards a maximum levitation height of approximately 10 μm.

As a demonstration of the parallelizability of the approach presented herein, we actuated 16 individual microbeads in parallel. Fig. 5 displays four frames that illustrate the parallel actuation (compare Video S2†). All 16 beads were successfully moved in square trajectories without losing any particles. Furthermore, no significant heating of the chip due to the increased power dissipation could be observed.

Fig. 5 Parallel actuation of 16 individual microbeads (scale bar in (a) corresponds to 50 μm; compare Video S2†). The particle positions and directions of motion are marked by circles and arrows, respectively. (a)–(d) show exemplary frames from an actuation experiment in which sixteen particles are moved along a square-shaped trajectory.

3-Dimensional actuation

In order to allow full 3-dimensional actuation, switching protocols that can transfer the particle from one position in the array to another are required. Here, a trap configuration using only the upper set of wires for the generation of dielectrophoretic forces and the lower set of wires for the generation of magnetic forces is used. Consequently, the switching procedures with respect to the x- and y-axes differ from each other. Fig. 6a shows a schematic of an actuation step along the y-axis. As indicated, the particle only crosses lower wires when being moved in this direction, while its position relative to the upper wires remains constant. Thus, the configuration of the AC inputs does not need to be changed during the process. As for the lower wires, a switching procedure that involves an intermediate step is most effective (see the ESI† for a more detailed description). In order to facilitate the translocation of the particle from its initial to its target position, this intermediate step was used to create a trap above the lower wire that was supposed to be crossed. Fig. 6b–d show an image sequence of a particle being actuated with this protocol at relative times of 0, 1, and 2 s, respectively. The white markers in Fig. 6c and d show the particle's positions as extracted via digital image analysis.⁴⁵ The shaded regions in Fig. 6b indicate the approximate position of the lower set of wires. At the start of the switching sequence (t = 0 s), the particle is trapped in the bottom right of the frame in between two of the indicated wires. At t = 1 s, the particle is shifted along the y-axis to the approximate middle of the center wire by the intermediate configuration described in the ESI.† Finally, at t = 2 s, the transfer is completed by activating a trap at the target position.

Fig. 6 Moving a levitating particle along the x- and y-axes (compare Videos S3 and S4†). (a) Schematic of an actuation step along the y-axis. The particle (brown) is levitating in the focal plane (illustrated in grey) at a z-position of approximately 10 μm. (b)–(d) Image sequence of a particle being moved along the y-axis during levitation (z-position approx. 10 μm above the chip surface, relative times are 0, 1, and 2 s, respectively). The white markers indicate the particle's trajectory as detected via digital image analysis. The shaded regions mark the approximate position of the lower set of wires. (e) Schematic of an actuation step along the x-axis. (f)–(h) Image sequence of a particle being moved along the x-axis during levitation (z-position approx. 10 μm above the chip surface, relative times are 0, 1, and 2 s, respectively). The shaded regions mark the approximate position of the upper set of wires. Scale bar amounts to 10 μm and corresponds to b–g as well. For clarity, the wires are marked by the white regions in b and f.

Fig. 6e shows a schematic of particle transport along the x-axis. In contrast to the switching procedure along the y-axis, the particle crosses the upper set of wires instead of the lower set. Consequently, the DC configuration of the lower wires can be held constant while the AC configuration applied to the upper wires has to be changed. Fig. 6f–h show an image sequence of a particle being moved along the x-axis. The images were taken at relative time points of t = 0, 1, and 2 s. The shaded regions in Fig. 6f indicate the approximate position of the upper set of wires. At the beginning of the transfer, the particle is trapped in the bottom left of the frame (t = 0 s, Fig. 6f). Subsequently, an intermediate step holding the particle over the approximate center of the wire to be crossed was activated (see Fig. 6g). This intermediate step is discussed in more detail in the ESI.† Finally, to complete the transfer, a trap at the target position was activated (Fig. 6h). The actuation procedures described above can be used to move the particle along the z-, y-, and x-axes of the system. This actuation can be performed continuously in the case of the particles z-position and in increments in the case of the x- and y-positions. In combination, this allows complex trajectories. One example of such a trajectory is shown in Fig. 7. In this experiment, a trajectory writing the letters ‘FZJ’ (acronym for Forschungszentrum Jülich) was traced by combining the actuation unit operations described above. Fig. 7a shows the positional data obtained from a video recorded in the levitation plane (z = 10 μm) via digital image analysis (compare Video S4†). In between the individual segments of the letters, the particle is lowered to the chip's surface, where it is actuated using only magnetic forces. By combining data from video material obtained in the levitation plane and at the chip's surface, the full trajectory of the particle can be reconstructed (Fig. 7b).

Fig. 7 3-Dimensional actuation of a single magnetic bead along a complex trajectory (compare Video S5†). (a) The particle positions detected in the levitation plane (white markers) write out the letters ‘FZJ’. Scale bar: 15 μm. (b) Combined data from two videos recorded in the levitation plane (open circles) and at the chip's surface (filled circles) is used to reconstruct the full trajectory of the particle (dashed line). In between the individual segments of the letters, the particle is lowered to the chip plane, where it is moved by magnetic actuation only.

Force calculation

An important aspect of chip-based particle actuation is the force that can be applied. Assuming that the overall actuation force (i.e. the sum of the magnetic and the dielectrophoretic force) is in constant equilibrium with the viscous drag force gives: F⃑_act = −F⃑_drag = 6πηR_hydrv⃑, where η is the viscosity of the medium, R_hydr is the hydrodynamic radius of the particle, and v⃑ its velocity. Using positional data obtained from a particle levitating at a z-position of approximately 10 μm, the x- and y-components of the actuation force were calculated. Fig. 8a and b show plots of the positional data obtained from analyzing 70 jumps along the y- and x-directions, respectively. For each axis, 35 jumps along the positive direction and 35 jumps along the negative direction were analyzed and the corresponding components of the actuation force were calculated as described in the Methods section. Both plots indicate forces in the low pN regime. Comparing the magnetic and the dielectrophoretic actuation (i.e. along the y- and x-axes, respectively), stronger forces in the case of the dielectrophoretic actuation can be noted. The magnetic force gives peak values of approximately 0.5 pN, while the maximum values for the dielectrophoretic force amount to approximately 1.25 pN. Consequently, the time the particle takes to reach a stable position is significantly shorter in Fig. 8b.

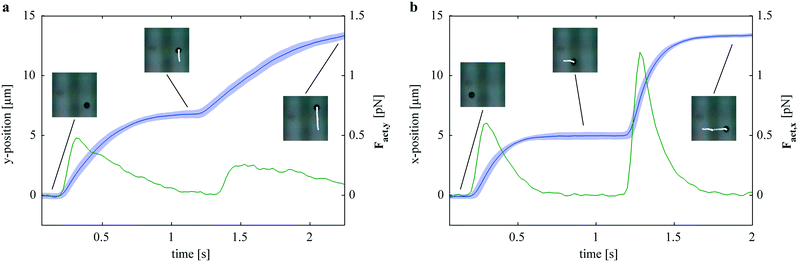Fig. 8 Y- and x-components of the actuation force calculated from positional data. (a) Average positional data ± standard deviation (blue line and shaded region, respectively) of 70 actuation events along the y-axis (35 in the positive and 35 in the negative y-directions). The green line represents the y-component of the actuation force calculated as described in the text. The inlays indicate the time points corresponding to Fig. 6b–d. (b) Average positional data ± standard deviation (blue line and shaded region, respectively) of 70 actuation events along the x-axis (35 in the positive and 35 in the negative x-directions). The green line represents the x-component of the actuation force calculated as described in the text, the inlays indicate the time points corresponding to Fig. 6f–h.

During the actuation, the amplitude of the DC signal is modified in order to maintain the particle's z-position constant. The z-component of the actuation force is thus zero. Thus, the magnetic and dielectrophoretic forces along the z-axis have to be of equal magnitude but of opposing sign. Fig. 9 shows an analytical simulation of the z-component of the magnetic force at z = 10 μm. The x-position of the particle relative to the upper set of wires corresponds to Fig. 6b–d. The individual curves correspond to the initial, intermediate, and final state (blue, green, and red, respectively) of the DC input during the switching procedure. During all three states, the z-component of the magnetic force is in the range of 0.2–0.3 pN. In order to maintain a constant levitation height, the z-component of the dielectrophoretic force has to be in the same range. It has to be considered, however, that this does not account for high AC input amplitudes of more than 15 V. In this case, the z-components of the magnetic and the dielectrophoretic force do not need to be of equal magnitude as the levitation height is mainly determined by the position of the local minimum in the electric field.

Fig. 9 Simulated z-component of the magnetic force for a jump along the y-direction. During the first step of the jump (blue curve), the particle is located at y = 0. During the second step (green curve), it is transferred to a y-position of 7 μm. Finally, the transfer is concluded by shifting the particle to its target position at y = 14 μm. The peak forces during all three states are in the range of 0.2–0.3 pN.

Discussion

In this paper, we present a chip-based actuation scheme that allows control over an individual microbead's position with respect to all three dimensions of space. Our method makes use of a combination of attractive magnetophoretic and repellent dielectrophoretic force fields to generate stable traps in the vicinity of the chip's surface. The combined use of magnetophoresis and dielectrophoresis for three-dimensional particle actuation has been demonstrated before. This includes meandering wire structures,³⁹ CMOS fabricated pixel arrays,⁴⁸ or approaches using multipolar dielectrophoresis.^49–52 Here, we show a control approach using a combination of magnetophoresis and dielectrophoresis that allows actuation of particles with respect to all three dimensions of space. At the same time, our approach only uses surface-integrated actuators and relies on standard microfabrication technology.

Using appropriate field configurations and amplitudes, our method is able to control a micrometer-sized bead within a distance of several micrometers away from the chip's surface. At the chip's surface, the particle can be moved with a velocity in the range of approximately 30 μm s⁻¹ (with respect to the x- and y-axes; data not shown). During levitation, we achieved an average velocity of approximately 7 μm s⁻¹ (with respect to the x- and y-axes). The actuation protocols presented here can be seamlessly combined to achieve more complex trajectories as demonstrated in Fig. 7.

The lateral resolution of the actuation is mainly defined by the wires' dimensions and pitch. Using the geometry and control schemes presented herein, the trap separation is in the range of several micrometers (compare Fig. 8). This is considerably higher than conventional magnetic or optical tweezers, which—laterally—are limited by stage motor precision in the nanometer range.^53,54 Nevertheless, in microwire crossbar arrays, the resolution can be improved by using thinner wires at a lower pitch. In addition, traps that are spaced below the grid pitch can be realized using more advanced control schemes (see the ESI†). Regarding the resolution normal to the chip's surface, the data in Fig. 4 shows a resolution of approximately 1–2 μm. In this context, the limiting factors are the AC amplitude applied by the function generator, as well as the focal depth of the objective. Our control unit allows adjustments of down to 0.1 V corresponding to approximately 0.1 μm. The optical limit for the detection of the particle's position, however, corresponds to ±0.5 μm. Normal to the chip's surface, the resolution thus mainly depends on the numerical aperture of the applied optics and could be improved using e.g. diffraction-based position detection.

Using our current chip design and power supply, the forces that can be exerted on the particle during the actuation are in the low pN regime. As demonstrated in the experiments above, this is sufficient to maintain reliable control over an individual bead. For many biophysical applications, however, forces in the hundreds of pN or even nN can be required.⁵⁵ In principle, forces of higher magnitudes should be achievable by simply increasing the amplitudes of the DC and AC signals. The trap position in our system is controlled by the relative magnitudes of the magnetic and the dielectrophoretic forces exerted on the particle. For field strengths below the saturation magnetization or polarization, both of these forces scale with ∇B⃑² and ∇E⃑_RMS², a 2-fold increase in the corresponding field strengths will yield a 4-fold increase in the trapping energy. However, concerning the DC generation of magnetic fields, this requires adjustments to the chip design (e.g. thicker wires or materials with better thermal conductivity) to limit excessive Joule heating of the wires. Similarly, the effect of high-amplitude electrical fields on e.g. biological systems has to be considered in this context.

Regarding the actuation of particles of various sizes, both the magnetic and the dielectrophoretic force scale with R³. Consequently, the trapping position generated by our system is independent of the particle's size. In particular with regard to smaller particles, however, the influence of Brownian motion has to be considered. While an increase of the applied AC and DC amplitudes could be used to increase the trapping energy relative to k_BT, thermal dissipation has to be considered.

Our method can easily be scaled up to the actuation of multiple particles in parallel and can be integrated in lab-on-a-chip platforms in a straight-forward way. We have exemplarily shown the parallel actuation of up to 16 beads. During parallel actuation, our method is able to generate traps with a minimum spacing of approximately 40 μm in order to ensure unambiguous transfer of a given particle to its destination. Similar to the above mentioned limits in resolution, this could be further decreased by using thinner wires or more advanced control schemes. During the parallel actuation, we simultaneously operated 16 wires without observing notable effects of thermal dissipation. Nevertheless, this aspect should be considered when scaling the method up to, for instance, thousands or even millions of particles.

Conceptually, the approach is not restricted to magnetic beads. A given object with a magnetic moment and a permittivity sufficiently different from the surrounding medium can be controlled as described above. This includes magnetically functionalized water-in-oil or oil-in-water emulsions, as well as magnetically tagged cells or capsules.^56–58 Regarding the actuation of cells, the effect of Debye screening in ionic media has to be taken into account when applying dielectrophoretic forces.

In conclusion, we present an actuation concept for micrometer-sized particles that is compatible with standard microtechnology fabrication methods and allows full three-dimensional control over the particle. We believe that this approach represents a flexible tool that will be useful in various experimental settings relying on precise manipulation of microscale objects. Examples for such settings include single-cell sorting and manipulation,^59–62 bead-bound sequencing assays,^63,64 or droplet-based drug screening technologies.^65–67

Acknowledgements

The authors would like to acknowledge Marko Banzet for cleanroom processing, Norbert Wolters for help with designing and building the power supply, and the Helmholtz Young Investigators Programme for funding. Furthermore, we gratefully acknowledge funding by the Bernstein Center Munich (grant number 01GQ1004A, BMBF).

References

1. F. Crick and A. Hughes, Exp. Cell Res., 1950, 37–80.
2. A. Ashkin, Phys. Rev. Lett., 1970, 24–27.
3. D. G. Grier, Nature, 2003, 424, 810–816.
4. X. Ding, S.-C. S. Lin, B. Kiraly, H. Yue, S. Li, I.-K. Chiang, J. Shi, S. J. Benkovic and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11105–11109.
5. B. G. Hosu, K. Jakab, P. Bánki, F. I. Tóth and G. Forgacs, Rev. Sci. Instrum., 2003, 74, 4158–4163.
6. J. R. Moffitt, Y. R. Chemla, S. B. Smith and C. Bustamante, Annu. Rev. Biochem., 2008, 77, 205–228.
7. J. Lipfert, J. W. J. Kerssemakers, T. Jager and N. H. Dekker, Nat. Methods, 2010, 7, 977–980.
8. I. De Vlaminck and C. Dekker, Annu. Rev. Biophys., 2012, 41, 453–472.
9. X. J. A. Janssen, J. Lipfert, T. Jager, R. Daudey, J. Beekman and N. H. Dekker, Nano Lett., 2012, 12, 3634–3639.
10. F. Kriegel, N. Ermann and J. Lipfert, J. Struct. Biol., 2016 DOI:10.1016/j.jsb.2016.06.022.
11. L. Chen, A. Offenhäusser and H.-J. Krause, Rev. Sci. Instrum., 2015, 86, 044701.
12. B. A. Berghuis, M. Köber, T. van Laar and N. H. Dekker, Methods, 2016, 105, 90–98.
13. L. Chen, W. Li, V. Maybeck, A. Offenhäusser and H.-J. Krause, Biomaterials, 2016, 106, 240–249.
14. A. Freikamp, A. Mehlich, C. Klingner and C. Grashoff, J. Struct. Biol., 2016 DOI:10.1016/j.jsb.2016.03.011.
15. N. Ribeck and O. a Saleh, Rev. Sci. Instrum., 2008, 79, 094301.
16. R. T. Dame, M. C. Noom and G. J. L. Wuite, Nature, 2006, 444, 387–390.
17. M. A. M. Gijs, Microfluid. Nanofluid., 2004, 1, 22–40.
18. N. Pamme, Lab Chip, 2006, 6, 24–38.
19. M. A. M. Gijs, F. Lacharme and U. Lehmann, Chem. Rev., 2010, 110, 1518–1563.
20. A. van Reenen, A. M. de Jong, J. M. J. den Toonder and M. W. J. Prins, Lab Chip, 2014, 14, 1966–1986.
21. R. Pethig, Biomicrofluidics, 2010, 4, 022811.
22. B. G. Hawkins, C. Huang, S. Arasanipalai and B. J. Kirby, Anal. Chem., 2011, 83, 3507–3515.
23. J. P. Smith, C. Huang and B. J. Kirby, Biomicrofluidics, 2015, 9, 014116.
24. M. Hejazian, W. Li and N.-T. Nguyen, Lab Chip, 2014, 959–970.
25. J. H. Kang, H. Driscoll, M. Super and D. E. Ingber, Appl. Phys. Lett., 2016, 108, 213702.
26. C. Murray, E. Pao, P. Tseng, S. Aftab, R. Kulkarni, M. Rettig and D. Di Carlo, Small, 2016, 12, 1891–1899.
27. H. Lee, A. M. Purdon and R. M. Westervelt, Appl. Phys. Lett., 2004, 85, 1063–1065.
28. P. Tseng, J. W. Judy and D. Di Carlo, Nat. Methods, 2012, 9, 1113–1119.
29. M. Irmscher, A. M. de Jong, H. Kress and M. W. J. Prins, Biophys. J., 2012, 102, 698–708.
30. J. Dobson, Nat. Nanotechnol., 2008, 3, 139–143.
31. H. Huang, S. Delikanli, H. Zeng, D. M. Ferkey and A. Pralle, Nat. Nanotechnol., 2010, 5, 602–606.
32. A. Kunze, C. Murray, A. K. Tay and D. Di Carlo, Biophys. J., 2016, 110, 466a.
33. Y. Huang, X. B. Wang, F. F. Becker and P. R. Gascoyne, Biophys. J., 1997, 73, 1118–1129.
34. U. Kim, C.-W. Shu, K. Y. Dane, P. S. Daugherty, J. Y. J. Wang and H. T. Soh, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20708–20712.
35. A. Valero, T. Braschler, A. Rauch, N. Demierre, Y. Barral and P. Renaud, Lab Chip, 2011, 11, 1754–1760.
36. Q. Cao, X. Han and L. Li, Lab Chip, 2014, 14, 2762.
37. T. Deng, G. M. Whitesides, M. Radhakrishnan, G. Zabow and M. Prentiss, Appl. Phys. Lett., 2001, 78, 1775–1777.
38. A. Rida, V. Fernandez and M. A. M. Gijs, Appl. Phys. Lett., 2003, 83, 2396–2398.
39. C. Liu, L. Lagae, R. Wirix-Speetjens and G. Borghs, J. Appl. Phys., 2007, 101, 024913.
40. C. Liu, L. Lagae and G. Borghs, Appl. Phys. Lett., 2007, 90, 184109.
41. Q. Ramadan, D. P. Poenar and C. Yu, Microfluid. Nanofluid., 2008, 6, 53–62.
42. S. S. Shevkoplyas, A. C. Siegel, R. M. Westervelt, M. G. Prentiss and G. M. Whitesides, Lab Chip, 2007, 7, 1294–1302.
43. C. S. Lee, H. Lee and R. M. Westervelt, Appl. Phys. Lett., 2001, 79, 3308–3310.
44. P. Rinklin, H.-J. Krause and B. Wolfrum, Phys. Status Solidi A, 2012, 209, 871–874.
45. P. Rinklin, H.-J. Krause and B. Wolfrum, Appl. Phys. Lett., 2012, 100, 014107.
46. B. J. Kirby, Micro- and Nanoscale Fluid Mechanics, Cambridge University Press, New York, 1st edn, 2013.
47. L. E. Helseth, Langmuir, 2005, 21, 7276–7279.
48. D. Issadore, T. Franke, K. A. Brown, T. P. Hunt and R. M. Westervelt, J. Microelectromech. Syst., 2009, 18, 1220–1225.
49. N. Manaresi, A. Romani, G. Medoro, L. Altomare, A. Leonardi, M. Tartagni and R. Guerrieri, IEEE J. Solid-State Circuits, 2003, 38, 2297–2305.
50. A. Rosenthal and J. Voldman, Biophys. J., 2005, 88, 2193–2205.
51. R. S. Thomas, H. Morgan and N. G. Green, Lab Chip, 2009, 9, 1534–1540.
52. K. A. Brown and R. M. Westervelt, Nano Lett., 2011, 11, 3197–3201.
53. D. Dulin, T. J. Cui, J. Cnossen, M. W. Docter, J. Lipfert and N. H. Dekker, Biophys. J., 2015, 109, 2113–2125.
54. F. E. Kemmerich, M. Swoboda, D. J. Kauert, M. S. Grieb, S. Hahn, F. W. Schwarz, R. Seidel and M. Schlierf, Nano Lett., 2016, 16, 381–386.
55. K. C. Neuman and A. Nagy, Nat. Methods, 2008, 5, 491–505.
56. B. Zebli, A. S. Susha, G. B. Sukhorukov, A. L. Rogach and W. J. Parak, Langmuir, 2005, 21, 4262–4265.
57. G. Sukhorukov, A. Rogach, M. Garstka, S. Springer, W. Parak, A. Muñoz-Javier, O. Kreft, A. Skirtach, A. Susha, Y. Ramaye, R. Palankar and M. Winterhalter, Small, 2007, 3, 944–955.
58. S. Carregal-Romero, M. Ochs and W. J. Parak, Nanophotonics, 2012, 1, 171–180.
59. P. Zhang, L. Ren, X. Zhang, Y. Shan, Y. Wang, Y. Ji, H. Yin, W. E. Huang, J. Xu and B. Ma, Anal. Chem., 2015, 87, 2282–2289.
60. C. Faigle, F. Lautenschläger, G. Whyte, P. Homewood, E. Martín-Badosa and J. Guck, Lab Chip, 2015, 15, 1267–1275.
61. F. Guo, Z. Mao, Y. Chen, Z. Xie, J. P. Lata, P. Li, L. Ren, J. Liu, J. Yang, M. Dao, S. Suresh and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 1522–1527.
62. D. McIlvenna, W. E. Huang, P. Davison, A. Glidle, J. Cooper and H. Yin, Lab Chip, 2016, 16, 1420–1429.
63. D. Horejsh, F. Martini, F. Poccia, G. Ippolito, A. D. Caro and M. R. Capobianchi, Nucleic Acids Res., 2005, 33, e13.
64. J.-C. Wang, H.-Y. Ku, D.-B. Shieh and H.-S. Chuang, Biomicrofluidics, 2016, 10, 014113.
65. L. Yu, M. C. W. Chen and K. C. Cheung, Lab Chip, 2010, 10, 2424.
66. O. J. Miller, A. E. Harrak, T. Mangeat, J.-C. Baret, L. Frenz, B. E. Debs, E. Mayot, M. L. Samuels, E. K. Rooney, P. Dieu, M. Galvan, D. R. Link and A. D. Griffiths, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 378–383.
67. N. Shembekar, C. Chaipan, R. Utharala and C. A. Merten, Lab Chip, 2016, 16, 1314–1331.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed description of the electric field distribution, the switching protocols, and the driving circuitry available online. Videos S1–S5 show single particle levitation, parallel actuation of 16 microbeads, horizontal and vertical actuation during levitation, as well as realization of a complex 3D trajectory, respectively. See DOI: 10.1039/c6lc00887a

---