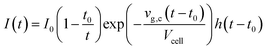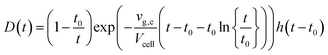Recent developments in the design of rapid response cells for laser ablation-inductively coupled plasma-mass spectrometry and their impact on bioimaging applications

Abstract

This review covers developments in the design of Laser Ablation (LA) cells, the associated transport tubing assembly, and their coupling to Inductively Coupled Plasma-Mass Spectrometry (ICP-MS) instrumentation. Recent ablation cell designs have reduced the pulse response duration for a single laser shot to <10 ms, using the criterion of the full peak width at 1% of the height of the maximum signal intensity. The evolution towards these low dispersion systems has been profoundly influenced by our understanding of processes driving the initial dispersion, of the design aspects of the cell and tubing that influence transport-induced dispersion and transport efficiency, and of limitations imposed by the temporal resolution of ICP-MS instruments, all of which are discussed. Rapid response LA-ICP-MS systems greatly benefit throughput and sensitivity, which are key parameters in 2D and 3D imaging at high lateral resolution. The analysis and imaging of biological material has come to the forefront as a key application of LA-ICP-MS. The impact of the technical developments in LA-ICP-MS systems on emerging applications, including multiplexed metal-tagged antibody detection (for immunohistochemistry), nanoparticle and compound hypo- and hyperaccumulation, and (intra-) cellular/histological studies, is also discussed.

---

Introduction

Laser Ablation-Inductively Coupled Plasma-Mass Spectrometry (LA-ICP-MS) is an established quantitative elemental analysis and mapping technique, characterized by its low detection limits, full elemental mass spectrum coverage, high spatial resolution, limited sample preparation, and wide linear dynamic range. In the past years, studies in the fields of proteomics, metallomics and nanotechnology have expanded the range of applications for the technique, e.g., the visualization of the distribution of drugs and tagged markers in biological tissue sections and single cells,^2–4 quantitative elemental and isotope ratio determinations in tissue,^5–7 and the uptake of nanoparticles.^8,9 The figures of merit of the technique, relating to sample throughput, sensitivity and spatial resolution, depend in a large part on the ability of the ablation setup to rapidly remove the aerosol from the ablation site to the ICP-MS instrument in a manner that minimizes the mass losses and the dispersion induced in the aerosol cloud. Current systems deployed in the field produce a signal response to a single shot (sometimes referred to as washout time) in the region of multiple hundreds of ms to a second. Pulse repetition rates that exceed the level at which pulse response peaks are separated are often adopted. Unless signal deconvolution is employed, the response from multiple ablation positions is convolved, and thus, the spatial response is distorted in the scan direction. When the responses of ablation positions are resolved in the time domain, the rate of information acquisition is limited to the reciprocal of the response duration. Recent developments have improved both the pulse response duration and transport efficiency. This review article provides a condensed overview of the latest developments in cell design, and related aspects, and the implications of the newfound capabilities for the applications of LA-ICP-MS within the biochemical, biological, and biomedical fields with a particular emphasis on high-resolution imaging. The scope of this review was limited to articles written in English, and focusses on literature reporting ablation cell designs supported by experimental data which demonstrate a characteristic pulse response width of 100 ms or less, and literature covering emerging biological and imaging applications in the past 5 years. The pulse response duration of ablation cells is expressed in this review as the full peak width of the ICP-MS unit detector signal response to a single laser shot, at a fraction of the height of the maximum intensity of the peak, e.g., 0.5, 0.1, 0.01 (respectively FWHM, FW0.1M, and FW0.01M), unless mentioned otherwise. Within this review ‘low dispersion’ and ‘rapid response’ are used as interchangeable terms. The authors apologize for any relevant work not included in this review article.

Rapid response ablation cells

Over the past decades, a handful of research groups have invested in developing efficient ablation cell designs based on their understanding of the underlying physics and the fundamental studies and models describing them. It was identified early on that aerosol dispersion induced by the ablation cell is one of the important factors limiting the performance of LA-ICP-MS. The figure of merit preferred to characterize the aerosol dispersion is the pulse response duration. A condensed overview of compiled data on this metric for selected ablation cells is presented here below.

State-of-the-art figures of merit

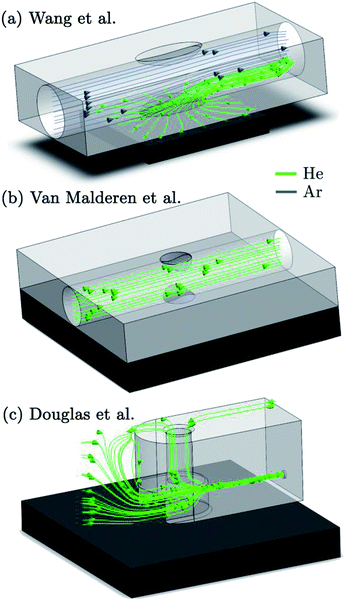
In one early study, Leach and Hieftje¹⁰ explored the inverse relationship between the system volume, and the peak width of pulse responses. The selection of the smallest cell and identification of the optimal He–Ar gas mixture composition yielded a transient signal of 85 ms at FWHM for U. Following the lead of Bogaerts et al., computational fluid dynamics (CFD) modelling based on Reynolds-averaged or Favre-averaged Navier–Stokes models has taken a prominent role in the study and simulation of the aerosol and flow behaviour within the ablation cell and ICP,^11–14e.g., for visualizing the pressure gradients and kinetic energy (KE) of the flow in turbulent regions. The visualization of streamlines opens a pathway to improve design aspects of a virtual prototype of an ablation cell by an iterative in silico process, hence optimizing the FD behaviour prior to manufacturing. Lindner et al.,¹⁵e.g., reported on the FD behaviour of a non-contact, low dispersion ‘High Efficiency Aerosol Dispersion’ (HEAD) cell, based on aerosol extraction via venturi-driven pressure reduction using a realizable k–ε model. The simulation suggested that the aerosol dispersion of the last iteration of the design could be reduced to less than 10 ms.¹⁵ The importance of a laminar flow regime, aerodynamically favourable outlets, and the relative position of the ablation site to the outlet have been demonstrated by Gurevich et al.,¹⁶ who reported a chamber characterized by a signal peak with a FW0.1M of less than 100 ms. The proximity of the ablation site to the outlet was reported to be a critical factor in a cyclonic flux cell design by Monticelli et al.,¹⁷ which delivers a transient peak down to 20 ms at FW0.1M, with a strong dependence on this distance. A more recent design by Wang et al.¹⁸ (Fig. 1a) brought the dispersion down to a consistent 30 ms at the FW0.01M level. Gundlach-Graham et al.¹⁹ reported that the latest iteration of the cell, which is based on the same working principle, has improved the dispersion to 9 ms at the FW0.01M level. An ablation cell reported by Van Malderen et al.²⁰ (Fig. 1b), focusing on regions-of-interest smaller than 0.25 mm², delivers transient peaks of 5 ms at the FW0.01M level. Douglas et al.²¹ also recently reported a low dispersion interface, consisting of a two-volume ‘Sniffer’ cell (Fig. 1c) and an integrated ‘Dual Concentric Injector’ (DCI), which produced signals of 5 ms at FW0.01M. The arrival of three new aerosol capture and transport interfaces characterized by a pulse response of <10 ms at FW0.01M, demonstrates that considerable progress has been made within the past few years. Sensitivity improvements have been reported all-round, e.g., the ‘sniffer’ cell was reported to yield an increase in absolute sensitivity (counts per mole) in the order of 5–10 fold compared to conventional setups. Low dispersion cells are expected to find their way to all LA-ICP-MS and related applications, though their adoption may be hampered by the absence of affordable, fast, sensitive, simultaneous mass spectrometer systems.

Fig. 1 Overview of 3 of the currently fastest ablation cell designs. The dark gray block represents a 7.5 × 7.5 × 1 mm sample. The scaling for each cell was performed separately, due to their size differences. The streamlines represent gas flows predicted by CFD.

Trends in instrumentation development

The following subsections present a general overview of the core concepts influencing the speed and efficiency of aerosol capture, transport, and detection, and their impact on ablation cell and transport conduit design.^22–25 These developments and insights are stepping stones to further progress ablation cell technology.

Cell design

The main strategy to minimize aerosol dispersion in the cell is confinement of the ejected particles, through gas flows, pressure, or cell walls, forming a controlled environment less than a few cm³ in volume, and preventing further expansion of the ablation plume inside the cavity of the chamber, which would inevitably enlarge the initial dispersion of the aerosol. The residence time of particles in the cell is not governed exclusively by the cell volume and shape, it also depends on the local gas velocity, pressure, and flow regime, as well as the particle size distribution and initial dispersion and momentum of the aerosol in the cell.^26,27 Confinement of the plume, either by gas flows or walls can simultaneously maintain a high local velocity of the carrier gas flow. In most designs this is dealt with by capturing the aerosol in a cup, i.e. a separate enclosure of small volume, or tube floating above the sample, whilst an XY(Z) stage or gantry is used to adjust the relative position of the fully-enclosed sample with respect to the aerosol capture component. Laser ablation designs can be subdivided based on the angle under which the carrier flow is extracting the aerosol plume. In the HEAD cell,²⁸ the aerosol was extracted vertically using a He flow; an Ar auxiliary/sheath gas flow was added co-axially to the He flow just above the ablation site. CFD simulation suggested that the He carrier flow resides in a laminar flow regime and shows limited mixing with the Ar sheath flow. Major differences in relative speed or density of the core-annular laminar flow at fluid inlets or joints can limit intermixing of the flows.^29,30 Autrique et al.^11,31 explored the CFD behaviour of a cell designed for vertical extraction of the aerosol by a carrier gas, with an optional auxiliary flow, parallel to the sample, shielding the fused silica window and guiding the suspended aerosol into an outlet that is co-axial to the inlet of the auxiliary flow. Such design features are reflected in the non-contact ablation cell designed by Wang et al.¹⁸ (Fig. 1a), in which the auxiliary flow inlet–outlet conduit is brought much closer to the sample surface, enabling a more efficient uptake of the particles in the carrier/sheath gas flow. Monticelli et al.¹⁷ designed a unique cell in which the plume is fully confined by a cyclonic gas flow. The drag/centrifugal force balance acting on the particles, results in a minimum curvature radius of the particle trajectories, estimated to be 0.1 mm under typical experimental conditions. Cell designs which introduce the aerosol directly into the transport line – sometimes referred to as a tube cell design – have been considered by Bleiner,³² Summerfield et al.³³ and Van Malderen et al.²⁰ (Fig. 1b) as a result of their envisaged short washout times.^20,32,33 The generated vapour cloud expands inside the transport line itself, and is constrained by the tube walls. The condensed aerosol is then carried with the carrier gas flow. A configuration reported by Douglas and Managh et al.²¹ (Fig. 1c) captures the aerosol in a fluid-dynamic optimized capture cavity/cup, which uses walls, elevated pressure, and a combination of a co-axial and orthogonal flows to confine the plume expansion and transfer the aerosol into a small capillary. Using a carrier flow parallel to the normal of the target surface (away from the surface) has been hypothesised to favour aerosol extraction, as the momentum of the carrier flow is opposite to the gravitational force and along the fastest ablation debris velocity component.^34,35 Extraction using a flow with a momentum parallel to the surface, generally orthogonal to most particle trajectories, could potentially negate the dispersion of the aerosol plume along the normal of the target surface. The stopping power (mass density), shorter mean free path, lower ionization efficiency, and particle size-independent transport characteristics, favour Ar as a carrier gas over He, however, the high particle entrainment efficiency (limiting the surface condensate deposition), reduced plasma shielding (higher thermal conductivity), higher breakdown threshold at atmospheric pressures, and lower dynamic viscosity favour a He environment.^27,36–40 These traits can be exploited to achieve narrow peak profiles most efficiently by conducting the ablation in He, with an option to utilize Ar as a sheath flow and make-up gas.¹⁰ A core concept of cell design is optimizing the design for flows in the laminar or laminar–turbulent transition regime, so as to avoid dispersion by turbulence, whilst enabling timely transport to limit the effect of diffusion on the aerosol dispersion. The initial dispersion of the aerosol, after thermalization – the process of particle-buffer gas interaction towards a thermal equilibrium, is determined in part by the position, the velocity and angular distributions of velocity vectors of particles at ejection, e.g., in He, particle ejection takes places at angles close to the normal.¹⁰ The particle ejection velocities on the far end of the shifted Maxwell–Boltzmann velocity distribution are in the order of 10^3–4 ms⁻¹, and critically dependent on the laser characteristics such as energy density, pulse length, spot size, and target properties.⁴¹ Bleiner et al.⁴² reported ion angular spreads to be dependent on the metal, and the bulk of fast ions to be ejected close to the normal. The evolution of the velocity component of the ejected particles on a ps–μs timescale depends on, among other factors, buffer gas properties, and the KE and development of the laser-induced shock wave (SW), which in turn is influenced by all the aforementioned parameters.^34,43 Ar is the preferred buffer gas to shield walls from particle impact due to its ability to decelerate the contact front faster, compared to He, as a result of its higher collision frequency – Ar has a relative larger collisional cross-section (dipole moment, polarizability), and mass.^16,43 The stopping distance of the particles is also a function of the environment pressure.⁴³ Bleiner et al.³⁵ estimated the peak stopping power of static Ar at atmospheric pressure to be ∼0.4 keV mm⁻¹ on the axial component in the early expansion stage, which suggests that a minimum gas buffer thickness of 10 mm is required to mitigate high KE debris impacting the walls at velocities above erosive threshold values. Conversely, Gurevich and Hergenröder¹⁶ estimated the upper limits of the stopping distance of particle with sizes between 10–2000 nm, in He or Ar under atmospheric pressure, to be less than 2 mm, using a laser energy of 1 mJ. The stopping power is a function of time and space, as the collision frequency varies with the thermalized KE. When the stopping distance of particles falls short of the cell walls, the reflection of the SW – the SW density front edge outruns the contact front and bulk of ejected particles – may compress or disperse the aerosol cloud, as has been observed in laser-induced breakdown spectroscopy.^44–49 As such, the expansion of the condensing plume can also be curbed and restricted by walls, and the sample itself (cf. Mach reflection of the SW).^50,51 Compression of the laser-induced plasma by the SW may create a hotter, denser plasma, resulting in an enhanced photon emission.⁴⁴ Shadowgraphy has been used to study the SW and particle ejection phenomena in detail, and has, among many other aspects, confirmed that the blast wave follows a behaviour close to the Sedov–Taylor solution.⁵² Laser-induced breakdown can be initiated by the high temperature environment in the expanding plume, in combination with single- and multi-photon ionization (PI), photoexcitation (PE), electron-neutral inverse bremsstrahlung (IB) by ejected species, and, to a lesser degree, electron-ion IB.^53,54 Complete removal of particles from the cell volume between subsequent sampling events decreases the chances of unpredictable (for ns-lasers) particle-induced plasma breakdown, which can promote plume expansion horizontal to the sample surface, inducing depositional losses.^40,55 Plasma shielding, i.e. photon absorption by the breakdown plasma, optically attenuates the incident laser beam intensity reaching the sample surface in ns pulse length laser systems.^38,51 The process is driven primarily by IB – photon absorption at high electron densities resulting in the excitation of the free electrons to a higher state in the continuum, PE, PI, and Mie scattering. Photon absorption in gas layers behind the SW and ensuing heat expansion can accelerate the SW (contact) front in the direction of the incoming laser pulse in a regime called laser-supported detonation, as part of the plasma shielding process.^51,56 It has also been suggested that the ions within the vapour cloud could undergo double layer ion acceleration by ambipolar diffusion as a result of charge separation.^57–59 In short, the initial dispersion is guided by the interplay of many physical processes, governed by environmental conditions, and laser beam and sample characteristics. The sample characteristics, aerosol particle size, and phase distribution are linked, as the condensational growth conditions in the supersaturated vapour shifts with the thermal conductivity of the sweep gas, and the spatial, size and phase distribution of condensation nuclei (i.e. ejected particles), which critically depend on the sample structure, composition, morphology and mechanical properties. This relationship can be compounded by the uptake of particles ejected by exfoliation and spallation, reablation of deposited material and melt splashing/droplet expulsion (by the recoil SW).^36,60 When the pulse length exceeds the local thermal relaxation time (sub-ps range) of the sample material, zone heating arises. Extensive melting can impact the phase distribution of the ejecta, once again, changing the ablation cell washout characteristics. An additional flow in the ablation cell design, or a carrier flow along the normal of the sample can promote the uptake of these particles.¹⁸ Particle growth can also be achieved through aggregation (agglomeration) and coalescence of particles. The particle size distribution and particle structure should be highlighted as an important aspect, as the particle transport mechanics critically depend on the slip and drag coefficients of the particles, and therefore the aerosol dispersion will be affected. Furthermore, the degree of elemental fractionation is governed to a large extent by the incomplete vaporization, atomization and ionization of mesoscopic particulates >200–500 nm in size, in combination with non-stoichiometric sampling (differential partitioning results in a particle-size dependent elemental composition), which is natively linked to the laser unit, ICP-MS unit and target characteristics.^61–68 A recent paper by Zhang et al.⁶⁹ provides a comprehensive overview of elemental fractionation and matrix effects. The particle size distribution can be acquired experimentally by, e.g., optical laser scattering, differential mobility analysis or gravimetric determination of the yield in particle impactors. On a side note, the higher rate of evaporation of volatile over refractory elements in the melt created in the zone heating process also induces cumulative compositional disparity between deposited and ablated material, leading to fractionation.⁷⁰ Thermal diffusion processes are also expected to increase the mobility of analytes in the heat-affected zone (HAZ) around each ablation crater (zone refinement).⁷¹ By lowering the sample bulk temperature by cryogenic cooling, thermal expansion of the HAZ and the volume under a metastable superheated state is slowed down, reducing the area affected by visible thermal degradation and vaporisation.^72–74 Furthermore, the thermoelastic stress required to fracture tissue decreases as a result of the cryogenic conditions on the tensile strength.

Turbulence in aerosol transport

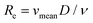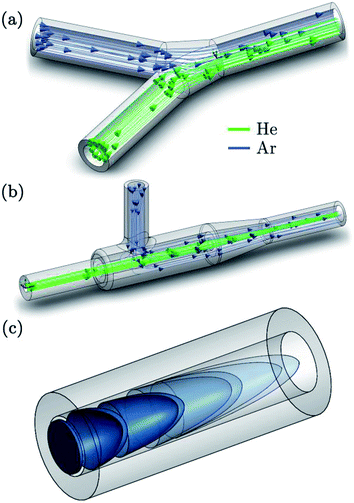
Once leaving the ablation cell, the aerosol is conducted to the ICP-MS instrument through flexible polymer tubing, which is typically a few mm in internal diameter and can be up to several m in length. This conduit has long been recognised as a potential source of material loss and a contributor to aerosol dispersion.⁷⁵ Reynolds numbers (with v_mean the mean fluid velocity, D the hydraulic diameter, and 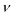the kinematic viscosity) easily allow identification of the flow regime. Gas flows in the tubing are generally within the laminar flow regime (R_e < 2100) under typical gas flow rates, and thus, follow a parabolic velocity profile³⁹v(r) = v_max(1 − r²/R²) with v the velocity at distance r of the center axis of a cylinder of radius R for subsonic velocities (v_max < 0.2v_sound). This Hagen–Poiseuille flow creates temporal axial dispersion through Taylor–Aris dispersion (Fig. 2c) and diffusion. On the other hand, turbulent flows in a conduit are controlled by turbulent diffusion, rather than shear forces, which gives rise to erratic inter-layer mixing, and an average velocity flow profile uniform over the entire cross-section, with the exception of thin boundary layers near the conduit walls.³⁰ Early experimental studies by Bleiner and Günther,²⁶ and Leach and Hieftje,¹⁰ demonstrated that dispersion increases with increasing transport volume for single shot LA-ICP-MS. This is a function of the tube diameter as well as its length, since the slower gas velocity in wider tubes allows for longer diffusion time. In a study by Summerfield et al.³³ a tube cell design was used to eliminate chamber effects and enable a focussed study of transport characteristics. Washout time was found to increase with increasing tubing length,¹⁰ with the inclusion of valves, and in particular with the presence of bends. Sharp bends in the tubing will disrupt the flow dynamics because the outer radius flow experiences a higher velocity than inner radius, inducing swirling or rotation as a result of shear stress. Inertial deposition, as well as gravitational settling, in conduits of small radius has been shown to be particle-size dependent, inducing additional elemental fractionation.^76–78 The flow path in early setups was intersected by a Y- or T-junction, for the addition of an Ar make-up gas. Computational modelling by Autrique et al.¹¹ highlighted this junction as a major source of turbulence in the flow (Fig. 2a). In this simulation, the introduction of a make-up gas pushed the carrier gas towards the wall of the tubing, which induced surface friction and the formation of eddies near to the wall region. Furthermore, divergences in the tubing, for instance where the tubing connected onto the Y-junction, and later onto the torch, produced a clear turbulent flow pattern. Turbulence and eddy formation can be observed when the inner diameter of the conduit is changed or if dead volumes are present.⁵⁰ These fluid dynamic instabilities may trap smaller particles in small scale eddies, increasing the width of the transient peak. Similar problems are present in GC and (UP or HP) LC. The issue was addressed by co-axial mixing bulbs^26,50,79 (Fig. 2b), where the make-up gas was added on-axis to the carrier gas flow, through a concentric outer tube. The simulation thus stimulated the deployment of a laminar flow gas connector in the field. Several groups have reported designs that avoid the use of a gas connector. These systems are exceptionally fast and all produce signals of 30 ms FW0.01M or considerably below.^19,20 In the tube cell designs, ablation takes place through an opening in the transport tubing, with material directed orthogonally into the laminar carrier gas stream. In Van Malderen's cell, this tubing also passed through, and effectively became, the inner injector of the ICP torch. In this way, the ablation cell, transport conduit and ICP torch could be considered as an integrated device, and divergences in conduit diameter were completely eliminated. The DCI interface²¹ uses an unbroken fused silica conduit, which passes through the injector of the ICP torch, to transport the aerosol from the ablation cell directly into the plasma. The conduit could be extended up to 12 mm beyond the injector, past the turbulent region at the base of the plasma. This was thought to help keep material on axis with the orifices in the cones, which may have contributed to an improvement in absolute sensitivity, as well as speed. From the above studies, it appears that optimum transport characteristics can be achieved through the use of a short, straight and unbroken conduit, of narrow and constant diameter. Optimally, the conduit would be integrated into both the cell and the ICP torch. However, the practicality of some lab geometries may understandably restrict the implementation of these ideal conditions, particularly with regards to minimising tubing lengths and the avoidance of bends. It may be that optimum performance would be best achieved by better integration of LA with ICP-MS instrumentation.

Fig. 2 Schematic and CFD simulation to demonstrate processes that drive aerosol dispersion. The gas mixing processes in a Y-connector piece (a) and a coaxial mixing bulb (b) control downstream eddy formation and gas composition. The Taylor dispersion process acting upon an aerosol cloud injected uniformly across the cross-section, induced by the between-layer velocity differences, is displayed in (c).

In-torch ablation

The concept of ablating material within the ICP torch was first reported by Liu and Horlick,⁸⁰ in conjunction with optical emission spectrometry (OES), and was later adapted by Tanner and Günther for use with mass spectrometry (MS).^81–84 In the MS arrangement, the laser beam was focussed through a small hole in the top of the torch box and onto the sample, which was mounted behind the injector on a small holder. The bulk of the response signal occurred within the first 1–2 ms, with the remainder stretching out over ∼30 ms. The arrangement has very limited practical applicability due to the restrictions on sample size and sample movement placed by the dimensions of the torch, and is limited to high melting point samples, due to the proximity of the target to the plasma. In-torch ablation is therefore mentioned in this review purely as a theoretical benchmark for the characterisation of new interfaces. It should be noted that in this configuration the aerosol particles still traverse the plasma, hence, the particles are transported over a distance of a few cm in atmospheric pressures before being extracted. As such, in practice, ablated particulates may become entrained in the turbulent flows at the base of the plasma within the in-torch design, thus methods that keep material aligned with the central channel of the plasma, or a sample configuration in closer proximity to the extraction site may eventually produce higher performance.¹²

Ablation yield – transport efficiency

The ultimate sensitivity of the technique is driven by the ablation yield and the overall efficiency of the entrainment of ejected particles and their transport from the ablation site to the mass analyser. The laser interaction and particle formation processes, affecting the mobility of the aerosol, are profoundly influenced by the sample composition. In a study by O'Connor et al.⁸⁵ the addition of a laser radiation absorbing compound (vanillic acid, pyrazinoic acid or nicotinic acid) to a sediment improved the ablation efficiency. Particle losses can occur through gravitational settling and non-stoichiometric particle entrainment of μm-sized particles, diffusional losses – disproportionally affecting nm-sized particles, aerosol condensation, carrier gas leaks and inertial deposition on walls in the cell geometry obstructing the carrier flow.^31,86 Selective particle losses in the size-segregation process will change the particle size distribution, inducing elemental fractionation, as demonstrated by Koch et al.⁷⁵ and Outridge et al.⁷¹ The cell geometry has limited influence on the aerosol transport efficiency, under the conditions that no dead volumes of low local flow velocity in which particles can settle, are present, and particle deposition on the window and walls of the cell and tubing is negligible.^31,87 Avoiding dead volumes within the cell is readily achieved by adopting a fluid-dynamic optimized design – eliminating sharp angles and corners which may trap particles – and positioning the inlets such as to cover the entire volume to be flushed.^26,27,88 Any trapped particles will be released slowly over time, resulting in broader response peaks or signal tailing, and/or higher background levels. An impact of debris on the wall may result in spattering, sputtering, adsorption or impingement of particles. Particle deposition on the cell walls – and the accompanied loss of material – can be mitigated by expanding the cell diameter,¹⁰ increasing the volume of gas between the ablation site and cell walls to buffer the particle velocity, or by decreasing the initial dispersion of the aerosol in the cell by increasing the stopping power of the gas (or fluid), e.g., by increasing the environmental pressure. A complete development of the ‘mushroom cloud’ plume⁸⁹ is not a necessary condition for achieving complete sample transport. Direct effects of the deposition processes are a decline of the aerosol transport efficiency as associated with the (non-stoichiometric) particle losses, and longer washout times as particles are detaching or being sputtered from the surface, with which they impacted, at a slower pace relative to the flush rate of the cell. Effects such as erosion may occur at high collision frequencies, as well as cross-contamination to subsequent ablation positions and samples. Transport efficiency in LA-ICP-MS using ns-lasers were reported in early studies^26,86,90 to be ≳40% for He as a carrier gas, as determined by optical particle counting (OPC) and chemical analysis of filtered particles. More recently, Garcia et al.³¹ reported efficiencies > 80–90% for fs lasers. Monticelli et al. reported a near to 100% recovery for the cyclonic design in combination with a fs laser unit. Back condensation of the vapour cloud on the target surface and losses in the impactor have not been taken into account in these studies. Recently, Niehaus et al.⁹¹ reported on particle transport characteristics for particles generated by ablation of a gelatine section, a matrix that compares well to a biological matrix. A variation of the transport tube length was not found to increase the loss of particles. Based on OPC measurements, the same study reported a positive correlation between the fluence and the portion of μm-sized particles in the particle size distribution, as well as between the fluence and ablation yield – this linear relationship quickly levels off at high fluence levels. The laser wavelength and energy density can have a profound influence on the ablation yield in biological matrices. The sample-specific characteristics, e.g., the mass ratio of extracellular matrix (e.g., collagen) to the total tissue, mediate the ablation threshold, attenuation length, scattering properties, and thermal conductivity of the target which impact the surface temperature profile, mechanical response, and ejected particle size and phase during ablation. Morphology of the sample, e.g., the presence of porosities or fractures, and surface roughness/reflectivity will also influence the ablation yield. In the UV region, photochemical processes such as electron excitation (one- and multi-photon processes) can directly break chemical bonds, e.g., covalent and ionic bonds and crosslinks. Thermal processes (vibrational excitation) on the other hand will induce melting and evaporation at fluence levels near or below the ablation threshold. At higher fluence levels, the rapid energy transfer can induce vaporization by phase explosion, with the ejection of μm-sized particles and spallation of fragments.⁷³ Explosive boiling and mechanical expansion are driven by spinodal breakdown, i.e. the decomposition of the irradiated volume, which resides within a superheated meta-stable phase, into a mixture of liquid and gas.⁹² Explosive boiling occurs when the irradiated volume is saturated homogeneously by nucleation bubbles. The time lag of nucleation depends on the nucleation rate and the dimensions of critical nuclei, which are larger for metallic matrices than for organic ones, as a result of heat delocalization (higher thermal conductivity).⁶⁰ The ablation threshold is generally lower for biological samples than for metals and minerals. The laser–surface interaction can induce other morphological changes, e.g., structural changes as a result of the laser SW propagating inside the solid, or microfoaming, e.g., in gelatine targets.^93–95 It should be noted that thermal processes play a more pronounced role in the ablation of biological matrices, relative to silicate, ceramic and polymer matrices, for these processes are a major source of fractionation.⁹¹ In contrast to geochemical matrices, wavelengths < 200 nm are not required to achieve efficient coupling to a biological matrix, however, thermal effects near the ablation zone become more pronounced at longer wavelengths. Biological samples are typically characterized by an optical penetration depth, i.e. the reciprocal of the absorption coefficient reduced by scattering effects, in the order of several μm,⁷³ whilst in metals it is limited to tens of nm.⁶⁰ The ablation depth and mass yield per shot is thus generally higher in biological samples than for metals. Claverie et al.⁹⁶ identified that their high repetition rate fs-laser ablation strategy yielded ablation rates for polyacrylamide gel 3 orders of magnitude higher than typical ablation rates in glasses or metals, and that the particle size distribution of fs-lasers was shifted towards smaller particles, though micrometric agglomerates were formed when the particle density was high. IR laser wavelengths induce evaporation-driven ablation, based on the presence of water in biological matrices, characterized by significant absorption at wavelengths > 1000 nm and <200 nm, peaking around 2940 nm, and <170 nm.^97,98 IR wavelengths impose diffraction limits on the beam's waist dimensions and generate more pronounced cracking and melting in targets depleted of water. It can be noted that at UV wavelengths a higher efficiency of photoionization can be observed. The relevant chromophores are the peptide bonds in proteins in the deep UV region (absorption peak centred around ∼190 nm), and DNA (purine and pyrimidine bases), melanin, tryptophan, tyrosine, and phenylalanine at longer UV wavelengths.⁷³ The review by Vogel et al.⁷³ provides a detailed description of the effect of pulsed lasers on tissues. The multitude of complex interacting processes and experimental parameters convolutes any prediction of the ablation yield, which, together with the aerosol dispersion and atomization, ionization, transmission, and detection efficiencies, governs the S/N ratios achievable, and by extension the minimum beam waist size, impacting the spatial resolution. The mass loaded into the plasma, assumed to be proportional to the area under the peak profile, is an important metric to evaluate relevant particle loss processes, as discussed hereinabove, which bias the stoichiometric elemental ratios. As the particle density – which is closely related to the ratio of ablated mass/cell volume, particle size distribution, and particle kinetic energy can be linked to the rate and extent of deposition and diffusion processes, the mass and mass flux at every point in space and time within the limited volume of low-dispersion ablation cells and their transport tubing should be monitored as key indicators of particle loss. The particle uptake and entrainment process on the other hand is relevant to the peak profile, as a signal spike can be identified on the profile tail for every fragment that is released after a delay period and successfully reaches the detector, broadening the overall peak width. The occurrence of these memory effects may inhibit rapid washout despite of low initial and induced aerosol dispersion in a low-dispersion aerosol transport system, and will invariably deteriorate the limit of detection or bias the response for subsequent shots.

Mass spectrometers

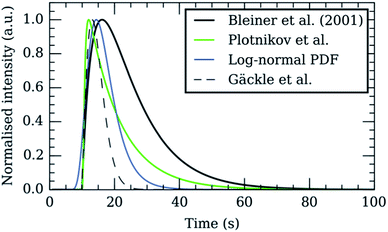
Whilst improving the washout time has several advantages, many of the current generation ICP-MS instruments were not designed to meet the challenges of fast transient analysis. A detailed analysis of common mass analysers and detectors used in the field of ICP-MS and their limitations for measuring short transient signals was previously published by Tanner et al.⁹⁹ Primary considerations include data acquisition and readout speed, minimization of dead time in the duty cycle, and maintenance of plasma stability on the millisecond time scale under highly variable plasma load. The capacity to detect multiple nuclides (pseudo-) simultaneously is important to isotope ratio determination studies, LA imaging, nanoparticle analysis with NPs consisting of ≥2 elements, and standardization approaches, but we will first consider the hardware specifications required for single nuclide monitoring. The importance of data acquisition speed was recognized from the early in-torch experiments (as discussed above), where a quadrupole mass spectrometer was used to profile transient peaks of ∼4 ms FW0.1M.⁸¹ In the original study, the time resolution of the mass spectrometer was limited to 0.5 ms (the minimum dwell time of the instrument), which recorded a log-normal peak shape, with 8 data points within the bulk of the peak. In a subsequent publication, the standard detection system was bypassed, and a digital oscilloscope recorded the signal from the analog detection stage of the mass spectrometer at 20 μs intervals.⁸³ The improved time resolution revealed a finer, bimodal peak structure, which comprised two overlapping Gaussian functions. Several other research groups have used plug-in devices to upgrade the data acquisition characteristics of commercial quadrupole^100–102 (Q), sector-field¹⁰³ (SF) and time-of-flight¹⁰⁴ (TOF) mass spectrometers. In recent years, ICP-MS instrument manufacturers have also begun to take note of the importance of time resolution, in reaction to the development of single particle analysis. This is reflected in recent product launches of ICP-quadrupole mass spectrometers by, e.g., Perkin Elmer (NexION® 350, 10 μs dwell time),¹⁰⁵ Agilent Technologies® (Agilent® 7900, 100 μs dwell time),¹⁰⁶ Thermo Scientific™ (iCAP Q™, 100 μs dwell time)¹⁰⁷ and AnalytikJena® (PlasmaQuant® MS, 50 μs dwell time).¹⁰⁸ Once acquisition speed is improved, the existence of ‘blind time’ in the duty cycle, where no signal is measured, becomes apparent. Blind times of up to 0.9 ms have been reported for ICP-Q-MS¹⁰⁹ and 3–4 ms for electrostatic mode scanning in ICP-SF-MS instruments.¹¹⁰ The reported losses predominantly result from re-setting of electronics after each acquisition segment, in contrast to dead time, i.e. time during which signal loss occurs as a result of electronic unawareness to ion detection whilst processing the previous pulse. The blind time may disproportionally affect fast transient signals compared to their slower counterparts. The extent of the data loss is dependent on the position of the peak within the duty cycle, which is variable and difficult to predict, but must be accounted for during data processing.¹¹⁰ Data losses and the effects of undersampling the transient signal are even more severe when simultaneous analysis of multiple elements/isotopes is required, especially as laser firing times are desynchronized from the dwell interval frequency. Quadrupole and single detector sector-field instruments are fundamentally restricted in their ability to perform this type of analysis because they detect elements sequentially. In other words, whilst one isotope is measured, data for the other elements/isotopes is not acquired, limiting sensitivity and precision. Multi-collector ICP-MS enables simultaneous measurement of elements of similar mass with high sensitivity.¹¹¹ Craig et al. recently demonstrated the use of multi-collector ICP-MS with the DCI/sniffer interface to measure uranium isotope ratios in sub-micron particles.¹¹² However, the use of slow Faraday detectors in parallel with ion counters placed restrictions on the minimum time resolution that could be achieved. Furthermore, using the mixed detector array for transient analysis was reported to introduce a form of spectral skew, which was more pronounced for the signals acquired using the DCI/sniffer interface compared to those from a much slower cell.¹¹² An alternative option is ICP-TOF-MS, which provides pseudo-simultaneous analysis (ions are sampled simultaneously but read-out sequentially) of a large part of the full mass range, with potentially fast data acquisition and readout. The feasibility of coupling an ICP to a TOF-MS was demonstrated as early as 1993,¹¹³ but these instruments are not as popular as ICP-Q-MS or ICP-SF-MS. ICP-TOF-MS has yet to reach the sensitivity of ICP-Q/SF-MS, however, improved S/N ratios provided by state-of-the-art LA cells, improved transmission efficiencies, and higher duty cycles may compensate for this limitation. In 2008, Tanner and Günther combined an ICP generator and interface from a quadrupole instrument with a commercial TOF-MS to measure Zn/Cu ratios in the context of in-torch LA.⁸⁴ The prototype system had five orders of magnitude poorer sensitivity compared to commercial ICP-Q-MS, but provided 30 μs time resolution. Based on this work a commercial instrument, ‘icpTOF’, was developed by TofWerk (Thun, Switzerland), which has been applied to other fast-transient applications.¹¹⁴ The ‘icpTOF’ data processing hardware can output mass spectra with 41 216 mass channels in the mass range (m/z = 2–257) with mass resolving power R = M/ΔM ≈ 3000 at frequencies of up to 667 Hz (1.5 ms/full elemental mass spectrum).¹¹⁵ Another commercial ICP-TOF-MS instrument, which has been coupled to a low dispersion ablation cell² is the ‘CyTOF’ instrument by Fluidigm (South San Francisco, CA, USA). Fluidigm's instruments provide a time resolution of 13 μs and sensitivities approaching those of ICP-SF-MS, but at the expense of reduced mass resolving power R ≈ 900–1000 and a restricted mass range (m/z = 75–209).² Quadrupoles or variants thereof are implemented in ICP-TOF-MS as a multi-notch mass filter to remove abundant plasma background ions and prevent detector saturation, or as a high-pass or low-pass filter to speed up data acquisition. GBC Scientific Equipment Pty Ltd (Melbourne, Victoria, Australia) offers the OptiMass 9500, a full range (m/z = 1–260) ICP-TOF-MS, with a spectral generation rate of 100 Hz and mass resolving power R ≈ 1500 at mid mass range.¹¹⁶ ICP – Mattauch–Herzog geometry SF – MS and distance-of-flight array detectors currently lack the S/N ratio to produce meaningful data at the time-resolution that would be required for pulse-to-pulse separation.^115,117 Spatially dispersive mass spectrometry may however in the future overcome the current limitations imposed upon the linear dynamic range of detectors, through the use of discrete detection channels in array detectors, the abundance sensitivity, the mass range, and the duty cycle. The linear dynamic range of the detectors in MS spans between 6 and 10 orders of magnitude. This might be of concern as the temporal compression of the signal produces substantial increases in relative sensitivity [counts s⁻¹ fmol⁻¹], even in the absence of increases in absolute sensitivity [counts fmol⁻¹], which can cause detector saturation at large beam waist sizes or higher analyte concentrations. In summary, there is no ‘ideal’ ICP-MS instrument type currently available that provides simultaneous multi-element detection across the full elemental mass range, with fast data readout, minimal blind time, wide linear dynamic detection range, high mass resolution, and high sensitivity. The increasing trend towards fast transient ICP-MS, not only for laser ablation imaging, but also for the single particle characterization promotes the adoption of low dispersion cells.

Fundamental considerations

Peak profile shape

The shape of a signal peak arising from the response for a single shot is an important parameter in the performance of a LA-ICP-MS system, and is therefore often used to benchmark these systems in terms of aerosol dispersion. Attempts to model the peak profile have supported our understanding of the aerosol entrainment/elution/transport processes, thus allowing the ablation cell design to be adapted in such a way that the limiting physical processes, are addressed. The single pulse response (SPR) can be constructed as a convolution of the aerosol particle release function and the setup transfer function (STF), which can be considered as the system response function. In 2001, Bleiner et al.^26,39 reported on a theoretical model for the SPR in an ideal mixing system (Fig. 3), by modelling the dispersion and diffusion in the system during particle transport. In a first approximation, a linear relationship can be established between the cell-induced dispersion and its volume.^26,118 Accounting for a non-steady velocity profile in the transport line – assuming a laminar flow – an aerosol delivery function at time t was derived:^26,119

Fig. 3 Theoretical models proposed in literature, provided with matching initial parameters: v_g,c = 10 ml s⁻¹, V = 100 ml, t₀ = 10 s. The log-normal probability density function (PDF) was added as a reference to its shape.

With v_g,c the carrier gas flow rate, I₀ an analyte-specific response factor proportional to the integrated response – and by extension the concentration of the analyte, V_cell the volume of the cell, t₀ the minimum particle transit time through the system, and h a Heaviside step function h(t − t₀) = {0, t < t₀; 1, t ≥ t₀}. The exponential decay of the signal has been observed widely, and appears in the factor relating to the rate of aerosol evacuation of the function.^119–121 Plotnikov et al.¹²² expanded upon this model, by introducing an additional exponential parameter:

With k a parameter introduced to describe the aerodynamic properties of the cell. The model (Fig. 3) observes mass conservation, and is self-consistent in this aspect, and was provided a physical meaning by Bleiner et al.³⁹ An alternate model, building on Bleiner's model, was suggested by Gäckle et al.,^123,124 in which the particle density at the margins of the cross-section of the conduit converges to the initial analyte density in the cell (under ideal mixing conditions). A total dispersion function was derived:

The model also attempts to account for the extraction yield by the interface by limiting the observed signal to the region of the cross-section around the centre axis.¹²³ Plotnikov et al.¹²⁵ and Bleiner et al.³⁹ have argued that the model does not satisfy continuity, as the integrated area under the profile depends on transport parameters. Bleiner et al.³⁹ proposed a CFD model based on the model by Plotnikov et al. that accounts for the influence of gas characteristics and particle size distribution. The overall aerosol dispersion will depend on the particle size distribution, which is closely related to the ablation process itself, due to size-dependent segregation during transport.^96,126 Despite efforts to derive all physical parameters relevant to the kernel, describing and predicting the SPR, current models remain incomplete as some processes have been ignored or disregarded, e.g., ionization,¹⁴ diffusion and turbulence in the plasma,¹² the geometry of the ablation damage, temporal changes in ablation yield linked to target composition variability, and the initial dispersion of the aerosol (a homogenous distribution of aerosol density within the cell has been assumed). Some of these effects can be accounted for in a straightforward manner by descriptive functions convolved with the I₀ profile, but other require an overhaul of the model. For the fastest cells,^21,127 a Gaussian-like peak profile has been reported, in which the front dispersion has become comparable to the trailing dispersion. An approximately symmetrical profile would be expected only if radial diffusion and/or pressure driven gas flow expansion were major contributors to dispersion and turbulence-, ablation-, and velocity gradient-induced dispersion were of minor influence. Empirically derived STF, e.g., a linear combination of log-normal distributions,¹²⁷ can also model the peak profile. Multiple studies have reported a bimodal peak profile shape.^16,21,83 It has been hypothesized that particle-size segregation in turbulent streamlines forms the basis of the phenomena. As noted by Russo et al.,¹²⁸ the particle distribution created by fs-lasers trends towards smaller particles, and a narrower profile, which partly eliminates size-segregation based on differences in the relative velocity, originating from the link between particle mass, mean-free path length and hydrodynamic cross-section. Additional information on laser ablation models can be found in the literature.^51,129 Deconvolution of the transient response in the time domain can improve the lateral or depth resolution by resolving the signal response for each laser shot, i.e. reversing the image blurring effects that result from pulse mixing. The deconvolution can be readily achieved through regularized or parameterized multivariate regression,¹²² or a non-affine transformation.¹¹⁹ There is, however, a trade-off between pulse response overlap and lateral resolution/accuracy/contrast ratio in the elemental image. It should be noted that a higher repetition rate will not necessarily increase the lateral resolution, as the S/N ratio of deconvolution algorithms aggravates with the overlap and number of parameters involved in the combined SPF. Within this approach, the peak profile model is used as a kernel function for the deconvolution. The signal response is modelled as a superimposition of SPR functions, e.g., implemented as a convolution of the SPR with the Dirac δ function.¹¹⁹ Bleiner et al.,¹¹⁹e.g., demonstrated data deconvolution through factorization. Plotnikov et al.¹²² proposed an algorithm to reconstruct the response peak for every pulse based on multivariate regression and regularization of the detector response, which was modelled as a superimposition of the SPR (fitted towards the experimental spectrum by the iterative Levenberg–Marquardt algorithm). Deconvolution approaches allow pixel-by-pixel scanning method to be conducted at higher repetition rates and scanning speeds, without compromising on spatial resolution.

Ablation approaches

The evolution to low dispersion cell designs, enabling single-shot analysis, creates new opportunities for alternative scanning methods that improve imaging speed and resolution. Until recently, the approach to image biological samples was restricted to raster scanning, i.e. the laser is scanned across the sample surface in a rectilinear line pattern, at speeds comparable to the beam waist size, and fired continuously at a repetition rate that exceeds the width of a single pulse peak profile by a factor 2 or higher. The response, after clipping the temporal response in the areas when the laser is not firing, and restructuring the response for every line chronologically, can be projected into a 2D image for every nuclide. The time-resolved response is however decoupled or distorted from the spatial coordinates corresponding to the response, as the aerosol dispersion is the determining factor in the distortion of downstream sampling positions and in the trade-off between resolution and scanning speed. The offset between the ablation positions and the transient detector can be compensated for by cross-referencing the time traces from the laser and ICP-MS unit via software, however, this ultimately does not improve lateral resolution. A higher resolution can be obtained whilst scanning and firing slower, however, the resolution will never be better than the spot size. A 2D or 3D nuclide distribution map can also be derived by resolving the response of multiple ablation positions in the time domain.¹²⁷ In other words, the aerosol is allowed to washout, with the integrated pulse response converted into the value of a single pixel, before an adjacent, non-overlapping location is sampled. This strategy generates spatially resolved pixel responses, which provides additional spatial resolution, but is only feasible when low dispersion ablation cells are employed, due to the inherent time constraints associated with the finite washout after each pulse. An early example of a 3D imaging approach in combination with resolved pixel acquisition via LA-ICP-MS was presented in a study by Peng et al.¹³⁰ on the near-surface U and C accumulation in a basaltic clast sample. They proposed sampling in a pattern of overlaid rectangular grids of ablation points, in which the layers were sequentially ablated. The use of a standard ablation cell resulted in a measurement time of 4–7 h per layer. The quantification protocol was based on normalization of the summed concentration of 8 major elements to a known stable value of 51.8 ± 1.1% wt, and forwarding the normalization factor to the signal intensity of all other elements. van Elteren et al.¹³¹ proposed a similar approach for 3D mapping of corroded glass: drilling a set of craters in a grid sequentially, whilst isolating every pulse response. Quantification was achieved by normalizing the sum of all oxides of all major and minor elements to 100% wt, an approach that was initially proposed for bulk analysis without internal standardization (IS).¹³² Chirinos et al.¹³³ adopted an identical drilling pattern. When every pulse can be isolated and integrated, the peak area can be normalized by internal standardization. Alternatively, when a simultaneous full-elemental mass spectrum MS unit is used, individual channels can be normalized to a factor assumed to be proportional to total mass ablated, such as the sum of ion counts of populated channels, or the sum of all molar concentrations, as proposed by Leach et al.¹³⁴ Recently, this was demonstrated by Gundlach-Graham et al.¹⁹ and Burger et al.,¹³⁵ in a study where the sum of the oxide forms of every detected element within their geological samples was utilized in the normalization of the results. The quantification of nuclide concentrations in multi-domain or multi-phase samples remains challenging for the 100% mass normalization procedure as the elemental sensitivities are ablation rate, and therefore, chemical-structure dependent. If a calibration standard is available for each domain, domain-boundaries would still prove challenging due to non-linear ablation effects. Although instability in the laser energy density is still present, the current generation of deep-UV ns- or fs-lasers has a laser energy density stability to within ∼1%, along with optical auto-focusing during ablation, which helps to minimize focus drift. Approaches based on scanning a 3D grid compare favourably to drilling the grid, as the steady-state fractionation in line scanning can be compensated for by tuning the ICP-MS unit, whilst fractionation during drilling is a transient phenomenon, and can be corrected for mathematically.¹³⁶ The effects of the crater aspect ratio on fractionation can be alleviated by alternative ablation approaches, e.g., trepanning (drilling according to a helical pattern).¹³⁷ For biological targets, the difficulties of applying quantification approaches are compounded by the complex morphology. Unfortunately, the C signal, for use as an IS is compromised by fractionation effects.¹³⁸ Temporal and spatial changes in ablation rate impede 3D imaging based on drilling approaches in biological samples. 3D imaging for biological samples however can be conducted by analysing sequential sections (serial sectioning), obtained via (cry)tome cutting of embedded or frozen organisms/organs/parts (Fig. 4). The choice of ablation approach for bioimaging may also have to take into account the strategy towards internal standardization or variants thereof, as such strategies often require complete ablation through tissue sections, and in some cases, ablation through a spiked coating below or above the tissue. The 2D images are stitched into a 3D stack of 2D images, either by manual alignment, or by image registration (Fig. 4d) based on marker points or selected elements such as P, which strongly outline the morphology of biological structures. A 3D volume can be reconstructed from the stack by stitching methods such as 3D Delaunay triangulation (Fig. 4e). Clustering algorithms, e.g., fuzzy C-means clustering, K-means clustering,¹³⁹ can then be used to isolate structures, e.g., biological compartments, within the 3D volume. Alternatively, isosurface rendering can extract surfaces from the volume. It can be easily envisaged that isolation of pulse responses through low dispersion ablation cells (Fig. 4b), in combination with topographical or morphological information would allow a computation of a 3D model (Fig. 4e) of the sample, in which the information and geometry for every ablated volume of every individual pulse is visualized as a single voxel, or a collection of voxels. Furthermore, analogous to software available in computer-aided manufacturing, the material removal process can be simulated, and arbitrary 3D and 2.5D ablation patterns can be adopted, e.g., to selectively ablate parts of the sample volume by tracking the morphology within the sample in 3D. In high-resolution LA-ICP-MS imaging, the laser beam waist size is intrinsically limited by: (i) the analytical sensitivity and (ii) the far-field diffraction limit. By virtue of their improved sensitivity, low dispersion ablation cells allow for smaller ablation spots. They also facilitate applications such as the selective ablation of individual cells, e.g., in combination with automated optical cell recognition software. The lateral resolution can be improved further by oversampling, i.e., overlapping the ablation positions, and reconstructing the I₀ profile through deconvolution, reducing the impact of the blurring effect on lateral resolution. Based on his previous work, Plotnikov et al.¹²⁵ pioneered deconvolution of the responses of overlapping ablation positions based on Fredholm integral equations of the first kind. Van Malderen et al.¹²⁷ recently reported a deconvolution approach based on the iterative Richardson–Lucy algorithm to retrieve spatially resolved information on a level below the beam waist dimensions in 2D and 3D imaging. Oversampling, whilst quantitatively removing the material at each ablation position, will improve the lateral distribution, as the response relates to the new edge of the tissue ablated, rather than the entire spot. The approach was reported by Drescher et al.⁸ for mapping of tissue sections. Analogous strategies can be encountered in other techniques, e.g., MALDI-MS.¹⁴⁰ In conclusion, low dispersion cells, especially in combination with simultaneous multi-element detection open up new sampling and normalization approaches that were previously inaccessible as a result of throughput or sensitivity constraints.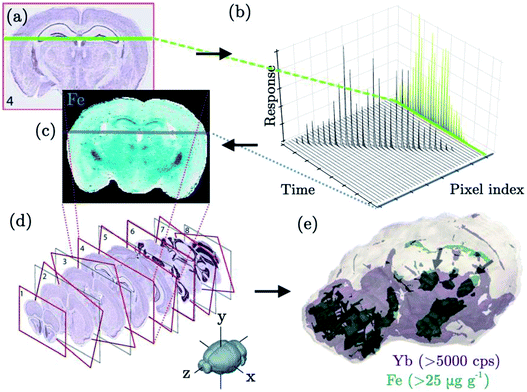

Fig. 4 Schematic representation of the hypothetical combination of low dispersion cells with single shot response isolation (b), producing spatially resolved images (c) of a tissue slice (a), and serial sectioning, in which a 3D volume (e) is reconstructed through image registration (d) of individual slices based on the P signal. Reformatted figure with components reprinted with permission of Paul et al.¹

Novel applications in bioimaging

The performance characteristics of low dispersion cells are advantageous for many applications spanning a variety of fields. Recent demonstrations of this level of performance include the analysis of corroded glass,¹²⁷ a multi-layer ceramic capacitor,²⁰ Opalinus clay rock,¹³⁵ a Seymchan pallasite meteorite,¹⁹ individual uranium particles,¹¹² fluid inclusions in quartz,¹⁴¹ biological tissue² and individual cells.²¹ The following sub-sections focus on novel applications involving the ablation of biological targets. These applications share a common requirement for high-speed, high-sensitivity and spatial resolution and therefore would strongly benefit from the use of low dispersion ablation cells.

High resolution imaging and single cell analysis

The use of LA-ICP-MS for bioimaging is fairly well established and has been thoroughly reviewed by various authors.^25,142,143 Typical applications include mapping endogenous metal distributions in organs¹⁴⁴ and determining the tissue penetration depth of administered drug complexes.^145–147 A common theme throughout these applications is the requirement for high spatial resolution to differentiate regions and structures of interest. This necessitates rapid washout, high repetition rates, and fast scanning speeds if imaging is to be completed within an acceptable time frame. Small scale structural features, for instance cortical fibres in ocular tissue, are obscured if larger spot sizes are used,⁶ whilst some emerging applications specifically demand lateral resolution on the level of cell structures.

The increasing development and use of cellular therapies has produced a requirement for strategies to monitor their persistence in vivo and their delivery to target organs. Managh et al. demonstrated that therapeutic cells can be individually tracked in recipients using a combination of elemental labelling and LA-ICP-MS detection.¹⁴⁸ Cells were labelled with a Gd-based MRI contrast agent, prior to infusion into a mouse model, and the Gd label was detected within extracted cell samples at 10 days post-infusion. Two subsequent publications have reported imaging of administered cells within tissue sections, using gold nanoparticles³ and Tm-based contrast agent labels,¹⁴⁹ respectively. The LA-ICP-MS approach offered several advantages over other detection methods for cell tracking; namely high sensitivity, the ability to selectively target and/or identify individual cells and compounds, and the capability to detect cells at periods when the labels would no longer be detectable by other techniques. However, a major limitation of these studies was the speed of analysis, which compares unfavourably to other elemental imaging techniques within the biological and clinical fields, e.g., fluorescence microscopy. In the vast majority of bioimaging literature, LA-ICP-MS is used as a research technique, but clearly for applications such as this, where the technology is proposed as a clinical or diagnostic aid, throughput becomes paramount. Douglas et al. therefore used a low dispersion LA-ICP-MS interface to analyse Gd-labelled cells from the aforementioned tracking study.²¹ Peak durations of less than 10 ms at FW0.1M were reported. Therefore, if low dispersion laser systems incorporated automated optical cell recognition software, then a more clinically acceptable analysis rate of >100 cells per s could be achieved. The authors also noted a 6-fold increase in absolute sensitivity when using the low dispersion interface, compared to conventional technology, which is similar to the gains observed for other ablation setups. This indicates that tracking proliferating cells with LA-ICP-MS could be feasible over a greater number of divisions. Zhai et al. recently demonstrated visualization of a fluorescent Au cluster probe, targeting integrin α_IIbβ₃, by confocal fluorescence microscopy and subsequent quantification of the number of integrin α_IIbβ₃ in a human erythroleukemia cell line on a single cell level.¹⁵⁰

Enhanced S/N ratios may also be beneficial when sub-cellular imaging is required. Giesen et al. imaged iodinated fibroblast cells using a 4 μm spot size, which is around one tenth of the size of a fibroblast cell nucleus.¹⁵¹ The iodine stain preferentially accumulated within the nucleus, which enabled differentiation of the nucleus and cytoplasmic regions on the basis of the ¹²⁷I signal. However, iodine suffers from a high instrumental background, so an alternative approach for staining cells using Tm containing maleimide–DOTA complex has since been proposed.¹⁵² Besides histology, sub-cellular resolution is also important in the emerging field of nano-toxicology. With the increasing use of nanomaterials for therapeutic applications, there is a requirement to quantify their accumulation within cells⁹ and to determine their cellular localization pattern following uptake. In 2012, Drescher and co-workers performed sub-cellular imaging of individual fibroblast cells using a 4 μm spot size.⁸ Au and Ag nanoparticle accumulation was localized to the perinuclear region of the cells. Subsequent studies have also reported the cellular distribution of smaller, 14 nm sized Au nanoparticles¹⁵³ and silica nanoparticles containing an inner Au or Ag core.¹⁵⁴ However, all of the aforementioned studies imaged fibroblast cells, which at ≥50 μm in diameter can be considered fairly large in size. Thus, the application would benefit from improved spatial resolution if the distribution of nanoparticles within smaller cells is to be studied.

Multiplexing

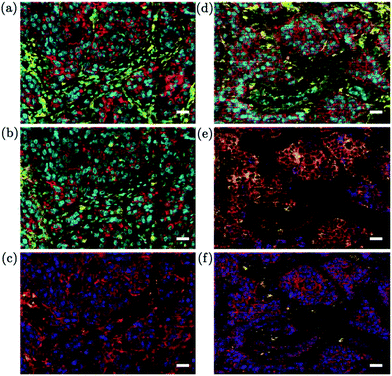
Multiparametric analysis of biomarkers is an emerging area that is expected to extend the reach of LA-ICP-MS to a new target audience. Biomarkers can be detected indirectly in cells or tissue sections through the application of metal-conjugated antibodies, which bind to their respective antigens on the cell surface. A range of metal-conjugated antibodies have been described in the literature,^155,156 many of which are now commercially available.¹⁵⁷ By the use of multiple antibodies, each labelled with a different metal or even a specific nuclide of a metal, simultaneous detection of multiple proteins, phenotype and function is possible using LA-ICP-MS. In an early example of this, Hutchinson et al. used Eu- and Ni-coupled antibodies to image amyloid precursor protein and αβ peptide in histological sections from a mouse model of Alzheimer's disease.¹⁵⁸ Other studies have imaged metal-conjugated antibodies in isolated cells,³ western blot immunoassays,¹⁵⁶ protein microarrays,¹⁵⁹ and sections of breast cancer tissue.^151,160,161 The advantages of using low dispersion ablation cells for biomarker analysis were demonstrated by Wang and co-workers, as part of the first publication describing the performance of their tube cell.¹⁸ The cell was coupled to a ICP-SF-MS instrument to image the distribution of ¹⁶⁵Ho-tagged anti-human epidermal growth factor 2 (HER2) antibody in breast cancer tissue. A very high lateral resolution, of ∼1 × 1 μm², enabled precise determination of HER2 on individual cell membranes, which was described as a crucial criterion for morphological assessment in cancer diagnostics. Importantly, superior sensitivity was observed for LA-ICP-MS using the tube cell compared to images of the same section analysed using micro-XRF with the same lateral resolution. Due to the limitations of ICP-SF-MS instruments for fast transient analysis (described previously in the Mass spectrometers section) only a single label was used in this experiment. However, in a later paper the tube cell was coupled to a pseudo-simultaneous detecting ICP-TOF-MS unit, which enabled multiplexed analysis.² Thirty two proteins were simultaneously measured, which enabled identification of specific cell sub-populations within a 0.5 mm² area of breast cancer tissue and highlighted tumor heterogeneity (Fig. 5). The 1 × 1 μm resolution was sufficient to clearly distinguish the nuclei, plasma membranes and stromal compartments of individual cells on the basis of their protein expression. It is noted that the CyTOF equipment used by Giesen et al. has been targeted towards workers in the clinical field, with many of the resulting publications based around flow cytometry appearing in journals relevant to the clinical field. Indeed, the authors of this review have observed a considerable interest in LA-ICP-MS technology from collaborators working in the field of immunology. However, continued improvement of the washout characteristics will be required to fully reach this potential new audience. The tube cell used for the above work has a reported washout time of 30 ms FW0.01M, thus a 20 Hz repetition rate and 20 μm s⁻¹ translation speed were used to ensure baseline resolution between shots for 1 × 1 μm image resolution. Using these parameters, it reportedly took 3.5 hours to image a 0.5 mm² area. The latest reported iteration of their cell improves the dispersion to 9 ms FW0.01M (NIST SRM 610; 10 μm diameter laser beam waist). This is a dramatic improvement on commercially available technology, but clearly, further improvement of the sample throughput would be greatly beneficial for clinical applications.

Fig. 5 Representative mass cytometry images of two luminal HER2+ breast cancer tissue samples. (a) Overlay of cytokeratin 8/18 (red), H3 (cyan) and vimentin (yellow). (b) Overlay of cytokeratin 7 (red), H3 (cyan) and CD44 (yellow). (c) Overlay of pan-actin (red), progesterone receptor (blue) and CD68 (yellow). (d) Overlay of HER2 (red), H3 (cyan) and vimentin (yellow). (e) Overlay of E-cadherin (red), cytokeratin 7 (yellow) and phosphorylation on S235/S236 on S6 (blue). (f) Overlay of β-catenin (red), estrogen receptor (blue) and CD68 (yellow). The white scale bars are 25 μm in length. Reprinted by permission from Macmillan Publishers Ltd: Nature Methods 11:417–422, © 2014.

3D imaging

The use of LA-ICP-MS for 3D imaging is a relatively recent concept, but with the development of faster LA technology it is one that is gaining momentum. Two new approaches to performing 3D imaging with low dispersion cells have already been reported this year,^127,135 both of which used non-biological targets. At the time of writing, there is relatively little literature covering 3D imaging of biological samples. Despite this, a 3D imaging approach would be highly beneficial in this area, as tissue inhomogeneity may result in an uncharacteristic representation of small scale features within individual 2D sections. 3D imaging could also prove useful to isolate hotspots in larger volumes such as organs, which might be missed when analysing a single cross-section. Additionally, small organisms could be fully ablated, to determine the distribution of targeted compounds in each body compartment. As discussed in a previous section and shown in Fig. 4, specific 3D imaging approaches tuned towards biological samples have been developed. In 2010, Hare et al. used a serial sectioning and imaging approach to create a 3D representation of Mn, Fe, Cu and Zn distribution within a mouse brain.¹⁶² Twelve sections from a single animal, each of 30 μm thickness, were consecutively ablated. Integrated Spectral Imaging Data Analysis Software (ISIDAS), an in-house Python-based program, was used to compile the individual data files and align 2D images of each slice using image registration¹ to create a 3D representation of the mouse brain. The same research group later applied a similar approach to create a 3D atlas of trace metals in the mouse brain.¹⁶³ A total of 46 sections were taken at 150 μm intervals. Each slice was 30 μm thick and covered a ∼10 mm² area, with imaging of each slice performed using a 80 μm spot size and 160 μm s⁻¹ scan speed. It is clear that such an approach requires a lengthy time commitment, which would be a limiting factor for some users. The above studies were reported to take 36 and 158 hours for the ablation of 12 and 46 sections, respectively. Improvements in acquisition speed, and the concurrent development of software to handle new data formats, may lead to the growing use of 3D LA-ICP-MS imaging and higher spatial resolution¹⁶⁴ in the future, in parallel to a similar ongoing evolution towards 3D imaging MS.^163,165

Conclusions and outlook

In the past few years, the development of low dispersion ablation cells has accelerated leading to new emerging applications of LA-ICP-MS in the biological and clinical fields. Despite this, further development of transport-efficient, low dispersion ablation cells is highly desirable. The optimum design criteria for low dispersion ablation cells can be summarized as: (i) a small volume, confined by solid walls or gas flows, in which the plume can expand, (ii) efficient uptake by utilizing the momentum and the characteristics of He, (iii) fluid-dynamic optimized design to transfer the aerosol by laminar flows to the transport conduit without creating advection/turbulence as a result of dead volume, (iv) minimisation of tubing lengths, bends and divergences in the conduit diameter and (v) utilization of the characteristics of Ar to achieve optimal transport and ionization conditions. The level of aerosol dispersion is pushing ever closer towards the aerosol dispersion of 1–2 ms achieved in in-torch ablation.^80,82–84 As the environment within an ablation cell can be isolated and controlled to a large extent, we may encounter cells in the future achieving even lower aerosol dispersion. It is becoming clear that fast (pseudo-) simultaneous mass analysers and detection systems have the potential to displace quadrupole and sector-field mass analysers for LA-ICP-MS mapping, as sequential mass filtering restricts the sampling speed. Detection of the full elemental mass spectrum, or a large part thereof, enables a more detailed look at the co-spatial distribution of elements, and calibration based on 100% wt normalization for every laser shot. An ICP-MS instrument capable of handling highly transient plasma loads, whilst offering simultaneous multi-element detection across the full mass range, wide linear dynamic range, fast data readout, minimal blind time, high mass resolution and high sensitivity, would make a good match to low dispersion laser ablation systems. 2D imaging of biological tissue samples is becoming an accepted approach for biomedical research and in some cases has been suggested as a clinical diagnostic aid. The sample preparation, calibration, standardization, ablation and image processing protocols to enable this analysis are well established in the literature. In order to better establish LA-ICP-MS for the analysis of biological samples by application-oriented users, who often desire a ‘sample in – press a button – results out’ instrument, further efforts are required, notably in instrument and software development. As the target audience widens and the complexity of experimental designs increases, requiring more replicates to be analysed in a set time span, new approaches to increase throughput are necessary. Sensitivity will grow in relative importance as new applications emerge requiring targeted nuclide analysis at lower lateral resolution. A handful of researchers are also looking into 3D imaging approaches, single-cell analysis, and multiplexing, all of which currently are niche applications, but show potential. The newly developed low dispersion cells are well suited to these challenges, as has already been demonstrated by specialised research groups. The body of literature and key concepts upon which this review article is based, provide key indicators for the further development of ablation cells.

Acknowledgements

The authors acknowledge financial and logistic support from the Flemish Research Foundation (FWO). Stijn Van Malderen is a PhD fellow of the FWO. Amy Managh acknowledges financial support through a Loughborough University Enterprise Fellowship (Engineering and Physical Sciences Research Council, Impact Acceleration Account).

References

1. B. Paul, D. J. Hare, D. P. Bishop, C. Paton, V. T. Nguyen, N. Cole, M. M. Niedwiecki, E. Andreozzi, A. Vais, J. L. Billings, L. Bray, A. I. Bush, G. McColl, B. R. Roberts, P. A. Adlard, D. I. Finkelstein, J. Hellstrom, J. M. Hergt, J. D. Woodhead and P. A. Doble, Chem. Sci., 2015, 6, 5383–5393.
2. C. Giesen, H. A. Wang, D. Schapiro, N. Zivanovic, A. Jacobs, B. Hattendorf, P. J. Schuffler, D. Grolimund, J. M. Buhmann, S. Brandt, Z. Varga, P. J. Wild, D. Günther and B. Bodenmiller, Nat. Methods, 2014, 11, 417–422.
3. A. J. Managh, R. W. Hutchinson, P. Riquelme, C. Broichhausen, A. K. Wege, U. Ritter, N. Ahrens, G. E. Koehl, L. Walter, C. Florian, H. J. Schlitt, H. J. Reid, E. K. Geissler, B. L. Sharp and J. A. Hutchinson, J. Immunol., 2014, 193, 2600–2608.
4. A. Izmer, D. Gholap, K. de Houwer, F. Cuyckens and F. Vanhaecke, J. Anal. At. Spectrom., 2012, 27, 413–418.
5. D. S. Urgast and J. Feldmann, J. Anal. At. Spectrom., 2013, 28, 1367–1371.
6. I. Konz, B. Fernandez, M. L. Fernandez, R. Pereiro, H. Gonzalez-Iglesias, M. Coca-Prados and A. Sanz-Medel, Anal. Bioanal. Chem., 2014, 406, 2343–2348.
7. M. R. Flórez, M. Aramendía, M. Resano, A. C. Lapeña, L. Balcaen and F. Vanhaecke, J. Anal. At. Spectrom., 2013, 28, 1005–1015.
8. D. Drescher, C. Giesen, H. Traub, U. Panne, J. Kneipp and N. Jakubowski, Anal. Chem., 2012, 84, 9684–9688.
9. M. Wang, L. N. Zheng, B. Wang, H. Q. Chen, Y. L. Zhao, Z. F. Chai, H. J. Reid, B. L. Sharp and W. Y. Feng, Anal. Chem., 2014, 86, 10252–10256.
10. A. M. Leach and G. M. Hieftje, Appl. Spectrosc., 2002, 56, 62–69.
11. D. Autrique, A. Bogaerts, H. Lindner, C. C. Garcia and K. Niemax, Spectrochim. Acta, Part B, 2008, 63, 257–270.
12. H. Lindner and A. Bogaerts, Spectrochim. Acta, Part B, 2011, 66, 421–431.
13. D. Asogan, B. L. Sharp, C. J. P. O'Connor, D. A. Green and J. Wilkins, J. Anal. At. Spectrom., 2011, 26, 631–634.
14. M. Aghaei and A. Bogaerts, J. Anal. At. Spectrom., 2016 10.1039/c5ja00162e.
15. H. Lindner, D. Autrique, J. Pisonero, D. Günther and A. Bogaerts, J. Anal. At. Spectrom., 2010, 25, 295–304.
16. E. L. Gurevich and R. Hergenröder, J. Anal. At. Spectrom., 2007, 22, 1043–1050.
17. D. Monticelli, E. L. Gurevich and R. Hergenröder, J. Anal. At. Spectrom., 2009, 24, 328–335.
18. H. A. Wang, D. Grolimund, C. Giesen, C. N. Borca, J. R. Shaw-Stewart, B. Bodenmiller and D. Günther, Anal. Chem., 2013, 85, 10107–10116.
19. A. Gundlach-Graham, M. Burger, S. Allner, G. Schwarz, H. A. Wang, L. Gyr, D. Grolimund, B. Hattendorf and D. Günther, Anal. Chem., 2015, 87, 8250–8258.
20. S. J. M. Van Malderen, J. T. van Elteren and F. Vanhaecke, J. Anal. At. Spectrom., 2015, 30, 119–125.
21. D. N. Douglas, A. J. Managh, H. J. Reid and B. L. Sharp, Anal. Chem., 2015, 87, 11285–11294.
22. T. Hirata, Anal. Sci., 2007, 23, 1195–1201.
23. B. Wu and J. S. Becker, Int. J. Mass Spectrom., 2012, 323, 34–40.
24. S. M. Monk and S. M. Lev, J. Anal. At. Spectrom., 2013, 28, 274–279.
25. J. S. Becker, A. Matusch and B. Wu, Anal. Chim. Acta, 2014, 835, 1–18.
26. D. Bleiner and D. Günther, J. Anal. At. Spectrom., 2001, 16, 449–456.
27. D. Bleiner and A. Bogaerts, Spectrochim. Acta, Part B, 2007, 62, 155–168.
28. J. Pisonero, D. Fliegel and D. Günther, J. Anal. At. Spectrom., 2006, 21, 922–931.
29. C. Kouris and J. Tsamopoulos, Chem. Eng. Sci., 2000, 55, 5509–5530.
30. R. Grigoriev and H. G. Schuster, Transport and Mixing in Laminar Flows: From Microfluidics to Oceanic Currents, Wiley-VCH, Wienham, Germany, 2012.
31. C. C. Garcia, H. Lindner and K. Niemax, Spectrochim. Acta, Part B, 2007, 62, 13–19.
32. D. Bleiner, Optimization of a Laser Ablation Inductively Coupled Plasma Mass Spectrometry System for the Detection of Short Transient Signals, Ph.D. thesis, ETH Zurich, 2002.
33. L. Summerfield, Winter Conference on Plasma Spectrochemistry, Tucson, Arizona, USA, 2012.
34. A. V. Gusarov and I. Smurov, J. Phys. D: Appl. Phys., 2001, 34, 1147–1156.
35. D. Bleiner and T. Lippert, J. Appl. Phys., 2009, 106, 123301.
36. S. M. Eggins, L. P. J. Kinsley and J. M. G. Shelley, Appl. Surf. Sci., 1998, 127–129, 278–286.
37. A. P. K. Leung, W. T. Chan, X. L. Mao and R. E. Russo, Anal. Chem., 1998, 70, 4709–4716.
38. A. P. K. Leung, W. T. Chan, X. L. Mao and R. E. Russo, Anal. Chem., 1998, 70, 4709–4716.
39. D. Bleiner and A. Bogaerts, J. Anal. At. Spectrom., 2006, 21, 1161–1174.
40. C. C. Garcia, H. Lindner and K. Niemax, J. Anal. At. Spectrom., 2009, 24, 14–26.
41. A. Bogaerts, Z. Chen and D. Bleiner, J. Anal. At. Spectrom., 2006, 21, 384–395.
42. D. Bleiner, A. Bogaerts, F. Belloni and V. Nassisi, J. Appl. Phys., 2007, 101, 083301.
43. S. Amoruso, J. Schou and J. G. Lunney, Appl. Phys. A: Mater. Sci. Process., 2008, 92, 907–911.
44. A. M. Popov, F. Colao and R. Fantoni, J. Anal. At. Spectrom., 2009, 24, 602–604.
45. A. M. Popov, F. Colao and R. Fantoni, J. Anal. At. Spectrom., 2010, 25, 837–848.
46. L. B. Guo, W. Hu, B. Y. Zhang, X. N. He, C. M. Li, Y. S. Zhou, Z. X. Cai, X. Y. Zeng and Y. F. Lu, Opt. Express, 2011, 19, 14067–14075.
47. Z. Wang, Z. Hou, S.-l. Lui, D. Jiang, J. Liu and Z. Li, Opt. Express, 2012, 20, A1011–A1018.
48. S. J. Choi, K.-j. Lee and J. J. Yoh, Spectrochim. Acta, Part B, 2014, 97, 113–117.
49. C. Li, L. Guo, X. He, Z. Hao, X. Li, M. Shen, X. Zeng and Y. Lu, J. Anal. At. Spectrom., 2014, 29, 638–643.
50. H. Lindner, D. Autrique, C. C. Garcia, K. Niemax and A. Bogaerts, Anal. Chem., 2009, 81, 4241–4248.
51. E. Tognoni and G. Cristoforetti, J. Anal. At. Spectrom., 2014, 29, 1318–1338.
52. X. Zeng, X. Mao, S. S. Mao, S.-B. Wen, R. Greif and R. E. Russo, Appl. Phys. Lett., 2006, 88, 061502.
53. A. Bogaerts and Z. Chen, Spectrochim. Acta, Part B, 2005, 60, 1280–1307.
54. D. Autrique and V. Alexiades, J. Appl. Phys., 2014, 115, 166101.
55. H. Lindner, K. H. Loper, D. W. Hahn and K. Niemax, Spectrochim. Acta, Part B, 2011, 66, 179–185.
56. R. G. Root, in Lasers-Induced Plasmas and Applications, ed. L. J. Radziemski and A. Cremers, Taylor & Francis, New York, 1989.
57. N. M. Bulgakova, A. V. Bulgakov and O. F. Bobrenok, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5624–5635.
58. S. Amoruso, X. Wang, C. Altucci, C. de Lisio, M. Armenante, R. Bruzzese, N. Spinelli and R. Velotta, Appl. Surf. Sci., 2002, 186, 358–363.
59. A. Lorusso, V. Nassisi, L. Velardi and M. V. Sicilano, J. Phys.: Conf. Ser., 2010, 227, 012037.
60. D. Bleiner and A. Bogaerts, Spectrochim. Acta, Part B, 2006, 61, 421–432.
61. R. E. Russo, X. L. Mao, O. V. Borisov and H. C. Liu, J. Anal. At. Spectrom., 2000, 15, 1115–1120.
62. M. Guillong and D. Günther, J. Anal. At. Spectrom., 2002, 17, 831–837.
63. D. B. Aeschliman, S. J. Bajic, D. P. Baldwin and R. S. Houk, Anal. Chem., 2004, 76, 3119–3125.
64. I. Kroslakova and D. Günther, J. Anal. At. Spectrom., 2007, 22, 51–62.
65. N. J. Saetveit, S. J. Bajic, D. P. Baldwin and R. S. Houk, J. Anal. At. Spectrom., 2008, 23, 54–61.
66. M. Gaboardi and M. Humayun, J. Anal. At. Spectrom., 2009, 24, 1188–1197.
67. J. Mikova, J. Kosler, H. P. Longerich, M. Wiedenbeck and J. M. Hanchar, J. Anal. At. Spectrom., 2009, 24, 1244–1252.
68. M. Ohata, D. Tabersky, R. Glaus, J. Koch, B. Hattendorf and D. Günther, J. Anal. At. Spectrom., 2014, 29, 1345–1353.
69. S. Zhang, M. He, Z. Yin, E. Zhu, W. Hang and B. Huang, J. Anal. At. Spectrom., 2016 10.1039/c5ja00273g.
70. M. Miclea, C. C. Garcia, I. Exius, H. Lindner and K. Niemax, Spectrochim. Acta, Part B, 2006, 61, 361–367.
71. P. M. Outridge, W. Doherty and D. C. Gregoire, Spectrochim. Acta, Part B, 1997, 52, 2093–2102.
72. J. Feldmann, A. Kindness and P. Ek, J. Anal. At. Spectrom., 2002, 17, 813–818.
73. A. Vogel and V. Venugopalan, Chem. Rev., 2003, 103, 577–644.
74. I. Konz, B. Fernandez, M. Luisa Fernandez, R. Pereiro and A. Sanz-Medel, Anal. Chim. Acta, 2014, 809, 88–96.
75. J. Koch, I. Feldmann, N. Jakubowski and K. Niemax, Spectrochim. Acta, Part B, 2002, 57, 975–985.
76. H.-R. Kuhn and D. Günther, J. Anal. At. Spectrom., 2004, 19, 1158–1164.
77. H. R. Kuhn, M. Guillong and D. Günther, Anal. Bioanal. Chem., 2004, 378, 1069–1074.
78. H. R. Kuhn, Laser ablation ICP-MS: fundamental investigations on aerosols generated by laser ablation at ambient pressure, Ph.D. thesis, ETH Zurich, 2005.
79. L. Halicz and D. Günther, J. Anal. At. Spectrom., 2004, 19, 1539–1545.
80. X. R. Liu and G. Horlick, Spectrochim. Acta, Part B, 1995, 50, 537–548.
81. M. Tanner and D. Günther, J. Anal. At. Spectrom., 2005, 20, 987–989.
82. M. Tanner and D. Günther, J. Anal. At. Spectrom., 2006, 21, 941–947.
83. M. Tanner and D. Günther, J. Anal. At. Spectrom., 2007, 22, 1189–1192.
84. M. Tanner and D. Günther, Anal. Bioanal. Chem., 2008, 391, 1211–1220.
85. C. O'Connor, M. R. Landon and B. L. Sharp, J. Anal. At. Spectrom., 2007, 22, 273–282.
86. S. H. Jeong, O. V. Borisov, J. H. Yoo, X. L. Mao and R. E. Russo, Anal. Chem., 1999, 71, 5123–5130.
87. D. Günther and B. Hattendorf, TrAC, Trends Anal. Chem., 2005, 24, 255–265.
88. D. Bleiner and H. Altorfer, J. Anal. At. Spectrom., 2005, 20, 754–756.
89. J. Koch, S. Schlamp, T. Rösgen, D. Fliegel and D. Günther, Spectrochim. Acta, Part B, 2007, 62, 20–29.
90. I. Horn and D. Günther, Appl. Surf. Sci., 2003, 207, 144–157.
91. R. Niehaus, M. Sperling and U. Karst, J. Anal. At. Spectrom., 2015, 30, 2056–2065.
92. P. Lorazo, L. J. Lewis and M. Meunier, Phys. Rev. Lett., 2003, 91, 225502.
93. G. Paltauf and H. Schmidtkloiber, Lasers Surg. Med., 1995, 16, 277–287.
94. M. Oujja, E. Rebollar, C. Abrusci, A. D. Amo, F. Catalina and M. Castillejo, J. Phys.: Conf. Ser., 2007, 59, 571–574.
95. S. Gaspard, M. Oujja, C. Abrusci, F. Catalina, S. Lazare, J. P. Desvergne and M. Castillejo, J. Photochem. Photobiol., A, 2008, 193, 187–192.
96. F. Claverie, C. Pécheyran, S. Mounicou, G. Ballihaut, B. Fernandez, J. Alexis, R. Lobinski and O. F. X. Donard, Spectrochim. Acta, Part B, 2009, 64, 649–658.
97. L. R. Painter, R. N. Hamm, E. T. Arakawa and R. D. Birkhoff, Phys. Rev. Lett., 1968, 21, 282–284.
98. Y. Li, B. Shrestha and A. Vertes, Anal. Chem., 2007, 79, 523–532.
99. M. Tanner and D. Günther, Anal. Chim. Acta, 2009, 633, 19–28.
100. S. E. Hobbs and J. W. Olesik, Anal. Chem., 1992, 64, 274–283.
101. T. Nomizu, H. Hayashi, N. Hoshino, T. Tanaka, H. Kawaguchi, K. Kitagawa and S. Kaneco, J. Anal. At. Spectrom., 2002, 17, 592–595.
102. I. Strenge and C. Engelhard, J. Anal. At. Spectrom., 2016 10.1039/c5ja00177c.
103. A. J. Managh, Single cell tracking of therapeutic cells using laser ablation-inductively coupled plasma-mass spectrometry, Ph.D. thesis, Loughborough University, 2014.
104. S. Willie, Z. Mester and R. E. Sturgeon, J. Anal. At. Spectrom., 2005, 20, 1358–1364.
105. Perkin Elmer, NexION® 350 ICP-MS, http://www.perkinelmer.co.uk/CMSResources/Images/44-157289BRO_NexION350ICPMSBrochure.pdf, accessed 06/09/2015.
106. Agilent Technologies, Agilent 7900 ICP-MS, https://www.agilent.com/cs/library/brochures/5991-3719EN.pdf, accessed 06/09/2015.
107. Thermo Scientific, iCAP Q ICP-MS, http://www.thermoscientific.com/content/dam/tfs/ATG/CMD/cmd-documents/bro/spec/ea/icp-ms/PS-43096-ICP-MS-iCAP-Q-PS43096-EN.pdf, accessed 06/09/2015.
108. Analytik Jena, PlasmaQuant® MS, https://www.analytik-jena.de/fileadmin/content/pdf_analytical_instrumentation/ICP/ICP-MS/Br_PlasmaQuant_MS_en.pdf, accessed 06/09/2015.
109. C. Degueldre and P. Y. Favarger, Talanta, 2004, 62, 1051–1054.
110. B. Ramkorun-Schmidt, S. A. Pergantis, D. Esteban-Fernandez, N. Jakubowski and D. Günther, Anal. Chem., 2015, 87, 8687–8694.
111. A. J. Walder and P. A. Freedman, J. Anal. At. Spectrom., 1992, 7, 571–575.
112. G. Craig, Improving the utility of LA-ICP-MS for isotope ratio analyses of single particles with application to uranium oxide, Ph.D. thesis, Loughborough University, 2015.
113. D. P. Myers and G. M. Hieftje, Microchem. J., 1993, 48, 259–277.
114. O. Borovinskaya, B. Hattendorf, M. Tanner, S. Gschwind and D. Günther, J. Anal. At. Spectrom., 2013, 28, 226–233.
115. A. Gundlach-Graham, E. A. Dennis, S. J. Ray, C. G. Enke, C. J. Barinaga, D. W. Koppenaal and G. M. Hieftje, J. Anal. At. Spectrom., 2015, 30, 139–147.
116. GBC Scientific Equipment Pty Ltd, OptiMass 9500 ICP-TOFMS, http://www.gbcsci.com/products/icp_tof/optimass.asp, accessed 06/09/2015.
117. J. A. Felton, G. D. Schilling, S. J. Ray, R. P. Sperline, M. B. Denton, C. J. Barinaga, D. W. Koppenaal and G. M. Hieftje, J. Anal. At. Spectrom., 2011, 26, 300–304.
118. L. Moenke-Blankenburg, M. Gackle, D. Günther and J. Kammel, Processes of laser ablation and vapor transport to the ICP, Royal Soc Chemistry, Cambridge, UK, 1990.
119. D. Bleiner, F. Belloni, D. Doria, A. Lorusso and V. Nassisi, J. Anal. At. Spectrom., 2005, 20, 1337–1343.
120. J. Triglav, J. T. van Elteren and V. S. Selih, Anal. Chem., 2010, 82, 8153–8160.
121. H. A. O. Wang, D. Grolimund, L. R. van Loon, K. Barmettler, C. N. Borca, B. Aeschimann and D. Günther, Anal. Chem., 2011, 83, 6259–6266.
122. A. Plotnikov, C. Vogt and K. Wetzig, J. Anal. At. Spectrom., 2002, 17, 1114–1120.
123. M. Gäckle and D. Merten, Spectrochim. Acta, Part B, 2004, 59, 1893–1905.
124. M. Gäckle and D. Merten, Spectrochim. Acta, Part B, 2005, 60, 1517–1530.
125. A. Plotnikov, C. Vogt, K. Wetzig and A. Kyriakopoulos, Spectrochim. Acta, Part B, 2008, 63, 474–483.
126. M. Guillong, I. Horn and D. Günther, J. Anal. At. Spectrom., 2003, 18, 1224–1230.
127. S. J. Van Malderen, J. T. van Elteren and F. Vanhaecke, Anal. Chem., 2015, 87, 6125–6132.
128. R. E. Russo, X. L. Mao, J. J. Gonzalez and S. S. Mao, J. Anal. At. Spectrom., 2002, 17, 1072–1075.
129. D. Bleiner, Computer modeling of laser ablation elemental microanalysis, in Mineralogical Association of Canada Short Course Series, ed. P. Sylvester, Mineralogical Association of Canada, Vancouver, Canada, 2008, vol. 40, ch. 3, pp. 35–52.
130. S. Peng, Q. H. Hu, R. P. Ewing, C. X. Liu and J. M. Zachara, Environ. Sci. Technol., 2012, 46, 2025–2032.
131. J. T. van Elteren, A. Izmer, M. Šala, E. F. Orsega, V. S. Šelih, S. Panighello and F. Vanhaecke, J. Anal. At. Spectrom., 2013, 28, 994.
132. B. Gratuze, J. Archaeol. Sci., 1999, 26, 869–881.
133. J. R. Chirinos, D. D. Oropeza, J. J. Gonzalez, H. Hou, M. Morey, V. Zorba and R. E. Russo, J. Anal. At. Spectrom., 2014, 29, 1292–1298.
134. A. M. Leach and G. M. Hieftje, J. Anal. At. Spectrom., 2000, 15, 1121–1124.
135. M. Burger, A. Gundlach-Graham, S. Allner, G. Schwarz, H. A. Wang, L. Gyr, S. Burgener, B. Hattendorf, D. Grolimund and D. Günther, Anal. Chem., 2015, 87, 8259–8267.
136. S. E. Jackson, Calibration strategies for elemental analysis by LA-ICP-MS, in Mineralogical Association of Canada Short Course Series, ed. P. Sylvester, Mineralogical Association of Canada, Vancouver, Canada, 2008, vol. 40, ch. 11, pp. 169–188.
137. R. E. Russo, X. Mao, J. J. Gonzalez, V. Zorba and J. Yoo, Anal. Chem., 2013, 85, 6162–6177.
138. D. A. Frick and D. Günther, J. Anal. At. Spectrom., 2012, 27, 1294.
139. A. M. Oros-Peusquens, A. Matusch, J. S. Becker and N. J. Shah, Int. J. Mass Spectrom., 2011, 307, 245–252.
140. J. C. Jurchen, S. S. Rubakhin and J. V. Sweedler, J. Am. Soc. Mass Spectrom., 2005, 16, 1654–1659.
141. M. Harlaux, O. Borovinskaya, D. A. Frick, D. Tabersky, S. Gschwind, A. Richard, D. Günther and J. Mercadier, J. Anal. At. Spectrom., 2015, 30, 1945–1969.
142. D. Pozebon, G. L. Scheffler, V. L. Dressler and M. A. G. Nunes, J. Anal. At. Spectrom., 2014, 29, 2204–2228.
143. D. J. Hare, E. J. New, M. D. de Jonge and G. McColl, Chem. Soc. Rev., 2015, 44, 5941–5958.
144. A. Matusch, C. Depboylu, C. Palm, B. Wu, G. U. Hoglinger, M. K. Schafer and J. S. Becker, J. Am. Soc. Mass Spectrom., 2010, 21, 161–171.
145. D. Gholap, J. Verhulst, W. Ceelen and F. Vanhaecke, Anal. Bioanal. Chem., 2012, 402, 2121–2129.
146. A. E. Egger, S. Theiner, C. Kornauth, P. Heffeter, W. Berger, B. K. Keppler and C. G. Hartinger, Metallomics, 2014, 6, 1616–1625.
147. A. E. Egger, C. Kornauth, W. Haslik, S. Hann, S. Theiner, G. Bayer, C. G. Hartinger, B. K. Keppler, U. Pluschnigh and R. M. Mader, Metallomics, 2015, 7, 508–515.
148. A. J. Managh, S. L. Edwards, A. Bushell, K. J. Wood, E. K. Geissler, J. A. Hutchinson, R. W. Hutchinson, H. J. Reid and B. L. Sharp, Anal. Chem., 2013, 85, 10627–10634.
149. O. Reifschneider, K. S. Wentker, K. Strobel, R. Schmidt, M. Masthoff, M. Sperling, C. Faber and U. Karst, Anal. Chem., 2015, 87, 4225–4230.
150. J. Zhai, Y. Wang, C. Xu, L. Zheng, M. Wang, W. Feng, L. Gao, L. Zhao, R. Liu, F. Gao, Y. Zhao, Z. Chai and X. Gao, Anal. Chem., 2015, 87, 2546–2549.
151. C. Giesen, L. Waentig, T. Mairinger, D. Drescher, J. Kneipp, P. H. Roos, U. Panne and N. Jakubowski, J. Anal. At. Spectrom., 2011, 26, 2160–2165.
152. L. Mueller, H. Traub, N. Jakubowski, D. Drescher, V. I. Baranov and J. Kneipp, Anal. Bioanal. Chem., 2014, 406, 6963–6977.
153. T. Büchner, D. Drescher, H. Traub, P. Schrade, S. Bachmann, N. Jakubowski and J. Kneipp, Anal. Bioanal. Chem., 2014, 406, 7003–7014.
154. D. Drescher, I. Zeise, H. Traub, P. Guttmann, S. Seifert, T. Büchner, N. Jakubowski, G. Schneider and J. Kneipp, Adv. Funct. Mater., 2014, 24, 3765–3775.
155. X. Lou, G. Zhang, I. Herrera, R. Kinach, O. Ornatsky, V. Baranov, M. Nitz and M. A. Winnik, Angew. Chem., 2007, 46, 6111–6114.
156. L. Waentig, N. Jakubowski, S. Hardt, C. Scheler, P. H. Roos and M. W. Linscheid, J. Anal. At. Spectrom., 2012, 27, 1311–1320.
157. Fluidigm, Maxpar® reagents, http://maxpar.fluidigm.com/product-catalog-metal.php, accessed 29/08/2015.
158. R. W. Hutchinson, A. G. Cox, C. W. McLeod, P. S. Marshall, A. Harper, E. L. Dawson and D. R. Howlett, Anal. Biochem., 2005, 346, 225–233.
159. L. Waentig, S. Techritz, N. Jakubowski and P. H. Roos, Analyst, 2013, 138, 6309–6315.
160. J. Seuma, J. Bunch, A. Cox, C. McLeod, J. Bell and C. Murray, Proteomics, 2008, 8, 3775–3784.
161. C. Giesen, T. Mairinger, L. Khoury, L. Waentig, N. Jakubowski and U. Panne, Anal. Chem., 2011, 83, 8177–8183.
162. D. J. Hare, J. L. George, R. Grimm, S. Wilkins, P. A. Adlard, R. A. Cherny, A. I. Bush, D. I. Finkelstein and P. Doble, Metallomics, 2010, 2, 745–753.
163. D. J. Hare, J. K. Lee, A. D. Beavis, A. van Gramberg, J. George, P. A. Adlard, D. I. Finkelstein and P. A. Doble, Anal. Chem., 2012, 84, 3990–3997.
164. I. Kuznetsov, J. Filevich, F. Dong, M. Woolston, W. Chao, E. H. Anderson, E. R. Bernstein, D. C. Crick, J. J. Rocca and C. S. Menoni, Nat. Commun., 2015, 6, 6944.
165. A. D. Palmer and T. Alexandrov, Anal. Chem., 2015, 87, 4055–4062.

---

Footnote

† These authors contributed equally.

---