Particle transport through an inductively coupled plasma torch: elemental droplet evaporation
M.
Aghaei
* and
A.
Bogaerts
Research group Plasmant, Chemistry Department, University of Antwerp, Antwerp, Belgium. E-mail: maryam.aghaei@uantwerpen.be
First published on 7th July 2015
Abstract
We studied the transport of copper droplets through an inductively coupled plasma, connected to the sampling cone of a mass spectrometer, by means of a computational model. The sample droplets are followed until they become evaporated. They are inserted as liquid particles from the central inlet and the effects of injection position (i.e. “on” and “off” axis), droplet diameter, as well as mass loading flow rate are investigated. It is shown that more “on-axis” injection of the droplets leads to a more straight path line, so that the droplets move less in the radial direction and are evaporated more on the central axis, enabling a better sample transfer efficiency to the sampler cone. Furthermore, there are optimum ranges of diameters and flow rates, which guarantee the proper position of evaporation along the torch, i.e. not too early, so that the sample can get lost in the torch, and not too late, which reduces the chance of becoming ionized before reaching the sampler.
1. Introduction
Inductively Coupled Plasma Mass Spectrometry (ICP-MS) is one of the most popular methods for determining trace elements and isotopes in a wide variety of samples.1,2 The sample to be analyzed is introduced, mostly as droplets, with a central gas, and will be subject to desolvation, vaporization, diffusion, ionization and excitation in the plasma. These individual processes are difficult to experimentally measure, in part because the sample is typically introduced as a polydisperse aerosol consisting of millions of droplets per second entering the ICP. Droplets with different initial diameters complete desolvation at different times and at different locations in the plasma. The smallest droplets are completely vaporized and produce rapidly diffusing atoms and ions, while the largest droplets may not be completely vaporized until they have passed through the analytical zone of the ICP. Furthermore, the cloud of atoms and ions produced from one droplet will overlap with those produced from other droplets, because of rapid diffusion in the hot plasma.3,4 To improve the analytical capabilities of ICP-MS, it is of great importance to study the material transport through the ICP. Such studies have been carried out both experimentally3–33 and computationally.34–55Olesik3 published an outstanding article to investigate the fate of individual sample droplets in an ICP, using the monodisperse dried microparticulate injector (MDMI). The diffusion process of a single element (Sr) after injection of droplets, or particles from dried droplets, was demonstrated by laser induced fluorescence3 and by side-on optical emission spectroscopy.5 Assuming that the largest droplets entering the ICP are the last to be completely vaporized, the maximum size droplet that is completely vaporized in the ICP could be estimated. By controlling the droplet size delivered into the ICP and observing the initial appearance of analyte emission, the height in the plasma where droplets of a particular size were completely desolvated could be determined.5 In,4 the measurement of monodisperse droplet desolvation in an ICP using droplet size dependent peaks in Mie scattering intensity was described. The introduction of isolated, monodisperse droplets of a sample was also used already long time ago to measure droplet desolvation rates in flames by Hieftje and coworkers.6–8 Single particle and single reproducible microdroplet injection into the analytical flames and electrothermal atomizers was applied and demonstrated as excellent probes to study the atomization processes with temporal and spatial resolution by optical spectroscopy.
Kinzer and Olesik3,9 determined by means of the MDMI and laser induced fluorescence image detection that the addition of high concentrations of concomitant species, such as NaCl, leads to a decrease in the number of analyte ions produced from each droplet of the sample solution. Lazar and Farnsworth10 observed a similar behavior. Furthermore, these groups reported that the initial appearance of emission was earlier when high concentrations of efficiently ionized elements were added to the sample.10–12 Monnig and Koirtyohann13 concluded by means of laser light scattering that the transition from the initial radiation zone to the analytical zone of the ICP was related to the completion of the aerosol droplet vaporization. Correlations between the number of scattering events from an individual incompletely desolvated droplet and the increase in atom emission intensity and decrease in ion emission intensities were reported in.14,15
Houk and coworkers16–20 studied the trajectory of the atomizing droplets and the diffusion of analytes during their transport through the ICP by means of spectral imaging with fast cameras. With a concentric nebulizer, emission from vapor clouds surrounding the aerosol droplets or particles was observed16 and a comparison between wet droplets and solid particles was made.17 Particle effects in laser ablation (LA) ICP-MS were studied and the dried solution aerosols from a microconcentric nebulizer were compared with solid particles from LA.18–20 Moreover, Jorabchi et al.21 applied Mie scattering to determine the droplet velocities in the ICP from particle image velocimetry and particle tracking velocimetry.
At the Niemax lab, a comprehensive study was conducted by end-on and side-on optical emission spectroscopy (OES), applying monodisperse microdroplets (MDMDs). The authors showed that the spatial positions where analyte atomization and ionization start and are accomplished depend on the injector gas flow rate, the droplet diameter, and the amount of analyte.22–28 The position of atomization is determining the size of the analyte cloud at a particular position. This is in particular important for ICP-MS because the size of the analyte ion clouds determines the detection efficiency.
Günther and coworkers detected nanoparticles by ICP-MS, which were carried by MDMDs.29 In,30 the vaporization process of laser-produced aerosols and the subsequent diffusion losses occurring inside the ICP were investigated using 2D OES and ICP-quadrupole (Q)MS of individual particles. Na- and Ca-specific OES of metallic vs. oxidic aerosols revealed axial shifts in the onset and maximum positions of atomic emission, which were in the range of a few millimeters. These shifts were found to arise from composition-dependent particle/aerosol penetration depths, resulting in varying ion extraction efficiencies through the vacuum interface due to delayed analyte diffusion. Vanhaecke and coworkers31 also discussed the phenomenon of varying atom or ion mass-specific penetration depths.
The transport efficiency of particles is also crucial for LA-ICP-MS. Depending on the LA parameters chosen, the material to be analyzed and the carrier gas, different kinds of aerosols in terms of particle size distribution, morphology, and composition are being formed.30,32 Therefore, all processes, starting from the LA until the MS/OES system, are subject to this dependence and may affect the accuracy of analysis. As indicated in,33 larger particles may vaporize incompletely or at different axial positions inside the ICP because of composition-dependent melting and vaporization enthalpies. This results in variable sizes of atom/ion clouds in front of the MS interface, which gives rise to non-representative ion extraction.
It is clear that for a general optimization, several parameters, such as the gas flow rates, the diameter of the injector inlet, the size of the analyte droplets, the sample mass, the diffusion rates of the elements studied, the position of the sampler of the MS, as well as the diameter and the pressure drop at the MS orifice, have to be taken into account.28 However, the difficulty is that these parameters are dependent on each other. We believe that the optimization needs support by numerical simulations of the ICP with sampler interface, taking into account all important physical processes involved.
Barnes et al.34 developed the first model for the “spectrochemical ICP”, which was a modification of Miller's model.35 The latter model solved a 2D energy equation with 1D electromagnetic field equations to calculate the 2D temperature field in the torch. Subsequently, Barnes et al.36 predicted the temperature and velocity fields, the evaporation and decomposition of dry particles along with the plasma continuum and analyte emission profiles. However, these models did not account for the local cooling of the plasma due to the presence of the particles or aerosol.
Boulos was the first to develop a model for studying the plasma–particle interaction.37 Based on this model, Mostaghimi, Proulx and Boulos investigated the flow and temperature fields in the ICP,38–42 and these simulations were combined with experiments in collaboration with Barnes.40,41 However, the operating conditions were not always applicable to analytical chemistry purposes and the ICP torch was not connected to a MS interface, so the relevance for ICP-MS was limited.
Benson, Montaser and colleagues performed an interesting computational study on droplet heating, desolvation and evaporation in an ICP.43,44 The total desolvation rate of sample droplets in an argon ICP was investigated through the development of a two-phase continuum flow computer model. The desolvation model was extended by equations determining the trajectories of the particles through the plasma. The model was used to calculate the behavior of aerosol droplets from a direct injection high efficiency nebulizer (DIHEN). Two separate techniques, i.e., based on the Stokes equation and a direct simulation Monte Carlo (DSMC) treatment for determining the droplet trajectories, were compared. Moreover, droplet coalescence along with transport, heating and desolvation was studied, considering droplet–droplet interactions.43,44
Hieftje's group45,46 also studied particle melting, boiling, and vaporization inside the ICP torch. The calculations were performed for various droplet sizes and ICP operating conditions. The effects of central channel gas flow rate and ICP power on the desolvation process were investigated. However, in this study, as well as in the work by Benson et al.,43,44 the initial set of plasma conditions (temperatures, number densities, and flow velocities) were generated by a separate code, and were needed as input to start up the particle transport modeling. Also, the energy loss by the plasma due to droplet evaporation was not taken into account because these models dealt with the plasma temperature and velocity and the droplet desolvation and trajectories separately.
Mostaghimi et al.47 presented an outstanding mathematical model to study the droplet desolvation and trajectories, in combination with the plasma behavior, within the ICP torch. A stochastic technique combined with the Monte Carlo method was used to determine the droplet trajectories and collisions. This model was implemented into a 2D time-dependent rf ICP model. Plasma–droplet interactions were modeled by adding source terms to the conservation equations of mass, momentum and energy of the gas phase. However, ionization was not included in this model and the sampler cone was not inserted.
The first model to describe the effect of the sampler cone in ICP-MS was presented by Spencer et al.,48,49 who applied a DSMC algorithm to simulate the flow of neutral argon gas through the first vacuum stage of ICP-MS. However, the upstream density and plasma temperature gradients were not included and no plasma was assumed in these models.
Lindner and Bogaerts50 presented the first “self-consistent” model for an atmospheric pressure ICP, operating at typical analytical chemistry conditions, including ionization, as well as transport parameters, calculated self-consistently for the gas mixture under study. Indeed, the other models described above typically apply transport parameters (e.g. viscosity) from literature. This, however, limits the applicability to mixtures where the data for exactly that mixture (i.e., species and relative concentrations) are known. Especially the ionization degree is dependent on the actual composition of the plasma, which strongly affects the transport parameters. In,50 only data from pure species (e.g. argon) were taken from literature and the resulting transport parameters for the mixtures can then be calculated in a kinetic model. This makes it possible to apply the model to a wider variety of gas mixtures, including carrier gas and sample material.
We have modified the above model by connecting the ICP torch to a mass spectrometer interface cone.51 By means of this model, we showed for the first time the effect of the presence of a cooled, grounded sampler, and the sudden pressure drop behind it, on the plasma characteristics, including the electron and ion density profiles inside the torch, both in the coil region as well as very close to the sampler. We performed calculations for a wide range of gas flow rates and applied power, and also for various sizes of the injector inlet and sampler orifice.52,53 Furthermore, special attention was paid to the recirculation of the gas flow inside the ICP torch.54 In the present work, the model is further extended by the sample introduction. As the first step, a model for elemental droplets is built, where chemical reactions do not play a role. This case is relevant as it applies to LA-ICP-MS, where the sample is injected as ablated elemental particles. Copper droplets are taken as a case study and inserted from the central inlet and tracked through the ICP torch.
2. Computational model
The 2D axisymmetric ICP-MS model is based on solving partial differential equations for the gas flow dynamics (i.e., the Navier–Stokes equations) coupled with the energy conservation and Maxwell equations. It is built within the commercial computational fluid dynamics (CFD) program FLUENT 16.0.0 (ANSYS). The power coupling into the ICP is a source term in the energy conservation equation, whereas the emitted radiation is treated as a loss term. Some self-written codes (user defined functions, UDFs) were added in order to calculate the electromagnetic fields (based on the Maxwell equations), the amount of ionization (by solving the Saha–Eggert equation, assuming local thermal equilibrium, LTE), as well as the material parameters, i.e., electrical conductivity, viscosity, heat capacity, thermal conductivity and diffusion coefficients as a function of the actual gas composition and plasma temperature. Since the Reynolds number of the flow, even on the sampler (=115.6), is far from the turbulence regime, the flow is assumed to be laminar. A validation of this model by experiments was provided in.54,55 Typical calculation results obtained with the model include the gas flow behavior, as well as the plasma temperature and electron density profiles.50–55The sample introduction is modelled with the so-called “discrete phase model (DPM)”.56 In this model, the introduced samples need to be in a fluid phase, either liquid or gas. Therefore, in this work, we introduced copper in liquid phase to the ICP. As the argon flow entering the torch is at room temperature, the introduced copper droplets turn into solid phase. Thus, we assume that some kind of hypothetical particles with thermophysical properties of liquid copper are introduced from the central inlet and carried with the gas flow (with the properties of liquid), up to reaching the vaporization point, thus not including the melting process. This assumption is made to apply the DPM in our calculations, and we believe it is justified, because the latent heat of melting for copper (203.5 kJ kg−1) is much smaller than the latent heat of vaporization (5310 kJ kg−1) and melting can thus be ignored in our calculations.
The trajectory of each droplet is calculated by integrating the force balance (i.e. Newton equation) acting on the droplets. The main force is the drag force, which is a function of the molecular viscosity of the fluid, the mass density and the diameter of the droplets. In this work a variation of the Stokes drag law, including the so-called Cunningham correction factor,57 is applied. The effect of Brownian motion is also included in the model.
Besides their transport throughout the torch, the particles in liquid phase will undergo heating, vaporization and finally ionization. For the elemental droplets, a heat and mass balance equation is applied, which relates the particle temperature to the convective and diffusive heat transfer, and calculates the mass transfer to the vapor phase by means of a vaporization rate based on thermodynamic relations.58–60 The heat lost or gained by the particle as it traverses each computational cell will also appear as a source or sink of heat in the subsequent calculation of the continuous phase energy equation. Once the injected material is in the gas phase, it will be treated as individual atoms in the same way as for the carrier gas, i.e., by solving the Navier–Stokes equations and the Saha–Eggert equation to calculate the ionization degree of the sample material at the local plasma temperature, assuming LTE. From the ionization degree and the (mass and charge) conservation equations, the number densities of electrons and of the atoms and ions of the sample material can be calculated. The ionization model is added to FLUENT as a self-written code.
For any injected material several material parameters are needed, both in liquid phase (i.e., as droplets), mainly taken from,61 and in gas phase (i.e., after vaporization). Some parameters, i.e., the viscosity, thermal conductivity and diffusion coefficients, are a function of the local gas composition and plasma temperature, and are again inserted in the model as UDFs. The diffusion coefficient of copper droplets in Ar gas is taken from62 as a function of temperature.
To implement the discrete phase model (DPM) into the ICP-MS model, a FLUENT model is built including the injection properties, material parameters and the physical models applicable for elemental droplets, i.e. transport, heating, vaporization, boiling and ionization as well as the particle transport UDFs. The solution strategy is first to obtain stable plasma properties for Ar in the continuous phase model (CPM), i.e. for the plasma temperature, velocity and electron density. Subsequently, the particles are introduced into the ICP with the DPM, and the calculation in the CPM is combined with the DPM till convergence is reached. In each iteration, the exchange of mass, momentum and energy between plasma and droplets is calculated and both the DPM and CPM are updated. Finally, we can track the particles to determine their position, their phase (liquid or vapor), velocity and temperature.
3. Results and discussions
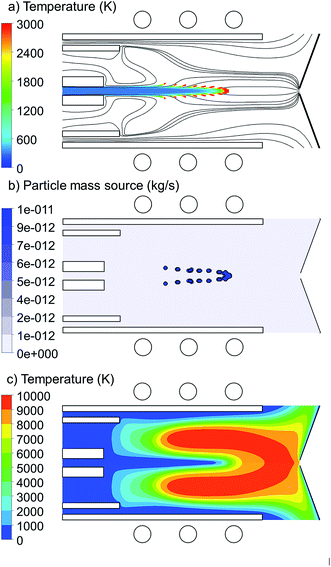
Copper droplets are inserted from the central inlet with 1.5 mm width and they are tracked through the torch up to the sampler position (i.e. 41.5 mm distance from the central inlet). The total applied power is 1000 W and the carrier, auxiliary and cooling gas flow rates are 1.0, 0.4 and 12.0 L min−1, respectively. The general properties of the copper droplet introduction are shown in Fig. 1. The copper droplet flow rate is 100 ng s−1 and the droplet diameter is 1 μm.In Fig. 1(a), the 2D trajectories of the injected copper droplets, colored according to their temperature, are shown, as well as the Ar gas flow path lines originating from the central, intermediate and outer inlets, colored in black. The Ar streamlines shows the path lines which the copper droplets can follow. It is seen that the droplets enter the torch at room temperature and are gradually heated until they reach the evaporation temperature (=2830 K). As soon as they are evaporated, they disappear from the droplet path lines and from then on we are able to trace them in the gas phase domain.
Fig. 1(b) shows the 2D mass transfer rate (also called mass source) of the copper droplets to the gas phase. It is expressed in kg s−1, as is common in this type of calculations. However, by dividing by the mass density and accounting for the conversion of units, it can easily be transferred into L min−1. For instance, the maximum value of 1 × 10−11 kg s−1 corresponds to 8.4 × 10−11 L min−1. We can deduce from both Fig. 1(a) and (b) that this group of droplets, which are all injected from the central inlet, are not evaporated at the same position in the torch. This can be explained by the radial expansion of the Ar gas flow path lines (Fig. 1(a)). In fact it is shown in Fig. 1(a) that not all of the carrier Ar gas flow goes straight to the sampler. This expansion was discussed in detail in51–54 and depends on the size of the central inlet, the size of the sampler orifice, the Ar gas flow rates from the central, intermediate and outer inlet, and the external power. Due to the radial expansion, the outer gas path lines reach the higher temperature regions in the torch earlier (see Fig. 1(c)). Therefore, they are heated up and the droplets following these path lines start to evaporate at earlier positions, while the droplets which follow the path lines with less radial expansion stay longer at the central axis and travel for a longer distance through the central cooled channel. Furthermore, the analyte atoms will diffuse and become ionized, forming ion vapor clouds with increasing diameter downstream the plasma.8,28 It should be realized that early evaporation and more radial expansion from the central axis may cause that some part of the sample ions does not reach the sampler orifice, which thus represents a loss.28 Moreover, even if they are not lost, it may cause a delay in detection time, as was observed in.63 We found that the exact position of injection, as well as the size of the injected droplets, has a significant effect on the radial expansion from the central axis, and thus on the evaporation position. Therefore, Section 3.1 and 3.2 will be devoted to investigate the effects of injection position and size of the copper droplets, respectively.
The 2D temperature profile of the plasma is shown in Fig. 1(c). Since the copper droplet flow rate is ten orders of magnitude lower than the Ar flow rate (i.e., 100 ng s−1 corresponds to only 8.36 × 10−10 L min−1), the temperature profile shows no differences from the case when pure Ar is injected into the torch.51 However, when increasing the copper droplet flow rate to the order of 500 μg s−1, a cooling effect due to the evaporation of the sample droplets is observed, which will be discussed in Section 3.3.
3.1. Effect of droplet injection position
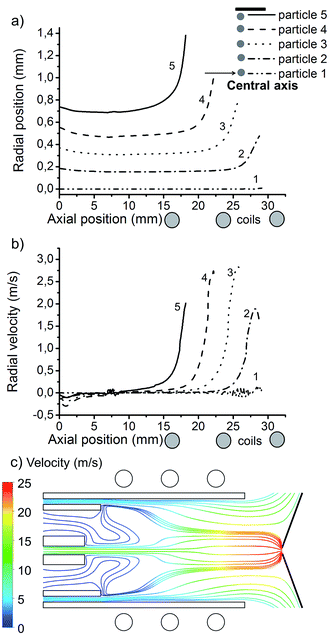
In Fig. 2, we introduced 5 different copper droplets of 1 μm diameter, with flow rate of 100 ng s−1, from different initial radial positions at the central inlet. A schematic picture of the droplets position at the central inlet as well as the load coils are also indicated in Fig. 2, for clarity. Particle 1 is introduced exactly on the central axis, while particle 5 is introduced at a radial position of 0.74 mm from the central axis.Fig. 2(a) shows the radial position of the 5 droplets as a function of their axial position in the ICP torch, as long as they are in the liquid phase. It can be seen that each particle follows a different trajectory by entering from a different initial position. Also, the radial expansion of each trajectory starts at a different axial position. It is shown that the central particle stays on axis along its journey before evaporation while the outer particle starts to move in the radial direction already at 15 mm from its introduction position at the inlet. This can be explained by the trajectory and the different velocities of the three argon gas flows, considering the lengths of the central and intermediate inlets, which are 7.2 mm and 10 mm, respectively. The Ar gas flow path lines, originating from the central, intermediate and outer inlets, colored by velocity, are plotted in Fig. 2(c). Indeed, when two layers of fluid in contact with each other move at different speeds, there will be a shear force depending on the flow viscosity between them.64 It was already demonstrated in our previous work51,54 that the auxiliary gas flow does not always move in the forward direction inside the torch and the carrier gas flow also experiences a radial expansion in the coil region. According to the different initial gas flow rates, each gas flow moves with a different velocity. Note that the auxiliary gas can enter more freely than the carrier and cooling gas due to its wider inlet. In fact the slower auxiliary gas flow comes in contact earlier with the faster carrier gas flow (at 7.2 mm from the entrance) than with the cooling gas flow (at 10 mm from the entrance) because of a difference in the length of the inlets. Therefore, the auxiliary gas flow goes straight, as long as it is only affected by a shear force from the carrier gas flow and after 10 mm away from the entrance, it comes into contact with the cooling gas flow and feels a shear force from the cooling gas flow, which results in a backward turn and again a forward motion of the auxiliary gas flow. More details about this gas flow can be found in ref. 54. Meanwhile, when the auxiliary gas flows backward, it leaves more space for the carrier gas, so that the carrier gas can move in the radial direction in the torch inside the coil region (see Fig. 2(c)). As a result of this radial movement, the outer particle (i.e. particle 5) which follows one of the outer path lines of the carrier gas flow, moves earlier in the radial direction than the particle injected along the central axis (i.e. particle 1).
Not only the radial position of the particles is affected by the initial injection position, but also their radial velocity, as shown in Fig. 2(b). Hence, different particles move with different radial speed from the central axis (in the range of 0 to 3 m s−1) at different positions. Note that the maximum radial velocity does not belong to particle 5 but to particle 3. In fact, the outer particle is already starting to become evaporated while the other particles are still moving in the radial direction (see Fig. 2(b)). Moreover, particle 1 experiences almost no radial velocity but it will reach the highest axial velocity (as can be deduced from Fig. 2(c)).
We believe that any deviation from the central axis leads to a longer transit time and a loss of intensity, which should be avoided. Also, the radial movement of the sample particles to the outer region of the torch lowers the chance that the sample exits through the sampler cone. Hence, the detection efficiency becomes lower as some part of the sample is lost in the torch and not effectively sampled through the plasma–vacuum interface. Moreover, the group of Farnsworth and Spencer studied the velocity profiles of argon flow entering the MS vacuum stages, by means of experiments and computations, respectively, and concluded that any deviation of analyte from the central axis affects the transmission between the first and second vacuum stages. In fact, the gas flows passing through the sampling cone off-axis, will expand off-axis in the first vacuum stage and therefore they get lost in the skimming process.48,49,65–68
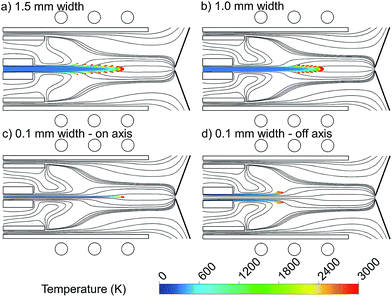
To study the importance of injection position at the central inlet in more detail, we made different setups with exactly the same conditions, in which only the specific width of the central inlet from which the copper droplets are introduced is different. Fig. 3 shows the 2D trajectories of 1 μm copper droplets, introduced with a flow rate of 100 ng s−1 from (a) the whole 1.5 mm width of the central inlet, (b) the central 1 mm width of the central inlet, (c) the central 0.1 mm (i.e., “on-axis”) and (d) the outer 0.1 mm of the central inlet (i.e., “off-axis”), colored according to their temperature. The Ar gas flow path lines originating from the central, intermediate and outer inlets are also shown, colored in black.
Comparing Fig. 3(a) and (b), i.e., when the droplets are introduced from 1.5 mm and 1 mm width, respectively, we see that when the central inlet is narrower, the droplets stay for a longer time on a straight line to the sampler, they diffuse less, and move later from the central axis. This means that the vapor cloud is produced later and closer to the central channel, which is more efficient to deliver the sample to the sampler. This is explained by the radial expansion of the Ar flow path line as discussed above, as well as by diffusion of copper droplets in the Ar flow. The detection efficiency in ICP-MS is best when the diffusion of analyte ions at the position of the MS sampler is small.27 This can be accomplished by shifting the evaporation position. Furthermore, note that the plasma temperature in the analyte – plasma interaction region has to be as high as possible to guarantee the most effective atomization and ionization. By means of OES with end-on and side-on observation of the plasma, Niemax et al. determined the location of atomization in the ICP and the spatial distribution of diffused analyte ions at positions where the MS interface is typically placed in ICP-MS. They indicated that both a downstream shift of the atomization and high temperature can be achieved by using injectors with a small inner diameter and high injector gas flow rates.27,28
To be more precise about this conclusion, we introduced copper droplets only on-axis and off-axis in Fig. 3(c) and (d), respectively. Fig. 3(c) shows that when the droplets are injected exactly from the center of the inlet, they stay on-axis along the torch until they become evaporated. Indeed, the central Ar gas path line does not deviate from the central axis and thus it carries the copper droplets to the sampler in a straight way. This is not the case in Fig. 3(d) when the droplets are injected only off-axis (i.e., we introduced them only from the outer 0.05 mm of the central inlet, hence again 1 mm width in total). Fig. 3(d) indicates that when the droplets are injected off-axis, they may move more in the radial direction, and they will not come closer to the central axis again.
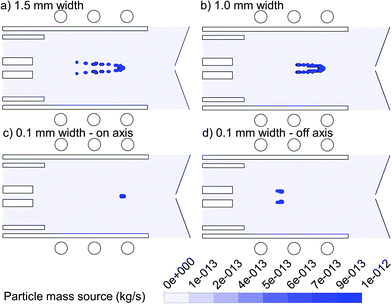
In Fig. 4, the 2D mass transfer rates of the 1 μm copper droplets to the gas phase, again introduced with a flow rate of 100 ng s−1 from the same positions as in Fig. 3, are depicted. As discussed above, the wider the area of droplet injection, the more radial expansion occurs for the droplets as well as for the vapor cloud. Thus we can conclude that the position of vapor production in both the axial and radial direction depends strongly on the exact initial injection position.
3.2. Effect of droplet diameter
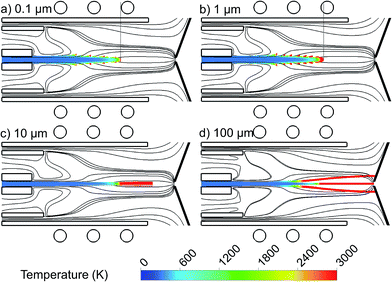
The 2D trajectories of copper droplets, introduced with a flow rate of 100 ng s−1 from the whole 1.5 mm width of the central inlet, with a diameter of 0.1 μm, 1 μm, 10 μm and 100 μm, colored according to their temperature, are presented in Fig. 5(a–d). The Ar gas flow path lines originating from the central, intermediate and outer inlets, colored in black, are also plotted again, for clarity. Note that further decreasing the droplet diameter to e.g., 0.01 μm did not give rise to stable calculation results, at least for the operating and geometrical conditions under consideration here.It can be seen that the smaller droplets, i.e. with 0.1 and 1 μm diameter, are evaporated earlier in the torch. Larger droplets need more heating to become evaporated. Therefore, they move deeper into the region with higher temperature. The droplets of 10 μm diameter (Fig. 5(c)) stay in the liquid phase all the way along the torch and they evaporate very late, after the coil region and almost outside of the length of the torch. Furthermore, the droplets with 100 μm diameter never become evaporated at the conditions under study, as shown in Fig. 5(d), and they stay in the liquid phase even when reaching the sampler. The droplets travelling on-axis might thus be able to enter the vacuum stage behind the sampler while they are still in liquid phase, which is unfavourable and lowers the detection efficiency of the ICP.27,33 Moreover, the droplets which move in the radial direction will hit the cooled, grounded sampler cone and get stuck there, which results also in sample loss. We can conclude that in the current setup, copper droplets with a diameter smaller than 10 μm will become evaporated early enough in the ICP torch, while larger droplets cannot be sampled efficiently. We expect that there will be an optimum range of droplet diameter for each setup which guarantees the full evaporation of the injected droplets inside the torch. We plan to study this optimum range for different setups as soon as the ionization of the copper droplets is included in our model.
Our results are in qualitative agreement with experiments. Indeed, it is indicated in27,28 that larger droplets of analyte solution penetrate deeper into the ICP than smaller droplets, before they are desolvated and atomization of the analyte residuum can start. It means that the size of the analyte ion cloud from larger droplets is smaller at the position of the sampler. This effect was demonstrated with droplets of Ca solution of 49 μm and 30 μm diameter. For example, 0.4 mm above the top of the torch, the Ca ion cloud from the 49 μm droplets was about six times smaller than that from the 30 μm droplets. Moreover, a linear relationship was observed between the square of the droplet diameter and time (which can be correlated with the penetration depth into the plasma).6,7 Finally, Olesik and Hobbs5 concluded, based on emission measurements with the MDMI, that droplets of 16 μm diameter or larger survive for 8 mm above the load coil (ALC) while droplets of 31 μm diameter or larger survive for 18 mm ALC in the ICP at a carrier gas flow rate of 0.8 L min−1.
3.3. Effect of mass loading flow rate
We performed calculations for a wide range of copper droplet flow rates, i.e. from 1 ng s−1 to 500 μg s−1, and the results are presented in Fig. 6 and 7. Fig. 6 illustrates the 2D temperature profiles in the plasma, when 1 μm copper droplets are introduced from the whole 1.5 mm width of the central inlet, with a flow rate of 1 ng s−1, 100 μg s−1, and 500 μg s−1.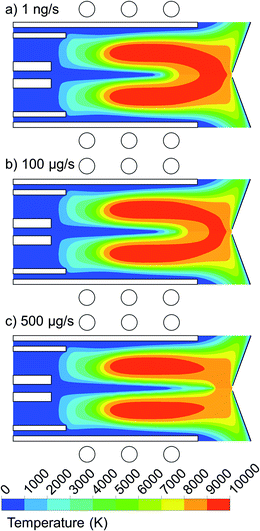 | ||
| Fig. 6 2D temperature profiles when introducing 1 μm copper droplets from the whole 1.5 mm width of the central inlet with flow rate of (a) 1 ng s−1, (b) 100 μg s−1 and (c) 500 μg s−1. | ||
As can be seen from Fig. 6(a) and (b), a mass loading flow rate up to 100 μg s−1 has only a minor effect on the plasma temperature profile, and only in the central region, which is slightly cooled by heat conduction to the copper droplets. This cooling effect is more pronounced when the mass loading flow rate rises to 500 μg s−1 (see Fig. 6(c)). Indeed, a larger amount of the injected material needs to be heated up by the Ar gas flow before getting evaporated. This is an unfavorable effect because it will decrease the ionization rate of the copper sample. We thus conclude that for the conditions under study, the mass loading flow rate for pure copper droplets should be below 100 μg s−1 (or 0.1 mg s−1), so that the plasma temperature is not affected by the sample introduction and stays high enough to enable enough ionization of the copper samples.27 However, it should be mentioned that here we inject pure copper droplets and not samples diluted in water. In the latter case, when droplets are penetrating into the torch, the plasma is affected by desolvation, dissociation of the water molecules, and by excitation and ionization of their products, i.e., the hydrogen and oxygen atoms and OH radicals, and there is only a minor fraction of real sample that is subject to excitation and ionization, while in our case, the droplets consist of pure copper, that is all subject to evaporation, excitation and ionization. Therefore, we expect that the local cooling effect of the plasma is less significant, for the same mass loading flow rates, when the samples are diluted in water. At the experimental conditions applied in,22 local cooling of the ICP during desolvation was observed from a ∼4% decrease of the Ar line intensity for a mass loading flow rate of 3 mg s−1 of 52 μm Si solution droplets.
However, as indicated in,25,42 in ICP spectrochemical analysis, the aerosol feed rates are usually sufficiently small, i.e. around 0.1 g min−1 (or 1.7 mg s−1) or less, so that the plasma–droplet interaction effects could be safely neglected. On the other hand, at other conditions, i.e., a torch size of 7 × 25 cm, flow rates of 3, 3, and 14 L min−1 for carrier gas, auxiliary gas and cooling gas, respectively, 3 kW applied power and frequency of 3 MHz, as used for plasma spray coating,69 a (dense) mass loading ratio of about 0.19 g copper/g argon was demonstrated to result in a temperature drop on the axis by about 2000 K. However, these conditions are clearly different from the conditions typically used for analytical purposes.
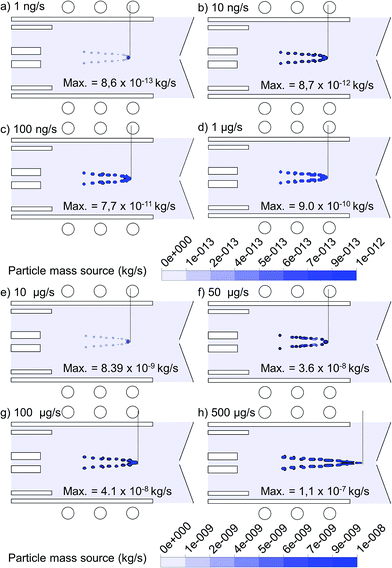
The 2D mass transfer rate of 1 μm copper droplets to the gas phase, introduced from the whole 1.5 mm width of the central inlet, is depicted in Fig. 7 for flow rates varying between 1 ng s−1 and 500 μg s−1. Note that the plotting scale is different for the four upper cases compared to the four lower cases. To make the comparison more feasible, the exact value of the maximum mass transfer rate, which occurs at the center of the plotted contours for each case, is also indicated in Fig. 7. As expected, the maximum mass transfer rate from the liquid to the vapor phase increases with the mass loading flow rate. The increase is more or less linear up to 10 μg s−1, but above this value, the mass transfer rate does not rise to the same extent as the mass loading flow rate, indicating that not all copper droplets become evaporated. Likewise, the position of evaporation stays almost the same up to 10 μg s−1 (i.e.Fig. 7(a) to (e)), but it shifts towards the sampler cone for still higher mass loading flow rates (i.e.Fig. 7(f) to (h)), because of the cooling effect, so that the copper droplets need a longer time to become evaporated. The dashed line in each frame indicates the depth of evaporation along the torch. It can be deduced from Fig. 7(h) that a mass loading flow rate of 500 μg s−1 causes a long evaporation depth, even till outside the torch, which lowers the chance of efficient ionization.
4. Conclusion
We have computationally investigated the introduction of copper elemental droplets in an ICP, in order to obtain a better insight into the particle transport through the ICP torch and to optimize the detection efficiency of inserted samples. The droplets are introduced from the central inlet at different positions, including “on-axis” and “off-axis”. Our calculations show that depending on the injection position, each droplet follows different path lines in the torch and sometimes it can expand in the radial direction from the central axis. Our model provides us the axial and radial position at which the evaporation occurs, which depends on the droplet temperature along the torch. It also shows to what extent the vapor cloud moves in the radial direction and deviates from the central axis. In the case of on-axis injection, the droplets move in a more straight line along the torch and experience a later evaporation compared with off-axis injection. This reduces the probability of losing the sample inside the torch or the occurrence of a detection delay by preventing the droplets from early radial movement inside the torch. Therefore, the sample species can reach the sampler orifice with a higher transmission efficiency. Also, it ensures less expansion in the first vacuum stage and therefore less sample lost through the skimmer. Moreover, our calculations predict that the optimum copper droplet diameter is below 10 μm for the conditions under study (i.e., geometrical setup, Ar gas flow rates and external power), to ensure that the injected droplets become evaporated early enough inside the torch and efficiently enter the sampler orifice. Larger particles do not become vaporized when reaching the sampler and are either stuck at the sampler cone or they enter the vacuum stage behind the sampler in the liquid phase, which are both unfavorable. Finally, we also studied the effect of mass loading flow rate on the plasma temperature. Below 100 μg s−1, the introduction of copper droplets almost does not affect the plasma temperature. However, at higher mass loading flow rates (shown here up to 500 μg s−1), the plasma is significantly cooled down by heat transfer to the copper droplets. As a consequence, the evaporation occurs closer to the sampler cone, which reduces the probability that the copper sample can still be ionized. The calculated results are compared with experiments and good qualitative agreement is reached. In our next study, we will extend our model to include the ionization of the sample material, which is a crucial step to predict more precisely the optimum parameters needed to increase the efficiency of particle transport through the ICP torch as well as transfer to the mass spectrometer.Acknowledgements
The authors are very grateful to H. Lindner for the many fundamental and fruitful discussions. They are also gratefully acknowledge financial support from the Fonds voor Wetenschappelijk Onderzoek (FWO).References
- J. A. C. Broekaert, Analytical atomic spectrometry with flames and plasmas, Wiley, Weinheim, 2005 Search PubMed.
- A. Montaser, Inductively coupled plasma mass spectrometry, Wiley, New York, 1998 Search PubMed.
- J. W. Olesik, Investigating the fate of individual sample droplets in inductively coupled plasmas, Appl. Spectrosc., 1997, 51, 158A–175A CrossRef CAS.
- J. W. Olesik and J. A. Kinzer, Measurement of monodisperse droplet desolvation in an inductively coupled plasma using droplet size dependent peaks in Mie scattering intensity, Spectrochim. Acta, Part B, 2006, 61, 696–704 CrossRef.
- J. W. Olesik and S. E. Hobbs, Monodisperse dried microparticulate injector: a new tool for studying fundamental processes in inductively coupled plasmas, Anal. Chem., 1994, 66, 3371–3378 CrossRef CAS.
- G. M. Hieftje and H. V. Malmstadt, Unique system for studying flame spectrometric processes, Anal. Chem., 1968, 40, 1860–1867 CrossRef CAS.
- N. C. Clampitt and G. M. Hieftje, Mechanism of desolvation of sample droplets in flame spectrometry, Anal. Chem., 1972, 44, 1211–1218 CrossRef CAS.
- C. B. Boss and G. M. Hieftje, Calculation of the velocity of a desolvating aerosol droplet in an analytical flame, Anal. Chem., 1977, 49, 2112–2114 CrossRef CAS.
- J. A. Kinzer, Capillary Electrophoresis—Inductively Coupled Plasma Spectrometry (CE–ICP): Elemental speciation and fundamental studies of matrix effects in the ICP, Ph.D. Thesis, The Ohio State University, 1997.
- A. C. Lazar and P. B. Farnsworth, Matrix effect studies in the inductively coupled plasma with monodisperse droplets. Part II: the influence of matrix on spatially integrated ion density, Appl. Spectrosc., 1999, 53, 465–470 CrossRef CAS.
- A. C. Lazar and P. B. Farnsworth, Investigation of the analytical performance of an MDMI-ICP-AES system, Appl. Spectrosc., 1997, 51, 617–624 CrossRef CAS.
- I. I. Stewart and J. W. Olesik, Time-resolved measurements with single droplet introduction to investigate space-charge effects in plasma mass spectrometry, J. Am. Soc. Mass Spectrom., 1999, 10, 159–174 CrossRef CAS PubMed.
- C. A. Monnig and S. R. Koirtyohann, Mie scattering from sample aerosol inside the inductively coupled plasma, Anal. Chem., 1985, 57, 2533–2576 CrossRef CAS.
- J. W. Olesik, L. J. Smith and E. J. Williamsen, Signal fluctuations due to individual droplets in inductively coupled plasma atomic emission spectrometry, Anal. Chem., 1989, 61, 2002–2008 CrossRef CAS PubMed.
- J. W. Olesik and J. C. Fister III, Incompletely desolvated droplets in argon inductively coupled plasmas: their number, original size and effect on emission intensities, Spectrochim. Acta, Part B, 1991, 46, 851–868 CrossRef.
- R. K. Winge, J. S. Crain and R. S. Houk, A high speed photographic study of plasma fluctuations and undissociated particles in ICP-MS, J. Anal. At. Spectrom., 1991, 6, 601–604 RSC.
- R. S. Houk, R. K. Winge and X. Chen, High speed photographic study of wet droplets and solid particles in the inductively coupled plasma, J. Anal. At. Spectrom., 1997, 12, 1139–1148 RSC.
- D. B. Aeschliman, S. J. Bajic, D. P. Baldwin and R. S. Houk, High-speed digital photographic study of an inductively coupled plasma during laser ablation: comparison of dried solution aerosols from a microconcentric nebulizer and solid particles from laser ablation, J. Anal. At. Spectrom., 2003, 18, 1008–1014 RSC.
- D. C. Perdian, S. J. Bajic, D. P. Baldwin and R. S. Houk, Time-resolved studies of particle effects in laser ablation inductively coupled plasma-mass spectrometry – Part 1, J. Anal. At. Spectrom., 2009, 23, 325–335 RSC.
- D. C. Perdian, S. J. Bajic, D. P. Baldwin and R. S. Houk, Time-resolved studies of particle effects in laser ablation inductively coupled plasma-mass spectrometry – Part 2, J. Anal. At. Spectrom., 2009, 23, 336–341 RSC.
- K. Jorabchi, R. G. Brennan, J. A. Levine and A. Montaser, Interferometric droplet imaging for in situ aerosol characterization in an inductively couple d plasma, J. Anal. At. Spectrom., 2006, 21, 839–846 RSC.
- S. Groh, C. C. Garcia, A. Murtazin, V. Horvatic and K. Niemax, Local effects of atomizing analyte droplets on the plasma parameters of the inductively coupled plasma, Spectrochim. Acta, Part B, 2009, 64, 247–254 CrossRef.
- C. C. Garcia, A. Murtazin, S. Groh, M. Becker and K. Niemax, Characterization of particles made by desolvation of monodisperse microdroplets of analyte solutions and particle suspensions for nanoparticle characterization in inductively coupled plasma spectrometry, Spectrochim. Acta, Part B, 2010, 65, 80–85 CrossRef.
- C. C. Garcia, S. Groh, A. Murtazin, V. Horvatic and K. Niemax, Characterization of single Au and SiO2 nano- and microparticles by ICP-OES using monodisperse droplets of standard solutions for calibration, J. Anal. At. Spectrom., 2010, 25, 645–653 RSC.
- S. Groh, P. Diwakar, C. C. Garcia, A. Murtazin, D. W. Hahn and K. Niemax, 100% efficient sub-nanoliter sample introduction in laser induced breakdown spectroscopy and inductively coupled plasma spectrometry: implications for ultralow sample volumes, Anal. Chem., 2010, 82, 2568–2573 CrossRef CAS PubMed.
- A. Murtazin, S. Groh and K. Niemax, Measurement of element mass distributions in particle ensembles applying ICP-OES, J. Anal. At. Spectrom., 2010, 25, 1395–1401 RSC.
- A. Murtazin, S. Groh and K. Niemax, Investigation of sample introduction- and plasma-related matrix effects in inductively coupled plasma spectrometry applying single analyte droplet and particle injection, Spectrochim. Acta, Part B, 2012, 67, 3–16 CrossRef CAS.
- K. Niemax, Considerations about the detection efficiency in inductively coupled plasma mass spectrometry, Spectrochim. Acta, Part B, 2012, 76, 65–69 CrossRef CAS.
- S. Gschwind, L. Flamigni, J. Koch, O. Borovinskaya, S. Groh, K. Niemax and D. Günther, Capabilities of inductively coupled plasma mass spectrometry for the detection of nanoparticles carried by monodisperse micro-droplets, J. Anal. At. Spectrom., 2011, 26, 1166–1174 RSC.
- L. Flamigni, J. Koch and D. Günther, Experimental and theoretical investigations about the vaporization of laser-produced aerosols and individual particles inside inductively coupled plasmas - Implications for the extraction efficiency of ions prior to mass spectrometry, Spectrochim. Acta, Part B, 2012, 76, 70–76 CrossRef CAS.
- F. Vanhaecke, R. Dams and C. Vandecastelle, Zone model as an explanation for signal behavior and non-spectral interferences in inductively-coupled plasma mass spectrometry, J. Anal. At. Spectrom., 1993, 8, 433–438 RSC.
- P. M. Outridge, W. Doherty and D. C. Gregoire, The formation of trace element-enriched particulates during laser ablation of refractory materials, Spectrochim. Acta, Part B, 1996, 51, 1451–1462 CrossRef.
- J. Koch and D. Günther, Review of the state-of-the-art of laser ablation inductively coupled plasma mass spectrometry, Appl. Spectrosc., 2011, 65, 155A–162A CrossRef CAS PubMed.
- R. M. Barnes and R. G. Schleicher, Computer simulation of RF induction-heated argon plasma discharges at atmospheric pressure for spectrochemical analysis-I. Preliminary investigations, Spectrochim. Acta, Part B, 1975, 30, 109–134 CrossRef.
- R. C. Miller and R. J. Ayen, Temperature profiles and energy balances for an inductively coupled plasma torch, J. Appl. Phys., 1969, 40, 5260–5273 CrossRef.
- R. M. Barnes and S. Nikdel, Temperature and velocity profiles and energy balances for an inductively coupled plasma discharge in nitrogen, J. Appl. Phys., 1976, 47, 3929–3934 CrossRef CAS.
- M. I. Boulos, Heating of powders in the fire ball of an induction plasma, IEEE Trans. Plasma Sci., 1978, PS-6, 93–106 CrossRef.
- J. Mostaghimi and E. Pfender, Effects of metallic vapor on the properties of an argon arc plasma, Plasma Chem. Plasma Process., 1984, 4, 199–217 CrossRef CAS.
- J. Mostaghimi, P. Proulx and M. I. Boulos, An analysis of the computer modeling of the flow and temperature fields in an inductively coupled plasma, Numer. Heat Tran., 1985, 8, 187–201 Search PubMed.
- P. Yang, R. M. Barnes, J. Mostaghimi and M. I. Boulos, Application of a two-dimensional model in the simulation of an analytical inductively coupled plasma discharge, Spectrochim. Acta, Part B, 1989, 44, 657–666 CrossRef.
- J. Mostaghimi, P. Proulx, M. Boulos and R. M. Barnes, Computer modeling of the emission patterns for a spectrochemical ICP, Spectrochim. Acta, Part B, 1985, 40, 153–166 CrossRef.
- M. Cai, D. A. Haydar, A. Montaser and J. Mostaghimi, Computer simulation of argon-nitrogen and argon-oxygen inductively coupled plasmas, Spectrochim. Acta, Part B, 1997, 52, 369–386 CrossRef.
- C. M. Benson, S. F. Gimelshein, D. A. Levin and A. Montaser, Simulation of droplet heating and desolvation in an inductively coupled plasma- Part I, Spectrochim. Acta, Part B, 2001, 56, 1097–1112 CrossRef.
- C. M. Benson, J. Zhong, S. F. Gimelshein, D. A. Levin and A. Montaser, Simulation of droplet heating and desolvation in inductively coupled plasma-Part II: Coalescence in the Plasma, Spectrochim. Acta, Part B, 2003, 58, 1453–1471 CrossRef.
- A. Horner, G. C. Y. Chan, S. A. Lehn and G. M. Hieftje, Computerized simulation of solute-particle vaporization in an inductively-coupled plasma, Spectrochim. Acta, Part B, 2008, 63, 217–233 CrossRef.
- J. A. Horner and G. M. Hieftje, Computerized simulation of mixed-solute-particle vaporization in an inductively coupled plasma, Spectrochim. Acta, Part B, 1998, 53, 1235–1259 CrossRef.
- Y. Shan and J. Mostaghimi, Numerical simulation of aerosol droplets desolvation in a radio frequency inductively coupled plasma, Spectrochim. Acta, Part B, 2003, 58, 1959–1977 CrossRef.
- R. L. Spencer, J. Krogel, J. Palmer, A. Payne, A. Sampson, W. Somers and C. N. Woods, Modeling the gas flow upstream and in the sampling nozzle of the inductively coupled plasma mass spectrometer via the direct simulation monte carlo algorithm, Spectrochim. Acta, Part B, 2009, 64, 215–221 CrossRef.
- R. L. Spencer, N. Taylor and P. B. Farnsworth, Comparison of calculated and experimental flow velocities from the sampling cone of an inductively coupled plasma mass spectrometer, Spectrochim. Acta, Part B, 2009, 64, 921–924 CrossRef.
- H. Lindner and A. Bogaerts, Multi-element model for the simulation of inductively coupled plasmas: Effects of helium addition to the central gas stream, Spectrochim. Acta, Part B, 2011, 66, 421–431 CrossRef CAS.
- M. Aghaei, H. Lindner and A. Bogaerts, Effect of a mass spectrometer interface on inductively coupled plasma characteristics: a computational study, J. Anal. At. Spectrom., 2012, 27, 604–610 RSC.
- M. Aghaei, H. Lindner and A. Bogaerts, Optimization of operating parameters for inductively coupled plasma mass spectrometry: a computational study, Spectrochim. Acta, Part B, 2012, 76, 56–64 CrossRef CAS.
- M. Aghaei, H. Lindner and A. Bogaerts, Effect of sampling cone position and diameter on the gas flow dynamics in an ICP, J. Anal. At. Spectrom., 2013, 28, 1485–1492 RSC.
- M. Aghaei, L. Flamigni, H. Lindner, D. Günther and A. Bogaerts, Occurrence of gas flow rotational motion inside the ICP torch: a computational and experimental study, J. Anal. At. Spectrom., 2014, 29, 249–261 RSC.
- H. Lindner, A. Murtazin, S. Groh, K. Niemax and A. Bogaerts, Simulation and experimental studies on plasma temperature, flow velocity and injector diameter effects for an inductively coupled plasma, Anal. Chem., 2011, 83, 9260–9266 CrossRef CAS PubMed.
- ANSYS FLUENT 16 Documentation, Theory Guide, 2015 Search PubMed.
- H. Ounis, G. Ahmadi and J. B. McLaughlin, Brownian diffusion of submicrometer particles in the viscouse sublayer, J. Colloid Interface Sci., 1991, 143, 66–277 CrossRef.
- W. E. Ranz and W. R. Marshall, Vaporation from drops, Part I, Chem. Eng. Prog., 1952, 48, 141–146 CAS.
- W. E. Ranz and W. R. Marshall, Evaporation from drops, Part II, Chem. Eng. Prog., 1952, 48, 173–180 CAS.
- K. K. Y. Kuo, Principles of combustion, John Wiley and sons, New York, 1986 Search PubMed.
- D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press LLC, Boca Raton, Florida, 83rd edn, 2002 Search PubMed.
- A. B. Murphy, A comparison of treatments of diffusion in thermal plasmas, J. Phys. D: Appl. Phys., 1996, 29, 1922–1932 CrossRef CAS.
- O. Borovinskaya, M. Aghaei, L. Flamigni, B. Hattendorf, M. Tanner, A. Bogaerts and D. Günther, Diffusion- and velocity-driven spatial separation of analytes from single droplets entering an ICP off-axis, J. Anal. At. Spectrom., 2014, 29, 262–271 RSC.
- L. D. Landau and E. M. Lifshitz, Fluid Mechanics, Pergamon Press, Oxford, 2nd edn, 1987 Search PubMed.
- P. Farnsworth, R. Spencer, W. N. Radicic, N. Taylor, J. Macedone and H. Ma, A comparison of ion and atom behavior in the first stage of an inductively coupled plasma mass spectrometer vacuum interface: Evidence of the effect of an ambipolar electric field, Spectrochim. Acta, Part B, 2009, 64(9), 905–910 CrossRef.
- J. E. Patterson, B. S. Duersch and P. B. Farnsworth, Optically determined velocity distributions of metastable argon in the second stage of an inductively coupled plasma mass spectrometer, Spectrochim. Acta, Part B, 1999, 54, 537–544 CrossRef.
- W. N. Radicic, J. B. Olsen, R. V. Nielson, J. H. Macedone and P. B. Farnsworth, Characterization of the supersonic expansion in the vacuum interface of an inductively coupled plasma mass spectrometer by high-resolution diode laser spectroscopy, Spectrochim. Acta, Part B, 2006, 61, 686–695 CrossRef.
- J. H. Macedone, A. A. Mills and P. B. Farnsworth, Optical measurements of ion trajectories through the vacuum interface of an inductively coupled plasma mass spectrometer, Appl. Spectrosc., 2004, 58(4), 463–467 CrossRef CAS PubMed.
- P. Proulx, J. Mostaghimi and M. I. Boulos, Plasma-particle interaction effects in induction plasma modeling under dense loading conditions, Int. J. Heat Mass Transfer, 1985, 28, 1327–1336 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |