Pb isotope analysis of ng size samples by TIMS equipped with a 1013 Ω resistor using a 207Pb–204Pb double spike
Martijn
Klaver
*,
Richard J.
Smeets
,
Janne M.
Koornneef
,
Gareth R.
Davies
and
Pieter Z.
Vroon
Department of Geology and Geochemistry, VU University Amsterdam, De Boelelaan 1085, 1081HV Amsterdam, The Netherlands. E-mail: martijn.klaver@vu.nl; Tel: +31 (0)20 5983725
First published on 11th May 2015
Abstract
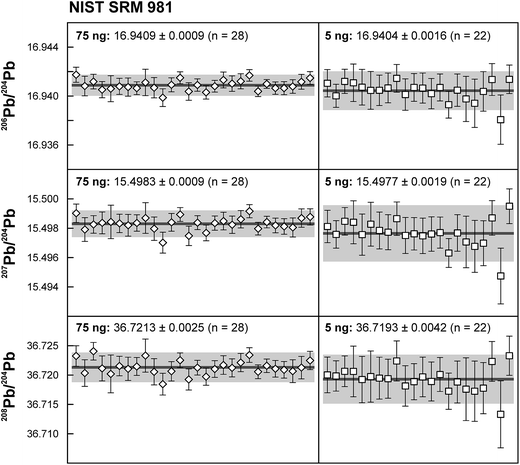
The use of the double spike technique to correct for instrumental mass fractionation has yielded high precision results for lead isotope measurements by thermal ionisation mass spectrometry (TIMS), but the applicability to ng size Pb samples is hampered by the small size of the 204Pb ion beam in the natural isotope composition analysis. To overcome this limitation, we successfully demonstrate the application of a 1013 Ω resistor in the Faraday cup amplifier feedback loop used for the collection of 204Pb in combination with a newly produced 207Pb–204Pb double spike to correct for instrumental mass fractionation. The use of a 1013 Ω resistor for the collection of the small 204Pb ion beam leads to a tenfold improvement in the signal-to-noise ratio, but necessitates an external gain correction using a secondary standard and careful monitoring of the ion beam stability. SRM 981 aliquots of 5 ng display unparalleled reproducibility of 90–125 ppm (2 SD) and are in excellent agreement with recommended values: 206Pb/204Pb = 16.9404 ± 0.0016, 207Pb/204Pb = 15.4977 ± 0.0019 and 206Pb/204Pb = 36.7193 ± 0.0042 (2 SD, n = 22). Comparable high quality data have been obtained for 5 ng aliquots of geological reference materials AGV-1 and BCR-1 (e.g.206Pb/204Pb = 18.9399 ± 0.0011 and 18.8208 ± 0.0011 respectively), indicating that analytical blank contribution is negligible for sample sizes down to 5 ng. With further reduction in, or precise correction for, analytical blanks, the combination of the double spike technique with high-resistance amplifiers has the potential to produce highly accurate and precise (<200 ppm) Pb isotope data for samples below the ng level. This methodology will open a range of research possibilities presently impeded by the low amount of Pb available for analysis.
1. Introduction
Lead isotopes are a powerful geochemical tool to investigate a wide variety of geological and environmental processes. In addition, the combination of the decay chains of 238U, 235U and 232Th, producing 206Pb, 207Pb and 208Pb respectively, represents one of the most robust geochronological tools available. Recent improvements in clean lab technology have pushed analytical procedure blanks down to and below the pg level, thereby enabling precise measurement of ng quantities of lead, for instance for microsampling of volcanic minerals1 or provenance studies.2 The accuracy of lead isotope measurements, however, is severely hampered by the difficulty in correcting for instrumental mass fractionation.3 In contrast with other radiogenic isotope systems such as Sr, Nd, Hf and Os, no stable isotope pair with an accepted constant ratio is available to correct for instrumental mass fractionation as only 204Pb is not produced by radioactive decay. In the last decades, multiple approaches have been proposed to overcome this problem. Reasonably accurate correction for instrumental mass fractionation in multi-collector inductively-coupled plasma mass spectrometry (MC-ICPMS) measurements can be achieved through sample-standard bracketing or Tl-spiking.3–5 Disadvantages of MC-ICPMS, however, are a higher background, isobaric interference of 204Hg from the Ar plasma, memory effects and large instrumental mass fractionation.3 In addition, the ion yield is up to an order of magnitude lower compared to thermal ionisation mass spectrometry (TIMS).3,6 Due to the high ion yield that is achievable with TIMS (up to 10% (ref. 7 and 8)), this is the most suitable method for measurement of ng or smaller sized lead samples.9–11 Arguably the most accurate method to correct for instrumental mass fractionation in TIMS measurements is the use of the double spike method.3,6 In contrast with isotope dilution, the double spike technique is not used to determine absolute element concentrations, but offers a mathematical solution to correct for instrumental mass fractionation (see Section 2). The conventional lead double spike technique, employing a double spike consisting of two stable isotopes of lead (e.g.207Pb–204Pb), has proven to be highly accurate and reproducible for large (>10 ng) sample sizes for both TIMS6,12 and MC-ICPMS.4,5 Its application to small (<10 ng) sample sizes, however, is hampered by two problems: (i) two measurements are required per sample: an unspiked and a spiked analysis. At least 20% of the total sample is required for the spiked analysis, and hence less sample is available for the natural analysis, thereby limiting the total ion beam size; and (ii) the precision of the measurement is largely controlled by the small size of the 204Pb ion beam in the natural run, which comprises only ∼1.4% of the total lead. The first problem can be overcome by the use of a 202Pb–205Pb spike, which eliminates the need for two mass spectrometric measurements and is not influenced by the uncertainty on the small 204Pb ion beam,11,13 but this technique has its own intrinsic weaknesses. A 202Pb–205Pb spike is radioactive, is not commercially available and suffers from interference by BaPO2+ and organic molecules. In addition, the problem of low 204Pb remains when 20xPb/204Pb data are desired and is compounded by the fact that typically small 202Pb and 205Pb ion beams are measured due to the expense of the spike. An elegant way to circumvent the problem of the small 204Pb ion beam is the use of two double spikes.14 In this technique, the natural sample is first spiked with a 204Pb–205Pb spike to augment the 204Pb ion beam intensity, after which a 207Pb–204Pb spike is used to correct for instrumental mass fractionation. The use of two spikes, however, introduces an additional source of error and organic molecular interference cannot be monitored at mass 205. Hence, a conventional double spike technique is expected to produce superior results once the limitation of the small 204Pb ion beam is overcome. In this paper, we investigate the use of an amplifier fitted with a state-of-the-art 1013 Ω resistor in the feedback loop for the collection of the small 204Pb ion beam. Compared to default 1011 Ω resistors, the use of a high-resistance 1013 Ω resistor results in a 100 times higher signal intensity while the noise increases with a factor of only √100, and thus a tenfold improvement in the signal to noise ratio.15 This allows the measurement of ion currents that are in the range normally covered by ion counting using a secondary electron multiplier (SEM), thereby taking advantage of the superior stability of a Faraday detector compared to SEM. The successful application of multiple 1013 Ω resistors has been demonstrated for the measurement of sub-ng Sr and Nd samples,15,16 but has not been investigated previously for Pb isotopes. We present an analytical protocol for the precise measurement of ng size Pb samples using a newly produced 207Pb–204Pb double spike in combination with a 1013 Ω resistor. The protocol is evaluated with NIST standard reference material (SRM) 981 and USGS reference materials AGV-1 and BCR-1.2. Principles of the double spike technique
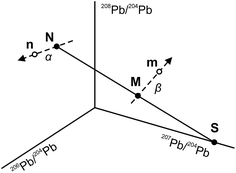
The use of the double spike technique to correct for instrumental mass fractionation is applicable to any element with at least four isotopes. It was first proposed by Dodson17 and is now regularly used to obtain high-precision isotope data for many elements, including Pb, Fe, Zn, Os etc.18 The fundamentals of the double spike technique have been discussed extensively in the literature5,6,17–19 and only a short summary is provided here. Two mass spectrometric measurements are required per sample, one for the unspiked sample (the natural analysis) and one for a mixture of the sample with a double spike (the spiked analysis). In four isotope space, these two measurements define three lines (Fig. 1): a mixing line between the sample and the double spike, on which the mixture is located, and two mass fractionation vectors that displace the measured compositions from the true, mass fractionation corrected compositions. Provided that the composition of the double spike is well known, the nine equations that define the three lines can be solved to yield the mass fractionation factor α for the natural run and hence the mass fractionation corrected composition of the sample. Note that the absolute concentration of the double spike is not an input parameter and does not need to be precisely constrained.3. Analytical techniques
3.1. The VUA 207Pb–204Pb double spike
A 207Pb–204Pb double spike was made at the VU University Amsterdam (VUA Pb DS) from 204Pb and 207Pb single spikes obtained from Oak Ridge National Laboratory. An optimal double spike composition was calculated using the double spike toolbox18 and was designed to introduce minimal error magnification on 207Pb/204Pb. The VUA Pb DS has a 207Pb/204Pb of 0.79086 ± 7 (Table 2), which allows large flexibility in the sample-double spike ratio without significantly increasing the error magnification. The isotope composition of the VUA Pb DS was calibrated against standard reference material NIST SRM 982 using the isotope ratios reported by Thirlwall.43.2. Ion-exchange chemistry
Single aliquots of USGS reference materials AGV-1 and BCR-1 used in this study were digested using PTFE Parr bombs and subsequently dissolved in 0.7 M HBr. Double sub-boiling distilled reagents were used for sample dissolution and ion-exchange chemistry to ensure low blank levels. All PTFE and PFA laboratory equipment is cleaned by sub-boiling in pro-analysis quality ∼6 M HNO3 and ∼6 M HCl for two hours each, followed by two 4–7 day leaching steps at 130 °C with double distilled 6 M HCl/1–2 M HF and 0.25 M HBr respectively. Laboratory equipment that has contained the Pb double spike is used at least once for any other purpose (e.g. Sr or Nd isotope analysis) before being reconsidered for Pb again to minimise double spike memory effects. For the purification of Pb, a double column pass anion-exchange technique was employed with disposable polyethylene pipette-tip columns fitted with a polyethylene filter (mesh 35 μm). The columns were loaded with 50 μl of Bio-Rad® AG 1-X8 200–400 mesh resin and cleaned three times with alternating 1.5 ml 1 M HF, 6.5 M HCl and milli-Q water before conditioning with 0.7 M HBr. Subsequently, 0.5 ml aliquots of the sample solutions dissolved in 0.7 M HBr, corresponding to the desired amount of Pb (typically 75 ng Pb for regular samples and 5 ng for the small standards used in this study), were loaded onto the columns. The matrix was washed out with 1 ml 0.7 M HBr followed by a rinse with 0.15 ml 3.0 M HCl and elution of the Pb fraction was accomplished with 0.4 ml 6.5 M HCl. The Pb fractions were dried down while the columns were conditioned with 0.7 M HBr. Subsequently, the Pb fractions were re-dissolved in 0.5 ml 0.7 M HBr, loaded onto the same columns and Pb was extracted as in the first column pass. The purified Pb fractions were dried down and nitrated twice with 2 drops of concentrated HNO3 to eliminate organic material. Over the 1.5 years of this study, total procedural blanks, including sample destruction in PTFE Parr bombs, were 5–13 pg, but have stabilized at 6 ± 1 pg Pb after implementation of the rigorous column cleaning procedure described above. Columns blanks are 3–6 pg, suggesting that the ion-exchange chemistry is the largest contributor to the total procedural blank.3.3. Mass spectrometry
Samples and standards were measured for isotope composition by TIMS using a Thermo Scientific TRITON Plus instrument. A summary of the analytical method is shown in Table 1. For the natural analysis, the samples were re-dissolved in 3 μl 10% HNO3 before loading on outgassed zone-refined rhenium filaments. First, 1.5 μl of silica gel prepared by the method of Gerstenberger & Haase7 was loaded to which 2 μl (i.e., two-thirds) of the sample was added drop by drop. The solution was evaporated at 1.0 A to allow effective mixing of the lead with the silica gel. Subsequently, the filament current was increased to 2.0 A to fuse the silica gel and evaporate excess H3PO4 from the silica gel. An aliquot of the VUA Pb DS and ∼0.5 ml dilute HNO3 were added to the remaining one-third of the samples, which were left to equilibrate overnight at 120 °C to ensure effective sample-spike homogenisation. Ideally, an amount of double spike Pb equivalent to the remaining amount of sample Pb was added, but the sample-spike ratio can be varied up to an order of magnitude without significantly increasing the error magnification. The spiked Pb fractions were dried down and loaded similarly to the natural analysis except that the complete sample was loaded. Loading blanks are systematically <150 fg and therefore differential loading blanks between the natural and spiked runs are assumed to be negligible.| Cup configuration | |||||
|---|---|---|---|---|---|
| Faraday cup | L2 | L1 | C | H1 | H2 |
| Isotope | 204Pb | 205Organics | 206Pb | 207Pb | 208Pb |
| N-runs >5 ng Pb S-runs | N-runs <5 ng Pb | |
|---|---|---|
| Resistor Faraday cup L2 (204Pb) | 1011 Ω | 1013 Ω |
| Resistor other Faraday cups | 1011 Ω | 1011 Ω |
| Baseline (defocused beam) | 32 s – every block | 660 s – during warm-up |
| Gain calibration | Software routine | External correction to in-house Pb standard |
| Data acquisition | 6–8 blocks of 20 cycles | 2–4 blocks of 100 cycles |
| Integration time | 8.389 s | 8.389 s |
| Idle time | 3 s | 10 s |
| Run temperature | 1160–1240 °C | 1160–1240 °C |
For the analysis of the unspiked samples larger than 5 ng Pb and all spiked analyses, regular 1011 Ω resistors were used. Samples were heated to obtain a slightly growing ion beam in the temperature range 1160–1230 °C. After beam optimization, data were acquired in static multi-collector mode in six to eight blocks of 20 cycles each without the use of the Triton's amplifier rotation option (see Table 1). A baseline measurement of 32 s was performed in between blocks by defocusing the ion beam. An amplifier gain calibration was performed at least daily. For the analysis of unspiked samples, a regular sample size of ca. 50 ng will yield a stable 208Pb beam with an intensity of 4–7 × 10−11 A that can easily be maintained for the duration of a measurement (roughly 30 minutes) in the temperature range 1160–1240 °C. Measurements obtained at a filament temperature in excess of 1250 °C display a decrease in 207Pb/204Pb of up to 150 ppm while 206Pb/204Pb and 208Pb/204Pb are unaffected. Similar anomalous behaviour of 207Pb on TIMS has been discussed in detail by Thirlwall6 and Doucelance and Manhès,20 who concluded that isobaric interference was not the cause of the 207Pb anomaly. Our results also show no evidence of isobaric interference in this temperature range. Organic molecular interference is monitored at mass 205, but an observable signal at T > 1130 °C was present in less than 1% of the analyses and was usually absent above 1180 °C. Hence, the origin of the anomalous behaviour of 207Pb remains unresolved, but is likely a nuclear effect.21,22 Rather than applying a correction for the anomalous behaviour of 207Pb, we exclude any data acquired at T > 1250 °C. For the unspiked analysis of sample sizes ≤5 ng Pb, a 1013 Ω resistor is used for the detection of 204Pb in combination with regular 1011 Ω resistors for the other isotopes. As it is not possible to calibrate the gain factor of the 1013 Ω resistor directly, an external reference solution is measured at least daily,15 as will be discussed in detail in Section 4.2. A 660 s baseline measurement is carried out during sample warm-up15 to save acquisition time, and after beam optimization data are acquired continuously for 200–400 cycles. A detailed discussion of measurement conditions is provided in Section 4.2.
3.4. Data reduction
By employing the exponential law to correct for mass fractionation, the double spike inversion cannot be solved algebraically and has to be processed individually per sample in an offline spreadsheet. First, the natural and spiked data were subjected to an artificial mass fractionation correction to the average 208Pb/206Pb ratio of the first block of the unspiked analysis. This allows a realistic estimate of the analytical uncertainties to be made6 and, as the same correction was applied to both the natural and spiked data, this artificial correction will cancel out during the subsequent double spike inversion. The corrected data were subjected to a 2-sigma outlier test and a variance-covariance matrix of these data was used for algebraic error propagation. Average 206Pb/204Pb, 207Pb/204Pb and 208Pb/204Pb ratios of the natural and spiked analysis were entered in the double spike inversion, following the solution presented by Rudge et al.18 To correct for instrumental mass fractionation according to the exponential law, the double spike equation was solved iteratively using a Newton–Raphson method and a linear fractionation correction as a first approximation. Uncertainties were propagated algebraically,18,23 taking into account the strong error correlation (r > 0.90) between 20xPb/204Pb ratios. The error magnification factor (defined as 2 SE uncertainty of the double spike corrected 206Pb/204Pb ratio over the artificially corrected 206Pb/204Pb ratio) is dependant predominantly on the precision of the spiked run, but was almost always less than 1.20.4. Results and discussion
4.1. Reproducibility of 75 ng standards with the double spike technique
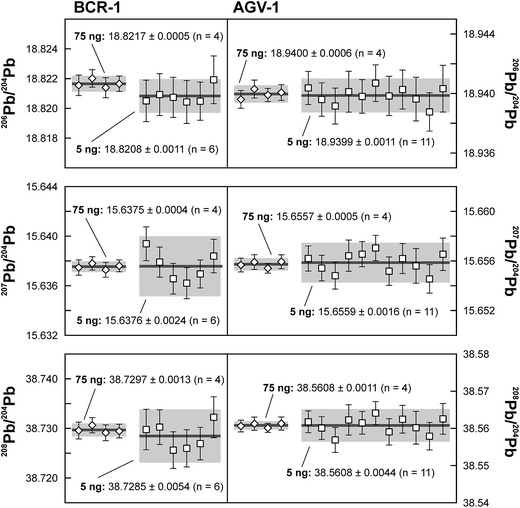
Repeated analyses of standard reference material (SRM) 981 were used to assess the reproducibility (2 standard deviation of the results acquired during the 1.5 years of this study) of the double spike method. All analyses of SRM 981 represent an individual double spike measurement: a 75 ng aliquot of SRM 981 was evaporated in a clean PFA vial and was loaded, measured and spiked in an identical way as for samples. We argue that this approach allows a more realistic estimate to be made of the performance of the double spike technique rather than using a single spiked SRM 981 measurement to correct all standard measurements. The data acquired for SRM 981 over the last 1.5 years display excellent reproducibility (51, 59 and 69 ppm 2 SD for 206Pb/204Pb, 207Pb/204Pb and 208Pb/204Pb respectively) and are in perfect agreement with recommended values (Fig. 2 and Table 2). To test the reproducibility of the analytical procedure with geological matrices, USGS reference materials AGV-1 and BCR-1 were periodically included as unknowns in sample sets measured over the course of this study. These reference materials were selected on the basis of their superior homogeneity compared to AGV-2, BCR-2 and other “-2” USGS standards, which are characterized by significant Pb isotope inhomogeneity.5,24 Nevertheless, we opted for processing aliquots of a single dissolution of AGV-1 and BCR-1 to eliminate any doubt with regard to standard inhomogeneity in order to assess the reproducibility of the ion-exchange and mass spectrometric procedures. Results obtained for AGV-1 and BCR-1 are shown in Fig. 3 and Table 2. The reproducibility for both standards is comparable to SRM 981 and the results agree within analytical uncertainty with published MC-ICPMS double spike corrected5 and MC-ICPMS Tl-corrected25 data. Hence, we conclude that the results obtained for AGV-1 and BCR-1 are of the same high quality as the SRM 981 data and that the chemical purification procedure has no effect on the accuracy and reproducibility of the Pb isotope data.| Study | Instrument | Ref. | 206Pb/204Pb | 2 SD | 207Pb/204Pb | 2 SD | 208Pb/204Pb | 2 SD |
|---|---|---|---|---|---|---|---|---|
| a Triple spike. b 2× double spike. c Batch 61/13. d Batch 20/3. | ||||||||
| VUA Pb 207Pb–204Pb DS | 0.002346 | 0.000025 | 0.790861 | 0.000070 | 0.001977 | 0.000052 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| NIST SRM 981 – double spike | ||||||||
| This study – 75 ng (n = 28) | TIMS | 16.9409 | 0.0009 | 15.4983 | 0.0009 | 36.7213 | 0.0025 | |
| This study – 5 ng (n = 22) | TIMS | 16.9404 | 0.0016 | 15.4977 | 0.0019 | 36.7193 | 0.0042 | |
| NIST SRM 981 recommended value | 3 | 16.9412 | 0.0003 | 15.4988 | 0.0006 | 36.7233 | 0.0013 | |
| Woodhead et al., 1995 | TIMS | 12 | 16.937 | 0.0040 | 15.492 | 0.0048 | 36.708 | 0.0128 |
| Galer and Abouchami, 1998 | TIMSa | 26 | 16.9405 | 0.0015 | 15.4963 | 0.0016 | 36.7219 | 0.0044 |
| Thirlwall, 2002 | TIMS | 4 | 16.9408 | 0.0021 | 15.4980 | 0.0025 | 36.722 | 0.0080 |
| Thirlwall, 2002 | MC-ICPMS | 4 | 16.9417 | 0.0029 | 15.4996 | 0.0031 | 36.724 | 0.0080 |
| Kuritani and Nakamura, 2003 | TIMSb | 14 | 16.9414 | 0.0028 | 15.4992 | 0.0029 | 36.723 | 0.0075 |
| Baker et al., 2004 | MC-ICPMS | 5 | 16.9416 | 0.0013 | 15.5000 | 0.0015 | 36.7262 | 0.0031 |
| Taylor et al., 2015 | TIMS | 3 | 16.9402 | 0.0027 | 15.4981 | 0.0027 | 36.7222 | 0.0075 |
| Taylor et al., 2015 | TIMS | 3 | 16.9403 | 0.0029 | 15.5000 | 0.0038 | 36.7224 | 0.0090 |
| Taylor et al., 2015 | MC-ICPMS | 3 | 16.9415 | 0.0022 | 15.4985 | 0.0021 | 36.7212 | 0.0063 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| AGV-1 | ||||||||
| This study – 75 ng (n = 4) | TIMS DS | 18.9400 | 0.0006 | 15.6557 | 0.0005 | 38.5608 | 0.0011 | |
| This study – 5 ng (n = 11) | TIMS DS | 18.9399 | 0.0011 | 15.6559 | 0.0016 | 38.5608 | 0.0044 | |
| Woodhead and Hergt, 2000 | TIMS DSc | 28 | 18.942 | 0.001 | 15.659 | 0.003 | 38.566 | 0.007 |
| Woodhead and Hergt, 2000 | TIMS DSd | 28 | 18.954 | 0.003 | 15.672 | 0.002 | 38.599 | 0.007 |
| Kuritani and Nakamura, 2002 | TIMS | 27 | 18.938 | 0.003 | 15.650 | 0.004 | 38.554 | 0.019 |
| Baker et al., 2004 | MC-ICPMS DS | 5 | 18.942 | 0.002 | 15.658 | 0.002 | 38.569 | 0.006 |
| Weis et al., 2006 | MC-ICPMS Tl | 25 | 18.9399 | 0.0063 | 15.6531 | 0.0038 | 38.5599 | 0.0096 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| BCR-1 | ||||||||
| This study – 75 ng (n = 4) | TIMS DS | 18.8217 | 0.0005 | 15.6375 | 0.0004 | 38.7297 | 0.0013 | |
| This study – 5 ng (n = 6) | TIMS DS | 18.8208 | 0.0011 | 15.6376 | 0.0024 | 38.7285 | 0.0054 | |
| Woodhead and Hergt, 2000 | TIMS-DS | 28 | 18.814 | 0.006 | 15.630 | 0.005 | 38.703 | 0.015 |
| Kuritani and Nakamura, 2002 | TIMS | 27 | 18.817 | 0.005 | 15.631 | 0.004 | 38.720 | 0.015 |
| Baker et al., 2004 | MC-ICPMS DS | 5 | 18.822 | 0.003 | 15.639 | 0.003 | 38.739 | 0.008 |
| Weis et al., 2006 | MC-ICPMS Tl | 25 | 18.8225 | 0.0031 | 15.6363 | 0.0033 | 38.7321 | 0.0073 |
4.2. Measurement of small Pb samples using a 1013 Ω resistor
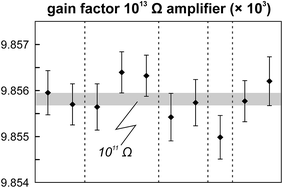
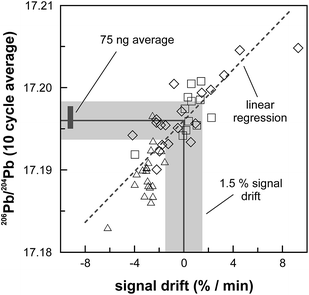
The internal precision (2 standard error) of lead isotope analyses using the double spike technique depends predominantly on the uncertainty in the measurement of 204Pb in the natural run. The low 204Pb signal intensity is the main limiting factor in the successful application of the double spike technique to small lead samples. To potentially improve the precision, we evaluated the use a 1013 Ω resistor in the feedback loop of the Faraday cup amplifier for the detection of the small 204Pb ion beam. The use of this high-resistance amplifier has proven to be superior to ion counting by SEM and default 1011 Ω resistors at signal intensities between 3.2 × 10−15 and 2.5 × 10−13 A.15 Online calibration of the amplifier gain factor of the 1013 Ω resistor through an internal reference current (3.33333 V on a 1011 Ω resistor) is not possible. Therefore, the amplifier gain factor was calculated through the measurement of a reference solution, in this case an in-house CPI Pb standard. The isotope composition of this reference solution has been determined through repeated double spike analysis of 75 ng aliquots (206Pb/204Pb = 17.8996 ± 0.0002; 207Pb/204Pb = 15.5645 ± 0.0003; 208Pb/204Pb = 38.0177 ± 0.0009; 2 SD, n = 3). During analytical sessions with the 1013 Ω amplifier, the in-house CPI standard was measured at least daily using a 1013 Ω resistor for 204Pb. As 206Pb and 208Pb data are obtained on regular, gain corrected 1011 Ω resistors, 208Pb/206Pb was used to correct for instrumental mass fractionation. Subsequently, the fractionation corrected 206Pb/204Pb, 207Pb/204Pb and 208Pb/204Pb ratios can be used to calculate the relative gain factor of the amplifier equipped with the 1013 Ω resistor that was used for the collection of 204Pb. The three independently calculated gain factors (relative to 206Pb, 207Pb and 208Pb) were identical within error and the average calculated gain factor was inserted in the amplifier system table of the TRITON software such that the gain correction was performed online. The gain factor for the 1013 Ω resistor was found to vary by less than 100 ppm (2 SD) over a 6 month period; day-by-day variation is even less (<50 ppm 2 SD; Fig. 4). Hence, we conclude that using an external reference solution to determine the gain factor of the 1013 Ω resistor is reproducible and capable of producing results that are both accurate and precise.A complicating issue found when analysing with a combination of amplifiers with 1011 and 1013 Ω resistors is the difference in signal response and decay times, which introduces a bias when the ion beam is unstable (Fig. 5). For a growing ion beam, the longer response time of the amplifier with a 1013 Ω resistor causes the 204Pb signal intensity to lag behind, leading to relatively high 20xPb/204Pb. For a diminishing ion beam, the effect is opposite and leads to 20xPb/204Pb that are too low. The successful application of an amplifier with a 1013 Ω resistor therefore requires that the ion beam intensity is kept as stable as possible, with a maximum drift of 1.5% in ion beam intensity per minute (Fig. 5). This is easily achieved by gently increasing or decreasing the filament current during data acquisition but requires careful monitoring of the ion beam stability. With these problems overcome, we tested the applicability of the double spike technique in combination with an amplifier with a 1013 Ω resistor for 5 ng aliquots of SRM 981, AGV-1 and BCR-1. Similar to the 75 ng data, all SRM 981 analyses represent individual aliquots, and in the case of AGV-1 and BCR-1 individual column passes, that were treated as unknown samples. Typical sample loads of ∼3.5 ng (i.e., two-thirds of the 5 ng aliquot) for the natural run yield a 208Pb signal intensity of 3–6 × 10−12 A, roughly ten times lower compared to typical 50 ng loads, which can be maintained for at least one hour in the temperature range 1170–1250 °C. This results in a 204Pb ion beam intensity of 8–15 × 10−14 A, in the range for which a 1013 Ω resistor has proven to be superior to ion-counting and regular 1011 Ω resistors.15 Once a stable ion signal has been obtained, data are acquired continuously for 200 to 400 cycles (Table 1). Generally, data acquisition was terminated after 200 cycles as longer analyses did have a smaller internal precision (2 standard error) but the reproducibility did not improve.
4.3. High-precision results for 5 ng standards
On the basis of the calculated Johnson–Nyquist noise of the 1011 and 1013 Ω resistors,15 it is expected that the on average ten times lower signal intensity of the 5 ng SRM 981 standards will result in an internal precision (2 SE) that is only a factor 1.5 times worse compared to the 75 ng standards. The reproducibility and internal precision of the measurements of 5 ng aliquots of SRM 981 (Fig. 3 and Table 2) agree with this prediction and are comparable to the results obtained for the 75 ng aliquots. This is partly due to the longer data acquisition time for the analysis of the 5 ng standards, but predominantly the result of the use of the 1013 Ω resistor for the collection of the 204Pb ion beam. In theory, the 1013 Ω resistor has a roughly ten times higher signal to noise ratio than default 1011 Ω resistors,15 which should drastically improve the counting statistics of the 204Pb ion beam and therefore the internal precision of 20xPb/204Pb data. We have compared data acquired for 3.5 ng SRM 981 aliquots with a 1013 Ω and a regular 1011 Ω resistor for the collection of 204Pb. Typical internal precision for 206Pb/204Pb is ca. 70 ppm (2 SE) using a 1013 Ω resistor, which is over a factor two better than the ca. 160 ppm acquired with a 1011 Ω resistor. These results confirm that a higher internal precision can be achieved with a 1013 Ω resistor than with regular amplifiers for ion beam intensities <2.5 × 10−13 A. We report a reproducibility of 90–125 ppm for the 5 ng aliquots of SRM 981, which is only a factor of ∼1.8 worse than the 50–70 ppm obtained for 75 ng aliquots (Table 2). Considering that the precision and reproducibility are largely controlled by the uncertainty in the ∼3.5 ng unspiked analysis, the 90–125 ppm reproducibility presents a marked improvement compared to the range of 170–900 ppm reported in previous studies for 2–5 ng Pb samples.10,11,14,27 In addition, the excellent reproducibility indicates that the external gain correction and necessity of maintaining a stable ion beam inherent to the use of a 1013 Ω resistor do not introduce a bias nor have an adverse effect on the reproducibility.To evaluate the effect of the ion exchange procedure used for samples with a geological matrix on the analytical results, 5 ng aliquots of a single dissolution of BCR-1 and AGV-1 were processed. Given the typical column blank levels of 3–6 pg, the contribution by the analytical blank is expected not be of influence in the results. This is confirmed by the results for these USGS reference materials, which are in good agreement with results obtained on 75 ng aliquots and published values (Fig. 3 and Table 2). Typical internal precision and reproducibility for AGV-1 and BCR-1 are similar to the 5 ng SRM 981 results, indicating that analytical blanks are negligible for sample sizes down to 5 ng.
Preliminary tests indicate sample sizes much less than 5 ng can also be measured successfully using a 1013 Ω resistor for the collection of 204Pb. The internal precision for 2 ng, 500 pg and 200 pg sample loads of SRM 981 is not significantly worse than for ∼3.5 ng aliquots, despite lower signal intensities, provided that a stable ion beam can be maintained for 200–400 cycles. For example, for a 200 pg SRM 981 standard, a 204Pb ion current of ∼3 × 10−14 A can easily be maintained for ca. 1 hour, resulting in an internal precision of 120 ppm (2 SE) for 206Pb/204Pb. The limiting factor in obtaining precise and accurate results for <5 ng samples, however, is the analytical blank. We have limited this study to sample sizes 1000 times larger than the currently lowest achievable blank level of ∼5 pg. Clearly, introducing a blank correction could overcome this limitation, but an accurate blank correction requires that the isotope composition of the analytical blank is well known, which might be problematic when memory effect of laboratory equipment is the largest contributor. Nevertheless, with a further reduction in blank levels and the implementation of an analytical blank correction, the double spike procedure in combination with a 1013 Ω resistor for 204Pb has the potential to produce precise and accurate measurements of sample sizes down to or even below 1 ng. Internal precision and reproducibility are on par with or even better than other those obtained with a 202Pb–205Pb spike.11 The main advantages of the use of a 207Pb–204Pb double spike in combination with a 1013 Ω resistor, when compared to a 202Pb–205Pb spike, are the wider availability of the spike and higher reproducibility when accurate 20xPb/204Pb data are desired. In comparison with the standard TIMS approach of applying a constant instrumental mass fractionation correction of typically 0.06–0.15% per a.m.u.,3,9 the double spike technique has proven to be superior in terms of accuracy and reproducibility.3 Therefore, the disadvantage of sacrificing 20–35% of the total amount of sample for the spiked analysis is easily compensated by the greatly enhanced reproducibility.
5. Conclusions
This study demonstrates the successful application of the double spike technique to obtain high-precision lead isotope data for ng size samples. Repeated analyses of 75 ng aliquots of SRM 981, using a newly developed 207Pb–204Pb double spike to correct for instrumental mass fractionation, are highly reproducible (50–70 ppm) and in excellent agreement with recommended values. The use of a 1013 Ω resistor in the Faraday cup amplifier feedback loop allows the accurate and precise measurement of ion currents <2.5 × 10−13 A and thereby enables the measurement of the small 204Pb ion beam in sample sizes ≤5 ng. Minor complications that are intrinsic to the use of a 1013 Ω resistor include the necessity of an external gain calibration and stable ion beam, but these have been overcome. Results for 5 ng SRM 981 aliquots obtained with a 1013 Ω amplifier for the collection of 204Pb are accurate and show unparalleled reproducibility of 90 ppm (2 SD) for 206Pb/204Pb. Similar reproducibility is achieved for 5 ng aliquots of USGS reference materials AGV-1 and BCR-1, indicating that sample matrix and ion exchange procedure have no adverse effect on data quality and that the analytical blank contribution is negligible for sample sizes down to 5 ng. With further reductions in blank levels, the double spike technique in combination with a 1013 Ω resistor for the collection of 204Pb allows high-precision Pb isotope data to be obtained when sub-ng quantities of Pb are available. This new analytical achievement has the potential to open a range of possibilities for research in cosmochemistry, high-precision U–Pb dating and microsampling of geological and archaeological materials.Acknowledgements
Jurriën Knibbe and Marlies ter Voorde are greatly acknowledged for their useful advice and discussions on the maths behind the double spike solution and error propagation. Suzette Timmerman, Stefan de Graaf and Alex Sakes provided assistance with TIMS analyses and preparation. The manuscript benefited from the constructive comments made by three anonymous reviewers. The TRITON facility at VUA is funded by NWO through grant number 834.10.001 and funding for JMK and GRD was provided by the ERC Synergy grant, Nexus 1492.References
- J. Davidson, D. Morgan, B. Charlier, R. Harlou and J. Hora, Annu. Rev. Earth Planet. Sci., 2007, 35, 273–311 CrossRef CAS.
- L. Font, G. van der Peijl, I. van Wetten, P. Vroon, B. van der Wagt and G. Davies, J. Anal. At. Spectrom., 2012, 27, 719–732 RSC.
- R. N. Taylor, O. Ishizuka, A. Michalik, J. A. Milton and I. W. Croudace, J. Anal. At. Spectrom., 2015, 30, 198–213 RSC.
- M. Thirlwall, Chem. Geol., 2002, 184, 255–279 CrossRef CAS.
- J. Baker, D. Peate, T. Waight and C. Meyzen, Chem. Geol., 2004, 211, 275–303 CrossRef CAS.
- M. Thirlwall, Chem. Geol., 2000, 163, 299–322 CrossRef CAS.
- H. Gerstenberger and G. Haase, Chem. Geol., 1997, 136, 309–312 CrossRef.
- M. H. Huyskens, T. Iizuka and Y. Amelin, J. Anal. At. Spectrom., 2012, 27, 1439–1446 RSC.
- C. Sarkar, D. G. Pearson, L. M. Heaman and S. J. Woodland, Chem. Geol., 2015, 395, 27–40 CrossRef CAS.
- M. Paul, L. Bridgestock, M. Rehkämper, T. van DeFlierdt and D. Weiss, Anal. Chim. Acta, 2015, 863, 59–69 CrossRef CAS PubMed.
- Y. Amelin and W. Davis, J. Anal. At. Spectrom., 2006, 21, 1053–1061 RSC.
- J. D. Woodhead, F. Volker and M. McCulloch, Analyst, 1995, 120, 35–39 RSC.
- W. Todt, R. A. Cliff, A. Hanser and A. Hofmann, Earth Processes: Reading the Isotopic Code, 1996, 429–437 Search PubMed.
- T. Kuritani and E. Nakamura, J. Anal. At. Spectrom., 2003, 18, 1464–1470 RSC.
- J. Koornneef, C. Bouman, J. Schwieters and G. Davies, Anal. Chim. Acta, 2014, 819, 49–55 CrossRef PubMed.
- J. M. Koornneef, I. Nikogosian, M. J. van Bergen, R. Smeets, C. Bouman and G. R. Davies, Chem. Geol., 2015 Search PubMed.
- M. H. Dodson, Journal of Scientific Instruments, 1963, 40(6), 289–295 CrossRef.
- J. F. Rudge, B. C. Reynolds and B. Bourdon, Chem. Geol., 2009, 265, 420–431 CrossRef.
- B. Hamelin, G. Manhes, F. Albarede and C. J. Allegre, Geochim. Cosmochim. Acta, 1985, 49, 173–182 CrossRef CAS.
- R. Doucelance and G. Manhès, Chem. Geol., 2001, 176, 361–377 CrossRef CAS.
- Y. Amelin, D. Davis and W. Davis, Geochim. Cosmochim. Acta, Suppl., 2005, 69, 215 Search PubMed.
- G. Manhes and C. Göpel, Geochim. Cosmochim. Acta, 2007, 71, A618 Search PubMed.
- N. McLean, J. F. Bowring and S. A. Bowring, Geochem., Geophys., Geosyst., 2011, 12(6), Q0AA18 CrossRef.
- M. Elburg, P. Vroon, B. van der Wagt and A. Tchalikian, Chem. Geol., 2005, 223, 196–207 CrossRef CAS.
- D. Weis, B. Kieffer, C. Maerschalk, J. Barling, J. de Jong, G. A. Williams, D. Hanano, W. Pretorius, N. Mattielli, J. S. Scoates, A. Goolaerts, R. M. Friedman and J. B. Mahoney, Geochem., Geophys., Geosyst., 2006, 7, Q08006 CrossRef.
- S. Galer and W. Abouchami, Mineral. Mag. A, 1998, 62, 491–492 Search PubMed.
- T. Kuritani and E. Nakamura, Chem. Geol., 2002, 186, 31–43 CrossRef CAS.
- J. D. Woodhead and J. M. Hergt, Geostand. Newsl., 2000, 24, 33–38 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |