DOI:
10.1039/C5IB00202H
(Paper)
Integr. Biol., 2016,
8, 216-229
Fully quantified spectral imaging reveals in vivo membrane protein interactions†
Received
12th August 2015
, Accepted 9th January 2016
First published on 20th January 2016
Abstract
Here we introduce the fully quantified spectral imaging (FSI) method as a new tool to probe the stoichiometry and stability of protein complexes in biological membranes. The FSI method yields two dimensional membrane concentrations and FRET efficiencies in native plasma membranes. It can be used to characterize the association of membrane proteins: to differentiate between monomers, dimers, or oligomers, to produce binding (association) curves, and to measure the free energies of association in the membrane. We use the FSI method to study the lateral interactions of Vascular Endothelial Growth Factor Receptor 2 (VEGFR2), a member of the receptor tyrosine kinase (RTK) superfamily, in plasma membranes, in vivo. The knowledge gained through the use of the new method challenges the current understanding of VEGFR2 signaling.
Insight, innovation, integration
Out of the many interactions that occur between biological macromolecules, the interactions between membrane proteins are the least understood due to lack of adequate quantitative experimental methodologies. Yet, these interactions regulate vital cellular processes such as signal transduction, nutrient uptake, and motility. Here we introduce a new quantitative fluorescence imaging methodology with unique capabilities to probe the stoichiometry and stability of protein complexes in biological membranes, in vivo. The method yields new knowledge about VEGFR2, an anti-cancer target known to control angiogenesis, the growth of new blood vessels from pre-existing ones. The method can be applied to many membrane proteins, such as RTKs, GPCRs, channels, and adhesion molecules, and may ultimately aid the development of diverse molecular therapies.
|
Introduction
The function of membrane proteins is often regulated through protein–protein interactions in cellular membranes.1 While methods to study interactions between soluble proteins are well established, methodologies to quantify membrane protein interactions have been slow to emerge.2,3 Great challenges remain, particularly for complex membrane proteins, which cannot be overexpressed in large quantities, and cannot be purified and properly reconstituted in model systems.4–6 Here we introduce a method, fully quantified spectral imaging (FSI), which yields both two-dimensional membrane concentrations and FRET efficiencies, and ultimately reports on the stoichiometry and stability of protein complexes in live cells. We use the method to gain new knowledge about the lateral interactions of Vascular Endothelial Growth Factor Receptor 2 (VEGFR2), a member of the receptor tyrosine kinase (RTK) superfamily, in plasma membranes of live cells.
RTKs epitomize functional regulation through lateral interaction in the plasma membrane.7,8 RTK dimerization is necessary for RTK function, as contacts between the intracellular kinase domains lead to kinase cross-phosphorylation and initiation of downstream signaling cascades that control cell growth, differentiation and motility during development and in the adult, and in many pathologies such as cancers and growth disorders.7 While RTK dimerization has been long assumed to occur in response to ligand binding,9 recent work has suggested that RTKs have a propensity to interact even in the absence of bound ligand, thus challenging the canonical view of RTK ligand-induced dimerization and activation.10–12 Yet, the mode of activation of many RTKs has thus far remained controversial, and is still a topic of intense investigations and debate.
VEGFR2 is a critically important member of the RTK superfamily, as it is the main regulator of angiogenesis, i.e. the development of new blood vessels from pre-existing ones.13,14 Thus, VEGFR2 signaling plays profound roles in embryogenesis, organ development, and in wound healing.13,15,16 It is also tightly linked to cancer, as the growth of all solid tumors require the recruitment of new blood vessels to supply nutrients.14,17 Like most RTKs, VEGFR2 consists of an extracellular (EC) domain, a single transmembrane (TM) domain, and an intracellular catalytic domain. The VEGFR2 EC domain is one of the largest in the RTK superfamily, composed of 7 Ig-like subdomains referred to as D1 (at the N-terminus) to D7 (proximal to the membrane).
VEGFR2 is assumed to be monomeric in the absence of ligand. This view has been supported by electron micrographs of the isolated VEGFR2 EC domains, showing only monomers and no dimers in solution, in the absence of ligand.18 Yet, the crystal structure of isolated D7 subdomain dimers reveals robust D7–D7 interactions in the crystal.19 This contradiction has been rationalized by postulating that D7–D7 interactions occur only in the presence of ligand, but not between unliganded receptors.20 However, the interactions between VEGFR2 EC domains in the absence of ligand have not been measured in the context of the two-dimensional plasma membrane.
Recent work has suggested that VEGFR2 TM domains have a propensity to dimerize in model systems.21,22 Thus, both the reduced dimensionality of the membrane,23 and the dimerization propensity of the TM domain, may provide the driving force for the EC domains to dimerize when anchored to the TM domains in the plasma membranes. We therefore investigated the ability of a VEGFR2 construct composed of the EC and TM domains to form dimers in the plasma membrane in the absence of ligand. We also investigated the specificity of the interactions between the EC domain by mutating a critical amino acid in D7, known to stabilize D7–D7 contacts in the D7 crystals.
The FSI method, developed here and used to study VEGFR2 interactions, utilizes two excitation wavelengths, pixel-level full spectrum acquisition, and pixel-level fluorescence calibration curves. It yields approximation-free measurement of the apparent FRET efficiency, as well as the donor- and acceptor-labeled receptor surface densities in the plasma membrane. Ultimately, the method allows us to acquire a complete binding (association) curve, and yields quantitative information about in vivo VEGFR2 interactions in the plasma membrane. The knowledge gained here through the use of the FSI methodology is new and challenges the current understanding of VEGFR2 signaling. Since VEGFR2 controls the development of blood vessels in a variety of solid tumors, the new knowledge can help guide the development of new VEGFR2 inhibitors as anti-cancer therapies.
Fully quantified spectral imaging (FSI) and analysis of membrane protein interactions
1. Theory
Here we derive the equations of the fully quantified spectral imaging (FSI) method. In the FSI method, two scans are performed: a “FRET scan” at λ1, in which the donor is primarily excited and an “Acceptor scan” at λ2 in which the acceptor is maximally excited. By using these two scans and calibration curves of fluorescence versus known concentration of donor and acceptor “solution standards,” one can solve for the full donor fluorescence and the acceptor fluorescence in the absence of FRET, as discussed below.
The fluorescence of the donor in the presence of the acceptor, FDAλn, and the fluorescence of the acceptor in the presence of the donor, FADλn, at both excitation wavelengths, λ1 and λ2, can be written as a sum of two terms:
| | | FADλn = FAλn + FARET,λn | (1.1) |
In
eqn (1.1),
FDλn and
FAλn (
n = 1, 2) are the donor and acceptor fluorescence emission spectra after direct excitation at
λ1 and
λ2, in the absence of FRET.
FDRET,λn and
FARET,λn are the loss and gain of fluorescence by the donor and the acceptor fluorophores due to FRET, respectively.
As derived in ref. 24, a relationship exists between FDRET,λn and FARET,λn. If one considers the number of FRET events from a donor to an acceptor molecule during the excitation period, NRET, then a fraction of those events, QD, would be detected as photons from the donor molecule, FDRET,λn. This relationship is shown below in eqn (1.2):
Similarly, once transferred to the acceptor molecule, a fraction of those excitation events,
QA, will be detected as photons emitted from the acceptor:
QD and
QA in
eqn (1.2) and (1.3) are the quantum yields of the donor and acceptor fluorophores, respectively. By solving for
NRET and equating
eqn (1.2) and (1.3), we arrive at a general and indispensable relationship between
FDRET,λn and
FARET,λn:
| |  | (1.4) |
The “apparent FRET efficiency” of energy transfer,
Eapp, is a measure of the interaction between the donor and the acceptor. It can be written in terms of “donor quenching” or the loss of fluorescence by the donor due to resonant energy transfer to an acceptor:
| |  | (1.5) |
By solving for
FDRET,λ1 in
eqn (1.1) and substituting into
eqn (1.2), we arrive at the commonly seen equation for the donor-quenched FRET efficiency:
| |  | (1.6) |
Thus, we see that we need an expression for the fluorescence of the donor in the absence of FRET,
FDλ1, in order to calculate the donor-quenched apparent FRET efficiency.
Calculation of FDλ1, the unquenched donor fluorescence in the absence of FRET.
Rearranging eqn (1.1) for FDλ1 gives eqn (1.7):| | | FDλ1 = FDAλ1 + FDRET,λ1 | (1.7) |
Using eqn (1.4), we, express FDRET,λ1 in terms of the ratio of quantum yields of the donor and acceptor, and FARET,λ1, as shown below in eqn (1.8):| | 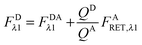 | (1.8) |
By solving eqn (1.1) for FARET,λ1, and inserting into eqn (1.8), we, arrive at the following relation:| | 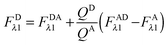 | (1.9) |
The first term, FDAλ1, is determined as shown below in section cotransfected samples and unmixing.
In the literature, the assumption is often made that FAλ1 ≈ 0 and EDqapp is estimated based on this assumption.24 Here we show, however, that FAλ1 can be determined exactly using eqn (1.23) below, derived in section Fluorescent protein solution standards. The exact expression for FDλ1 is:
| | 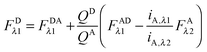 | (1.10) |
where
iA,λ1 and
iA,λ2 are concentration calibration constants, namely the slopes of the acceptor fluorescence
versus concentration calibration curves.
F
A
λ2 is determined using information acquired in an “Acceptor scan” of the sample as described next. Thus, FDλ1 can be calculated exactly using eqn (1.10).
Calculation of FAλ2, the fluorescence of the acceptor in the absence of FRET.
By rearranging eqn (1.1) to solve for FAλ2 and utilizing the fundamental relationship (1.4), we arrive at eqn (1.11) below:| | 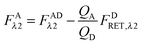 | (1.11) |
We write FDRET,λ2 in terms of the ratios of the donor standard slopes at λ1 and λ2 (see eqn (1.23) in section Fluorescent protein solution standards below), and we obtain eqn (1.12):| | 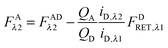 | (1.12) |
By using the fundamental relationship (1.4), we solve for FDRET,λ1 in terms of FARET,λ1 and the ratio of the donor and acceptor quantum yields. Insertion into eqn (1.12) above allows for the quantum yields to cancel, giving eqn (1.13) below:| | 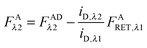 | (1.13) |
Solving for FARET,λ1 in eqn (1.1) and inserting into eqn (1.13) brings us to eqn (1.14):| | 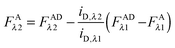 | (1.14) |
Finally, we convert from FAλ1 to FAλ2 using the ratios of the calibration slopes as derived in section Fluorescent protein solution standards, arriving at eqn (1.15):| | 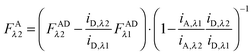 | (1.15) |
FAλ2 in eqn (1.15) is written exactly in terms of quantities that can be measured experimentally.
Eqn (1.15), along with eqn (1.10), provides an approximation-free calculation of FDλ1, and allows for the calculation of EDapp according to eqn (1.6). In addition, eqn (1.15) allows the calculation of the donor and acceptor concentrations, based on their fluorescence and the calibration slopes i of the intensity versus concentration, at the fluorophores' primary excitation wavelengths, as shown in eqn (1.16a) and (1.16b):
| | 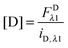 | (1.16a) |
| | 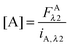 | (1.16b) |
The relevant equations are collected below:
Fluorescent protein solution standards.
The FSI method relies on calibration curves obtained by imaging solution standards of the donor and acceptor fluorophores of known concentration. Given that the total fluorescence from a volume of solution containing excited fluorescent molecules is proportional to the number of fluorescent molecules present in the solution, we can write:25
| | | FFP,B = kFPNFP,B = kFP[FP]BdV | (1.17) |
Here, FFP,B, stands for the total integrated fluorescence emission of the fluorophore (in our case, a fluorescent protein) in a bulk solution. kFP is a proportionality constant that accounts for the dependence of fluorescence on quantum yield, excitation rate and wavelength, and other physical parameters. Eqn (1.17) yields an explicit dependence of the fluorescence from a bulk solution of fluorophores on the concentration of the fluorescent protein and the excitation volume.
The same relationship (1.17) can be written when the fluorophore is attached to a protein of interest, by fusing the gene encoding the fluorescent protein to the gene of interest, with B replaced by S, representing the sample of interest.
| | | FFP,S = kFPNFP,S = kFP[FP]SdV | (1.18) |
Equating the proportionality constant,
kFP, of
eqn (1.17) and (1.18), we obtain
eqn (1.19):
| | 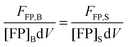 | (1.19) |
Rearranging
eqn (1.19) and solving for the concentration of the fluorescent protein in the sample, we obtain:
| | 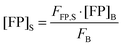 | (1.20) |
Thus, the concentration of the fluorophore in the sample can be calculated from the known concentration and fluorescence intensity of the fluorophore in the bulk solution, and the experimentally determined fluorescence intensity of the fluorescent protein in the sample.
By rearranging eqn (1.20) and adding the subscripts 1 and 2 to represent two different known concentrations of the fluorescent protein solution standards, we arrive at:
By subtracting and rearranging these equations, we obtain
eqn (1.21):
| | 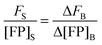 | (1.21) |
In the limit of
Δ→ 0, the ratio of the change in bulk fluorescence to the change in bulk solution standard concentration is replaced by
i, the slope of a line fit to a solution standard fluorescence intensity
versus concentration calibration curve:
| | 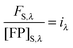 | (1.22) |
Eqn (1.22) allows the calculation of the concentration of the fluorophore in the sample from its fluorescence intensity upon excitation at a specific wavelength. Imaging the same sample at the two different excitation wavelengths,
λ1 and
λ2, and equating the concentrations in
eqn (1.22), yields the following relations:
| | 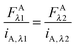 | (1.23a) |
| | 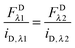 | (1.23b) |
These relations allow the conversion of donor or acceptor fluorescence at one wavelength to the fluorescence at the other excitation wavelength through the ratios of the slopes of the fluorescence calibration curves.
As stated above, the two excitation wavelengths are chosen based on the fluorescence and emission properties of the fluorescent proteins utilized: λ1 is chosen to primarily excite the donor; and λ2 is chosen to maximally excite the acceptor. Several concentrations of soluble fluorescent proteins are imaged at both excitation wavelengths, and a line is fit to the integrated intensity versus concentration data for every pixel of the sample image (see Fig. 1A). The four slopes, iD,λ1, iD,λ2, iA,λ1, and iD,λ2, are calculated for every pixel, for both the donor and acceptor fluorescent protein solution standards, at the two excitation wavelengths, λ1 and λ2.
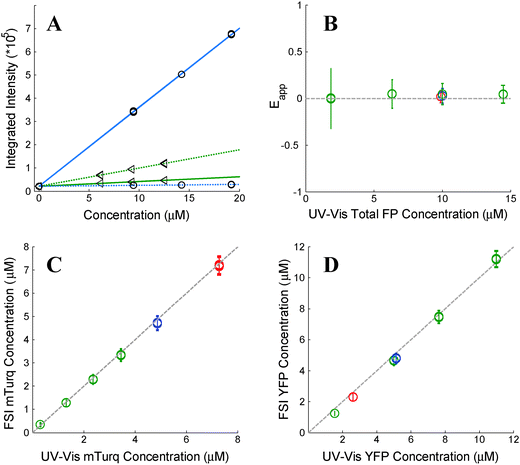 |
| | Fig. 1 Verification of the FSI method. (A) Calibration. Images of soluble donor and acceptor solution standards are acquired for three known solution concentrations, along with images of buffer-only (PBS) controls at two excitation wavelengths, λ1 = 840 nm and λ2 = 960 nm. After integration of the fluorescence over the emission wavelengths, a line is fit to every pixel's integrated intensity vs. concentration solution standard data, yielding the slopes iD,λ1, iD,λ2, iA,λ1, and iD,λ2. The solid and dashed lines are the best fit lines to the measured integrated intensity versus concentration data with excitation at λ1 and at λ2, respectively. The best-fit lines for the donor and the acceptor are shown in blue and green, respectively. (B) FRET Efficiencies measured for mixtures of soluble mTurq and YFP, as a function of total protein concentration. Dashed line: y = 0. (C) Comparison of mTurq concentrations, measured with FSI and NanoDrop. Dashed line: y = x. (D) Comparison of YFP concentrations, measured with FSI and NanoDrop. Dashed line: y = x. Red: 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mTurqiouse 1 mTurqiouse![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) YFP; yellow: 1 YFP; yellow: 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mTurqiouse 1 mTurqiouse![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) YFP; green: 3 YFP; green: 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mTurqiouse 1 mTurqiouse![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) YFP. Dashed lines. YFP. Dashed lines. | |
Donor- and acceptor-only expressing samples.
Donor-only and acceptor-only samples are imaged in order to acquire the donor and acceptor emission spectra as a function of emission wavelength. A large region of a singly-transfected cell membrane is selected and the emission spectra for every pixel are averaged and smoothed over all emission wavelengths.26 The donor and acceptor spectra are then normalized to their maximum value, so that the values range between 0 and 1, providing FD(λ) and FA(λ), which are used for spectral decomposition (unmixing) of pixels in the cotransfected samples, as discussed below. The integrals of these normalized spectra over the emission wavelengths are denoted as wD and wA. The total integrated fluorescence is then calculated by multiplication of the best fit coefficients of the normalized donor and acceptor spectra with their respective wD and wA values (see section cotransfected samples and unmixing below).
We observe that the fluorescence properties of the fluorescent proteins are the same in the cytosol and in PBS buffer. We measure the emission spectra for singly transfected cells in each experiment. The shape of the spectra and the peak emission positions are the same as in spectra measured in buffer with a fluorometer.27
Cotransfected samples and unmixing.
The analysis of the emission spectra from the pixels of a co-transfected cell expressing both the donor and the acceptor fluorophores, excited in a “FRET scan” at λ1, and in an “Acceptor Scan” at λ2, provides the information needed to calculate the concentrations of donor and acceptor fluorophores and the apparent FRET efficiency, Eapp.28 The fluorescence emission spectrum from a pixel of the cotransfected cell at both excitation wavelengths is assumed to be a linear sum of three contributions: the fluorescence of the donor in the presence of the acceptor, FDA(λ), the fluorescence of the acceptor in the presence of the donor, FAD(λ), and a background contribution. This is represented below in eqn (1.24):| | | F(λ)pixelλ1,λ2 = FDA(λ) + FAD(λ) + background(λ) | (1.24) |
We modeled the pixel-level background contribution as a line, as shown below in eqn (1.25).| | | F(λ)pixelλ1,λ2 = kDAλ1,λ2·FD(λ) + kADλ1,λ2·FA(λ) + aλ + b | (1.25) |
Linear least squares optimization yields the “best fit” coefficients i.e., kDAλ1,λ2, kADλ1,λ2, and background (a and b in eqn (1.25)) that minimizes the chi-squared value for the fit.29 The pixel-level integrated intensities of the donor in the presence of the acceptor and of the acceptor in the presence of the donor are then readily calculated, as shown below in eqn (1.26a) and (1.26b):24| | | FDAλ1,λ2 = kDAλ1,λ2·wD | (1.26a) |
| | | FADλ1,λ2 = kADλ1,λ2·wA | (1.26b) |
Verification.
To validate the capabilities of the FSI method to accurately yield pixel-level concentrations and FRET efficiencies, we performed experiments with mixtures of purified mTurqoise and YFP soluble fluorescent proteins. We imaged six different samples, and we acquired four FRET and acceptor images for each sample. In three of these samples, the concentration was held constant (∼10 μM) while the donor (mTurqoise) to acceptor (YFP) ratio was varied. The other three samples contained a fixed donor to acceptor ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) while the total FP concentration was varied from 2 to 14 μM. Concentrations of mTurquoise and YFP in the samples were first measured via UV-Vis spectroscopy using NanoDrop. Next, the solutions were imaged in a FRET scan with excitation at 840 nm and an acceptor scan with excitation at 960 nm in the two-photon microscope. Spectral unmixing and the FSI equations were then used to obtain the FRET efficiencies (Fig. 1B) and the concentrations of mTurqoise and YFP in the sample mixtures (Fig. 1C and D).
3) while the total FP concentration was varied from 2 to 14 μM. Concentrations of mTurquoise and YFP in the samples were first measured via UV-Vis spectroscopy using NanoDrop. Next, the solutions were imaged in a FRET scan with excitation at 840 nm and an acceptor scan with excitation at 960 nm in the two-photon microscope. Spectral unmixing and the FSI equations were then used to obtain the FRET efficiencies (Fig. 1B) and the concentrations of mTurqoise and YFP in the sample mixtures (Fig. 1C and D).
The concentrations of the fluorescent proteins determined with the FSI method are in complete agreement with the fluorescent protein concentrations measurements obtained via UV-Vis absorption measurements. Furthermore, we measure zero concentration dependence on the FRET efficiency, indicating a lack of interactions between the fluorescent proteins. This is expected for three-dimensional solutions of monomeric fluorescent proteins. Changing the excitation wavelength to 800 nm, and thus the amount of intrinsic acceptor excitation during the FRET scan (Fig. 3B), had no effect on the measured concentrations and FRET efficiencies (see ESI,† Fig. S2). Thus, we see that the FSI equations are able to extract the proper fluorophore concentrations over a wide range of total concentrations and donor to acceptor ratios.
2. Implementation
Image acquisition.
Spectral images with two-photon excitation are acquired with a Mai Tai laser (Spectra Physics) and the OptiMis True Line Spectral Imaging system (Aurora Spectral Technologies) utilizing a Zeiss Observer wide field microscope with a 63× NA 1.2 water immersion objective as described in detail in ref. 30. Two images of each cell are acquired: a “FRET scan” with primary donor excitation at 840 nm and an “Acceptor Scan” with primary acceptor excitation at 960 nm. A 35 ms line scan time of full-field (300 × 440 pixels) images is utilized for the spectral image acquisition. Each spectral image requires approximately 15 seconds to acquire at full spectral resolution, with approximately 30 seconds required between scans for two photon laser emission wavelength tuning.
The FSI equations described in the Theory section are implemented in a MATLAB graphical user interface designed with MATLAB's GUI development tool, GUIDE. Linear least squares, or unmixing, is utilized to determine the best-fit kDAλ1,λ2 and kADλ1,λ2 values for the donor and acceptor components of the measured spectrum in every pixel (see Fig. 3).
Noise analysis and image registration are described in ESI.†
Membrane region selection.
Cell images are inspected for membrane regions of uniform diffraction limited fluorescence. The fluorescence of the labeled proteins in the stretched membrane appears as a diffraction limited line that is approximately 600 nm wide (see Fig. 2, bottom). One or two regions of homogenous fluorescence, ∼3 microns in length, are selected from each cell. Under 63× magnification of the microscope objective, the 16 μm pixels of the CCD are square, with a 254 nm side length, as shown in ESI,† Fig. S4. The proper pixels are automatically selected in each region by selecting several points along the path length of the fluorescence. Connecting lines are drawn between these points, and the unit normal vectors to the vectors pointing from point i to point i + 1 are defined. A region half-width of 1.7 pixels is then used to draw a polygon that outlines the fluorescence of the selected region (see ESI,† Fig. S5). With this, a region 3.4 pixels in width is outlined. The masking operation used to select pixels chooses the pixels such that their centers fall within the polygon of the region selected. Thus, the regions selected are 3 to 4 pixels wide, depending on the location and orientation of the line of fluorescence with respect to the CCD array.
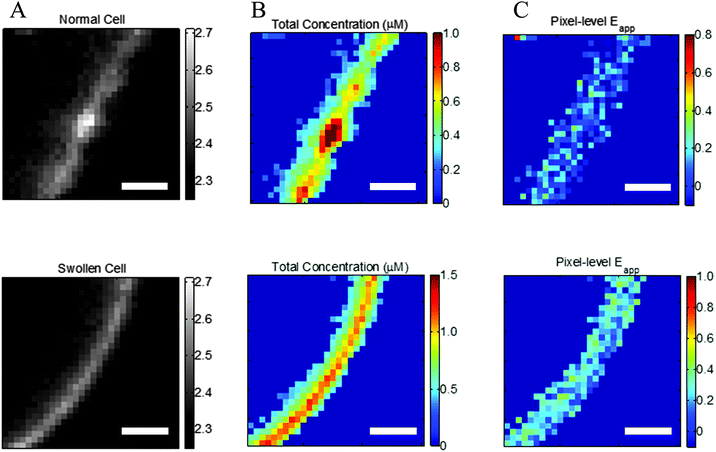 |
| | Fig. 2 Effect of reversible cell swelling on membrane topology and FRET. Top: Intact cell. Bottom: Swollen cell. (A) Selected membrane region. (B) Map of pixel-level total concentrations. (C) Map of pixel-level FRET efficiencies. In the intact cell, there is no correlation between the pixel-level apparent FRET efficiencies and the total concentration, in violation of the law of mass action. Scale bar: 2 μm. | |
Calculation of region-level Eapp and receptor surface densities.
The apparent pixel-level fluorophore (receptor) concentrations calculated during the image analysis must be integrated across the diffraction limited segment in order to properly determine the 2D surface density from the fluorescence and the calibration curves. To do so, FD, FA, and FAD are integrated (summed) over every pixel selected in the region, 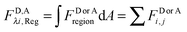 . The apparent FRET efficiency of the region is then calculated as
. The apparent FRET efficiency of the region is then calculated as 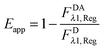 .
.
The total integrated fluorescence intensities for the region, FDλ1,Reg, and FAλ2,Reg, are then divided by the arc length, s, of the selected region to calculate the average integrated fluorescence per unit length of membrane (in units of pixel). We assume a perpendicular orientation of the membrane with respect to the focal plane. We also assume that the fluorescence originates from an infinitely thin sheet within the width of one pixel, or 254 nm. To obtain the fluorescence that would be emitted by a full voxel of chromophores, the integrated fluorescence per unit pixel-length is multiplied by the pixel width, 254 nm. By dividing the full voxel fluorescence by the average slope, 〈iD,Aλi〉, and performing the appropriate unit conversion from micromolar concentrations to receptors per unit area (in units of rec per nm2), the average receptor surface density for the region is calculated, as shown below in eqn (1.27).
| |  | (1.27) |
The need for reversible osmotic stress.
Correct two-dimensional concentrations in the membrane, and thus association curves and association free energies, cannot be determined if the cells are not subjected to reversible osmotic stress. This is consequence of the complex topology of the membrane within a voxel that is nearly a micron thick.31,32Fig. 2A, top, shows a membrane patch from an intact cell, with diffraction limited features clearly visible, whereas Fig. 2A, bottom, shows a membrane patch from a swollen cell. The membrane of the intact cell has a complex topology which is unknown, while the membrane of the swollen cell is perpendicular to the focal plane. The apparent pixel-level concentrations, and the apparent FRET efficiencies, calculated with the FSI method under the assumption that the membrane is perpendicular to the focal plane, are shown in Fig. 2B and C. For the intact cell, we see wide variations in fluorophore concentrations, but no such variations in FRET efficiencies. According to the kinetic theory of FRET, in a dimerizing system, the total fraction of dimers is dependent upon the total concentration of receptors, and thus a higher concentration must necessarily yield higher pixel-level FRET efficiency. The lack of correlation therefore demonstrates that the results for the intact cell have no physical meaning.
To understand the consequence of working with intact cells, about 250 intact cells expressing EC + TM VEGFR2 were imaged and 513 regions of membrane were analyzed. The resultant FRET efficiency versus concentration data is shown in ESI,† Fig. S6, along with the complementary results for swollen cells. In addition to greatly increased scatter and the presence of negative FRET efficiencies, we see that the apparent concentrations appear much higher in intact cells despite the fact that the same protein is being expressed, a consequence of the membrane folds and wrinkles within the voxel thickness. Notably, the range of FRET efficiencies that are physically realistic are similar in the case of intact and swollen cells, suggesting that the interactions between membrane receptors are very similar in both systems. Thus, swelling does not appear to have an effect on membrane protein–protein interactions, but enables measurements of two-dimensional membrane protein concentrations. On the other hand, the use of intact cells yields erroneous concentrations and thus precludes the calculations of association constants for membrane proteins.
3. Interpretation: thermodynamic analysis of apparent FRET efficiencies and concentration measurements
Receptor dimerization and oligomerization.
The FRET efficiencies of oligomers of donor-labeled and acceptor-labeled proteins are calculated using the “kinetic theory of FRET”, as derived by Raicu:33,34| | 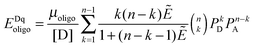 | (3.1) |
In eqn (3.1), n represents the oligomer order. μoligo is the concentration of oligomers. PD and PA are the fractions of donors and acceptors in the oligomer. For large numbers of molecules, these are equal to the fraction of donor and acceptors, respectively: xD and 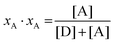 , with [D] and [A] representing the donor and acceptor concentrations, and xD + xA = 1.
, with [D] and [A] representing the donor and acceptor concentrations, and xD + xA = 1.
Eqn (3.1) gives the theoretical apparent donor-quenched energy transfer efficiency for mixtures of monomers and oligomers, assuming an equal donor to acceptor distance for all D–A pairs in the oligomer. For the case of n = 2, a dimer, this is always correct as there is only one donor and one acceptor in the dimer pair. For trimers and above, this is an approximation which minimizes the number of adjustable parameters in the theoretical model for FRET. This approximation is reasonable in our experiments, because the FPs are connected to the TM domains through long flexible GGS5 linkers.
We fit eqn (3.1) for n = 1 to 6, corresponding to the cases of monomer-only, monomer–dimer, monomer–trimer, monomer–tetramer, monomer–pentamer, and monomer–hexamer thermodynamic equilibria, to the experimental data as described below. We calculate the overall mean squared error (MSE) for all oligomer models. The model that yields the lowest mean squared error is the model that best represents the experimental FRET data.
The kinetic model for FRET, however, does not take into account stochastic FRET, or FRET that occurs due to random approach of donors and acceptors in the membrane within distances of ∼100 Å or so.35 Stochastic FRET can represent a significant contribution to the measured FRET efficiency in the case of a monomer–dimer equilibrium, but it decreases significantly as a function of oligomer size. As such, here we correct for stochastic FRET in the dimer case (see ref. 36 for details), but we do not apply a proximity FRET correction for higher order oligomers.
Next we derive the case for a monomer–dimer equilibrium by letting n = 2 in eqn (3.1) above and multiplying by [T]/[T]:
| | 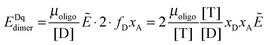 | (3.2) |
The fraction of dimers,
fd, can be written as a function of an equilibrium association constant,
KA, and total receptor concentration, [T],
i.e. fd(
KA, [T]). To do so, we begin by writing down the equation for the fraction of dimers:
| | 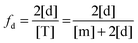 | (3.4) |
Here, [m] is the concentration of monomeric receptors and [d] is the concentration of dimeric receptors. For the two-state monomer–dimer equilibrium, we define the equilibrium association constant,
KA:
| | 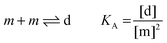 | (3.5) |
First, we solve for the fraction of monomers:
| | 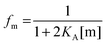 | (3.6) |
Since [T] = [m] + 2[d] = [m] + 2
KA[m]
2, we use the quadratic equation to solve for [m] as a function of the coefficients of the polynomial,
KA and [T]. There are two real roots to this equation, one positive and one negative. We use the positive root as the physical solution.
| | 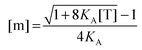 | (3.7) |
| | 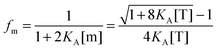 | (3.8) |
By using the relationship
fd +
fm = 1, we solve for the fraction of dimers,
fD, as a function of
KA and [T]:
| | 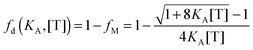 | (3.9) |
FRET for a mixed population of monomers and dimers can be calculated from the dimeric fraction
fd(
KA, [T]) according to
eqn (3.10):
| | | EDqdimer = fD(KA, [T])xAẼ | (3.10) |
To this FRET prediction, we add a contribution for stochastic FRET
36 and complete the theoretical model for the apparent FRET efficiency for the case of a monomer–dimer equilibrium:
| | Eapp,theory,i ≈ E(KA, [A]i)proximity + xA,i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) · ·![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fD(K, [T]i)Ẽ fD(K, [T]i)Ẽ | (3.11) |
Next, we vary the
Ẽ and
K values, and we choose the model which minimizes the MSE as the best model to represent the data. The MSE is calculated according to:
| | 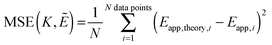 | (3.12) |
We follow the same basic procedure for fitting of higher order oligomerization models, except that there is no proximity FRET correction:
Eapp ≈
EDqoligo. As discussed above, this approximation is justified as the stochastic FRET contribution to the signal decreases significantly as a function of oligomer order.
36
The analytic solutions for the roots become more intractable when n ≥ 3, and there is no analytic solution for the roots of a polynomial greater than order five. Instead of writing down the solution for the fraction of oligomers as a function of total receptor concentration, we utilize a MATLAB root finding function to calculate the roots of the binding polynomial. We take the largest real root as the physical solution to the n'th order polynomial which yields [mi] as a function of KA and [Ti].
The general procedure for n = 3 (trimers) is now described, and the same procedure is applied to tetrameric, pentameric, and hexameric model fitting. For the case of a monomer–trimer equilibrium, the theoretical apparent FRET efficiency is described by letting n = 3 in eqn (3.1).
| | 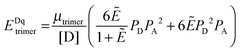 | (3.13) |
Letting
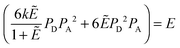
and multiplying the right side by [T]/[T] we have:
| | 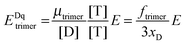 | (3.14) |
Now that we have a theoretical representation for the FRET efficiency, we focus on the fraction of trimers.
| | 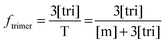 | (3.15) |
Here, [tri] is the concentration of trimeric receptors. Next, we express the fraction of trimers in terms of the equilibrium association constant and the total receptor concentration. For the two-state monomer–trimer equilibrium model, we write:
| |
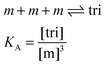
| (3.16) |
Writing the total concentration of macromolecules in terms of
KA and [m] and rearranging the third order polynomial in [m] gives:
| | | 3KA[m]3 + [m] − [T] = 0 | (3.17) |
Next, we use a root-finding algorithm to find the largest positive, real root, [m](
KA, [T]) and write the fraction of trimers as:
| | 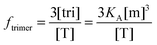 | (3.18) |
Finally, we vary the
E and
KA values, and we calculate the mean squared error as:
| | 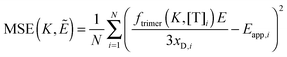 | (3.19) |
Experimental methods
Fluorescent proteins
Soluble monomeric YFP and mTurquoise with an N-terminal 6× His tag were expressed and purified to near-milimolar concentrations as described.27 Fluorescent protein stocks were buffer exchanged into PBS buffer with a 20 kDa MWCO concentrator (Pierce #87751) and filtered with a 0.2 μm syringe filter. For each imaging session, the stocks were then diluted in buffer to micromolar concentrations to produce 100%, 75%, and 50% fluorescent protein solution standards. The mTurquoise and YFP solution standard concentrations were measured in a 1 cm path length quartz cuvette using NanoDrop 2000C (Thermo Scientific). Molar absorption coefficients of 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 mol cm−1 and 30
400 mol cm−1 and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mol cm−1 were used to calculate the concentrations of the solution standards from the YFP and mTurquoise absorption maxima of 514 nm and 434 nm, respectively. Images of the 100%, 75%, 50% FP solution standards and a PBS buffer-only control were acquired at both excitation wavelengths and were used for the calculation of the pixel-level slope values, as described in the Theory section.
000 mol cm−1 were used to calculate the concentrations of the solution standards from the YFP and mTurquoise absorption maxima of 514 nm and 434 nm, respectively. Images of the 100%, 75%, 50% FP solution standards and a PBS buffer-only control were acquired at both excitation wavelengths and were used for the calculation of the pixel-level slope values, as described in the Theory section.
Plasmid constructs
A pBE plasmid encoding for the VEGFR2 signal sequence, extracellular domain, transmembrane domain, a 15 amino acid GGS linker, and yellow fluorescent protein (YFP) was received from Dr Kurt Ballmer-Hofer, Paul Scherrer Institute, and was the starting product for the mutagenesis required for this work. The A206K mutation was introduced into YFP using QuikChange to render it monomeric. The pcDNA 3.1 + VEGFR2-EC-TM-(GGS)5-mTurqoise construct was created by ligating a double-digested PCR insert of the mTurqoise gene between the AgeI and XbaI restriction sites that flank the fluorescent protein sequence, thus replacing YFP with mTurqoise. Ligations were performed with the Roche Rapid DNA Ligation Kit (#11635379001), according to the manufacturer's protocol.
Cell culture and transient transfection
HEK293T cells used for the expression of the VEGFR2-EC-TM-FP plasmid constructs were a kind gift from Dr D. Wirtz, Johns Hopkins University. The cells were cultured in DMEM supplemented with 10% FBS and 20 mM glucose, at 37 °C in a 5% CO2 environment.
Twenty four hours prior to transfection, HEK293T cells were seeded in collagen-coated, glass bottom 35 mm Petri dishes (MatTek, P35GCOL-1.5-14-C) at a density of 2.5 × 105 cells per dish to achieve ∼60 percent confluency at the time of transfection, 24 hours later. Single transfections were performed with a total 3 μg of plasmid DNA and cotransfections were performed with a total 4–9 μg of plasmid DNA, using the Lipofectamine 3000 (Invitrogen) according to the manufacturer's protocol. A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 donor to acceptor plasmid ratio was used in all cotransfection experiments.
3 donor to acceptor plasmid ratio was used in all cotransfection experiments.
We found that the addition of 10 mM sodium butyrate greatly enhanced expression of the pcDNA 3.1 + VEGFR2 EC-TM-(GGS)3-FP construct in HEK293T cells.37,38 Thus, six hours after transfection, 10 mM sodium butyrate was added to the cells. Twelve hours after transfection, the cells were rinsed twice with phenol-red free, serum free DMEM (Sigma, D2902) to remove all traces of phenol red and the cells were serum starved for at least 12 hours in the presence of 10 mM sodium butyrate, prior to the application of osmotic stress and imaging.
Cells under reversible osmotic stress
Hypotonic swelling media was composed of serum-free media, diluted 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 with diH2O, buffered with 25 mM HEPES, and 0.2 μm sterile filtered. Just prior to imaging, the starvation media was aspirated from the Petri dishes and was gently replaced with 1 mL of 37 °C hypotonic swelling media.39 The cells in each dish were allowed to stabilize for at least 10 minutes before imaging, and swollen cell images were acquired for up to two hours per dish post swelling.
9 with diH2O, buffered with 25 mM HEPES, and 0.2 μm sterile filtered. Just prior to imaging, the starvation media was aspirated from the Petri dishes and was gently replaced with 1 mL of 37 °C hypotonic swelling media.39 The cells in each dish were allowed to stabilize for at least 10 minutes before imaging, and swollen cell images were acquired for up to two hours per dish post swelling.
mTurquoise two-photon absorption measurement
The mTurquoise two-photon absorption measurement was performed with the OptiMiS spectral imaging system (Aurora Spectral Technologies) and a Mai-Tai two-photon excitation source (Spectra-Physics) with the output power fixed at 150 mW. Soluble mTurquoise was imaged at excitation wavelengths ranging from 760 nm through 1020 nm, in 20 nm steps. Four spectral images of two separate samples were acquired for each excitation wavelength. A circular region was selected in all images at each excitation wavelength, and the emission spectra were integrated, averaged, and normalized to produce the two-photon absorption spectrum, with respect to mTurquoise emission.
Results
1. VEGFR2 EC + TM forms dimers in the absence of ligand
We use the FSI method to study the lateral interactions between VEGFR2 EC + TM constructs in which the intracellular domain has been substituted with either mTurquoise (mTurq) or YFP, a FRET pair of fluorescent proteins.40,41 The schematic of the constructs, with fluorescent proteins attached to VEGFR2 TM domains via (GGS)5 flexible linkers, is shown in Fig. 3A.
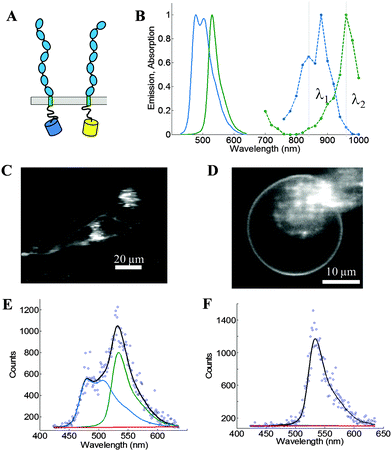 |
| | Fig. 3 The FSI method, applied to VEGFR2 EC + TM in cells under reversible osmotic stress. (A) The VEGFR2 EC + TM constructs used in the experiments. Fluorescent proteins (mTurq and YFP, a FRET pair) were attached to the TM domain via a flexible (GGS)5 linker. (B) mTurq (blue) and YFP (green) spectral properties, with emission shown as solid lines and two-photon absorption shown as dashed lines. The two vertical lines (grey) at 840 nm and 960 nm represent the excitation wavelengths λ1 and λ2 utilized in the FRET and acceptor scans, respectively. (C) HEK293T cells expressing VEGFR2 EC + TM-mTurq and EC + TM-YFP. (D) A HEK293T cell under reversible osmotic stress displays large stretches of homogenous membrane fluorescence. These cells are subjected to spectral imaging at two different infrared wavelengths. The FSI methodology yields approximation-free measurements of the apparent FRET efficiency, the EC + TM-mTurq concentration, and the EC + TM-YFP concentration. (E and F) A single pixel's fluorescence signal (blue circles) in the FRET (E) and acceptor (F) scans is decomposed as a linear sum (black line) of the donor (blue line), acceptor (green line), and background (red line) contributions. | |
Fig. 3B shows the emission and two-photon excitation spectra of mTurq and YFP. The pixel-level emission spectra of VEGFR2 EC + TM-mTurq and VEGFR2 EC + TM-YFP, expressed in HEK 293T cells, are integrated to produce cell images in Fig. 3C.
Measurements of dimer and oligomer stabilities (free energies of oligomerization) in membranes require knowledge of the 2D concentration of the proteins in the membrane and thus, detailed knowledge of membrane topologies and membrane areas.42 The topology of the plasma membrane of cells, however, is very complex because cells possess 2 to 3 times the membrane needed to sustain their shape31,32 (Fig. 3C, see also Fig. 2). It has been shown, however, that the plasma membrane topology can be controlled in a completely reversible and non-lethal manner by subjecting cells to reversible osmotic stress.39 As a result of the osmotic stress, cells disassemble their caveolae (60–80 nm cup-shaped invaginations) and “un-wrinkle” their membranes.39Fig. 3C and D compare the appearance of HEK293T cells, expressing VEGFR2 EC + TM, before and after the application of the reversible osmotic stress. The treatment results in a simple vesicle-like membrane topology,43 such that the 2D area of the membrane at the focal plane can be calculated precisely. Here we use such live cells under reversible osmotic stress to characterize VEGFR2 EC + TM interactions, in conjunction with the FSI method.
Full emission spectra for each pixel are acquired in two scans: a “FRET scan” at λ1, in which the donor, mTurq, is primarily excited (Fig. 3E and 2) an “Acceptor scan” at λ2 in which the acceptor, YFP, is maximally excited (Fig. 3F). The emission spectra are then unmixed to yield the donor and acceptor fluorescence contributions, for each pixel.
We use the integrated pixel-level donor and acceptor fluorescence contributions for both scans (Fig. 3E and F), as well as a pixel-level fluorescence versus intensity calibration (Fig. 1A), to measure the apparent FRET efficiency, as well as the donor and acceptor labeled receptor surface densities, in μm-sized membrane regions of plasma membrane with known topology (shown in ESI,† Fig. S4 and S5). Results for the wild-type VEGFR2 EC + TM are shown in Fig. 4 in blue. Altogether, 1024 regions, ∼3 μm in length, of homogenous membrane fluorescence in 538 HEK293T cells, co-transfected with VEGFR2 EC + TM-mTurq and VEGFR2 EC + TM-YFP, were chosen for analysis. The mole fraction of VEGFR2 EC + TM-YFP (the acceptor-tagged receptors), for each membrane region, is shown in Fig. 4A (blue bars). The average values agree closely with those expected for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 donor-to-acceptor ratio used in transfection. Fig. 4B shows the measured VEGFR2 EC + TM-YFP concentrations versus the measured VEGFR2 EC + TM-mTurq receptor concentrations (blue symbols), for each membrane region. There is a high variability in total receptor expression levels due to transient transfection of the HEK293T cells. In the FSI methodology, this variability is embraced and utilized to ultimately produce binding curves for the receptors. The measured apparent FRET efficiency versus total receptor concentration for wild-type VEGFR2 EC + TM is shown in Fig. 4C (blue symbols). We see that the apparent FRET efficiency increases as a function of the total receptor concentration, suggesting a concentration dependent protein–protein association in the membrane.
3 donor-to-acceptor ratio used in transfection. Fig. 4B shows the measured VEGFR2 EC + TM-YFP concentrations versus the measured VEGFR2 EC + TM-mTurq receptor concentrations (blue symbols), for each membrane region. There is a high variability in total receptor expression levels due to transient transfection of the HEK293T cells. In the FSI methodology, this variability is embraced and utilized to ultimately produce binding curves for the receptors. The measured apparent FRET efficiency versus total receptor concentration for wild-type VEGFR2 EC + TM is shown in Fig. 4C (blue symbols). We see that the apparent FRET efficiency increases as a function of the total receptor concentration, suggesting a concentration dependent protein–protein association in the membrane.
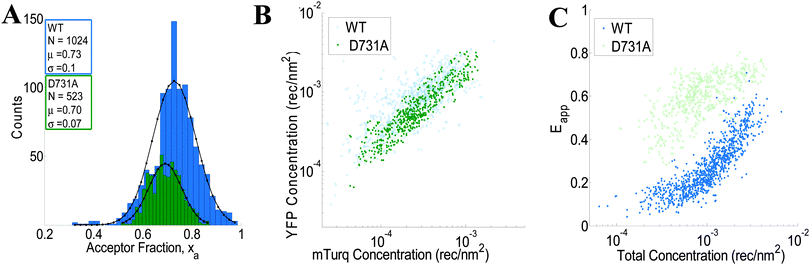 |
| | Fig. 4 FSI data for VEGFR2 EC + TM (blue) and the VEGFR2 EC(D731A) + TM (green) constructs in membrane regions of transiently transfected HEK-293T cells under reversible osmotic stress. (A) Histograms of the measured acceptor fractions, xa, for the wild type and mutant constructs. A Gaussian was fit to each peak, with the mean and standard deviation shown in the box. (B) The measured acceptor-tagged receptor density versus the measured donor-tagged receptor surface density. (C) The measured apparent FRET efficiency versus the total receptor concentration for the VEGF2 EC + TM and the D731A mutant constructs. | |
The wild-type VEGFR2 EC + TM data in Fig. 4 are used to determine the type of oligomer in the membrane (dimer, trimer, tetramer, etc.) that best describes the data. The kinetic theory of FRET33 is used to compute the theoretical apparent FRET efficiency as a function of total concentration for different oligomeric models (e.g., monomer-only, monomer–dimer, monomer–trimer, monomer–tetramer, etc.). These models, which include a contribution for stochastic FRET35,36 were fitted to the data. Theoretical binding curves for a particular oligomeric association model depend on two unknown parameters: the monomer–oligomer association constant K and the Intrinsic FRET, or the pairwise FRET efficiency. The Intrinsic FRET (the pairwise FRET efficiency) is a structural parameter which depends on the average separation between the fluorescent proteins in the oligomer, but not on the association constant, K.42 The least squared error is calculated for each oligomeric model, along with the optimal K and Intrinsic FRET values. The model which gives the lowest mean squared error (MSE) is considered the best overall model to represent the data.
For wild-type VEGFR2 EC + TM, the best-fit is achieved for the monomer–dimer equilibrium model, which yields the lowest overall MSE (Fig. 5A). Fig. 5B compares the measured apparent FRET efficiency and the best-fit theoretical apparent FRET efficiency for VEGFR2 EC + TM. The corresponding dimerization curve is shown in Fig. 5C. With respect to K0 = 1 (rec per nm2)−1, the apparent Gibbs free energy, −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(K/K0), of VEGFR2 EC + TM dimerization is −3.5 ± 0.1 kcal mol−1. The Intrinsic FRET for the donor–acceptor pair in the VEGFR2 EC + TM dimer is 0.85 ± 0.05, corresponding to a donor-to-acceptor distance of 4.1 nm (95% confidence interval: 3.8 to 4.3 nm).
ln(K/K0), of VEGFR2 EC + TM dimerization is −3.5 ± 0.1 kcal mol−1. The Intrinsic FRET for the donor–acceptor pair in the VEGFR2 EC + TM dimer is 0.85 ± 0.05, corresponding to a donor-to-acceptor distance of 4.1 nm (95% confidence interval: 3.8 to 4.3 nm).
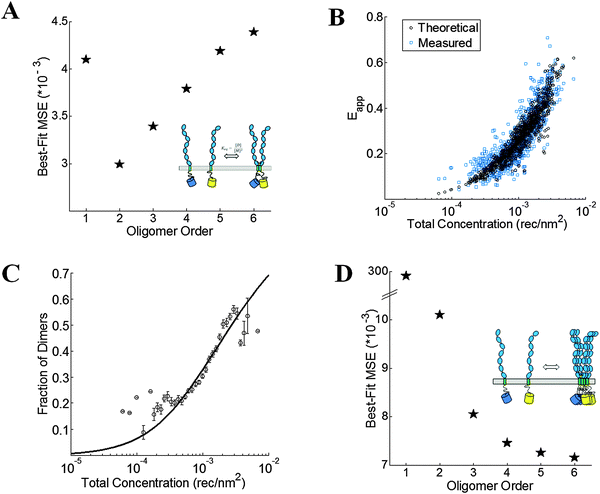 |
| | Fig. 5 VEGFR2 EC + TM forms dimers in the plasma membrane. (A) The minimum mean squared error (MSE) versus oligomer order for monomer-only, monomer–dimer, monomer–trimer, monomer–tetramer equilibria, monomer–pentamer, and monomer–hexamer equilibria for the wild-type. The MSE is the lowest for the dimer model. (B) The measured (blue squares) and best-fit theoretical apparent FRET efficiency (black squares) versus total receptor concentration for the dimer. (C) The dimeric fractions, calculated using eqn (3.3) are binned, and are shown together with the best-fit dimerization curve. (D) The MSE versus oligomer order for the D371A mutant. The lack of a minimum in the MSE vs. oligomer order plot suggests the formation of non-specific large aggregates due to the D371A mutation. | |
2. The D731A mutant forms oligomers in the absence of ligand
The crystal structure of the isolated D7 VEGFR2 EC domains (PDB entry 3KQV) shows a very prominent salt bridge between residues D731 and R726, joining two adjacent molecules in the dimer.19 To study if this salt bridge plays a role in VEGFR2 EC + TM dimer stabilization in the absence of ligand, we introduced a D731A mutation in VEGFR2 EC + TM and measured the self-association of this mutant in the plasma membrane with the FSI method. 278 swollen cells expressing the D731A mutant were imaged, and 523 ∼ 3 μm membrane regions in these cells were analyzed to yield FRET efficiencies, donor concentrations, and acceptor concentrations. The results are shown in Fig. 4 in green. While we expected that the D731A mutation would destabilize the VEGFR2 dimer and thus decrease the FRET efficiencies and dimerization propensity, we instead observed a very large increase in FRET over all receptor concentrations.
Next we sought to determine the type of oligomeric interaction in the membrane that best describes the mutant data. The MSE for tetramers, pentamers and hexamers are all very similar, with no apparent minimum in the MSE as the oligomer order was increased (Fig. 5D). Thus, no single oligomeric model greater than a dimer could be singled out as providing the best fit to the data (Fig. 5D). This FRET signature is likely due to the formation of large aggregates, or due to heterogeneous populations of mutant VEGFR2 oligomers, undergoing non-specific associations. The MSEs for all these oligomers, however, were much smaller than the dimer MSE. Thus, the data analysis indicates that the D731A mutation induced higher-order oligomerization of VEGFR2 EC + TM in the plasma membrane.
Discussion
FSI, a powerful tool in membrane protein research
Membrane proteins have been notoriously difficult to study, especially in the environment of the live cell membrane. Membrane proteins are very hydrophobic, and are not amenable to traditional biophysical characterization techniques developed for soluble, cytosolic proteins.2,3 Crystal structures have been slow to emerge for many membrane proteins,44 and there are no crystal structures of full-length RTK dimers. Thus, most of our knowledge about the structure and function of RTKs comes from investigations of either their isolated soluble domains, their transmembrane portions reconstituted into micelles or bicelles, or through biochemical assays of phosphorylation such as Western Blotting.22,45–48 Here we demonstrate the utility of the FSI methodology to probe membrane protein interactions. Thus, the FSI method augments the arsenal of experimental methodologies that are available to membrane protein researchers.
The primary limitation of the FSI method, as applied to membrane protein association, is that the proteins need to be expressed over a broad concentration range, such that dimer/oligomer binding models can be fitted to the experimental data. High expression, however, is a requirement for many experimental techniques used in protein research, not just the FSI method.
The FSI method offers significant advantages over previous FRET spectral methods.24,28,49,50 First, by adding a second excitation wavelength, FSI expands the set of basic equations introduced earlier, thereby obtaining exact solutions to the donor and acceptor fluorescence in the absence of FRET.24,28,51 Indeed, the FSI approximation-free calculations are possible only upon the acquisition of a FRET spectral image and an acceptor spectral image, at two different excitation wavelengths. The experimentalist has a great flexibility in the choice of fluorophores, as well as in the choice of λ1 and λ2, the two excitation wavelengths. Second, by utilizing calibration curves of fluorescence versus known concentration of donor and acceptor solution standards, we determine true protein concentrations, in this case two-dimensional donor and acceptor surface densities in the plasma membrane. By utilizing the slope of the fluorescence obtained by imaging fluorescent protein solution standards at several known concentrations, we improve on methods that use a single calibration standard imaged at two wavelengths.
Cells under reversible osmotic stress as a model system
The native cell membrane folds into a very complex and irregular surface with many invaginations.31,32,39 As a result of this complex topology, pixel-level fluorescence intensities can vary greatly in neighboring regions of the native cell membrane (Fig. 2B). Thus, a single slice through the focal plane of the cell does not yield information about membrane orientation and topology, and does not allow us to convert the pixel-level fluorescence into to a receptor surface density. The hypotonically swollen cell, however, allows us to determine the two-dimensional protein concentration in the membrane, and to study membrane protein interactions in quantitative terms. The geometry of a swollen cell mimics that of a large, cell-derived vesicle,43 in which we see large stretches of homogenous fluorescence that trace an arc of a sphere. This geometry allows us to assume a perpendicular orientation of the membrane with respect to the focal plane. This assumption is critical for the proper calculation of the receptor surface density in the membrane and without it, receptor concentrations cannot be determined. Yet, the application of the osmotic stress is non-lethal and entirely reversible,39 and thus measurements of free energies of association are performed in live cells.
The experiments in cells under reversible osmotic stress report on the intrinsic propensities of receptor association in the plasma membrane. Thus, in these experiments we extract the fundamental rules that guide the behavior of the receptors. Membrane curvature, lipid domains and other heterogeneities may modulate the local effective concentrations of the receptors. In all cases, however, the dimeric fraction of receptors can be predicted if the local concentrations are known, based on binding curves acquired with the FSI method.
The FSI methodology reveals new knowledge about VEGFR2 interactions in the membrane
Here we sought to investigate the specificity of the 2D interactions between VEGFR2 EC domains in cellular membranes by destabilizing an inter-molecular salt bridge observed in crystal structures of isolated D7 dimers. The mutagenesis of an aspartic acid involved in this interaction, D731, to alanine did not destabilize the VEGFR2 EC + TM dimers, as we expected. Instead, the mutation introduced a very large, surprising perturbation in the receptor interactions, leading to receptor oligomerization. It is curious that engineered VEGFR2 TM domain mutations can also alter the oligomerization state of the isolated TM domain, inducing trimer formation.21 It can be argued, therefore, that mutations that are rationally designed by researchers to interrogate the function of VEGFR2, and RTKs in general, may have similar profound effects that complicate data interpretation.
The large perturbation in interactions, observed here, suggests that the Asp–Arg salt bridge between the D7 domains is important for VEGFR2 dimerization in the absence of ligand, as it ensures that VEGFR2 forms a dimer and not a higher-order oligomer. The mutagenesis therefore reveals that sequence-specific D7–D7 contacts occur in the VEGFR2 EC domain in the absence of ligand. This is fundamentally novel discovery, as D7–D7 interaction are currently believed to occur only upon ligand binding.20 Our understanding of VEGFR2 activation, therefore, is likely incomplete, and deserves further investigation. Here we report on a method that can help the broad scientific community study the association of any RTK, to differentiate between monomers, dimers, or oligomers, and to reveal novel aspects of RTK signaling that have remained well hidden from us, despite many years of fruitful RTK research.
Implications
Therapies that exert control over the activity of VEGFR2 are desperately needed in the clinic. A therapy that inhibits angiogenesis would be applicable to many human cancers, while a pro-angiogenic therapy would be beneficial in ischemia, such as in coronary artery disease, stroke, and chronic wounds.52–54 Here, with the use of the new FSI method, we show that the current paradigm of VEGFR2 activation is incomplete. Thus, the lack of basic knowledge about VEGFR2 dimerization and activation at the molecular level is likely a very significant hurdle to the development of effective treatments that target VEGFR2 signaling. The FSI method, therefore, addresses a large gap in methodology and knowledge that may eventually lead to new therapies that improve human health.
Author contribution
C. K., M. S., and V. R. derived the equations of the FSI method. C. K. developed the image analysis software, the data analysis software, and performed the experiments. C. K and K. H. wrote the paper.
Acknowledgements
Supported by NSF MCB 1157687 and NIH GM068619 (to KH), a NSF Graduate Research Fellowship DGE-1232825 (to CK), and NSF PFI-1114305 and NSF PHY-1058470 (to VR). We thank Dr Ballmer-Hofer for the VEGFR2 EC + TM-(GGS)-YFP plasmid, Dr Sarvenaz Sarabipour for engineering the A206K mutation in YFP, and for creating the VEGFR2 EC + TM-(GGS)-mTurq plasmid, and S. Workman and B. Tsou for help with data analysis.
References
- H. K. B. Simmerman and L. R. Jones, Phospholamban: Protein structure mechanism of action and role in cardiac function, Physiol. Rev., 1998, 78, 921–947 CAS
 .
.
-
H. Hong, N. H. Joh, J. U. Bowie and L. K. Tamm, Methods for Measuring the Thermodynamic Stability of Membrane Proteins, Methods in Enzymology: Biothermodynamics, 2009, pp. 213–236 Search PubMed
 .
.
- E. Li, W. C. Wimley and K. Hristova, Transmembrane helix dimerization: Beyond the search for sequence motifs, Biochim. Biophys. Acta, Biomembr., 2012, 1818, 183–193 CrossRef CAS PubMed
 .
.
- S. H. White and W. C. Wimley, Membrane protein folding and stability: Physical principles, Annu. Rev. Biophys. Biomol. Struct., 1999, 28, 319–365 CrossRef CAS PubMed
 .
.
- J.-L. Popot and D. M. Engelman, Helical membrane protein folding stability and evolution, Annu. Rev. Biochem., 2000, 69, 881–922 CrossRef CAS PubMed
 .
.
- K. R. MacKenzie, Folding and stability of alpha-helical integral membrane proteins, Chem. Rev., 2006, 106, 1931–1977 CrossRef CAS PubMed
 .
.
- M. A Lemmon and J. Schlessinger, Cell Signaling by Receptor Tyrosine Kinases, Cell, 2010, 141, 1117–1134 CrossRef PubMed
 .
.
- J. Schlessinger, Cell signaling by receptor tyrosine kinases, Cell, 2000, 103, 211–225 CrossRef CAS PubMed
 .
.
- W. J. Fantl, D. E. Johnson and L. T. Williams, Signaling by Receptor Tyrosine Kinases, Annu. Rev. Biochem., 1993, 62, 453–481 CrossRef CAS PubMed
 .
.
- C. C. Lin, F. A. Melo, R. Ghosh, K. M. Suen, L. J. Stagg, J. Kirkpatrick, S. T. Arold, Z. Ahmed and J. E. Ladbury, Inhibition of Basal FGF Receptor Signaling by Dimeric Grb2, Cell, 2012, 149, 1514–1524 CrossRef CAS PubMed
 .
.
- S. T. Low-Nam, K. A. Lidke, P. J. Cutler, R. C. Roovers, P. M. van Bergen en Henegouwen, B. S. Wilson and D. S. Lidke, ErbB1 dimerization is promoted by domain co-confinement and stabilized by ligand binding, Nat. Struct. Mol. Biol., 2011, 18, 1244–1249 CAS
 .
.
- I. Chung, R. Akita, R. Vandlen, D. Toomre, J. Schlessinger and I. Mellman, Spatial control of EGF receptor activation by reversible dimerization on living cells, Nature, 2010, 464, U783–U163 CrossRef PubMed
 .
.
- N. Ferrara, H. P. Gerber and J. LeCouter, The biology of VEGF and its receptors, Nat. Med., 2003, 9, 669–676 CrossRef CAS PubMed
 .
.
- M. Shibuya and L. Claesson-Welsh, Signal transduction by VEGF receptors in regulation of angiogenesis and lymphangiogenesis, Exp. Cell Res., 2006, 312, 549–560 CrossRef CAS PubMed
 .
.
- A. K. Olsson, A. Dimberg, J. Kreuger and L. Claesson-Welsh, VEGF receptor signalling – in control of vascular function, Nat. Rev. Mol. Cell Biol., 2006, 7, 359–371 CrossRef CAS PubMed
 .
.
- R. Roskoski Jr., VEGF receptor protein-tyrosine kinases: structure and regulation, Biochem. Biophys. Res. Commun., 2008, 375, 287–291 CrossRef PubMed
 .
.
- S. Koch, S. Tugues, X. Li, L. Gualandi and L. Claesson-Welsh, Signal transduction by vascular endothelial growth factor receptors, Biochem. J., 2011, 437, 169–183 CrossRef CAS PubMed
 .
.
- C. Ruch, G. Skiniotis, M. O. Steinmetz, T. Walz and K. Ballmer-Hofer, Structure of a VEGF-VEGF receptor complex determined by electron microscopy, Nat. Struct. Mol. Biol., 2007, 14, 249–250 CAS
 .
.
- Y. Yang, P. Xie, Y. Opatowsky and J. Schlessinger, Direct contacts between extracellular membrane-proximal domains are required for VEGF receptor activation and cell signaling, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 1906–1911 CrossRef CAS PubMed
 .
.
- C. A. Hyde, A. Giese, E. Stuttfeld, S. J. Abram, D. Villemagne, T. Schleier, H. K. Binz and K. Ballmer-Hofer, Targeting extracellular domains D4 and D7 of vascular endothelial growth factor receptor 2 reveals allosteric
receptor regulatory sites, Mol. Cell. Biol., 2012, 32, 3802–3813 CrossRef CAS PubMed
 .
.
- S. Manni, K. S. Mineev, D. Usmanova, E. N. Lyukmanova, M. A. Shulepko, M. P. Kirpichnikov, J. Winter, M. Matkovic, X. Deupi, A. S. Arseniev and K. Ballmer-Hofer, Structural and Functional Characterization of Alternative Transmembrane Domain Conformations in VEGF Receptor 2 Activation, Structure, 2014, 22, 1077–1089 CrossRef CAS PubMed
 .
.
- C. Finger, C. Escher and D. Schneider, The Single Transmembrane Domains of Human Receptor Tyrosine Kinases Encode Self-Interactions, Sci. Signaling, 2009, 2 CrossRef CAS PubMed
 , ra56.
, ra56.
- B. Grasberger, A. P. Minton, C. DeLisi and H. Metzger, Interaction Between Proteins Localized in Membranes, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 6258–6262 CrossRef CAS
 .
.
- V. Raicu, M. R. Stoneman, R. Fung, M. Melnichuk, D. B. Jansma, L. F. Pisterzi, S. Rath, M. Fox, J. W. Wells and D. K. Saldin, Determination of supramolecular structure and spatial distribution of protein complexes in living cells, Nat. Photonics, 2009, 3, 107–113 CrossRef CAS
 .
.
-
J. R. Lakowicz, Principles of fluorescence spectroscopy, Kluwer Academic/Plenum, 1999 Search PubMed
 .
.
- D. Garcia, Robust smoothing of gridded data in one and higher dimensions with missing values, Comput. Stat. Data Anal., 2010, 54, 1167–1178 CrossRef PubMed
 .
.
- S. Sarabipour, C. King and K. Hristova, Un-induced high-yield bacterial expression of fluorescent proteins, Anal. Biochem., 2014, 449, 155–157 CrossRef CAS PubMed
 .
.
- C. Thaler, S. V. Koushik, P. S. Blank and S. S. Vogel, Quantitative multiphoton spectral imaging and its use for measuring resonance energy transfer, Biophys. J., 2005, 89, 2736–2749 CrossRef CAS PubMed
 .
.
-
W. H. Press, B. P. Flannery, S. A. Teukolsky and W. T. Vetterling, Numerical Recipes, The Art of Scientific Computing, Cambridge University Press, Cambridge, 1989 Search PubMed
 .
.
- G. Biener, M. R. Stoneman, G. Acbas, J. D. Holz, M. Orlova, L. Komarova, S. Kuchin and V. Raicu, Development and Experimental Testing of an Optical Micro-Spectroscopic Technique Incorporating True Line-Scan Excitation, Int. J. Mol. Sci., 2014, 15, 261–276 CrossRef PubMed
 .
.
- J. Adler, A. I. Shevchuk, P. Novak, Y. E. Korchev and I. Parmryd, Plasma membrane topography and interpretation of single-particle tracks, Nat. Methods, 2010, 7, 170–171 CrossRef CAS PubMed
 .
.
- I. Parmryd and B. Onfelt, Consequences of membrane topography, FEBS J., 2013, 280, 2775–2784 CrossRef CAS PubMed
 .
.
- V. Raicu, Efficiency of resonance energy transfer in homo-oligomeric complexes of proteins, J. Biol. Phys., 2007, 33, 109–127 CrossRef CAS PubMed
 .
.
- S. Patowary, L. F. Pisterzi, G. Biener, J. D. Holz, J. A. Oliver, J. W. Wells and V. Raicu, Experimental Verification of the Kinetic Theory of FRET Using Optical Microspectroscopy and Obligate Oligomers, Biophys. J., 2015, 108, 1613–1622 CrossRef CAS PubMed
 .
.
- P. K. Wolber and B. S. Hudson, An analytic solution to the Förster energy transfer problem in two dimensions, Biophys. J., 1979, 28, 197–210 CrossRef CAS PubMed
 .
.
- C. King, S. Sarabipour, P. Byrne, D. J. Leahy and K. Hristova, The FRET signatures of non-interacting proteins in membranes: simulations and experiments, Biophys. J., 2014, 106, 1309–1317 CrossRef CAS PubMed
 .
.
- J. Kruh, Effects of Sodium-Butyrate, A New Pharmacological Agent, on Cells in Culture, Mol. Cell. Biochem., 1982, 42, 65–82 CAS
 .
.
- Y. Soneoka, P. M. Cannon, E. E. Ramsdale, J. C. Griffiths, G. Romano, S. M. Kingsman and A. J. Kingsman, A Transient 3-Plasmid Expression System for the Production of High-Titer Retroviral Vectors, Nucleic
Acids Res., 1995, 23, 628–633 CrossRef CAS PubMed
 .
.
- B. Sinha, D. Koster, R. Ruez, P. Gonnord, M. Bastiani, D. Abankwa, R. V. Stan, G. Butler-Browne, B. Vedie, L. Johannes, N. Morone, R. G. Parton, G. Raposo, P. Sens, C. Lamaze and P. Nassoy, Cells respond to mechanical stress by rapid disassembly of caveolae, Cell, 2011, 144, 402–413 CrossRef CAS PubMed
 .
.
- N. C. Shaner, P. A. Steinbach and R. Y. Tsien, A guide to choosing fluorescent proteins, Nat. Methods, 2005, 2, 905–909 CrossRef CAS PubMed
 .
.
- D. W. Piston and G. J. Kremers, Fluorescent protein FRET: the good, the bad and the ugly, Trends Biochem. Sci., 2007, 32, 407–414 CrossRef CAS PubMed
 .
.
- L. Chen, L. Novicky, M. Merzlyakov, T. Hristov and K. Hristova, Measuring the Energetics of Membrane Protein Dimerization in Mammalian Membranes, J. Am. Chem. Soc., 2010, 132, 3628–3635 CrossRef CAS PubMed
 .
.
- S. Sarabipour, R. B. Chan, B. Zhou, G. Di Paolo and K. Hristova, Analytical characterization of plasma membrane-derived vesicles produced via osmotic and chemical vesiculation, Biochim. Biophys. Acta, 2015, 1848, 1591–1598 CrossRef CAS PubMed
 .
.
- S. H. White, The progress of membrane protein structure determination, Protein Sci., 2004, 13, 1948–1949 CrossRef CAS PubMed
 .
.
- M. S. Brozzo, S. Bjelic, K. Kisko, T. Schleier, V. M. Leppanen, K. Alitalo, F. K. Winkler and K. Ballmer-Hofer, Thermodynamic and structural description of allosterically regulated VEGFR-2 dimerization, Blood, 2012, 119, 1781–1788 CrossRef CAS PubMed
 .
.
- J. K. Nagy, F. W. Lau, J. U. Bowie and C. R. Sanders, Mapping the oligomeric interface of diacylglycerol kinase by engineered thiol cross-linking: Homologous sites in the transmembrane domain, Biochemistry, 2000, 39, 4154–4164 CrossRef CAS PubMed
 .
.
- J. Waltenberger, L. Claessonwelsh, A. Siegbahn, M. Shibuya and C. H. Heldin, Different Signal-Transduction Properties of Kdr and Flt1, 2 Receptors for Vascular Endothelial Growth-Factor, J. Biol. Chem., 1994, 269, 26988–26995 CAS
 .
.
- T. Takahashi, S. Yamaguchi, K. Chida and M. Shibuya, A single autophosphorylation site on KDR/Flk-1 is essential for VEGF-A-dependent activation of PLC-gamma and DNA synthesis in vascular endothelial cells, EMBO J., 2001, 20, 2768–2778 CrossRef CAS PubMed
 .
.
- J. Kim, X. Li, M. S. Kang, K. B. Im, A. Genovesio and R. Grailhe, Quantification of protein interaction in living cells by two-photon spectral imaging with fluorescent protein fluorescence resonance energy transfer pair devoid of acceptor bleed-through, Cytometry, Part A, 2012, 81, 112–119 CrossRef PubMed
 .
.
- D. R. Singh, M. M. Mohammad, S. Patowary, M. R. Stoneman, J. A. Oliver, L. Movileanu and V. Raicu, Determination of the quaternary structure of a bacterial ATP-binding cassette (ABC) transporter in living cells, Integr. Biol., 2013, 5, 312–323 RSC
 .
.
-
S. S. Vogel, P. S. Blank, S. V. Koushik and C. Thaler, Spectral imaging and its use in the measurement of Forster resonance energy transfer in living cells, in Laboratory Techniques in Biochemistry and Molecular Biology, ed. T. W. J. Gadella Jr., 2015, pp. 351–394 Search PubMed
 .
.
- F. Mac Gabhann, A. A. Qutub, B. H. Annex and A. S. Popel, Systems biology of pro-angiogenic therapies targeting the VEGF system, Wiley Interdiscip. Rev.: Syst. Biol. Med., 2010, 2, 694–707 CrossRef CAS PubMed
 .
.
- A. Nessa, S. A. Latif, N. I. Siddiqui, M. A. Hussain, M. R. Bhuiyan, M. A. Hossain, A. Akther and M. Rahman, Angiogenesis-a novel therapeutic approach for ischemic heart disease, Mymensingh Med. J., 2009, 18, 264–272 CAS
 .
.
- T. Matsumoto and L. Claesson-Welsh, VEGF
receptor signal transduction, Sci. STKE, 2001, 2001, re21 CAS
 .
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ib00202h |
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article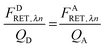
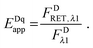
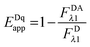
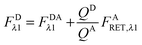
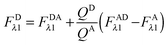
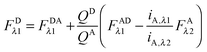
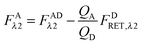
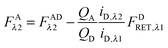
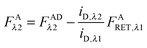
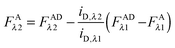
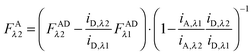
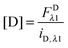
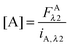
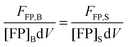
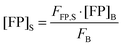
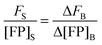
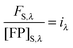
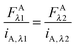
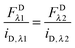
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) while the total FP concentration was varied from 2 to 14 μM. Concentrations of mTurquoise and YFP in the samples were first measured via UV-Vis spectroscopy using NanoDrop. Next, the solutions were imaged in a FRET scan with excitation at 840 nm and an acceptor scan with excitation at 960 nm in the two-photon microscope. Spectral unmixing and the FSI equations were then used to obtain the FRET efficiencies (Fig. 1B) and the concentrations of mTurqoise and YFP in the sample mixtures (Fig. 1C and D).
3) while the total FP concentration was varied from 2 to 14 μM. Concentrations of mTurquoise and YFP in the samples were first measured via UV-Vis spectroscopy using NanoDrop. Next, the solutions were imaged in a FRET scan with excitation at 840 nm and an acceptor scan with excitation at 960 nm in the two-photon microscope. Spectral unmixing and the FSI equations were then used to obtain the FRET efficiencies (Fig. 1B) and the concentrations of mTurqoise and YFP in the sample mixtures (Fig. 1C and D).
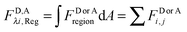 . The apparent FRET efficiency of the region is then calculated as
. The apparent FRET efficiency of the region is then calculated as 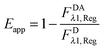 .
.

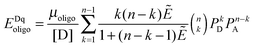
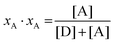 , with [D] and [A] representing the donor and acceptor concentrations, and xD + xA = 1.
, with [D] and [A] representing the donor and acceptor concentrations, and xD + xA = 1.
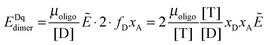
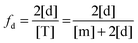
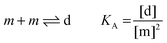
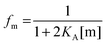
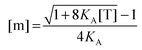
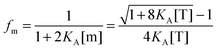
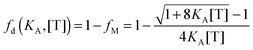
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ·
·![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fD(K, [T]i)Ẽ
fD(K, [T]i)Ẽ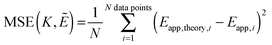
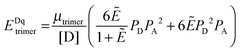
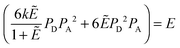 and multiplying the right side by [T]/[T] we have:
and multiplying the right side by [T]/[T] we have: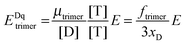
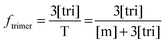
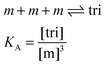
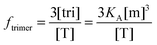
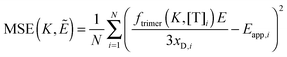
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 mol cm−1 and 30
400 mol cm−1 and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mol cm−1 were used to calculate the concentrations of the solution standards from the YFP and mTurquoise absorption maxima of 514 nm and 434 nm, respectively. Images of the 100%, 75%, 50% FP solution standards and a PBS buffer-only control were acquired at both excitation wavelengths and were used for the calculation of the pixel-level slope values, as described in the Theory section.
000 mol cm−1 were used to calculate the concentrations of the solution standards from the YFP and mTurquoise absorption maxima of 514 nm and 434 nm, respectively. Images of the 100%, 75%, 50% FP solution standards and a PBS buffer-only control were acquired at both excitation wavelengths and were used for the calculation of the pixel-level slope values, as described in the Theory section.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 donor to acceptor plasmid ratio was used in all cotransfection experiments.
3 donor to acceptor plasmid ratio was used in all cotransfection experiments.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 with diH2O, buffered with 25 mM HEPES, and 0.2 μm sterile filtered. Just prior to imaging, the starvation media was aspirated from the Petri dishes and was gently replaced with 1 mL of 37 °C hypotonic swelling media.39 The cells in each dish were allowed to stabilize for at least 10 minutes before imaging, and swollen cell images were acquired for up to two hours per dish post swelling.
9 with diH2O, buffered with 25 mM HEPES, and 0.2 μm sterile filtered. Just prior to imaging, the starvation media was aspirated from the Petri dishes and was gently replaced with 1 mL of 37 °C hypotonic swelling media.39 The cells in each dish were allowed to stabilize for at least 10 minutes before imaging, and swollen cell images were acquired for up to two hours per dish post swelling.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 donor-to-acceptor ratio used in transfection. Fig. 4B shows the measured VEGFR2 EC + TM-YFP concentrations versus the measured VEGFR2 EC + TM-mTurq receptor concentrations (blue symbols), for each membrane region. There is a high variability in total receptor expression levels due to transient transfection of the HEK293T cells. In the FSI methodology, this variability is embraced and utilized to ultimately produce binding curves for the receptors. The measured apparent FRET efficiency versus total receptor concentration for wild-type VEGFR2 EC + TM is shown in Fig. 4C (blue symbols). We see that the apparent FRET efficiency increases as a function of the total receptor concentration, suggesting a concentration dependent protein–protein association in the membrane.
3 donor-to-acceptor ratio used in transfection. Fig. 4B shows the measured VEGFR2 EC + TM-YFP concentrations versus the measured VEGFR2 EC + TM-mTurq receptor concentrations (blue symbols), for each membrane region. There is a high variability in total receptor expression levels due to transient transfection of the HEK293T cells. In the FSI methodology, this variability is embraced and utilized to ultimately produce binding curves for the receptors. The measured apparent FRET efficiency versus total receptor concentration for wild-type VEGFR2 EC + TM is shown in Fig. 4C (blue symbols). We see that the apparent FRET efficiency increases as a function of the total receptor concentration, suggesting a concentration dependent protein–protein association in the membrane.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(K/K0), of VEGFR2 EC + TM dimerization is −3.5 ± 0.1 kcal mol−1. The Intrinsic FRET for the donor–acceptor pair in the VEGFR2 EC + TM dimer is 0.85 ± 0.05, corresponding to a donor-to-acceptor distance of 4.1 nm (95% confidence interval: 3.8 to 4.3 nm).
ln(K/K0), of VEGFR2 EC + TM dimerization is −3.5 ± 0.1 kcal mol−1. The Intrinsic FRET for the donor–acceptor pair in the VEGFR2 EC + TM dimer is 0.85 ± 0.05, corresponding to a donor-to-acceptor distance of 4.1 nm (95% confidence interval: 3.8 to 4.3 nm).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
, ra56.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.