Open Access Article
Open Access ArticleReactive trajectories of the Ru2+/3+ self-exchange reaction and the connection to Marcus' theory
Ambuj
Tiwari
ab and
Bernd
Ensing
*abc
aVan't Hoff Institute for Molecular Sciences, Universiteit van Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands. E-mail: b.ensing@uva.nl
bAmsterdam Center for Multiscale Modeling, Science Park 904, 1098 XH Amsterdam, The Netherlands
cCatalan Institute of Nanoscience and Nanotechnology (ICN2), CSIC and The Barcelona Institute of Science and Technology, Campus UAB, Bellaterra, 08193 Barcelona, Spain
First published on 5th October 2016
Abstract
Outer sphere electron transfer between two ions in aqueous solution is a rare event on the time scale of first principles molecular dynamics simulations. We have used transition path sampling to generate an ensemble of reactive trajectories of the self-exchange reaction between a pair of Ru2+ and Ru3+ ions in water. To distinguish between the reactant and product states, we use as an order parameter the position of the maximally localised Wannier center associated with the transferring electron. This allows us to align the trajectories with respect to the moment of barrier crossing and compute statistical averages over the path ensemble. We compare our order parameter with two typical reaction coordinates used in applications of Marcus theory of electron transfer: the vertical gap energy and the solvent electrostatic potential at the ions.
Introduction
Electron transfer is the fundamental process in reduction and oxidation (i.e. redox) chemistry, taking place for example in metal corrosion, fuel cell reactions, and photo-synthesis. Early pioneering studies of the prototypical self-exchange reaction between two metal ions in aqueous solution, as illustrated by eqn (1),| Mn+ + M*(n+1)+ → M(n+1)+ + M*n+ | (1) |
As with most chemical reactions, the self-exchange reaction is an activated process, in which the system has to surpass a transition state of high (free) energy, which renders direct sampling of an electron transfer reaction in an MD simulation highly improbable. This so-called rare event problem was tackled in the early work by using enhanced sampling techniques, such as umbrella sampling6,7 or free energy perturbation,10 which bias the simulation along an appropriate reaction coordinate, for example the position of the electron.
Unfortunately, it is not so easy to bias the electron transfer process in combination with a quantum-chemical many-electron description of the system, such as with density functional theory (DFT). The reason is that the position of the excess electron, in the reactant state, the product state, or somewhere in between, is governed by the configurational state of the polar solvent environment, which is difficult to capture with a reaction coordinate. The method of constrained-DFT12–14 offers alternatively the possibility to use the electron position as the reaction coordinate, although this constraint also confines the orbital to a certain shape.
Instead, most DFT studies on electron transfer focus on half-reactions. With the half-reaction approach, introduced by Warshel,5,10 and further developed for DFT-MD simulation by Sprik and co-workers,15–20 the redox potential and reorganisation free energy is computed from the average energy needed to add (or remove) an electron to (or from) the system containing only the solvated donor or acceptor species. This approach has been extensively applied to investigate the redox properties of transition metals,16–19,21,22 organic molecules,20,23–25 and proteins26,27 in explicit solvent. However, the half-reaction approach does not provide direct information on the electron transfer between a donor and acceptor species, such as their average distance, as the model only considers one of the two species at once.
We have recently returned to the problem of direct simulation of electron transfer between donor and acceptor species with DFT-MD.28 Using transition path sampling (TPS) simulations,29,30 we can generate an ensemble of reactive trajectories that sample the unbiased dynamics of an electron transfer process. Analysis of the trajectories provides unique information on the transition state ensemble, such as the donor–acceptor distance, the solvent structure in the transition state and the dynamics of the process. Particularly interesting would be an analysis of relevant order parameters or collective variables that correlate with the vertical energy gap, ΔE, which is the reaction coordinate used in Marcus theory. However, direct computation of ΔE is difficult within the DFT-MD simulations, as it requires constraining the position of the electron.
Here, we analyse a DFT-MD/TPS ensemble of reactive trajectories of the self-exchange reaction between a pair of Ru2+ and Ru3+ ions in water solvent. Rather than computing ΔE, we obtain statistics of the energy to insert or delete an electron (ΔEins, ΔEdel) to the system along the reactive trajectory. We first sample these two vertical gap energies for the pair of Ru2+ and Ru3+ ions in an equilibrium simulation to reconstruct the free energy landscape, which we compare to that obtained using the half-reaction approach. We then sample ΔEins and ΔEdel along the reactive trajectories, and compare the sum as a reaction coordinate to the solvent electrostatic potential and an order parameter based on the position of the transferring electron.
In the following, we first briefly summarise the theory of electron transfer as applied in half-reaction simulations, we discuss the issues associated with the use of periodic boundary conditions, and we present the computational details of our combined transition path sampling and DFT-MD simulations. The results are presented in three subsections covering the redox properties obtained with the half-reaction approach, our equilibrium DFT-MD simulations of the pair of Ru2+ and Ru3+ ions in water, and analysis of the reactive trajectories of the electron transfer obtained with TPS. This is followed by the conclusions.
1 Methods
1.1 Theory of electron transfer
At the DFT level of theory, redox properties of ions and molecules in explicit solvent are most conveniently computed using the half-reaction approach, which is based on Marcus' theory of electron transfer and can be connected to the half-reactions that take place in electrochemical cell experiments. The central quantity to be measured is the vertical energy gap, ΔE, which is the energy needed to add (or delete) an electron to (or from) the solute in a given nuclear configuration. This gap energy plays the role of the reaction coordinate and it quantifies the state of the polarised medium when the solute is an ion. In the case of a molecular solute, ΔE also captures the state of the molecule itself. In remarkably many cases (but not always25), the response of both the polarised medium and the molecular solute, as measured by ΔE, is largely linear with respect to the amount of charge loaded to or from the solute.Consider the reduction of an oxidant (O) to a reductant (R),
| O + e− → R, | (2) |
| ΔE = ER(rN) − EO(rN), | (3) |
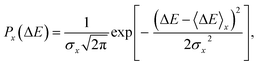 | (4) |
ΔAx(ΔE) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[P(ΔE)], ln[P(ΔE)], | (5) |
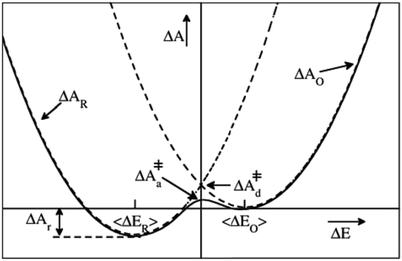 | ||
| Fig. 1 Schematic illustration of a parabolic free energy landscape of electron transfer. The dashed lines depict Marcus' diabatic free energy curves, which cross at the diabatic free energy barrier ΔA‡d. The solid line shows the adiabatic free energy profile, with a somewhat lower barrier ΔA‡a, due to the coupling of the electronic reactant and product states. The difference between ΔA‡d and ΔA‡a is generally much smaller than depicted here. For a half-reaction written in the conventional reduction form (eqn (2)) and the definition of the reaction coordinate, ΔE, from eqn (3), the reaction thus takes place from right to left. | ||
The overall reaction free energy is a particularly simple function of the average gap energies when linear response holds:
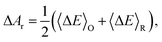 | (6) |
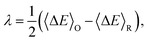 | (7) |
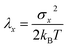 | (8) |
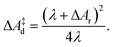 | (9) |
In practice, the diabatic free energy curves are computed by sampling ΔE along two equilibrium DFT-MD simulations; one in the oxidised state where the energy needed to add an electron is computed and one in the reduced state in which the energy to delete an electron is sampled. In Section 2.1, we will set the stage by applying this approach to compute the redox properties of the Ru2+/Ru3+ couple, which can be compared to the extensive studies on this system by Blumberger and Sprik.17–19,22,31
As pointed out in the introduction, the half-reaction framework cannot be so easily applied to study directly the full reaction, i.e. the electron transfer reaction between a donor molecule and an acceptor molecule. In the full reaction case, ΔE would be the energy to bring the electron from the donor to the acceptor at a fixed configuration. This ΔE can be decomposed into two terms: (1) the energy needed to delete the electron from the donor, ΔEdel, and (2) the energy needed to insert the electron at the acceptor, ΔEins. The first term is easy to compute as long as the transferring electron resides at the highest occupied orbital (HOMO) of the system. But the second term cannot be computed with ground-state DFT without additional constraints, since the electron would return to the donor in the electronic ground-state. Of course, we can compute the energy needed to insert an electron at the acceptor before removing the electron from the donor, ΔEins,before, but that energy would contain an additional interaction energy of the inserted electron with the other electron still at the donor, plus higher order terms in a polarisable environment.
If we consider this additional electron interaction as a correction to the ΔEins,before term, the ΔE of moving an electron from donor to acceptor at a given nuclear configuration can thus be computed using the half-reaction technique of inserting an electron and deleting an electron:
| ΔE = ΔEdel + ΔEins + Ucorr. | (10) |
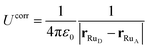 | (11) |
1.2 Periodic boundary conditions and finite size effects
One of the complications of DFT-MD simulations of molecular processes in condensed materials, and in particular of half-reactions in aqueous solution, is related to the rather small size of the systems and the periodic boundary conditions to mimic the extended phase. The long-range electrostatic interactions are computed using Ewald summation, which is of course almost always much better than using a cutoff, but is nevertheless not without its own issues. The problem is that the half-reaction approach is typically applied to systems that are not neutral, and, moreover, the method requires the calculation of energy differences between systems that carry different charges.Although in principle a charged system embedded in infinite arrays of periodic copies would have an infinite energy, Ewald summation removes the divergent term in a manner that is commonly interpreted as adding a uniformly smeared out background charge. The density of the background charge is −q/L3 and thus depends on the box size, L. The charged system interacts with the background charge so that the energy of the system contains a “self-interaction” term that is a function of the box size and shape. For a charged particle in a cubic cell, this (Wigner) self-interaction is:
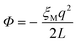 | (12) |
For a charged particle dissolved in a polar medium such as water, it turns out that the self-interaction energy is largely compensated by the screening of the solvent, effectively reducing this L−1 dependent term by a factor of 1/ε, with ε the dielectric constant, which is approximately 80 for ambient water. The L−1-dependence of the solvent comes from the repulsion of the polarised solvent in the unit cell with that in the periodic images, which solvate the periodic image of the charged particle in their own cell, rather than the original ion.
Although the L−1-dependent self-interaction is thus largely canceled in a high-dielectric solvent, higher order terms in L remain that arise from the finite size of the ion, which creates a cavity with a radius R in the medium in all periodic images. The total energy difference due to (Ewald) periodic boundary conditions (PBC) with respect to that of a continuum Bohr model19,34,35 (B) is:
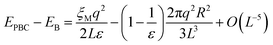 | (13) |
In the half-reaction approach presented above, the reaction free energy, ΔAr (eqn (6)), and the reorganisation free energy, λ (eqn (7)), are computed from sampled energy differences, ΔE, of the system with and without an extra charge. Sprik et al. found that for ΔAr the box size dependence is dominated by the L−3 term, whereas λ scales as L−1. Blumberger and Lamoureux showed that for the full electron transfer reaction, in which the electron moves from donor to acceptor, the box size dependence of the reorganisation free energy is much less severe. This is perhaps not surprising, since in that case only the dipole is changed, but not the total charge.22
The dipole term depends on the distance between the donor and the acceptor. In Fig. 2, we show the P(ΔEET) (top panel) and the free energy curve computed with eqn (5) (bottom panel) computed with simple force field MD simulations of a pair of Ru2+ and Ru3+ aqua complexes, constrained at different donor–acceptor distances, d, ranging from 6 to 14.5 Å, solvated in 1000 water molecules in a cubic box with L = 31.04 Å. As expected, the curves show a clear dependence on the donor–acceptor distance.
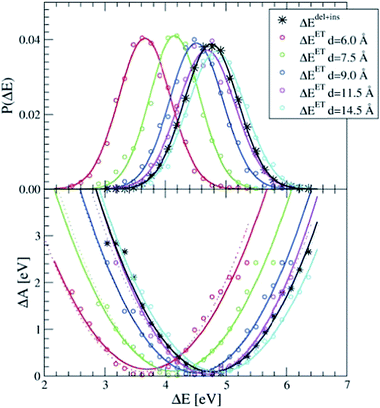 | ||
| Fig. 2 The apparent dependence on the distance between the Ru2+ and Ru3+ ions of the energy gap probability (top) and the free energy curves (bottom) computed with force field MD simulations. The curves obtained from ΔEdel+ins (in black) are not distance dependent. The lines are Gaussian (top) and parabolic (bottom) fits through the measured data (circles). Dashed lines in the bottom panel are computed by adding to ΔEdel+ins the Ucorr term of eqn (10) as explained in the text. | ||
The black curves in Fig. 2 were computed using the insertion–deletion scheme, with ΔEdel+ins = ΔEdel + ΔEins, i.e. the first two terms of eqn (10), which are, within the statistical accuracy, independent of the Ru–Ru distance. The missing Ucorr term of eqn (10) can be computed as the difference in ΔEdel+ins between a system containing the two ruthenium point charges (without solvent) with, and without, periodic boundary conditions. Adding this to the ΔEdel+ins indeed recovers perfectly the ΔEET curves, as shown by the dotted lines in the bottom panel of Fig. 2.
For the DFT-MD simulations that we discuss hereafter, the box size dependence and the Ucorr term also contain contributions due to the instantaneous electronic polarisation. The aim of this work, however, is not to obtain quantitative numbers for the redox properties, but rather, to connect the reaction coordinates used in Marcus theory and the half-reaction method to our equilibrium and TPS simulations of the full electron transfer reaction.
1.3 Transition path sampling
We use an adapted 2-way TPS algorithm of shooting and shifting moves to generate reactive trajectories, starting from an initial path obtained from a biased MD simulations as explained hereafter. Here, reactive trajectory refers to a trajectory that starts in the stable reactant state and ends in the stable product state, or vice versa. The shooting move proceeds in the usual way. That is, each new trajectory starts from a randomly chosen configuration from the previous trajectory, by adding small perturbations to all atomic momenta, and performing two MD simulations, one forward and one backward (by reversing all velocities) in time (hence, “2-way TPS”). The shooting move is accepted if the new trajectory connects the reactant and product states, or rejected otherwise. The perturbations are done by adding random momenta from a 5 Kelvin Maxwell–Boltzmann distribution to the original momenta, removing any total momentum, and rescaling to the original temperature. This resulted in an average acceptance ratio of the shooting move of 0.46. Instead of the original shifting move, we locate the configuration on the previous trajectory that is closest to halfway for the electron transfer process. The shooting configuration was subsequently chosen from a fixed number of saved restart files ranging from 1000 MD steps (i.e. 500 fs) before and after this central time frame. By using this fixed number of restart files to randomly choose the shooting configuration from, the TPS algorithm obeys detailed balance. The actual trajectory length was not fixed however, and ranged typically between 2 and 3 ps.The initial reactive trajectory was obtained from a 1 ps constrained MD simulation that started from an equilibrated system, in which the six ruthenium–oxygen distances of the hexaaqua Ru2+ complex were forced to decrease by 0.3 Å. By the time that the constrained coordination shell becomes smaller than that of the (free) Ru3+ complex, an electron is expelled from the Ru2+ complex and taken up by the Ru3+ complex soon after. A second constrained simulation was initiated from a frame just after the forced electron transfer took place, in which the six Ru–O distances were kept constant. This second trajectory was used to generate initial unconstrained reactive trajectories, by applying the TPS shooting move but without perturbing the nuclear momenta.
The stable reactant and product states are defined by the numbers of d-electrons at each of the ruthenium ions; six on one and five on the other, or vice versa. Counting the number of electrons is conveniently done by transforming the occupied orbitals into maximally localised Wannier functions36,37 (MLWFs) and computing the distances of the MLWF centers to each of the Ru ions. The MLWFs are computed every 10 MD steps on-the-fly along each TPS trajectory. We define as an order parameter:
| ξET = (dRu–X − dRu′–X)/dRu–Ru′, | (14) |
The TPS algorithm of generating reactive trajectories described here was implemented using a bash script that would launch the forward and backward DFT-MD simulations (further detailed below), accept or reject the trajectories, choose a new starting configuration, perturb the momenta, and launch the next simulations, and so forth.
1.4 Density functional theory-based molecular dynamics
The DFT-MD simulations were performed using the CP2K software package.38 The electronic structure part of CP2K, called QUICKSTEP,39 uses the combined Gaussian and plane-wave (GPW) method40 for the calculation of forces and energies. The GPW method is based on the Kohn–Sham formulation of density functional theory and employs a hybrid scheme of Gaussian and plane wave functions. First principles simulations with CP2K sample directly the Born–Oppenheimer surface.In the DFT-MD simulations, the norm-conserving pseudopotentials of Goedecker et al. (GTH)41 were applied to replace the core electrons. We employed the BLYP42,43 exchange–correlation functional, augmented with Grimme's D2 dispersion correction44,45 to include van der Waals interactions. The BLYP-D level of theory has been extensively used and tested by the scientific community for the description of various structural and dynamical properties of liquid water and aqueous solutions (see e.g.ref. 46 and 47), including the Ru2+/3+ redox couple.17 The Gaussian basis set consisted of a double-zeta valence basis set with a single set of polarisation functions (DZVP) optimised for the use with the GTH pseudopotentials. A charge density cutoff of 280 Ry was used for the auxiliary plane-wave basis set. For the plane-wave grid, we applied the nearest neighbour smoothing operator NN10. A CSVR thermostat48 with a time constant of 500 fs was used to generate an NVT ensemble. The temperature was set to 300 K. Periodic boundary conditions were applied to a cubic box with an edge length of 12.4138 Å for the simulations with two Ru ions and 64 water molecules. For the single ion with 32 water molecules, the box dimension was 9.86 Å. The simulations here were carried out on the Dutch national supercomputer Cartesius using 24 processors in parallel.
2 Results
We first compute the redox properties of the Ru2+/Ru3+ couple using the half-reaction approach. Next, we investigate the pair of aqueous Ru2+ and Ru3+ ions in equilibrium. Thirdly, we analyse the reactive trajectories of the self-exchange reaction harvested with TPS.2.1 Redox properties using the half-reaction approach
The Ru2+/Ru3+ redox couple was one of the first systems to which Sprik and co-workers applied their half-reaction approach. Here we present the same redox properties computed with the CP2K program at the BLYP+D2/DZVP/280 Ry level of theory for a single ion with 32 water molecules in a cubic box with an edge of L = 9.86 Å subject to periodic boundary conditions. Two equilibrium DFT-MD simulations were performed, one of Ru2+ and one of Ru3+, with a length of 10 ps, of which the last 5 ps were used to sample ΔE.The P(ΔE) distributions are shown in the top-panel of Fig. 3. The histograms of ΔE, shown by the circles are fitted very well by Gaussian functions (solid lines), as expected, however, the widths of the two distributions, measured by σ, are not exactly the same. The Ru2+/Ru3+ system is known to obey Marcus linear response theory rather well,17–19,22,31 so the deviation seen here must be due to statistical errors.
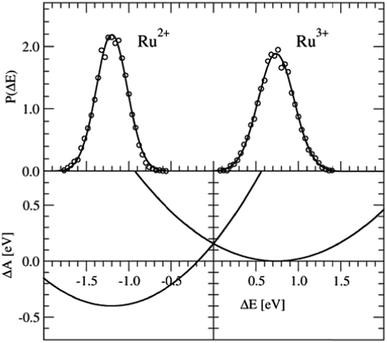 | ||
| Fig. 3 Top panel: Vertical energy gap distributions for the Ru3+ + e− → Ru2+ half-reaction. The circles show the histogram values obtained from the simulation data; the solid lines are Gaussian fit functions. Bottom panel: Free energy curves obtained from the Gaussian functions using eqn (5). | ||
The derived redox properties are compiled in Table 1. The uneven standard deviations of ΔE in the oxidised and reduced states leads to a significant discrepancy between λO and λR. We have previously seen that the fluctuations in ΔE are easily underestimated in the rather short DFT-MD simulations, and that λ computed from the averages (eqn (7)) is the safer estimate for the reorganisation free energy.25 Our results are in reasonable agreement with the early work of Blumberger and Sprik, although in that work an external chemical potential was applied to enforce alignment of the minima of the parabolic curves, and the parabola were fitted to the combined O and R data-sets resulting in a more symmetric free energy landscape.
2.2 Free energy curves of the combined Ru2+ and Ru3+ ions
Four independent DFT-MD simulations were performed for a pair of Ru2+ and Ru3+ ions solvated by 64 water molecules in a cubic box with L = 12.41 Å subject to periodic boundaries. These simulations had different starting configurations, but they had in common that in all cases the Ru3+ complex was deprotonated. From two of the simulations, we removed at the start the excess proton from the solvent, yielding a total charge of +4 for the system. The other two systems had a charge of +5. In the latter, the extra proton diffused through the solvent via the Grotthuss mechanisms, and was not seen to jump back onto the deprotonated ruthenium complex during the simulation. Rather than adding explicit counter ions, which would make the sampling more cumbersome, the system has a neutralising uniform background counter-charge via the Ewald summation, as further detailed in the Methods section. The simulations had a length of 50 ps, of which the last 30 ps were used for analysis.Fig. 4 shows in the top panel the distributions, P(ΔEdel) (red curve), P(ΔEins) (blue), and P(ΔEdel+ins) (black). The solid lines are Gaussian functions fitted to the histograms of the data, which are shown in circles for the system without the solvated proton. The fitted Gaussian functions are also shown for the system with the excess proton, with dashed lines, to illustrate that the computed distributions are remarkably independent from the total charge of the system; apart from a small deviation between the blue curves, the distributions obtained from the two systems are, considering the statistical uncertainty, equal to each other.
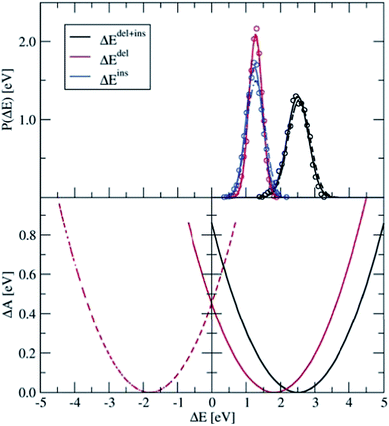 | ||
| Fig. 4 Top panel: Distributions of ΔEdel, ΔEins, and ΔEdel + ΔEins, computed for the Ru2+ + Ru3+ system (circles), which are fitted by Gaussian functions (lines). The solid lines show the results for the 4+ charged system, from which the excess proton was removed; the dashed line shows the results for the 5+ charged system. Bottom panel: Parabolic free energy curve obtained from the Gaussian fit function (solid black line) using eqn (5) and the final free energy curves (red) that are shifted based on λdel+ins as explained in the text. | ||
The distribution of the energy needed to insert an electron at the Ru3+ ion is somewhat broader than that of the energy needed to delete an electron at the Ru2+ ion. This trend is in agreement with what we found earlier for the PO(ΔE) and PR(ΔE) distributions with the half-reaction approach (see Fig. 3), although this is probably a coincidence. The more plausible cause for the different widths is the different coordination shells of the Ru2+ and Ru3+ ions here, the former being coordinated by six water ligands whereas the latter contains five water ligands and one hydroxo ligand. This difference between the oxidised and reduced Ru ions could indeed cause such a non-linear effect.
The first and second moments of the distributions, together with the derived reorganisation free energies are listed in Table 2. The average energy to delete an electron from the system is in perfect agreement with −〈ΔER〉 of the half-reaction (Table 1) and also σ matches very well. However, this must be somewhat fortuitous, considering the different box sizes and the effect that the nearby Ru3+ complex must have in the current case of the full reaction. Also σins is in excellent agreement with σO of the half-reaction, however the average 〈ΔEins〉 is significantly shifted with respect to 〈ΔEO〉. This discrepancy is mainly due to the different coordination shells between the Ru3+ complexes, which contain a hydroxo ligand in the current full reaction case, while for the half-reaction none of the water ligands were deprotonated.
The lower panel of Fig. 4 shows the parabolic free energy profile obtained from the P(ΔEdel+ins) distribution, using eqn (6) (solid black line). Note however, that this profile is shifted with respect to that of the actual electron transfer from Ru2+ to Ru3+, as we did not include the correction term, Ucorr, from eqn (10). But since ΔAr = 0 for the self-exchange reaction, the average 〈ΔE〉 must equal λdel+ins. Here we neglect the fluctuation part of the correction term, which is expected to be small. In Fig. 4, the shifted free energy curve is shown in red, together with its counterpart of the reverse electron transfer reaction (red dashed). The obtained reorganisation free energy, λdel+ins = 1.73 eV is in reasonable agreement with earlier estimates using constrained-DFT (1.62 eV),31 static quantum-chemistry methods (1.95 eV),49 and experimental measurement (2.0 eV).50 Finally, the diabatic free energy barrier for the Ru2+/Ru3+ self-exchange reaction is computed with eqn (9) to be ΔA‡d = 0.43 eV.
2.3 Transition path sampling
We employed the TPS technique in combination with DFT-MD to generate in total eight sequences of reactive trajectories of the self-exchange reaction between a Ru2+ ion and a Ru3+ ion in water. During the initial constrained MD simulations to generate an initial path (as explained in the Method section), not only an electron transferred, but also a proton was donated by one of the aqua ligands of the Ru3+ complex to the solvent. The first four TPS sequences were generated with this proton in the water solvent. The second four TPS sequences were generated after removal of the solvated proton. The first seven sequences contain 50 reactive trajectories. A typical “path tree” of such a sequence is shown in Fig. 5. The eighth sequence contained 180 (accepted) paths. The acceptance ratio over all paths was 0.46. The simulation length of each forward or backward path ranged from 0.5 to 1.5 ps, as seen from the path tree.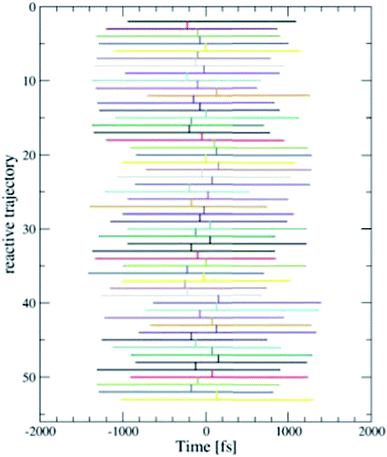 | ||
| Fig. 5 One of the eight TPS “path trees”, showing the length of each path and the shooting time where the next path branches off a previous one. Only the accepted paths are shown. | ||
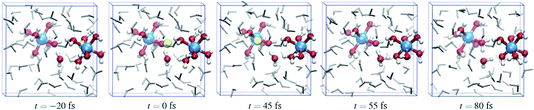
Fig. 6 shows a cartoon of snapshots from a representative reactive trajectory. The octahedrally coordinated ruthenium complexes are shown in ball-stick representation (Ru is blue, O is red, and H is white), while the other solvent water molecules are shown as grey sticks. In the first panel the Wannier center is seen, as a yellow sphere, to depart from the Ru2+ ion. The Ru3+ complex on the left side has five water ligands and one hydroxo ligand, which points toward the electron donor complex and is hydrated by a solvent water molecule also drawn in ball-stick representation. In the second panel, the Wannier center is halfway between the donor and acceptor complexes, and 45 fs later the electron is taken up by the acceptor species in panel 3. Panels 4 and 5 show the subsequent proton transfer from the (hitherto) Ru2+ complex to the acceptor complex, via a bridging solvent water molecule.
The distance between the Ru ions fluctuates around 7 Å. The electron transfer is in all reactive trajectories accompanied by the proton transfer, in no preferential order (as should be expected by time-reversibility). Further details of this proton-coupled electron transfer mechanism are discussed in a separate publication;28 instead here we will focus on how we can connect the reactive trajectories of the adiabatic electron transfer to the redox quantities from Marcus theory.
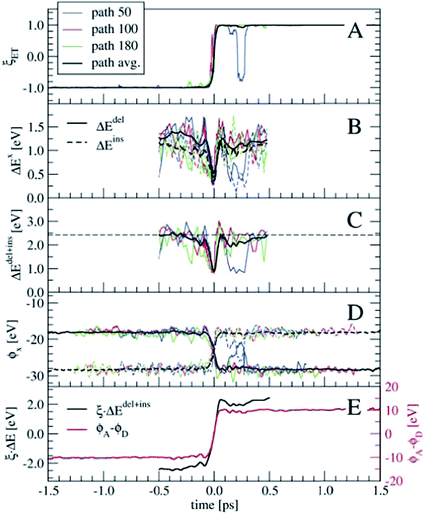
In order to perform a statistical analysis over the TPS sequences of reactive trajectories, we have to align the trajectories by time. We take the moment of electron transfer in each path as the zero of the time scale, which we compute by fitting the reaction coordinate values ξET (see eqn (14)) along each trajectory by the switch function f(t) = tanh[a × (t − t0)], with the parameter t0 defining the moment of electron transfer. Fig. 7 shows ξET, which quantifies the position of the Wannier center, for three trajectories. Also the average ξET over the sequence of 180 paths is shown (black line). The blue line shows a reactive event in which the electron recrossed back toward the donor and again to the acceptor moiety. However, such barrier recrossings are rather scarce in this electron transfer process. Seen from the average ξET, the actual electron transfer, that is, passing from the reactant state definition to the product state definition takes about 102 fs.
Having aligned the trajectories, statistics of other order parameters can be obtained from the TPS ensemble. Panels B and C of Fig. 7 show ΔEdel, ΔEins, and ΔEdel+ins, computed from t = −0.5 to t = 0.5 ps. The fluctuations seen in the three individual path traces are very large just before and after the electron transfer event, however around t = 0 they all show a clear spike toward zero. Only for a few trajectories the ΔE values are zero at t = 0, which probably means that our time resolution was not fine enough to see this in the other trajectories. The horizontal dashed line in panel C denotes the average 〈ΔEdel+ins〉 = 2.42 eV from the equilibrium simulation (see also Table 2), which is an indication that our relatively short 2–3 ps trajectories indeed connect the stable reactant and product states, and do not sample only the top region of a free energy barrier.
Another interesting property, already suggested by Marcus, is the solvent electrostatic potential, ϕx, x = (D, A) acting on the donor (D) and acceptor (A) ions respectively. These potentials are shown in panel D of Fig. 7. Here, the potentials are approximated by summing the classical Coulomb interaction over all solvent nuclei and associated Wannier centers using the minimum image convention and neglecting the long-range part. The electrostatic potentials are remarkably symmetric with respect to their switching at t = 0. Note that all these order parameters show clearly the barrier recrossing event in path 50 (blue lines) in agreement with the Wannier center position.
Both the ΔEdel+ins and ϕx quantities can be used as reaction coordinates for the electron transfer process. The ΔEdel+ins parameter does not by itself distinguish between the reactant and product states, as it does not change sign unlike the original ΔE. This can be remedied by keeping track of which of the Ru ions is involved in the electron deletion and insertion processes. Alternatively, the ΔEdel+ins can be multiplied with ξET, which is shown in panel E in Fig. 7 (black line, left-hand-side axis) for the averaged quantities. For the electrostatic potential, we take the difference between ϕA and ϕD, which is also shown in panel E (red line, right-hand-side axis). Both these combined order parameters switch smoothly from the reactant state to the product state, crossing zero at t = 0.
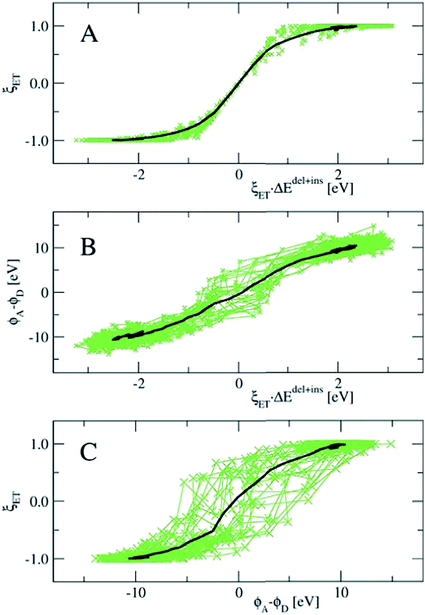
In Fig. 8, we show the correlation between the three order parameters, by projecting 18 reactive trajectories, taken from the long sequence at an interval of 10, as green points and lines in pairs of the order parameters. The gap energy ΔEdel+ins, multiplied with ξET, is shown versus the Wannier center position, ξET, in the top panel, and versus the solvent potential difference, ϕA − ϕD, in the middle panel. The bottom panel shows ϕA − ϕDversus ξET. Starting with the top panel, we notice that there is a strong correlation between the gap energy and the Wannier center position, and that their relation is not linear. Since ΔE captures the linear response of the solvent polarisation to the amount of charge displaced, the latter being quantified here by ξET, this is somewhat surprising. Note however, that ξET is obtained from the sampling of adiabatic electron transfer events only (see also Fig. 1, in which the adiabatic profile deviates from the parabolic curves near the barrier). If diabatic electron transfer events could have been included in the statistics of ξET at gap energies left and right from the center at ΔE = 0, the curve would have been more straight.
Note also that the fluctuations seen in ΔE in the reactant and product states (i.e. at ξET = −1 and ξET = 1 respectively) disappear at ξET = 0. In other words, not only the average gap energy is zero at barrier crossing, but the gap energy for all reactive trajectories is zero at barrier crossing. However, since ΔE (i.e. the solvent polarisation) governs the electron position, and not the other way around, this means that a simulation in which the electron position is fixed in the middle, ΔE would exhibit the same fluctuations as it would in the reactant or product state, whereas, vice versa, a simulation at fixed ΔE = 0, would show very little fluctuations in the electron position.
Panel B in Fig. 8 shows that there is a good, almost linear, correlation between ΔE and the difference in solvent electrostatic potential. However, the correlation with ξET in panel C clearly shows that this potential difference does not uniquely determine the electron position. This could be caused by the approximate nature of the calculation of the electrostatic potential order parameters here, using pairwise sums over nuclei and Wannier center distances, but it could also mean that other interactions play a role. For example, we found that the correlation of ΔE with the solvent electrostatic potential computed using the atomic Mulliken charges would significantly improve when this electrostatic potential was multiplied by a factor depending on the amount of charge transfer from the Ru ion to the aqua ligands in each configuration (data not shown).
3 Conclusions
We have used transition path sampling combined with first principles DFT-MD simulations to investigate the proton-coupled electron transfer reaction taking place between a pair of ruthenium(II/III) ions in aqueous solution. Until now, the main approach to study this prototypical self-exchange reaction at the DFT level of theory was by means of the half-reaction approach. Here, we first applied this approach to construct the diabatic free energy landscape and compute the overall reaction and reorganisation free energies, based on Marcus' linear response theory of electron transfer. Next, we performed equilibrium DFT-MD simulations of a pair of donor and acceptor ions in solution. As it is not possible for the full reaction to sample the vertical gap energy, ΔE, of transferring the electron from the donor ion to the acceptor ion, the gap energy was probed indirectly as the sum of the energy needed to delete an electron from the donor ion, ΔEdel, and the energy required to insert an electron at the acceptor ion, ΔEins. This allowed us to compute the free energy profiles of the full diabatic electron transfer reaction.The reactive trajectories generated with DFT-MD/TPS remain always in the electronic ground-state, and thus sample the adiabatic electron transfer landscape. To define the stable reactant and product states, we used as the order parameter, the position of the center of a maximally localised Wannier function associated with the transferring electron. The moment of barrier crossing along each path was set as the reference of the time scale to align the paths and compute averages over the paths. In particular, we have computed the ΔEdel+ins along the electron transfer reaction and also the solvent electrostatic potential at the ruthenium ions, both of which are important ingredients in Marcus' theory of electron transfer.
Correlating the Wannier center position with ΔEdel+ins shows that there is a one-to-one mapping between the order parameters in the neighbourhood of the transition state, where both order parameters pass through zero. This means that the electron position is strictly governed by the value of ΔEdel+ins when it is close to zero. The relation between these two order parameters was surprisingly non-linear however, which we believe to be due to the sampling of only adiabatic electron transfer events. Instead the correlation of the difference between the electrostatic potential at the ruthenium ions shows fluctuations in the electrostatic potential that are not different during electron transfer with respect to that in the stable states. This suggests that the solvent electrostatic potential difference is not a very good reaction coordinate for electron transfer, as it does not determine strictly the amount of electron transfer.
Acknowledgements
This work is part of the Industrial Partnership Programme (IPP) ‘Computational sciences for energy research’ of the Foundation for Fundamental Research on Matter (FOM), which is part of the Netherlands Organisation for Scientific Research (NWO). This research programme is co-financed by Shell Global Solutions International B.V. The calculations were carried out on the Dutch national e-infrastructure with the support of the SURF Cooperative.References
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 979–989 CrossRef CAS.
- R. A. Marcus, Discuss. Faraday Soc., 1960, 29, 21–31 RSC.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 679–701 CrossRef CAS.
- A. Warshel, J. Phys. Chem., 1982, 86, 2218 CrossRef CAS.
- J. K. Hwang and A. Warshel, J. Am. Chem. Soc., 1987, 109, 715 CrossRef CAS.
- R. A. Kuharski, J. S. Bader, D. Chandler, M. Sprik, M. L. Klein and R. W. Impey, J. Chem. Phys., 1988, 89, 3248–3257 CrossRef CAS.
- E. A. Carter and J. T. Hynes, J. Phys. Chem., 1989, 93, 2184–2187 CrossRef CAS.
- M. Tachiya, J. Phys. Chem., 1989, 93, 7050–7052 CrossRef CAS.
- G. King and A. Warshel, J. Chem. Phys., 1990, 93, 8682 CrossRef CAS.
- J. S. Bader, R. A. Kuharski and D. Chandler, J. Chem. Phys., 1990, 93, 230–236 CrossRef CAS.
- Q. Wu and T. Van Voorhis, Phys. Rev. Lett., 2005, 72, 024502 Search PubMed.
- H. Oberhofer and J. Blumberger, J. Chem. Phys., 2009, 131, 064101 CrossRef PubMed.
- T. Van Voorhis, T. Kowalczyk, B. Kaduk, L.-P. Wang, C.-L. Cheng and Q. Wu, Annu. Rev. Phys. Chem., 2010, 61, 149–170 CrossRef CAS PubMed.
- I. Tavernelli, R. Vuilleumier and M. Sprik, Phys. Rev. Lett., 2002, 88, 213002 CrossRef PubMed.
- J. Blumberger, L. Bernasconi, I. Tavernelli, R. Vuilleumier and M. Sprik, J. Am. Chem. Soc., 2004, 126, 3928–3938 CrossRef CAS PubMed.
- J. Blumberger and M. Sprik, J. Phys. Chem. B, 2005, 109, 6793–6804 CrossRef CAS PubMed.
- J. Blumberger and M. Sprik, Theor. Chem. Acc., 2006, 115, 113–126 CrossRef CAS.
- R. Ayala and M. Sprik, J. Chem. Theory Comput., 2006, 2, 1403–1415 CrossRef CAS PubMed.
- F. Costanzo, M. Sulpizi, R. G. D. Valle and M. Sprik, J. Chem. Phys., 2011, 134, 244508 CrossRef PubMed.
- P. H.-L. Sit, M. Cococcioni and N. Marzari, Phys. Rev. Lett., 2006, 97, 028303 CrossRef PubMed.
- J. Blumberger and G. Lamoureux, Mol. Phys., 2008, 106, 1597–1611 CrossRef CAS.
- J. VandeVondele, R. Lynden-Bell, E. J. Meijer and M. Sprik, J. Phys. Chem. B, 2006, 110, 3614–3623 CrossRef CAS PubMed.
- J. Cheng, M. Sulpizi and M. Sprik, J. Chem. Phys., 2009, 131, 154504 CrossRef PubMed.
- M. Kılıç and B. Ensing, J. Chem. Theory Comput., 2013, 9, 3889–3899 CrossRef PubMed.
- J. Blumberger and M. L. Klein, J. Am. Chem. Soc., 2006, 128, 13854 CrossRef CAS PubMed.
- J. Blumberger, Phys. Chem. Chem. Phys., 2008, 10, 5651 RSC.
- B. Ensing, Manuscript submitted.
- P. G. Bolhuis, D. Chandler, C. Dellago and P. L. Geissler, Annu. Rev. Phys. Chem., 2002, 53, 291–318 CrossRef CAS PubMed.
- C. Dellago and P. G. Bolhuis, Mol. Simul., 2004, 30, 795–799 CrossRef CAS.
- H. Oberhofer and J. Blumberger, Angew. Chem., 2010, 122, 3713–3716 CrossRef.
- F. Figueirido, G. S. Del Buono and R. M. Levy, J. Chem. Phys., 1995, 103, 6133 CrossRef CAS.
- G. Hummer, L. R. Pratt and A. E. García, J. Phys. Chem., 1996, 100, 1206–1215 CrossRef CAS.
- G. Hummer, L. R. Pratt and A. E. García, J. Chem. Phys., 1997, 107, 9275–9277 CrossRef CAS.
- P. H. Hünenberger and J. A. McCammon, J. Chem. Phys., 1999, 110, 1856–1872 CrossRef.
- N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Rev. Mod. Phys., 2012, 84, 1419 CrossRef CAS.
- A. Ambrosetti and P. L. Silvestrelli, Introduction to Maximally Localized Wannier Functions, in Reviews in Computational Chemistry, ed. A. L. Parrill and K. B. Lipkowitz, John Wiley & Sons, Inc, Hoboken, NJ, 2016, vol. 29, ch. 6 Search PubMed.
- The CP2K developers group, http://www.cp2k.org.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477–488 CrossRef CAS.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- J. Schmidt, J. VandeVondele, I.-F. W. Kuo, D. Sebastiani, J. I. Siepmann, J. Hutter and C. J. Mundy, J. Phys. Chem. B, 2009, 113, 11959–11964 CrossRef CAS PubMed.
- M. J. Gillan, D. Alfè and A. Michaelides, J. Chem. Phys., 2016, 144, 130901 CrossRef PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- F. P. Rotzinger, J. Chem. Soc., Dalton Trans., 2002, 719–728 RSC.
- P. Bernhard, L. Helm, A. Ludi and A. E. Merbach, J. Am. Chem. Soc., 1985, 107, 312–317 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |