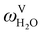DOI:
10.1039/C6FD00041J
(Paper)
Faraday Discuss., 2016,
192, 337-390
On the use of molecular-based thermodynamic models to assess the performance of solvents for CO2 capture processes: monoethanolamine solutions
Received
7th March 2016
, Accepted 15th April 2016
First published on 15th April 2016
Abstract
Predictive models play an important role in the design of post-combustion processes for the capture of carbon dioxide (CO2) emitted from power plants. A rate-based absorber model is presented to investigate the reactive capture of CO2 using aqueous monoethanolamine (MEA) as a solvent, integrating a predictive molecular-based equation of state: SAFT-VR SW (Statistical Associating Fluid Theory-Variable Range, Square Well). A distinctive physical approach is adopted to model the chemical equilibria inherent in the process. This eliminates the need to consider reaction products explicitly and greatly reduces the amount of experimental data required to model the absorber compared to the more commonly employed chemical approaches. The predictive capabilities of the absorber model are analyzed for profiles from 10 pilot plant runs by considering two scenarios: (i) no pilot-plant data are used in the model development; (ii) only a limited set of pilot-plant data are used. Within the first scenario, the mass fraction of CO2 in the clean gas is underestimated in all but one of the cases, indicating that a best-case performance of the solvent can be obtained with this predictive approach. Within the second scenario a single parameter is estimated based on data from a single pilot plant run to correct for the dramatic changes in the diffusivity of CO2 in the reactive solvent. This parameter is found to be transferable for a broad range of operating conditions. A sensitivity analysis is then conducted, and the liquid viscosity and diffusivity are found to be key properties for the prediction of the composition profiles. The temperature and composition profiles are sensitive to thermodynamic properties that correspond to major sources of heat generation or dissipation. The proposed modelling framework can be used as an early assessment of solvents to aid in narrowing the search space, and can help in determining target solvents for experiments and more detailed modelling.
1 Introduction
Carbon dioxide (CO2) emissions play a major role in climate change and particularly in global warming. Fossil fuel power plants are the major fixed point-source emitters of CO2. In response to the threat posed by global warming, the Roadmap for 2050 set by the European Commission in 2011 suggested a reduction of greenhouse gas emissions in Europe to 25% by 2020 and to 80% by 2050.1 In the recent Paris climate conference (COP21), an agreement was made between participating parties to cut greenhouse gas emissions to a level that limits the global average temperature to “well below” 2 °C above pre-industrial levels and to “pursue efforts to limit the temperature increase to 1.5 °C”.2 In this context, the development of carbon capture systems must be addressed in the short term, and amine-based post-combustion capture processes are seen as the most promising near-term technology in terms of development and applicability, e.g. see Mac Dowell et al.3 In this technique, absorption is achieved both physically and chemically, so that significant CO2 removal can take place even at challenging low partial pressures of the greenhouse gas. The major advantage of this technology is that it can be retrofitted to existing power plants.
There are however several concerns with this technology, in particular the large energy requirements associated with solvent regeneration, the degradation of the solvent, which is exacerbated by the presence of oxygen in the flue gas, and the environmental and health impact that may result from solvent losses and solvent degradation products. These issues are particularly important because of the scale of deployment required to have a meaningful impact on CO2 emissions. There are significant experimental programmes to identify new solvents4–12 and several pilot-plant studies are under way.13–21 Modelling studies can play an invaluable and complementary role in addressing some of these issues, including the choice of solvent and operating conditions that yield optimal performance.
A key challenge in realising the benefits of a model-based design approach is the development of models that can accurately predict the behaviour of the CO2 capture process under different conditions and for a range of solvents. This is particularly difficult in the case of CO2 absorption due to the complex reaction chemistry that occurs and the large number of ionic species present in the process. For example, in the case of absorption of CO2 using the most common solvent, an aqueous solution of monoethanolamine (MEA, HOC2H4NH2), the key reactions are:22–28
| CO2 + HOC2H4NH2 ⇌ HOC2H4NH2+CO2− |
| HOC2H4NH2+CO2− + HOC2H4NH2 ⇌ HOC2H4NHCO2− + HOC2H4NH3+ |
| HOC2H4NH2+CO2− + H2O ⇌ HOC2H4NHCO2− + H3O+ |
| HOC2H4NHCO2− + H2O ⇌ HOC2H4NH2 + HCO3− |
| HOC2H4NH2+CO2− + H2O ⇌ HOC2H4NH3+ + HCO3− |
| HOC2H4NH2+ + H2O ⇌ HOC2H4NH2 + H3O+ |
The main overall reaction products are therefore the zwitterion (HOC
2H
4NH
2+CO
2−), the carbamate (HOC
2H
4NHCO
2− + HOC
2H
4NH
3+), and bicarbonate (HCO
3−).
Given the complexity of the underlying chemical and physical phenomena, detailed models of the thermodynamics, kinetics, and process units relevant to the absorption systems have been developed for the simulation, optimisation, and design of CO2 capture processes for a given solvent, as for example in the work of Kucka et al.,29 Zhang et al.,30 and Kale et al.31 The elucidation and characterization of the speciation, reaction mechanism, equilibria, and kinetics for mixtures relevant to CO2 chemisorption are required before detailed models can be developed, and this necessitates extensive experimental investigation. The types of data that are required include data specific to the solvent involved, such as reliable physicochemical (e.g. vapour–liquid equilibrium (VLE) and liquid-phase speciation) and kinetic (including reaction rate constants and diffusion coefficients) data, and information regarding the effect of the column specifications, for instance the type of packing material employed. This presents a significant barrier to the rapid development of improved processes for carbon capture.
To overcome this difficulty, the task of identifying solvents that lead to improved CO2 absorption processes can be subdivided into two main steps. The first is the rapid identification of a list of promising solvents by assessing a wide solvent search space as fully as possible, analyzing key performance indicators that relate closely to process performance, energetics, environmental impact, and solvent degradation. To minimize the reliance on experimental data and accelerate the search for new solvents, models that make it possible to predict physical and chemical properties from molecular structure are highly desirable. The motivation for this first step is to reduce the number of solvents to be considered in more detail, and the models used should therefore offer broad predictive capabilities, which may require making simplifying assumptions in the model development. In the second step, promising solvents can be further analyzed and some of the assumptions made in the first step can be re-assessed. Once a list of candidate solvents is obtained, experiments can be conducted on a subset of these solvents, with the aim of obtaining the information required for a more detailed evaluation of each solvent and the corresponding carbon dioxide process.
To explore the space of possible solvents, there is a need to develop models that offer adequate predictive capabilities without exhaustive reliance on experimental data, and that can provide a quantitative insight into the behaviour of the process; the use of a thermodynamic model to capture the phase and chemical equilibria of mixtures of carbon dioxide, water, and alkanolamine within a process model is investigated in our current paper, as a means of obtaining an estimate of the performance of the absorption. As an initial assessment of the method, we focus on MEA because as a ubiquitous solvent for CO2 capture there is extensive experimental data available to test the validity of the predictions. Before presenting the model, we first place the proposed approach in the context of other modelling work in the area.
There is an extensive body of literature concerning the modelling and simulation of CO2 absorption in packed columns. The modelling approaches that have been proposed to date differ in the choice of thermodynamic and kinetic models, and, where appropriate, heat- and mass-transfer models. Most of the effort has been focused on the performance of aqueous monoethanolamine solutions, due to their widespread industrial use and the availability of pilot-plant data, although there have been some models developed for other solvents, notably aminomethylpropanol (AMP).16,32–35 In modelling an absorber, the column is usually divided into hypothetical stages, each representing a (sometimes infinitesimal) section of packing in the column.36,37 Each stage can be modelled using either an equilibrium or a rate-based model. In an equilibrium model, vapour–liquid equilibrium is assumed at each stage, everywhere on the stage. A rate-based model accounts for heat- and mass-transfer limitations. For chemisorption processes with fast reaction kinetics, as is the case for the process of interest,28,38 a rate-based process is more reliable. Indeed, Lawal et al.39 have compared the two approaches using the same physical property model and concluded that the rate-based model provides a better description of the pilot-plant14 temperature profiles where aqueous MEA was used as a solvent. A similar comparison was made by Afkhamipour and Mofarahi35 for CO2 absorption in AMP solution, and a rate-based model was found to give a better representation of the temperature and composition profiles of the pilot-plant runs.13
When using a rate-based approach, an important aspect in model development is the choice of approach to treat heat- and mass-transfer phenomena. The concentration and temperature profiles across hypothetical films in a two-film model can be imposed, taking into account the effect of chemical reactions on mass transfer with an enhancement factor, defined as the ratio of the amount of gas absorbed in a reacting liquid to the amount which would be absorbed if there were no reaction.40–42 The enhancement factor varies along the length of the column and can often be adjusted to pilot-plant data. This is the route followed in most models of CO2 absorption (e.g. Tontiwachwuthikul et al.,13 Sivasubramanian et al.,43 Pintola et al.,44 Pacheco and Rochelle,45 Al-Baghli et al.,46 Tobiesen et al.,47 Faramarzi et al.,48 Khan et al.,49 Neveux et al.,50 Saimpert et al.,51 Jayarathna et al.,52 Afkhamipour and Mofarahi53). A comparative review of the rate-based models that have been used to specifically treat CO2 absorption in aqueous MEA solutions can be found in ref. 54.
As an improvement on the standard film theory, Tobiesen et al.47 developed a penetration model, where the two films at the interface are described continuously, which was found to describe their own pilot-plant data well. A more rigorous approach is that followed by Kucka et al.,29 in which the Maxwell–Stefan formalism is used together with a discretization of the film. This more detailed model leads to better predictions of the concentration and temperature profiles at the pilot-plant scale13 than other models, without the need to adjust any parameters to pilot-plant data.29 The Maxwell–Stefan formalism has also been applied by Lawal et al.55 and Biliyok et al.56 Kale et al.31 have investigated a rate-based model with film discretization, and studied the sensitivity of the calculations to several key parameters. They found that good predictions of column profiles can be obtained with a sufficiently fine discretization.
In all rate-based models, empirical mass-transfer correlations are required to account for the type of packing used and the operating conditions. The correlations of Onda et al.57,58 and Bravo and Fair59 were developed specifically for random packing, whereas the correlations of Rocha et al.60 were developed for structured packing, but can be applied to random packing by using an equivalence relation linking the random packing characteristics to the structured packing. Correlations developed by Billet and Schultes61 are also available as they apply to both structured and random packing. In a detailed comparison applied to a model of a CO2 capture pilot plant presented by Faramarzi et al.,48 it appears that the main operating conditions to consider when choosing a mass-transfer correlation are the flow rates of the flue gas and the lean solvent.
Another important consideration in modelling CO2 absorption is the representation of the chemical reactions and fluid-phase equilibria of the mixture of MEA, CO2 and H2O. In the earliest absorber models, the thermodynamics of the gas and liquid phases were described with the assumption of ideal gas and ideal solution behaviour. This is the case for example of the model developed by Pandya62 and later used by Tontiwachwuthikul et al.13 However, this model was too simplified to describe the complex interactions between the CO2 and the solvent, and may not be suitable when transferred to other solvents. Two different approaches are typically followed when developing more accurate models of mixtures exhibiting reaction equilibria: those based on physical theories and those based on chemical theories. Most commonly, a chemical approach (e.g. see refs 30 and 63–67) is adopted. In such approaches, all of the reaction species in solution are modelled explicitly, requiring the a priori specification of the relevant reaction schemes and their corresponding temperature-dependent equilibrium constants. Hence, the use of a chemical approach requires experimental data on the concentration of species in solution at various temperatures.
Most models proposed to date that specifically treat CO2–amine–H2O systems are based on this class of chemical approach; an explicit treatment of the major ionic and non-ionic species formed due to reaction is adopted. Such methods rely on the use of reaction kinetics and equilibrium constants derived from experimental data specific to each reaction.29,30,68–73 The methodology of combining the electrolyte-NRTL (eNRTL) approach68,74 with a Henry's constant to describe CO2 solubility has attracted much interest and has been used in recent studies.55 The eNRTL approach has also been corrected for inconsistencies by Bollas et al.75 More recently, Zhang et al.30 developed a detailed model of the CO2–MEA–H2O amine system using a chemical approach: an eNRTL66 model was developed for the treatment of the liquid phase, the perturbed chain statistical associating fluid theory (PC-SAFT)76 was used to obtain the vapour phase fugacity coefficients, and Henry's law constants were obtained to provide a full description of the phase equilibria. While this approach arguably provides the most accurate representation of the behaviour of these mixtures to date, a major drawback of these models is that they contain a large number of parameters, requiring ample experimental data for VLE and reaction kinetics, thus making it difficult to use for different conditions and solvents. A similar approach29 is to combine the Soave–Rechlich–Kwong (SRK) equation of state (EoS)77 with the eNRTL model. Tobiesen et al.47 have adapted an activity coefficient model from Hoff78 to correlate VLE experimental data, using an experimentally-derived equilibrium constant.79 In order to reduce the number of parameters to be determined and the computational effort needed to solve the vapour–liquid equilibrium, Gabrielsen et al.80 developed their own thermodynamic model to determine the VLE of MEA, CO2 and H2O. They proposed a simple correlation derived from experimental data of CO2 solubility in aqueous MEA, which is valid for MEA over the conditions considered: in this case CO2 loading (defined as the number of moles of CO2 per mole of MEA in the liquid phase) varied from 0 to 0.5 at 313 K and 393 K. As a simplification, a single chemical equilibrium reaction (carbamate formation) was considered, reducing the number of adjustable parameters required.
The combined reaction and activity coefficient models developed to date provide an accurate representation of CO2–MEA–H2O systems over a range of conditions. However, extensive parameterization is required and the model parameters obtained are not transferable to other solvents. These models are therefore more suited for their application in step two of the solvent selection process, the detailed quantitative analysis of the performance of the most promising solvents.
An alternative treatment of reactions follows a physical approach. Such approaches have previously been proposed to model the phase and chemical equilibria of mixtures of alkanolamines, CO2, and H2O.81–84 This methodology is based on a version of the molecular statistical associating fluid theory (SAFT) EoS,85,86 in which a square-well intermolecular potential of variable range is used (SAFT-VR).87,88 More recently,89,90 models for aqueous solutions of CO2 and primary alkanolamine have been developed within a group contribution re-formulation of the SAFT-VR EoS (SAFT-γ SW),91,92 where a similar physical treatment of reactions was applied. In these approaches, the reaction products are considered as associated aggregates of the reactants and are not modelled as independent chemical species. Aggregation is driven by short-range association sites incorporated in the molecular models, by means of appropriate site–site interactions. Appropriate association schemes are chosen in order to form the desired reaction products (e.g. carbamate, zwitterion, etc.). In the SAFT approach, the concentration of each aggregated species in the mixture can be determined from the fraction of association sites that are not bonded.93 In cases where chemical equilibrium can be assumed and under some appropriate approximations (e.g. a constant site–site binding energy), such an approach has been shown to be equivalent to the chemical models used to date in which the aggregated chemical species are modelled explicitly.94 The equivalence of the chemical and physical approaches means that the parameters within SAFT can be related to the experimental equilibrium constant. The thermodynamic properties of the mixture can thus be determined by specifying the concentration of the reactants, the pressure, temperature, and the parameters describing the interactions between reactant species (including the types, number, energy, and bonding volume of association sites). The physical approach applied to CO2 and aqueous MEA has been found to provide excellent predictions of the concentration of the key reaction products.84,90 Physical approaches are particularly well-suited to the exploration of a wide solvent space in that models can be developed entirely from experimental VLE data (e.g. vapour pressure and saturated liquid density) and no data on energetics or speciation are required. In addition, parameters can often be transferred from one compound to another compound on the basis of similarities in molecular chemistry, and the resulting predictions are found to be valid over wide ranges of compositions, temperatures, and pressures. These characteristics make SAFT-VR models, which are based on a physical representation of chemical equilibrium, a suitable platform for the exploration of a large space of solvent candidates. While the evaluation of potential solvents can be carried out on the basis of thermodynamics alone, it would be more valuable to obtain an evaluation of each solvent based on performance metrics that relate to a specific absorption process; this possibility is investigated in our current work.
The use of the SAFT-VR thermodynamic approach within process models of CO2 absorption has previously been explored for high-pressure physical absorption in alkanes,95 ethers and ether derivatives,96 and also for chemisorption. In an early study the modelling of the absorption process was also considered and explored in the context of solvent-blend design.97 The absorber model was further developed98 showing reliable results for a set of pilot-plant data. Mac Dowell et al.99 have proposed a dynamic model of a CO2 absorber, based on the SAFT-VR thermodynamic treatment, which has been used in in-depth studies of the control100 and economics101,102 of post-combustion CO2 capture processes. Qualitative agreement with data from two pilot-plant runs from ref. 13 was found in these studies.99–101 The column profiles obtained by Mac Dowell et al.99 are somewhat difficult to interpret as the location of the data points reported in the paper does not match the location of the sensors reported in the physical pilot plant. Nevertheless, the findings of this body of work indicate that a physical approach to the modelling the chemical and physical equilibria allows one to capture the process behaviour accurately with a limited set of parameters.
Overall, the models developed to date can be used to adequately represent the general behaviour of the absorber column. However, only the model of Tontiwachwuthikul et al.13 provides an accurate description of the temperature of the rich solvent at the outlet, and in all of the published models, the bulge in the temperature profile, which is a well-known characteristic of this absorption process,103 is reproduced qualitatively but not quantitatively. Existing models reproduce either its magnitude or its location along the column, but not both.
In view of the foregoing discussion, the potential benefits of a novel absorption model in which a SAFT-VR thermodynamic treatment and a rate-based column model are integrated are explored here for CO2 absorption in aqueous MEA. The proposed approach is based on a two-film model. Because the reactions are treated implicitly with the SAFT-VR EoS, only the key molecular species (i.e. MEA, CO2, H2O, and N2) need to be taken into account explicitly at the level of mass and energy balances. The detailed model presented in our current paper includes several modifications over previous work,97,104 leading to enhanced model reliability. In Section 2, we describe the SAFT-VR EoS and the heat- and mass-transfer relations used in the rate-based absorber model. The validation of the model, its predictive capabilities, and a sensitivity analysis are presented in Section 3. Two scenarios are investigated, corresponding to different levels of data availability: in the first scenario, it is assumed that no pilot-plant data are available, and the suitability of the model to provide a best-case analysis of process performance is studied; in the second scenario, one pilot-plant run is considered and employed to obtain a more realistic quantification of mass-transfer limitations. The transferability of this analysis is then tested for data at other conditions.
2 Modelling methodology
The development of a rate-based model of a CO2 absorber is described in this section. In subsection 2.1, the thermodynamic model used for the VLE and the chemical equilibrium is presented. The non-equilibrium stage approach is introduced in Subsection 2.2.
2.1 Thermodynamic model
The treatment of the chemical-reaction equilibria relevant to the absorption process is a key aspect of the modelling strategy adopted in our work. In the physical approach followed here, the chemical and physical interactions are treated on an equal footing within the SAFT-VR SW EoS.87,88 Background information is provided in this section to help the reader better understand the models used and the underlying assumptions.
The SAFT family of equations stems from the first-order thermodynamic perturbation theory (TPT1) of Wertheim.93,105–109 In SAFT approaches molecules are modelled as chains of fused spherical segments with embedded short-range association sites incorporated to mediate hydrogen bonding which leads to aggregate formation (speciation). The EoS is developed in terms of the Helmholtz free energy using a perturbation approach, such that the free energy of a chain molecule is obtained with respect to the properties (free energy and radial distribution function) of a reference monomeric (non-bonded) system. The original SAFT85,86 EoS has been revisited and modified by a number of researchers so that several versions are now available.76,87,88,110–116 A historical account of perturbation theories for polar and associating liquids has recently been presented by Gubbins.117
In the SAFT-VR formulation87,88 employed here, a square-well (SW) potential is used to describe the interaction between spherical molecular segments of the reference fluid. The more recent versions of the SAFT-VR EoS incorporate the Mie (generalized Lennard-Jones) potential (SAFT-VR Mie116), and allow for a more reliable representation of the near-critical region and second derivative properties (e.g. heat capacities) which depend mainly on the specific form of the repulsive part of the potential.114,116,118,119 Additionally, group contribution (GC)120 versions of the SAFT-VR EoSs, namely SAFT-γ SW91,92 and SAFT-γ Mie,121 have also been proposed. These offer additional predictive capabilities in that the properties of a new solvent that has never been synthesized can be predicted (without data specific to that solvent) provided that the interaction parameters for the functional groups appearing in that molecule are available. The assessment of the integration of the molecular-based SAFT-VR SW EoS within an absorption model presented in our current paper can readily be extended to a GC formulation.
In the SAFT-VR SW approach, a molecule i is modelled as a chain of mi fused homonuclear spherical segments of diameter σii. The interactions between two identical segments are described by a square-well potential of range λii and depth εii (cf.Fig. 1). For each molecule i, the number of site types Ns,i must be defined, as well as the number of sites of each type a, Ns,ia. The sites are characterized by SW site–site energetic εHBab,ii and range rc;ab,ii parameters (cf.Fig. 1).
 |
| | Fig. 1 The square-well potentials for a monomer, Φmono, and association between the sites, Φassoc, employed in the SAFT-VR approach. (a) Φmono is characterized by a hard-core with a diameter σ, range of attraction λσ and depth ε. (b) Φassoc is defined by an off-centre potential of depth εHBab and of range rc;ab. (c) The centre of the site is at a distance rd from the centre of the segment. | |
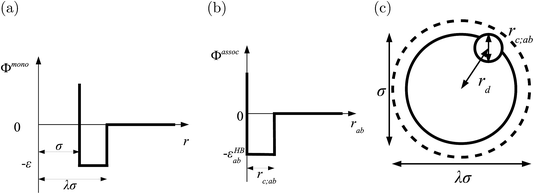
In order to model mixtures, combining rules based on the Lorentz–Berthelot form (cf. Haslam et al.122) are used to describe the unlike interaction between segments on two different molecules i and j:
| | 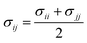 | (1) |
| | 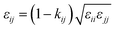 | (2) |
| | 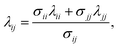 | (3) |
where
kij is an adjustable parameter that characterizes the unlike dispersion attractive interaction. Parameters to describe association between different molecules are estimated using experimental data for the specific mixtures of interest, or for chemically similar mixtures.
82,84
In recent work82,84,89,90 the reactions involved in aqueous amine solutions of CO2 are treated implicitly within the SAFT-VR and SAFT-γ frameworks, with the products of the chemical reaction represented as aggregates of the reactant molecules. In the case of MEA the overall set of reactions can be reduced to28
| CO2 + HOC2H4NH2 ⇌ [HOC2H4NH2+ + CO2−], |
| [HOC2H4NH2+ + CO2−] + HOC2H4NH2 ⇌ HOC2H4NH+3 + HOC2H4NHCO2−, |
and association sites that mimic the complexation of CO
2 and amine are introduced in the SAFT-VR molecular models. The reaction products can thus be modelled as neutral aggregates of CO
2 and MEA, bonded at association sites as shown in
Fig. 2. An accurate overall representation of the vapour–liquid phase equilibria of MEA + CO
2 + H
2O can be obtained in this manner by estimating the molecular parameters from experimental fluid-phase equilibria data, for both the pure components and mixtures. One important implication of the physical treatment of chemical equilibrium is that there is no need to explicitly specify a reaction scheme or reaction products. The types of products formed (
e.g. carbamates or bicarbonates) are dictated by the association scheme chosen (number of sites and strength of their interactions), and the relative extent of formation of the different products depends on the temperature-independent intermolecular parameters that describe the association energies. The fraction of molecules bonded at a given site is an output of the SAFT-VR approach and the distribution of reaction products can be determined from a statistical analysis of the values of these fractions at the thermodynamic state of interest.
94 Thus, although no speciation data are used in deriving the SAFT-VR parameters, the speciation equilibria can nonetheless be predicted successfully.
84,90
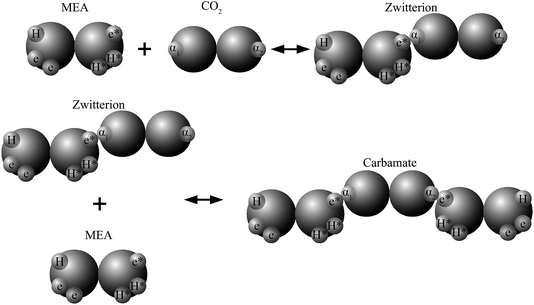 |
| | Fig. 2 Schematic representation of the association scheme between MEA and CO2 (in aqueous media) with a SAFT treatment showing two reaction products. | |
This type of physical approach greatly reduces the number of parameters needed to describe the mixture compared to explicit approaches such as eNRTL, in which every species must be described as a separate entity and temperature-dependent equilibrium constants must be derived for all the relevant reactions. The SAFT-VR approach has been shown to be applicable to the absorption of CO2 for a wide range of aqueous alkanolamine solutions.84 In many cases, it is possible to transfer parameters from one alkanolamine to another based on molecular similarity, further reducing the need for experimental data.
One key assumption in adopting this type of physical approach is that all reactions are assumed to be at equilibrium, which is only applicable to processes in the physical regime, i.e. where mass transfer is the rate limiting process. In the case where a specific treatment of the charged electrolytic species is required, the SAFT-VR approach123–128 can be coupled to a chemical approach as appropriate. It is also possible to represent some or all species explicitly where chemical reactions that are not at equilibrium can then be modelled via a separate kinetic model. We do not follow this route here, which would fall within the class of chemical approaches, but instead assess the adequacy of the physical approach.
The molecules considered in our study are MEA, H2O, CO2, and N2. A schematic of the molecular models used in the SAFT-VR SW treatment is presented in Fig. 3. The values of all parameters are listed Tables 1–4. The MEA molecule is represented as 2 tangent spherical segments with 2 association sites of type e (electron lone pairs on the oxygen atom), 1 site of type e* (corresponding to the lone pair on the nitrogen atom), 1 site of type H (the hydrogen atom on the hydroxyl group), and two sites of type H* (hydrogen atoms on the amine group).82 The H2O is represented as 1 spherical segment with 2 e sites and 2 H sites.129 The CO2 model comprises 2 tangent segments and has 1 α1 site and 1 α2 site (acceptor sites) that interact only with the e* sites of MEA.84 The N2 molecule is modelled as a fused non-spherical diatomic, with an aspect ratio of m = 1.4, and does not have association sites as it is chemically inert and apolar.104,130 A site of type e/e* can bond with a site H/H* and vice versa. For example, when an e site from MEA and an H site from water come within the cut-off range  of each other, there is a site–site hydrogen-bonding associative interaction of strength
of each other, there is a site–site hydrogen-bonding associative interaction of strength  . A representative example of the good overall description of the temperature and pressure dependence of the absorption VLE behaviour of CO2 in aqueous MEA obtained with the SAFT-VR SW models can be seen in Fig. 4 over several orders of magnitude for the partial pressure of CO2. In the standard Wertheim TPT1 treatment at the heart of the SAFT EoS, association into linear-chain, branched-chain, and network aggregates are considered. Association into ring-like structures131–134 (and even double bonding135 and bond cooperativity136) can be taken into account but this is not considered for the systems described in our current work.
. A representative example of the good overall description of the temperature and pressure dependence of the absorption VLE behaviour of CO2 in aqueous MEA obtained with the SAFT-VR SW models can be seen in Fig. 4 over several orders of magnitude for the partial pressure of CO2. In the standard Wertheim TPT1 treatment at the heart of the SAFT EoS, association into linear-chain, branched-chain, and network aggregates are considered. Association into ring-like structures131–134 (and even double bonding135 and bond cooperativity136) can be taken into account but this is not considered for the systems described in our current work.
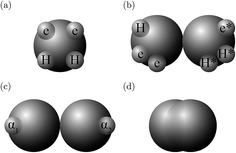 |
| | Fig. 3 A schematic of the molecular models used in the SAFT-VR SW approach: (a) H2O, (b) MEA, (c) CO2, and (d) N2. | |
Table 1 The SAFT-VR parameters characterising the pure-component models used in our work: the number of segments mi, the diameter of the spherical core σii, the depth εii and range λii of the dispersive square-well potential, and the type and the number of hydrogen-bonding sites
|
i
|
m
i
|
σ
ii
(Å) |
ε
ii
/k (K) |
λ
ii
|
e-sites |
H-sites |
e*-sites |
H*-sites |
α1-sites |
α2-sites |
Source |
| H2O |
1.0 |
3.03420 |
250.00 |
1.78890 |
2 |
2 |
0 |
0 |
0 |
0 |
Clark et al.129 |
| MEA |
2.0 |
3.57229 |
305.00 |
1.58280 |
2 |
1 |
1 |
2 |
0 |
0 |
Mac Dowell et al.82 |
| CO2 |
2.0 |
2.78640 |
179.27 |
1.51573 |
0 |
0 |
0 |
0 |
1 |
1 |
Rodríguez et al.84 |
| N2 |
1.4 |
3.07357 |
74.587 |
1.58795 |
0 |
0 |
0 |
0 |
0 |
0 |
Mac Dowell104 |
Table 2 Binary interaction parameters for the mixtures relevant to our work. kij characterizes the strength of the unlike dispersion interaction between molecules of types i and j, cf.eqn (2)
|
i + j |
k
ij
|
Source |
| MEA + CO2 |
0.4788 |
Rodríguez et al.84 |
| MEA + H2O |
0.01 |
Mac Dowell et al.82 |
| MEA + N2 |
0.03 |
Mac Dowell104 |
| CO2 + H2O |
−0.06 |
Mac Dowell et al.82 |
| CO2 + N2 |
−0.0599 |
Mac Dowell104 |
| H2O + N2 |
−0.3635 |
Mac Dowell104 |
Table 3 The site–site association energies εHBab,ij for MEA, H2O, and CO2 (cf.Fig. 3). The interaction matrix is symmetrical, i.e. εHBeH,ii = εHBHe,ii; the lower diagonal part has been left blank and is implied. The unlike association between sites of the same type is assumed to be symmetric, i.e. εHBeH,ij = εHBHe,ij = εHBeH,ji = εHBHe,ji (ref. 82 and 84)
|
|
ε
HB
ab,ij/k (K) |
| MEA |
H2O |
CO2 |
| |
a/b |
e |
H |
e* |
H* |
e |
H |
α1 |
α2 |
| MEA |
e |
0 |
2357.79 |
0 |
900 |
0 |
1780.7121 |
0 |
0 |
| H |
— |
0 |
550 |
0 |
1780.7121 |
0 |
0 |
0 |
| e* |
— |
— |
0 |
960 |
0 |
1517.1049 |
5200 |
3982.66 |
| H* |
— |
— |
— |
0 |
1517.1049 |
0 |
0 |
0 |
| H2O |
e |
— |
— |
— |
— |
0 |
1400.00 |
0 |
0 |
| H |
— |
— |
— |
— |
— |
0 |
0 |
0 |
| CO2 |
α1 |
— |
— |
— |
— |
— |
— |
0 |
0 |
| α2 |
— |
— |
— |
— |
— |
— |
0 |
0 |
Table 4 The site–site range parameters rc;ab,ij for mixtures containing MEA, H2O, and CO2 (cf.Fig. 3). The interaction matrix is symmetrical, i.e. rc;eH,ii = rc;He,ii, and so the lower diagonal part has been left blank. The unlike association between sites of the same type is assumed to be symmetric, i.e. rc;eH,ij = rc;He,ij = rc;eH,ji = rc;He,ji (ref. 82 and 84)
|
|
r
c;ab,ij (Å) |
| MEA |
H2O |
CO2 |
| |
a/b |
e |
H |
e* |
H* |
e |
H |
α1 |
α2 |
| MEA |
e |
0 |
2.08979 |
0 |
2.65064 |
0 |
2.10763 |
0 |
0 |
| H |
— |
0 |
2.65064 |
0 |
2.10763 |
0 |
0 |
0 |
| e* |
— |
— |
0 |
2.32894 |
0 |
2.22626 |
1.97978 |
1.96999 |
| H* |
— |
— |
— |
0 |
2.22626 |
0 |
0 |
0 |
| H2O |
e |
— |
— |
— |
— |
0 |
2.10822 |
0 |
0 |
| H |
— |
— |
— |
— |
— |
0 |
0 |
0 |
| CO2 |
α1 |
— |
— |
— |
— |
— |
— |
0 |
0 |
| α2 |
— |
— |
— |
— |
— |
— |
0 |
0 |
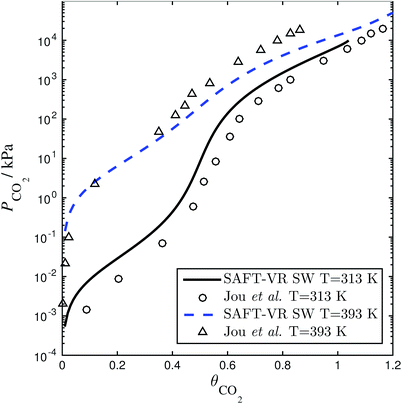 |
| | Fig. 4 Solubility of CO2 in a 30 wt% aqueous solution of MEA expressed as the CO2 loading (defined as the number of moles of CO2 per mole of MEA in the liquid solvent) as a function of the partial pressure. The SAFT-VR model predictions (dashed and continuous curves) using parameters from Rodríguez et al.84 are compared with the experimental data (triangles and circles) from Jou et al.159 | |
2.2 Non-equilibrium absorber model
The absorber is a counter-current vapour–liquid multistage separation column, with a liquid feed at the top stage and a vapour feed at the bottom stage. The vapour product comes off the top stage and the liquid product off the bottom stage. The inside of the column is filled with an inert packing material designed to maximize mass transfer between the vapour and the liquid and to minimize the pressure drop. The vapour and liquid compositions vary continuously with packing height.
The modelling of such a column can be either discrete or continuous in the vertical direction. In a discrete model, the column is divided into hypothetical stages, each of which represents a section of packing in the packed column. For rate-based models, a greater number of stages provides a better description.36 Taken to the limit, the use of an infinite number of stages is equivalent to modelling the column continuously. Although both models could be used; we choose the discrete approach for our study.
The modelling of the stages can be equilibrium or rate-based. In an equilibrium model, it is assumed that vapour–liquid equilibrium is achieved at each stage, everywhere on the stage. A rate-based model accounts for limitations due to transport phenomena. Due to the complexity of the process modelled in the current system, a rate-based approach is chosen over an equilibrium one in order to capture some of the key physical phenomena.137,138
For the absorber model, the assumption is made that the two phases are distinct, and each phase is perfectly mixed at each stage. A diagram of a non-equilibrium stage is presented in Fig. 5. Vapour from the stage below is brought into contact with liquid from the stage above and the two phases exchange mass and energy through their common interface represented in the diagram by the wavy line. In a rate-based model, separate mass balances are considered for each phase. The two phases are in contact through their interface where material lost by the vapour phase is gained by the liquid phase. The heat transfer is treated in a similar way. There is one energy balance in each phase, and the phases are linked via the rate of energy transferred across the phase interface. The compositions of the two phases at the interface are determined assuming equilibrium conditions at the interface.
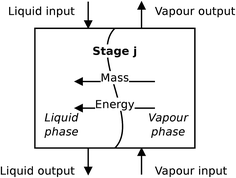 |
| | Fig. 5 A schematic of a non-equilibrium stage. This stage represents a section of packing in a packed column. | |
The behaviour at the phase interface in the rate-based stages is described with a two-film theory.137 Each phase is split into two parts: the bulk phase and the film in which the heat and mass transfer occur. In the bulk phase, the concentration, pressure, and temperature are assumed to be uniform, whereas there could be a gradient in composition and temperature in the film. A liquid–gas interface between the two films is sketched in Fig. 6, where the profiles for the composition of component i, temperature, and pressure are represented.
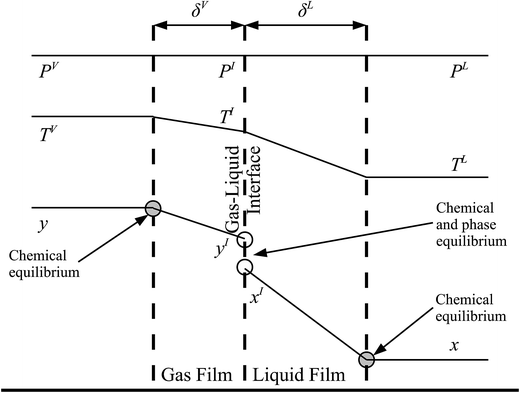 |
| | Fig. 6 A schematic of the two-film model of a column stage. δV and δL represent the thickness of the gas and liquid films, respectively. PV, PI, and PL are the pressure in the bulk vapour phase, at the gas–liquid interface, and in the bulk liquid, respectively. As can be seen an isobaric profile is assumed. The temperatures of the bulk vapour phase, at the gas–liquid interface, and of the bulk liquid are denoted by TV, TI, and TL, respectively. Finally, yi and xi are the mole fractions of component i in the bulk vapour and liquid phases, respectively, and yIi and xIi are the mole fractions of component i at the vapour–liquid interface in the vapour and the liquid phases, respectively. | |
The following assumptions are made:
• The model is steady state.
• The bulk phases and films are at chemical equilibrium everywhere (i.e. the reaction rates are faster than the mass transfer rates).25,28
• The interface is at phase and chemical equilibrium.
• The interfacial surface area is the same for both heat and mass transfer.
• The effective area is equal to the wetted area.
• The absorption column is considered to be adiabatic.
• There is no pressure drop along the column.
2.3 Model equations
In this subsection, we present the equations used to model a packed column subsection (stage). The equations are grouped into different categories: energy and mass balances, rate equations, equilibrium equations, mass-transfer correlations, heat-transfer correlations, and diffusion correlations. We list explicitly all of the model equations to clarify the radically different approach followed here. One important model parameter τ is introduced to account for a scaling of the CO2 diffusivity. This parameter will be estimated from experimental data. In the following equations, the subscript i refers to the ith component, j to the jth stage, c is the total number of components, and Ns is the number of stages in the column. The number of stages is fixed to 50 which is amply sufficient to assure numerical convergence without significantly impacting the computational time.
2.3.1 Heat and mass balances.
The liquid and vapour phase mole balances for component i on stage j are given by| | | Lj−1xi,j−1 + NLi,j = Ljxi,j, i = 1, 2…, c; j = 1, 2…, Ns | (4) |
| | | Vj+1yi,j+1 − NVi,j = Vjyi,j, i = 1, 2…, c; j = 1, 2…, Ns, | (5) |
where Lj and Vj (mol s−1) are the total liquid and vapour molar flow rate leaving stage j respectively, xi,j and yi,j are the bulk liquid and vapour mole fractions of component i on stage j, NLi,j (mol s−1) is the net gain of species i in the liquid phase due to interphase transport for stage j, and NVi,j (mol s−1) is the net loss of species i in the vapour phase due to interphase transport for stage j.
The mole fractions in the streams leaving each stage must sum to unity:
| | 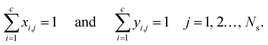 | (6) |
The energy balances for the liquid and vapour phases respectively are
| | Lj−1HLj−1(TLj−1, VLj−1, ![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) j−1) + ELj = LjHLj(TLj, VLj, j−1) + ELj = LjHLj(TLj, VLj, ![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) j), j = 1, 2…, Ns, j), j = 1, 2…, Ns, | (7) |
| | Vj+1HVj+1(TVj+1, VVj+1, ![[y with combining low line]](https://www.rsc.org/images/entities/i_char_0079_0332.gif) j+1) − EVj = VjHVj(TVj, VVj, j+1) − EVj = VjHVj(TVj, VVj, ![[y with combining low line]](https://www.rsc.org/images/entities/i_char_0079_0332.gif) j), j = 1, 2…, Ns, j), j = 1, 2…, Ns, | (8) |
where
HLj and
HVj (J mol
−1) are the molar enthalpies of the liquid and gas phases of stage
j, respectively.
ELj (W) is the net gain of energy of the liquid phase through the interface at stage
j, and
EVj (W) is the net loss of energy from the vapour phase through the interface at stage
j. The molar enthalpies
HLj and
HVj are determined from SAFT-VR as functions of the temperature of the bulk phases,
TLj and
TVj (K), the molar volumes of the phases,
VLj and
VVj (m
3 mol
−1), and the composition (vectors) of the phases,
![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) j
j and
![[y with combining low line]](https://www.rsc.org/images/entities/i_char_0079_0332.gif) j
j.
There is no accumulation of mass or energy at the vapour–liquid interface:
| | | NLi,j = NVi,j, i = 1, 2…, c; j = 1, 2…, Ns, | (9) |
| | | ELj = EVj, i = 1, 2…, c; j = 1, 2…, Ns. | (10) |
2.3.2 Rate equations: mass transfer.
According to the film model for mass transfer, we define the mass-transfer rates as follows:| | | NLi,j = kLi,jaT,j(CI,Li,j − CLi,j), i = 1, 2…, c; j = 1, 2…, Ns, | (11) |
| | | NVi,j = kVi,jaT,j(CVi,j − CI,Vi,j), i = 1, 2…, c; j = 1, 2…, Ns, | (12) |
where aT,j (m2) is the total interfacial area on stage j available for heat or mass transfer, kLi,j (m s−1) is the liquid-phase mass-transfer coefficient for component i of stage j, kVi,j (m s−1) is the vapour-phase mass-transfer coefficient for component i of stage j, CLi,j and CVi,j (mol m−3) are the concentrations of component i in the bulk liquid and vapour phases of stage j, and CI,Li,j and CI,Vi,j (mol m−3) are the concentrations of component i at the vapour–liquid interface in the liquid and vapour phases of stage j.
The total area for heat and mass transfer is given by the product of the effective specific area and the stage volume:
| | | aT,j = a′jAsectionDz, j = 1, 2…, Ns, | (13) |
where
a′
j (m
2 m
−3) is the interfacial area density on stage
j,
Asection (m
2) is the cross sectional area of the column, and
Dz (m) is the stage height given by
hpacking/
Ns, with
hpacking (m) as the total packing height.
2.3.3 Rate equations: heat transfer.
The energy fluxes in the liquid and gas phases at stage j are given by the sum of the conductive and diffusive heat fluxes:| | | ELj = QLcond,j + QLdiff,j, j = 1, 2…, Ns, | (14) |
| | | EVj = QVcond,j + QVdiff,j, j = 1, 2…, Ns, | (15) |
where QLcond,j and QLdiff,j (W) are the conductive and diffusive heat fluxes at the interface into the liquid phase on stage j, and QVcond,j and QVdiff,j (W) are the conductive and diffusive heat fluxes at the interface out of the vapour phase on stage j.
The conductive heat-transfer rate into the liquid phase and out of the vapour phase on stage j are driven by temperature gradients between the bulk phases and the interface, and are given by
| | | QLcond,j = hLT,jaT,j(TIj − TLj), j = 1, 2…, Ns, | (16) |
| | | QVcond,j = hVT,jaT,j(TVj − TIj), j = 1, 2…, Ns, | (17) |
where
hLT,j and
hVT,j (W m
−2 K
−1) are the heat-transfer coefficients in the liquid and gas phases on stage
j, respectively, and
TIj (K) is the temperature at the vapour–liquid interface on stage
j.
The diffusive heat fluxes account for the variation in enthalpy in the liquid and vapour streams associated with the transfer of mass from one phase to another. This is obtained based on the individual component fluxes and the corresponding enthalpies of the pure components:
| | 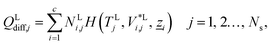 | (18) |
| | 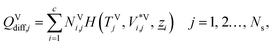 | (19) |
where
H(
TLj,
V*Li,j,
![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif) i
i) and
H(
TVj,
V*Vi,j,
![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif) i
i) (J mol
−1) are the molar enthalpies of pure component
i in the bulk liquid and vapour phase respectively, as calculated with SAFT-VR SW. The variable
![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif) i
i denotes the molar composition vector of a stream consisting of pure component
i defined by
zk,i = 1 if
i =
k and
zk,i = 0 otherwise.
V*Li,j and
V*Vi,j (m
3 mol
−1) are the molar volumes of pure component
i at stage
j in the bulk liquid and vapour phases respectively, obtained from
| | PLj = P(TLj, V*Li,j, ![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif) i), i = 1, 2…, c; j = 1, 2…, Ns, i), i = 1, 2…, c; j = 1, 2…, Ns, | (20) |
| | PVj = P(TVj, V*Vi,j, ![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif) i), i = 1, 2…, c; j = 1, 2…, Ns, i), i = 1, 2…, c; j = 1, 2…, Ns, | (21) |
where
PLj and
PVj (MPa) are the pressure of the bulk liquid and vapour phases at stage
j respectively and
P(
TLj,
V*Li,j,
![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif) i
i) and
P(
TLj,
V*Li,j,
![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif) i
i) represent evaluations of the pressure using the SAFT-VR SW EoS.
When equating the vapour and liquid fluxes, one obtains an expression which includes the difference between the enthalpies in the vapour phase and in the liquid phase for a pure component i; this is the enthalpy of vaporization of this component. As we will see, the enthalpy of vaporization of water plays a significant role in the process. We assume that the contribution of N2 to the change of enthalpy between the two phases is negligible as its mass transfer is very small, and that the enthalpy of vaporization of CO2 is negligible as the operating conditions are close to or above its critical point. In the case where only one phase is stable for a pure component at the conditions of interest, as is typically the case for CO2, one can access the hypothetical phase information by providing an adequate initial guess for the molar volume to the SAFT-VR SW EoS.
2.3.4 Equilibrium relations.
Both chemical and phase equilibria are assumed to prevail at the interface so that the conditions of equality of pressure, temperature, and chemical potential must be satisfied:| | μ(TIj, VI,Vj, ![[y with combining low line]](https://www.rsc.org/images/entities/i_char_0079_0332.gif) Ij) = μ(TIj, VI,Lj, Ij) = μ(TIj, VI,Lj, ![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) Ij) = μI,Li,j = μI,Vi,j, i = 1, 2…, c; j = 1, 2…, Ns, Ij) = μI,Li,j = μI,Vi,j, i = 1, 2…, c; j = 1, 2…, Ns, | (22) |
| | P(TIj, VI,Vj, ![[y with combining low line]](https://www.rsc.org/images/entities/i_char_0079_0332.gif) Ij) = P(TIj, VI,Lj, Ij) = P(TIj, VI,Lj, ![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) Ij) = PIj, j = 1, 2…, Ns, Ij) = PIj, j = 1, 2…, Ns, | (23) |
where μI,Li,j and μI,Vi,j (J mol−1) are the chemical potentials of component i on stage j in the liquid and vapour phases respectively, VI,Lj and VI,Vj (m3 mol−1) are the molar volumes of the liquid phase and the vapour phases at the vapour–liquid interface (I) on stage j, and PIj (MPa) is the pressure at the liquid–vapour interface on stage j. The chemical potentials and the molar volume are determined using the SAFT-VR SW EoS.
The mole fractions at the interface must sum to unity:
| | 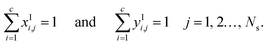 | (24) |
Each stage is assumed to be in mechanical equilibrium, so that
| | | PVj = PLj = PIj, j = 2…, Ns, | (25) |
where
| | PVj = P(TVj, VVj, ![[y with combining low line]](https://www.rsc.org/images/entities/i_char_0079_0332.gif) j), j = 1, 2…, Ns, j), j = 1, 2…, Ns, | (26) |
| | PLj = P(TLj, VLj, ![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) j), j), ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j = 1, 2…, Ns. j = 1, 2…, Ns. | (27) |
Finally, the column pressure drop is assumed to be negligible.
| | | PVj = PVj+1, j = 1, 2…, Ns. | (28) |
All pressure terms present in the model are thus equated to the pressure of the gas inlet stream,
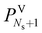
. This assumption can easily be removed at a later stage of the model development. Preliminary results have indicated that the pressure drop has a negligible effect on the process used for the validation of our model.
The equations presented in the remainder of this section apply to each stage. The subscript j has been omitted for the purpose of clarity.
2.3.5 Mass-transfer correlations.
The interfacial area, the liquid-phase mass-transfer coefficient, and the gas-phase mass-transfer coefficient are obtained using the correlations from Onda et al.57,58 Other correlations are available, the most commonly used being the ones developed by Rocha et al.60 and Billet and Schultes.61 Faramarzi et al.48 compared the performance of the correlations and found that all three provide a good description; they expressed a slight preference for the correlations of Rocha et al.60 but could not draw a general conclusion applicable to all operating conditions. The correlations of Rocha et al.60 apply to structured packing and have to be adapted for use in random packing, whereas those developed by Onda et al.57,58 have been developed specifically using random Berl saddle packing, the same as the one employed in the pilot plant by Tontiwachwuthikul et al.13 This last set of correlations is sometimes reparameterized when used in commercial software such as Aspen or ProTreat. The correlations developed by Onda et al.,57,58 as reported by Treybal,139 are implemented in our model of the absorber column. The liquid-phase mass-transfer coefficient for component i is given by| | 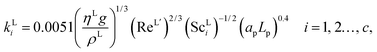 | (29) |
where ρL (kg m−3) is the density of the liquid phase, ηL (kg m−1 s−1) is the dynamic viscosity of the liquid phase, g (m s−2) is the gravitational acceleration, ReL′ is the liquid-phase Reynolds number based on the interfacial area, ScLi is the Schmidt number of component i in the liquid phase, ap (m2 m−3) is the specific surface area of the packing, and Lp (m) is the nominal packing size.
The Reynolds number and the Schmidt number for component i in the liquid phase are
| | 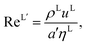 | (30) |
| | 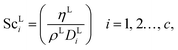 | (31) |
where
DLi (m
2 s
−1) is the diffusion coefficient of component
i in the liquid phase,
uL (m s
−1) is the liquid velocity, and
a′ is the interfacial area density defined in
eqn (35).
The vapour-phase mass-transfer coefficient is obtained from
| | | kVi = 2apDViReV0.7ScV1/3i(apLp)−2, i = 1, 2…, c, | (32) |
where
DVi (m
2 s
−1) is the diffusivity of component
i in the vapour-phase, Re
V is the vapour-phase Reynolds number, and Sc
Vi is the Schmidt number of component
i in the vapour phase.
The Reynolds number and the Schmidt number for the vapour phase are
| | 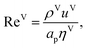 | (33) |
| | 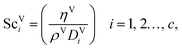 | (34) |
where
ρV (kg m
−3) is the density of the vapour phase,
ηV (kg m
−1 s
−1) is the dynamic viscosity of the vapour phase, and
uV (m s
−1) is the vapour velocity.
The interfacial area density a′ is obtained from57,58
| | 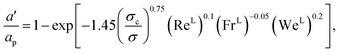 | (35) |
where
σc (N m
−1) is the critical surface tension of the packing material,
σ (N m
−1) is the vapour–liquid surface tension, Re
L is the liquid-phase Reynolds number based on the specific surface area, Fr
L is the liquid-phase Froude number, and We
L is the liquid-phase Weber number. The interfacial area density, together with the three dimensionless numbers used in
eqn (35), are properties of the mixture, not properties of individual components.
The expressions for the dimensionless numbers are
| | 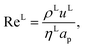 | (36) |
| | 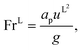 | (37) |
| | 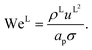 | (38) |
The velocities of each phase are
| | 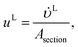 | (39) |
| | 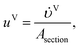 | (40) |
where
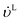
and
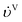
(m
3 s
−1) are the volumetric flow rates of the liquid and gas phase, respectively.
2.3.6 Heat-transfer correlations.
For the gas and liquid heat-transfer coefficients we use the correlations presented in Treybal's Mass Transfer Operations.139 Once again these expressions apply to each stage. The expression for the liquid-phase heat-transfer coefficient is| | 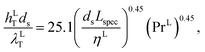 | (41) |
where hLT (W m−2 K−1) is the liquid-phase heat-transfer coefficient, ds (m) is the diameter of a sphere of the same surface area as a single packing particle (not the same as ap), λLT (W m−1 K−1) is the liquid thermal conductivity, Lspec (kg s−1) is the specific liquid flow rate, and PrL is the liquid-phase Prandtl number. The latter is obtained from the following expression:| | 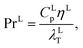 | (42) |
where CLp (J kg−1 K−1) is the specific isobaric heat capacity of the liquid phase. The vapour-phase heat-transfer coefficient is given by| | 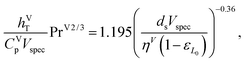 | (43) |
where hVT (W m−2 K−1) is the vapour-phase heat-transfer coefficient, CVp (J kg−1 K−1) is the specific isobaric heat capacity of the vapour phase, PrV is the Prandtl number for the gas phase, Vspec (kg s−1) is the specific vapour flow rate, and εL0 is the operating void space in the packing (assumed to be equal to the void fraction ε). The Prandtl number for the gas phase is obtained from| | 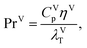 | (44) |
where λVT (W m−1 K−1) is the vapour thermal conductivity.
2.3.7 Vapour-phase diffusion coefficient.
The vapour-phase diffusion coefficient used in eqn (34) is obtained from the expression of Fuller and co-workers140–142 as reported by Poling et al.77 It is assumed that the components are diffusing through air:| | 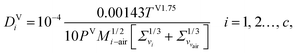 | (45) |
where Σv (Å) is the atomic diffusion volume, and Mi–air is given by| | | Mi–air = 2[(1/Mair) + (1/Mi)]−1, i = 1, 2…, c, | (46) |
where Mi (g mol−1) is the molar mass of component i.
2.3.8 Liquid-phase diffusion coefficient.
The liquid-phase binary diffusion coefficients are described with different correlations. The mutual diffusion coefficients of CO2 at very low concentration in pure MEA and pure H2O are derived from the Wilke–Chang correlation:77,143| | 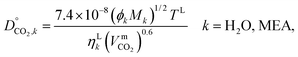 | (47) |
where ϕk is the “association factor” of solvent k, and 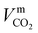 (cm3 mol−1) is the molar volume of CO2 at its normal boiling temperature.
(cm3 mol−1) is the molar volume of CO2 at its normal boiling temperature.
These mutual diffusion coefficients are used in the correlation of Takahashi et al.144 to determine the diffusivity of CO2 in a liquid mixture of H2O and MEA:
| | 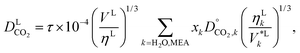 | (48) |
where we have introduced the scaling prefactor
τ to the correlation. We refer to
eqn (48) as the effective diffusivity (ED) correlation. The presence of this scaling factor provides an effective approach to modelling several effects that are not accounted for due to the use of a chemical approach and the consequent implicit treatment of the reaction products: the acceleration of mass-transfer due to the depletion of CO
2via chemical reactions;
40 the reduction in mass transfer due to the ion pairs formed and their electrostatic interaction with other species;
40 and the reduction in the mass transfer due to CO
2 being present in larger aggregated products (bicarbonate and carbonate species). The latter effect was observed by Han
et al.145 in a molecular-dynamics study of the transport properties of CO
2 in MEA, indicating a significant decrease in the diffusion coefficient with increasing CO
2 loading. The value of the parameter
τ and its impact on model predictions are discussed in Section 3. Finally, the Perkins and Geankoplis
146 method is used to calculate the diffusivity of H
2O, MEA, and N
2 in the liquid phase:
| | 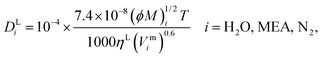 | (49) |
where
Vmi (cm
3 mol
−1) is the molar volume of component
i at its normal boiling temperature, and the term (
ϕM)
i (g mol
−1) represents the “association factor” of component
i in the liquid mixture which is derived from
| | 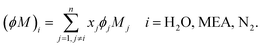 | (50) |
The other correlations of experimental data used in our model are listed in
Table 5.
Table 5 Correlations used in the process model of the absorber
| Physical property |
Component |
Source |
| Liquid-phase viscosity |
H2O |
Westmeier160 |
| MEA |
Leibush and Shorina161 |
| Mixture |
Maham et al.162 |
| Vapour-phase viscosity |
|
Kestin et al.163 |
| Vapour–liquid surface tension |
|
Vazquez et al.152 |
| Heat conductivity |
|
Haynes164 |
| Liquid heat capacity |
H2O |
Laliberte165 |
| MEA |
Mundhwa and Henni166 |
| Vapour heat capacity |
H2O |
Riddick et al.167 |
| N2 |
Vargaftik168 |
| CO2 |
Bender et al.169 |
| Liquid-phase diffusion coefficient |
CO2 |
Takahashi et al.144 |
| H2O, MEA, N2 |
Perkins and Geankoplis146 |
| Vapour-phase diffusion coefficient |
CO2, H2O, MEA, N2 |
Poling et al.77 |
3 Results
The model described in Section 2.2 is implemented in gPROMS147 and an in-house implementation of the SAFT-VR SW EoS148 is accessed via a Foreign Object Interface.
In this section, we investigate the predictive capabilities of the proposed model by thorough comparisons with the pilot-plant data obtained by Tontiwachwuthikul et al.13 The inputs required to model these data and relevant assumptions are discussed in Section 3.1. As discussed in Section 3.2, we first assume that there are no pilot-plant data available for the solvent in question and analyze the suitability of the model for the provision of a best-case analysis of the process performance. It is then assumed that only one pilot-plant run is available and the corresponding concentration profiles are used to estimate the single parameter τ, related to mass-transfer limitations, as summarized in Section 3.3. The transferability of this parameter is assessed by comparing model predictions against data for other pilot-plant runs. Finally, in Section 3.4, the sensitivity of the model to several parameters is explored, providing insights into the behaviour of CO2 absorption columns.
3.1 Model inputs
The absorption column studied by Tontiwachwuthikul et al.13 has an internal diameter of 0.1 m and a total packed height of 6.6 m; care has to be taken not to mistake the total column height of 7.2 m with the packed height, which is the relevant dimension in modelling the absorber. The absorption column internals are randomly packed 12.7 mm ceramic Berl saddles. The gas inlet stream is assumed to be free of MEA and the liquid solvent inlet stream free of N2. The input values used are listed in Table 6 and the characteristics of the column and the packing are listed in Table 7. Some of the data needed for the simulation of the process were not explicitly reported by Tontiwachwuthikul et al.:13 in particular, the temperature of the flue gas, and the concentration of water in the flue gas. Close inspection of an earlier paper detailing the experimental apparatus149 reveals that the temperature of the flue gas is controlled to be that of the lean solvent with a thermostatic bath. The inlet vapour stream is composed of ambient air and bottled CO2. Typical values of the relative humidity of air (defined as the mole fraction of water vapour divided by the mole fraction of air saturated with water at the same temperature and pressure) lie between 20% to 70%, which, at 20 °C and 1 bar, corresponds to a mass fraction of H2O 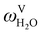 in the flue gas of between 0.003 and 0.01.150 A sensitivity analysis of the extent of humidity indicates that the variation of
in the flue gas of between 0.003 and 0.01.150 A sensitivity analysis of the extent of humidity indicates that the variation of 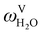 between 0 and 0.072 (corresponding to a mole fraction 0.12) has a negligible impact on the temperature and composition profiles. The effect of the amount of water in the flue gas is discussed in more detail in Section 3.3.2. For our working model, the nominal amount of water in the inlet flue gas is fixed to
between 0 and 0.072 (corresponding to a mole fraction 0.12) has a negligible impact on the temperature and composition profiles. The effect of the amount of water in the flue gas is discussed in more detail in Section 3.3.2. For our working model, the nominal amount of water in the inlet flue gas is fixed to 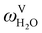 = 0.0058, corresponding to 50% humidity at 20 °C and 1 bar.
= 0.0058, corresponding to 50% humidity at 20 °C and 1 bar.
Table 6 Inputs to absorber column model for Runs T13 to T22 (ref. 13)
| Input variable |
T13 |
T14 |
T15 |
T16 |
T17 |
T18 |
T19 |
T20 |
T21 |
T22 |
| Inlet gas flow (mol m−2 s−1) |
17.54 |
17.54 |
18.4 |
17.51 |
17.54 |
18.29 |
16.72 |
18.32 |
13.72 |
18.3 |
| Inlet gas pressure (MPa) |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
| Inlet gas temperature (K) |
292.15 |
292.15 |
292.15 |
292.15 |
293.15 |
293.15 |
292.15 |
292.15 |
292.15 |
292.15 |
| Inlet gas CO2 mole fraction |
0.153 |
0.156 |
0.195 |
0.155 |
0.156 |
0.191 |
0.115 |
0.192 |
0.191 |
0.191 |
| Inlet gas H2O mass fraction |
0.0058 |
0.0058 |
0.0058 |
0.0058 |
0.0058 |
0.0058 |
0.0058 |
0.0058 |
0.0058 |
0.0058 |
| Inlet liquid flow (m3 m−2 h−1) |
13.5 |
13.5 |
13.5 |
9.5 |
13.5 |
9.5 |
13.5 |
9.5 |
9.5 |
9.5 |
| Inlet liquid temperature (K) |
292.15 |
292.15 |
292.15 |
292.15 |
293.15 |
293.15 |
292.15 |
292.15 |
292.15 |
292.15 |
| Inlet MEA concentration (kmol m−3) |
2.00 |
2.00 |
2.03 |
2.08 |
3.08 |
2.00 |
2.00 |
2.55 |
2.00 |
3.00 |
| Lean loading θCO2 |
10−4 |
0.118 |
10−4 |
10−4 |
0.237 |
10−4 |
10−4 |
10−4 |
10−4 |
10−4 |
Table 7 Characteristics of the column and the packing
| Name |
Value |
Source |
|
A
section (m2) |
0.00785 |
Tontiwachwuthikul et al.13 |
|
a
p (m2 m−3) |
466 |
Treybal139 |
|
σ
c (N m−1) |
61 |
Ref. 170 pg. 18–34, Tables 18–11 |
|
L
p (m) |
0.0127 |
Tontiwachwuthikul et al.13 |
|
ε
|
0.63 |
Ref. 139 pg. 198, Table 6.3 |
|
D
z (m) |
0.132 |
Tontiwachwuthikul et al.13 |
|
d
s (m) |
0.31622 |
Ref. 139 pg. 206, Table 6.5 |
3.2 Scenario 1
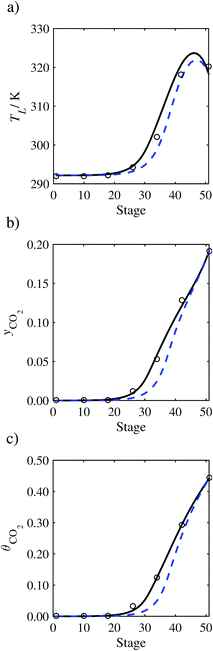
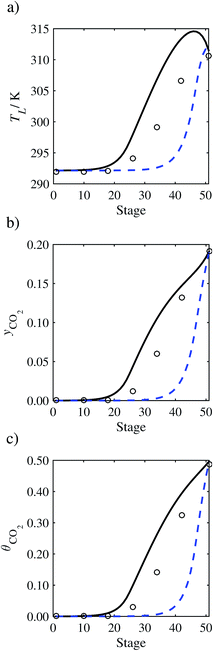
In the absence of pilot-plant data, the scaling factor τ for the diffusion coefficient of CO2, cf.eqn (48), is set to 1. The predictions with τ = 1 are presented in Fig. 7 and Fig. 9–17 as dashed curves. In all but one case (Run T18, Fig. 14), the rate of absorption of CO2 throughout the column is found to be over-predicted as the estimates for the gas-phase CO2 concentration profiles yCO2 all fall under the measured values. With the exception of Run T18, the temperature profiles TL and the liquid-phase CO2 loading profiles θCO2 are similarly under-predicted. Complete absorption occurs at approximately stage 30, whilst an analysis of the pilot-plant data suggests that this occurs between stages 10 to 20. The size of the column required to achieve maximum absorption is therefore underestimated based on these predictions alone.
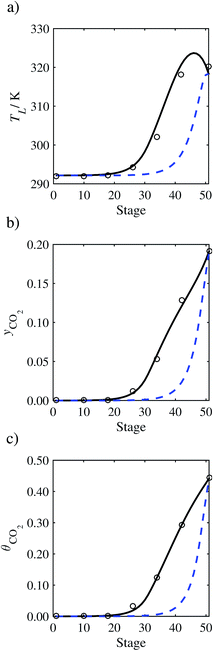 |
| | Fig. 7 Comparison of the pilot-plant data (circles)13 and the result of our model (curves) for Run T22 for the absorption of CO2 in an 18 wt% solution of MEA. The dashed curves represent the results obtained without scaling the CO2 diffusivity (τ = 1) and the continuous curves the results obtained with the ED correlation (eqn (48)) by scaling the CO2 diffusivity in the liquid phase to 4.1% of its original value (τ = 0.041). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading (defined as the number of moles of CO2 per mole of MEA in the liquid phase). Stage 50 corresponds to the bottom of the column. | |
 |
| | Fig. 8 Sensitivity analysis of the mass transfer correlation on the profiles predicted with our model compared with the experimental pilot-plant data of Run T2213: mass-transfer correlations from Onda et al.57,58 (continuous curve); mass-transfer correlations from Rocha et al.60,151 (a) Temperature profile for the liquid phase, (b) gas phase CO2 concentration profile, and (c) liquid phase CO2 loading. Stage 50 corresponds to the bottom of the column. | |
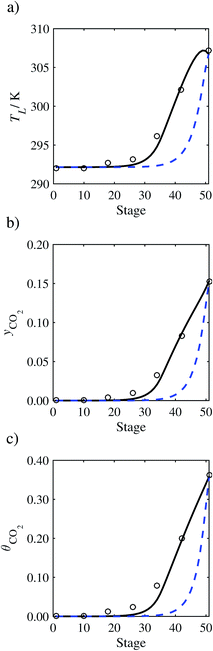 |
| | Fig. 9 Comparison of the pilot-plant data (circles)13 and the result of our model (curves) for Run T13. The dashed curves represent the results obtained without scaling the CO2 diffusivity (τ = 1) and the continuous curves the results obtained with the ED correlation (eqn (48))by scaling the CO2 diffusivity in the liquid phase to 4.1% of its original value (τ = 0.041). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading. Stage 50 corresponds to the bottom of the column. | |
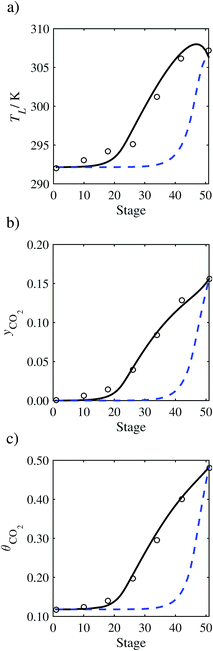 |
| | Fig. 10 Comparison of the pilot-plant data (circles)13 and the result of our model (curves) for Run T14. The dashed curves represent the results obtained without scaling the CO2 diffusivity (τ = 1) and the continuous curves the results obtained with the ED correlation (eqn (48)) by scaling the CO2 diffusivity in the liquid phase to 4.1% of its original value (τ = 0.041). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading. Stage 50 corresponds to the bottom of the column. | |
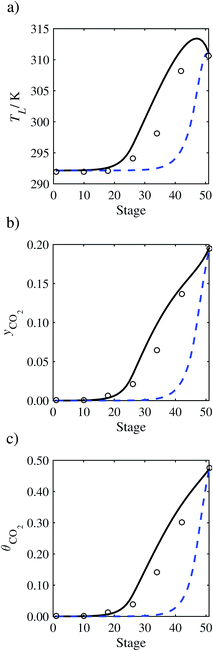 |
| | Fig. 11 Comparison of the pilot-plant data (circles)13 and the result of our model (curves) for Run T15. The dashed curves represent the results obtained without scaling the CO2 diffusivity (τ = 1) and the continuous curves the results obtained with the ED correlation (eqn (48)) by scaling the CO2 diffusivity in the liquid phase to 4.1% of its original value (τ = 0.041). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading. Stage 50 corresponds to the bottom of the column. | |
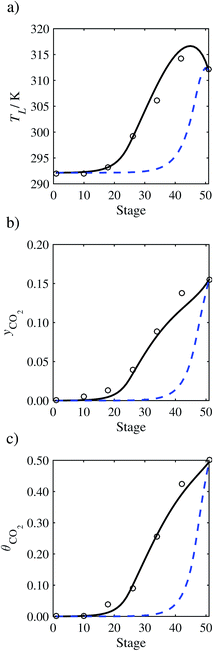 |
| | Fig. 12 Comparison of the pilot-plant data (circles)13 and the result of our model (curves) for Run T16. The dashed curves represent the results obtained without scaling the CO2 diffusivity (τ = 1) and the continuous curves the results obtained with the ED correlation (eqn (48)) by scaling the CO2 diffusivity in the liquid phase to 4.1% of its original value (τ = 0.041). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading. Stage 50 corresponds to the bottom of the column. | |
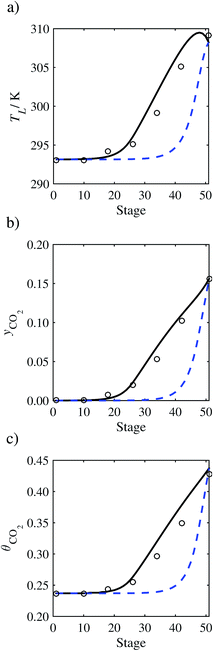 |
| | Fig. 13 Comparison of the pilot-plant data (cirlces)13 and the result of our model (curves) for Run T17. The dashed curves represent the results obtained without scaling the CO2 diffusivity (τ = 1) and the continuous curves the results obtained with the ED correlation (eqn (48)) by scaling the CO2 diffusivity in the liquid phase to 4.1% of its original value (τ = 0.041). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading. Stage 50 corresponds to the bottom of the column. | |
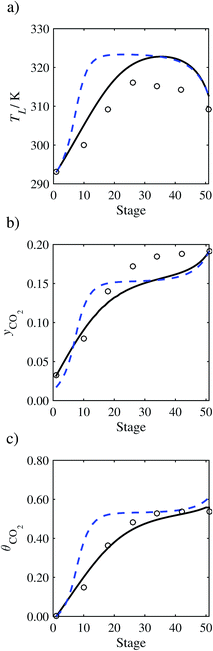 |
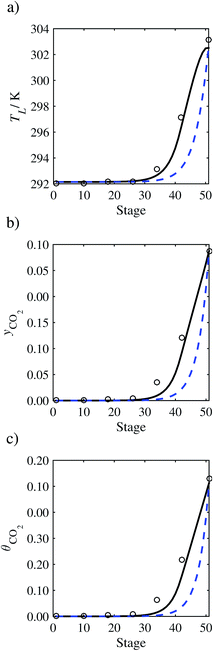
| | Fig. 14 Comparison of the pilot-plant data (cirlces)13 and the result of our model (curves) for Run T18. The dashed curves represent the results obtained without scaling the CO2 diffusivity (τ = 1) and the continuous curves the results obtained with the ED correlation (eqn (48)) by scaling the CO2 diffusivity in the liquid phase to 4.1% of its original value (τ = 0.041). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading. Stage 50 corresponds to the bottom of the column. | |
 |
| | Fig. 15 Comparison of the pilot-plant data (cirlces)13 and the result of our model (curves) for Run T19. The dashed curves represent the results obtained without scaling the CO2 diffusivity (τ = 1) and the continuous curves the results obtained with the ED correlation (eqn (48)) by scaling the CO2 diffusivity in the liquid phase to 4.1% of its original value (τ = 0.041). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading. Stage 50 corresponds to the bottom of the column. | |
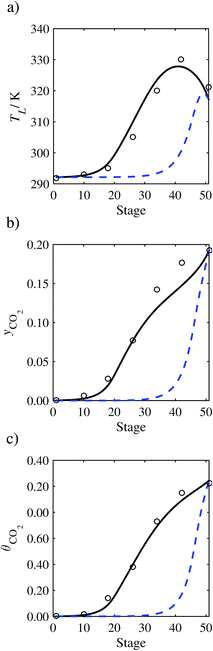 |
| | Fig. 16 Comparison of the pilot-plant data (cirlces)13 and the result of our model (curves) for Run T20. The dashed curves represent the results obtained without scaling the CO2 diffusivity (τ = 1) and the continuous curves the results obtained with the ED correlation (eqn (48)) by scaling the CO2 diffusivity in the liquid phase to 4.1% of its original value (τ = 0.041). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading. Stage 50 corresponds to the bottom of the column. | |
 |
| | Fig. 17 Comparison of the pilot-plant data (cirlces)13 and the result of our model (curves) for Run T21. The dashed curves represent the results obtained without scaling the CO2 diffusivity (τ = 1) and the continuous curves the results obtained with the ED correlation (eqn (48)) by scaling the CO2 diffusivity in the liquid phase to 4.1% of its original value (τ = 0.041). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading. Stage 50 corresponds to the bottom of the column. | |
In Run T18 (Fig. 14), there are two competing effects: the overestimation of the absorption of CO2 tends to increase the temperature of the liquid phase, which in turn tends to decrease the extent of absorption of CO2 in the liquid. Since this is the only run in which the CO2 in the inlet gas is not completely absorbed within the column, the cooling effect of the liquid feed is not as apparent as in other runs. Given the relatively low recovery of CO2 and the fact that equilibrium is not reached at the bottom of the column, our findings indicate that the model is best used as an indicator of process performance by modelling a sufficiently large absorber to achieve equilibrium.
In general, an optimistic prediction of process performance is thus obtained with the model when no pilot-plant data are used (τ = 1). Indeed, although the depletion of CO2 through chemical reactions has an accelerating effect on mass transfer, the reduced diffusivities of the product species lead to an overall reduction in mass transfer rates. This suggests that the proposed predictive model could be used to obtain a preliminary assessment of novel solvents in the absence of pilot-plant data: if their best-case (τ = 1) performance is found to be significantly less than that of MEA or another suitable benchmark, these solvents would be eliminated from further consideration without undertaking an experimental programme.
3.3 Scenario 2
3.3.1 Estimation of the scaling factor.
In order to investigate whether the proposed model can be used to provide quantitative agreement with the pilot-plant runs, the value of τ is now estimated by fitting to selected pilot-plant data. In keeping with our requirement to rely on only a limited amount of experimental data in the first step of the solvent selection process (and the exploration of a large space of solvents), the value τ is estimated from only one pilot-plant run (Run T22 of Tontiwachwuthikul et al.13). Additionally, this value is determined by minimizing the absolute deviation between the model predictions and the gas and liquid composition profiles, yCO2 and θCO2. The resulting temperature profile for Run T22 is hence predicted rather than correlated. The value of τ in the ED correlation (eqn (48)) that results in the minimum deviation from the compositional pilot-plant data corresponds to a scaling of the liquid-phase diffusivity to 4.1% of its original value (i.e., τ = 0.041). The liquid-phase temperature, gas-phase CO2 concentration, and liquid-phase CO2 concentration profiles for Run T22, determined with and without the scaling factor for the diffusivity of CO2, are represented in Fig. 7 as continuous and dashed curves, respectively.
As the parameter τ is estimated from pilot-plant data, this may be correcting any potential errors in the chosen mass-transfer correlation rather than the diffusivity alone. To the best of our knowledge, there is no published experimental data for the diffusion of the carbamate product in aqueous MEA. In order to assess the impact of the choice of mass-transfer correlation on the value of τ, we also implement the mass-transfer correlations of Rocha et al.60,151 in our current model of the absorber with the same scaling factor of τ = 0.041. The liquid-phase temperature, gas-phase CO2 concentration, and liquid-phase CO2 concentration profiles for Run T22 obtained with the two different mass transfer correlations are compared in Fig. 8. It can be seen that the profiles obtained are very similar: with the correlation of Rocha et al.60,151 there is a slight underestimation of the composition of CO2 in the liquid and gas phases, though one should bear in mind that the diffusivity parameter is determined from the data using the correlation of Onda et al.57,58 Both mass-transfer correlations predict the experimental temperature profiles equally well. In conclusion, the value of τ is found to be essentially independent of the choice of the mass-transfer correlation (at least for this set of process conditions), confirming our hypothesis that a scaling of the diffusivity is necessary to accurately model the process.
3.3.2 Model predictions.
Other runs with the MEA absorption pilot plant can now be simulated in a predictive manner with the ED correlation (eqn (48)) using the value of the diffusivity parameter (τ = 0.041) obtained based on Run T22. The predictions for the profiles of the temperature in the liquid phase, the gas-phase CO2 concentration, and liquid-phase CO2 loading for the different Runs T13 to T21 are represented in Fig. 9–17 with continuous curves. These runs represent a variety of operating conditions in terms of amine concentration, inlet liquid-phase CO2 loading, inlet gas-phase CO2 concentration, and gas-to-liquid flow rate ratio (see Table 6).
Good agreement is found between the model predictions and the pilot-plant data for Runs T13, T14, T16, T17, T19, and T20 in relation to the liquid-phase temperature and the liquid- and gas-phase compositions along the entire length of the column. There is a slight over-prediction of the temperature and the composition profile for Runs T15 and T21, though the compositions at the top and at the bottom of the column are accurately described. The outlet liquid temperature for Run T18 is overestimated by about 12 K; there is a good match between the model predictions and the experimental values for the composition profiles. A good representation of the temperature bulges for Runs T16 and T20 can be seen in terms of their location along the column, and the amplitude is predicted accurately for both of these runs. To the best of our knowledge, no other published model provides a description of the temperature bulge to this level of fidelity.29,33,48,99
In all runs except Run T18, flat profiles are observed toward the top of the column. This plateau means that a maximum in the absorption is reached, indicating that equilibrium is achieved not only at the vapour–liquid interface but also between the bulk liquid and the bulk vapour phases. As a result the profiles are not be affected by making the column any higher. This plateau is depicted in Fig. 18 for Run T22. It is apparent that the temperatures of the liquid phase, the vapour phase, and the vapour–liquid interface are all equal between stages 1 and 15 (i.e. at the top of the column). Similarly, the CO2 gas-phase composition in the bulk vapour phase and at the vapour interface are equal between stages 1 and 15, as are the CO2 loadings in the liquid phase and at the interface. The profiles for the temperature of the liquid phase and the temperature at the interface are found to be almost identical, suggesting that all the heat-transfer resistance is in the vapour film.
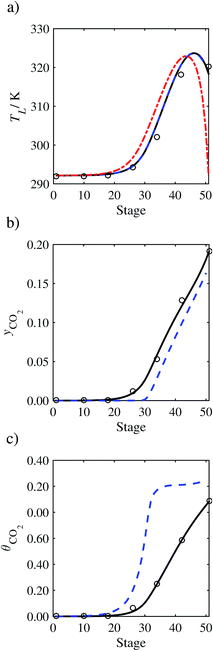 |
| | Fig. 18 Pilot plant data for Run T22 of Tontiwachwuthikul et al.13 Comparison of the predictions of our model for: (a) the temperature of the bulk liquid phase (continuous curve), the temperature at the vapour–liquid interface (dashed curve indistinguishable from the continuous curve), and the temperature of the bulk vapour phase (dot-dashed curve); (b) the gas-phase CO2 concentration in the bulk vapour phase (continuous curve) and at the interface (dashed curve); (c) the liquid-phase CO2 loading in the bulk liquid phase (continuous curve) and at the interface (dashed curve). | |
Run T18 stands out from this set of runs as it does not exhibit a plateau in the profiles as found for the other operating conditions, meaning that the whole length of the column is used for absorption. The lack of a plateau region is clearly apparent from Fig. 19. From Table 6, one can see that Run T18 corresponds to the lowest amount of MEA in the lean solvent and the highest amount of CO2 in the flue gas compared to the other runs. As a result the whole column is required for absorption. In other runs, the totality of CO2 is absorbed as the gas travels up the column between stages 50 and 15, so that lean solvent flowing at the top of the absorber (stages 1 to 15) has essentially no CO2 left to absorb. Run T18 is the only run where there is still CO2 in the gas stream leaving the absorber, so the lean solvent starts absorbing CO2 as soon as it enters the column at the top. These differences explain why a larger discrepancy is observed between the predicted and measured profiles for Run T18.
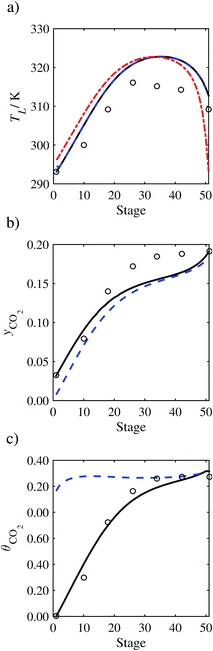 |
| | Fig. 19 Pilot plant data for Run T18 of Tontiwachwuthikul et al.13 Comparison of the predictions of our model for: (a) the temperature of the bulk liquid phase (continuous curve), the temperature at the vapour–liquid interface (dashed curve indistinguishable from the continuous curve), and the temperature of the bulk vapour phase (dot-dashed curve); (b) the gas-phase CO2 concentration in the bulk vapour phase (continuous curve) and at the interface (dashed curve); (c) the liquid-phase CO2 loading in the bulk liquid phase (continuous curve) and at the interface (dashed curve). | |
The behaviour of Runs T15, T18, and T21 could be represented more accurately by estimating specific values of τ for these runs. However, this would not be in keeping with our objective to develop a predictive modelling platform to support solvent-design activities. The good overall quantitative agreement achieved with a unique value of τ indicates that the scaling factor can be applied in a transferable manner at different operating conditions (at least for similar types of column packing).
An analysis of the deviation between the column profiles presented here and those obtained when a different run is chosen to estimate τ is also undertaken. The same method is applied to estimate τ with the ED correlation (eqn (48)) based on pilot plant Runs T13–T21. The values of τ range between 0.027 (for Run T19) and 0.076 (for Run T21). These extreme values are then used to predict the column profiles (for TL, yCO2, and θCO2). The absolute errors between the values for each variable obtained with τ = 0.041 (for Run T22) and the values obtained from the extreme values of τ are calculated, and averaged over all of the stages and column profiles. The calculated mean errors are 4.35 K for TL, 0.080 for θCO2 and 0.023 for yCO2. These values provide an indication of the error bounds for the profiles presented in our current work, based on choosing any single pilot plant run arbitrarily to estimate the value of τ.
3.4 Sensitivity analysis
A sensitivity analysis is now employed to assess the relative importance of selected mass- and heat-transfer parameters. Different key parameters in the model are altered to observe their impact on the predicted profiles. The properties considered are listed in Table 8.
Table 8 Sensitivity analysis of key properties in the model
| Parameter description |
Variation |
Effect |
| Vapour diffusivity |
Doubled |
Negligible effect |
| Halved |
| Liquid diffusivity |
Doubled |
Significant effect |
| Halved |
See Fig. 20 |
| Vapour viscosity |
Doubled |
Negligible effect |
| Halved |
| Liquid viscosity |
Doubled |
Significant effect |
| Halved |
See Fig. 21 |
| Surface tension |
+10 mN m−1 |
Negligible effect |
| −10 mN m−1 |
see Fig. 22 |
| Heat transfer in the liquid |
×10 |
Negligible effect |
| ÷10 |
| Heat transfer in the vapour |
×10 |
Limited effect |
| ÷10 |
See Fig. 23 |
| Heat of vaporization of water |
Doubled |
Significant effect |
| Halved |
See Fig. 24 |
| Mass fraction of water in inlet flue gas |
Varied between 0 and 0.072 |
Negligible effect |
| See Fig. 25 |
3.4.1 Mass transfer.
In the model, mass transfer is mediated via mass-transfer coefficients.57,58 These coefficients are highly dependent on the viscosity, the diffusivity, and to a certain degree, the surface tension of the fluid considered; these properties are thus considered as key parameters in the model and their influence on the temperature and composition profiles are assessed. The values of the parameters assessed in the sensitivity analysis are varied within physically realistic ranges. We should note that though marked variations are expected for the diffusivity and viscosity for a reacting system of this type, the change in the vapour–liquid surface tension is expected to be somewhat less dramatic. The values of the vapour and liquid diffusivities are doubled and halved, and the vapour–liquid surface tension is varied within ± 10 mN m−1 from the nominal value. Varying the diffusivity or viscosity in the gas phase has no discernable effect on the temperature profile of the liquid or the composition profiles. However, varying these properties in the liquid phase results in a significant variation in the profiles. The effect on the profiles due to the variation of the liquid viscosity and the diffusivity in the liquid phase is represented in Fig. 20 and 21. Varying the vapour–liquid interfacial tension produces a less significant variation in the profiles as can be seen in Fig. 22. The data that are originally considered for the surface-tension correlation in our model are for a mixture of only H2O and MEA.152 Jayarathna et al.153 have recently published experimental data of the surface tension of mixtures of H2O, MEA and CO2, finding an increase in the vapour–liquid interfacial tension on absorption of CO2. A new correlation from these data is also implemented in our process model. A comparison of the temperature and composition profiles obtained with the two different correlations is shown in Fig. 22. The difference in the profiles is negligible so changing the surface tension correlation is not considered necessary in this case. This also suggests that the process model is less sensitive to realistic changes in the interfacial tension than for corresponding changes in the diffusivity and viscosity. We should note that the vapour–liquid surface tension can also be determined from the SAFT-VR EOS within a density-functional treatment.84,154–156 We do not however pursue this approach here as the full DFT of the ternary H2O–MEA–CO2 mixture is computationally challenging, and as has just been discussed the use of the correlations for the surface tension of the H2O–MEA binary system provides a good representation of the pilot-plant data for the full mixture. The use of SAFT-VR DFT will be considered in future studies.
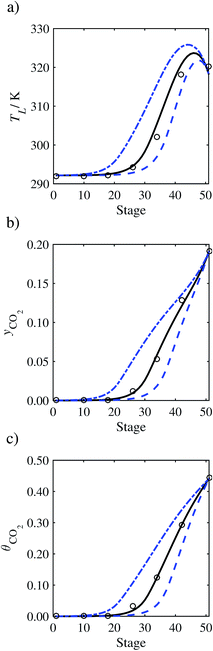 |
| | Fig. 20 Sensitivity analysis of the CO2 diffusivity in the liquid phase on the profiles predicted with our model in terms of the scaling parameter τ compared with the experimental pilot-plant data of Run T22 of Tontiwachwuthikul et al.:13τ = 0.041 (continuous curve), τ = 0.082 (dashed curve), and τ = 0.021 (dot-dashed curve). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading. | |
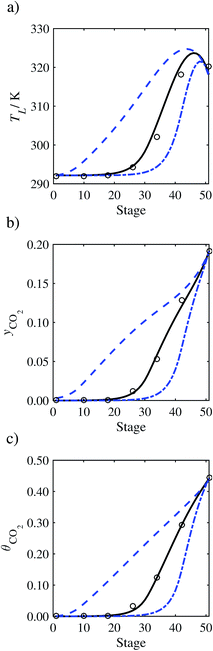 |
| | Fig. 21 Sensitivity analysis of the liquid viscosity on the profiles predicted with our model compared with the experimental pilot-plant data of Run T22 of Tontiwachwuthikul et al.:13 nominal value (continuous curve), viscosity doubled (dashed curve), and viscosity halved (dot-dashed curve). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading. | |
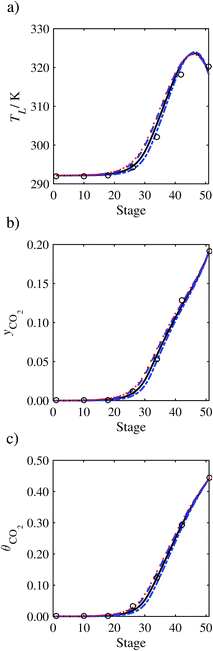 |
| | Fig. 22 Sensitivity analysis of the vapour–liquid surface tension on the profiles predicted with our model compared with the experimental pilot-plant data of Run T22 of Tontiwachwuthikul et al.:13 nominal value (continuous curve),152 +10 mN m−1 (dashed curve), −10 mN m−1 (dot-dashed curve), and the surface tension correlation for the loaded MEA solution obtained from Jayarathna et al.153 (dotted curve). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading. | |
It should be noted that the values of the mole fractions and temperatures at the outlets are not affected by the variations of the surface tension or the viscosity and diffusivity in the liquid phase. It would be safe to assume that under these operating conditions, where the residence time is large enough for the system to reach equilibrium, the outlet values are determined solely by thermodynamic considerations while the composition profiles are mostly dependent on mass transfer.
3.4.2 Heat transfer.
The major source of heat in the absorption process is a consequence of the exothermic reaction between MEA and CO2, which occurs in the liquid phase. This heat can then be transferred to the vapour phase. Another major element in the energy balance is the heat associated with the transfer of water from one phase to the other. In the model, the heat transfer is mediated via heat-transfer coefficients.139 Two notable thermal parameters can be identified in the model: the heat-transfer coefficient for the liquid phase, and the heat-transfer coefficient for the gas phase. In addition, the magnitude of the enthalpy changes as the components are transferred from one phase to another or as the temperature changes in the gas and liquid streams affects the overall temperature profile. For instance, Kvamsdal and Rochelle103 and Faramarzi et al.48 have identified heat capacities as sensitive properties for the temperature profiles. Here, we consider the impact of the heat of vaporization of water on the model predictions. Although it is a well characterized thermodynamic quantity, its variation provides insights into the behaviour of the column.
The value of the heat of vaporization of water is doubled and halved relative to the value predicted with the SAFT-VR EoS, and the values of the heat transfer coefficients are multiplied by 10 and divided by 10 (Table 8). The variation of the liquid heat-transfer coefficient has no visible effect on the liquid-phase temperature and composition profiles. The effects on the profiles resulting from varying the heat-transfer coefficients and the heat of vaporization of water are presented in Fig. 23 and 24, respectively.
 |
| | Fig. 23 Sensitivity analysis of the vapour-phase heat-transfer coefficient on the profiles predicted with our model compared with the experimental pilot-plant data of Run T22 of Tontiwachwuthikul et al.:13 Nominal value (continuous curve), coefficient value multiplied by 10 (dashed curve), and coefficient value divided by 10 (dot-dashed curve). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading. | |
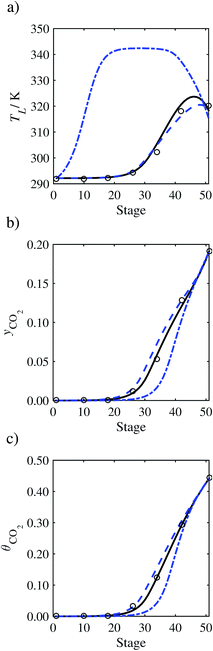 |
| | Fig. 24 Sensitivity analysis of the enthalpy of vaporization of water on the profiles predicted with our model compared with the experimental pilot-plant data of Run T22 of Tontiwachwuthikul et al.:13 Nominal value (continuous curve), enthalpy doubled (dashed curve), and enthalpy halved (dot-dashed curve). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading. | |
As can be seen from Fig. 23, despite a variation of one order of magnitude in the vapour heat-transfer coefficient, the effect on the temperature profile is very limited. It can be concluded that for the operating conditions under consideration, the model is insensitive to the heat-transfer coefficients and there is no need to investigate heat-transfer correlations further.
The variation of the heat of vaporization of water is found to have a significant impact on the liquid phase temperature profile when its value is doubled, and a lesser impact on the composition profiles; it has a limited effect on the end-point values. An increase in the heat of vaporization magnifies the amplitude of the temperature bulge, whereas a reduction eliminates the bulge. This suggests that the heat of vaporization of H2O is responsible for the rate at which the liquid heats up and cools down. A similar effect is observed when a sensitivity analysis is carried out on the heat of absorption of CO2, however the analysis is not presented here because the adjustment of both properties leads to similar (but opposite) corrections to the energy balance. The key elements to predict the temperature bulge accurately are therefore the enthalpy of absorption of CO2 and the enthalpy of vaporization of water. The absorption of CO2 releases energy that heats both phases. As the gas temperature increases upon entering the column, water is transferred from the liquid phase to the gas phase through evaporation to maintain saturation; this results in an absorption of energy, and a consequent decrease in temperature.
In conclusion, the competition between these two thermal effects (the absorption of CO2 increases the temperature and the vaporization of water decreases the temperature) is responsible for the observed and predicted temperature bulge. This interpretation is consistent with that reported in Mac Dowell et al.99
3.4.3 Effect of humidity in the flue gas.
The amount of water in the flue gas is considered to be important in determining the position of the temperature bulge in the absorber.103,157 In the case of the pilot plants examined by Tontiwachwuthikul et al.13 and Dugas,14 the inlet flue gas is not saturated in water, while the flue gas is saturated in the pilot-plant studies of Tobiesen et al.47 and Gabrielsen et al.16 In order to assess the impact of humidity in our model of the absorber, we vary the amount of water in the inlet flue gas from 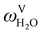 = 0 to 0.072 (corresponding to a mole fraction of 0.12) (water-rich). The effect on the profiles is represented in Fig. 25. It is apparent that varying the amount of water in the flue gas does not have a significant impact on the composition profiles. The effect is visible only for the liquid-phase temperature profile, where the outlet temperature value is higher by approximately 5 K for the saturated gas
= 0 to 0.072 (corresponding to a mole fraction of 0.12) (water-rich). The effect on the profiles is represented in Fig. 25. It is apparent that varying the amount of water in the flue gas does not have a significant impact on the composition profiles. The effect is visible only for the liquid-phase temperature profile, where the outlet temperature value is higher by approximately 5 K for the saturated gas  = 0.072 than for the dry gas
= 0.072 than for the dry gas  = 0. Biliyok et al.56 also find that increasing the moisture content of the flue gas affects the absorber temperature profile, however the increase in temperature is more significant in their study because a larger change in moisture content is considered (
= 0. Biliyok et al.56 also find that increasing the moisture content of the flue gas affects the absorber temperature profile, however the increase in temperature is more significant in their study because a larger change in moisture content is considered ( varies between 0.015 and 0.15, where the latter value represents a two-phase aqueous system). The negligible effect on the composition profiles is in contrast to the work of Mac Dowell et al.99 who found a large effect of the humidity of the inlet gas on the flux profiles in the mass transfer zone.
varies between 0.015 and 0.15, where the latter value represents a two-phase aqueous system). The negligible effect on the composition profiles is in contrast to the work of Mac Dowell et al.99 who found a large effect of the humidity of the inlet gas on the flux profiles in the mass transfer zone.
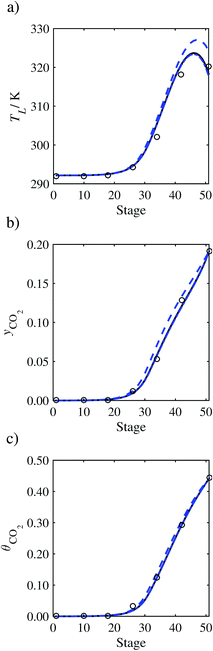 |
| | Fig. 25 Sensitivity analysis of the amount of water in the inlet flue gas on the profiles predicted with our model compared with the experimental pilot-plant data of Run T22 of Tontiwachwuthikul et al.:13 Nominal value (continuous curve), yH2O = 0.072 (dashed curve), and yH2O = 0 (dot-dashed curve). (a) Temperature profile for the liquid phase, (b) gas-phase CO2 concentration profile, and (c) liquid-phase CO2 loading. | |
4 Conclusions
An absorber model for CO2 capture is developed with the aim of being as predictive as possible, in order to support solvent-design activities prior to extensive experimental investigations. The heat and mass transfer are described with rate-based equations, in common with many other process models. Unusually, however, a physical approach is taken to model the chemical reactions taking place in the absorber. Both vapour–liquid equilibrium and chemical equilibrium are treated within the SAFT-VR thermodynamic framework, ensuring a consistent and accurate representation of the physical interactions in the system under the assumption that the reaction kinetics are not rate-determining. This approach lends itself to straightforward extension to other solvents, as a consequence of the transferable nature of the SAFT molecular models and the relatively small number of parameters and data required to develop them.
Without making use of pilot-plant data in model development, we find that the proposed model can generally be used to obtain a best-case performance of the solvent in question. This modelling approach is valuable for narrowing the solvent search space as solvents may be quickly rejected by comparing their performance in such a test. With very limited pilot-plant data we find that by adjusting a single parameter in the ED correlation for the mass transfer, that corrects for the diffusivity of CO2 in the liquid phase, the model can be used to predict with quantitative accuracy a variety of different operating conditions. Excellent predictions are obtained for the liquid-phase temperature profiles and the liquid- and gas-phase compositions along the column in most cases, with moderate deviations in some instances. The comparison of the absorption performance of different solvents via this method may further aid in the narrowing of the solvent search space, and then a more quantitative comparison could be carried out.
Following accurate predictions of the column profiles, a careful sensitivity analysis is conducted. We find that the liquid viscosity and diffusivity are key properties for the prediction of the composition profiles. The column profiles are also shown to be sensitive to the thermodynamic properties that are major sources of heat generation or dissipation.
The main benefit of the proposed modelling framework, which is based on the physical modelling of the underlying chemical reactions, is the ability to assess new solvents for which there may be limited data. This can be further enhanced through the adoption of a group-contribution EoS, which makes use of the same physical concepts, such as the SAFT-γ Mie EoS.121 The modification of the proposed model to use this group-contribution approach is straightforward and offers an additional predictive capability as new solvents may be analyzed for which no experimental data are available. Additionally, it is clear that an extension of the work presented here to the desorption process and the coupling of the absorber and desorber is required.158 This would allow for a more comprehensive predictive assessment of new solvents and for the rapid evaluation of many alternative multifunctional amines for the optimal capture of CO2 from flue gas.
Nomenclature
![[small upsilon, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e158.gif) L
L
| Volumetric flow rate of the liquid phase (m3 s−1) |
![[small upsilon, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e158.gif) V
V
| Volumetric flow rate of the vapour phase (m3 s−1) |
|
ε
| Void fraction (-) |
|
ε
L0
| Operating void space in the packing (-) |
|
η
L
| Dynamic viscosity of the liquid phase (kg m−1 s−1) |
|
η
V
| Dynamic viscosity of the vapour phase (kg m−1 s−1) |
|
λ
LT
| Liquid thermal conductivity (W m−1 K−1) |
|
λ
VT
| Vapour thermal conductivity (W m−1 K−1) |
|
λ
ij
| Parameter of the attractive range of the intermolecular potential between two segments i and j (-) |
|
μ
L
i,j
| Chemical potential of component i in the liquid phase on stage j (J mol−1) |
|
μ
V
i,j
| Chemical potential of component i in the gas phase on stage j (J mol−1) |
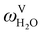
| Mass fraction of water in the vapour phase |
|
ϕM
| Association factor for the liquid mixture (-) |
|
ϕ
j
| Association factor of solvent j (-) |
|
ρ
L
| Density of the liquid phase (kg m−3) |
|
ρ
V
| Density of the vapour phase (kg m−3) |
|
σ
| Vapour–liquid surface tension (N m−1) |
|
σ
c
| Critical surface tension of the packing material (N m−1) |
|
Σ
v
| Atomic diffusion volume (Å) |
|
σ
ii
| Diameter of segments forming molecule i (Å) |
|
τ
| Scaling factor for the liquid diffusivity of CO2 in the solvent (-) |
|
θ
CO2
| CO2 loading in the liquid phase (-) |
![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) j
j
| Vector of liquid mole fractions on stage j (-) |
![[y with combining low line]](https://www.rsc.org/images/entities/i_char_0079_0332.gif) j
j
| Vector of vapour mole fractions on stage j (-) |
![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif) i
i
| Molar composition vector of a stream consisting of pure component i (-) |
|
ε
HB
ab,ij/k | Depth of the interaction potential between association site a on molecule i and site b of molecule j (K) |
|
ε
ij
/k | Depth of the intermolecular potential between two segments i and j (K) |
|
a′j | Interfacial area density on stage j (m2 m−3) |
|
a
p
| Specific surface area of the packing (m2 m−3) |
|
A
section
| Cross-sectional area of the column (m2) |
|
a
T,j
| Total interfacial area available for heat or mass transfer on stage j (m2) |
|
c
| Total number of components |
|
C
L
i,j
| Concentration of component i in the liquid phase on stage j (mol m−3) |
|
C
V
i,j
| Concentration of component i in the vapour phase on stage j (mol m−3) |
|
C
I,L
i
| Concentration of component i at the liquid–vapour interface in the liquid phase (mol m−3) |
|
C
I,V
i
| Concentration of component i at the liquid–vapour interface in the vapour phase (mol m−3) |
|
C
Lp
| Specific isobaric heat capacity of the liquid phase (J kg−1 K−1) |
|
C
Vp
| Specific isobaric heat capacity of the vapour phase (J kg−1 K−1) |
|
D
L
i
| Diffusion coefficient of component i in the liquid phase (m2 s−1) |
|
D
V
i
| Diffusion coefficient of component i in the vapour phase (m2 s−1) |
|
D
°
i,j
| Mutual diffusion coefficient of solute i at very low concentrations in solvent j (cm2 s−1) |
|
d
s
| Diameter of a sphere of the same surface as a single packing particle (m) |
|
D
z
| Stage height (m) |
|
E
L
j
| Net gain of energy of the liquid phase on stage j (W) |
|
E
V
j
| Net loss of energy from the vapour phase on stage j (W) |
| FrL | Liquid-phase Froude number (-) |
|
g
| Gravitational acceleration (m s−2) |
|
H
L
j
| Enthalpy of the liquid phase on stage j (J mol−1) |
|
H
V
j
| Enthalpy of the vapour phase on stage j (J mol−1) |
|
h
packing
| Total packing height (m) |
|
h
LT,j
| Liquid-phase heat-transfer coefficient on stage j (W m−2 K−1) |
|
h
VT,j
| Vapour-phase heat-transfer coefficient on stage j (W m−2 K−1) |
|
k
| Boltzmann constant (J K−1) |
|
k
L
j
| Liquid-phase mass-transfer coefficient on stage j (m s−1) |
|
k
V
j
| Vapour-phase mass-transfer coefficient on stage j (m s−1) |
|
k
ij
| Binary interaction parameter used to compute the strength of the interactions between segments i and j (-) |
|
L
j
| Liquid molar flow rate leaving stage j (mol s−1) |
|
L
p
| Nominal packing size (m) |
|
L
spec
| Specific liquid flow rate (kg s−1) |
|
M
i
| Molecular weight of component i (g mol−1) |
|
m
i
| Number of segments in the molecule i |
|
N
L
i,j
| Net gain of species i in the liquid phase due to interphase transport on stage j (mol s−1) |
|
N
V
i,j
| Net loss of species i in the vapour phase due to interphase transport on stage j (mol s−1) |
|
N
s
| Number of stage in the column |
|
N
s,ia
| Number of sites of type a on molecule i |
|
N
s,i
| Number of site types for molecule i |
|
P
I
j
| Pressure at the vapour–liquid interface on stage j (MPa) |
|
P
L
j
| Pressure in the liquid phase on stage j (MPa) |
|
P
V
j
| Pressure in the vapour phase on stage j (MPa) |
| PrV | Prandtl number for the vapour phase (-) |
|
Q
Lcond,j
| Conductive heat flux in the liquid phase on stage j (W) |
|
Q
Ldiff,j
| Diffusive heat flux in the liquid phase on stage j (W) |
|
Q
Vcond,j
| Conductive heat flux in the vapour phase on stage j (W) |
|
Q
Vdiff,j
| Diffusive heat flux in the vapour phase on stage j (W) |
|
r
c;ab,ij
| Attractive range of the interaction potential between association site a on molecule i and site b of molecule j (Å) |
| ReL | Liquid-phase Reynolds number based on the interfacial area (-) |
| ReV | Vapour-phase Reynolds number (-) |
| ScLi | Schmidt number of component i in the liquid phase (-) |
| ScVi | Schmidt number of component i in the vapour phase (-) |
|
T
I
j
| Temperature at the vapour–liquid interface on stage j (K) |
|
T
L
j
| Temperature of the liquid phase on stage j (K) |
|
T
V
j
| Temperature of the vapour phase on stage j (K) |
|
u
L
| Liquid velocity (m s−1) |
|
u
V
| Vapour velocity (m s−1) |
|
V
L
j
| Molar volume of the liquid phase on stage j (cm3 mol−1) |
|
V
V
j
| Molar volume of the vapour phase on stage j (cm3 mol−1) |
|
V
*L
i,j
| Molar volume of the pure component i in the bulk liquid phase on stage j (cm3 mol−1) |
|
V
*V
i,j
| Molar volume of the pure component i in the bulk vapour phase on stage j (cm3 mol−1) |
|
V
I,L
j
| Molar volume of the liquid phase at the vapour–liquid interface on stage j (cm3 mol−1) |
|
V
I,V
j
| Molar volume of the gas phase at the vapour–liquid interface on stage j (cm3 mol−1) |
|
V
m
i
| Molar volume of solute i at its normal boiling temperature (cm3 mol−1) |
|
V
j
| Vapour molar flow rate leaving stage j (mol s−1) |
|
V
spec
| Specific vapour flow rate (kg s−1) |
| WeL | Liquid-phase Weber number (-) |
| ReL′ | Liquid-phase Reynolds number based on the specific surface area (-) |
Acknowledgements
We are very grateful to Leila Faramarzi and Georgios Kontogeorgis for helpful discussions regarding details of the pilot-plant and mass-transfer correlations. C. V. B. and E. G thank the Department of Chemical Engineering of Imperial College London and Engineering and Physical Sciences Research Council (EPSRC) of the UK for the award of PhD studentships. Additional funding to the Molecular Systems Engineering Group from the EPSRC (grants GR/T17595, GR/N35991, EP/E016340, EP/J003840/1, and EP/J014958) is also gratefully acknowledged.
References
-
The European Commission, A Roadmap for Moving to a Competitive Low Carbon Economy in 2050, http://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:52011DC0112%26from=EN, 2011 Search PubMed.
-
UNFCCC, Adoption of the Paris Agreement, https://unfccc.int/resource/docs/2015/cop21/eng/l09r01.pdf, 2015 Search PubMed.
- N. Mac Dowell, N. Florin, A. Buchard, J. Hallett, A. Galindo, G. Jackson, C. S. Adjiman, C. K. Williams, N. Shah and P. S. Fennell, Energy Environ. Sci., 2010, 3, 1645–1669 CAS.
- S. Paul, A. K. Ghoshal and B. Mandal, Chem. Eng. J., 2008, 144, 352–360 CrossRef CAS.
- H. P. Mangalapally, R. Notz, S. Hoch, N. Asprion, G. Sieder, H. Garcia and H. Hasse, Energy Proc., 2009, 1, 963–970 CrossRef CAS.
- A. Bardow, K. Steur and J. Gross, Ind. Eng. Chem. Res., 2010, 49, 2834–2840 CrossRef CAS.
- F. Barzagli, M. Di Vaira, F. Mani and M. Peruzzini, ChemSusChem, 2012, 5, 1724–1731 CrossRef CAS PubMed.
- H. P. Mangalapally, R. Notz, N. Asprion, G. Sieder, H. Garcia and H. Hasse, Int. J. Greenhouse Gas Control, 2012, 8, 205–216 CrossRef CAS.
- J. Li, C. You, L. Chen, Y. Ye, Z. Qi and K. Sundmacher, Ind. Eng. Chem. Res., 2012, 51, 12081–12088 CrossRef CAS.
- Y. K. Salkuyeh and M. Mofarahi, Int. J. Energy Res., 2013, 37, 973–981 CrossRef CAS.
- S. Chen, S. Chen, X. Fei, Y. Zhang and L. Qin, Ind. Eng. Chem. Res., 2015, 54, 7212–7218 CrossRef CAS.
- P. V. Kortunov, M. Siskin, L. S. Baugh and D. C. Calabro, Energy Fuels, 2015, 29, 5940–5966 CrossRef CAS.
- P. Tontiwachwuthikul, A. Meisen and C. J. Lim, Chem. Eng. Sci., 1992, 47, 381–390 CrossRef CAS.
-
R. E. Dugas, PhD thesis, The University of Texas at Austin, 2006.
- F. A. Tobiesen and H. F. Svendsen, Ind. Eng. Chem. Res., 2006, 45, 2489–2496 CrossRef CAS.
- J. Gabrielsen, H. F. Svendsen, M. L. Michelsen, E. H. Stenby and G. M. Kontogeorgis, Chem. Eng. Sci., 2007, 62, 2397–2413 CrossRef CAS.
- H. Habaki, J. M. Perera, S. E. Kentish, G. W. Stevens and W. Fei, Sep. Sci. Technol., 2007, 42, 701–716 CrossRef CAS.
- H. R. Godini and D. Mowla, Chem. Eng. Res. Des., 2008, 86, 401–409 CrossRef CAS.
- A. J. Cottrell, J. M. McGregor, J. Jansen, Y. Artanto, N. Dave, S. Morgan, P. Pearson, M. I. Attalla, L. Wardhaugh, H. Yu, A. Allport and P. H. M. Feron, Energy Proc., 2009, 1, 1003–1010 CrossRef CAS.
- R. Notz, H. P. Mangalapally and H. Hasse, Int. J. Greenhouse Gas Control, 2012, 6, 84–112 CrossRef CAS.
- M. Akram, U. Ali, T. Best, S. Blakey, K. Finney and M. Pourkashanian, Int. J. Greenhouse Gas Control, 2016, 47, 137–150 CrossRef CAS.
-
G. Astarita, Mass Transfer with Chemical Reaction, Elsevier, 1967 Search PubMed.
- H. Hikita, S. Asai, H. Ishikawa and M. Honda, Chem. Eng. J., 1977, 13, 7–12 CrossRef CAS.
- P. V. Danckwerts, Chem. Eng. Sci., 1979, 34, 443–446 CrossRef CAS.
- S. S. Laddha and P. V. Danckwerts, Chem. Eng. Sci., 1981, 36, 479–482 CrossRef CAS.
-
G. Astarita, D. W. Savage and A. Brito, Gas Treating with Chemical Solvents, John Wiley & Sons, 1983 Search PubMed.
- D. E. Penny and T. J. Ritter, J. Chem. Soc., Faraday Trans. 1, 1983, 79, 2103–2109 RSC.
- P. M. M. Blauwhoff, G. F. Versteeg and W. P. M. Van Swaaij, Chem. Eng. Sci., 1984, 39, 207–225 CrossRef CAS.
- L. Kucka, I. Muller, E. Y. Kenig and A. Górak, Chem. Eng. Sci., 2003, 58, 3571–3578 CrossRef CAS.
- Y. Zhang, H. Que and C.-C. Chen, Fluid Phase Equilib., 2011, 311, 67–75 CrossRef CAS.
- C. Kale, A. Górak and H. Schoenmakers, Int. J. Greenhouse Gas Control, 2013, 17, 294–308 CrossRef CAS.
- A. Aboudheir, P. Tontiwachwuthikul and R. Idem, Ind. Eng. Chem. Res., 2006, 45, 2553–2557 CrossRef CAS.
- J. Gabrielsen, M. L. Michelsen, E. H. Stenby and G. M. Kontogeorgis, AIChE J., 2006, 52, 3443–3451 CrossRef CAS.
- W.-J. Choi, J.-B. Seo, S.-W. Cho, S.-W. Park and K.-J. Oh, Korean J. Chem. Eng., 2009, 26, 705–710 CrossRef CAS.
- M. Afkhamipour and M. Mofarahi, Int. J. Greenhouse Gas Control, 2013, 15, 186–199 CrossRef CAS.
-
R. Taylor and R. Krishna, Multicomponent Mass Transfer, John Wiley & Sons, 1993 Search PubMed.
-
F. M. Khoury, Multistage Separation Processes, CRC Press, 2005 Search PubMed.
- J. Ying and D. A. Eimer, Ind. Eng. Chem. Res., 2013, 52, 2548–2559 CrossRef CAS.
- A. Lawal, M. Wang, P. Stephenson and H. Yeung, Fuel, 2009, 88, 2455–2462 CrossRef CAS.
-
P. V. Danckwerts, Gas-Liquid Reactions, McGraw-Hill, 1970 Search PubMed.
- W. J. DeCoursey, Chem. Eng. Sci., 1982, 37, 1483–1489 CrossRef CAS.
- W. P. M. van Swaaij and G. F. Versteeg, Chem. Eng. Sci., 1992, 47, 3181–3195 CrossRef CAS.
- M. S. Sivasubramanian, H. Sardar and R. H. Weiland, Oil Gas J., 1985, 83, 133–136 CAS.
- T. Pintola, P. Tontiwachwuthikul and A. Meisen, Gas Sep. Purif., 1993, 7, 47–52 CrossRef CAS.
- M. A. Pacheco and G. T. Rochelle, Ind. Eng. Chem. Res., 1998, 37, 4107–4117 CrossRef CAS.
- N. A. Al-Baghli, S. A. Pruess, V. F. Yesavage and M. S. Selim, Fluid Phase Equilib., 2001, 185, 31–43 CrossRef CAS.
- F. A. Tobiesen, H. F. Svendsen and O. Juliussen, AIChE J., 2007, 53, 846–865 CrossRef CAS.
- L. Faramarzi, G. M. Kontogeorgis, M. L. Michelsen, K. Thomsen and E. H. Stenby, Ind. Eng. Chem. Res., 2010, 49, 3751–3759 CrossRef CAS.
- F. Khan, V. Krishnamoorthi and T. Mahmud, Chem. Eng. Res. Des., 2011, 89, 1600–1608 CrossRef CAS.
- T. Neveux, Y. L. Moullec, J.-P. Corriou and E. Favre, Ind. Eng. Chem. Res., 2013, 52, 4266–4279 CrossRef CAS.
- M. Saimpert, G. Puxty, S. Qureshi, L. Wardhaugh and A. Cousins, Chem. Eng. Sci., 2013, 96, 10–25 CrossRef CAS.
- S. A. Jayarathna, B. Lie and M. C. Melaaen, Comput. Chem. Eng., 2013, 53, 178–189 CrossRef CAS.
- M. Afkhamipour and M. Mofarahi, Int. J. Greenhouse Gas Control, 2014, 25, 9–22 CrossRef CAS.
- M. Llano-Restrepo and E. Araujo-Lopez, Int. J. Greenhouse Gas Control, 2015, 42, 258–287 CrossRef CAS.
- A. Lawal, M. Wang, P. Stephenson, G. Koumpouras and H. Yeung, Fuel, 2010, 89, 2791–2801 CrossRef CAS.
- C. Biliyok, A. Lawal, M. Wang and F. Seibert, Int. J. Greenhouse Gas Control, 2012, 9, 428–445 CrossRef CAS.
- K. Onda, E. Sada and H. Takeuchi, J. Chem. Eng. Jpn., 1968, 1, 62–66 CrossRef CAS.
- K. Onda, H. Takeuchi and Y. Okumoto, J. Chem. Eng. Jpn., 1968, 1, 56–62 CrossRef CAS.
- J. L. Bravo and J. R. Fair, Ind. Eng. Chem. Process Des. Dev., 1982, 21, 162–170 CAS.
- J. A. Rocha, J. L. Bravo and J. R. Fair, Ind. Eng. Chem. Res., 1996, 35, 1660–1667 CrossRef CAS.
- R. Billet and M. Schultes, Chem. Eng. Res. Des., 1999, 77, 498–504 CrossRef CAS.
- J. D. Pandya, Chem. Eng. Commun., 1983, 19, 343–361 CrossRef CAS.
- F. Dolezalek, Z. Phys. Chem., 1908, 64, 727–747 Search PubMed.
- A. Fredenslund, R. L. Jones and J. M. Prausnitz, AIChE J., 1975, 21, 1086–1099 CrossRef CAS.
-
J. M. Prausnitz, R. N. Lichtenthaler and E. G. de Azevedo, Molecular Thermodynamics of Fluid-phase Equilibria, Pearson Education, 1998 Search PubMed.
- Y. Song and C.-C. Chen, Ind. Eng. Chem. Res., 2009, 48, 7788–7797 CrossRef CAS.
-
A. Fredenslund, Vapor-liquid equilibria using UNIFAC: a group-contribution method, Elsevier, 2012 Search PubMed.
- D. M. Austgen, G. T. Rochelle, X. Peng and C. C. Chen, Ind. Eng. Chem. Res., 1989, 28, 1060–1073 CrossRef CAS.
- D. M. Austgen, G. T. Rochelle and C. C. Chen, Ind. Eng. Chem. Res., 1991, 30, 543–555 CrossRef CAS.
- L. Kucka, E. Y. Kenig and A. Górak, Ind. Eng. Chem. Res., 2002, 41, 5952–5957 CrossRef CAS.
- C. Noeres, E. Y. Kenig and A. Górak, Chem. Eng. Process., 2003, 42, 157–178 CrossRef CAS.
- E. Y. Kenig, L. Kucka and A. Górak, Chem. Eng. Technol., 2003, 26, 631–646 CrossRef CAS.
- L. Kucka, J. Richter, E. Y. Kenig and A. Górak, Sep. Purif. Technol., 2003, 31, 163–175 CrossRef CAS.
- C.-C. Chen and L. B. Evans, AIChE J., 1986, 32, 444–454 CrossRef CAS.
- G. M. Bollas, C. C. Chen and P. I. Barton, AIChE J., 2008, 54, 1608–1624 CrossRef CAS.
- J. Gross and G. Sadowski, Ind. Eng. Chem. Res., 2001, 40, 1244–1260 CrossRef CAS.
-
B. E. Poling, J. M. Prausnitz and J. P. O'Connell, The Properties of Gases and Liquids, McGraw-Hill, 5th edn, 2001 Search PubMed.
-
K. A. Hoff, PhD thesis, Norges Teknisk-Naturvitenskapelige Universitet, 2003.
- R. H. Weiland, M. Rawal and R. G. Rice, AIChE J., 1982, 28, 963–973 CrossRef CAS.
- J. Gabrielsen, M. L. Michelsen, E. H. Stenby and G. M. Kontogeorgis, Ind. Eng. Chem. Res., 2005, 44, 3348–3354 CrossRef CAS.
- J. Button and K. Gubbins, Fluid Phase Equilib., 1999, 158, 175–181 CrossRef.
- N. Mac Dowell, F. Llovell, C. S. Adjiman, G. Jackson and A. Galindo, Ind. Eng. Chem. Res., 2010, 49, 1883–1899 CrossRef CAS.
- N. Mac Dowell, F. E. Pereira, F. Llovell, F. J. Blas, C. S. Adjiman, G. Jackson and A. Galindo, J. Phys. Chem. B, 2011, 115, 8155–8168 CrossRef CAS PubMed.
- J. Rodríguez, N. Mac Dowell, F. Llovell, C. S. Adjiman, G. Jackson and A. Galindo, Mol. Phys., 2012, 110, 1325–1348 CrossRef.
- W. G. Chapman, K. E. Gubbins, G. Jackson and M. Radosz, Fluid Phase Equilib., 1989, 52, 31–38 CrossRef CAS.
- W. G. Chapman, K. E. Gubbins, G. Jackson and M. Radosz, Ind. Eng. Chem. Res., 1990, 29, 1709–1721 CrossRef CAS.
- A. Gil-Villegas, A. Galindo, P. J. Whitehead, S. J. Mills, G. Jackson and A. N. Burgess, J. Chem. Phys., 1997, 106, 4168–4186 CrossRef CAS.
- A. Galindo, L. A. Davies, A. Gil-Villegas and G. Jackson, Mol. Phys., 1998, 93, 241–252 CrossRef CAS.
- A. Chremos, E. Forte, V. Papaioannou, A. Galindo, G. Jackson and C. S. Adjiman, Chem. Eng. Trans., 2013, 35, 427–432 Search PubMed.
- A. Chremos, E. Forte, V. Papaioannou, A. Galindo, G. Jackson and C. S. Adjiman, Fluid Phase Equilib., 2016, 407, 280–297 CrossRef CAS.
- A. Lymperiadis, C. S. Adjiman, A. Galindo and G. Jackson, J. Chem. Phys., 2007, 127, 234903 CrossRef PubMed.
- A. Lymperiadis, C. S. Adjiman, G. Jackson and A. Galindo, Fluid Phase Equilib., 2008, 274, 85–104 CrossRef CAS.
- G. Jackson, W. G. Chapman and K. E. Gubbins, Mol. Phys., 1988, 65, 1–31 CrossRef CAS.
- I. G. Economou and M. D. Donohue, AIChE J., 1991, 37, 1875–1894 CrossRef CAS.
- F. E. Pereira, E. Keskes, A. Galindo, G. Jackson and C. S. Adjiman, Comput. Chem. Eng., 2011, 35, 474–491 CrossRef CAS.
- J. Burger, V. Papaioannou, S. Gopinath, G. Jackson, A. Galindo and C. S. Adjiman, AIChE J., 2015, 61, 3249–3269 CrossRef CAS.
- N. Mac Dowell, A. Galindo, G. Jackson and C. S. Adjiman, Comput.-Aided Chem. Eng., 2010, 28, 1231–1236 CAS.
- C. V. Brand, J. Rodríguez, A. Galindo, G. Jackson and C. S. Adjiman, Comput.-Aided Chem. Eng., 2012, 31, 930–934 CAS.
- N. Mac Dowell, N. J. Samsatli and N. Shah, Int. J. Greenhouse Gas Control, 2013, 12, 247–258 CrossRef CAS.
- A. Arce, N. Mac Dowell, N. Shah and L. F. Vega, Int. J. Greenhouse Gas Control, 2012, 11, 236–250 CrossRef.
- N. Mac Dowell and N. Shah, Int. J. Greenhouse Gas Control, 2013, 13, 44–58 CrossRef CAS.
- A. Alhajaj, N. Mac Dowell and N. Shah, Int. J. Greenhouse Gas Control, 2016, 44, 26–41 CrossRef CAS.
- H. M. Kvamsdal and G. T. Rochelle, Ind. Eng. Chem. Res., 2008, 47, 867–875 CrossRef CAS.
-
N. Mac Dowell, PhD thesis, Imperial College London, 2010.
- M. S. Wertheim, J. Stat. Phys., 1984, 35, 19–34 CrossRef.
- M. S. Wertheim, J. Stat. Phys., 1984, 35, 35–47 CrossRef.
- M. S. Wertheim, J. Stat. Phys., 1986, 42, 459–476 CrossRef.
- M. S. Wertheim, J. Stat. Phys., 1986, 42, 477–492 CrossRef.
- W. G. Chapman, G. Jackson and K. E. Gubbins, Mol. Phys., 1988, 65, 1057–1079 CrossRef CAS.
- S. H. Huang and M. Radosz, Ind. Eng. Chem. Res., 1990, 29, 2284–2294 CrossRef CAS.
- S. H. Huang and M. Radosz, Ind. Eng. Chem. Res., 1991, 30, 1994–2005 CrossRef CAS.
- F. J. Blas and L. F. Vega, Mol. Phys., 1997, 92, 135–150 CrossRef CAS.
- J. Gross and G. Sadowski, Ind. Eng. Chem. Res., 2002, 41, 5510–5515 CrossRef CAS.
- T. Lafitte, D. Bessières, M. M. Piñeiro and J.-L. Daridon, J. Chem. Phys., 2006, 124, 024509 CrossRef PubMed.
- T. Lafitte, M. M. Piñeiro, J.-L. Daridon and D. Bessières, J. Phys. Chem. B, 2007, 111, 3447–3461 CrossRef CAS PubMed.
- T. Lafitte, A. Apostolakou, C. Avendaño, A. Galindo, C. S. Adjiman, E. A. Müller and G. Jackson, J. Chem. Phys., 2013, 139, 154504 CrossRef PubMed.
- K. E. Gubbins, Fluid Phase Equilib., 2016, 416, 3–17 CrossRef CAS.
- S. Dufal, T. Lafitte, A. Galindo, G. Jackson and A. J. Haslam, AIChE J., 2015, 61, 2891–2912 CrossRef CAS.
- S. Dufal, T. Lafitte, A. J. Haslam, A. Galindo, G. N. I. Clark, C. Vega and G. Jackson, Mol. Phys., 2015, 113, 948–984 CrossRef CAS.
-
V. Papaioannou, C. S. Adjiman, G. Jackson and A. Galindo, Group contribution methodologies for the prediction of thermodynamic properties and phase behaviour in mixtures, in Molecular Systems Engineering, ed. C. S. Adjman and A. Galindo, Wiley-VCH, Germany, 2010, vol. 6, ch. 4, pp. 135–172 Search PubMed.
- V. Papaioannou, T. Lafitte, C. Avendaño, C. S. Adjiman, G. Jackson, E. A. Müller and A. Galindo, J. Chem. Phys., 2014, 140, 054107 CrossRef PubMed.
- A. J. Haslam, A. Galindo and G. Jackson, Fluid Phase Equilib., 2008, 266, 105–128 CrossRef CAS.
- A. Galindo, A. Gil-Villegas, G. Jackson and A. N. Burgess, J. Phys. Chem. B, 1999, 103, 10272–10281 CrossRef CAS.
- A. Gil-Villegas, A. Galindo and G. Jackson, Mol. Phys., 2001, 99, 531–546 CrossRef CAS.
- B. H. Patel, P. Paricaud, A. Galindo and G. C. Maitland, Ind. Eng. Chem. Res., 2003, 42, 3809–3823 CrossRef CAS.
- B. Behzadi, B. Patel, A. Galindo and C. Ghotbi, Fluid Phase Equilib., 2005, 236, 241–255 CrossRef CAS.
- P. Paricaud, L. Tazi and J. M. Borgard, Int. J. Hydrogen Energy, 2010, 35, 978–991 CrossRef CAS.
- J. M. A. Schreckenberg, S. Dufal, A. J. Haslam, C. S. Adjiman, G. Jackson and A. Galindo, Mol. Phys., 2014, 112, 2339–2364 CrossRef CAS.
- G. N. I. Clark, A. J. Haslam, A. Galindo and G. Jackson, Mol. Phys., 2006, 104, 3561–3581 CrossRef CAS.
- P. Paricaud, A. Galindo and G. Jackson, Ind. Eng. Chem. Res., 2004, 43, 6871–6889 CrossRef CAS.
- R. P. Sear and G. Jackson, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 386–394 CrossRef CAS.
- D. Ghonasgi, V. Perez and W. G. Chapman, J. Chem. Phys., 1994, 101, 6880–6887 CrossRef.
- R. P. Sear and G. Jackson, Mol. Phys., 1996, 87, 517–521 CAS.
- A. Galindo, S. J. Burton, G. Jackson, D. P. Visco Jr and D. A. Kofke, Mol. Phys., 2002, 100, 2241–2259 CrossRef CAS.
- R. P. Sear and G. Jackson, Mol. Phys., 1994, 82, 1033–1048 CrossRef CAS.
- R. P. Sear and G. Jackson, J. Chem. Phys., 1996, 105, 1113–1120 CrossRef CAS.
- R. Krishnamurthy and R. Taylor, AIChE J., 1985, 31, 449–455 CrossRef CAS.
- R. Krishnamurthy and R. Taylor, AIChE J., 1985, 31, 456–465 CrossRef CAS.
-
R. E. Treybal, Mass-Transfer Operations, McGraw-Hill, 3rd edn, 1981 Search PubMed.
- E. N. Fuller and J. C. Giddings, J. Chromatogr. Sci., 1965, 3, 222–227 CrossRef CAS.
- E. N. Fuller, P. D. Schettler and J. C. Giddings, Ind. Eng. Chem., 1966, 58, 18–27 CrossRef CAS.
- E. N. Fuller, K. Ensley and J. C. Giddings, J. Phys. Chem., 1969, 73, 3679–3685 CrossRef CAS.
- C. Wilke and P. Chang, AIChE J., 1955, 1, 264–270 CrossRef CAS.
- M. Takahashi, Y. Kobayashi and H. Takeuchi, J. Chem. Eng. Data, 1982, 27, 328–331 CrossRef CAS.
- B. Han, Y. Sun, M. Fan and H. Cheng, J. Phys. Chem. B, 2013, 117, 5971–5977 CrossRef CAS PubMed.
- L. R. Perkins and C. J. Geankoplis, Chem. Eng. Sci., 1969, 24, 1035–1042 CrossRef CAS.
- Process Systems Enterprise, gPROMS v4.0, 1997–2015, http://www.psenterprise.com/gproms.
-
N. M. Kakalis, A. I. Kakhu and C. C. Pantelides, Proc. 6th International Conf. on Foundations of Computer Aided Process Design, CACHE Publications, 2004, pp. 537–40 Search PubMed.
- P. Tontiwachwuthikul, A. Meisen and C. J. Lim, Can. J. Chem. Eng., 1989, 67, 602–607 CrossRef CAS.
-
ASHRAE, 2011 ASHRAE Handbook, ASHRAE, 2011 Search PubMed.
- J. A. Rocha, J. L. Bravo and J. R. Fair, Ind. Eng. Chem. Res., 1993, 32, 641–651 CrossRef CAS.
- G. Vazquez, E. Alvarez, J. M. Navaza, R. Rendo and E. Romero, J. Chem. Eng. Data, 1997, 42, 57–59 CrossRef CAS.
- S. A. Jayarathna, A. Weerasooriya, S. Dayarathna, D. A. Eimer and M. C. Melaaen, J. Chem. Eng. Data, 2013, 58, 986–992 CrossRef CAS.
- G. J. Gloor, G. Jackson, F. J. Blas, E. M. del Río and E. de Miguel, J. Chem. Phys., 2004, 121, 12740–12759 CrossRef CAS PubMed.
- G. J. Gloor, G. Jackson, F. J. Blas, E. M. del Río and E. de Miguel, J. Phys. Chem. C, 2007, 111, 15513–15522 CAS.
- F. Llovell, A. Galindo, F. J. Blas and G. Jackson, J. Chem. Phys., 2010, 133, 024704 CrossRef PubMed.
- H. M. Kvamsdal, J. Hetland, G. Haugen, H. F. Svendsen, F. Major, V. Kårstad and G. Tjellander, Int. J. Greenhouse Gas Control, 2010, 4, 613–622 CrossRef CAS.
- C. V. Brand, J. Rodriguez, A. Galindo, G. Jackson and C. S. Adjiman, Energy Procedia, 2013, 37, 1566–1571 CrossRef CAS.
- F. Y. Jou, A. E. Mather and F. D. Otto, Can. J. Chem. Eng., 1995, 73, 140–147 CrossRef CAS.
- S. Westmeier, Chem. Tech. (Leipzig, Ger.), 1977, 29, 218–222 CAS.
- A. G. Leibush and E. D. Shorina, Zh. Prikl. Khim., 1947, 20, 69–76 CAS.
- Y. Maham, C. N. Liew and A. E. Mather, J. Solution Chem., 2002, 31, 743–756 CrossRef CAS.
- J. Kestin, Y. Kobayashi and R. T. Wood, Physica, 1966, 32, 1065–1089 CrossRef CAS.
-
W. N. Haynes, Handbook of Chemistry and Physics, CRC Press, 2011 Search PubMed.
- M. Laliberte, J. Chem. Eng. Data, 2009, 54, 1725–1760 CrossRef CAS.
- M. Mundhwa and A. Henni, J. Chem. Eng. Data, 2007, 52, 491–498 CrossRef CAS.
-
J. A. Riddick, W. B. Bunger and T. K. Sakano, Organic Solvents, Wiley, New York, 4th edn, 1986 Search PubMed.
- N. B. Vargaftik, Moskva, 1972, 433–434 Search PubMed.
- R. Bender, K. Bier and G. Maurer, Ber. Bunsen-Ges. Phys. Chem., 1981, 85, 778–784 CrossRef CAS.
-
R. H. Perry and D. W. Green, Perry's Chemical Engineers' Handbook, McGraw Hill, 6th edn, 2008 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Claire S.
Adjiman
*
and
Claire S.
Adjiman
*
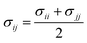
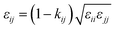
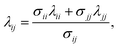

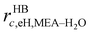 of each other, there is a site–site hydrogen-bonding associative interaction of strength
of each other, there is a site–site hydrogen-bonding associative interaction of strength  . A representative example of the good overall description of the temperature and pressure dependence of the absorption VLE behaviour of CO2 in aqueous MEA obtained with the SAFT-VR SW models can be seen in Fig. 4 over several orders of magnitude for the partial pressure of CO2. In the standard Wertheim TPT1 treatment at the heart of the SAFT EoS, association into linear-chain, branched-chain, and network aggregates are considered. Association into ring-like structures131–134 (and even double bonding135 and bond cooperativity136) can be taken into account but this is not considered for the systems described in our current work.
. A representative example of the good overall description of the temperature and pressure dependence of the absorption VLE behaviour of CO2 in aqueous MEA obtained with the SAFT-VR SW models can be seen in Fig. 4 over several orders of magnitude for the partial pressure of CO2. In the standard Wertheim TPT1 treatment at the heart of the SAFT EoS, association into linear-chain, branched-chain, and network aggregates are considered. Association into ring-like structures131–134 (and even double bonding135 and bond cooperativity136) can be taken into account but this is not considered for the systems described in our current work.


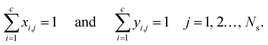
![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) j−1) + ELj = LjHLj(TLj, VLj,
j−1) + ELj = LjHLj(TLj, VLj, ![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) j), j = 1, 2…, Ns,
j), j = 1, 2…, Ns,![[y with combining low line]](https://www.rsc.org/images/entities/i_char_0079_0332.gif) j+1) − EVj = VjHVj(TVj, VVj,
j+1) − EVj = VjHVj(TVj, VVj, ![[y with combining low line]](https://www.rsc.org/images/entities/i_char_0079_0332.gif) j), j = 1, 2…, Ns,
j), j = 1, 2…, Ns,![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) j and
j and ![[y with combining low line]](https://www.rsc.org/images/entities/i_char_0079_0332.gif) j.
j.
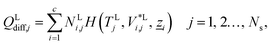
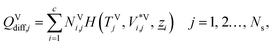
![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif) i) and H(TVj, V*Vi,j,
i) and H(TVj, V*Vi,j, ![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif) i) (J mol−1) are the molar enthalpies of pure component i in the bulk liquid and vapour phase respectively, as calculated with SAFT-VR SW. The variable
i) (J mol−1) are the molar enthalpies of pure component i in the bulk liquid and vapour phase respectively, as calculated with SAFT-VR SW. The variable ![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif) i denotes the molar composition vector of a stream consisting of pure component i defined by zk,i = 1 if i = k and zk,i = 0 otherwise. V*Li,j and V*Vi,j (m3 mol−1) are the molar volumes of pure component i at stage j in the bulk liquid and vapour phases respectively, obtained from
i denotes the molar composition vector of a stream consisting of pure component i defined by zk,i = 1 if i = k and zk,i = 0 otherwise. V*Li,j and V*Vi,j (m3 mol−1) are the molar volumes of pure component i at stage j in the bulk liquid and vapour phases respectively, obtained from![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif) i), i = 1, 2…, c; j = 1, 2…, Ns,
i), i = 1, 2…, c; j = 1, 2…, Ns,![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif) i), i = 1, 2…, c; j = 1, 2…, Ns,
i), i = 1, 2…, c; j = 1, 2…, Ns,![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif) i) and P(TLj, V*Li,j,
i) and P(TLj, V*Li,j, ![[z with combining low line]](https://www.rsc.org/images/entities/i_char_007a_0332.gif) i) represent evaluations of the pressure using the SAFT-VR SW EoS.
i) represent evaluations of the pressure using the SAFT-VR SW EoS.
![[y with combining low line]](https://www.rsc.org/images/entities/i_char_0079_0332.gif) Ij) = μ(TIj, VI,Lj,
Ij) = μ(TIj, VI,Lj, ![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) Ij) = μI,Li,j = μI,Vi,j, i = 1, 2…, c; j = 1, 2…, Ns,
Ij) = μI,Li,j = μI,Vi,j, i = 1, 2…, c; j = 1, 2…, Ns,![[y with combining low line]](https://www.rsc.org/images/entities/i_char_0079_0332.gif) Ij) = P(TIj, VI,Lj,
Ij) = P(TIj, VI,Lj, ![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) Ij) = PIj, j = 1, 2…, Ns,
Ij) = PIj, j = 1, 2…, Ns,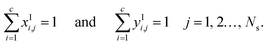
![[y with combining low line]](https://www.rsc.org/images/entities/i_char_0079_0332.gif) j), j = 1, 2…, Ns,
j), j = 1, 2…, Ns,![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) j),
j), ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j = 1, 2…, Ns.
j = 1, 2…, Ns.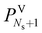 . This assumption can easily be removed at a later stage of the model development. Preliminary results have indicated that the pressure drop has a negligible effect on the process used for the validation of our model.
. This assumption can easily be removed at a later stage of the model development. Preliminary results have indicated that the pressure drop has a negligible effect on the process used for the validation of our model.
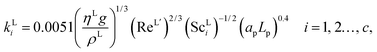
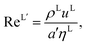
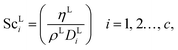
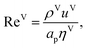
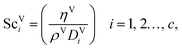
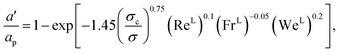
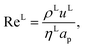
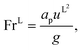
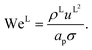
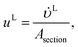
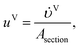
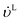 and
and 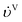 (m3 s−1) are the volumetric flow rates of the liquid and gas phase, respectively.
(m3 s−1) are the volumetric flow rates of the liquid and gas phase, respectively.
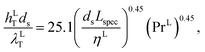
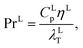
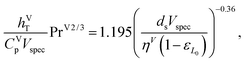
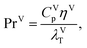
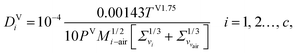
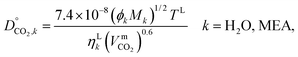
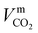 (cm3 mol−1) is the molar volume of CO2 at its normal boiling temperature.
(cm3 mol−1) is the molar volume of CO2 at its normal boiling temperature.
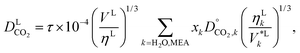
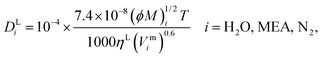
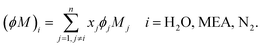
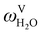 in the flue gas of between 0.003 and 0.01.150 A sensitivity analysis of the extent of humidity indicates that the variation of
in the flue gas of between 0.003 and 0.01.150 A sensitivity analysis of the extent of humidity indicates that the variation of 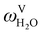 between 0 and 0.072 (corresponding to a mole fraction 0.12) has a negligible impact on the temperature and composition profiles. The effect of the amount of water in the flue gas is discussed in more detail in Section 3.3.2. For our working model, the nominal amount of water in the inlet flue gas is fixed to
between 0 and 0.072 (corresponding to a mole fraction 0.12) has a negligible impact on the temperature and composition profiles. The effect of the amount of water in the flue gas is discussed in more detail in Section 3.3.2. For our working model, the nominal amount of water in the inlet flue gas is fixed to 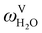 = 0.0058, corresponding to 50% humidity at 20 °C and 1 bar.
= 0.0058, corresponding to 50% humidity at 20 °C and 1 bar.


















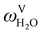 = 0 to 0.072 (corresponding to a mole fraction of 0.12) (water-rich). The effect on the profiles is represented in Fig. 25. It is apparent that varying the amount of water in the flue gas does not have a significant impact on the composition profiles. The effect is visible only for the liquid-phase temperature profile, where the outlet temperature value is higher by approximately 5 K for the saturated gas
= 0 to 0.072 (corresponding to a mole fraction of 0.12) (water-rich). The effect on the profiles is represented in Fig. 25. It is apparent that varying the amount of water in the flue gas does not have a significant impact on the composition profiles. The effect is visible only for the liquid-phase temperature profile, where the outlet temperature value is higher by approximately 5 K for the saturated gas 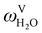 = 0.072 than for the dry gas
= 0.072 than for the dry gas 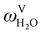 = 0. Biliyok et al.56 also find that increasing the moisture content of the flue gas affects the absorber temperature profile, however the increase in temperature is more significant in their study because a larger change in moisture content is considered (
= 0. Biliyok et al.56 also find that increasing the moisture content of the flue gas affects the absorber temperature profile, however the increase in temperature is more significant in their study because a larger change in moisture content is considered (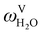 varies between 0.015 and 0.15, where the latter value represents a two-phase aqueous system). The negligible effect on the composition profiles is in contrast to the work of Mac Dowell et al.99 who found a large effect of the humidity of the inlet gas on the flux profiles in the mass transfer zone.
varies between 0.015 and 0.15, where the latter value represents a two-phase aqueous system). The negligible effect on the composition profiles is in contrast to the work of Mac Dowell et al.99 who found a large effect of the humidity of the inlet gas on the flux profiles in the mass transfer zone.




![[small upsilon, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e158.gif)