Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Micro-ratcheted surfaces for a heat engine biomass conveyor†
Christoph
Krumm‡
a,
Saurabh
Maduskar‡
a,
Alex D.
Paulsen
ab,
Anthony D.
Anderson
a,
Nicholas L.
Barberio
a,
Jonathan N.
Damen
a,
Connor A.
Beach
a,
Satish
Kumar
a and
Paul J.
Dauenhauer
*ab
aDepartment of Chemical Engineering and Materials Science, University of Minnesota, 421 Washington Ave. SE, Minneapolis, MN 55455, USA. E-mail: hauer@umn.edu
bCatalysis Center for Energy Innovation, a U.S. Department of Energy – Energy Frontier Research Center, Web: http://www.efrc.udel.edu
First published on 7th March 2016
Abstract
Cellulosic particles on surfaces consisting of microstructured, asymmetric ratchets (100 by 400 μm) were observed to spontaneously move orthogonal to ratchet wells above the cellulose reactive Leidenfrost temperature (>750 °C). Evaluation of the accelerating particles supported the mechanism of propelling viscous forces (50–200 nN) from rectified pyrolysis vapors, thus providing the first example of biomass conveyors with no moving parts driven by high temperature for biofuel reactors.
Broader contextHigh temperature biomass reactors (>300 °C) commonly utilize moving augers or conveyors to transport and inject lignocellulosic particles for gasification, torrefaction, pyrolysis and combustion for energy and biofuels applications. In this work, cellulosic particles are shown to spontaneously move on a patterned metal surface of asymmetric ratchets at reactor temperatures with limited resistance to flow. Ratcheted metal surfaces utilize heat to propel particles without moving parts while creating a lubricating layer of gas/vapor between the particle and hot surface. The ability to controllably move organic solid particles and fibers within high temperature systems provides a simple alternative for transporting and processing difficult-to-handle solid feedstocks. |
Lignocellulosic biomass grows in sufficient quantities to impact fuel and chemical production,1,2 but converting solid, low-density feedstocks to energy-rich liquids remains one of the major challenges of the 21st century. Implementation of thermochemical biofuels via pyrolysis, gasification, and torrefaction utilizes high temperature catalytic reactors to rapidly break down biomass within a few seconds for further upgrading and refining.3,4 At temperatures exceeding 400 °C, thermolytic scission of biopolymers, achieved primarily through cleavage of ether linkages that connect biomass monomers, produces a volatile mixture of hundreds of organic compounds referred to as ‘bio-oil’.5–7 Optimization of pyrolytic chemistry can potentially occur through integration of catalysts and/or control of the reacting environment (e.g. rapid heat transfer),8,9 but limited understanding of the reactions, particles, and processing equipment has prevented significant improvements in thermochemical technologies for biofuels.10,11
Advances in thermochemical biomass reactors will likely come from higher throughput and improved chemical control of reacting lignocellulosic particles, such as fibers and wood chips, via direct particle ablation. While fluid/bubbling bed reactors provide even, gas-to-solid heating of particles, ablative-type reactors utilize direct contact between biomass particles and surfaces in a variety of methods such as screw and auger conveyors. Reacting particles in contact with engineered surfaces exhibit at least an order of magnitude faster heat transfer relative to hot gases,12 allowing for rapid thermal pyrolysis to organic vapors and the potential for dramatically higher reactor space velocities.
Despite the potential of new ablative reactor technologies, little is known regarding the behavior of lignocellulosic materials in contact with high temperature surfaces (>500 °C). Woody fibers and grasses rich in carbohydrates, such as cellulose and hemicellulose, are known to thermally degrade to short-lived liquid intermediates with millisecond lifetime before evaporating to bio-oil.13,14 Comprised of oligomers of the parent biopolymer, molten cellulose droplets have been observed to wet ceramic surfaces at moderate temperatures, coalesce, bubble, and spontaneously eject aerosols.15 More recently, intermediate cellulose liquids were revealed to exhibit a ‘reactive Leidenfrost effect,’ whereby the droplet of molten cellulose levitates above polished silicon surfaces at temperatures exceeding 750 °C.16
In this work, we demonstrate the first capability to control the behavior and motion of microcrystalline cellulosic particles using engineered surfaces at the conditions common to thermochemical reactors. As depicted in the photograph of Fig. 1, a particle of cellulose about one millimeter in size is self-propelled on a hot surface (800 °C) consisting of micrometer-scale ratchets.17–19 Using backlit photography within an inert environment (nitrogen atmosphere), the Fig. 1 image depicts the heated ratchet surface, the cellulose particle, and the particle's orientation above the surface. Additionally, as the particle spontaneously moves from left to right, evolved organic chemicals form a vapor cloud contrail indicating the motion of the particle.
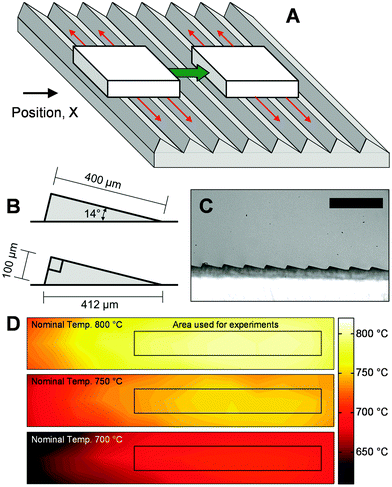
The self-propelled cellulose particles were examined via high-speed photography conducted within a closed container filled with nitrogen gas to eliminate high temperature oxidation of organic vapors. A glass window above the surface allowed for photography of the heated, ratcheted surface at either an angle (∼45°) or from the side (0–5°) as described in the ESI.† The microstructured surface was comprised of a stainless steel block (10.2 by 3.8 by 1.9 cm) which was micro-machined with the ratchet pattern depicted in Fig. 2B; ratchets consisted of aligned rows of 400 μm by 100 μm triangles visible in the photograph of Fig. 2C. Two 500 watt heating cartridges were inserted into the stainless steel block, and the temperature was controlled by a PID control loop measuring the temperature of the middle of the block via a thermocouple within a thermowell. Spatial mapping of the heated surface via emission spectroscopy indicated even heating to the set point temperature ±5 °C within the surface region used for experiments as depicted in Fig. 2D. Particles of cellulose were comprised of 1.0–2.0 mg of microcrystalline cellulose pressed into approximately one millimeter cubes.†
In the experiments depicted in Fig. 3, cellulose particles were dropped using tweezers (visible in the first frame) to impact the ratcheted surface (800 °C) with minimal horizontal momentum; this moment was identified as time zero in panels A and B. In Fig. 3A, sequential image frames in increments of 250 milliseconds obtained from low-angle photography with backlighting clearly show that the particle accelerates; the particle is farther apart in each subsequent frame. Additionally, the particle becomes increasingly blurry in sequential frames as it accelerates, and in some images, the vapor contrail following the particle is visible as a result of the back lighting. While the solid cellulose particle is moderately translucent, the bottom of the particle appears dark, consistent with formation of intermediate liquid cellulose. In all frames, the particle appears to sit on top of the ratchet points; insufficient resolution exists to determine the spacing between the ratchet point and the liquid at the bottom of the particle.
The full motion of cellulose particles is visible when viewed from above with front lighting as depicted in Fig. 3B. As shown in sequential frames, cellulose particles move orthogonal to the ratchet wells with only minimal movement parallel to the wells. When viewing the complete set of sequential images in the video,† more complex behavior is observed such as particle rotation. Moderate rotation is visible in the frames of Fig. 3B. Additionally, particles will undergo periods of aggressive acceleration, followed by a collision between the solid cellulose particle and the solid ratchet. After the surface collision, particles will either slow or stop before undergoing a second period of aggressive acceleration. In Fig. 3B, a surface collision occurred between 150 ms and 300 ms; continuous acceleration was observed from 300 ms to 400 ms.
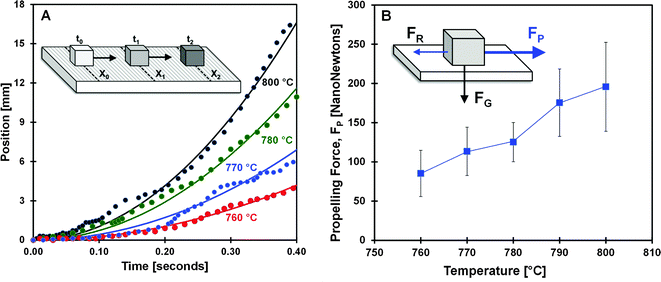
The periods of rapid, smooth particle acceleration were characterized by measuring particle position with time. As shown in Fig. 4A, the position of four different particles at 760, 770, 780 and 800 °C indicate that increasing temperature produces increased particle acceleration. For each data set, a simple model depicted as a parabolic line assumes continuous particle acceleration. Comparison between the model and the fine structure of the experimental data reveals the complex behavior of vibrating and rotating of the solid particle while maintaining overall approximately constant acceleration. The position and acceleration of about ten particles was characterized at each temperature, and the resulting particle force was determined by Newton's law as shown in Fig. 4B. Between 760 and 800 °C, particles exhibited accelerations of 0.05–0.20 m s−2, and the force applied to the particle due to the ratchet surface more than doubled from about 80 nN to 200 nN. Particles were never observed to achieve a terminal velocity.
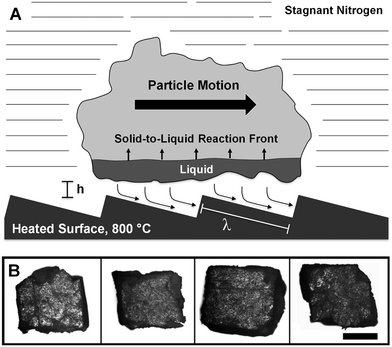
The behavior of self-propelled cellulose can be interpreted from similar motion of liquid water on ratcheted surfaces.17 Volatile liquids exhibiting the Leidenfrost effect are known to levitate above non-porous surfaces with gas/vapor production rates sufficient to propel droplets in random directions.20 However, Link et al. have discovered that ratcheted surfaces directly control droplet motion in the direction across the long face of the asymmetric ratchet as depicted in Fig. 2A.17 It has since been concluded that vapor production and flow over the ratchet is the primary cause of motion. Heat conducted within the thin film layer from the surface leads to vapor generation, which supports the droplet. The ratchet serves to rectify the vapor, such that it flows along the longer ratchet surface and exhibits viscous stress on the levitating droplet propelling it forward.17,21,22 This mechanism was further supported with vapor flow tracking by high speed photography and flow simulation.23,24
The mechanism by which cellulose particles are propelled is likely similar to that proposed by Link et al. with the additional complexity of the reaction chemistry associated with conversion of solid cellulose to intermediate liquid cellulose and subsequent vapor generation below the particle. In a similar analysis by Dupeux, et al.,23 the Reynolds number characterizing the vapor flow below the particle is obtained from the ratio of inertia (of order ρU2/λ) with viscous resistance (of order ηU/h2), where ρ is the vapor density, U is the average vapor velocity, h is the thickness of the vapor film, η is the dynamic viscosity, and λ is the long ratchet dimension of 400 μm. The Reynolds number Re = ρUh2/ηλ is then calculated from estimated parameters pertaining to the cellulose pyrolysis vapor within the film between the particle and ratchet surfaces. Using the measured particle velocities of ∼3 cm s−1 as the approximate characteristic velocity and the film thickness of ∼50 μm above the ratchet surface, the resulting Reynolds number is 0.01 < Re < 0.1, indicating the importance of viscous stress on the particle from organic vapor flow. Other parameters and their justification are described in the ESI.†
The viscous fluid beneath the solid/liquid cellulose particle propels it forward via shear force. As shown previously,17,23 Poiseuille flow resulting from a pressure differential between the top and the bottom of the ratchet applies viscous stress to the bottom of the particle. Using the method of Linke et al.,17,25 the horizontal propelling force, FP, force is estimated as,
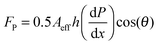 | (1) |
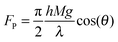 | (2) |
The hot, ratcheted surface could potentially be utilized with lignocellulosic biomass by increasing either the mass of applied particles or their applied force to the ratcheted surface. Lignin and lignocellulose particles have also been shown to liquefy at pyrolysis/gasification conditions and aggressively produce gases and vapors necessary for the reactive Leidenfrost effect.14,26 While the apparent force of particles measured in this work appears low (∼80–200 nN for ∼1 mg cellulose particles), this range of forces is in accordance with previously studied systems of liquid droplets on hot ratchets when scaling for the droplet size and applied droplet/particle pressure to the surface. As previously described, an increase in the force normal to the ratchet surface has been shown to increase the propelling force by two orders of magnitude from 1.0 μN to 100 μN.23 Heavier particles will exhibit greater propelling force as predicted in eqn (2). Water droplets on ratcheted surfaces examined by Linke et al. exhibited propelling forces of ∼1–10 μN, but the droplets of 2–8 mm diameter weighed considerably more (∼10–100 mg) than the cellulose particles examined here. Similarly, an increase in weight of larger biomass fibers (1–2 mm diameter, 1–2 cm length), stalks, and wood chips as well as the aggregate weight of a mixture of particles as exists within an auger/conveyor or reactor could increase the normal force to the ratchet surface and further enhance the viscous propelling force.
Applying the ratcheted surface to industrial biomass systems could enable a high temperature biomass conveyor with no moving parts. For example, application of ratchets to the inside surface of heated tubes oriented such that particles on the surface are propelled forward could allow for continuous flow of wood fibers lubricated by reactant gases. With a mixture of biomass fibers, the bulk of the mass can serve to push the external layer of fibers against the ratchets, thus enhancing the propelling viscous force. As shown in Fig. 3C, cellulose fibers will flow up an incline, indicating that the viscous propelling force can overcome the resistive component of the gravitational force. The ability to inject a complex mixture of solid particles with poor flow characteristics could improve the design of auger reactors or even eliminate the need for solid injectors in high temperature reactors such as pyrolyzers or gasifiers.
To evaluate the potential for applying high temperature ratchets to real biomass materials, particles of lignocellulosic biomass including wheat straw and poplar wood (same size as cellulose particles in Fig. 3) were applied to the ratchet system described in Fig. 2 at 790 °C. For these conditions, lignocellulosic particles were observed to pyrolyze, generate vapors, lift off the surface, and self-propel. However, introduction of real biomass presents numerous variables including the role of water content, grain/fiber orientation, particle shape, and lignin/carbohydrate/ash content which will likely enhance or reduce the self-propulsion mechanism. It remains to be evaluated in future work how complex lignocellulosic particles can be applied to ratcheted surface within the extensive range of particle properties (e.g. fiber orientation, composition, moisture content) and biomass auger/feeder/reactor applications.
Author contributions
C. K., S. M., P. J. D. and S. K. were authors. High speed photography was conducted by C. K., A. D. P., A. D. A., N. L. B., and J. N. D. Particles were prepared and analyzed by A. D. A. and N. L. B., S. M., and C. A. B.Acknowledgements
Financial support was provided from the Catalysis Center for Energy Innovation, a U.S. Department of Energy – Energy Frontier Research Center (http://www.efrc.udel.edu) under Award DE-SC0001004. Funding supported researchers N. L. B., P. J. D. and the cost of materials.References
- U.S. Department of Energy, U.S. Billion-Ton Update: Biomass Supply for a Bioenergy and Bioproducts Industry. R. D. Perlack and B. J. Stokes (Leads), Oak Ridge National Laboratory, Oak Ridge, 2011, TN. ORNL/TM-2011/224, 227p.
- R. Slade, R. Gross and A. Bauen, Energy Environ. Sci., 2011, 4, 2645 Search PubMed.
- A. V. Bridgwater, D. Meier and D. Radlein, Org. Geochem., 1999, 30, 1479–1493 CrossRef CAS.
- K. Wang, J. Zhang, B. H. Shanks and R. C. Brown, Green Chem., 2015, 17, 557–564 RSC.
- R. Vinu and L. J. Broadbelt, Energy Environ. Sci., 2012, 5, 9808–9826 CAS.
- M. R. Hurt, et al. , Anal. Chem., 2013, 85, 10927–10934 CrossRef CAS PubMed.
- M. S. Mettler, et al. , Energy Environ. Sci., 2012, 5, 5414–5424 CAS.
- A. D. Paulsen, M. S. Mettler and P. J. Dauenhauer, Energy Fuels, 2013, 27, 2126–2134 CrossRef CAS.
- M. S. Mettler, A. D. Paulsen, D. G. Vlachos and P. J. Dauenhauer, Catal. Sci. Technol., 2014, 4, 3822–3825 CAS.
- M. S. Mettler, D. G. Vlachos and P. J. Dauenhauer, Energy Environ. Sci., 2012, 5, 7797–7809 CAS.
- C. Di Blasi, Prog. Energy Combust. Sci., 2008, 34, 47–90 CrossRef CAS.
- A. D. Paulsen, B. R. Hough, C. L. Williams, A. R. Teixeira, D. T. Schwartz, J. Pfaendtner and P. J. Dauenhauer, ChemSusChem, 2014, 7(3), 765–776 CrossRef CAS PubMed.
- O. Boutin, M. Ferrer and J. Lédé, J. Anal. Appl. Pyrolysis, 1998, 47, 13–31 CrossRef CAS.
- P. J. Dauenhauer, J. L. Colby, C. M. Balonek, W. J. Suszynski and L. D. Schmidt, Green Chem., 2009, 11, 1555 RSC.
- A. R. Teixeira, K. G. Mooney, J. S. Kruger, C. L. Williams, W. J. Suszynski, L. D. Schmidt, D. P. Schmidt and P. J. Dauenhauer, Energy Environ. Sci., 2011, 4, 4306 CAS.
- A. R. Teixeira, C. Krumm, K. P. Vinter, A. D. Paulsen, C. Zhu, S. Maduskar, K. E. Joseph, K. Greco, M. Stelatto, E. Davis, B. Vincent, R. Hermann, W. Suszynski, L. D. Schmidt, W. Fan, J. P. Rothstein and P. J. Dauenhauer, Sci. Rep., 2015, 5, 11238 CrossRef PubMed.
- H. Linke, Appl. Phys. A: Mater. Sci. Process., 2002, 75, 167 CrossRef CAS.
- A. Buguin, L. Talini and P. Silberzan, Appl. Phys. A: Mater. Sci. Process., 2002, 75, 207–212 CrossRef CAS.
- H. Linke, B. J. Aleman, L. D. Melling, M. J. Taormina, M. J. Francis, C. C. Dow-Hygelund, V. Narayanan, R. P. Taylor and A. Stout, Phys. Rev. Lett., 2006, 96, 154502 CrossRef CAS PubMed.
- D. Quéré, Annu. Rev. Fluid Mech., 2013, 45, 197–215 CrossRef.
- T. R. Cousins, R. E. Goldsteni, J. W. Jaworski and A. I. Pesci, J. Fluid Mech., 2012, 696, 215–227 CrossRef.
- G. Lagubeau, M. Le Merrer, C. Clanet and D. Quéré, Nat. Phys., 2011, 7, 395 CrossRef CAS.
- G. Dupeux, M. Le Merrer, G. Lagubeau, C. Clanet, S. Hardt and D. Quéré, Europhys. Lett., 2011, 96, 58001 CrossRef.
- S. Hardt, S. Tiwari and T. Baier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 063015 CrossRef PubMed.
- R. L. Panton, Incompressible Flow, John Wiley and Sons, New York, 1996 Search PubMed.
- J. Lede, H. Z. Li and J. Villermaux, J. Anal. Appl. Pyrolysis, 1987, 10, 291–308 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ee00519e |
| ‡ Authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2016 |