Design of an artificial photosynthetic system for production of alcohols in high concentration from CO2
Meenesh R.
Singh
 a and
Alexis T.
Bell
*ab
a and
Alexis T.
Bell
*ab
aJoint Center for Artificial Photosynthesis, Material Science Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
bThe Dow Professor of Sustainable Chemistry, Department of Chemical & Biomolecular Engineering, University of California, 107 Gilman Hall, Berkeley, CA 94720-1462, USA. E-mail: alexbell@berkeley.edu; Tel: +1-510-642-1536
First published on 6th November 2015
Abstract
Artificial photosynthesis of liquid fuels is a potential source for clean energy. Alcohols are particularly attractive products because of their high energy density and market value per amount of energy input. The major challenges in photo/electrochemical synthesis of alcohols from sunlight, water and CO2 are low product selectivity, high membrane fuel-crossover losses, and high cost of product separation from the electrolyte. Here we propose an artificial photosynthesis scheme for direct synthesis and separation to almost pure ethanol with minimum product crossover using saturated salt electrolytes. The ethanol produced in the saturated salt electrolytes can be readily phase separated into a microemulsion, which can be collected as pure products in a liquid–liquid extractor. A novel design of an integrated artificial photosynthetic system is proposed that continuously produces >90 wt% pure ethanol using a polycrystalline copper cathode at a current density of 0.85 mA cm−2. The annual production rate of >90 wt% ethanol using such a photosynthesis system operating at 10 mA cm−2 (12% solar-to-fuel (STF) efficiency) can be 15.27 million gallons per year per square kilometer, which corresponds to 7% of the industrial ethanol production capacity of California.
Broader contextArtificial photosynthesis offer a means for mitigating global warming while also supporting future energy demands. Although artificial photosynthetic systems can have ten-fold higher efficiency than the natural photosynthesis, the energy penalty due to membrane crossover losses and product separation from the electrolyte are some of the challenges that may prevent deployment and scale-up of such systems. Here we propose a novel artificial photosynthetic system that can produce alcohols such as ethanol of >90 wt% purity with minimal membrane crossover losses. The annual production rate of ethanol using such a photosynthesis system operating at 10 mA cm−2 (12% solar-to-fuel (STF) efficiency) can be 15.27 million gallons per year per square kilometer, which corresponds to 7% of the industrial ethanol production capacity of California. |
1. Introduction
An efficient, stable, and scalable artificial photosynthetic system could provide a sustainable source of carbon-neutral fuels. Solar-driven photo-electrochemical CO2 reduction (CO2R) devices based on various catalysts and light absorbers with varying levels of integration have been demonstrated experimentally,1–5 and investigated theoretically in detail.6,7 Such devices typically operate at near-neutral pH using bicarbonate electrolyte, cation- or anion-exchange membrane, and pure CO2 feed. The products produced with highest selectivity include H2, CO, CH4, C2H4, HCOOH, CH3OH, C2H5OH, and C3H7OH. The selectivity to these gaseous and liquid products strongly depends on the choice catalyst.8 For example, the reported selectivity to ethanol and methanol are in the range of 10–30%9–13 and 40–90%,8,14,15 respectively. However, the reported productivity or partial current density of ethanol is about an order of magnitude higher than that for the methanol.9,14 It is notable that liquid fuels, such as alcohols, have higher energy density (∼20 MJ L−1) and higher market value per amount of energy input (∼10 ¢ kW h−1) than light hydrocarbons, such as methane and ethene.7In contrast to gaseous products, alcohols have much higher solubility in the electrolyte and hence are more difficult to separate.16 The higher solubility of alcohols also leads to higher membrane-crossover losses due to oxidation of these products at the anode. Another issue is the low concentration of alcohols present in the catholyte. For example, the maximum achievable concentration of ethanol is <1 mol% when the rate of ethanol generation is equal to 10 mA cm−2 and the membrane separating the catholyte from the anolyte is Nafion.17,18 The energy required to distill such low concentrations of ethanol from the electrolyte is approximately 40.68/0.01 = 4068 kJ mol−1, which is much higher than its lower heating value of 1235 kJ mol−1.7 Alternatively, the catholyte can be heated to evaporate a dilute ethanol–water stream, which can be catalytically upgraded to a C3–C15 blendstock by passage over a zeolite catalysts.19 However, such upgrading also reduces the net energy efficiency for converting sunlight to fuels. Consequently, there is a need for developing an artificial photosynthetic system that can separate alcohols from the electrolyte directly with minimum membrane crossover losses and energy demand for product concentration.
Separation of alcohols from water is challenging due to formation of azeotropic mixtures. The two widely employed techniques to separate alcohol–water mixtures are distillation and extraction. Distillation of alcohol–water mixtures (<10 mol%) requires multiple distillation columns and is an energy intensive process.20 As an alternative, alcohol–water mixtures can be separated into two immiscible, water-rich and alcohol-rich, phases by the addition of salts.21–24 In this technique, the raffinate phase requires downstream processing to recover salt by evaporating excess water. Alcohol separation using salt has been studied extensively,22–25 and implemented for the separation of alcohol from dilute aqueous solutions present in fermenters.21 Based on the same principle, we propose the operation of electrolyzers with saturated salt electrolytes that allows instantaneous phase-separation of alcohols at the cathode into microemulsion, which can be readily collected as pure products without requiring a salt-recovery system. Therefore the objective of this study is to evaluate an artificial photosynthetic system that integrates production and separation of alcohols, focusing on ethanol for illustrative purposes since it can be produced with relatively high yields. However, the proposed method is not limited to ethanol and could be used to separate other water soluble products, such as methanol.
2. Modeling
2.1 Mass balance of liquid fuels in a solar-fuel generator
A simple mass balance on the alcohol in catholyte can be developed based on the production of alcohol at the cathode and the amount of alcohol diffusing across the membrane separating anolyte and catholyte.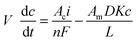 | (1) |
The solution of eqn (1) provides the concentration of alcohol as a function of current density and membrane properties, such that
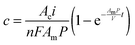 | (2) |
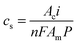 | (3) |
 | (4) |
2.2 Phase equilibrium of salt–ethanol–water mixtures
The solubility of organic molecules in aqueous systems decreases with increase in the salt concentration, and the phase equilibrium for salt–water–organics mixtures have been thoroughly investigated for various systems.22 Phase separation of alcohols in saturated salt electrolytes is due to the “salting-out” effect, a phenomenon in which salt binds strongly with water thereby weakening the water organic interactions and causing the organic to phase separate.26 The phase diagram of salt–organics–water mixtures has a binodal curve dividing the two-phase from the single, miscible phase region and tie lines representing the equilibrium composition of the liquid phases, which are strongly dependent of the salt composition and temperature. While various salts might be used as electrolytes, cesium carbonate is particularly attractive because is known to promote CO2 reduction,27–29 and can also be used to phase-separate ethanol produced at the cathode.23 The experimentally measured binodal curve for cesium carbonate–water–ethanol mixture at 20 °C is given by the following empirical equation:23ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) w1 = −0.064 − 1.477w20.5 − 1.481w2 − 2.749w22 − 2.872w23 w1 = −0.064 − 1.477w20.5 − 1.481w2 − 2.749w22 − 2.872w23 | (5) |
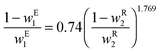 | (6) |
3. Results and discussion
3.1 Achievable concentrations of liquid fuels
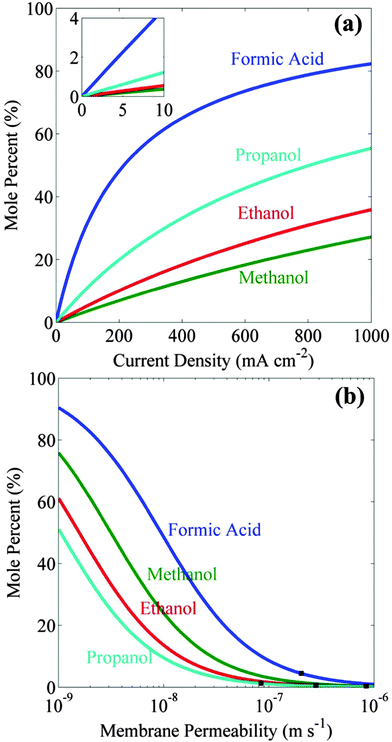
Fig. 1a shows the increase in the steady-state concentrations of formic acid, methanol, ethanol, and propanol as functions of the cell current densities. These concentrations were determined assuming equal areas of catalyst (same as the area of the cathode) and ion-exchange membrane, and are based on the permeability of formic acid,30 and alcohols18 through Nafion 117. The steady-state concentration of formic acid is higher than that of alcohols because of its higher stoichiometric number (0.5) per electron transferred. Since the diffusion coefficient of alcohols in Nafion 117 decreases with increasing the size of the alcohol, the steady-state concentration of alcohol increases with increasing alcohol size. It should be noted, though, that high product concentration can only be achieved at high (>100 mA cm−2) product current densities and require very long (>45 h) times to reach 99% of the steady-state concentration.Artificial photosynthetic systems are usually limited by light absorption and therefore operate at product current densities <10 mA cm−2.7 Reference to Fig. 1a shows that achievable concentrations at this current density are 4.4 mol% for formic acid, 0.4 mol% for methanol, 0.6 mol% for ethanol, and 1.2 mol% for propanol. These concentrations can be increased by using an ion-exchange membrane with lower fuel permeabilities than Nafion 117. Fig. 1b shows the steady-state concentrations of liquid fuels at 10 mA cm−2 increases with decreasing membrane permeability (DK/L). It can be seen that an order of magnitude decrease in the membrane mass-transfer coefficient increases the concentration of formic acid up to 32 mol%, methanol up to 4 mol%, ethanol up to 5 mol%, and propanol up to 11 mol%. This analysis provides an upper limit on the achievable concentrations of liquid fuel in the artificial photosynthetic system using a state-of-the-art ion-exchange membrane with an order of magnitude lower fuel permeability than characteristic of Nafion 117.
3.2 Phase diagram of cesium carbonate–water–ethanol mixtures
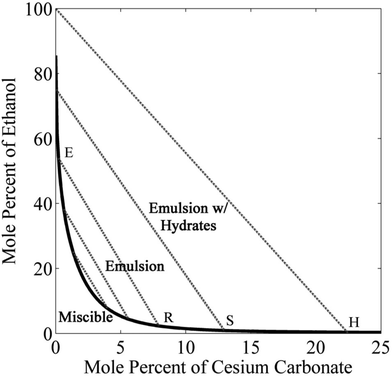
Fig. 2 shows the binodal curve (or solubility curve) for ethanol and cesium carbonate in water, obtained using eqn (5). Ethanol and water are completely miscible; however, slight addition of cesium carbonate drastically reduces the solubility of ethanol to 60 mol%. The solubility of ethanol can be further decreased by increasing the concentration of cesium carbonate. The lowest concentration of ethanol is 0.9 mol% at the solubility limit of cesium carbonate in water (13 mol%). On the left side of the binodal curve, all three components of the mixture coexist in one liquid phase. On the right side of the binodal curve, an ethanol-rich microemulsion can be formed in the water-rich phase. The composition of the emulsion is given by the tie lines (dotted lines) in Fig. 2, which are obtained using eqn (6). The left end of the tie line is the composition of the extract phase (the ethanol-rich phase) and the right end of the tie line is the composition of the raffinate phase (the water-rich phase). There is an interesting region in the phase diagram of cesium carbonate–water–ethanol mixtures, where three phases such as ethanol-rich, water-rich, and hydrates of cesium carbonate can coexists. The concentration of ethanol in the extract phase of this triple-phase region can be as high as 100 mol%.3.3 Advanced artificial photosynthetic system
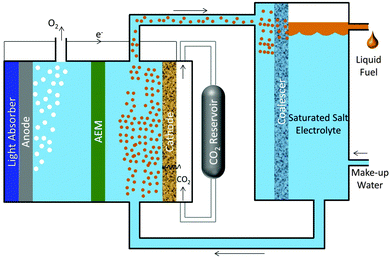
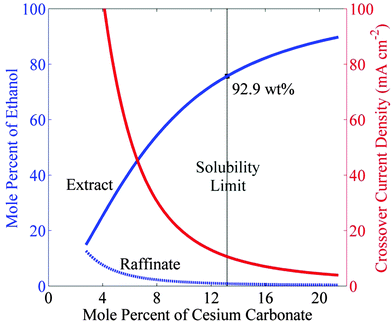
Fig. 3 shows a scheme for a photosynthetic system utilizing salt-based, liquid–liquid extraction of fuels. In this scheme, a photoelectrochemical cell or PV-electrolyzer can be used consisting of photoanode or anode, a porous cathode with a gas-diffusion layer impregnated with a saturated salt (Cs2CO3) electrolyte. The anolyte compartment is separated from the catholyte compartment by an anion-exchange membrane (AEM). Since CO2 is sparingly soluble in a saturated salt electrolyte,31 it must be supplied through a gas-diffusion layer. Electrochemical reduction of gaseous CO2 in such cell configuration has been tested at current densities >300 mA cm−2.13,32 A continuous flow of catholyte is required to collect CO2 reduction products, so that they do not contaminate the CO2 feed. Based on the phase equilibrium thermodynamics for the cesium carbonate–water–ethanol system shown in Fig. 2, the ethanol produced at the cathode will form a microemulsion in the saturated cesium carbonate electrolyte. The microemulsion is then fed to a settler, where it passes through a coalescer and is collected as a liquid containing >90 wt% pure ethanol. The make-up water feed to the settler balances the amount of water removed with the extract phase and consumed at the cathode. The bottom phase containing salt and water is recycled to the photo/electrochemical cell.Fig. 4 shows the equilibrium concentration of ethanol in the extract and the raffinate phases as a function of the concentration of cesium carbonate. The concentration of ethanol reaches 75.7 mol% (or 92.9 wt%) in the extract phase and 0.87 mol% (or 0.6 wt%) in the raffinate phase, when the Cs2CO3 reaches its solubility limit (13 mol%) in water. Ethanol in the raffinate phase will diffuse across the anion-exchange membrane and undergo oxidization at the anode. The crossover current density of ethanol is given as
| icrossover = nFPc | (7) |
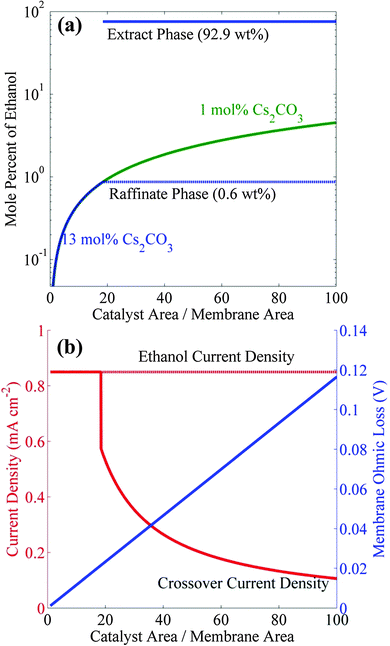
Polycrystalline copper can produce 0.85 mA cm−2 of ethanol with a Faradaic efficiency (FE) of 11% at about −1.1 V vs. RHE.9,17 A photo/electrochemical cell consisting of an IrO2 anode (or any earth-abundant materials such as NiFe or Ni) and a Cu cathode separated by Nafion 117 can be operated at −1.1 vs. RHE to generate such current densities in Cs2CO3 electrolyte.27 However, as noted above, rate of ethanol generation is well below the threshold current density to form a microemulsion in a 13 wt% CsCO3 solution (10.6 mA cm−2), and all of the ethanol produced will cross over to the anolyte compartment and be consumed. One way to circumvent this situation is to increase the ratio of catalyst-to-membrane areas well above 1.0. Fig. 5a shows the increase in catholyte ethanol concentration with increasing ratio of Cu catalyst area to Nafion 117 area for two different electrolytes −1 mol% and 13 mol% cesium carbonate and an ethanol partial current density of 0.85 mA cm−2. It can be seen that the ethanol concentration in 1 mol% Cs2CO3 only be increased to 4.5 mol% by increasing the catalyst-to-membrane area ratio to 100. Reference to Fig. 2 shows that ethanol will not phase-separate in 1 mol% Cs2CO3 because the required concentration of ethanol for phase-separation is 30 mol%. However, the required ethanol concentration for phase-separation is only 0.87 mol% in 13 mol% Cs2CO3, a level can be attained by increasing the catalyst-to-membrane area ratio to >18.46. Under these circumstances, the microemulsion will contain 93 wt% ethanol. Although the formation of microemulsion is only dependent on the partial current density of ethanol and the catalyst-to-membrane area, the FE of ethanol formation can affect the current and voltage efficiencies which directly affect the solar-to-fuel (STF) efficiency of this process. Increasing the FE of ethanol to >11% will decrease the side-reactions (which will increase the current efficiency) and also reduce the ohmic losses associated with the side-reactions (which will increase the voltage efficiency). Therefore, identification of novel catalysts that can produce ethanol at higher FE (>11%) and current density (>1 mA cm−2) will not only increase the productivity of ethanol microemulsion but will also increase its efficiency.
There are two consequences of increasing the catalyst-to-membrane areas. The first is a decrease in the ethanol-crossover current density and the second is an increase in the ohmic loss across the membrane. Fig. 5b shows that the crossover current density is equal to the ethanol current density until the onset of phase separation occurs at the catalyst-to-membrane (Cu cathode-to-Nafion membrane) area ratio of 18.46, after which the crossover current density rapidly decreases with further increasing catalyst-to-membrane area ratio, since the ethanol in the electrolyte is already at the saturation limit. The ohmic loss across the membrane increases linearly with increasing catalyst-to-membrane area ratio, and for the area ratio of 18.46 the crossover current density is equal to 0.6 mA cm−2, which means that the net rate of ethanol formation will be 0.85 − 0.60 = 0.25 mA cm−2; however, the ohmic loss across the membrane will only be 20 mV. The crossover current density could be reduced from 0.6 mA cm−2 to 0.1 mA cm−2 by decreasing the membrane ethanol permeability by six fold relative to Nafion 117, and in this case, the net ethanol current density will become 0.85 − 0.1 = 0.75 mA cm−2.
Under such conditions, increasing the partial current density of ethanol will not change its concentration in the microemulsion but will increase the volumetric flowrate of emulsion. The net molar flow rate of ethanol can be written as
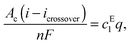 | (8) |
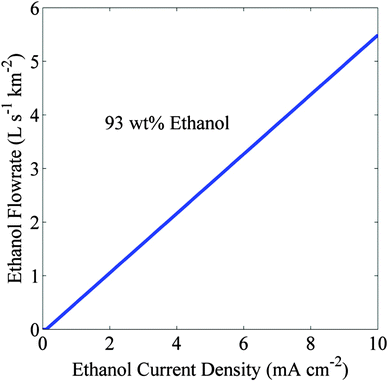 | ||
| Fig. 6 Flowrate of 93 wt% ethanol generated over a square kilometer area versus partial current density. Electrolyte is 13 mol% Cs2CO3 and the crossover current density is 0.1 mA cm−2. | ||
Although the proposed scheme should be able to produce pure liquid products continuously, there can be some operational challenges. These include (i) stability of materials used to make the cell in saturated Cs2CO3 electrolyte of pH = 10, (ii) power required to pump saturated Cs2CO3 electrolyte, and (iii) crystallization of salt due to electrodialysis. We consider that these concerns are all surmountable for the following reasons. Advances in electrolysis alkaline electrolytes have led to the development of various materials that are stable in base.34 For example, acrylic polymer can be used for the cell body, Selemion for the membrane, copper for the cathode, and IrO2 for anode, all of which are known to be stable in an alkaline environment. The viscosity of saturated CsCl electrolyte is 0.87 cP;35 therefore, if we assume a similar viscosity for Cs2CO3, the pumping requirement will be similar to that for water. From Fig. 6, the required recycle rate of Cs2CO3 electrolyte is 5.7 L s−1 km−2 at 10 mA cm−2 of ethanol current density. Assuming that a 10 cm diameter and 1 km long pipe is used to supply the saturated Cs2CO3 electrolyte to a 1 km2 wide array of artificial photosynthetic cells at a rate of 5.7 L s−1 km−2, the additional pressure required to pump the electrolyte would be 1.95 kPa which is equivalent to the energy consumption of 9.46 × 10−2 J mol−1. Therefore, the energy required to recycle the saturated salt is negligible as compared to the energy density of ethanol (1235 kJ mol−1) produced at the cathode.
The stability of saturated salt electrolytes is related to their tendency to crystallize at the cathode due to electrodialysis. Electrodialysis causes cations to migrate from anolyte to catholyte, resulting in an increase in salt concentration above saturation limit in the catholyte. This phenomenon can be prevented or minimized using an anion-exchange membrane such as Selemion, which would block cations but allow charge carriers such as bicarbonate and carbonate anions to pass through the membrane. Even if a small flux of cations did occur through the anion-exchange membrane, the increase in the salt concentration above its saturation limit would not be expected to induce nucleation (or crystallization) until the cation concentration increased beyond the metastable zone width. The metastable zone width of most salts is in the range of 10–15% above their saturation concentration.36,37 Therefore the concentration of saturated Cs2CO3 electrolyte can be increased from 4.96 mol L−1 (or 13 mol%) to 5.45 mol L−1 (or 14.28 mol%) without causing crystallization. At 10 mA cm−2 of ethanol current density, the predicted increase in the salt concentration at the cathode is about 5 mol L−1, which is within the metastable zone width (4.96–5.45 mol L−1). Therefore, the saturated salt electrolyte in the proposed scheme (Fig. 3) will not crystallize when operated in the current density regime used typically for artificial photosynthesis.
4. Conclusions and perspectives
We have summarized the challenges associated with the production of pure alcohol fuels such methanol, ethanol, and propanol using artificial photosynthesis and provide a scheme to benefit such production. The maximum achievable concentrations of various alcohols in the catholyte are of the order of 1 mol% at partial current densities of 10 mA cm−2. However such concentrations can only be achieved about 100 h of batch operation and result in 100% fuel-crossover if a Nafion 117 membrane is used to separate the catholyte and anolyte compartments. Reducing the alcohol permeability of the ion-exchange membrane by an order of magnitude only increases the liquid fuel concentration to 10 mol%, but also raises the batch operation time needed to achieve this concentration to 1000 h. To overcome these limitations, we propose an artificial photosynthetic system (Fig. 3) that utilizes concentrated salt electrolytes to phase-separate ethanol (or other organics) into microemulsion; and thereby reduce alcohol crossover and increase product collection efficiency. These design principles can also be applied to an artificial photosynthetic system producing methanol, where methanol can be separated from the aqueous mixture using various salts such as LiCl, NaCl, K2SO4, and NaHCO3.22,24 The foremost requirement for design of such systems is the availability of phase diagrams for alcohol–salt–water mixtures, which can also be defined using existing thermodynamic models.24,26 The proposed system has an additional advantage; it does not require a salt-recovery process and the phase-separated salt–water mixture can be recycled back to the photo/electrochemical cell. The use of cesium carbonate as the electrolyte and a gas-diffusion electrode will enhance the rate of CO2 reduction reaction.13,27,32 We show that photo/electrochemical reduction using 13 mol% cesium carbonate, and a catalyst-to-membrane area of 100 (or a catalyst-to-membrane area of 18.46 with a membrane ethanol permeability six-fold lower than that of Nafion 117) results in the formation of a microemulsion containing 93 wt% ethanol, while still producing 0.85 mA cm−2 ethanol at 0.1 mA cm−2 of crossover and an ohmic loss across the membrane of 117 (or 20) mV. The annual production rate of 93 wt% ethanol produced directly from such artificial photosynthetic system operating at 10 mA cm−2 (or 12% STF efficiency) will be 15.27 million gallons per year per square kilometer, which is 7% of the capacity for industrial ethanol production in California.Acknowledgements
This material is based on the work performed by the Joint Center for Artificial Photosynthesis, a DOE Energy Innovation Hub, supported through the Office of Science of the U.S. Department of Energy under Award number DE-SC0004993.References
- T. Sekimoto, S. Shinagawa, Y. Uetake, K. Noda, M. Deguchi, S. Yotsuhashi and K. Ohkawa, Appl. Phys. Lett., 2015, 106, 073902 CrossRef.
- Y. Sugano, A. Ono, R. Kitagawa, J. Tamura, M. Yamagiwa, Y. Kudo, E. Tsutsumi and S. Mikoshiba, RSC Adv., 2015, 5, 54246–54252 RSC.
- J. L. White, J. T. Herb, J. J. Kaczur, P. W. Majsztrik and A. B. Bocarsly, J. CO2 Util., 2014, 7, 1–5 CrossRef CAS.
- T. Arai, S. Sato and T. Morikawa, Energy Environ. Sci., 2015, 8, 1998–2002 CAS.
- M. Schreier, L. Curvat, F. Giordano, L. Steier, A. Abate, S. M. Zakeeruddin, J. Luo, M. T. Mayer and M. Grätzel, Nat. Commun., 2015, 6, 7326, DOI:10.1038/ncomms8326.
- M. R. Singh, E. L. Clark and A. T. Bell, Phys. Chem. Chem. Phys., 2015, 17, 18924–18936 RSC.
- M. R. Singh, E. L. Clark and A. T. Bell, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E6111–E6118, DOI:10.1073/pnas.1519212112.
- Y. Hori, Modern aspects of electrochemistry, Springer, 2008, pp. 89–189 Search PubMed.
- K. P. Kuhl, E. R. Cave, D. N. Abram and T. F. Jaramillo, Energy Environ. Sci., 2012, 5, 7050–7059 CAS.
- D. Ren, Y. Deng, A. D. Handoko, C. S. Chen, S. Malkhandi and B. S. Yeo, ACS Catal., 2015, 5, 2814–2821 CrossRef CAS.
- N. Ullah, I. Ali, M. Jansen and S. Omanovic, Can. J. Chem. Eng., 2015, 93, 55–62 CrossRef CAS.
- C. W. Li, J. Ciston and M. W. Kanan, Nature, 2014, 508, 504–507 CrossRef CAS PubMed.
- M. Schwartz, R. L. Cook, V. M. Kehoe, R. C. MacDuff, J. Patel and A. F. Sammells, J. Electrochem. Soc., 1993, 140, 614–618 CrossRef CAS.
- E. E. Barton, D. M. Rampulla and A. B. Bocarsly, J. Am. Chem. Soc., 2008, 130, 6342–6344 CrossRef CAS PubMed.
- D. P. Summers, S. Leach and K. W. Frese, J. Electroanal. Chem. Interfacial Electrochem., 1986, 205, 219–232 CrossRef CAS.
- D. W. Green, Perry's chemical engineers' handbook, McGraw-Hill, New York, 2008 Search PubMed.
- E. L. Clark, M. R. Singh, Y. Kwon and A. T. Bell, Anal. Chem., 2015, 87, 8013–8020 CrossRef CAS PubMed.
- D. Rivin, C. Kendrick, P. Gibson and N. Schneider, Polymer, 2001, 42, 623–635 CrossRef CAS.
- C. K. Narula and B. H. Davison, US Pat., US20150011813 A1, 2014 Search PubMed.
- H.-J. Huang, S. Ramaswamy, U. Tschirner and B. Ramarao, Sep. Purif. Technol., 2008, 62, 1–21 CrossRef CAS.
- J. C. Card and L. M. Farrell, Separation of alcohol-water mixtures using salts, Oak Ridge National Lab., TN, USA, 1982 Search PubMed.
- H. Zerres and J. Prausnitz, AIChE J., 1994, 40, 676–691 CrossRef CAS.
- M. Hu, Q. Zhai and Z. Liu, J. Chem. Eng. Data, 2004, 49, 717–719 CrossRef CAS.
- M. C. Iliuta, K. Thomsen and P. Rasmussen, Chem. Eng. Sci., 2000, 55, 2673–2686 CrossRef CAS.
- M. Hu, Q. Zhai, Z. Liu and S. Xia, J. Chem. Eng. Data, 2003, 48, 1561–1564 CrossRef CAS.
- J. M. Prausnitz, R. N. Lichtenthaler and E. G. de Azevedo, Molecular thermodynamics of fluid-phase equilibria, Pearson Education, 1998 Search PubMed.
- A. Murata and Y. Hori, Bull. Chem. Soc. Jpn., 1991, 64, 123–127 CrossRef CAS.
- G. Kyriacou and A. Anagnostopoulos, J. Appl. Electrochem., 1993, 23, 483–486 CrossRef CAS.
- M. R. Thorson, K. I. Siil and P. J. Kenis, J. Electrochem. Soc., 2013, 160, F69–F74 CrossRef CAS.
- Y.-W. Rhee, S. Y. Ha and R. I. Masel, J. Power Sources, 2003, 117, 35–38 CrossRef CAS.
- U. Riebesell, V. J. Fabry, L. Hansson and J.-P. Gattuso, Guide to best practices for ocean acidification research and data reporting, Publications Office of the European Union Luxembourg, 2010 Search PubMed.
- R. L. Cook, R. C. MacDuff and A. F. Sammells, J. Electrochem. Soc., 1990, 137, 607–608 CrossRef CAS.
- http://www.neo.ne.gov/statshtml/122.htm .
- K. Zeng and D. Zhang, Prog. Energy Combust. Sci., 2010, 36, 307–326 CrossRef CAS.
- D. E. Goldsack and R. Franchetto, Can. J. Chem., 1977, 55, 1062–1072 CrossRef CAS.
- A. Mersmann and K. Bartosch, J. Cryst. Growth, 1998, 183, 240–250 CrossRef CAS.
- P. H. Karpinski and J. Nývlt, Cryst. Res. Technol., 1983, 18, 959–965 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |