Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A combined experimental and computational study on supramolecular assemblies in hetero-tetranuclear nickel(II)–cadmium(II) complexes with N2O4-donor compartmental Schiff bases†
Sourav
Roy
a,
Anik
Bhattacharyya
a,
Sourav
Purkait
a,
Antonio
Bauzá
b,
Antonio
Frontera
 *b and
Shouvik
Chattopadhyay
*a
*b and
Shouvik
Chattopadhyay
*a
aDepartment of Chemistry, Inorganic Section, Jadavpur University, Kolkata - 700032, India. E-mail: shouvik.chem@gmail.com; Tel: +913324572941
bDepartamento de Química, Universitat de les Illes Balears, Crta. deValldemossa km 7.5, 07122 Palma, Baleares, Spain. E-mail: toni.frontera@uib.es
First published on 29th July 2016
Abstract
Two new hetero-tetranuclear nickel(II)/cadmium(II) complexes, a cubane [(CH3CO2)2Ni2(L1)2Cd2(NCS)2] (1) and a linear tetramer [(DMSO)2NiL2Cd(NCS)(μ1,3-SCN)Ni(DMSO)L2Cd(NCS)2] (2) {where H2L1 = N,N′-bis(3-methoxysalicylidene)propane-1,3-diamine and H2L2 = N,N′-bis(3-ethoxysalicylidene)propane-1,3-diamine are potential octadentate compartmental Schiff bases}, were synthesized and characterized. The structures of both complexes were confirmed by single crystal X-ray diffraction studies. Complex 1 contained a Ni2Cd2O4 cubane core, whereas complex 2 featured an end-to-end thiocyanate-bridged tetranuclear moiety. Furthermore, complex 1 showed C–H⋯H–C interactions, whereas a unique S⋯π interaction was observed in complex 2. Theoretical studies were performed using several computational tools such as NBO and AIM analyses. Both complexes showed photoluminescence in DMSO medium at room temperature upon irradiation with ultraviolet light. The lifetimes of the excited states were ∼27 ns.
Introduction
The condensation of various diamines and salicylaldehyde gives H2salen-type Schiff bases, which are very well-known chelating ligands to synthetic inorganic chemists for the preparation of di- and polynuclear complexes.1 The di-negative anionic forms of these Schiff bases generally act as tetradentate N2O2-donor chelating ligands to produce mononuclear complexes,2 which can cleverly be utilized as ligands (metallo-ligands) to coordinate a second metal ion by exploiting the interesting bridging ability of the phenoxo oxygen atoms, thereby forming multinuclear complexes.3 The use of 3-alkoxysalicyalaldehyde instead of salicylaldehyde itself is more beneficial as it produces compartmental octadentate Schiff bases (with inner N2O2 and outer O4 cores), which can again be used efficiently to prepare various homo-polynuclear complexes.4 These high-nuclearity transition and non-transition metal complexes have attracted much attention for their unusual physical properties5 and relevance to biological function in metalloproteins.6 Among these, phenoxo-bridged tetrameric nickel(II) clusters have been extensively studied to explore the relationship between their structural features and the strength of the magnetic exchange interaction between the nickel(II) clusters.7 Reports on the formation of heteronuclear tetramers, however, are relatively fewer in the literature.8Supramolecular interactions have been shown to play an important role in structural biology and supramolecular chemistry.9 The harmonization of various biological and physico-chemical methods is frequently implemented by the amalgamation of many non-covalent supramolecular interactions.10 A good number of familiar, strong, directional non-covalent interactions, such as hydrogen bonding and halogen bonding, have been used to manage multi-component supramolecular assemblies.11 In addition, π⋯π stacking, cation⋯π, C–H⋯π, lone pair⋯π and anion⋯π interactions are also extremely significant in this field12 and can manage the structures of bio-molecules such as proteins and DNA, several host–guest systems, enzyme–substrate binding.13 They can also participate in crystal engineering, drug–receptor interactions, enzyme inhibition, protein folding, etc.14 As a matter of fact, S⋯π interactions are crucial in the mechanism of sulphide![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) quinone oxidoreductase.14d Their omnipresent role in such diverse fields has attracted the attention of theoretical chemists to investigate and try to understand the nature of these weak non-covalent interactions, and, as a result, the importance of these no-covalent interactions have been analyzed by various researchers using combined theoretical and experimental methods.15
quinone oxidoreductase.14d Their omnipresent role in such diverse fields has attracted the attention of theoretical chemists to investigate and try to understand the nature of these weak non-covalent interactions, and, as a result, the importance of these no-covalent interactions have been analyzed by various researchers using combined theoretical and experimental methods.15
In the present work, two similar compartmental N2O4-donor Schiff bases were used to prepare two hetero-tetranuclear nickel(II)/cadmium(II) complexes: a cubane and a linear tetramer with Ni2Cd2O4 cores. These are the first examples of any hetero-tetranuclear nickel(II)/cadmium(II) complexes with H2salen-type Schiff bases. The unconventional supramolecular interactions found in the crystal packing of these complexes were theoretically analyzed focusing attention on the remarkable S⋯π interactions and also on the C–H⋯H–C interactions. Herein, we would like to report the synthesis, characterization, X-ray crystal structure, photoluminescence properties and results of the DFT study on the supramolecular architectures of these two new hetero-tetranuclear nickel(II)/cadmium(II) complexes.
Experimental section
Nickel(II) thiocyanate tetrahydrate was prepared in the laboratory following the literature method.16 All the other materials were commercially available, reagent grade and used as purchased from Sigma-Aldrich without further purification.Preparations
Preparation of H2L1 [N,N′-bis(3-methoxysalicylidene)propane-1,3-diamine]. A methanol solution (10 ml) of 3-methoxysalicylaldehyde (304 mg, 2 mmol) and 1,3-diaminopropane (0.13 ml, 1 mmol) was refluxed for ca. 1 h to form H2L1. The ligand was not isolated and was used directly for the synthesis of complex 1.
Preparation of H2L2 [N,N′-bis(3-ethoxysalicylidene)propane-1,3-diamine]. This ligand was prepared using a similar method as that used for H2L1 except that 3-ethoxysalicylaldehyde (332 mg, 2 mmol) was used instead of 3-methoxysalicylaldehyde. It was also not isolated and was used directly for the synthesis of complex 2.
Preparation of [(CH3CO2)2Ni2(L1)2Cd2(NCS)2] (1). A methanol (10 ml) solution of cadmium(II) acetate dihydrate (270 mg, 1 mmol) was added to the methanol solution (20 ml) of H2L1 and the resulting solution was stirred for 15 min. A methanol (10 ml) solution of nickel(II) thiocyanate tetrahydrate (250 mg, 1 mmol) was then added to it. The stirring was continued for about 2 h. Single crystals, suitable for X-ray diffraction, were obtained after 3–4 days on slow evaporation of the solution in open atmosphere.
Yield: 460 mg (72%); based on nickel(II). Anal. Calc. for C44H46Cd2Ni2O12S2N6 (FW = 1257.21): C, 42.04; H, 3.69; N, 6.68; Found: C, 41.9; H, 3.5; N, 6.7%. FT-IR (KBr, cm−1): 1630 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N); 2067 (C
N); 2067 (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N). UV-VIS [λmax(nm)] [εmax(L mol−1 cm−1)] (DMSO): 239 (2.55 × 104); 375 (3.4 × 103); 668 (5.86); 901 (13.84).
N). UV-VIS [λmax(nm)] [εmax(L mol−1 cm−1)] (DMSO): 239 (2.55 × 104); 375 (3.4 × 103); 668 (5.86); 901 (13.84).
Preparation of [(DMSO)2NiL2Cd(NCS)(μ1,3-SCN)Ni(DMSO)L2Cd(NCS)2] (2). This ligand was prepared using a similar method as that used for complex 1 except that H2L2 was used instead of H2L1. A few drops of DMSO were added and the resulting solution was kept for crystallization. Single crystals, suitable for X-ray diffraction, were obtained after 3–4 days on slow evaporation of the solution in open atmosphere.
Yield: 570 mg (74%); based on nickel(II). Anal. Calc. for C52H66Cd2Ni2O11S7N8 (FW = 1545.82): C, 40.40; H, 4.30; N, 7.25; Found: C, 40.2; H, 4.2; N, 7.3%. FT-IR (KBr, cm−1): 1628 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N); 2034, 2068 (C
N); 2034, 2068 (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N). UV-VIS [λmax(nm)] [εmax(L mol−1 cm−1)] (DMSO): 236 (2.75 × 104); 378 (3.6 × 103); 672 (7.46); 902 (8.64).
N). UV-VIS [λmax(nm)] [εmax(L mol−1 cm−1)] (DMSO): 236 (2.75 × 104); 378 (3.6 × 103); 672 (7.46); 902 (8.64).
Physical measurements
Elemental analyses (carbon, hydrogen and nitrogen) were performed using a Perkin Elmer 240C elemental analyzer. IR spectra in KBr (4500–500 cm−1) were recorded with a Perkin Elmer Spectrum Two spectrophotometer. Electronic spectra in DMSO were recorded on a Perkin Elmer Lambda 35 UV-visible spectrophotometer. Steady-state photoluminescence spectra in DMSO were obtained with a Shimadzu RF-5301PC spectrofluorometer at room temperature. Time-dependent photoluminescence spectra were recorded using a Hamamatsu MCP photomultiplier (R3809) and were analyzed using IBHDAS6 software. Powder X-ray diffraction was performed on a Bruker D8 instrument with Cu Kα radiation. In this process, the complexes were ground with a mortar and pestle to prepare fine powders. The powders were then dispersed with alcohol onto a zero background holder (ZBH). The alcohol was allowed to evaporate to provide a nice, even coating of powder adhered to the sample holder.X-ray crystallography
Suitable single crystals of complexes 1 and 2 were used for the data collection using a Bruker SMART APEX II diffractometer equipped with graphite-monochromated Mo Kα radiation (λ = 0.71073 Å) at 100 K. The molecular structures were solved by a direct method and refined by full-matrix least squares on F2 using the SHELX-2014 package.17 Non-hydrogen atoms were refined using anisotropic thermal parameters. The hydrogen atoms were placed in their geometrically idealized positions and constrained to ride on their parent atoms. Multi-scan empirical absorption corrections were applied to the data using the program SADABS.18 Details of the crystallographic data and refinement details are given in Table 1.| Complex | 1 | 2 |
|---|---|---|
| Formula | C44H46Cd2Ni2O12S2N6 | C52H66Cd2Ni2O11S7N8 |
| Formula weight | 1257.21 | 1545.82 |
| Temperature (K) | 100 | 100 |
| Crystal system | Triclinic | Monoclinic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P21/n |
| a (Å) | 15.313(10) | 12.070(3) |
| b (Å) | 15.334(1) | 20.252(5) |
| c (Å) | 23.219(16) | 26.697(7) |
| α (°) | 74.682(4) | 90 |
| β (°) | 77.101(4) | 93.663(1) |
| γ (°) | 89.888(4) | 90 |
| Z | 4 | 4 |
| d calc (g cm−3) | 1.632 | 1.577 |
| μ (mm−1) | 1.689 | 1.497 |
| F (000) | 2528 | 3144 |
| Total reflections | 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 609 609 |
93![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 652 652 |
| Unique reflections | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 091 091 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 581 581 |
| Observed data [I > 2σ(I)] | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053 053 |
8813 |
| No. of parameters | 1225 | 743 |
| R (int) | 0.067 | 0.049 |
| R 1, wR2 (all data) | 0.0944, 0.2010 | 0.0619, 0.1054 |
| R 1, wR2 [I > 2σ(I)] | 0.0783, 0.1941 | 0.0416, 0.0942 |
The crystal structure of complex 1 was somewhat problematic. The unit cell included some highly disordered solvent molecules, which could not be modelled as discrete atomic sites. We employed PLATON/SQUEEZE to calculate the diffraction contribution of the solvent molecules and thereby were able to produce a set of solvent-free diffraction intensities. Details about the SQUEEZE procedure are given in the CIF file.
Theoretical methods
The calculations of the non-covalent interactions were carried out using TURBOMOLE version 7.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 using the M06-2X/def2-TZVP level of theory. To evaluate the interactions in the solid state, we used the crystallographic coordinates and optimized the position of the H atoms. In the large assemblies computed for complex 1, the SVP basis set was used instead of the time-consuming def2-TZVP basis set. This procedure and level of theory have been successfully used before to evaluate similar interactions.20 The interaction energies were computed by calculating the difference between the energies of isolated monomers and their assembly. The interaction energies were corrected for the Basis Set Superposition Error (BSSE) using the counterpoise method.21
19 using the M06-2X/def2-TZVP level of theory. To evaluate the interactions in the solid state, we used the crystallographic coordinates and optimized the position of the H atoms. In the large assemblies computed for complex 1, the SVP basis set was used instead of the time-consuming def2-TZVP basis set. This procedure and level of theory have been successfully used before to evaluate similar interactions.20 The interaction energies were computed by calculating the difference between the energies of isolated monomers and their assembly. The interaction energies were corrected for the Basis Set Superposition Error (BSSE) using the counterpoise method.21
The Natural Bond Orbital (NBO) method22 was employed to analyze the charge-transfer interactions between the occupied and empty orbitals using the NBO-3.1 program included within the Gaussian-09 program. Bader's “Atoms in molecules” theory was used to study the interactions discussed herein by means of the AIMall calculation package.23
Results and discussion
Synthesis
1,3-Diaminopropane was refluxed with 3-methoxysalicylaldehyde and 3-ethoxysalicylaldehyde, respectively, to form two potential octadentate Schiff base ligands, H2L1 and H2L2, respectively, following the literature method.24 These Schiff bases (H2L1 and H2L2) on reaction with cadmium(II) acetate dihydrate, followed by the addition of nickel(II) thiocyanate tetrahydrate, gave two heteronuclear complexes. The formation of both complexes is shown in Scheme 1. | ||
| Scheme 1 Preparation of the ligands and complexes. Only the cubane core of complex 1 is shown for clarity. | ||
Description of the structures
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . The complex contains two independent hetero-tetranuclear units (A and B) with equivalent geometries. A perspective view of unit A is shown in Fig. 1. The cubane core and the coordinating atoms are highlighted in Fig. 2. The cubane core of unit B has a similar structure, as shown in Fig. S1 {ESI†}. The important bond lengths of unit A are given in Table 2. The important bond lengths of unit B and the bond angles (units A and B) are gathered in Tables S1–S3.†
. The complex contains two independent hetero-tetranuclear units (A and B) with equivalent geometries. A perspective view of unit A is shown in Fig. 1. The cubane core and the coordinating atoms are highlighted in Fig. 2. The cubane core of unit B has a similar structure, as shown in Fig. S1 {ESI†}. The important bond lengths of unit A are given in Table 2. The important bond lengths of unit B and the bond angles (units A and B) are gathered in Tables S1–S3.†
 | ||
| Fig. 1 Perspective view of complex 1 (unit A). Only the Cd2Ni2O4 cubane core has been labelled. Hydrogen atoms have been omitted for clarity. | ||
 | ||
| Fig. 2 Perspective view of the Cd2Ni2O4 cubane core of unit A, along with the coordinating atoms and bridging acetate ligands. | ||
| Complex | 1 | 2 | Complex | 1 | 2 |
|---|---|---|---|---|---|
| Cd(1)–O(1) | 2.364(7) | 2.238(2) | Ni(1)–O(2) | 2.059(7) | — |
| Cd(1)–O(2) | 2.390(6) | 2.220(3) | Ni(1)–O(5) | 2.190(7) | — |
| Cd(1)–O(3) | 2.551(8) | 2.581(4) | Ni(1)–O(10) | 2.078(8) | — |
| Cd(1)–O(4) | 2.507(9) | 2.639(4) | Ni(2)–N(3) | 2.040(9) | — |
| Cd(2)–O(6) | 2.390(6) | 2.232(3) | Ni(2)–O(5) | 2.072(6) | — |
| Cd(2)–O(7) | 2.584(8) | 2.245(3) | Ni(2)–O(1) | 2.177(7) | — |
| Cd(2)–O(8) | 2.538(9) | 2.543(3) | Ni(2)–N(4) | 2.062(8) | — |
| Ni(1)–N(2) | 2.059(9) | 2.034(4) | Cd(1)–N(6) | — | 2.194(6) |
| Ni(1)–N(1) | 2.043(9) | 2.036(4) | Cd(1)–N(7) | — | 2.150(6) |
| Ni(1)–O(1) | 2.085(6) | 2.022(3) | Cd(2)–O(9) | — | 2.669(3) |
| Ni(2)–O(11) | 2.093(8) | 2.107(4) | Cd(2)–S(7) | — | 2.521(15) |
| Ni(2)–O(6) | 2.062(7) | 2.024(3) | Cd(2)–N(10) | — | 2.175(4) |
| Cd(1)–O(6) | 2.310(6) | — | Ni(1)–N(5) | — | 2.141(4) |
| Cd(1)–O(9) | 2.202(8) | — | Ni(1)–O(2) | — | 2.011(4) |
| Cd(1)–N(5) | 2.188(11) | — | Ni(1)–O(5) | — | 2.112(3) |
| Cd(2)–O(2) | 2.311(6) | — | Ni(2)–O(7) | — | 2.021(3) |
| Cd(2)–O(5) | 2.352(7) | — | Ni(2)–O(10) | — | 2.100(3) |
| Cd(2)–O(12) | 2.214(8) | — | Ni(2)–N(8) | — | 2.031(4) |
| Cd(2)–N(6) | 2.189(11) | — | Ni(2)–N(9) | — | 2.025(4) |
The molecular structure of unit A is built from isolated heteronuclear molecules of [(CH3CO2)2Ni2(L1)2Cd2(NCS)2], in which both nickel(II) centres are hexacoordinated having pseudo-octahedral geometries while cadmium(II) centres are heptacoordinated. H2L1 is a potential octadentate compartmental Schiff base with inner N2O2 and outer O4 compartments. Nickel(II) centres occupy the inner N2O2 compartment, while each cadmium(II) resides in the outer O4 compartment. Each nickel(II) centre is attached with two imine nitrogen atoms, [N(1) and N(2) for Ni(1); N(3) and N(4) for Ni(2)] and two phenoxo oxygen atoms, [O(1) and O(2) for Ni(1); O(5) and O(6) for Ni(2)] of the deprotonated Schiff base (L1)2− constituting the equatorial plane. The fifth coordination site of each nickel(II) centre is occupied by another phenoxo oxygen atom, [O(5) for Ni(1) and O(1) for Ni(2)], from the second deprotonated Schiff base. The octahedral geometries around both nickel(II) centres are fulfilled by the coordination of two oxygen atoms [O(10) for Ni(1), which bridge between Ni(1) and Cd(1), and O(11) for Ni(2), which bridges between Ni(2) and Cd(2)] from the two bridging acetates. For the Ni(1) centre, the deviation of the coordinating atoms, O(1), O(2), N(1) and N(2) in the basal plane from the mean plane passing through them are 0.002(6), 0.008(6), 0.008(9) and 0.002(8) Å, respectively. The deviation of Ni(1) from the same plane is −0.020(13) Å. For the Ni(2) centre, the deviation of the coordinating atoms O(5), O(6), N(3) and N(4) in the basal plane from the mean plane passing through them are 0.007(6), −0.014(6), −0.013(9) and 0.006(8) Å, respectively. The deviation of Ni(2) from the same plane is 0.015(1) Å. Each cadmium(II) resides in outer O4 compartment coordinated by two phenoxo [O(1) and O(2) for Cd(1); O(5) and O(6) for Cd(2)] and two methoxo oxygen atoms [O(3) and O(4) for Cd(1); O(7) and O(8) for Cd(2)]. The fifth coordination site in each cadmium(II) is occupied by two terminal N-bonded thiocyanates [N(5) for Cd(1) and N(6) for Cd(2)]. Phenoxo oxygen atom [O(6) for Cd(1) and O(2) for Cd(2)] coordinates in the sixth coordination site of each cadmium(II) centre axially. The pentagonal bipyramidal geometry around each cadmium(II) is completed by the coordination of oxygen atom [O(9) for Cd(1) and O(12) for Cd(2)] of the bridging acetate groups.
Cadmium(II) and nickel(II) centres in the cubane unit reside in an identical environment. Within the cubane unit, the Cd(1)–Ni(1), Ni(2)–Cd(2) and Ni(2)–Ni(1) distances are significantly shorter (∼3.32 Å) compared to the Cd(1)–Ni(2) and Cd(2)–Ni(1) distances (∼3.44 Å), while the Cd(1)–Cd(2) distance is relatively longer (∼3.69 Å). The cubane core has six faces. The Cd2O2 face is opposite the Ni2O2 face. The bridging angles M–O–M (M = metal) are comparable (∼103°). The saturated six-membered chelate rings [Ni(1)–N(1)–C(9)–C(10)–C(11)–N(2)] and [Ni(2)–N(3)–C(31)–C(32)–C(33)–N(4)] have envelope conformations with the puckering parameters: q = 0.523(14) Å; θ = 143.3(12)°; ϕ = 354(2)° and q = 0.503(13) Å; θ = 144.9(12)°; ϕ = 2(2)°, respectively.25 The structure of unit B is similar to that of unit A and is described in the ESI.†
Complex 1 shows significant C–H⋯π interactions. The hydrogen atom, H(9B), attached to carbon atom, C(9), is involved in an intra-molecular C–H⋯π interaction with the phenyl ring [C(24)–C(25)–C(26)–C(27)–C(28)–C(29)]. Similarly the hydrogen atom, H(55B), attached to carbon atom, C(55), is involved in another intra-molecular C–H⋯π interaction with the phenyl ring, C(68)–C(69)–C(70)–C(71)–C(72)–C(73). Another intra-molecular C–H⋯π interaction is observed between the hydrogen atom, H(75A), attached to carbon atom, C(75A), with the phenyl ring, C(57)–C(58)–C(59)–C(60)–C(61)–C(62). The hydrogen atom, H(36), attached to carbon atom, C(36), shows another C–H⋯π interaction with the phenyl ring, C(68)–C(69)–C(70)–C(71)–C(72)–C(73). These C–H⋯π interactions are shown in Fig. S2 {ESI†}. The hydrogen atom, H(80), attached to carbon atom, C(80), shows an inter-molecular C–H⋯π interaction with a symmetry related (x, 1 + y, z) phenyl ring [C(2)–C(3)–C(4)–C (5)–C(6)–C(7)], as shown in Fig. S3.† Another C–H⋯π inter-molecular interaction is observed between the hydrogen atom, H(49), attached to carbon atom, C(49), with the symmetry related (−1 + x, y, z) phenyl ring [C(24)–C(25)–C(26)–C(27)–C(28)–C(29)], as shown in Fig. S4.† The hydrogen atom, H(14), attached to carbon atom, C(14), is involved in another inter-molecular C–H⋯π interaction with the symmetry related (1 + x, −1 + y, z) phenyl ring [C(57)–C(58)–C(59)–C(60)–C(61)–C(62)], as shown in Fig. S5.† The details of the geometric features of the C–H⋯π interactions are given in Table 3.
| Complex | X–H⋯Cg(Ring) | H⋯Cg (Å) | C–H⋯Cg (°) | C⋯Cg (Å) |
|---|---|---|---|---|
| Symmetry transformations: a = 1 + x, −1 + y, z; b = −1 + x, y, z; c = x, 1 + y, z; d = −x, 2 − y, −z; e = ½ + x, 3/2 − y, ½ + z. Cg(8) = centre of gravity of the ring [C(2)–C(3)–C(4)–C(5)–C(6)–C(7)]; Cg(10) = centre of gravity of the ring [C(24)–C(25)–C(26)–C(27)–C(28)–C(29)]; Cg(20) = centre of gravity of the ring [C(57)–C(58)–C(59)–C(60)–C(61)–C(62)]; Cg(21) = centre of gravity of the ring [C(68)–C(69)–C(70)–C(71)–C(72)–C(73)] for complex 1 and Cg(13) = centre of gravity of the ring [C(7)–C(8)–C(9)–C(10)–C(11)–C(12)]; Cg(14) = centre of gravity of the ring [C(18)–C(19)–C(20)–C(21)–C(22)–C(23)]; for complex 2. | ||||
| 1 | C(14)–H(14)⋯Cg(20)a | 2.83 | 135 | 3.549(15) |
| C(36)–H(36)⋯Cg(21) | 2.84 | 129 | 3.495(15) | |
| C(49)–H(49)⋯Cg(10)b | 2.90 | 126 | 3.527(15) | |
| C(9)–H(9B)⋯Cg(10) | 2.93 | 151 | 3.807(14) | |
| C(55)–H(55B)⋯Cg(21) | 2.97 | 148 | 3.830(15) | |
| C(75)–H(75A)⋯Cg(20) | 2.97 | 150 | 3.842(15) | |
| C(80)–H(80)⋯Cg(8)c | 2.86 | 134 | 3.566(15) | |
| 2 | C(48)–H(48A)⋯Cg(14)d | 2.91 | 133 | 3.634(6) |
| C(41)–H(41)⋯Cg(13)e | 2.85 | 149 | 3.672(7) | |
| C(29)–H(29)⋯Cg(13) | 2.98 | 153 | 3.829(6) | |
 | ||
| Fig. 3 Perspective view of complex 2 with selective atom numbering. Hydrogen atoms have been omitted for clarity. | ||
 | ||
| Fig. 4 Perspective view of the tetranuclear unit of complex 2 with selective atom numbering. Only the metal centres with coordinating atoms and the bridging thiocyanate are shown for clarity. | ||
The dinuclear unit D has a similar structure to unit C. Unit D contains nickel(II) and cadmium(II) centres, Ni(2), Cd(2), which are bridged by two phenoxo oxygen atoms, O(6) and O(7), with a Ni(2)⋯Cd(2) distance of 3.300(6) Å. Ni(2) is coordinated by two imine nitrogen atoms, N(8) and N(9), and two phenoxo oxygen atoms, O(6) and O(7), of the deprotonated potential octadentate Schiff base ligand (L2)2−. The remaining two coordination sites of Ni(2) are occupied by two oxygen atoms, O(10) and O(11), from two DMSO molecules. On the other hand, Cd(2) is coordinated by two phenoxo oxygen atoms, O(6) and O(7), two ethoxy oxygen atoms, O(8) and O(9), and one nitrogen atom, N(10), from one terminal thiocyanate. The sixth coordination site of Cd(2) is occupied by a sulphur atom, S(7), of an end-to-end bridged thiocyanate, which links the two pseudo-dinuclear units C and D. The saturated six-membered chelate ring [Ni(2)–N(8)–C(35)–C(36)–C(37)–N(9)] has an envelope conformation with the puckering parameters: q = 0.528(6) Å; θ = 144.1(5)°; ϕ = 3.5(10)°.25 The Ni(1)⋯Cd(2) separation in the tetranuclear unit is 6.42(7) Å.
Complex 2 shows three C–H⋯π interactions. The hydrogen atom, H(48A), attached to carbon atom, C(48), is involved in an inter-molecular (between two C units) C–H⋯π interaction with a symmetry related (−x, 2 − y, −z) phenyl ring [C(18)–C(19)–C(20)–C(21)–C(22)–C(23)] to form a supramolecular dimer. One intra-molecular C–H⋯π interaction is observed between two different subunits of the complex having different symmetries. The hydrogen atom, H(29), attached to carbon atom, C(29), is involved in an intra-molecular (between the C and D units) C–H⋯π interaction with a phenyl ring [C(7)–C(8)–C(9)–C(10)–C(11)–C(12)]. These interactions are shown in Fig. S6 {ESI†}. The hydrogen atom, H(41), attached to carbon atom, C(41), is involved in another inter-molecular (between the C and D units) C–H⋯π interaction with the symmetry related (1/2 + x, 3/2 − y, ½ + z) phenyl ring, C(7)–C(8)–C(9)–C(10)–C(11)–C(12) to form another supramolecular dimer, as shown in Fig. S7.† The details of the geometric features of the C–H⋯π interactions are given in Table 3. In addition to these C–H⋯π interactions, complex 2 also shows S⋯π interactions. A remarkable S⋯π interaction is observed between the lone pair of disordered sulphur atoms with the C–N and C–S orbitals of the thiocyanate [N(7)–C(2)–S(9)], attached with Cd(1). In this S⋯π interaction, DMSO acts as an electron-rich moiety (electron donor) while thiocyanate acts as an electron acceptor in spite of its anionic character. Details of this S⋯π interaction are explored in the theoretical part of this study below.
Theoretical study
The theoretical study was divided into two parts. Firstly, the surprisingly different architecture observed in the solid state of the two complexes was rationalized taking into account that the only difference between the H2salen-type Schiff bases is the alkoxy substituent (methoxy or ethoxy). The supramolecular assemblies observed in the crystal packing of complexes 1 and 2 has also been analyzed.As described above, in the cubane assembly, each cadmium(II) centre is heptacoordinated, being coordinated by two phenoxo and two methoxo oxygen atoms, with the fifth coordination site in the equatorial plane being occupied by a terminal N-bonded thiocyanate. This coordination mode, which is required for the formation of the cubane, is only possible for the methoxy substituted ligand, since the steric hindrance of both ethoxy groups prevents the formation of the heptacoordinated cadmium atom (only four atoms in the equatorial plane) in the L2 ligand (Fig. 6). As a matter of fact, the cadmium ions are hexacoordinated in compound 2, giving rise to a totally different complex.
In the crystal structure of 2, the nickel(II) and cadmium(II) metal centres are bridged by only one NCS ligand, in which the nickel(II) of the C unit is connected with the cadmium(II) of the D unit through the NCS bridge. On the other hand, the nickel(II) of the D unit is not coordinated by the NCS ligand from the C unit but is rather coordinated by two DMSO molecules. One of both DMSO molecules establishes a non-covalent S⋯π interaction, which is studied below. The coordination of this DMSO molecule prevents the formation of the doubly NCS-bridged structure. We analysed this issue by means of DFT calculations. We optimized the hypothetical double bridge structure and compared the formation energy with the one observed experimentally. The results are shown in Fig. 7, and it can be observed that the dissymmetric assembly observed experimentally is 14.4 kcal mol−1 more stable that the doubly bridged structure. A likely explanation is that both assemblies present the same number of metal–ligand coordination bonds but the experimentally observed complex has some additional stabilization from the intra-molecular non-covalent interactions established by the DMSO molecule.
 | ||
| Fig. 7 Optimized geometries of the dissymmetric assembly of complex 2 (left) and the hypothetical doubly bridged assembly. The formation energy is also indicated. | ||
The second part of the theoretical study is devoted to analysing the unconventional non-covalent interactions found in the crystal packing of complexes 1 and 2, focusing our attention to the C–H⋯H–C interactions and the remarkable S⋯π interactions. In 1, we analyzed the interesting C–H⋯H–C interactions observed between the organic ligand and acetate coligand in the solid-state structure. In 2, we analyzed the remarkable and unprecedented S⋯π interaction observed in the solid-state structure by using several computational tools, such as NBO and AIM analyses. The importance of the C–H⋯H–C interaction was highlighted by Alvarez and coworkers.26 Dihydrogen contacts in alkanes are among the weakest inter-molecular interactions (∼−0.4 kcal mol−1 for the methane dimer); however, they are cumulative, resulting in larger dimerization energies in some cases (e.g. long open chains). For example, the complexation energy computed for the dimer of n-hexane is −4.5 kcal mol−1.26
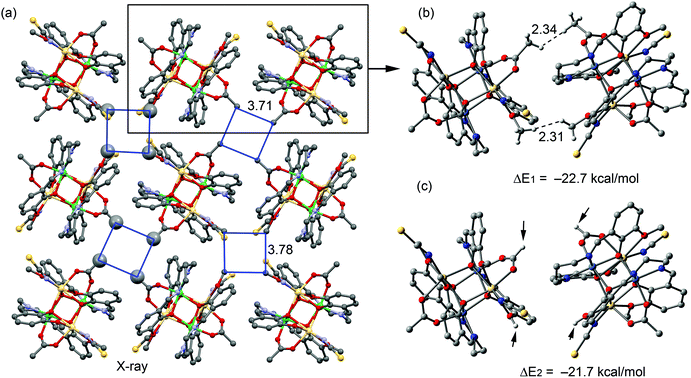
It is also worthy to emphasize that supramolecular chemists usually analyze the conventional non-covalent interactions in the X-ray structures (shorter than the sum of the van der Waals radii), ignoring longer interactions in the crystal structures. Evidently, this is a simplistic view of the crystal packing since interactions slightly longer also have an impact. Bearing this in mind, we studied the interesting crystal packing observed in 1 (Fig. 8a), where 2D planes are found in the solid state governed basically by the long range dispersion and C–H⋯H–C interactions. Curiously, the tetranuclear complexes are arranged in such a way that four methyl groups belonging to the acetate ligands of four different complexes point to the same void space (Fig. 8a). In a similar way, four methyl groups of the methoxy substituent of the aromatic ligand also point to the void space of the 2D plane (the blue lines in Fig. 8a). Moreover, the formation of the 2D plane is due to the van der Waals dispersion interactions between the bulk of the molecules. In order to evaluate the contribution of the C–H⋯H–C interactions involving the methyl groups, we used a theoretical model consisting of one dimer taken from this 2D plane, as shown in Fig. 8b (using the crystallographic coordinates). We computed its interaction energy, which is ΔE1 = −22.7 kcal mol−1 and which could be attributed to the contribution of two CH3⋯H3C interactions (in one, the –CH3 groups are from the acetate and in the other they are from the methoxy group, see dashed lines) along with the long range interactions. In an effort to estimate the contribution of the C–H⋯H–C interaction, we computed an additional model, where the methyl groups were changed by hydrogen atoms (the small arrows in Fig. 8c). As a result, the interaction is modestly reduced to ΔE2 = −21.7 kcal mol−1, which is the contribution of the van der Waals dispersion interactions between the bulk of the two molecules. The difference between both interaction energies (ΔE1 − ΔE2 = −1 kcal mol−1) is the contribution of the CH3⋯H3C interactions. This value is in good agreement with the reported calculations of the methane dimer.
In complex 2, we analyzed the disordered DMSO molecule observed in its solid-state X-ray structure (Fig. 9a). The sulphur atom is disordered in two positions and in one of both the sulphur atom is in contact with the central carbon atom of the bridging thiocyanate. This interaction can be viewed as a contact between the electron-rich sulphur atom with the π-system of the thiocyanate. In fact, we previously demonstrated27 the ability of pseudo-halide ligands (thiocyanate and selenocyanate) to interact with either H bonds (via the ending atoms) or lone pair donors (via the central carbon atom). We evaluated energetically the difference between the two disordered positions at the M06-2X/def2-TZVP level of theory, and the one with the S⋯π interaction was more stable by 3 kcal mol−1, which can be attributed to this interaction.
 | ||
| Fig. 9 (a) X-ray solid-state structure of 2; (b, c) theoretical models used to evaluate the S⋯π interaction. H atoms omitted for clarity. Distances in Å. | ||
At this point, in order to investigate the S⋯π interaction from an orbital point of view, we performed Natural Bond Orbital (NBO) calculations in the model of Fig. 9c, focusing our attention on the second-order perturbation analysis, which is very useful to study donor–acceptor interactions.28 Interestingly, we found that the lone pair (lp orbital) of the sulphur atom of DMSO interacts with the C–N and C–S antibonding orbitals (BD*) of the thiocyanate, with a concomitant second-order stabilization energy of E(2) = 0.98 kcal mol−1 for the LP(S) → BD*(CN) interaction and E(2) = 0.05 kcal mol−1 for the LP(S) → BD*(CS) orbital interaction. Therefore, the global orbital stabilization energy that can be attributed to the S⋯π interaction is approximately 1.03 kcal mol−1 in the dimer (∼33% of the total interaction energy). This analysis confirms both the existence of the interaction and also that the DMSO is acting as an electron-rich moiety (electron donor) and the thiocyanate moiety as an electron acceptor, in spite of its anionic character. This is likely due to the double coordination of the thiocyanate to two divalent metal centres [nickel(II) and cadmium(II)], which drastically increases the π-acidity of the ligand. We also computed the AIM analysis of the model of complex 2 shown in Fig. 9c in order to investigate the distribution of the critical points, which is shown in Fig. 10. A bond critical point and bond path that connects the sulphur atom of the DMSO with the sulphur atom of the pseudo-halide ligand can be observed, thus confirming the S⋯π interaction. The rest of the critical points and bond paths in this assembly have been omitted for clarity.
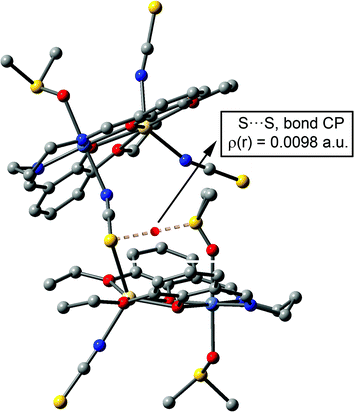 | ||
| Fig. 10 Representation of the bond critical point (red sphere) and bond path connecting the S atom of DMSO to the S atom of the pseudo-halide ligand (dashed line). H atoms omitted for clarity. | ||
IR and electronic spectra and the photophysical study
In the IR spectra of both complexes, distinct bands due to the azomethine (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) groups within the range of 1626–1632 cm−1 are routinely noticed.29 A strong band at 2067 cm−1 indicates the presence of terminal N-bonded thiocyanate in complex 1. There are two strong bands at 2034 and 2068 cm−1 in complex 2, indicating the presence of terminal (N-bonded) and end-to-end bridged thiocyanate30 respectively, which are also evident from the crystal structure determination.
N) groups within the range of 1626–1632 cm−1 are routinely noticed.29 A strong band at 2067 cm−1 indicates the presence of terminal N-bonded thiocyanate in complex 1. There are two strong bands at 2034 and 2068 cm−1 in complex 2, indicating the presence of terminal (N-bonded) and end-to-end bridged thiocyanate30 respectively, which are also evident from the crystal structure determination.
As cadmium(II) is a d10 system, no d–d bands are observed due to cadmium(II). The intense absorption bands at shorter wavelengths (∼375 nm) may be assigned to metal-to-ligand charge-transfer bands (MLCT) due to both the nickel(II) and cadmium(II) centres.31a In the visible range, two absorption bands around 670 nm and 900 nm are observed. These bands may be assigned as 3T1g(F) ← 3A2g(F) and 3T2g(F) ← 3A2g(F), respectively.31b,c The higher energy d–d band, 3T1g(P) ← 3A2g(F), expected for octahedral nickel(II), cannot be observed as it is obscured by strong charge-transfer transitions (∼375 nm).31c The bands at ∼270 nm may be assigned as ligand centred π* ← π transitions.32
Both complexes exhibit fluorescence in DMSO medium. The fluorescence data are listed in Table 4 (without solvent correction). These are assigned as intra-ligand (π* ← π) fluorescence.32 The mean lifetimes (Γavg) of the exited states are 27.7 ns (for 1) and 26.8 ns (for 2) at room temperature (Table 4). Decay profiles (Fig. 11) were fitted to a multi-exponential model:
where αi and τi are the pre-exponential factor and excited-state luminescence decay time associated with the i-th component, respectively.
| Complex | Absorption (nm) | Emission (nm) | A 1 (%) | τ 1 (ns) | A 2 (%) | τ 2 (ns) | Γ avg (ns) | χ 2 |
|---|---|---|---|---|---|---|---|---|
| 1 | 375 | 453 | 33.64 | 6.94 | 66.36 | 30.12 | 27.7 | 1.1098 |
| 2 | 378 | 456 | 33.64 | 7.21 | 66.36 | 29.20 | 26.8 | 1.1481 |
PXRD
The experimental PXRD patterns of the bulk products were in good agreement with the simulated XRD patterns from the single crystal X-ray diffraction results, indicating consistency of the bulk sample. The simulated patterns of the complexes were calculated from the single crystal structural data (Cif) using the CCDC Mercury software.Concluding remarks
Synthesis and X-ray characterization of two new hetero-tetranuclear nickel(II)–cadmium(II) complexes with Schiff base ligands have been described in this paper. Between the complexes, complex 1 was a phenoxo-bridged cubane and complex 2 was a linear tetramer with Ni2Cd2O4 cores. The linear tetramer consisted of two pseudo-dinuclear units, joined through a single end-to-end thiocyanate bridge. The solid-state structure of complex 1 showed the participation of the organic ligand and acetate group in C–H⋯H–C interactions, which were evaluated energetically by means of DFT calculations. Moreover, the disorder of the DMSO molecule was studied in complex 2, since one of the disordered DMSO molecules presented an unprecedented S⋯π interaction, where the π-system was provided by the thiocyanate. This unexpected interaction was evidenced by means of several computational tools, such as NBO and AIM analyses.Acknowledgements
Crystallographic data were collected at the DST-FIST, India funded Single Crystal Diffractometer Facility at the Department of Chemistry, Jadavpur University. We thank the MINECO of Spain (projects CTQ2014-57393-C2-1-P and CONSOLIDER INGENIO 2010 CSD2010-00065, FEDER funds). We thank the CTI (UIB) for computational facilities.Notes and references
- (a) A. Hazari, L. K. Das, A. Bauzá, A. Frontera and A. Ghosh, Dalton Trans., 2016, 45, 5730–5740 RSC; (b) P. Seth, S. Giri and A. Ghosh, Dalton Trans., 2015, 44, 12863–12870 RSC; (c) B. J. Kennedy and K. S. Murray, Inorg. Chem., 1985, 24, 1552–1557 CrossRef CAS; (d) A. van den Bergen, K. S. Murray, B. O. West and A. N. Buckley, J. Chem. Soc. A, 1969, 2051–2060 RSC; (e) E. Uhlig, Coord. Chem. Rev., 1973, 10, 227–264 CrossRef CAS; (f) S. Yamada, Coord. Chem. Rev., 1999, 190, 537–555 CrossRef; (g) P. Mukherjee, C. Biswas, M. G. B. Drew and A. Ghosh, Polyhedron, 2007, 26, 3121–3128 CrossRef CAS; (h) L. S. Felices, E. C. Escudero-Adán, J. Benet-Buchholz and A. W. Kleij, Inorg. Chem., 2009, 48, 846–853 CrossRef PubMed; (i) S. A. Fairhurst, D. L. Hughes, G. J. Leigh, J. R. Sanders and J. Weisner, J. Chem. Soc., Dalton Trans., 1994, 2591–2598 RSC; (j) R. M. Clarke and T. Storr, Dalton Trans., 2014, 43, 9380–9391 RSC; (k) X. Yanga, R. A. Jonesb and S. Huanga, Coord. Chem. Rev., 2014, 273–274, 63–75 CrossRef.
- (a) N. Sarkar, P. K. Bhaumik and S. Chattopadhyay, Polyhedron, 2016, 115, 37–46 CrossRef CAS; (b) P. Bhowmik, H. P. Nayek, M. Corbella, N. Aliaga-Alcalde and S. Chattopadhyay, Dalton Trans., 2011, 40, 7916–7926 RSC; (c) E. Ĺopez-Torres and M. A. Mendiola, Dalton Trans., 2009, 7639–7647 RSC; (d) M. Sutradhar, T. Roy Barman, M. G. B. Drew and E. Rentschler, J. Mol. Struct., 2013, 1041, 44–49 CrossRef CAS; (e) D. A. Rotsch, K. M. Reinig, E. M. Weis, A. B. Taylor, C. L. Barnesa and S. S. Jurisson, Dalton Trans., 2013, 42, 11614–11625 RSC; (f) S. Chandra and R. Kumar, Transition Met. Chem., 2004, 29, 269–275 CrossRef CAS; (g) S. A. Schuetz, C. M. Silvernail, C. D. Incarvito, A. L. Rheingold, J. L. Clark, V. W. Day and J. A. Belot, Inorg. Chem., 2004, 43, 6203–6214 CrossRef CAS PubMed; (h) S. Mohebbi and M. Abdi, J. Coord. Chem., 2008, 61, 3410–3419 CrossRef CAS; (i) A. Ray, S. Banerjee, G. M. Rosair, V. Gramlich and S. Mitra, Struct. Chem., 2008, 19, 459–465 CrossRef CAS; (j) D. Mandal, P. B. Chatterjee, S. Bhattacharya, K.-Y. Choi, R. Clérac and M. Chaudhury, Inorg. Chem., 2009, 48, 1826–1835 CrossRef CAS PubMed; (k) A. Vlad, M.-F. Zaltariov, S. Shova, M. Cazacu, M. Avadanei, A. Soroceanu and P. Samoila, Polyhedron, 2016, 115, 76–85 CrossRef CAS.
- (a) S. Bhattacharya and S. Mohanta, Inorg. Chim. Acta, 2015, 432, 169–175 CrossRef CAS; (b) P. A. Vigato and S. Tamburini, Coord. Chem. Rev., 2008, 252, 1871–1995 CrossRef CAS; (c) L. K. Das, C. J. Gómez-García, M. G. B. Drew and A. Ghosh, Polyhedron, 2015, 87, 311–320 CrossRef CAS; (d) P. Chakraborty and S. Mohanta, Polyhedron, 2015, 87, 98–108 CrossRef CAS.
- (a) S. Bhattacharya, A. Jana and S. Mohanta, CrystEngComm, 2013, 15, 10374–10382 RSC; (b) A. Biswas, L. Mandal, S. Mondal, C. R. Lucas and S. Mohanta, CrystEngComm, 2013, 15, 5888–5897 RSC; (c) P. Bhowmik, H. P. Nayek, M. Corbella, N. Aliaga-Alcalde and S. Chattopadhyay, Dalton Trans., 2011, 40, 7916–7926 RSC; (d) P. Bhowmik, S. Jana, P. P. Jana, K. Harms and S. Chattopadhyay, Inorg. Chim. Acta, 2012, 390, 53–60 CrossRef CAS; (e) P. Bhowmik, S. Jana, P. P. Jana, K. Harms and S. Chattopadhyay, Inorg. Chem. Commun., 2012, 18, 50–56 CrossRef CAS; (f) P. Bhowmik, S. Jana and S. Chattopadhyay, Polyhedron, 2012, 44, 11–17 CrossRef CAS; (g) P. Bhowmik, K. Harms and S. Chattopadhyay, Polyhedron, 2013, 49, 113–120 CrossRef CAS; (h) P. Bhowmik, N. Aliaga-Alcalde, V. Gómez, M. Corbella and S. Chattopadhyay, Polyhedron, 2013, 49, 269–276 CrossRef CAS; (i) P. Bhowmik, S. Chatterjee and S. Chattopadhyay, Polyhedron, 2013, 63, 214–221 CrossRef CAS.
- (a) K. Bhattacharya, M. Maity, S. Md T. Abtab, M. C. Majee and M. Chaudhury, Inorg. Chem., 2013, 52, 9597–9605 CrossRef CAS PubMed; (b) A. Jana, R. Koner, T. Weyhermueller, P. Lemoine, M. Ghosh and S. Mohanta, Inorg. Chim. Acta, 2011, 375, 263–270 CrossRef CAS.
- (a) E. Evangelio, N. P. Rath and L. M. Mirica, Dalton Trans., 2012, 41, 8010–8021 RSC; (b) X. Gong, Y.-Y. Ge, M. Fang, Z.-G. Gu, S.-R. Zheng, W.-S. Li, S.-J. Hu, S.-B. Lib and Y.-P. Cai, CrystEngComm, 2011, 13, 6911–6915 RSC.
- (a) S. Sasmal, S. Hazra, P. Kundu, S. Majumder, N. Aliaga-Alcalde, E. Ruiz and S. Mohanta, Inorg. Chem., 2010, 49, 9517–9526 CrossRef CAS PubMed; (b) S. Hazra, R. Koner, P. Lemoine, E. C. Sañudo and S. Mohanta, Eur. J. Inorg. Chem., 2009, 3458–3466 CrossRef CAS; (c) J. P. Wikstrom, A. Y. Nazarenko, W. M. Reiff and E. V. Rybak-Akimova, Inorg. Chim. Acta, 2007, 360, 3733–3740 CrossRef CAS; (d) B. Biswas, U. Pieper, T. Weyhermuller and P. Chaudhuri, Inorg. Chem., 2009, 48, 6781–6793 CrossRef CAS PubMed; (e) J. M. Clemente-Juan, B. Chansou, B. Donnadieu and J. Tuchagues, Inorg. Chem., 2000, 39, 5515–5519 CrossRef CAS PubMed; (f) S.-Y. Zhang, W.-Q. Chen, B. Hu, Y.-M. Chen, W. Li and Y. Li, Inorg. Chem. Commun., 2012, 16, 74–77 CrossRef CAS; (g) S.-H. Zhang, N. Li, C.-M. Ge, C. Fenga and L.-F. Ma, Dalton Trans., 2011, 40, 3000–3007 RSC.
- (a) H. Y. Kwak, D. W. Ryu, H. C. Kim, E. K. Koh, B. K. Chod and C. S. Hong, Dalton Trans., 2009, 1954–1961 RSC; (b) H. Chen, C.-B. Ma, D.-Q. Yuan, M.-Q. Hu, H.-M. Wen, Q.-T. Liu and C.-N. Chen, Inorg. Chem., 2011, 50, 10342–10352 CrossRef CAS PubMed.
- (a) S. Biswas, C. J. Gómez-García, J. M. Clemente-Juan, S. Benmansour and A. Ghosh, Inorg. Chem., 2014, 53, 2441–2449 CrossRef CAS PubMed; (b) L. K. Das and A. Ghosh, CrystEngComm, 2013, 15, 9444–9456 RSC; (c) S. L. Roderick and B. W. Matthews, Biochemistry, 1993, 32, 3907–3912 CrossRef CAS PubMed; (d) K. Ghosh, S. Roy, A. Ghosh, A. Banerjee, A. Bauzá, A. Frontera and S. Chattopadhyay, Polyhedron, 2016, 112, 6–17 CrossRef CAS.
- (a) J. Chen, J. Tang, J. Zhou, L. Zhang, G. Chen and D. Tang, Anal. Chim. Acta, 2014, 810, 10–16 CrossRef CAS PubMed; (b) K. Mahata and M. Schmittel, J. Am. Chem. Soc., 2009, 131, 16544–16554 CrossRef CAS PubMed.
- (a) Y.-S. Yang, Y.-P. Yang, M. Liu, Q.-M. Qiu, Q.-H. Jin, J.-J. Sun, H. Chen, Y.-C. Dai and Q.-X. Meng, Polyhedron, 2015, 85, 912–917 CrossRef CAS; (b) Y. Shen, N. Ma, L. Wu and H.-H. Song, Inorg. Chim. Acta, 2015, 429, 51–60 CrossRef CAS; (c) A. Bhattacharyya, P. K. Bhaumik, P. P. Jana and S. Chattopadhyay, Polyhedron, 2014, 78, 40–45 CrossRef CAS; (d) S. Carboni, C. Gennari, L. Pignataro and U. Piarulli, Dalton Trans., 2011, 40, 4355–4373 RSC.
- (a) C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534 CrossRef CAS; (b) S. K. Burley and G. A. Petsko, Science, 1985, 229, 23–28 CAS; (c) K. S. Kim, P. Tarakeshwar and J. Y. Lee, Chem. Rev., 2000, 100, 4145–4185 CrossRef CAS PubMed; (d) J. C. Ma and D. A. Dougherty, Chem. Rev., 1997, 97, 1303–1324 CrossRef CAS PubMed; (e) K. S. Kim, J. Y. Lee, S. J. Lee, T.-K. Ha and D. H. Kim, J. Am. Chem. Soc., 1994, 116, 7399–7400 CrossRef CAS; (f) M. Nishio, M. Hirota and Y. Umezawa, in The C–H/p Interaction: Evidence, Nature, Consequences, Wiley-VCH, New York, 1998 Search PubMed; (g) M. Nishio, CrystEngComm, 2004, 6, 130–156 RSC; (h) M. Egli and S. Sarkhel, Acc. Chem. Res., 2007, 40, 197–205 CrossRef CAS PubMed; (i) T. J. Mooibroek, P. Gamez and J. Reedijk, CrystEngComm, 2008, 10, 1501–1515 RSC; (j) J. Ran and P. Hobza, J. Chem. Theory Comput., 2009, 5, 1180–1185 CrossRef CAS PubMed; (k) M. Barceló-Oliver, C. Estarellas, A. García-Raso, A. Terrón, A. Frontera, D. Quiñonero, E. Molins and P. M. Deyà, CrystEngComm, 2010, 12, 362–365 RSC; (l) D. Quiñonero, C. Garau, C. Rotger, A. Frontera, P. Ballester, A. Costa and P. M. Deyà, Angew. Chem., Int. Ed., 2002, 41, 3389–3392 CrossRef.
- (a) D. Paolantoni, J. Rubio-Magnieto, S. Cantel, J. Martinez, P. Dumy, M. Surin and S. Ulrich, Chem. Commun., 2014, 50, 14257 RSC; (b) S. Jana, K. Harms and S. Chattopadhyay, J. Coord. Chem., 2014, 67, 2954–2966 CrossRef CAS; (c) C. Estarellas, A. Frontera, D. Quiæonero and P. M. Deyà, Angew. Chem., Int. Ed., 2011, 50, 415 CrossRef CAS PubMed.
- (a) S. Naskar, D. Mishra, R. J. Butcher and S. K. Chattopadhyay, Polyhedron, 2007, 26, 3703–3714 CrossRef CAS; (b) L. M. Salonen, M. Ellermann and F. Diederich, Angew. Chem., Int. Ed., 2011, 50, 4808 CrossRef CAS PubMed; (c) J. Xiao, P. Broz, A. W. Puri, E. Deu, M. Morell, D. M. Monack and M. Bogyo, J. Am. Chem. Soc., 2013, 135, 9130–9138 CrossRef CAS PubMed; (d) A. Bauzá, D. Quiñonero, P. M. Deyà and A. Frontera, Chem. – Asian J., 2013, 8, 2708–2713 CrossRef PubMed.
- (a) A. Hazari, L. K. Das, A. Bauza, A. Frontera and A. Ghosh, Dalton Trans., 2014, 43, 8007 RSC; (b) P. Seth, A. Bauza, A. Frontera and A. Ghosh, Inorg. Chem. Commun., 2014, 41, 1 CrossRef CAS; (c) A. Bhattacharyya, P. K. Bhaumik, A. Bauza, P. P. Jana, A. Frontera, M. G. B. Drew and S. Chattopadhyay, RSC Adv., 2014, 4, 58643 RSC; (d) H. S. Jena, RSC Adv., 2014, 4, 3028 RSC; (e) H. S. Jena, Inorg. Chim. Acta, 2014, 410, 156 CrossRef CAS; (f) S. Naiya, M. G. B. Drew, C. Estarellas, A. Frontera and A. Ghosh, Inorg. Chim. Acta, 2010, 363, 3904 CrossRef CAS; (g) C. Murcia-García, A. Bauzá, G. Schnakenburg, A. Frontera and R. Streubel, CrystEngComm, 2015, 17, 1769 RSC.
- K. P. Sarma and R. K. Poddar, Transition Met. Chem., 1984, 9, 135–138 CrossRef CAS.
- (a) G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed; (b) G. M. Sheldrick, SHELXS-97 and SHELXL-97: Program for Structure Solution, University of Göttingen, Institute fur Anorganische Chemieder Universitat, Gottingen, Germany, 1997 Search PubMed.
- G. M. Sheldrick, SADABS: Software for Empirical Absorption Correction, University of Göttingen, Institute fur Anorganische Chemieder Universitat, Gottingen, Germany, 1999–2003 Search PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- (a) A. Bauzá, A. Terrón, M. Barceló-Oliver, A. García-Raso and A. Frontera, Inorg. Chim. Acta, 2016 DOI:10.1016/j.ica.2015.04.028; (b) D. Sadhukhan, M. Maiti, G. Pilet, A. Bauzá, A. Frontera and S. Mitra, Eur. J. Inorg. Chem., 2015, 11, 1958–1972 CrossRef; (c) M. Mirzaei, H. Eshtiagh-Hosseini, Z. Bolouri, Z. Rahmati, A. Esmaeilzadeh, A. Hassanpoor, A. Bauza, P. Ballester, M. Barceló-Oliver, J. T. Mague, B. Notash and A. Frontera, Cryst. Growth Des., 2015, 15, 1351–1361 CrossRef CAS; (d) P. Chakraborty, S. Purkait, S. Mondal, A. Bauzá, A. Frontera, C. Massera and D. Das, CrystEngComm, 2015, 17, 4680–4690 RSC.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- T. A. Keith, TK Gristmill Software, AIMAll (Version 13.05.06), Overland Park, KS, USA, 2013 Search PubMed.
- (a) P. Bhowmik, S. Jana, P. P. Jana, K. Harms and S. Chattopadhyay, Inorg. Chim. Acta, 2012, 390, 53–60 CrossRef CAS; (b) S. Bhattacharya and S. Mohanta, Inorg. Chim. Acta, 2015, 432, 169–175 CrossRef CAS.
- (a) D. Cremer and J. A. Pople, J. Am. Chem. Soc., 1975, 97, 1354–1358 CrossRef CAS; (b) D. Cremer, Acta Crystallogr., Sect. B: Struct. Sci., 1984, 40, 498–500 CrossRef; (c) J. C. A. Boeyens, J. Cryst. Mol. Struct., 1978, 8, 317–320 CrossRef.
- (a) J. Echeverría, G. Aullón, D. Danovich, S. Shaik and S. Alvarez, Nat. Chem., 2011, 3, 323–330 CrossRef PubMed; (b) D. Danovich, S. Shaik, F. Neese, J. Echeverría, G. Aullón and S. Alvarez, J. Chem. Theory Comput., 2013, 9, 1977–1991 CrossRef CAS PubMed.
- A. Hazari, L. K. Das, A. Bauzá, A. Frontera and A. Ghosh, Dalton Trans., 2014, 43, 8007–8015 RSC.
- F. Weinhold, J. Comput. Chem., 2012, 33, 2363–2379 CrossRef CAS PubMed.
- A. Bhattacharyya, S. Roy, J. Chakraborty and S. Chattopadhyay, Polyhedron, 2016, 112, 109–117 CrossRef CAS.
- (a) S. Roy and S. Chattopadhyay, Inorg. Chim. Acta, 2015, 433, 72–77 CrossRef CAS; (b) S. Thakurta, R. J. Butcher, C. J. Gomez-Garcia, E. Garribba and S. Mitra, Inorg. Chim. Acta, 2010, 363, 3981–3986 CrossRef CAS.
- (a) B. Machura, I. Nawrop, R. Kruszynski and M. Dulski, Polyhedron, 2013, 54, 272–284 CrossRef CAS; (b) A. Bhattacharyya, P. K. Bhaumik, M. Das, A. Bauzá, P. P. Jana, K. Harms, A. Frontera and S. Chattopadhyay, Polyhedron, 2015, 101, 257–269 CrossRef CAS; (c) S. Chattopadhyay, M. G. B. Drew and A. Ghosh, Polyhedron, 2007, 26, 3513–3522 CrossRef CAS.
- A. Bhattacharyya, P. K. Bhaumik, P. P. Jana and S. Chattopadhyay, Polyhedron, 2014, 78, 40–45 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1445222 for 1 and 1445223 for 2. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6dt02587k |
| This journal is © The Royal Society of Chemistry 2016 |