Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Silver(I) complexes with 1′-(diphenylphosphino)-1-cyanoferrocene: the art of improvisation in coordination†
Karel
Škoch
a,
Filip
Uhlík
b,
Ivana
Císařová
a and
Petr
Štěpnička
*a
aDepartment of Inorganic Chemistry, Faculty of Science, Charles University in Prague, Hlavova 2030, 128 40 Prague, Czech Republic. E-mail: petr.stepnicka@natur.cuni.cz
bDepartment of Physical and Macromolecular Chemistry, Faculty of Science, Charles University in Prague, Hlavova 2030, 128 40 Prague, Czech Republic
First published on 1st June 2016
Abstract
1′-(Diphenylphosphino)-1-cyanoferrocene (1) reacts with silver(I) halides at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
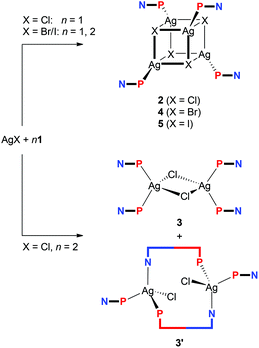
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 metal-to-ligand ratio to afford the heterocubane complexes [Ag(μ3-X)(1-κP)]4, where X = Cl (2), Br (4), and I (5). In addition, the reaction with AgCl with 2 equiv. of 1 leads to chloride-bridged dimer [(μ-Cl)2{Ag(1-κP)2}2] (3) and, presumably, also to [(μ(P,N)-1){AgCl(1-κP)}]2 (3′). While similar reactions with AgCN furnished only the insoluble coordination polymer [(1-κP)2Ag(NC)Ag(CN)]n (6), those with AgSCN afforded the heterocubane [Ag(1-κP)(μ-SCN-S,S,N)]4 (7) and the thiocyanato-bridged disilver(I) complex [Ag(1-κP)2(μ-SCN-S,N)]2 (8), thereby resembling reactions in the AgCl–1 system. Attempted reactions with AgF led to ill-defined products, among which [Ag(1-κP)2(μ-HF2)]2 (9) and [(μ-SiF6){Ag(1-κP)2}2] (10) could be identified. The latter compound was prepared also from Ag2[SiF6] and 1. Reactions between 1 and AgClO4 or Ag[BF4] afforded disilver complexes [(μ(P,N)-1)Ag(ClO4-κO)]2 (11) and [(μ(P,N)-1)Ag(BF4-κF)]2 (12) featuring pseudolinear Ag(I) centers that are weakly coordinated by the counter anions. A similar reaction with Ag[SbF6] followed by crystallization from ethyl acetate produced an analogous complex, albeit with coordinated solvent, [(μ(P,N)-1)Ag(AcOEt-κO)]2[SbF6]2 (13). Ultimately, a compound devoid of any additional ligands at the Ag(I) centers, [(μ(P,N)-1)Ag]2[B(C6H3(CF3)2-3,5)4]2 (14), was obtained from the reaction of 1 with silver(I) tetrakis[3,5-bis(trifluoromethyl)phenyl]borate. The reaction of Ag[BF4] with two equivalents of 1 produced unique coordination polymer [Ag(1-κP)(μ(P,N)-1)]n[BF4]n (15), the structure of which contained one of the phosphinoferrocene ligands coordinated as a P,N-chelate and the other forming a bridge to an adjacent Ag(I) center. All of these compounds were structurally characterized by single-crystal X-ray crystallography, revealing that the lengths of the bonds between silver and its anionic ligand(s) typically exceed the sum of the respective covalent radii, which is in line with the results of theoretical calculations at the density-functional theory (DFT) level, suggesting that standard covalent dative bonds are formed between silver and phosphorus (soft acid/soft base interactions) while the interactions between silver and the ligand's nitrile group (if coordinated) or the supporting anion are of predominantly electrostatic nature.
1 metal-to-ligand ratio to afford the heterocubane complexes [Ag(μ3-X)(1-κP)]4, where X = Cl (2), Br (4), and I (5). In addition, the reaction with AgCl with 2 equiv. of 1 leads to chloride-bridged dimer [(μ-Cl)2{Ag(1-κP)2}2] (3) and, presumably, also to [(μ(P,N)-1){AgCl(1-κP)}]2 (3′). While similar reactions with AgCN furnished only the insoluble coordination polymer [(1-κP)2Ag(NC)Ag(CN)]n (6), those with AgSCN afforded the heterocubane [Ag(1-κP)(μ-SCN-S,S,N)]4 (7) and the thiocyanato-bridged disilver(I) complex [Ag(1-κP)2(μ-SCN-S,N)]2 (8), thereby resembling reactions in the AgCl–1 system. Attempted reactions with AgF led to ill-defined products, among which [Ag(1-κP)2(μ-HF2)]2 (9) and [(μ-SiF6){Ag(1-κP)2}2] (10) could be identified. The latter compound was prepared also from Ag2[SiF6] and 1. Reactions between 1 and AgClO4 or Ag[BF4] afforded disilver complexes [(μ(P,N)-1)Ag(ClO4-κO)]2 (11) and [(μ(P,N)-1)Ag(BF4-κF)]2 (12) featuring pseudolinear Ag(I) centers that are weakly coordinated by the counter anions. A similar reaction with Ag[SbF6] followed by crystallization from ethyl acetate produced an analogous complex, albeit with coordinated solvent, [(μ(P,N)-1)Ag(AcOEt-κO)]2[SbF6]2 (13). Ultimately, a compound devoid of any additional ligands at the Ag(I) centers, [(μ(P,N)-1)Ag]2[B(C6H3(CF3)2-3,5)4]2 (14), was obtained from the reaction of 1 with silver(I) tetrakis[3,5-bis(trifluoromethyl)phenyl]borate. The reaction of Ag[BF4] with two equivalents of 1 produced unique coordination polymer [Ag(1-κP)(μ(P,N)-1)]n[BF4]n (15), the structure of which contained one of the phosphinoferrocene ligands coordinated as a P,N-chelate and the other forming a bridge to an adjacent Ag(I) center. All of these compounds were structurally characterized by single-crystal X-ray crystallography, revealing that the lengths of the bonds between silver and its anionic ligand(s) typically exceed the sum of the respective covalent radii, which is in line with the results of theoretical calculations at the density-functional theory (DFT) level, suggesting that standard covalent dative bonds are formed between silver and phosphorus (soft acid/soft base interactions) while the interactions between silver and the ligand's nitrile group (if coordinated) or the supporting anion are of predominantly electrostatic nature.
Introduction
Because of a d10 valence shell configuration, soft1 silver(I) ions have no stereochemical preference due to the lack of ligand field stabilization. As a result, the coordination geometry of Ag(I) complexes is determined by an interplay of electrostatic and steric factors and is, therefore, difficult to predict.2 Thus, although the Ag(I)–phosphine complexes are accessible through simple reactions of silver(I) salts with phosphines, they form a wide variety of structures ranging from mononuclear species to complicated multinuclear, often polymeric, assemblies and clusters.3 This also holds true for silver(I) complexes with 1,1′-bis(diphenylphosphino)ferrocene (dppf), an archetypal and widely studied bidentate metalloligand,4 which has been demonstrated in numerous systematic and focused studies devoted to Ag(I)–dppf complexes with various supporting (mostly simple anionic) ligands5,6 as well as on multimetallic complexes and transition metal clusters featuring Ag(I)(dppf) fragments.7 In contrast, the structural chemistry of Ag(I) complexes with other phosphinoferrocene donors remains largely unexplored, being limited to compounds prepared from (ferrocenylmethyl)diphenylphosphine,8 diferrocenyl(phenyl)phosphine,9 a cyclic ferrocene triphosphine10 or (2-ferrocenylethyl)phosphines (FcCH2CH2)nPH3−n (Fc = ferrocenyl, n = 1–3)11 for the non-functional ferrocene phosphines, and a handful of dppf congeners with one of their phosphine groups replaced by another functional moiety.12 To date, the latter compounds include only Ag(I) complexes with phosphino-chalcogen donors (A and B in Scheme 1)13 or phosphinoferrocene pyridines (C–E in Scheme 1)14 and Ag(I) carboxylates prepared from 1′-(diphenylphosphino)-1-ferrocenecarboxylic acid (Hdpf).15In view of our recent investigations into the coordination chemistry of 1′-(diphenylphosphino)-1-cyanoferrocene (1 in Scheme 1) that led to structurally unique Cu(I) complexes16 and hemilabile Au(I) complexes with favorable catalytic properties,17 we aimed to complete our study with this new, donor-unsymmetric dppf analogue by focusing on complexes with Ag(I). Attention was directed mainly to the structural chemistry of the 1–Ag(I) complexes because a search in the Cambridge Structural Database18 revealed that silver(I) complexes with phosphinonitrile donors whose crystal structure has been determined are very rare, consisting of [Ag{P(CH2CH2CN)3-κP}2]NO3 featuring linearly coordinated Ag(I) centers19 and complex [Ag2(μ-L)2(MeCN)2][SbF6]2, where L is 2,6-bis(diphenylphosphino)benzonitrile coordinated as a P,P′-bridge between the trigonal and tetrahedral Ag(I) centers.20
This contribution describes the structural characterization of products arising from the interactions of various AgX salts with phosphinonitrile 1 at varying metal-to-ligand ratios. Because of the specific features detected in the structures of some of these complexes, attention is also paid to the bonding situation in the representative complexes, which is discussed in view of the results of density-functional theory (DFT) computations.
Results and discussion
General comments
Considering the structural complexity of Ag(I)–phosphine complexes, the reaction studies were performed using silver(I) salts with a wide selection of counter anions and at varying metal-to-ligand ratios. The screening experiments were performed in deuterated solvents to allow for in situ NMR monitoring. Typically, ligand 1 was added to a suspension of the respective AgX salt (mostly at Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratios of 1
1 ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) in CDCl3, and the resulting mixture was stirred for 90 min, during which time the silver salt dissolved. After filtration, the reaction mixture was monitored by 1H and 31P{1H} NMR spectroscopy and, finally, crystallized by the addition of a poor solvent (sometimes after evaporation and re-dissolution). The conditions were kept as similar as possible to minimize possible influence of complexation and solvolytic equilibria21 on the reaction outcome.
2) in CDCl3, and the resulting mixture was stirred for 90 min, during which time the silver salt dissolved. After filtration, the reaction mixture was monitored by 1H and 31P{1H} NMR spectroscopy and, finally, crystallized by the addition of a poor solvent (sometimes after evaporation and re-dissolution). The conditions were kept as similar as possible to minimize possible influence of complexation and solvolytic equilibria21 on the reaction outcome.
Notably, the NMR spectra of the reaction mixtures provided little diagnostic information because the dynamic nature of the Ag–1 complexes resulted in a broadening and averaging of the NMR resonances.22 Little structural information was inferred also from the IR spectra of solid samples except for the characteristic bands due to C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretching vibrations that are observed in the narrow range of 2223–2228 cm−1 for compounds featuring uncoordinated nitrile groups (cf. 2225 cm−1 for ligand 1)16 and that shifted upon coordination of the nitrile group.
N stretching vibrations that are observed in the narrow range of 2223–2228 cm−1 for compounds featuring uncoordinated nitrile groups (cf. 2225 cm−1 for ligand 1)16 and that shifted upon coordination of the nitrile group.
Complexes with halide-supporting ligands
Aiming at a systematic survey of the coordination properties of 1 toward silver(I), attention was first paid to compounds resulting from the action of the phosphinonitrile on Ag(I) halides (Scheme 2).The 31P{1H} NMR spectrum of the solution obtained after addition of one molar equivalent of 1 into a suspension AgCl in CDCl3 showed a broad doublet at δP −1.4, confirming that the phosphinonitrile was indeed coordinated (cf. δP −17.7 for 1 in CDCl3).16 Moreover, the relatively large 1JAgP coupling constant of 604 Hz suggested that the reaction stoichiometry was very likely maintained in the reaction product (i.e., that “AgCl·1” was formed in situ).21,23 A subsequent crystallization from wet acetone–hexane afforded orange crystals of hydrated heterocubane 2·H2O, which was structurally characterized (see below). Unsolvated 2 could be similarly isolated from acetone–hexane (i.e., in the absence of added water). However, the crystals suffered from extensive disorder.
Upon increasing the amount of the ligand to two equivalents, the reaction in CDCl3 and crystallization by the addition of methyl tert-butyl ether and hexane furnished a mixture of two products. The dominating, larger orange prismatic crystals were identified by X-ray crystallography as dinuclear complex 3, in which two chloride ligands bridge two Ag(1-κP)2 units (Scheme 2). The minor product separated in the form of fine yellow needles was tentatively formulated as [(μ(P,N)-1){AgCl(1-κP)}]2 (3′) based on the similarity of its IR spectrum with the spectrum obtained for an analogous Cu(I) complex studied previously (see the ESI, Fig. S1†).16 Upon increasing the amount of 1 to 3 equiv., however, dimer 3 became the only crystalline product isolated from the reaction mixture under otherwise identical conditions, although 31P{1H} NMR indicates that some other species (or perhaps equilibria) might be involved (cf. δP of −5.0 and −6.9 for the AgCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures with Ag
1 mixtures with Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 = 1
1 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, respectively).
3, respectively).
In contrast, the similar reactions of 1 with the heavier silver(I) halides gave rise to heterocubanes [Ag(μ3-X)(1-κP)]4 (4: X = Br, 5: X = I) irrespective of the Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio (Ag
1 molar ratio (Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 = 1
1 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2). The bromide-bridged heterocubane was isolated in the form of a solvate 4·0.25H2O after crystallization from ethyl acetate–hexane. Under similar conditions, the iodide analogue was separated as 5·3AcOEt, while crystallization from chloroform–hexane provided 5·4CHCl3.
2). The bromide-bridged heterocubane was isolated in the form of a solvate 4·0.25H2O after crystallization from ethyl acetate–hexane. Under similar conditions, the iodide analogue was separated as 5·3AcOEt, while crystallization from chloroform–hexane provided 5·4CHCl3.
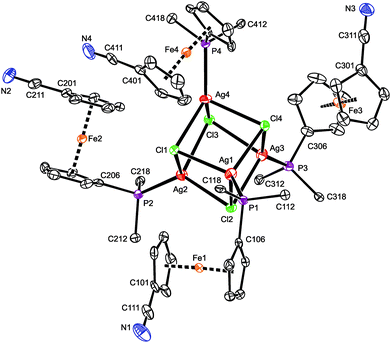
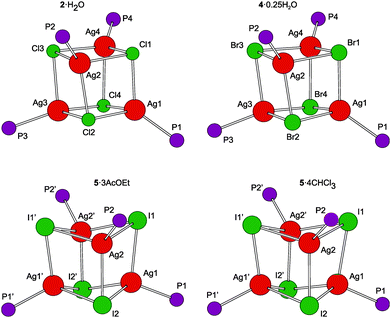
A representative crystal structure of 2·H2O is shown in Fig. 1, and all heterocubane cores are depicted in Fig. 2 (N.B. complete structural drawings for all compounds are presented in the ESI†). Selected geometric parameters for the heterocubanes are presented in Table 1 and 2, and in the ESI.†
| Parameter [n]a | 2·H2O | 4·0.25H2O | 5·3AcOEt | 5·4CHCl3 |
|---|---|---|---|---|
| a n gives the number of observed independent values for 2·H2O, 4·0.25H2O/5·3AcOEt and 5·4CHCl3. | ||||
| Ag–X [12/6] | 2.5550(7)–2.7481(7) | 2.6801(3)–2.8375(3) | 2.8215(3)–3.0094(3) | 2.8141(4)–3.0185(4) |
| Ag–P [4/2] | 2.3709(7)–2.3841(8) | 2.3947(5)–2.4083(5) | 2.4508(8) and 2.458(1) | 2.4535(8) and 2.4592(8) |
| Ag–X–Ag [12/6] | 78.98(2)–89.85(2) | 76.34(1)–86.72(1) | 65.99(1)–77.86(1) | 65.23(1)–75.57(1) |
| X–Ag–X [12/6] | 89.24(2)–102.02(2) | 91.11(1)–104.42(1) | 96.65(1)–113.77(1) | 99.35(1)–114.07(1) |
| P–Ag–X [12/6] | 104.62(3)–146.73(3) | 103.15(2)–143.41(2) | 104.26(2)–125.87(2) | 100.62(2)–125.02(2) |
The pairs of compounds 2·H2O/4·0.25H2O and 5·3AcOEt/5·4CHCl3 are essentially isostructural. The former structures actually differ only in the abundance of the water molecules in the crystal lattice. Apparently, the water molecules can penetrate into the structures built up from these bulky complexes without changing the overall crystal assembly. In fact, they fill the structural voids left between the complex molecules and form hydrogen bridges toward the in-cage halide ions and uncoordinated cyano groups (for a structural diagram, see the ESI, Fig. S3†). The latter interactions appear to be essential for the construction of a regular structural assembly because the structure determined for crystals of unsolvated 2 was disordered at the exterior of the heterocubane molecule mainly at the terminal C5H4CN moieties.24 The isostructural relationship between 5·3AcOEt and 5·4CHCl3 also indicates that the crystal structures of these compounds are determined mainly by the packing of the bulky building blocks, leaving vacancies that can be filled by solvent molecules whose size and shape determine the stoichiometry (i.e., relative amount) without affecting the crystal structure.
According to recent DFT calculations,25 closed heterocubanes are energetically favored over opened, chair-like assemblies for {MX(PH3)}4 tetramers with M = Cu and Ag. These cubanes can be described as distorted tetrahedral arrays of metal ions embedded within an X4 tetrahedron of the face-capping halide ions. However, their geometry can change rather broadly depending on the relative sizes of the M/X ions and the steric properties of the metal-bound ligands (possible crowding around the compact M4X4 unit), as well as on the symmetry of the crystal assembly.26 In the present case, the heterocubane units in the structures of 2·H2O and 4·0.25H2O lack any imposed symmetry, while those in 5·3AcOEt and 5·4CHCl3 reside on the crystallographic two-fold axes, which makes only their halves structurally independent.
The geometric data reported in Tables 1 and 2 indicate that the intra-cluster parameters vary considerably across the series of structurally characterized compounds as well as for the individual representatives. Both the particular data and asymmetry parameters Q, defined as a ratio of the Ag⋯Ag and X⋯X separations (diagonals) for the six faces of the cube-like Ag4X4 array given in Table S2,† suggest an increasing distortion of the heterocubane cores with an increasing size of the halide anion. The Ag–X bond distances are similar or longer than the sum of the respective covalent radii (∑rcov; Ag–Cl 2.47, Ag–Br 2.65, and Ag–I 2.84 Å)27 and expectedly lengthen upon replacing Cl with Br and then I, which is associated with a less pronounced elongation of the Ag–P bonds and, mainly, with a closing of the Ag–X–Ag angles and an opening of the X–Ag–X angles. Changes in the angles at the vertices of the heterocubane moiety manifest an increasing departure from a nearly planar rhomboidal shape of the Ag2X2 faces toward a butterfly-like arrangement resulting from a disparity between the sizes of atoms forming the cage. Typically, a short in-face Ag⋯Ag distance is associated with a long X⋯X contact and vice versa. All observed intermolecular Ag⋯Ag contacts were longer than double the covalent radius for silver (2rcov ≈ 2.90 Å).27 Moreover, because the large iodine anions are displaced from the heterocubane core, the Ag⋯Ag distances within the faces of the Ag4I4 core are slightly shorter than those observed for 2·H2O and 4·0.25H2O that are in turn quite similar. These trends are generally consistent with those observed for [AgX(PR3)]4 complexes resulting from simple phosphines (see ref. 26).
| Compound | Parameter | i/j = 1/2 | 1/3 | 1/4 | 2/3 | 2/4 | 3/4 |
|---|---|---|---|---|---|---|---|
| 2·H2O | Agi⋯Agj | 3.7212(3) | 3.5511(4) | 3.6119(3) | 3.4364(3) | 3.7043(3) | 3.7262(3) |
| Cli⋯Clj | 3.739(1) | 3.780(1) | 3.904(1) | 4.113(1) | 3.912(1) | 3.7503(9) | |
| 4·0.25H2O | Agi⋯Agj | 3.7784(2) | 3.5604(2) | 3.6163(2) | 3.4494(2) | 3.7107(2) | 3.7544(2) |
| Bri⋯Brj | 3.9458(3) | 4.0575(3) | 4.1661(3) | 4.3624(3) | 4.1831(3) | 3.9836(3) |
| Compound | Parameter | i/j = 1/2 | 1/1′ | 1/2′ | 2/2′ | 2/1′ | 1′/2′ |
|---|---|---|---|---|---|---|---|
| 5·3AcOEt | Agi⋯Agj | 3.1841(4) | 3.6670(3) | 3.4557(4) | 3.3812(4) | ≡1/2′ | ≡1/2 |
| Ii⋯Ij | 4.8029(3) | 4.5341(3) | 4.5938(3) | 4.3570(3) | ≡1/2′ | ≡1/2 | |
| 5·4CHCl3 | Agi⋯Agj | 3.1576(4) | 3.5773(4) | 3.3775(4) | 3.2264(4) | ≡1/2′ | ≡1/2 |
| Ii⋯Ij | 4.8117(3) | 4.6302(3) | 4.6286(3) | 4.4485(3) | ≡1/2′ | ≡1/2 |
The ferrocene moieties in the structure of the heterocubanes adopt their regular geometry. Their cyclopentadienyl rings are tilted by less than ca. 6° and assume conformations4a that direct the cyanide groups away from the central Ag4X4 moiety (see Fig. 1). This can be demonstrated by the dihedral angles τn = Cn01–Cgn1–Cgn2–Cn06, where Cgn1 and Cgn2 denote the centroids of the cyclopentadienyl rings C(n01–n05) and C(n06–n10), respectively. In the case of 2·H2O/4·0.25H2O, these angles are τ1 = −134.0(2)/−136.3(2)°, τ2 = 144.0(2)/143.1(2)°, τ3 = −155.8(2)/−153.6(2)°, and τ4 = −63.6(2)/−67.6(2)°, while for 5·3AcOEt/5·4CHCl3: τ1 = 135.1(3)/131.6(3)°, and τ2 = 75.4(3)/77.3(2)°.
The crystal structure of 3·CH2Cl2 (Fig. 3) reveals a symmetric dimeric structure in which two chloride anions bridge two equivalent Ag(1-κP)2 units, thereby completing the tetrahedral donor array around the Ag(I) ions. The atoms constituting the central Ag2Cl2 ring in the molecule of 3 are coplanar within 0.008(1) Å. The variation of the Ag–Cl bond lengths within this ring is marginal (ca. 0.02 Å), but the Ag2Cl2 core is rhomboidal in shape (Cl–Ag–Cl ≫ Ag–Cl–Ag). In addition, the adjacent P2Ag planes are not perpendicular to the Ag2Cl2 ring as expected for two regular, edge-sharing tetrahedra but appear tilted by 77.93(3)° (Ag1) and 81.78(3)° (Ag2) in mutually opposite directions. These distortions can be attributed to the steric strain imparted by the bulky, Ag-bound phosphine ligands (correspondingly, the P–Ag–P angles are the most opened among the interligand angles). Similar features and Ag-donor distances were described for an analogous triphenylphosphine complex, [Ag(μ-Cl)(PPh3)2]2·2CHCl3.28 As in 3·CH2Cl2, the Ag–Clbridge in the mentioned PPh3 complex (2.625(3) and 2.630(3) Å) is longer than the sum of the respective covalent radii (∑rcov = 2.47 Å).
The four structurally independent ferrocene units in the structure of 3·CH2Cl2 have similar opened conformations (τ = 154.9(2)° (Fe1), 156.5(2)° (Fe2), 153.7(2)° (Fe3), and 155.3(2)° (Fe4)) that divert their nitrile substituents from the sterically congested Ag(I) centers. These units also exert similar Fe–C distances and, consequently, the observed tilt angles do no exceed ca. 3°. The conformation of the substituents on the phosphorus atoms seems to be controlled through their spatial contacts and further stabilized via intramolecular, π⋯π stacking interactions of phenyl rings above and below the Ag2Cl2 ring.29
The experiments with simple Ag(I) halides were further extended to reactions of silver(I) pseudohalides, whose anions are potentially polydentate. The reactions of silver(I) cyanide with 1 at metal-to-ligand ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 produced identical, insoluble orange crystalline products, which were found to be coordination polymer 6 (Scheme 3), wherein the linear Ag(C
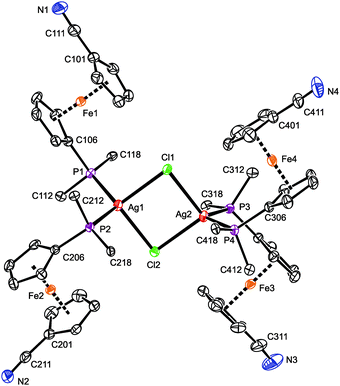
2 produced identical, insoluble orange crystalline products, which were found to be coordination polymer 6 (Scheme 3), wherein the linear Ag(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N-κC)2− moieties interconnect the Ag(1-κP)2+ fragments into an infinite zig-zag chain.30 Although formal, this description is supported by the structural parameters determined for solvated 6 (Fig. 4), showing that the Ag2–C bonds (Ag2–C50 = 2.055(2) Å; Ag2–C60 = 2.053(2) Å) are significantly shorter than the Ag1–N bonds (Ag1–N50 = 2.341(2) Å, Ag1–N60i = 2.344(2) Å; i = 1/2 + x, 1/2 − y, 1/2 + z). Such a formulation further corresponds to the high stability of the [Ag(CN)2]− ions31 that may be, together with solubility issues, responsible for the preferential formation of polymeric 6. Analogous complexes have been isolated from reactions of AgCN with triphenyl- and tricyclohexylphosphine.32,33
N-κC)2− moieties interconnect the Ag(1-κP)2+ fragments into an infinite zig-zag chain.30 Although formal, this description is supported by the structural parameters determined for solvated 6 (Fig. 4), showing that the Ag2–C bonds (Ag2–C50 = 2.055(2) Å; Ag2–C60 = 2.053(2) Å) are significantly shorter than the Ag1–N bonds (Ag1–N50 = 2.341(2) Å, Ag1–N60i = 2.344(2) Å; i = 1/2 + x, 1/2 − y, 1/2 + z). Such a formulation further corresponds to the high stability of the [Ag(CN)2]− ions31 that may be, together with solubility issues, responsible for the preferential formation of polymeric 6. Analogous complexes have been isolated from reactions of AgCN with triphenyl- and tricyclohexylphosphine.32,33
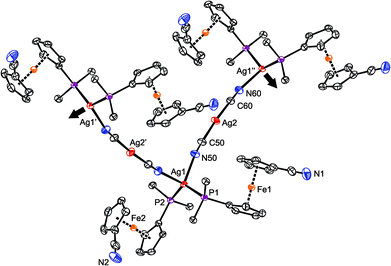 | ||
| Fig. 4 Section of the infinite chain in the structure of 6. The displacement ellipsoids are scaled to the 50% probability level. For clarity, only the pivotal atoms from the phenyl rings are shown, and the hydrogen atoms are omitted (for a complete drawing, see the ESI†). | ||
The Ag(CN)2− connecting moiety in the structure of 6 is essentially linear with a C50–Ag2–C60 angle of 175.86(9)° and possesses Ag–C distances similar to those determined for isolated dicyanoargentate(1−) anions.34 In contrast, the tetrahedral coordination environment of the second Ag(I) ion in the structure of 6 is severely distorted, apparently due to the steric demands of the phosphine ligands. This distortion can be demonstrated by the interligand angles at Ag1 ranging from 96.27(6)–130.30(2)°, with the limits set by the N50–Ag1–N60 (most acute) and P1–Ag1–P2 (most opened) angles. The Ag1–P distances are 2.4489(5) and 2.4527(5) Å for P1 and P2, respectively. Finally, the ferrocene units in the two structurally independent phosphinonitrile donors exert negligible tilting (1.7(1)° for Fe1, 2.7(1)° for Fe2), and their cyanide pendants are rotated away from the ligated Ag(I) ion so that the ferrocene units adopt conformations around anticlinal eclipsed (τ = 137.8(2)/−145.6(1)° for Fe1/Fe2; cf. ideal value: τ = 144°).
Unlike the previous case, the reactions of silver(I) thiocyanate with 1 (Scheme 3) led to different products when the amount of 1 was varied, virtually paralleling the reactivity patterns observed in the AgCl–1 system. Thus, the reaction of AgSCN with one molar equivalent of 1 led to a cuboidal tetrameric complex 7, whereas the reaction at a Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio of 1
P ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 produced a symmetrical, thiocyanato-bridged dimer [Ag(1-κP)2(μ-SCN-S,N)]2 (8). Complexes 7 and 8 have different 1H NMR signatures (in solution), and their 31P NMR resonances were observed at δPca. −1.0 and −2.6 ppm, respectively. The bands of the uncoordinated nitrile groups (νC
2 produced a symmetrical, thiocyanato-bridged dimer [Ag(1-κP)2(μ-SCN-S,N)]2 (8). Complexes 7 and 8 have different 1H NMR signatures (in solution), and their 31P NMR resonances were observed at δPca. −1.0 and −2.6 ppm, respectively. The bands of the uncoordinated nitrile groups (νC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N) in their IR spectra were observed at positions similar to 1–5. On the other hand, the absorptions attributable to stretching vibrations of the thiocyanate groups differ (νmax/cm−1; 7: 2122 m + 2094 vs 8: 2098 vs), reflecting different roles of these anionic ligands.
N) in their IR spectra were observed at positions similar to 1–5. On the other hand, the absorptions attributable to stretching vibrations of the thiocyanate groups differ (νmax/cm−1; 7: 2122 m + 2094 vs 8: 2098 vs), reflecting different roles of these anionic ligands.
Repeated crystallization experiments with 7 only yielded poor-quality crystals. For instance, those utilized for X-ray diffraction analysis contained heavily disordered chloroform (the pendant C5H4CN moieties were also partly disordered) and suffered from twinning. Although these complications lowered the overall precision, the structural determination is unambiguous.
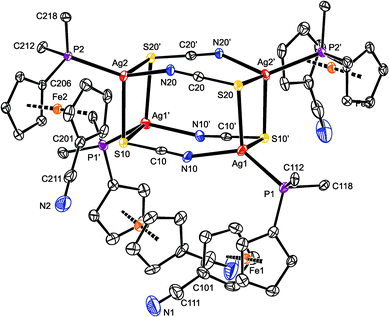
Compound 7 (Fig. 5) crystallized with four complete tetramers per monoclinic unit cell (space group P2/n) and with two halves of the [Ag(1-κP)(μ-SCN)]4 array in the asymmetric unit, each located around the crystallographic two-fold axis. The thiocyanate groups act as S,N-bridges between two silver atoms at the elongated Ag2(SCN)2 faces. Their sulfur atoms further coordinate silver atoms in adjacent Ag2(SCN)2 moieties and thus interlink the final cuboidal assembly. Such an arrangement formally corresponds with the bonding ability of the SC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N moiety, namely with the number of lone electron pairs available at the N and S atoms, and can be alternatively described as a dimer of dimers (i.e., as [{(1-κP)Ag(SCN)}2]2), as was suggested for the only analogous compound whose crystal structure was determined: [(Ph2PPy-κP)Ag(μ-SCN-S,S,N)]4 (Py = 2-pyridyl).35
N moiety, namely with the number of lone electron pairs available at the N and S atoms, and can be alternatively described as a dimer of dimers (i.e., as [{(1-κP)Ag(SCN)}2]2), as was suggested for the only analogous compound whose crystal structure was determined: [(Ph2PPy-κP)Ag(μ-SCN-S,S,N)]4 (Py = 2-pyridyl).35
The two independent heterocubanes found in the structure of 7 differ only marginally, and their geometry is generally similar to that of the mentioned Ph2PPy analogue. Each silver atom in 7 is surrounded by two sulfur atoms, a thiocyanate nitrogen and a phosphine phosphorus, forming a distorted tetrahedral donor set (see parameters in Table 3). The distances between Ag1 and the two bonded sulfur atoms (S20 and S10′) differ by ca. 0.13 Å. A similar feature is also observed for Ag4, while the Ag2 and Ag3 atoms bind to their two S-thiocyanate ligands more symmetrically. The SCN-bridged edges of the cuboidal assembly are bent at the nitrogen atoms (Ag–N–C angles: 151.2(4)–157.8(4)°), which in turn results in an expansion of the central part of the heterocubane core, albeit without any notable twisting at the Ag2(SCN)2 faces.36
| Molecule 1 | Molecule 2 | ||
|---|---|---|---|
| a The prime-labeled atoms are generated by crystallographic two-fold axes (N.B. the symmetry operations are different for molecules 1 and 2). | |||
| Ag1–S20 | 2.652(1) | Ag3–S40 | 2.660(1) |
| Ag1–N10 | 2.214(5) | Ag3–N30 | 2.227(5) |
| Ag1–S10′ | 2.782(1) | Ag3–S30′ | 2.770(2) |
| Ag1–P1 | 2.389(1) | Ag3–P3 | 2.391(1) |
| S20–Ag1–N10 | 96.7(1) | S40–Ag3–N30 | 97.0(1) |
| S20–Ag1–S10′ | 95.80(4) | S40–Ag3–S30′ | 96.62(4) |
| N10–Ag1–S10′ | 97.3(1) | N30–Ag3–S30′ | 96.3(1) |
| P1–Ag1–S20 | 122.19(5) | P3–Ag3–S40 | 121.23(5) |
| P1–Ag1–N10 | 132.8(1) | P3–Ag3–N30 | 131.8(1) |
| P1–Ag1–S10′ | 103.55(4) | P3–Ag3–S30′ | 106.18(5) |
| Ag2–S10 | 2.648(1) | Ag4–S30 | 2.638(1) |
| Ag2–N20 | 2.262(4) | Ag4–N40 | 2.241(5) |
| Ag2–S20′ | 2.660(1) | Ag4–S40′ | 2.672(2) |
| Ag2–P2 | 2.397(1) | Ag4–P4 | 2.387(1) |
| S10–Ag2–N20 | 100.2(1) | S30–Ag4–N40 | 100.5(1) |
| S10–Ag2–S20′ | 98.90(4) | S30–Ag4–S40′ | 99.56(4) |
| N20–Ag2–S20′ | 98.3(1) | N40–Ag4–S40′ | 100.8(1) |
| P2–Ag2–S10 | 110.44(4) | P4–Ag4–S30 | 110.88(5) |
| P2–Ag2–N20 | 126.3(1) | P4–Ag4–N40 | 127.5(1) |
| P2–Ag2–S20′ | 118.16(4) | P4–Ag4–S40′ | 113.69(5) |
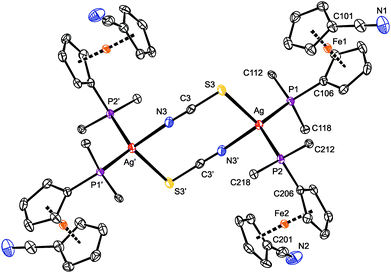
As indicated above, compound 8 is a dimer in which the thiocyanate anions interconnect two Ag(1-κP)2 units (Fig. 6). In the crystal, its molecules are arranged around the inversion centers and, hence, only their half is structurally independent. Analogous structures have been reported for [L2Ag(μ-SCN-S,N)]2 with various monophosphine (L = PPh3,37 P(C6H4Me-4)3,38 P(C6H4F-4)3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 39 and Ph2PPy)35 and chelating diphosphine donors.40 Similar to these compounds, the Ag–S3 and Ag–N3 distances in 8 are longer than the sum of the respective covalent radii (∑rcov = 2.50 (Ag/S) and 2.16 (Ag/N) Å).
39 and Ph2PPy)35 and chelating diphosphine donors.40 Similar to these compounds, the Ag–S3 and Ag–N3 distances in 8 are longer than the sum of the respective covalent radii (∑rcov = 2.50 (Ag/S) and 2.16 (Ag/N) Å).
The eight-membered ring in the structure of 8 is rectangular in shape due to the presence of the rigid, rod-like SCN bridges and the fact that the S–Ag–N angle of 93.79(4)° departs considerably from the tetrahedral value, being diminished due to the steric demands of the Ag-bound phosphines. The central (AgSCN)2 ring has a chair-like conformation (Fig. S11†) with the silver atoms displaced by 0.541(1) Å above and below the “central” (SCN)2 plane.41 The latter plane thus appears tilted by 14.2(7)° with respect to the {Ag, S3, N3′} plane but is perpendicular to the plane defined by atoms Ag, P1, and P2. Even in this case, the nitrile substituents at the ferrocene units remain uncoordinated and are directed away from the phosphine groups (τ = 152.0(1)° (Fe1) and 141.0(1)° (Fe2)).
To complete our investigation of the reactions of 1 with silver(I) halides and pseudohalides, reaction tests were also performed with silver(I) fluoride. Unfortunately, experiments with AgF were complicated by the highly hygroscopic nature of this salt and typically led to non-crystallizing, extensively decomposed reaction mixtures. Nonetheless, several of the repeated experiments performed with AgF and 1 at Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratios of both 1
1 ratios of both 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 provided few crystals (always along with a black tarry material) that were structurally characterized as a dimer similar to 3 but with linear HF2− bridges between the Ag(I) centers, [Ag(1-κP)2(μ-HF2)]2 (9). Unfortunately, all crystals obtained were affected by a substitutional disorder, resulting from the alternation of HF2− and chloride anions as the bridges in between the sterically encumbered Ag(1-κP)2 units.42 The chloride ions necessary for the formation of 3 most likely came from the starting silver(I) salt43 or arose via decomposition of the halogenated solvent. Yet another experiment at a Ag
2 provided few crystals (always along with a black tarry material) that were structurally characterized as a dimer similar to 3 but with linear HF2− bridges between the Ag(I) centers, [Ag(1-κP)2(μ-HF2)]2 (9). Unfortunately, all crystals obtained were affected by a substitutional disorder, resulting from the alternation of HF2− and chloride anions as the bridges in between the sterically encumbered Ag(1-κP)2 units.42 The chloride ions necessary for the formation of 3 most likely came from the starting silver(I) salt43 or arose via decomposition of the halogenated solvent. Yet another experiment at a Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of 1
1 molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 resulted in few crystals that—despite their low quality and extensive disorders—allowed the product to be unequivocally formulated as a hexafluorosilicate-bridged disilver(I) complex, [(μ-SiF6){Ag(1-κP)2}2] (10). Obviously, some hydrogen fluoride was formed by decomposition of the hygroscopic AgF during the crystallization, which in turn reacted with the starting AgF and 1 (or any 1–AgF intermediate) to afford compound 9 or attacked the glass tube used for crystallization, producing some H2[SiF6] (or any hexafluorosilicate salt) and then complex 10. These rather unexpected results prompted us to attempt at a reproducible synthesis of 10 and, mainly, to study the Ag(I)–1 complexes with “non-coordinating” supporting anions in more detail.
2 resulted in few crystals that—despite their low quality and extensive disorders—allowed the product to be unequivocally formulated as a hexafluorosilicate-bridged disilver(I) complex, [(μ-SiF6){Ag(1-κP)2}2] (10). Obviously, some hydrogen fluoride was formed by decomposition of the hygroscopic AgF during the crystallization, which in turn reacted with the starting AgF and 1 (or any 1–AgF intermediate) to afford compound 9 or attacked the glass tube used for crystallization, producing some H2[SiF6] (or any hexafluorosilicate salt) and then complex 10. These rather unexpected results prompted us to attempt at a reproducible synthesis of 10 and, mainly, to study the Ag(I)–1 complexes with “non-coordinating” supporting anions in more detail.
To prepare 10 in a rational manner, defined Ag2[SiF6] was synthesized from Ag2O and H2[SiF6] and reacted with four equivalents of the phosphinonitrile ligand in chloroform. The resulting mixture displayed a very broad 31P NMR resonance at around δP −2. The 19F NMR spectrum revealed one singlet at δF −131 with 29Si satellites (1JSiF = 115 Hz),44 suggesting a rapid interchange or no interaction between Ag(I) and the anion in solution. The IR spectrum of crystalline 10 contained band attributable to the ligand's C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N group and solvating acetone at 2223 cm−1 and 1705 cm−1, respectively, and a strong band due to the hexafluorosilicate anion (ν3 vibration at 749 cm−1).
N group and solvating acetone at 2223 cm−1 and 1705 cm−1, respectively, and a strong band due to the hexafluorosilicate anion (ν3 vibration at 749 cm−1).
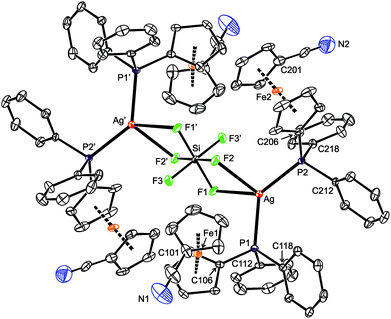
Crystallization from chloroform–acetone/hexane afforded orange crystals of 10·½CHCl3·½Me2CO, which were structurally characterized. The compound crystallizes with the symmetry of the monoclinic space group C2/c, with both the solvent molecules and the nitrile groups disordered (Fig. 7 and Table 4). Otherwise, however, the molecular symmetry is rather high because the silicon atom resides on the inversion center, which in turn renders only the half of the complex molecule structurally independent. The hexafluorosilicate anion, symmetrically placed between two Ag(1-κP)2, forms two Si–F→Ag bridges toward each silver(I) ion. Coordination of the [SiF6]2− anion results in a slight yet statistically significant elongation of the bridging Si–F bonds (cf. Si–F1/2 = 1.691(2)/1.704(2) Å vs. Si–F3 = 1.669(2) Å (ref. 45)), though without angular distortion of the octahedral anion (see the cis-F–Si–F angles in Table 4). Because the bridging fluorine atoms are a part of the [SiF6]2− anion and thus occur in constrained proximal positions, the donor array around Ag(I) departs from a regular tetrahedron even more than in the other structurally characterized compounds that comprise two Ag(I)(1-κP)2 moieties connected by anionic bridging ligands. This distortion is clearly manifested in the interligand angles ranging from 56.68(7)° for F1–Ag–F2 to 132.44(3)° for P1–Ag–P2. Because of the twisting, the {Ag, F1, F2} and {Ag, P1, P2} planes are rotated by 56.1(1)°, and the central Ag(μ-F)2Si(μ-F)2Ag moiety is undulated (the dihedral angle of the {Ag, F1, F2} and {Si, F1, F2} planes is 18.77(9)°; see Fig. S13†).
| Ag–P1 | 2.421(1) | P1–Ag–P2 | 132.44(3) |
| Ag–P2 | 2.4160(9) | P1–Ag–F1 | 89.93(6) |
| Ag–F1 | 2.542(2) | P1–Ag–F2 | 122.30(6) |
| Ag–F2 | 2.482(2) | P2–Ag–F1 | 130.00(6) |
| Si–F1 | 1.691(2) | P2–Ag–F2 | 103.08(6) |
| Si–F2 | 1.704(2) | F1–Ag–F2 | 56.68(7) |
| Si–F3 | 1.669(2) | cis-F–Si–F | 89.3(1)–90.7(1) |
While the Ag–P bond lengths in 10 fall within the common ranges and below the sum of the covalent radii (2.421(1) and 2.4160(9) for P1 and P2, respectively; ∑rcov = 2.52 Å), the Ag–F distances of 2.542(2) and 2.482(2) Å for F1 and F2, respectively, are considerably longer than the sum of the covalent radii (∑rcov = 2.02 Å) as well as the Ag–F separations in the “true” fluoride-bridged complex [(μ-F){AgL}2][BF4] (L = 1,3-bis(2,6-diisopropylphenyl)imidazol-2-ylidene; 2.0671(7) and 2.0672(7) Å).46 This suggests a predominantly electrostatic nature of the interaction between the Ag(I)(1-κP)2 units and the hexafluorosilicate anion whose closer contact is sterically hindered (N.B. the anion is surrounded by four sterically demanding phosphinoferrocene moieties). In fact, the structure of 10 can be adequately compared with only [Ag(MeCN)2]2[SiF6] in which the hexafluorosilicate anion interacts with four adjacent Ag(I) ions (twice via two and twice through one fluorine atom).47
DFT study of the bridged disilver(I) complexes
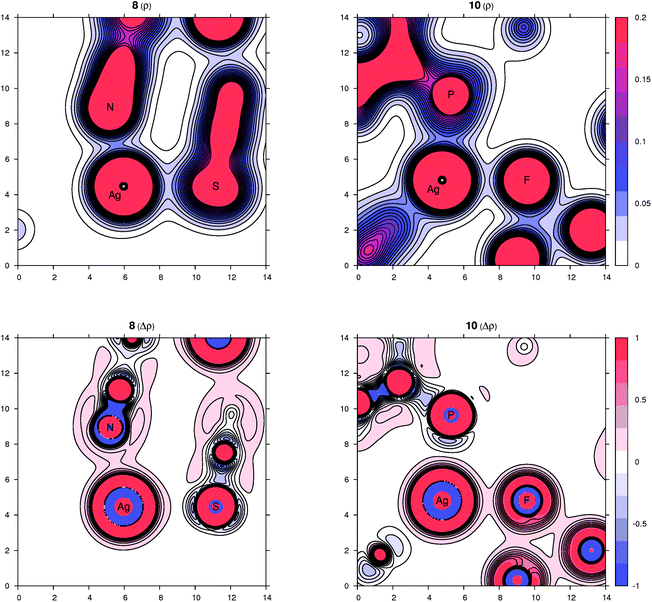
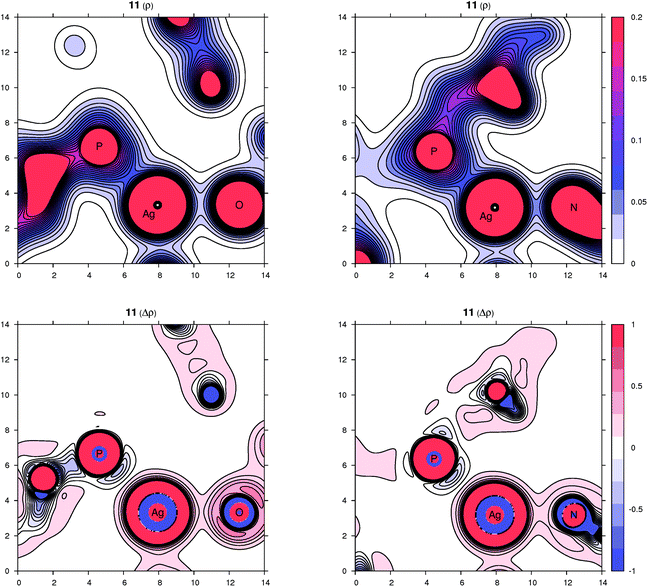
Peculiar structural features detected in the solid-state structures of 3·CH2Cl2, 8 and 10 led us to investigate the bonding situation in these compounds theoretically using DFT calculations (details are given in the ESI†). As mentioned earlier, in many cases, the observed bonding distances, particularly the Ag–X (X = S, N, Cl and F) “dative bonds” in these compounds, were found to be significantly longer than sum of the corresponding covalent radii, raising the question of whether the bonding has more ionic than covalent character. A useful clue about ionicity can be derived from the partial charges assigned by a population analysis. Although this assignment is somewhat arbitrary, as can be demonstrated by the sole existence of several dozens of such partitioning schemes, the concept of partial charges proved to be quite useful. We used a natural population analysis (NPA)48 that has a rather small basis-set dependence, but even the results of the basic Mulliken population analysis were similar. In general, there is no correlation between the charge transfer and strength of a donor–acceptor bond.49 For this reason, we also followed an unambiguous description of bonding using the properties of the experimentally observable electron density, applying the concepts from the Atoms in Molecules (AIM) theory.50 Herein, we give contour plots of the electron density in planes defined by the Ag center and two coordinated atoms as well as their Laplacian, the sum of the second partial derivatives with respect to coordinates. The latter quantity indicates the local concentration of electrons if negative and depletion if positive. Negative values of the density Laplacian around a critical bond point (the saddle point of the electron density) indicate the formation of a covalent bond with electrons concentrated in this region.49 For ionic bonds, no such negative region exists, and the density Laplacian remains positive. This property allows for distinguishing between different types of bonding.The bonding situation for compound 3 is depicted in Fig. 8 (for additional plots, see the ESI†). Already on the electron density map, one can see an increased bonding density between the Ag and P centers, but no such charge concentration between Ag and Cl. The same projection mapping the Laplacian of the electron density reveals a negative basin between Ag and P and a positive region between Ag and Cl. The NPA charges (in units of the elementary charge) for Ag, P and Cl in 3 are 0.52, 0.88 and −0.74, respectively, corroborating an ionic nature of the Ag–Cl bonding interaction.
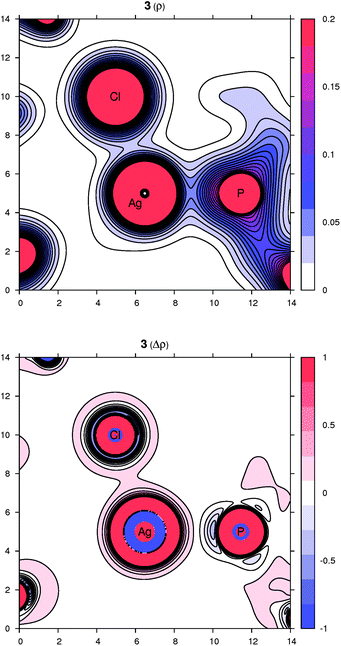 | ||
| Fig. 8 Contour plots of the electron density ρ(r) (top) and its Laplacian Δρ(r) (bottom) in the plane defined by Ag, P and Cl atoms for compound 3. All values are in atomic units. | ||
In complex 8, the other coordination partners of Ag(I) (besides the phosphine) are the N and S atoms of the thiocyanate ligand. The NPA charges for Ag, P, N and S are 0.48, 0.90, −0.59 and −0.30, respectively (the nitrogen in the SCN ligand is significantly more negative than sulfur, which corresponds to its higher electronegativity). The character of the nitrogen coordination can be thus described as more ionic, whereas that of sulfur is more covalent, as further indicated by a basin in the negative Laplacian of the electron density shown in Fig. 9. The situation observed for complex 10 (Fig. 9) is quite similar to 3. The sum of the covalent radii for Ag and F is again significantly shorter than the observed Ag–F separation, suggesting a prevalently electrostatic interaction between the Ag(I) center and bridging anion. This observation is in agreement with the calculated NPA partial charges for Ag, P, F and Si of 0.56, 0.88, −0.67 and 2.46, respectively, and also with the area of negative density Laplacian found between Ag and F (Fig. 9). In contrast, the P→Ag dative bonds retained their covalent nature in all studied cases (see additional plots in the ESI†).
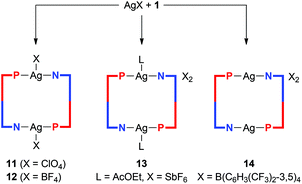
Complexes resulting from Ag(I) salts with weakly coordinating anions
The phosphinonitrile ligand 1 in all its Ag(I) complexes with anionic supporting ligands mentioned above behaves as a simple phosphine. In order to enforce the coordination of the nitrile moiety, we next investigated reactions between 1 and silver(I) salts with common “non-coordinating” anions,51viz. AgClO4, Ag[BF4] and Ag[SbF6]. Indeed, the reactions performed with these salts at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Ag
1 Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio afforded symmetric, dimer-like disilver(I) complexes 11–13 in which the two equivalent Ag(I) centers are connected by two P,N-bridging phosphinonitrile ligands (Scheme 4). However, the coordination environments of the Ag(I) ions (in the solid state) are completed by compensating anions (ClO4− and [BF4]−) or the solvent used during crystallization (ethyl acetate in the case of the [SbF6]− salt).
1 molar ratio afforded symmetric, dimer-like disilver(I) complexes 11–13 in which the two equivalent Ag(I) centers are connected by two P,N-bridging phosphinonitrile ligands (Scheme 4). However, the coordination environments of the Ag(I) ions (in the solid state) are completed by compensating anions (ClO4− and [BF4]−) or the solvent used during crystallization (ethyl acetate in the case of the [SbF6]− salt).
The IR spectra of solid perchlorate 11 and tetrafluoroborate 12 contain bands related to νC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N at 2272/2283 cm−1 and at 2275/2285 cm−1. The shift of these bands to higher energies relative to free 1 suggests a low contribution of π-back bonding to the C
N at 2272/2283 cm−1 and at 2275/2285 cm−1. The shift of these bands to higher energies relative to free 1 suggests a low contribution of π-back bonding to the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N→Ag interaction.52 Also observed are strong bands characteristic of the anions, namely composite ν3 bands of ClO4− and BF4− at 1025–1125 and 995–1100 cm−1, respectively.
N→Ag interaction.52 Also observed are strong bands characteristic of the anions, namely composite ν3 bands of ClO4− and BF4− at 1025–1125 and 995–1100 cm−1, respectively.
Because the product isolated from the reaction of 1 with Ag[SbF6] proved to be poorly soluble, it was recrystallized from ethyl acetate/hexane.53 Under such conditions, however, the plausible “primary” product was converted to [Ag{μ(P,N)-1}(AcOEt-κO)]2[SbF6]2 (13). The coordination of the solvent is indicated by a strong νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O band in the IR spectrum of the crystallized sample at 1703 cm−1, shifted toward lower energies with respect to ethyl acetate itself (1742 cm−1 in a CCl4 solution).54 The νC
O band in the IR spectrum of the crystallized sample at 1703 cm−1, shifted toward lower energies with respect to ethyl acetate itself (1742 cm−1 in a CCl4 solution).54 The νC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bands are observed at 2255 (m), 2267 (s) and 2280 (m) cm−1, while the [SbF6]− anion gives rise to a strong band at 661 cm−1.
N bands are observed at 2255 (m), 2267 (s) and 2280 (m) cm−1, while the [SbF6]− anion gives rise to a strong band at 661 cm−1.
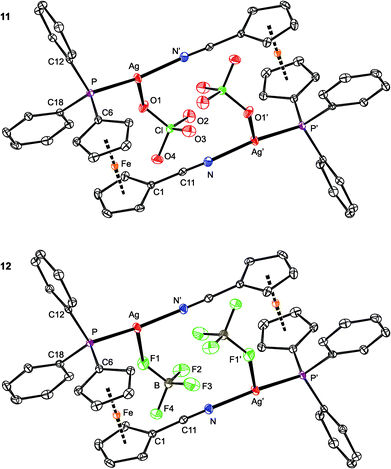
Compounds 11 and 12 are isostructural and crystallize as compact dimers around the crystallographic inversions centers (Fig. 10, parameters in Table 5). The O- and F-monodentate anions are located within the pocket defined by the bulky phosphinoferrocene moieties. While the Ag–P and Ag–N bond lengths are less than the sum of the covalent radii, suggesting a real bonding interaction, the distances between the silver(I) centers and O or F donor atoms from the anions markedly exceed the respective “threshold” values (∑rcov = 2.11 (Ag/O) and 2.02 (Ag/F) Å). The P–Ag–N angles in 11 and 12 are ca. 156° and 162°, respectively, with the more acute angle for 11 reflecting a closer approach of the “additional” donor to silver. Otherwise, however, these angles suggest the cationic Ag(I) centers to be essentially linearly dicoordinate, weakly interacting with the counter anions. Such a description is in line with the results of the DFT computations (vide infra).
| Parameter | 11 | 12 | 13 | 14 |
|---|---|---|---|---|
| X | O1 | F1 | O1S | None |
| a n.a. = not applicable. b Further data: Cl–O1 1.447(2), Cl–O2 1.419(2), Cl–O3 1.431(2), Cl–O4 1.440(2). c Further data: B–F1 1.398(3), B–F2 1.364(3), B–F3 1.365(3), B–F4 1.397(3). d Further data: C1S–O1S 1.211(5). | ||||
| Ag–P | 2.3564(7) | 2.3513(5) | 2.3583(9) | 2.3508(6) |
| Ag–N | 2.141(2) | 2.124(2) | 2.133(3) | 2.120(2) |
| Ag–X | 2.550(2) | 2.624(2) | 2.648(3) | n.a. |
| P–Ag–N | 156.50(6) | 161.87(5) | 161.67(8) | 169.36(7) |
| P–Ag–X | 112.59(4) | 109.79(4) | 92.90(7) | n.a. |
| N–Ag–X | 90.45(7) | 87.03(6) | 100.2(1) | n.a. |
| Ag⋯Ag | 5.6145(3) | 5.5859(3) | 5.9009(5) | 5.4674(3) |
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N N |
1.140(3) | 1.139(3) | 1.135(5) | 1.135(3) |
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N–Ag N–Ag |
171.7(2) | 171.2(2) | 170.8(3) | 168.8(2) |
| τ | 87.2(2) | 85.9(1) | −87.1(3) | 80.1(2) |
The ferrocene units in 11 and 12 exert negligible tilting (1.2(2)° and 1.6(1)°) and their substituents, now both involved in coordination, adopt positions approximately halfway between synclinal eclipsed (τ = 72°) and anticlinal staggered (τ = 108°). In such a conformation, the C6–P and C1–CN bonds are nearly perpendicular,55 giving rise to a side-by-side arrangement of the two Ag(1) subunits. The PPh2 moiety is oriented such that the Ag–P bond is directed inward the Ag2(1)2 core.56 The CN bond lengths in 11 and 12 are the same (within the 3σ-level) as in uncoordinated 1 (1.144(2) Å).16
As opposed to the structures of 11 and 12, the ethyl acetate in 13 is directed to the sides of the Ag2(1)2 core and displaced away from its center (Fig. 11). The coordinated oxygen atom is closer to the Ag-bound phosphorus, diminishing the P–Ag–O1S and opening the N–Ag–O1S angle. As judged from the displacement of the Ag atom from the plane of the directly bonded atoms, P, N′ and X [0.076(1) Å for 11 (X = O1), 0.116(1) Å for 12 (X = F1), and 0.227(1) Å for 13 (X = O1S)], twisting of the coordination environment of the Ag(I) ion increases from 11 through 12 to 13. On the other hand, the conformation of the ferrocene ligand in 13 is nearly the same as in 11 and 12.
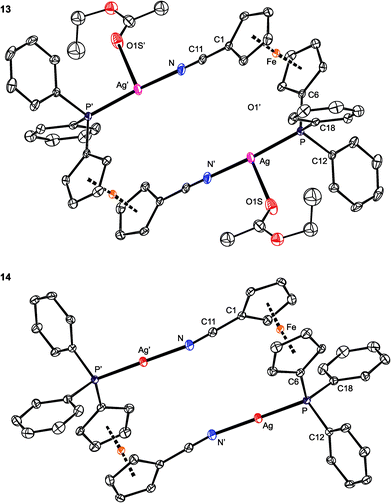 | ||
| Fig. 11 PLATON plots of the complex cations in the structures of 13 (top) and 14 (bottom). Displacement ellipsoids enclose the 30% probability level. All hydrogen atoms are omitted, and only one position of the disordered ethyl acetate is shown (for 13) for clarity. Complete structural diagrams are available in the ESI.† | ||
Eventually, the elusive [Ag2(1)2]2+ complex devoid of any additional ligands at the Ag(I) ions was obtained from the reaction between 1 and the silver(I) salt with tetrakis[3,5-bis(trifluoromethyl)phenyl]borate (BARF) anion (Scheme 4). The 31P NMR spectrum of 14 displays a doublet at δP 5.5 ppm with 1JAgP = 765 Hz, the relatively large 1JAgP coupling constant being in accordance with the presence of linear, sp-hybridized silver.23,57 The νC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bands in the IR spectrum of a crystalline sample are observed at 2282 (w) and 2258 (s) cm−1.
N bands in the IR spectrum of a crystalline sample are observed at 2282 (w) and 2258 (s) cm−1.
The structure of [Ag2{μ(P,N)-1}2][BARF]2 (14; see Fig. 11) resembles that of the analogous Au(I) complexes [Au2{μ(P,N)-1}2]X2, where X = N(SO2CF3)2 and [SbF6],17 consisting of discrete dimeric units [Au2(1)2]2+ and isolated anions. Because of the absence of an additional donor protruding into the coordination sphere of Ag(I), the Ag–P/N distances in 14 are slightly shorter, the P–Ag–N angle is less acute,58 and the ferrocene substituents are rotated closer to each other (τ = 80.1(2)°, tilt angle: 2.7(2)°) than in the structures of 11–13. Additionally, the Ag⋯Ag distances in 14 are the shortest among complexes 11–14, with the observed trend (14 < 12 < 11 < 13) reflecting the presence and size of the additional ligands coordinated to the [Ag2(1)2]2+ moiety.
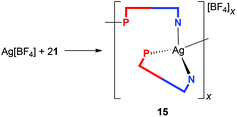
Upon increasing the amount of ligand 1 to 2 or even 3 equiv., the reaction with Ag[BF4] proceeded differently, leading to an unusual coordination polymer [Ag{μ(P,N)-1}(1-κ2P,N)]n[BF4]n (15 in Scheme 5).59 The IR spectrum of crystalline 15 contains three bands attributable to C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretching vibrations at 2242, 2228 and 2214 cm−1, all shifted to lower wavenumbers compared to those of the dimeric complex 12. The anion gives rise to a strong composite band between ca. 1085–1025 cm−1.
N stretching vibrations at 2242, 2228 and 2214 cm−1, all shifted to lower wavenumbers compared to those of the dimeric complex 12. The anion gives rise to a strong composite band between ca. 1085–1025 cm−1.
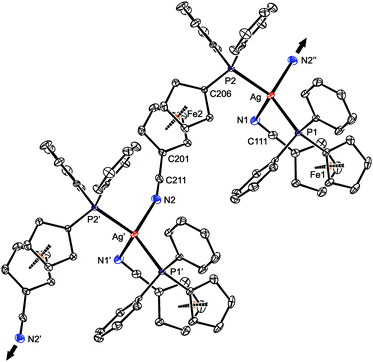
Presumably because of its polymeric nature, compound 15 proved to be very difficult to crystallize. Eventually, one of the numerous repeated experiments, during which the solvents, sample concentration, temperature and mode of crystallization were varied, produced crystals of solvate 15·AcOEt that were suitable for X-ray diffraction analysis. The crystal structure of 15·AcOEt (Fig. 12 and Table 6) revealed tetracoordinate Ag(I) centers, ligated from two bridging phosphinonitrile ligands responsible for linear propagation of the polymeric chain and further by another molecule of 1 bonded in a P,N-chelating manner. Such a particular combination of P,N-bridging60 and chelating coordination of a phosphinonitrile donor is unprecedented and leads to an abnormal geometry at the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N–Ag fragment.
N–Ag fragment.
| a Symmetry operations: i = x + 1, y, z; ii = x − 1, y, z. τn is the torsion angle Cn1–Cgn1–Cgn2–Cn6, φn is the dihedral angle of the cyclopentadienyl planes. | |||
|---|---|---|---|
| Ag–P1 | 2.4345(7) | Ag–P2 | 2.4402(7) |
| Ag–N1 | 2.485(2) | Ag–N2i | 2.330(2) |
| P1–Ag–N1 | 100.35(5) | P2–Ag–N2i | 99.65(6) |
| P1–Ag–N2i | 120.83(6) | P2–Ag–N1 | 108.90(6) |
| P1–Ag–P2 | 129.20(2) | N1–Ag–N2i | 90.94(8) |
| C111–N1 | 1.150(3) | C211–N2 | 1.136(3) |
| C101–C111–N1 | 178.7(3) | C201–C211–N2 | 177.9(3) |
| C111–N1–Ag | 109.4(2) | C211–N2–Agii | 159.9(2) |
| τ 1 | 5.6(2) | τ 2 | 144.6(2) |
| φ 1 | 5.3(2) | φ 2 | 2.1(1) |
As stated above, compound 15 is a coordination polymer in which one of the phosphinonitrile donors bridges two adjacent Ag(I) centers related by elemental translation along the crystallographic axis a in the space group P212121. The silver(I) ion in 15 possesses a distorted tetrahedral P2N2 donor set. While the Ag–P distances to the two phosphine groups are similar in length, the Ag–N1 separation pertaining to the chelating ligand is significantly longer (by ca. 0.16 Å) than the Ag–N2 bond involving the bridging phosphinonitrile, but both Ag–N distances are well below the sum of the covalent radii (∑rcov = 2.16 Å). The CN group of the bridging ligand is coordinated with a departure from linearity (Ag–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C ≈ 160°) but is still within the ranges common for Ag(I) complexes with nitrile donors (see the distribution in Fig. 13).18 In contrast, the Ag–N
C ≈ 160°) but is still within the ranges common for Ag(I) complexes with nitrile donors (see the distribution in Fig. 13).18 In contrast, the Ag–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C angle of ca. 109° found for the chelating ligand is unusually acute. Indeed, compounds with C
C angle of ca. 109° found for the chelating ligand is unusually acute. Indeed, compounds with C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N–Ag angles below 110° are not entirely unprecedented but remain quite scarce, being found in only 5 out of 1016 C
N–Ag angles below 110° are not entirely unprecedented but remain quite scarce, being found in only 5 out of 1016 C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N–Ag fragments (<0.5%)61 encountered in 853 structurally characterized Ag(I)–nitrile complexes featuring the C–C
N–Ag fragments (<0.5%)61 encountered in 853 structurally characterized Ag(I)–nitrile complexes featuring the C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N–Ag moieties (repeated structure determinations are not excluded). In neither case, however, the coordinated bent nitrile group is a part of a simple chelating ligand. Furthermore, the geometry encountered in the crystal structure of 15 also differentiates this compound from transition metal complexes with η2-coordinated nitriles, in which the C
N–Ag moieties (repeated structure determinations are not excluded). In neither case, however, the coordinated bent nitrile group is a part of a simple chelating ligand. Furthermore, the geometry encountered in the crystal structure of 15 also differentiates this compound from transition metal complexes with η2-coordinated nitriles, in which the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bonds are oriented laterally with respect to the metal center and bonded in an approximately symmetrical fashion (i.e., with d(M–CN) ≈ d(M–NC); cf. Ag–N1/C111 of 2.485(2)/3.065(3) Å in 15·AcOEt).62
N bonds are oriented laterally with respect to the metal center and bonded in an approximately symmetrical fashion (i.e., with d(M–CN) ≈ d(M–NC); cf. Ag–N1/C111 of 2.485(2)/3.065(3) Å in 15·AcOEt).62
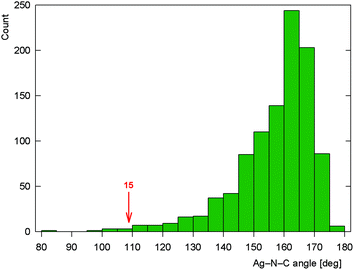 | ||
Fig. 13 Histogram showing the distribution of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N–Ag angles in the structurally characterized Ag–nitrile complexes (the angle encountered for chelating 1 in complex 15 is indicated). N–Ag angles in the structurally characterized Ag–nitrile complexes (the angle encountered for chelating 1 in complex 15 is indicated). | ||
Notably, the conformation of the flexible phosphinoferrocene ligands in 15 changes with their coordination mode. The ferrocene substituents in chelating 1 (Fe1) are nearly synclinal eclipsed, and the cyclopentadienyl rings are slightly tilted (by ca. 5°). In contrast, the ferrocene moiety in the bridging ligand has an opened conformation near ideal anticlinal eclipsed that allows for efficient bridging while maintaining a relatively compact arrangement without much steric crowding.
DFT study of the bonding situation in 11, 12 and 15
DFT calculations suggest that the bonding situation in dimeric complexes 11 and 12 is similar to that in compounds 3 and 10. The calculated NPA atomic charges on Ag, P and N are, in both cases, approximately 0.61, 0.88 and −0.42, respectively. The charges on the O atoms in the perchlorate anion in 11 range from −0.80 to −0.90 (the most negative being the O atom coordinated to silver), while those on the F atoms in the BF4− anion of 12 are all ca. −0.56. The ionic character of the coordination of ClO4− and BF4− was confirmed by the positive electron density Laplacians (see the ESI†).The coordination of the nitrile groups deserves more comments. In general, nitrile ligands are weak π-acceptors with usually insignificant π-back donation,52,63 which can be deduced from the negligible contribution of nitrile antibonding π* molecular orbitals (MOs) to the occupied MOs of the complex. The main components of the Ag–N coordination bond are thus the σ-donation of the nitrile lone pair to the silver(I) ion and the electrostatic interaction.52 These general conclusions from MO theory are supported by AIM concept. The relevant cross-sections containing the Ag and N atoms of the electron density map and its Laplacian are shown in Fig. 14 (see also the ESI†). The region of the N atom is essentially unperturbed upon coordination and shows a charge concentration corresponding to a slight distortion of the lone electron pair on N toward the Ag(I) center. The nitrile group becomes more polarized upon coordination, with partial charges changing from −0.32 (N) and 0.30 (C) for the free ligand to −0.44 (N) and 0.42 (C) for the coordinated one in both 11 and 12. Otherwise, the bonding region resembles the situation for the closed-shell interaction and corresponds to the Coulomb interaction between Ag and the nitrile group due to a significant partial charge on N.49,52
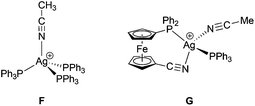
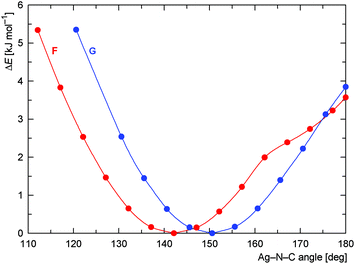
Neither σ-donation nor Coulomb interaction is sensitive to the Ag–N–C coordination angle, which explains the unusually small value of this angle observed for 15 and also applies to model compounds F and G (Scheme 6) that were studied instead of polymeric 15. The dependence of the (relative) energy on the coordination angle is shown in Fig. 15, where the all other coordinates were relaxed and the energy was minimized with respect to them. The minima are quite shallow corresponding to approximately 1–2kBT at room temperature, thus allowing for adjustment of the coordination angle due to other interactions without significant penalty.
Conclusions
Compound 1 combines two soft donor moieties of different nature and coordination properties. Its reactions with silver(I) salts containing common coordinating counter anions affords crystalline mixed-donor silver(I) complexes in which the phosphinonitrile ligand coordinates as a simple phosphine donor. The role of the supporting anions in the coordination of Ag(I) depends on their ligating ability, reaction stoichiometry and the solubility of the species present in the system. Thus, reactions with silver(I) halides and pseudohalides with a limited amount of 1 (i.e., at a Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of 1
1 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) produce complexes featuring multiply bridging anions such as the heterocubanes 2, 4, 5 and 7 or the polymeric complex 6 built up from alternating Ag(CN)2− and Ag(1-κP)2+ units. Increasing the amount of the phosphinonitrile ligand results in a preferential formation of compounds wherein the {Ag(1-κP)2}+ moieties are bridged by the same anions, but in a simple μ2-fashion (such in 3, 8 and 10). DFT computations indicate covalent interactions between the Ag(I) ion and phosphine phosphorus for these complexes (i.e., the formation of P→Ag dative bonds), while the interactions between silver and the anionic ligands are largely electrostatic, which in turn corresponds with an easy disintegration (or at least fluxional behavior) of these compounds in a solution.
1) produce complexes featuring multiply bridging anions such as the heterocubanes 2, 4, 5 and 7 or the polymeric complex 6 built up from alternating Ag(CN)2− and Ag(1-κP)2+ units. Increasing the amount of the phosphinonitrile ligand results in a preferential formation of compounds wherein the {Ag(1-κP)2}+ moieties are bridged by the same anions, but in a simple μ2-fashion (such in 3, 8 and 10). DFT computations indicate covalent interactions between the Ag(I) ion and phosphine phosphorus for these complexes (i.e., the formation of P→Ag dative bonds), while the interactions between silver and the anionic ligands are largely electrostatic, which in turn corresponds with an easy disintegration (or at least fluxional behavior) of these compounds in a solution.
In contrast, reactions with Ag(I) salts possessing relatively weaker coordinating anions at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 metal-to-1 ratio give rise to [Ag2(μ(P,N)-1)2]2+ cations in which the ligand's nitrile group completes the linear coordination environment of the Ag(I) ion. Counter anions with a higher propensity to coordinate form supportive weak interactions with the silver(I) ion (in the solid state), being replaceable by other donors including solvents. The “coordination” of both the nitrile moiety and the anionic ligands in these species has a prevalently electrostatic nature. Although rather counterintuitive, this bonding feature reflects the hard–soft nature of the Ag–N, Ag–O and Ag–F interactions and is also in agreement with the results of the previous theoretical studies.
1 metal-to-1 ratio give rise to [Ag2(μ(P,N)-1)2]2+ cations in which the ligand's nitrile group completes the linear coordination environment of the Ag(I) ion. Counter anions with a higher propensity to coordinate form supportive weak interactions with the silver(I) ion (in the solid state), being replaceable by other donors including solvents. The “coordination” of both the nitrile moiety and the anionic ligands in these species has a prevalently electrostatic nature. Although rather counterintuitive, this bonding feature reflects the hard–soft nature of the Ag–N, Ag–O and Ag–F interactions and is also in agreement with the results of the previous theoretical studies.
The results collected in this study indicate that the soft phosphine moiety can be regarded as the primary coordination site in Ag(I) complexes with ligand 1, forming strong covalent bonds toward the Ag(I) centers. On the other hand, the coordination of the nitrile group (as well as the counteranions) probably has a supportive character, being predominantly electrostatic and thus less directional. Consequently, the particular combination of donor moieties and structural flexibility of 1 renders this metalloligand capable of “improvising” in the silver(I) complexes depending on the roles played by other partners (ligands), mainly recruiting from the counter anions, that further increase the overall structural diversity of the resulting compounds.
Acknowledgements
The results reported in this paper were obtained with financial support from the Czech Science Foundation (project no. 13-08890S).Notes and references
- In the absolute hardness scale, the Ag(I) ion is the hardest among the univalent group 11 metal ions: R. G. Pearson, Inorg. Chem., 1988, 27, 734 CrossRef CAS
.
-
R. J. Lancashire, in Comprehensive Coordination Chemistry, ed. G. Wilkinson, R. D. Gillard and J. A. McCleverty, Pergamon Press, New York, NY, 1987, ch. 54, vol. 5, p. 775 Search PubMed
.
- R. Meijboom, R. J. Bowen and S. J. Bernes-Price, Coord. Chem. Rev., 2009, 253, 325 CrossRef CAS
.
-
(a)
K.-S. Gan and T. S. A. Hor, in Ferrocenes: Homogeneous Catalysis, Organic Synthesis, Materials Science, ed. A. Togni and T. Hayashi, Wiley-VCH, Weinheim, 1995, ch. 1, p. 3 Search PubMed
; (b) S. W. Chien and T. S. A. Hor, in Ferrocenes: Ligands, Materials and Biomolecules, ed. P. Štěpnička, Wiley, Chichester, 2008, ch. 2, p. 33 Search PubMed
; (c) G. Bandoli and A. Dolmella, Coord. Chem. Rev., 2000, 209, 161 CrossRef CAS
; (d) D. J. Young, S. W. Chien and T. S. A. Hor, Dalton Trans., 2012, 41, 12655 RSC
.
-
(a) T. S. A. Hor, S. P. Neo, C. S. Tan, T. C. W. Mak, K. W. P. Leung and R.-J. Wang, Inorg. Chem., 1992, 31, 4510 CrossRef CAS
; (b) S.-P. Neo, T. S. A. Hor, Z.-Y. Zhou and T. C. W. Mak, J. Organomet. Chem., 1994, 464, 113 CrossRef CAS
; (c) M. C. Gimeno, P. G. Jones, A. Laguna and C. Sarroca, J. Chem. Soc., Dalton Trans., 1995, 1473 RSC
; (d) Effendy, G. G. Lobbia, M. Pellei, C. Pettinari, C. Santini, B. W. Skelton and A. H. White, Inorg. Chim. Acta, 2001, 315, 153 CrossRef CAS
; (e) X. L. Lu, W. K. Leong, T. S. A. Hor and L. Y. Goh, J. Organomet. Chem., 2004, 689, 1746 CrossRef CAS
; (f) X. L. Lu, W. K. Leong, L. Y. Goh and T. S. A. Hor, Eur. J. Inorg. Chem., 2004, 2504 CrossRef CAS
; (g) Effendy, J. V. Hanna, F. Marchetti, D. Martini, C. Pettinari, R. Pettinari, B. W. Skelton and A. H. White, Inorg. Chim. Acta, 2004, 357, 1523 CrossRef CAS
; (h) G. G. Lobbia, M. Pellei, C. Pettinari, C. Santini, B. W. Skelton and A. H. White, Polyhedron, 2005, 24, 181 CrossRef CAS
; (i) C. Di Nicola, Effendy, C. Pettinari, B. W. Skelton, N. Somers and A. H. White, Inorg. Chim. Acta, 2005, 358, 695 CrossRef CAS
; (j) A. Cingolani, Effendy, C. Pettinari, B. W. Skelton and A. H. White, Inorg. Chim. Acta, 2006, 359, 2170 CrossRef CAS
; (k) P. Teo, L. L. Koh and T. S. A. Hor, Inorg. Chim. Acta, 2006, 359, 3435 CrossRef CAS
; (l) P. Teo, L. L. Koh and T. S. A. Hor, Chem. Commun., 2007, 4221 RSC
; (m) P. Teo, L. L. Koh and T. S. A. Hor, Inorg. Chem., 2008, 47, 9561 CrossRef CAS PubMed
; (n) C. Pettinari, J. Ngoune, A. Marinelli, B. W. Skelton and A. H. White, Inorg. Chim. Acta, 2009, 362, 3225 CrossRef CAS
; (o) J. Vincente, P. González-Herrero, Y. García-Sánchez and P. G. Jones, Inorg. Chem., 2009, 48, 2060 CrossRef PubMed
; (p) X. Yang, I. Isaac, C. Persau, R. Ahlrichs, O. Fuhr and D. Fenske, Inorg. Chim. Acta, 2014, 421, 233 CrossRef CAS
.
- For a structural study on complexes resulting from AgCN and dppf, 1,1′-bis(di-tert-butylphosphino)ferrocene or 1,1′-bis(dicyclohexylphosphino)ferrocene, see: M. Trivedi, Bhaskaran, G. Singh, A. Kumar and N. P. Rath, J. Organomet. Chem., 2014, 758, 9 CrossRef CAS
.
- Selected examples:
(a) I. D. Salter, S. A. Williams and T. Adatia, Polyhedron, 1995, 14, 2803 CrossRef CAS
; (b) I. D. Salter, V. Šik, S. A. Williams and T. Adatia, J. Chem. Soc., Dalton Trans., 1996, 643 RSC
; (c) D. Imhof, U. Burckhardt, K.-H. Dahmen, F. Joho and R. Nesper, Inorg. Chem., 1997, 36, 1813 CrossRef CAS PubMed
; (d) K.-T. Youm, Y. Kim, Y. Do and M.-J. Jun, Inorg. Chim. Acta, 2000, 310, 203 CrossRef CAS
; (e) Y. C. Neo, J. J. Vittal and T. S. A. Hor, J. Chem. Soc., Dalton Trans., 2002, 337 RSC
; (f) W.-Y. Wong, G.-L. Lu and K.-H. Choi, J. Organomet. Chem., 2002, 659, 107 CrossRef CAS
; (g) J. Lu, C.-C. Zhu, D.-C. Li and J.-M. Dou, J. Cluster Sci., 2012, 23, 545 CrossRef CAS
.
- E. M. Barranco, O. Crespo, M. C. Gimeno, A. Laguna, P. G. Jones and B. Ahrens, Inorg. Chem., 2000, 39, 680 CrossRef CAS PubMed
.
- M. C. Gimeno, P. G. Jones, A. Laguna and C. Sarroca, Polyhedron, 1998, 17, 3681 CrossRef CAS
.
- T. Mizuta, T. Aotani, Y. Imamura, K. Kubo and K. Miyoshi, Organometallics, 2008, 27, 2457 CrossRef CAS
.
- M. A. Fard, A. R. Kenaree, P. D. Boyle, P. J. Ragogna, J. B. Gilroy and J. F. Corrigan, Dalton Trans., 2016, 45, 2868 RSC
.
-
P. Štěpnička, in Ferrocenes: Ligands, Materials and Biomolecules, ed. P. Štěpnička, 2008, Wiley, Chichester, ch. 5, p. 177 Search PubMed
.
-
(a) N. J. Long, J. Martin, G. Opromolla, A. J. P. White, D. J. Williams and P. Zanello, J. Chem. Soc., Dalton Trans., 1999, 1981 RSC
; (b) J. E. Aguado, S. Canales, M. C. Gimeno, P. G. Jones, A. Laguna and M. D. Villacampa, Dalton Trans., 2005, 3005 RSC
.
- U. Siemeling, T. Klemann, C. Bruhn, J. Schulz and P. Štěpnička, Z. Anorg. Allg. Chem., 2011, 637, 1824 CrossRef CAS
.
- J. Kühnert, M. Lamač, T. Rüffer, B. Walfort, P. Štěpnička and H. Lang, J. Organomet. Chem., 2007, 692, 4303 CrossRef
.
- K. Škoch, I. Císařová and P. Štěpnička, Inorg. Chem., 2014, 53, 568 CrossRef PubMed
.
- K. Škoch, I. Císařová and P. Štěpnička, Chem. – Eur. J., 2015, 21, 15998 CrossRef PubMed
.
- According to a search in the Cambridge Structural Database, version 5.36 of November 2014 with updates from November 2014, February 2015 and May 2015.
- C. W. Liu, H. Pan, J. P. Fackler Jr., G. Wu, R. E. Wasylishen and M. Shang, J. Chem. Soc., Dalton Trans., 1995, 3691 RSC
.
- Two types of the complex cations are found in the crystal structure of [Ag(μ-L)2(MeCN)2][SbF6], differing by the distribution of the MeCN ligands, viz. [(MeCN)Ag(μ-L)2Ag(MeCN)]2+ and [Ag(μ-L)2Ag(MeCN)2]2+: P. W. Miller, M. Nieuwenhuyzen, J. P. H. Charmant and S. L. James, Inorg. Chem., 2008, 47, 8367 CrossRef CAS PubMed
.
-
(a) E. L. Muetterties and C. W. Alegranti, J. Am. Chem. Soc., 1970, 92, 4114 CrossRef CAS
; (b) E. L. Muetterties and C. W. Alegranti, J. Am. Chem. Soc., 1972, 94, 6386 CrossRef CAS
.
- NMR analysis of the crystallized products was often complicated by their very low solubility.
- R. G. Goel and P. Pilon, Inorg. Chem., 1978, 17, 2876 CrossRef CAS
.
- The cell parameters determined for unsolvated 2 are as follows: triclinic, space group P
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , a = 13.8254(3) Å, b = 17.5121(4) Å, c = 20.7672(5) Å; α = 74.567(1)°, β = 76.281(1)°, γ = 69.615(1)°.
, a = 13.8254(3) Å, b = 17.5121(4) Å, c = 20.7672(5) Å; α = 74.567(1)°, β = 76.281(1)°, γ = 69.615(1)°. - P. Schwerdtfeger, R. P. Krawczyk, A. Hammerl and R. Brown, Inorg. Chem., 2004, 43, 6707 CrossRef CAS PubMed
.
- This can be demonstrated by the structures of other [AgX(L)]4 clusters, where X = Cl, Br and I, and L = PPh3:
(a) B.-K. Teo and J. C. Calabrese, Inorg. Chem., 1976, 15, 2467 CrossRef CAS
; (b) B.-K. Teo and J. C. Calabrese, Inorg. Chem., 1976, 15, 2474 CrossRef CAS
; (c) B.-K. Teo and J. C. Calabrese, J. Chem. Soc., Chem. Commun., 1976, 185 RSC
; L = PEt3: (d) M. R. Churchill and B. G. DeBoer, Inorg. Chem., 1975, 14, 2502 CrossRef CAS
; (e) M. R. Churchill, J. Donahue and F. J. Rotella, Inorg. Chem., 1976, 15, 2752 CrossRef CAS
; and L = Ph2PBu: (f) R. J. Bowen, D. Camp, Effendy, P. C. Healy, B. W. Skelton and A. H. White, Aust. J. Chem., 1994, 47, 693 CrossRef CAS
.
- B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832 RSC
.
- G. A. Bowmaker, Effendy, J. V. Hanna, P. C. Healy, B. W. Skelton and A. H. White, J. Chem. Soc., Dalton Trans., 1993, 1387 RSC
.
- C(118–123)⋯C(318–323) interactions with centroid⋯centroid distance = 3.775(2) Å and dihedral angle = 2.1(1)°, and C(218–223)⋯C(418–423) contacts with centroid⋯centroid distance = 3.757(2) Å and dihedral angle = 5.1(1)°.
- The presence of two different cyanide groups is clearly manifested in the IR spectrum, displaying two bands at 2227 cm−1 (ligand 1) and at 2149 cm−1 (Ag(CN)2−). In an aqueous solution, the IR absorption of the [Ag(CN)2]− anion was observed at 2135 cm−1: L. H. Jones and R. A. Penneman, J. Chem. Phys., 1954, 22, 965 CrossRef CAS
.
- The stability constants determined for [Ag(CN)2]− in water (1 M NaClO4) and in nitromethane are log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β2 = 20.14(5) and >34, respectively.
(a) A. O. Gübeli and P. A. Côté, Can. J. Chem., 1972, 50, 1144 CrossRef
β2 = 20.14(5) and >34, respectively.
(a) A. O. Gübeli and P. A. Côté, Can. J. Chem., 1972, 50, 1144 CrossRef ; (b) J. Badoz-Lambling and J.-C. Bardin, C. R. Acad. Sci., Sect. C., Chim., 1968, 266, 95 CAS
.
-
(a) G. A. Bowmaker, Effendy, J. C. Reid, C. E. F. Rickard, B. W. Skelton and A. H. White, J. Chem. Soc., Dalton Trans., 1998, 2139 CAS
; (b) M. Ghazzali, M. H. Jaafar, S. Akerboom, A. Alsalme, K. Al-Farhan and J. Reedijk, Inorg. Chem. Commun., 2013, 36, 18 CrossRef CAS
.
- For the crystal structures of [(Cy3P)AgNCAgCN]n and [(Cy3P)2AgNCAgCN] in which linear (Ag(CN)2) and trigonal (Ag(NC)2(PCy3)) silver(I) centers coexist, see: Y.-Y. Lin, S.-W. Lai, C.-M. Che, Wen-Fu, Z.-Y. Zhou and N. Zhu, Inorg. Chem., 2005, 44, 1511 CrossRef CAS PubMed
.
-
(a) 1-Ethyl-3-methylimidazolium dicyanoargentate(1−), Ag–C = 2.06(2) Å: Y. Yoshida, K. Muroi, A. Otsuka, G. Saito, M. Takahashi and T. Yoko, Inorg. Chem., 2004, 43, 1458 CrossRef CAS PubMed
; (b) Bis(triphenylphospine)iminium dicyanoargentate(1−), Ag–C = 2.03(2) and 2.05(2) Å: M. Carcelli, C. Ferrari, C. Pelizzi, G. Pelizzi, G. Predieri and C. Solinas, J. Chem. Soc., Dalton Trans., 1992, 2127 RSC
.
- G. A. Bowmaker, C. Di Nicola, Effendy, J. V. Hanna, P. C. Healy, S. P. King, F. Marchetti, C. Pettinari, W. T. Robinson, B. W. Skelton, A. N. Sobolev, A. Tăbăcaru and A. H. White, Dalton Trans., 2013, 42, 277 RSC
.
- Compare the following non-bonding distances: Ag1⋯Ag2 = 5.6450(6) Å, S10⋯S20 = 5.553(2) Å; Ag3⋯Ag4 = 5.6247(6), S30⋯S40 = 5.535(2) Å.
- J. Howatson and B. Morosin, Cryst. Struct. Commun., 1973, 2, 51 CAS
(SciFinder Scholar, AN = 1973:89664).
-
(a) G. J. S. Venter, R. Meijboom and A. Roodt, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2007, 63, m3076 CAS
; (b) N. M. Khumalo, R. Meijboom, A. Muller and B. Omondi, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2010, 66, m451 CAS
.
- B. Omondi and R. Meijboom, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 69 CAS
.
-
(a) Effendy, C. Di Nicola, M. Fianchini, C. Pettinari, B. W. Skelton, N. Somers and A. H. White, Inorg. Chim. Acta, 2005, 358, 763 CrossRef CAS
; (b) L. Yang, C. Zhu and D. Li, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2011, 67, m2 CAS
.
- The (SCN)2 plane is defined by the atoms S3, N3, C3, S3′, N3′and C3′. These atoms are coplanar within ca. 0.001 Å.
- Selected crystallographic data: triclinic, P
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , a = 14.755(1), b = 16.940(2), c = 18.684(2) Å, α = 116.939(3)°, β = 90.455(4)°, γ = 104.733(4)° at T = 150(2) K.
, a = 14.755(1), b = 16.940(2), c = 18.684(2) Å, α = 116.939(3)°, β = 90.455(4)°, γ = 104.733(4)° at T = 150(2) K. - The Cl−/HF2−-bridged complex was isolated even when the samples were prepared and crystallized in halogen-free solvents.
- R. B. Johannesen, F. E. Brinckman and T. D. Coyle, J. Phys. Chem., 1968, 72, 660 CrossRef CAS
.
- Compare the observed Si–F bond lengths with those determined for M2[SiF6], where M = Na (av. 1.69 Å) and Me3NCH2CO2H (1.6627(9) and 1.6794(7) Å):
(a) G. F. Schäfer, Z. Kristallogr., 1986, 175, 269 Search PubMed
; (b) M. Fleck, V. V. Ghazaryan and A. M. Petrosyan, Z. Kristallogr., Cryst. Mater., 2013, 228, 240 CrossRef CAS
.
- C. D. Wyss, B. K. Tate, J. Bacsa, M. Wieliczko and J. P. Sadighi, Polyhedron, 2014, 84, 87 CrossRef CAS
.
- T. M. Klapötke, B. Krumm and M. Scherr, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, m2634 Search PubMed
.
- J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211 CrossRef CAS
.
- V. Jonas, G. Frenking and M. T. Reetz, J. Am. Chem. Soc., 1994, 116, 8741 CrossRef CAS
.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9 CrossRef CAS
.
- S. H. Strauss, Chem. Rev., 1993, 93, 927 CrossRef CAS
.
- M. L. Kuznetsov, Russ. Chem. Rev., 2002, 71, 265 CrossRef CAS
.
- Complexes 11 and 12 were crystallized from acetone/hexane and chloroform/hexane, respectively, with a small amount of MeCN added for better solubility.
- National Institute of Advanced Industrial Science and Technology. Spectral Database for Organic Compounds: SDBS; http://sdbs.db.aist.go.jp/sdbs/cgi-bin/cre_index.cgi, No. 889 (ethyl acetate) (accessed February 12, 2016).
- The angles between the vectors of the C6–P and C1–C11 bonds are 93.7(2)° in 11 and 95.7(1)° in 12.
- The vectors of the Ag–P bonds intersect the C(6–10) planes at 19.4(1)° in 11 and 18.91(8)° in 12.
- P. F. Barron, J. C. Dyason, P. C. Healy, L. M. Engelhardt, B. W. Skelton and A. H. White, J. Chem. Soc., Dalton Trans., 1986, 1965 RSC
.
- The P–Ag bond intersects the C(6–10) plane at an angle of 20.9(1)°, which falls between those in 11 and 12 (see ref. 56) and 13 (21.2(2)°).
- Notably, analogous reactions with AgClO4 (Ag
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 = 1
1 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) afforded only complex 11 (after crystallization), while no defined solid product could be isolated from an analogous experiment with Ag[SbF6].
2) afforded only complex 11 (after crystallization), while no defined solid product could be isolated from an analogous experiment with Ag[SbF6]. - Complexes with bridging phosphinonitrile donors have been postulated, e.g., in:
(a) P. Braunstein, D. Matt, Y. Dusausoy, J. Fischer, A. Mitschler and L. Ricard, J. Am. Chem. Soc., 1981, 103, 5115 CrossRef CAS
; (b) D. S. Barratt, A. Hosseiny, C. A. McAuliffe and C. Stacey, J. Chem. Soc., Dalton Trans., 1985, 135 RSC
. However, the only structurally characterized compounds of this type are several Cu(I) complexes with ligand 1 (see ref. 16).
-
(a) An Ag(I) complex with a macrocyclic N3O2 donor and coordinated cyanoethyl pendant arm completing an [5 + 1] pseudoctahedral coordination around the Ag center (Ag–N
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C of 86°m Ag–N ≈ 2.68 Å): Z. Ma, H. Shi, X. Deng, M. F. C. G. da Silva, L. M. D. R. S. Martins and A. J. L. Pombeiro, Dalton Trans., 2015, 44, 1388 RSC
C of 86°m Ag–N ≈ 2.68 Å): Z. Ma, H. Shi, X. Deng, M. F. C. G. da Silva, L. M. D. R. S. Martins and A. J. L. Pombeiro, Dalton Trans., 2015, 44, 1388 RSC ; (b) A cationic Ag–Fe complex with a pyridine-dipyrrinato ligand and solvating MeCN (Ag–N
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C of 105°): S. R. Halper, L. Do, J. R. Stork and S. M. Cohen, J. Am. Chem. Soc., 2006, 128, 15255 CrossRef CAS PubMed
C of 105°): S. R. Halper, L. Do, J. R. Stork and S. M. Cohen, J. Am. Chem. Soc., 2006, 128, 15255 CrossRef CAS PubMed ; (c) [(Ph2PPy-κP)2Ag(μ-Cl)2Ag(MeCN)(Ph2PPy-κP)] (Ag–N
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C = 106°; this angle is associated with a very long Ag–N distance, ca. 3.21 Å): A. Cingolani, Effendy, D. Martini, C. Pettinari, B. W. Skelton and A. H. White, Inorg. Chim. Acta, 2006, 359, 2183 CrossRef CAS
C = 106°; this angle is associated with a very long Ag–N distance, ca. 3.21 Å): A. Cingolani, Effendy, D. Martini, C. Pettinari, B. W. Skelton and A. H. White, Inorg. Chim. Acta, 2006, 359, 2183 CrossRef CAS ; (d) Ag(MeCN)3+ cation in the structure of a complicated polyoxometalate (Ag–N
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C = 109°): J. T. Rhule, W. A. Neiwert, K. I. Hardcastle, B. Do and C. L. Hill, J. Am. Chem. Soc., 2001, 123, 12101 CrossRef CAS PubMed
C = 109°): J. T. Rhule, W. A. Neiwert, K. I. Hardcastle, B. Do and C. L. Hill, J. Am. Chem. Soc., 2001, 123, 12101 CrossRef CAS PubMed ; (e) [Ag(L)(MeCN)]n(ClO4)n,(H2O)n (L = 2,6-diamino-3,5-dicyano-4-(3-quinolinyl)-2,5-heptadiene; Ag–N
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C = 110°): C.-W. Yeh, C.-H. Tsou, F.-C. Huang, A. Jong and M.-C. Suen, Polyhedron, 2014, 81, 273 CrossRef CAS
C = 110°): C.-W. Yeh, C.-H. Tsou, F.-C. Huang, A. Jong and M.-C. Suen, Polyhedron, 2014, 81, 273 CrossRef CAS .
- For representative examples, see:
(a) T. C. Wright, G. Wilkinson, M. Motevalli and M. B. Hursthouse, J. Chem. Soc., Dalton Trans., 1986, 2017 RSC
. (d(Mo–N)–d(Mo–C) ≈ 0.10 Å); (b) P. A. Chetcuti, C. B. Knobler and M. F. Hawthorne, Organometallics, 1988, 7, 650 CrossRef CAS
. (d(Ir–N)–d(Ir–C) = 0.07 and 0.15 Å); (c) J. Barrera, M. Sabat and W. D. Harman, Organometallics, 1993, 12, 4381 CrossRef CAS
. (d(W–N)–d(W–C) = 0.01 and 0.03 Å); (d) J. J. Garcia, N. M. Brunkan and W. D. Jones, J. Am. Chem. Soc., 2002, 124, 9547 CrossRef CAS PubMed
. (d(Ni–N)–d(Ni–C) = 0.07 Å).
- M. L. Kuznetsov, E. A. Klestova-Nadeeva and A. I. Dement'ev, J. Mol. Struct. (THEOCHEM), 2004, 671, 229 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Full experimental and characterization data for all newly prepared compounds, IR spectra of 3′ and [(μ(P,N)-1){CuCl(1-κP)}]2, complete structural drawings, a summary of relevant crystallographic data, additional plots of the calculated electron density and its Laplacian. CCDC 1470453–1470466. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6dt01843b |
| This journal is © The Royal Society of Chemistry 2016 |