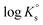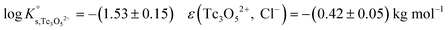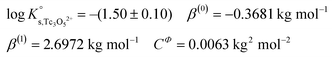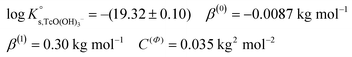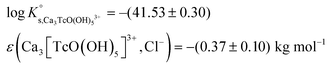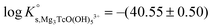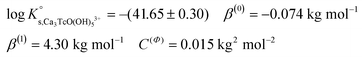Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermodynamic description of Tc(IV) solubility and hydrolysis in dilute to concentrated NaCl, MgCl2 and CaCl2 solutions†
Ezgi
Yalçıntaş
*,
Xavier
Gaona
*,
Marcus
Altmaier
,
Kathy
Dardenne
,
Robert
Polly
and
Horst
Geckeis
Institute for Nuclear Waste Disposal, Karlsruhe Institute of Technology, P.O. Box 3640, 76021 Karlsruhe, Germany. E-mail: ezgi.yalcintas@kit.edu; xavier.gaona@kit.edu
First published on 20th April 2016
Abstract
We present the first systematic investigation of Tc(IV) solubility, hydrolysis and speciation in dilute to concentrated NaCl, MgCl2 and CaCl2 systems, and comprehensive thermodynamic and activity models for the system Tc4+–H+–Na+–Mg2+–Ca2+–OH−–Cl−–H2O using both SIT and Pitzer approaches. The results are advancing the fundamental scientific understanding of Tc(IV) solution chemistry and are highly relevant in the applied context of nuclear waste disposal. The solubility of Tc(IV) was investigated in carbonate-free NaCl–NaOH (0.1–5.0 M), MgCl2 (0.25–4.5 M) and CaCl2 (0.25–4.5 M) solutions within 2 ≤ pHm ≤ 14.5. Undersaturation solubility experiments were performed under an Ar atmosphere at T = 22 ± 2 °C. Strongly reducing conditions (pe + pHm ≤ 2) were imposed with Na2S2O4, SnCl2 and Fe powder to stabilize technetium in the +IV redox state. The predominance of Tc(IV) in the aqueous phase was confirmed by solvent extraction and XANES/EXAFS spectroscopy. Solid phase characterization was accomplished after attaining thermodynamic equilibrium using XRD, SEM–EDS, XANES/EXAFS, TG–DTA and quantitative chemical analysis, and indicated that TcO2·0.6H2O(s) exerts solubility-control in all evaluated systems. The definition of the polyatomic Tc3O52+ species instead of TcO2+ is favoured under acidic conditions, consistently with slope analysis (mTcvs. pHm) of the solubility data gained in this work and spectroscopic evidence previously reported in the literature. The additional formation of Tc(IV)–OH/O–Cl aqueous species in concentrated chloride media ([Cl−] = 9 M) and pHm ≤ 4 is suggested by solubility and EXAFS data. The pH-independent behaviour of the solubility observed under weakly acidic to weakly alkaline pHm conditions can be explained with the equilibrium reaction TcO2·0.6H2O(s) + 0.4H2O(l) ⇔ TcO(OH)2(aq). Solubility data determined in dilute NaCl systems with pHm ≥ 11 follow a well-defined slope of +1, consistent with the predominance of TcO(OH)3− previously selected by NEA–TDB. In concentrated MgCl2 and CaCl2 solutions with pHm ≥ 8, the formation of the ternary Mg3[TcO(OH)5]3+ and Ca3[TcO(OH)5]3+ species is proposed based on the slope analysis of the solubility data, model calculations and previous observations for analogous An(IV) and Zr(IV) systems. The formation and stability of these hitherto unknown Tc(IV) species are supported by DFT calculations. Based on the newly generated experimental data and previous spectroscopic observations, new comprehensive chemical, thermodynamic and activity models (SIT, Pitzer) for these systems are derived.
1 Introduction
99Tc is a fission product of 235U and 239Pu forming with a high yield in nuclear reactors. The behaviour of 99Tc in repositories for radioactive waste needs to be properly assessed due to its redox sensitive character, very long half-life (t1/2 ∼ 2.13 × 105 a) and potential contribution to the dose rate of radioactive waste in the long-term. Two main oxidation states of Tc (+VII and +IV) control the potential release and migration of this radionuclide from the repository into the biosphere. Tc(VII) is the most stable oxidation state in suboxic/oxidizing environments, forming the highly mobile TcO4− anion over the entire pH range with very high solubility and very weak sorption properties.1 In contrast, Tc(IV) forms sparingly soluble oxides TcO2·xH2O(s) under reducing conditions, and thus it is expected to control the chemical behaviour of Tc under the redox conditions expected in deep underground repositories for radioactive waste.The geochemical conditions in underground repositories are mostly defined by the host-rock formation, composition of the groundwater, backfill material, waste inventories and waste form, among others. Although dilute conditions (I < 0.1 M) are normally expected for intruding waters in clay and crystalline host-rock formations, high saline (5 M < I < 15 M) systems are expected in certain sedimentary rocks and salt-rock formations. The latter systems are characterized by high concentrations of Na+, Mg2+, K+, Cl− and SO42− with lower contributions of Ca2+, HCO3−, F− and Br−.2 The use of cement-based materials for conditioning/stabilization of the waste or construction purposes in a repository potentially leads to an alteration of the geochemical media buffering the pH in the hyperalkaline range and inducing a significant increase in the Ca concentration (≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.02 M at pH ≈ 12.5).3 In concentrated salt brine systems, the interaction of MgCl2 with cement can further lead to the formation of concentrated CaCl2 systems (up to 2.0 M) with pHm ≈ 12 (pHm = −log
0.02 M at pH ≈ 12.5).3 In concentrated salt brine systems, the interaction of MgCl2 with cement can further lead to the formation of concentrated CaCl2 systems (up to 2.0 M) with pHm ≈ 12 (pHm = −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mH+).4 The solution chemistry of radionuclides in saline systems of high ionic strength cannot be predicted from data and model descriptions gained in dilute systems, mainly because of strong ion interaction processes taking place in the former, leading to a potential strong stabilisation or de-stabilisation of species in brine systems. Besides ion interaction processes which may significantly affect the chemical behaviour and thermodynamic equilibria, the presence of high concentrations of cations like Mg2+ or Ca2+ can further result in the formation of new aqueous species or solid compounds not observed in dilute systems. Apart from being an interesting research topic from the perspective of fundamental aquatic chemistry, this tendency can lead to completely different chemical properties and migration behaviour of radionuclides in salt brine systems, which therefore justifies dedicated research efforts.
mH+).4 The solution chemistry of radionuclides in saline systems of high ionic strength cannot be predicted from data and model descriptions gained in dilute systems, mainly because of strong ion interaction processes taking place in the former, leading to a potential strong stabilisation or de-stabilisation of species in brine systems. Besides ion interaction processes which may significantly affect the chemical behaviour and thermodynamic equilibria, the presence of high concentrations of cations like Mg2+ or Ca2+ can further result in the formation of new aqueous species or solid compounds not observed in dilute systems. Apart from being an interesting research topic from the perspective of fundamental aquatic chemistry, this tendency can lead to completely different chemical properties and migration behaviour of radionuclides in salt brine systems, which therefore justifies dedicated research efforts.
The solubility of Tc(IV) was previously investigated by a number of research groups, in most of the cases at low ionic strength. Meyer et al.5 studied the solubility of Tc(IV) in the pH range 1 to 10. Two different approaches were used for the preparation of the solid phase, namely electrodeposition of an oxide solid phase and the oxide precipitation onto sand particles from reduction of Tc(VII) by hydrazine. The authors determined the number of hydration waters in TcO2·xH2O(s) as (1.63 ± 0.28) by weighing the dried solid phases reduced under acidic and alkaline conditions. Based on their solubility data, Meyer and co-workers proposed a chemical model with TcO2+ and TcO(OH)+ species prevailing under acidic conditions. On the other hand, the chemical equilibrium TcO2·1.6H2O(s) ⇔ TcO(OH)2(aq) + 0.6H2O(l) was proposed to explain the very low and pH-independent solubility behaviour within 4 ≤ pH ≤ 10. Eriksen et al.6 performed solubility experiments with an electrodeposited Tc(IV) oxide as a function of pH and PCO2. Consistently with Meyer and co-workers, these authors observed a pH-independent solubility (≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 × 10−9 M) within the pH range 6 to 9.5. The increase in solubility with slope +1 observed above pH = 9.5 was interpreted as the formation of the TcO(OH)3− species in accordance with the chemical reaction TcO2·xH2O(s) ⇔ TcO(OH)3− + H+ + (x − 2)H2O(l) and
7 × 10−9 M) within the pH range 6 to 9.5. The increase in solubility with slope +1 observed above pH = 9.5 was interpreted as the formation of the TcO(OH)3− species in accordance with the chemical reaction TcO2·xH2O(s) ⇔ TcO(OH)3− + H+ + (x − 2)H2O(l) and 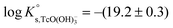 . Hess et al. (2004)7 conducted solubility experiments in dilute to concentrated saline systems (up to 5.0 M NaCl and 6.0 M HCl) under acidic to near-neutral pH conditions. Samples were equilibrated for up to 65 days. The solubility study was complemented with extensive solid and aqueous phase characterization, including XRD, UV-vis, XANES/EXAFS and liquid–liquid extraction. In spite of the high [Cl−] considered in the study, the authors only reported evidence on the formation of Tc(IV)–Cl species (TcCl4(aq) and TcCl62−) at pHm ≤ 1 and I ≥ 2.5 M. The transformation of TcO2·xH2O(s) to TcCl4(s) was also proposed to take place under these conditions. Above pHm ≈ 1, Hess and co-workers reported the predominance of Tc(IV) hydrolysis species and explained the significant increase in solubility observed in concentrated NaCl solutions exclusively by ion interaction processes. The authors derived comprehensive chemical, thermodynamic and activity models for Tc(IV) in acidic HCl–NaCl systems based on their solubility data at short equilibration times (t = 11 days) and the corresponding solid and aqueous phase characterization. The chemical model reported by Hess et al. is in agreement with previous publications available in the literature and with the current NEA–TDB data selection, although the authors reported greater
. Hess et al. (2004)7 conducted solubility experiments in dilute to concentrated saline systems (up to 5.0 M NaCl and 6.0 M HCl) under acidic to near-neutral pH conditions. Samples were equilibrated for up to 65 days. The solubility study was complemented with extensive solid and aqueous phase characterization, including XRD, UV-vis, XANES/EXAFS and liquid–liquid extraction. In spite of the high [Cl−] considered in the study, the authors only reported evidence on the formation of Tc(IV)–Cl species (TcCl4(aq) and TcCl62−) at pHm ≤ 1 and I ≥ 2.5 M. The transformation of TcO2·xH2O(s) to TcCl4(s) was also proposed to take place under these conditions. Above pHm ≈ 1, Hess and co-workers reported the predominance of Tc(IV) hydrolysis species and explained the significant increase in solubility observed in concentrated NaCl solutions exclusively by ion interaction processes. The authors derived comprehensive chemical, thermodynamic and activity models for Tc(IV) in acidic HCl–NaCl systems based on their solubility data at short equilibration times (t = 11 days) and the corresponding solid and aqueous phase characterization. The chemical model reported by Hess et al. is in agreement with previous publications available in the literature and with the current NEA–TDB data selection, although the authors reported greater 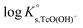 for the TcO(OH)+ species, which accordingly becomes predominant in the acidic pH region. Later, Liu et al. (2007)8 performed Tc(IV) solubility experiments in simulated ground water within 1 ≤ pH ≤ 12 and 10−4 M ≤ [CO32−] ≤ 0.05 M. The authors found a good agreement with previous publications and did not observe any relevant increase in Tc(IV) solubility due to carbonate complexation. Warwick et al.9 investigated the solubility of Tc(IV) reduced by Sn(II) and Fe(II) within the pH range 11.8 to 14.4. In contrast to the solubility data by Eriksen and co-workers, the authors only observed a slight increase of Tc(IV) solubility above pH = 13.5. Unfortunately, no solid phase characterization was conducted by the authors, and thus it can only be speculated that a more crystalline solid or alteration phase was eventually responsible for the control of the solubility in this study. Kobayashi and co-workers (2013)10 investigated the reduction of Tc(VII) to Tc(IV) in 0.1 M NaCl and the presence of various reducing systems. The authors compared their experimental results with thermodynamic calculations of the Tc(VII)/Tc(IV) redox border, with the aim of assessing the kinetics of the reduction process and the reliability of Eh–pH measurements. Recently, Yalcintas et al.11 extended the redox experiments by Kobayashi et al. to dilute and concentrated NaCl and MgCl2 solutions in order to evaluate the effect of elevated ionic strength on the redox behaviour of Tc. Besides the impact of salt concentration on the measured Eh values, a systematic increase in the concentration of Tc(IV) under acidic conditions was observed with increasing ionic strength, thus reflecting a relevant impact of ion interaction processes on the aquatic chemistry of Tc(IV).
for the TcO(OH)+ species, which accordingly becomes predominant in the acidic pH region. Later, Liu et al. (2007)8 performed Tc(IV) solubility experiments in simulated ground water within 1 ≤ pH ≤ 12 and 10−4 M ≤ [CO32−] ≤ 0.05 M. The authors found a good agreement with previous publications and did not observe any relevant increase in Tc(IV) solubility due to carbonate complexation. Warwick et al.9 investigated the solubility of Tc(IV) reduced by Sn(II) and Fe(II) within the pH range 11.8 to 14.4. In contrast to the solubility data by Eriksen and co-workers, the authors only observed a slight increase of Tc(IV) solubility above pH = 13.5. Unfortunately, no solid phase characterization was conducted by the authors, and thus it can only be speculated that a more crystalline solid or alteration phase was eventually responsible for the control of the solubility in this study. Kobayashi and co-workers (2013)10 investigated the reduction of Tc(VII) to Tc(IV) in 0.1 M NaCl and the presence of various reducing systems. The authors compared their experimental results with thermodynamic calculations of the Tc(VII)/Tc(IV) redox border, with the aim of assessing the kinetics of the reduction process and the reliability of Eh–pH measurements. Recently, Yalcintas et al.11 extended the redox experiments by Kobayashi et al. to dilute and concentrated NaCl and MgCl2 solutions in order to evaluate the effect of elevated ionic strength on the redox behaviour of Tc. Besides the impact of salt concentration on the measured Eh values, a systematic increase in the concentration of Tc(IV) under acidic conditions was observed with increasing ionic strength, thus reflecting a relevant impact of ion interaction processes on the aquatic chemistry of Tc(IV).
Besides these studies specifically targeting the determination of thermodynamic data, a number of spectroscopic investigations providing relevant insights into the speciation of Tc under acidic conditions have been published since 2000.12–16 Hence, Vichot et al. (2002) investigated the speciation of Tc(IV) in aqueous Cl− and SO42− media at pH ≈ 1.5 and I ≤ 3 M.12 Based on the evaluation of their EXAFS data, the authors proposed the formation of small sized polynuclear species independently of the composition of the background electrolyte. EXAFS data disregarded also the presence of Cl-backscatterers in the first coordination shell of Tc. In 2003, the same authors confirmed the formation and predominance of polymeric TcnOp(4n–2p)+ species up to pH = 3 using UV-vis spectroscopy, clearly contradicting the previously postulated predominance of the monomeric TcO2+ and TcO(OH)+ species. The authors interpreted their data with the formation of the trimer Tc3O44+, which shows clear analogies with the cluster M3O4·9H2O4+ previously described for Mo(IV).13 Poineau et al. (2006)16 investigated the aqueous speciation of Tc in 3.0 M HCl–NaCl solutions with 0 ≤ pH ≤ 1.5 using a combination of spectroscopic techniques (UV-vis/NIR and EXAFS). The authors confirmed the predominance of the Tc2OCl104− species at 0.1 ≤ pH ≤ 1.1, whereas TcCl62− and TcnOp(4n–2p)+ prevailed below and above this pH range, respectively.17
In spite of the abundant experimental studies focussing on the aquatic chemistry of Tc(IV), a number of open questions remain with regard to the chemical and thermodynamic models available for this system. Furthermore, the lack of systematic studies at elevated ionic strength hinders the development of accurate activity models able to predict the chemical behaviour of Tc(IV) at I ≠ 0 and directly impacts the possibilities to model Tc chemistry in salt media. In this context, the present study aims at a comprehensive and systematic investigation of Tc(IV) solubility and hydrolysis in dilute to concentrated NaCl, MgCl2 and CaCl2 systems relevant for different nuclear waste disposal concepts and scenarios. Solubility experiments are complemented with comprehensive solid and aqueous phase characterisation contributing to the development of an accurate chemical model for this system. The thermodynamic and activity models for the system Tc4+–H+–Na+–Mg2+–Ca2+–OH−–Cl−–H2O are derived based on the newly generated experimental data using SIT and Pitzer approaches.
1.1. Thermodynamic background
The first definition of TcO2+ as Tc(IV) cation prevailing under very acidic conditions dates back to the electrophoretic study by Gorski and Koch (1969),19 who reported a Tc(IV) species with charge +2 dominating at pH < 1.3. This formulation was adopted by the NEA–TDB, although more recent spectroscopic studies strongly hint towards the predominance of positively charged Tc(IV) polyatomic species under acidic conditions.12–16 In spite of selecting the TcO(OH)3− species, Rard and co-workers1 acknowledged the need of additional experimental studies focussing on the alkaline pH region due to the limited number of data points in the study of Eriksen et al. (1992).6 The lack of experimental studies at I > 0.1 M hindered the development of an activity model for Tc(IV), which remains as one of the main limitations of the current Tc(IV) thermodynamic selection in the NEA–TDB.
2 Materials and methods
2.1 Chemicals
All solutions were prepared with purified water (Milli-Q academic, Millipore) and purged for 2–3 hours with Ar before use. All sample preparation and handling procedures were performed in an Ar glovebox with <1 ppm O2 at T = 22 ± 2 °C. A purified and radiochemically well-characterized 99Tc stock solution (1.3 M NaTcO4) was used for the electrochemical preparation of the Tc(IV) stock suspension. NaCl (p.a.), MgCl2·6H2O (p.a.), Mg(OH)2(s), CaCl2·2H2O (p.a.), Ca(OH)2(s), sodium dithionite (Na2S2O4) and metallic iron powder (grain size 10 μm) were purchased from Merck. SnCl2, pH buffers PIPES , TRIS
, TRIS  and tetraphenylphosphonium chloride (TPPC) were obtained from Sigma-Aldrich. HCl and NaOH Titrisol© (Merck) were used for adjusting the pH of the solutions.
and tetraphenylphosphonium chloride (TPPC) were obtained from Sigma-Aldrich. HCl and NaOH Titrisol© (Merck) were used for adjusting the pH of the solutions.
2.2 pH and Eh measurements
The hydrogen ion concentration (pHm = −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mH+) was measured using combination pH electrodes (type ROSS, Orion) calibrated against standard pH buffers (2 ≤ pH ≤ 12, Merck). In salt solutions of ionic strength Im ≥ 0.1 mol kg−1, the measured pH value (pHexp) is an operational apparent value related to mH+ by pHm = pHexp + Am. The empirical correction factor Am entails both the liquid junction potential and the activity coefficient of H+. Am values determined as a function of NaCl, MgCl2 and CaCl2 concentrations are available in the literature.20,21 In NaCl–NaOH solutions with mOH− > 0.03 m, the H+ concentration was calculated from the given mOH− and the conditional ion product of water.18 In MgCl2 and CaCl2 solutions, the highest pHm (pHmax) is fixed by the precipitation of Mg(OH)2(s) and Ca(OH)2(s) (or corresponding hydroxochlorides at Ca or Mg concentrations above ≈2 m), which buffer pHm at ≈
mH+) was measured using combination pH electrodes (type ROSS, Orion) calibrated against standard pH buffers (2 ≤ pH ≤ 12, Merck). In salt solutions of ionic strength Im ≥ 0.1 mol kg−1, the measured pH value (pHexp) is an operational apparent value related to mH+ by pHm = pHexp + Am. The empirical correction factor Am entails both the liquid junction potential and the activity coefficient of H+. Am values determined as a function of NaCl, MgCl2 and CaCl2 concentrations are available in the literature.20,21 In NaCl–NaOH solutions with mOH− > 0.03 m, the H+ concentration was calculated from the given mOH− and the conditional ion product of water.18 In MgCl2 and CaCl2 solutions, the highest pHm (pHmax) is fixed by the precipitation of Mg(OH)2(s) and Ca(OH)2(s) (or corresponding hydroxochlorides at Ca or Mg concentrations above ≈2 m), which buffer pHm at ≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 and ≈
9 and ≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12, respectively.20
12, respectively.20
Redox potentials were measured with Pt combination electrodes with the Ag/AgCl reference system (Metrohm) and converted to Ehvs. the standard hydrogen electrode (SHE) by correction for the potential of the Ag/AgCl reference electrode (+208 mV for 3 M KCl at T = 22 °C). The measurement of Eh values in highly saline systems was previously discussed elsewhere.11
2.3 Sample preparation and characterization
The Tc(IV) solid phase used in this study was prepared by electrochemical reduction of a 0.01 M TcO4− solution in 1.0 M HCl at E ≈ −50 mV vs. SHE, followed by quantitative precipitation of the Tc(IV) suspension in 5 mM Na2S2O4 solution at pHm > 12. The resulting TcO2·xH2O(s) was aged for two months before further use.The solubility of Tc(IV) was studied from undersaturation conditions in 0.1–5.0 M NaCl, 0.25–4.5 M MgCl2 and 0.25–4.5 M CaCl2 solutions. A total of 52 independent batch samples were prepared in these background electrolytes. The pH values were adjusted at 1.5 ≤ pHm ≤ 14.5 by using HCl–NaCl–NaOH, HCl–MgCl2 and HCl–CaCl2 of appropriate ionic strength, as well as Mg(OH)2(s) and Ca(OH)2(s). 0.5 M PIPES and 1.0 M TRIS stock solutions were used for buffering the solubility samples at pHm ≈ 7 and pHm ≈ 8, respectively. In both cases, the final buffer concentration was 12 mM. Based on a previous comprehensive study on the redox chemistry of Tc(VII)/Tc(IV) in dilute to concentrated saline systems,11 Na2S2O4, SnCl2 and Fe powders (depending upon target pH) were used to stabilize the +IV redox state of Tc in the solubility samples. Background electrolyte solutions with adjusted pHm and Eh conditions were equilibrated for two weeks. About 5 mg of the Tc(IV) solid phase were washed three times with 1 mL of the respective pre-equilibrated matrix solution and added to 20 mL of the same matrix solution in 50 mL screw cap centrifuge vials (Nalgene™, Thermo Scientific). Those samples with expectedly high solubility were prepared in smaller volumes (1 to 5 mL) to avoid the complete dissolution of the Tc(IV) solid phase. pHm and mTc in the solubility samples were repeatedly measured at regular time intervals, usually from 3 to 600 days. During this time, samples were agitated manually about once per week. After reaching equilibrium conditions (stable pHm and mTc readings), the pH of some unbuffered samples was slightly shifted by addition of acidic or basic solutions of the same ionic strength to obtain additional data points in the solubility curve. This approach was strictly followed from pH values with lower to higher solubility, in order to avoid oversaturation conditions and the potential formation of colloidal phases.22
Tc concentration in solution was quantified by Liquid Scintillation Counting (LSC, Quantulus, Perkin Elmer) after 10 kD ultrafiltration (2–3 nm, Pall Life Sciences). Samples for LSC analysis were mixed with 10 mL of LSC-cocktail Ultima Gold XR (Perkin-Elmer). The detection limit of LSC for this system was calculated as ≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 × 10−10 M (signal of the blank +3 standard deviations). The error associated with the sorption of Tc on the ultrafiltration filters was found below the uncertainty of the measurement of mTc. The oxidation state of Tc in the aqueous phase was determined by solvent extraction as reported elsewhere.23,24 The supernatant of the sample was contacted with 50 mM TPPC in chloroform. After vigorous mixing for 1 minute and subsequent separation of the aqueous and organic phases by centrifugation, Tc concentration in the aqueous phase was determined by LSC. Since TcO4− is extracted to the organic solvent, the activity remaining in the aqueous phase is interpreted as Tc(IV).
4 × 10−10 M (signal of the blank +3 standard deviations). The error associated with the sorption of Tc on the ultrafiltration filters was found below the uncertainty of the measurement of mTc. The oxidation state of Tc in the aqueous phase was determined by solvent extraction as reported elsewhere.23,24 The supernatant of the sample was contacted with 50 mM TPPC in chloroform. After vigorous mixing for 1 minute and subsequent separation of the aqueous and organic phases by centrifugation, Tc concentration in the aqueous phase was determined by LSC. Since TcO4− is extracted to the organic solvent, the activity remaining in the aqueous phase is interpreted as Tc(IV).
Solid phase characterization was conducted for selected batch samples after attaining equilibrium conditions. A fraction of the solid phase (≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mg) was washed 3–5 times with ethanol under an Ar atmosphere to remove the salt-containing matrix solution. After the last cleaning step, the solid was re-suspended in approximately 20 μL ethanol, transferred to a capped silicon single crystal sample holder (Dome, Bruker), dried under an Ar atmosphere for a few minutes before sealing of the sample holder, and transferred outside the glovebox for the collection the XRD diffractogram. XRD measurements were performed on a Bruker AXS D8 Advance X-ray powder diffractometer at 10° ≤ 2θ ≤ 78° with incremental steps of 0.015° and a measurement time of 1.7 seconds per step. The spectra collected were compared with the JCPDS database (Joint Committee on Powder Diffraction Standards25). After XRD measurement, the solid phase was dissolved in 1 mL of 2–3% HNO3 and used for quantitative chemical analysis. The dissolved solid phase was analysed by LSC and inductively coupled plasma-optical emission spectroscopy (ICP-OES, Perkin-Elmer Optima 2000™) to determine the Tc and Na, Mg, or Ca contents, respectively. Analytical errors in the quantitative chemical analysis by LSC and ICP–OES can be safely considered to be below 10%. A second fraction of the washed solid was investigated in the selected samples by scanning electron microscope-energy disperse spectrometry (SEM–EDS) with the aim of characterizing the morphology and crystallinity of the solid phase, and to further assess its chemical composition. Measurements were performed with a FEI Quanta 650 FEG equipped with a Noran EDS unit.
1 mg) was washed 3–5 times with ethanol under an Ar atmosphere to remove the salt-containing matrix solution. After the last cleaning step, the solid was re-suspended in approximately 20 μL ethanol, transferred to a capped silicon single crystal sample holder (Dome, Bruker), dried under an Ar atmosphere for a few minutes before sealing of the sample holder, and transferred outside the glovebox for the collection the XRD diffractogram. XRD measurements were performed on a Bruker AXS D8 Advance X-ray powder diffractometer at 10° ≤ 2θ ≤ 78° with incremental steps of 0.015° and a measurement time of 1.7 seconds per step. The spectra collected were compared with the JCPDS database (Joint Committee on Powder Diffraction Standards25). After XRD measurement, the solid phase was dissolved in 1 mL of 2–3% HNO3 and used for quantitative chemical analysis. The dissolved solid phase was analysed by LSC and inductively coupled plasma-optical emission spectroscopy (ICP-OES, Perkin-Elmer Optima 2000™) to determine the Tc and Na, Mg, or Ca contents, respectively. Analytical errors in the quantitative chemical analysis by LSC and ICP–OES can be safely considered to be below 10%. A second fraction of the washed solid was investigated in the selected samples by scanning electron microscope-energy disperse spectrometry (SEM–EDS) with the aim of characterizing the morphology and crystallinity of the solid phase, and to further assess its chemical composition. Measurements were performed with a FEI Quanta 650 FEG equipped with a Noran EDS unit.
The number of hydration waters in the TcO2·xH2O(s) solid phase used in the present work before and after solubility experiments was quantified by thermogravimetric analysis (TG–DTA) using a Netzsch STA 449C equipment. Three samples were prepared for thermogravimetric analysis: (i) 6.6 mg of the original Tc(IV) solid phase prepared by electrolysis and consecutive precipitation in alkaline media (presence of Na2S2O4, pHm ≈ 12), (ii) 6.1 mg of the Tc(IV) solid phase equilibrated in 5.0 M NaCl (presence of Na2S2O4, pHm = 12, 13 and 14) and (iii) 1.4 mg of the Tc(IV) solid phase equilibrated in 4.5 M MgCl2 (presence of Sn(II), pHm = 4). All investigated samples were washed 3–5 times with ethanol under an Ar atmosphere to remove the salt-containing matrix solution. After the last cleaning step, the solid was left to dry under an Ar atmosphere for 2–3 days and transferred to a glovebox specifically dedicated to DTA analyses. Measurements were performed under an Ar atmosphere up to T = 200 °C at a rate of 5 K min−1.
2.4 XAFS measurements
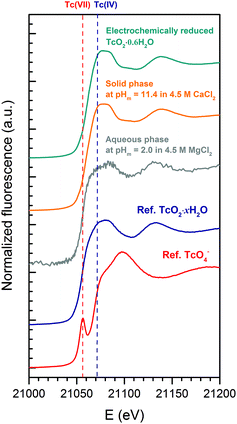
XAFS spectra were recorded at the INE-Beamline for Actinide Research at ANKA, KIT Campus North,26 in Karlsruhe, Germany. Both solid and aqueous phases were characterized by XANES/EXAFS to confirm the redox state of Tc and assess its coordination environment. Three samples were investigated: (i) the original Tc(IV) solid phase, (ii) a Tc(IV) solid phase equilibrated in 4.5 M CaCl2 at pHm = 11.4 and (iii) the supernatant solution of the solubility sample equilibrated in 4.5 M MgCl2 at pHm = 2.0 (mTc ≈ 3 × 10−3 m). In all cases, approximately 300 μL of the suspension were transferred to a 400 μL polyethylene vial under an Ar atmosphere and centrifuged at 4020g for 10 minutes to obtain a compacted solid phase at the bottom of the vial. The vials were mounted in a gas-tight cell with windows of the Kapton® film (polyimide) inside the Ar-glovebox and transported to the INE-Beamline. XAFS measurements were conducted within a few hours after sample preparation.Tc-K edge (21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 044 eV) XAFS spectra (3–4 replicates per sample) were recorded at room temperature under a continuous flow of Ar. Ge(422) crystals were used in the double crystal monochromator, Lemonnier-type operating in fixed-exit mode. The monochromatic beam is focused by a toroidal mirror, delivering a beam spot-size of ∼500 × 300 μm2 at the sample position at a photon energy of 18 keV. The parallel alignment of the crystal faces was detuned to ≈70% of the maximum beam intensity at the beginning of each scan. The incident intensity was held constant by means of a piezo-driven feedback system to the second crystal. The intensity of the incoming beam (I0) was monitored using an Ar filled ionization chamber at ambient pressure. Spectra were recorded in fluorescence mode using a five pixel LEGe solid state detector (Canberra, Belgium). Tc spectra were energy-calibrated with respect to the first inflection point in the XANES spectra of a Mo metal foil (20
044 eV) XAFS spectra (3–4 replicates per sample) were recorded at room temperature under a continuous flow of Ar. Ge(422) crystals were used in the double crystal monochromator, Lemonnier-type operating in fixed-exit mode. The monochromatic beam is focused by a toroidal mirror, delivering a beam spot-size of ∼500 × 300 μm2 at the sample position at a photon energy of 18 keV. The parallel alignment of the crystal faces was detuned to ≈70% of the maximum beam intensity at the beginning of each scan. The incident intensity was held constant by means of a piezo-driven feedback system to the second crystal. The intensity of the incoming beam (I0) was monitored using an Ar filled ionization chamber at ambient pressure. Spectra were recorded in fluorescence mode using a five pixel LEGe solid state detector (Canberra, Belgium). Tc spectra were energy-calibrated with respect to the first inflection point in the XANES spectra of a Mo metal foil (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 eV), which was measured simultaneously in transmission geometry.
000 eV), which was measured simultaneously in transmission geometry.
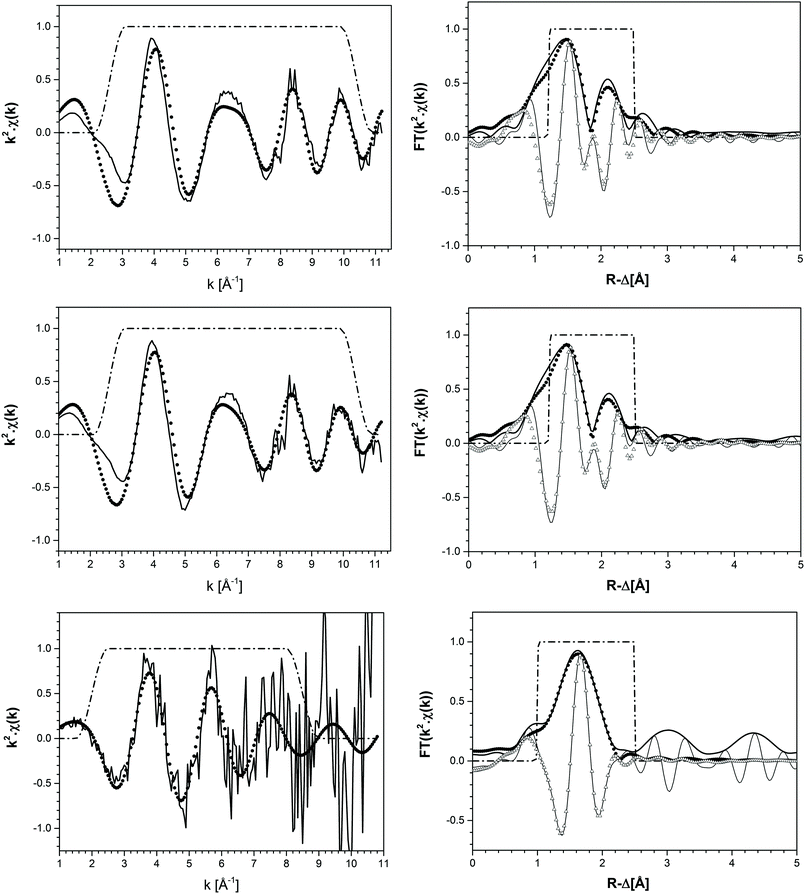
XANES/EXAFS data reduction and analysis were performed with the ATHENA/ARTEMIS package following standard procedures.27 Structural information was obtained following a multi-shell step-wise approach for the EXAFS data fitting. The fit included the neighbouring atomic distances (R), EXAFS Debye–Waller factors (σ2), coordination numbers (CN) and relative shift in ionization energy E0 (ΔE0). EXAFS spectra were Fourier transformed (FT) in the k-range between 2.6–10.4 Å−1 and 2.0–8.5 Å−1 using Hanning windows for solid and aqueous phases, respectively. The fit was performed in R-space (1.2–2.5 Å) using paths files calculated with Feff8.4 based on the TcO2 crystal structure reported in the ICSD database with record number 17–3151. The coordination number of O-shells was allowed to vary in the fit, whereas Tc- and Cl-shells were constrained to 1 and 1.4, respectively. The value of 1.4 for Cl in the fit of aqueous phases was obtained in a preliminary fit where CN(Cl) was defined such that the total CN(O) + CN(Cl) for the first coordination shell was equal to 6. The overall amplitude factor S02 was set to 0.75 to obtain a good match with the coordination number of ∼6 in the solid and reference samples.
2.5 Quantum chemical calculations
The stability of the complexes [TcO(OH)5]3− and Can[TcO(OH)5]2n−3 (n = 1–3) in gas and aqueous phases was investigated by quantum chemical calculations using a combination of multi reference ab initio methods and density functional theory (DFT). Only multi reference ab initio calculations on TcO (ref. 28) and density functional theory (DFT) calculations on TcO2+ (ref. 29) have been previously reported in the literature, whereas no accurate high-level multireference ab initio calculations on TcO2+ are available to date. Provided that TcO2+ is at the core of these complexes, the lack of these calculations prevents a theoretically sound characterization of the lowest electronic state. Consequently, we performed pilot studies on TcO2+ with high-level multireference Complete Active Space Self Consistent Field (CASSCF) and Multi Reference Configuration Interaction (MRCI) calculations to identify the electronic configuration of the ground states of these species.30 This is a very important pre-requisite for the theoretically sound application of DFT, which is restricted to single reference states. Calculations were first performed in the gas phase, and then extended to a simulated aqueous system consisting of a water cluster with 100 water molecules. This cluster was previously described by Müller et al. and Lenz and Ojamäa.31–333 Results and discussion
3.1 Solubility of Tc(IV) in dilute to concentrated NaCl solutions
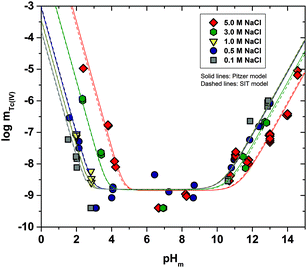
Fig. 1 shows the experimental solubility data obtained in the present work in dilute to concentrated NaCl systems, compared with solubility data previously reported in the literature (Meyer et al., 1991;5 Eriksen et al., 1992;6 Hess et al., 2004;7 Warwick et al., 20079). In the acidic pH region, experimental data in 0.1 M NaCl agree well with the previous solubility data in dilute systems reported by Meyer et al. (1991).5 The solubility of Tc(IV) within 2.5 ≤ pHm ≤ 4 increases up to 3 orders of magnitude with increasing ionic strength. This trend qualitatively agrees with previous experiments reported by Hess et al. (2004)7 (see also Fig. 1). Strong kinetics are observed for the sample at pHm ≈ 2 in 5.0 M NaCl, for which equilibrium is not attained even after 520 days of contact time. Note that slow kinetics were also observed by Hess and co-workers in their solubility experiments, in spite of considering significantly shorter equilibration times (≤61 days).All investigated NaCl systems follow a well-defined slope of −2 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mTc(IV)vs. pHm, dashed lines in Fig. 1) within the pHm-range 1.5 to 4, which indicates that 2 H+ are consumed in the chemical reaction controlling the solubility of Tc(IV) in this pH region. This observation agrees very well with the slope analysis in the study of Meyer et al.,5 whereas it is in disagreement with the slope of −1 proposed by Hess et al.7 Note that Hess and co-workers disregarded their solubility data at longer equilibration times for the slope analysis (and thus for the definition of their chemical model), which was mostly based on solubility data gained after 11 days of equilibration time. Provided the strong kinetics observed (both in the present work and in Hess et al.) for the solubility equilibria under acidic conditions, we consider that the interpretation by the latter authors is not representing the thermodynamic equilibrium under these conditions (see Fig. A1 in the ESI†).
mTc(IV)vs. pHm, dashed lines in Fig. 1) within the pHm-range 1.5 to 4, which indicates that 2 H+ are consumed in the chemical reaction controlling the solubility of Tc(IV) in this pH region. This observation agrees very well with the slope analysis in the study of Meyer et al.,5 whereas it is in disagreement with the slope of −1 proposed by Hess et al.7 Note that Hess and co-workers disregarded their solubility data at longer equilibration times for the slope analysis (and thus for the definition of their chemical model), which was mostly based on solubility data gained after 11 days of equilibration time. Provided the strong kinetics observed (both in the present work and in Hess et al.) for the solubility equilibria under acidic conditions, we consider that the interpretation by the latter authors is not representing the thermodynamic equilibrium under these conditions (see Fig. A1 in the ESI†).
At 4 ≤ pHm ≤ 9, a pH-independent solubility behaviour is observed in dilute to concentrated NaCl solutions, indicating that no H+ are exchanged in the chemical reaction controlling the solubility of Tc(IV) in this pH-region. The concentration of Tc is not affected by ionic strength either, and thus data in 0.1 M and 5.0 M NaCl show similar solubility. A very large scattering in mTc (1–1.5 log-units) is observed in this pH region. This behaviour is likely related with the very low solubility (close to the detection limit of LSC) and the expected predominance of neutral species in solution, which are prone to form oligomeric species and strongly sorb on surfaces (filters, vessel walls, solid phases, etc.). A similar behaviour was previously reported for An(III)/Ln(III) and An(IV).22,34 Meyer and co-workers reported very similar observations, i.e. pH- and ionic strength independent behaviour and large scattering of the solubility data. Although not discussed in the original publication, we hypothesize that the very stable Tc concentrations measured by Eriksen et al. (1992)6 within 6 ≤ pH ≤ 10 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mTc = –8.2) likely correspond to the detection limit of their quantification method.
mTc = –8.2) likely correspond to the detection limit of their quantification method.
The solubility of Tc(IV) increases with a well-defined slope of +1 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mTc(IV)vs. pHm) at pHm ≥ 11. Although the same slope is retained, the solubility decreases almost one order of magnitude when increasing the ionic strength from 0.1 to 5.0 M NaCl. Note that a similar trend with increasing ionic strength was reported for the solubility of Zr(IV) under alkaline to hyperalkaline pH conditions,21 where anionic hydrolysis species are dominant in solution. The solubility data and slope determined in this work in 0.1 M NaCl are consistent with the results reported by Eriksen et al. (1992).6 Significantly lower Tc(IV) solubility was observed by Warwick et al. (2007)9 within 12 ≤ pH ≤ 14. Unfortunately, the authors did not properly characterize the solid phase controlling the solubility. Although a solubility-control by a more crystalline Tc(IV) solid phase can be hypothesized, a direct comparison with the solubility data gained in this work is not feasible.
mTc(IV)vs. pHm) at pHm ≥ 11. Although the same slope is retained, the solubility decreases almost one order of magnitude when increasing the ionic strength from 0.1 to 5.0 M NaCl. Note that a similar trend with increasing ionic strength was reported for the solubility of Zr(IV) under alkaline to hyperalkaline pH conditions,21 where anionic hydrolysis species are dominant in solution. The solubility data and slope determined in this work in 0.1 M NaCl are consistent with the results reported by Eriksen et al. (1992).6 Significantly lower Tc(IV) solubility was observed by Warwick et al. (2007)9 within 12 ≤ pH ≤ 14. Unfortunately, the authors did not properly characterize the solid phase controlling the solubility. Although a solubility-control by a more crystalline Tc(IV) solid phase can be hypothesized, a direct comparison with the solubility data gained in this work is not feasible.
3.2 Solubility data of Tc(IV) in dilute to concentrated MgCl2 solutions
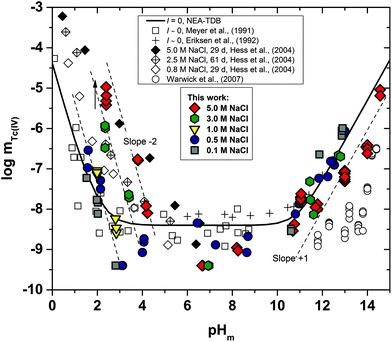
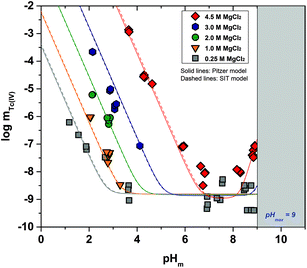
Fig. 2 shows the experimental solubility data obtained in the present work in dilute to concentrated MgCl2 systems. The solubility of Tc(IV) in the acidic pH region is nearly identical to the solubility data obtained in NaCl solutions with similar ionic strength, indicating that the same chemical reaction likely controls the solubility in both systems. Within the same pH-region, the solubility of Tc(IV) is significantly increased (up to 5 orders of magnitude) with the increasing MgCl2 concentration. This observation reflects very strong ion interaction processes taking place between cationic Tc(IV) hydrolysis species and Cl−, although the possible formation of new aqueous species must also be considered. The solubility curve becomes pH-independent in 4.5 M MgCl2 solutions with pHm ≤ 2 (dotted lines in Fig. 2). A similar behaviour was reported by Hess et al. (2004)7 at pHm ≤ 0.1 and pHm ≤ 0.75 in pure HCl and 5.0 M HCl–NaCl systems, respectively. Hess and co-workers explained this observation considering a solid phase transformation from TcO2·xH2O(s) to TcCl4(s) and assuming the predominance of TcCl4(aq) in the aqueous phase. In the present work, the aqueous speciation of Tc in 4.5 M MgCl2 solutions with pHm ≤ 2 has been investigated by XAFS and is discussed in section 3.4.3. Slow kinetics are observed in solubility samples in contact with [MgCl2] ≥ 2 M, where equilibrium conditions (stable pHm and mTc readings) are only attained after 200 days. Considering mTc data collected at longer equilibration times, the solubility curves of all evaluated MgCl2 systems follow a very well-defined slope of −2 within the pHm-range 2 to 6 (depending upon salt concentration). This is in excellent agreement with the solubility data obtained in the present work in NaCl systems and indicates that 2H+ are consumed in the chemical reaction controlling the solubility in this pH region.The solubility of Tc(IV) shows a pH-independent behaviour at 4 ≤ pHm ≤ 9 in 0.25 M MgCl2, in analogy with the NaCl systems. The pH-independent region is significantly smaller in 4.5 M MgCl2 (7 ≤ pHm ≤ 8), mainly due to the very relevant increase in the solubility under acidic pH conditions, but also because of a likely change in the aqueous speciation above pHm ≈ 8. As in the case of NaCl systems, the solubility of Tc(IV) in this pH region scatters within −8.2 ≥ log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mTc ≥ −9.4.
mTc ≥ −9.4.
A steep increase in the Tc(IV) solubility is observed in 4.5 M MgCl2 solutions with pHm ≈ 8. This behaviour differs from the findings gained in the NaCl systems, where the formation of anionic Tc(IV) hydrolysis species (and consequent increase of the solubility) takes only place at pHm ≈ 11. Similar observations were previously reported for Zr(IV) and An(IV) in concentrated alkaline CaCl2 solutions.21,35,36 Based on the collected spectroscopic evidence (EXAFS) and model calculations, the solubility behaviour of Zr(IV) and An(IV) under these conditions was explained with the formation of ternary Ca–Zr(IV)/An(IV)–OH aqueous species. The predominance of analogous Mg–Tc(IV)–OH aqueous species is accordingly suspected in concentrated alkaline MgCl2 solutions, in spite of the limitations in pHm posed by the precipitation of Mg–OH–Cl(s) (pHmax ≈ 9). In order to gain more conclusive insights into the aqueous chemistry of Tc(IV) in concentrated alkaline MCl2 (M = Mg2+, Ca2+) systems, the solubility of Tc(IV) was further investigated in dilute to concentrated alkaline CaCl2 solutions and is discussed in the following section.
3.3 Solubility data of Tc(IV) in dilute to concentrated CaCl2 solutions
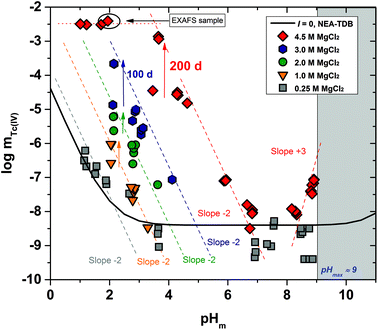
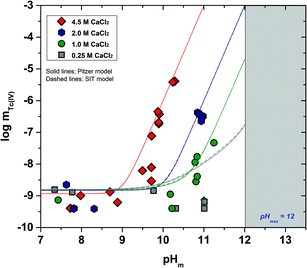
The experimental solubility data obtained in CaCl2 solutions within 7 ≤ pHm ≤ 12 are shown in Fig. 3. The solubility of Tc(IV) in 0.25 M CaCl2 follows a pH-independent behaviour up to pHm ≈ 11. A very steep but slow increase in solubility is observed in more concentrated CaCl2 systems. Hence, the solubility of Tc(IV) in 4.5 M CaCl2 increases 3 orders of magnitude within 9.5 ≤ pHm ≤ 10.5 following a well-defined slope of +3 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mTc(IV)vs. pHm, dashed line in Fig. 3). For this system, equilibrium conditions are not attained above pHm ≈ 10.5 even after 325 days. The very steep increase in solubility cannot be explained with the formation of TcO(OH)3− as described for NaCl systems, but rather points to the predominance of higher hydrolysis species strongly interacting with Ca2+ ions. In this context, the possible formation of ternary Ca–Tc(IV)–OH aqueous complexes is discussed in section 4 in combination with the outcome of DFT calculations summarized in section 3.4.4. The possible formation of ternary Ca–Tc(IV)–OH solid phases in concentrated hyperalkaline CaCl2 systems was assessed by EXAFS and is discussed in section 3.4.3.
mTc(IV)vs. pHm, dashed line in Fig. 3). For this system, equilibrium conditions are not attained above pHm ≈ 10.5 even after 325 days. The very steep increase in solubility cannot be explained with the formation of TcO(OH)3− as described for NaCl systems, but rather points to the predominance of higher hydrolysis species strongly interacting with Ca2+ ions. In this context, the possible formation of ternary Ca–Tc(IV)–OH aqueous complexes is discussed in section 4 in combination with the outcome of DFT calculations summarized in section 3.4.4. The possible formation of ternary Ca–Tc(IV)–OH solid phases in concentrated hyperalkaline CaCl2 systems was assessed by EXAFS and is discussed in section 3.4.3.
3.4 Tc aqueous and solid phase characterization
| Background electrolyte | Reducing system | pHm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
E
h![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b (mV) b (mV) |
%Tc(IV)c |
|---|---|---|---|---|
| a ± 0.05. b ± 50 mV. c ± 10%; n.m. = not measured. d Same sample also investigated by XAFS. | ||||
| 0.5 M NaCl | Na2S2O4 | 12.4 | −670 | 99 |
| 5.0 M NaCl | Sn(II) | 2.5 | 80 | 99 |
| 5.0 M NaCl | Na2S2O4 | 13.0 | −540 | 98 |
| 5.0 M NaCl | Na2S2O4 | 14.0 | −580 | 98 |
| 4.5 M MgCl2 | Sn(II) | 2.0 | n.m. | 13d |
| 4.5 M MgCl2 | Sn(II) | 4.0 | −50 | 52 |
| 4.5 M MgCl2 | Fe Powder | 8.9 | −170 | 91 |
| 4.5 M MgCl2 | Sn(II) | 9.0 | −175 | 94 |
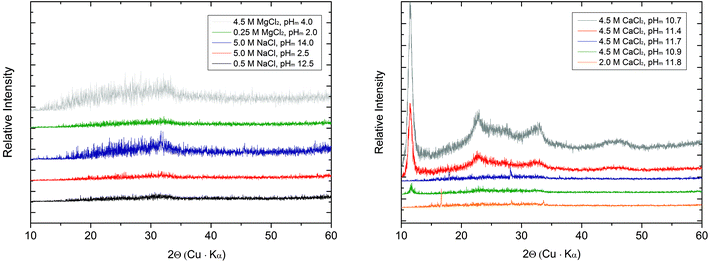 | ||
| Fig. 4 XRD patterns collected for Tc solid phases equilibrated in dilute to concentrated NaCl and MgCl2 solutions (left), and concentrated CaCl2 solutions (right). | ||
| Background electrolyte | Reducing system | pHm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
XRD | Chemical analysis |
|---|---|---|---|---|
Na![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tc Tc |
||||
| a ± 0.05, n.m. = not measured. b pH = pHmax, presence of Mg–OH–Cl(s) expected. c pH = pHmax, presence of Ca–OH–Cl(s) expected. | ||||
| 0.5 M NaCl | Na2S2O4 | 12.4 | am | <0.01 |
| 5.0 M NaCl | Sn(II) | 2.5 | am | <0.01 |
| 5.0 M NaCl | Na2S2O4 | 13.0 | n.m. | <0.01 |
| 5.0 M NaCl | Na2S2O4 | 14.0 | am | <0.01 |
Mg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tc Tc |
||||
| 0.25 M MgCl2 | Sn(II) | 2.0 | am | <0.01 |
| 4.5 M MgCl2 | Sn(II) | 4.0 | am | <0.01 |
| 4.5 M MgCl2 | Fe Powder | 8.9 | n.m. | 25.0b |
| 4.5 M MgCl2 | Sn(II) | 9.0 | n.m. | 0.3b |
Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tc Tc |
||||
| 2.0 M CaCl2 | Na2S2O4 | 11.8 | am | n.m. |
| 4.5 M CaCl2 | Sn(II) | 10.9 | am, (11.6, 23, 33) | 2.7c |
| 4.5 M CaCl2 | Na2S2O4 | 11.7 | am | 1.6c |
| 4.5 M CaCl2 | Sn(II) | 11.4 | am, (11.6, 23, 33) | n.m. |
| 4.5 M CaCl2 | Sn(II) | 10.7 | am, (11.6, 23, 33) | n.m. |
The SEM images (Fig. 5 and 6) of all investigated samples show the predominance of amorphous Tc aggregates, in good agreement with the observed absence of well-defined XRD patterns. The particle size of these aggregates varies between 50 and 80 nm. Quantitative chemical analyses (Table 3) show the absence of Na in the Tc solid phases controlling the solubility in NaCl systems, even for those phases equilibrated in 5.0 M NaCl solutions. Similarly, no Mg is detected in solid phases controlling the solubility under acidic conditions in 4.5 M MgCl2, whereas very high Mg content is quantified in alkaline samples with pHm ≈ pHmax. SEM images of the later samples confirm the presence of needle-like precipitates of Mg–OH–Cl(s) (Fig. 5, right). Similar observations are gained for Tc solid phases equilibrated in CaCl2 solutions with pHm ≈ pHmax, for which SEM pictures indicate the presence of Ca(OH)2(s) and/or Ca–OH–Cl(s) phases (Fig. 6). The absence of Na, Mg, or Ca in the Tc solid phases (except those at pHm ≈ pHmax) controlling the solubility in NaCl, MgCl2 and CaCl2 systems, in combination with the amorphous character of the solid confirmed by XRD and SEM, strongly points towards a solubility-control exerted by TcO2·xH2O(s).
TG–DTA analyses indicate a mass loss of 5–11% in the investigated solid phases, corresponding to x = 0.4–0.8 in TcO2·xH2O(s). These results highlight the similar hydration degree of the Tc(IV) solid phase in the different background electrolytes and salt concentrations considered in this study. The unweighted mean value of the number of hydration waters x = 0.6 ± 0.3 is considered in the following in the definition of the Tc(IV) solid phase used in this study: TcO2·0.6H2O(s). Note that a very discrepant number of hydration waters was previously reported by Meyer and co-workers,5 who measured x = 0.44–4.22 and 1.38–1.81 for solid phases obtained from acidic and alkaline deposition, respectively. Although the number of hydration waters has a minor influence on solubility phenomena and calculations in dilute systems, it becomes relevant in concentrated brines where water activities significantly lower than 1 arise (e.g. aw = 0.5083 in 4.0 M MgCl2).18
k 2-weighted Tc K-edge EXAFS spectra and corresponding Fourier transforms are shown in Fig. 8. Structural parameters of all investigated samples resulting from the fit of the EXAFS spectra are summarized in Table 4. The EXAFS fit of the original TcO2·0.6H2O(s) material shows an O-shell at 2.07 Å with a coordination number (CN) of 6.7, and a Tc-shell at 2.59 Å with CN = 1. These results are in excellent agreement with structural parameters reported in the literature for TcO2·xH2O(s).7 Similar structural parameters are obtained from the fit to EXAFS data of the Tc(IV) solid phase equilibrated in 4.5 M CaCl2 at pHm = 11.4. This observation indicates that no solid phase transformation occurred within the 325 days of equilibration time, and that TcO2·0.6H2O(s) remains as the solubility-controlling phase under these conditions. Hence, Tc(IV) solubility data obtained in [CaCl2] ≥ 2.0 M at pHm ≈ pHmax are not representative of a thermodynamic equilibrium and can only be explained by the very slow kinetics in the presence of Ca(OH)2(s) or Ca–OH–Cl(s) phases or eventually a solubility control by an unidentified surface “coating”.
| Sample | Path | CN | R (Å) | σ 2 (Å2) | ΔE0 (eV) | R-factor |
|---|---|---|---|---|---|---|
| Fit errors: CN: ± 20%, R: 0.01 Å, σ2: 0.001 Å2.a Held constant during the fit. | ||||||
| Original TcO2·0.6H2O(s) material | Tc–O | 6.7 | 2.07 | 0.010 | −5.146 | 0.002 |
| R-Space [1.2–2.5 Å] | Tc–Tc | 1.0a | 2.59 | 0.002 | ||
| k-Range [2.6–10.4 Å−1] | ||||||
| Tc(IV) solid phase in 4.5 M CaCl2 at pHm = 11.4 | Tc–O | 6.4 | 2.07 | 0.009 | −5.635 | 0.015 |
| R-Space [1.2–2.5 Å] | Tc–Tc | 1.0a | 2.59 | 0.003 | ||
| k-Range [2.6–10.4 Å−1] | ||||||
| Tc(IV)(aq) in 4.5 M MgCl2 at pHm = 2 | Tc–O | 3.5 | 2.21 | 0.002 | 0.842 | 0.010 |
| R-Space [1.0–2.5 Å] | Tc–Cl | 1.4a | 2.53 | 0.007 | ||
| k-Range [2.0–8.5 Å−1] | ||||||
The EXAFS fit of the supernatant solution in the solubility sample equilibrated in 4.5 M MgCl2 at pHm = 2 unequivocally shows the co-existence of O- (CN = 3.5, R = 2.21 Å) and Cl- (CN = 1.4, R = 2.53 Å) backscatterers in the first coordination sphere of Tc. The substitution of Tc–Cl by Tc–O interactions significantly worsens the fit. The addition of a Tc–Tc contribution at R = 2.77 Å decreased the residual of the fit (%R), although this farther shell was disregarded in the final model due to the limited k-range considered in the fit (2.0 ≤ k [Å−1] ≤ 8.5). These observations hint towards the possible formation of Tc(IV)–O/OH–Cl oligomers in acidic concentrated MgCl2 solutions. Note that Poineau and co-workers16 reported the predominance of the Tc2OCl104− species at pH = 0.3 and [Cl−] = 3.0 M. The structural parameters determined for this species by EXAFS for Tc–O (CN = 1.2, R = 1.79 Å) and Tc–Cl (CN = 4.7, R = 2.36 Å) interactions are significantly different compared to those determined in the present study, suggesting the predominance of a different aqueous species at pHm = 2.0 and [Cl−] = 9.0 M (present work). The formation of Tc(IV) – chloride species in acidic concentrated MgCl2 solutions is in line with the results obtained by liquid–liquid extraction. Hence, the solvent extraction method used in the present work has been reported to extract into the organic phase not only MO4− species, but also anionic chloride complexes.39
Tc(IV) solubility data obtained in concentrated CaCl2 solutions hint towards the formation of the previously unreported [TcO(OH)5]3− moiety in the aqueous phase, considering the slope of +3 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mTcvs. pHm) and the solubility control by TcO2·0.6H2O(s). In the absence of Ca in the background electrolyte (e.g. NaCl or KCl systems), TcO(OH)3− is the only anionic hydrolysis species forming under hyperalkaline pH conditions (see section 3.1 and references therein). As previously described for Zr(IV) and An(IV) (An = Th, Np, Pu), the formation of highly charged anionic hydrolysis species in concentrated alkaline CaCl2 solutions is stabilized by the contribution of Ca2+ in the second coordination sphere of the tetravalent cation.21,35,36 The number of Ca2+ ions participating in the complex formation was inferred from model calculations and EXAFS spectroscopy for Zr(IV) and Th(IV), and was based on the analogy with Th(IV) in the case of Np(IV) and Pu(IV). In this work, the stability of the Can[TcO(OH)5]2n−3 species (n = 1–3) was evaluated by large-scale DFT calculations. In order to understand the role of Ca2+ in the stabilization of the highly charged [TcO(OH)5]3− moiety, the stability of the latter in the absence of Ca2+ ions was also investigated.
mTcvs. pHm) and the solubility control by TcO2·0.6H2O(s). In the absence of Ca in the background electrolyte (e.g. NaCl or KCl systems), TcO(OH)3− is the only anionic hydrolysis species forming under hyperalkaline pH conditions (see section 3.1 and references therein). As previously described for Zr(IV) and An(IV) (An = Th, Np, Pu), the formation of highly charged anionic hydrolysis species in concentrated alkaline CaCl2 solutions is stabilized by the contribution of Ca2+ in the second coordination sphere of the tetravalent cation.21,35,36 The number of Ca2+ ions participating in the complex formation was inferred from model calculations and EXAFS spectroscopy for Zr(IV) and Th(IV), and was based on the analogy with Th(IV) in the case of Np(IV) and Pu(IV). In this work, the stability of the Can[TcO(OH)5]2n−3 species (n = 1–3) was evaluated by large-scale DFT calculations. In order to understand the role of Ca2+ in the stabilization of the highly charged [TcO(OH)5]3− moiety, the stability of the latter in the absence of Ca2+ ions was also investigated.
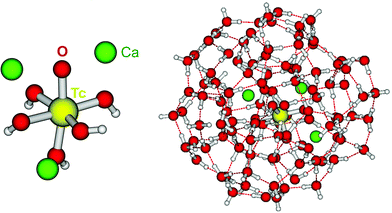
DFT calculations show that only the Ca3[TcO(OH)5]3+ species is stable both in the gas phase and enwrapped by one hundred water molecules (Fig. 9). In contrast, the Ca[TcO(OH)5]−, Ca2[TcO(OH)5]+ and [TcO(OH)5]3− species break apart both in the gas and aqueous phases, mostly due to the insufficient or inexistent charge compensation of the [TcO(OH)5]3− moiety. Tc(IV)–Ca distances optimized by DFT for the Ca3[TcO(OH)5]3+ species enwrapped by one hundred water molecules (RTc–Ca1 = 3.01 Å, RTc–Ca2 = 3.11 Å, RTc–Ca3 = 3.33 Å; average RTc–Ca = 3.15 Å) are in line with distances determined by EXAFS for Zr(IV)–Ca (R = 3.38 ± 0.02 Å) and Th(IV)–Ca (R = 3.98 ± 0.02 Å) in Ca3[Zr(OH)6]4+ and Ca4[Th(OH)8]4+, respectively.‡,40 The outcome of these theoretical calculations supports the predominance of the Ca3[TcO(OH)5]3+ species in concentrated CaCl2 systems, which otherwise cannot be assessed by spectroscopic means. The quantum chemical and DFT studies performed will be presented in more detail in a separate manuscript by R. Polly et al. currently under preparation.
4 Tc(IV) chemical, thermodynamic and activity models
Chemical models describing the aquatic chemistry and relevant equilibrium reactions of Tc(IV) in dilute to concentrated NaCl, MgCl2 and CaCl2 are evaluated in this section based on (i) the slope analyses (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mTcvs. pHm) of experimental solubility data determined in this work, (ii) detailed solid phase characterization and identification of solubility controlling compounds, (iii) spectroscopic (XANES, EXAFS) evidence gained in this work and previously reported in the literature, and (iv) the new structural information obtained by DFT calculations. After deriving the chemical model and defining the relevant equilibrium reactions for a given system, conditional solubility constants (log
mTcvs. pHm) of experimental solubility data determined in this work, (ii) detailed solid phase characterization and identification of solubility controlling compounds, (iii) spectroscopic (XANES, EXAFS) evidence gained in this work and previously reported in the literature, and (iv) the new structural information obtained by DFT calculations. After deriving the chemical model and defining the relevant equilibrium reactions for a given system, conditional solubility constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s) are determined for each investigated ionic strength, and extrapolated to I = 0 using both SIT and Pitzer activity models. SIT and Pitzer ion interaction coefficients are gained in the process of extrapolation conditional data to I = 0. Calculation of uncertainties throughout the complete process is based on the NEA guidelines for the assignment of uncertainties.41
K′s) are determined for each investigated ionic strength, and extrapolated to I = 0 using both SIT and Pitzer activity models. SIT and Pitzer ion interaction coefficients are gained in the process of extrapolation conditional data to I = 0. Calculation of uncertainties throughout the complete process is based on the NEA guidelines for the assignment of uncertainties.41
4.1 Acidic pH conditions (pHm ≤ 4)
Independent of the background electrolyte, the solubility of Tc(IV) in the acidic pH region systematically increases with increasing ionic strength. The increase of the solubility is very similar in NaCl and MgCl2 solutions of analogous ionic strength. The slope (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mTcvs. pHm) of −2 defined by solubility data under acidic conditions with 0.1 M ≤ I ≤ 13.5 M indicates that 2H+ are consumed in the chemical reaction controlling the solubility of Tc in this pH region. The combination of solvent extraction and XANES analysis confirms that no oxidation of Tc(IV) occurred in the aqueous or solid phases during the timeframe of the study. A pH-independent solubility behaviour is observed in 4.5 M MgCl2 systems with pHm ≤ 3.5. EXAFS characterization of the aqueous phase under these mCl− and pHm conditions confirms the presence of Cl-atoms in the first coordination sphere of Tc, thus supporting the formation of Tc(IV) chloro-complexes (see section 3.4.3). Although the equilibrium Tc(IV)−O/OH−Cl(s) ⇔ Tc(IV)−O/OH−Cl(aq) is suspected to control the aqueous chemistry of Tc(IV) under these conditions (see also discussion in Hess et al., 20047), solubility data determined in 4.5 M MgCl2 and pHm ≤ 2 have been disregarded in the chemical and thermodynamic models derived in this section and are omitted in the following discussion.
mTcvs. pHm) of −2 defined by solubility data under acidic conditions with 0.1 M ≤ I ≤ 13.5 M indicates that 2H+ are consumed in the chemical reaction controlling the solubility of Tc in this pH region. The combination of solvent extraction and XANES analysis confirms that no oxidation of Tc(IV) occurred in the aqueous or solid phases during the timeframe of the study. A pH-independent solubility behaviour is observed in 4.5 M MgCl2 systems with pHm ≤ 3.5. EXAFS characterization of the aqueous phase under these mCl− and pHm conditions confirms the presence of Cl-atoms in the first coordination sphere of Tc, thus supporting the formation of Tc(IV) chloro-complexes (see section 3.4.3). Although the equilibrium Tc(IV)−O/OH−Cl(s) ⇔ Tc(IV)−O/OH−Cl(aq) is suspected to control the aqueous chemistry of Tc(IV) under these conditions (see also discussion in Hess et al., 20047), solubility data determined in 4.5 M MgCl2 and pHm ≤ 2 have been disregarded in the chemical and thermodynamic models derived in this section and are omitted in the following discussion.
Provided the solubility-control exerted by TcO2·0.6H2O(s) (see sections 3.4.2 and 3.4.3), the slope of −2 defined by solubility data in acidic dilute to concentrated NaCl and MgCl2 solutions is consistent with the predominance of the TcnOm(OH)2+(2–4n+2m) species in the aqueous phase. Although NEA–TDB (consistently with previous publications) defined the formation of the TcO2+ species in this pH region, more recent spectroscopic studies strongly hint towards the predominance of cationic polynuclear Tc(IV) species.12–16 Based on the analogy with Mo(IV) and the proven formation of the cluster Mo3O4·9H2O4+, Vichot and co-workers13 proposed the formation of the trimeric Tc3O44+ species at pH ≤ 3. The predominance of trimeric Zr(IV) species was also favoured by Altmaier et al. (2008) to explain the solubility behaviour of Zr(OH)4(s) under acidic pH conditions.21 In view of the available experimental evidence and in analogy with Mo(IV) and Zr(IV), the predominance of the trimeric Tc3O52+ species in the acidic pH region is proposed in the present work. Note that the formation/predominance of other polyatomic species such as Tc2O32+ or Tc4O72+ is also consistent with the available solubility data and spectroscopic evidence, but has been disregarded in the chemical model derived in this work. The formation of the TcO(OH)+ species is not needed to properly explain the experimentally determined solubility data, and has been also disregarded in the chemical model considered in this work. The predominance of the latter species under acidic conditions was claimed by Hess and co-workers,7 but the large stability field proposed by the authors for TcO(OH)+ is ruled out in the present work due to the relevant experimental shortcomings discussed in section 3.1.
Besides the formation of Tc3O52+, the very large increase in solubility (>5 orders of magnitude!) between solubility data in dilute and concentrated chloride media may hint towards the formation of Tc(IV)–O/OH–Cl aqueous complexes in concentrated chloride solutions also beyond pHm > 4. Previous spectroscopic studies16 confirmed the predominance of the TcCl5(H2O)− and Tc2OCl104− species in 3.0 M NaCl solutions with pH < 1.1. Above this pH, the authors proposed the predominance of a polyatomic oxo-cation TcnO4n−2yy. In the present work, the formation of Tc(IV)–O/OH–Cl aqueous complexes in 4.5 M MgCl2 solutions with pHm ≤ 4 is also hinted by EXAFS. Besides this spectroscopic evidence, Tc(IV) solubility data follows a well-defined slope of −2 both in dilute and concentrated chloride solutions, thus indicating that the number of H+ involved in the solubility reaction is the same in both cases. Provided the proposed predominance of the Tc3O52+ species under acidic conditions with low mCl−, the possible formation of Tc(IV) chloro-complexes of the type Tc3O5Cl(2−m)m with 1 ≤ m ≤ 4 was also considered in the development of the chemical model. Thus, chemical reactions (1) and (2) are taken into account for the assessment of Tc(IV) solubility under acidic conditions:
| TcO2·0.6H2O(s) + 2/3 H+ ⇔ 1/3 Tc3O52+ + 0.93H2O(l) | (1) |
| TcO2·0.6H2O(s) + 2/3 H+ + m/3Cl− ⇔ 1/3 Tc3O5Cl(2−m)m + 0.93H2O(l) | (2) |
with
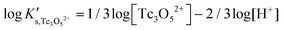 | (3) |
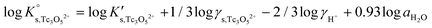 | (4) |
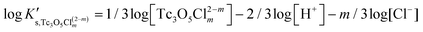 | (5) |
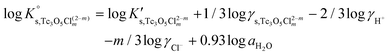 | (6) |
In the first step, different chemical models involving the formation of Tc3O52+ and Tc3O5Cl(2−m)m complexes were evaluated using the SIT approach. Then, the chemical model chosen was used to fit the corresponding conditional equilibrium constants with the Pitzer approach to derive 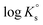 and ion interaction parameters.
and ion interaction parameters.
1. only the formation of Tc3O52+ was considered to explain Tc(IV) solubility data in dilute to concentrated NaCl and MgCl2 solutions.
2. Formation of both Tc3O52+ and Tc3O5Cl(2−m)m with 1 ≤ m ≤ 4 was considered to explain Tc(IV) solubility data in dilute to concentrated NaCl and MgCl2 solutions:
a. Use of Tc(IV) solubility data at low ionic strength (0.1 M NaCl) and ε(Tc3O52+, Cl−) = (0.15 ± 0.1) kg mol−1 estimated according to charge analogies42 to determine 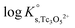 . Solubility data not explained by the contribution of this species are then fitted assuming the formation of Tc3O5Cl(2−m)m. Four independent models (including the formation of Tc(IV) chloro-complexes with 1 ≤ m ≤ 4) are evaluated.
. Solubility data not explained by the contribution of this species are then fitted assuming the formation of Tc3O5Cl(2−m)m. Four independent models (including the formation of Tc(IV) chloro-complexes with 1 ≤ m ≤ 4) are evaluated.
b. Use of Tc(IV) solubility data at [Cl−] ≤ 3.0 M to determine 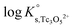 and ε(Tc3O52+, Cl−), and data at [Cl−] > 3.0 M to determine
and ε(Tc3O52+, Cl−), and data at [Cl−] > 3.0 M to determine 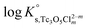 and ε(Tc3O5Cl(2−m)m,Na+/Cl−).
and ε(Tc3O5Cl(2−m)m,Na+/Cl−).
Approach 2a properly explains Tc(IV) solubility data in dilute to concentrated NaCl and MgCl2 solutions (data not shown). However, this approach suggests the predominance of Tc3O5Cl(2−m)m complexes at [Cl−] ≥ 0.5 M. This is in strong contradiction with previous spectroscopic observations, which confirmed the predominance of TcnO4n−2yy in NaCl systems with [Cl−] ≤ 3.0 M and pH > 1.1.
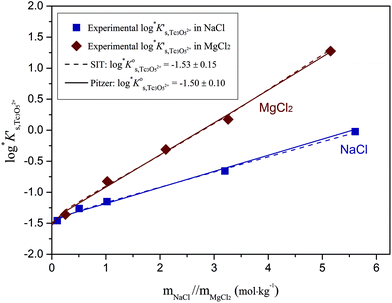
Approach 2b clearly overestimates the solubility of Tc(IV) (data not shown). Hence, 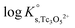 and ε(Tc3O52+, Cl−) derived from solubility data at [Cl−] ≤ 3.0 M are able to perfectly explain experimental observations gained up to [Cl−] = 9.0 M. Any additional contribution to the solubility provided by the definition of Tc3O5Cl(2−m)m species results in the overestimation of mTc(IV) in equilibrium with TcO2·0.6H2O(s). The outcome of approach 2b further indicates that the chemical model in approach 1 is the only one consistent with both solubility in dilute to concentrated NaCl and MgCl2 systems and spectroscopic observations available in the literature.12,17Fig. 10 shows the perfect agreement between the SIT-plots derived for NaCl and MgCl2 systems considering the only formation of Tc3O52+. This observation supports again that the same chemical model applies to dilute and concentrated chloride systems, and further that the formation of Tc(IV)–O/OH–Cl complexes can be disregarded under these pHm and mCl− conditions.
and ε(Tc3O52+, Cl−) derived from solubility data at [Cl−] ≤ 3.0 M are able to perfectly explain experimental observations gained up to [Cl−] = 9.0 M. Any additional contribution to the solubility provided by the definition of Tc3O5Cl(2−m)m species results in the overestimation of mTc(IV) in equilibrium with TcO2·0.6H2O(s). The outcome of approach 2b further indicates that the chemical model in approach 1 is the only one consistent with both solubility in dilute to concentrated NaCl and MgCl2 systems and spectroscopic observations available in the literature.12,17Fig. 10 shows the perfect agreement between the SIT-plots derived for NaCl and MgCl2 systems considering the only formation of Tc3O52+. This observation supports again that the same chemical model applies to dilute and concentrated chloride systems, and further that the formation of Tc(IV)–O/OH–Cl complexes can be disregarded under these pHm and mCl− conditions.
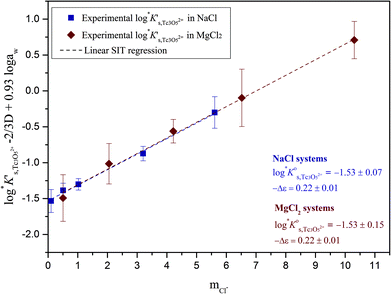 | ||
Fig. 10 SIT-plot for the solubility reaction TcO2·0.6H2O(s) + 2/3 H+ ⇔ 1/3 Tc3O52+ + 0.93H2O(l) considering experimental 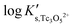 determined in dilute to concentrated NaCl and MgCl2 solutions. determined in dilute to concentrated NaCl and MgCl2 solutions. | ||
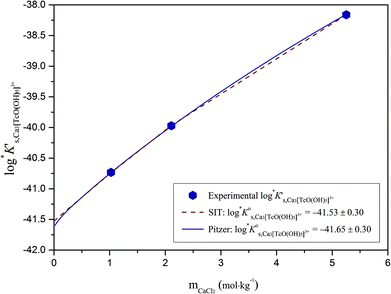
The y-intercept and slope determined by linear regression of the SIT-plots in Fig. 10 correspond to 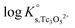 and −Δε (with −Δε = −1/3 ε(Tc3O52+, Cl−) + 2/3 ε(H+, Cl−)), respectively. The combination of −Δε and ε(H+, Cl−) reported in the NEA–TDB further allows the calculation of ε(Tc3O52+, Cl−). Excellent agreement is found between
and −Δε (with −Δε = −1/3 ε(Tc3O52+, Cl−) + 2/3 ε(H+, Cl−)), respectively. The combination of −Δε and ε(H+, Cl−) reported in the NEA–TDB further allows the calculation of ε(Tc3O52+, Cl−). Excellent agreement is found between 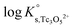 and ε(Tc3O52+, Cl−) derived from NaCl and MgCl2 systems. The final selection gained in this work is:
and ε(Tc3O52+, Cl−) derived from NaCl and MgCl2 systems. The final selection gained in this work is:
The SIT ion interaction coefficient determined for Tc3O52+ is much lower than that expected for a typical divalent cation according with charge-based correlations (ε(M2+, Cl−) = 0.15 ± 0.10 kg mol−1).42 However, the use of charge analogies for very large or oligomeric species must be considered with caution. The effect of size and the distribution of the formal charge throughout the voluminous species can lead to large deviations with respect to monomeric/simple species. Similar effects are observed for ternary Ca–M–OH complexes, as discussed in section 4.4.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γH+ and aw in eqn (4) are calculated from the parameters reported by Harvie et al.43 The binary parameter β(2) is only ≠0 for 2–2 electrolytes. The mixing parameters θ(Tc3O52+, Na+) and Ψ(Tc3O52+, Cl−, Na+) are set to zero.
γH+ and aw in eqn (4) are calculated from the parameters reported by Harvie et al.43 The binary parameter β(2) is only ≠0 for 2–2 electrolytes. The mixing parameters θ(Tc3O52+, Na+) and Ψ(Tc3O52+, Cl−, Na+) are set to zero. 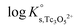 , β(0), β(1) and CΦ are fitted simultaneously for NaCl and MgCl2 systems by minimizing the difference between experimental and modelled log
, β(0), β(1) and CΦ are fitted simultaneously for NaCl and MgCl2 systems by minimizing the difference between experimental and modelled log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s,Tc3O52+ in both systems. The resulting values are:
K′s,Tc3O52+ in both systems. The resulting values are:
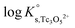 values derived using both SIT and Pitzer approaches are in excellent agreement. The value of β(0) resulting from the Pitzer fit is also in good agreement with the estimate calculated following the approach described by Grenthe et al.44 (β(0) = −0.32 kg mol−1).§
values derived using both SIT and Pitzer approaches are in excellent agreement. The value of β(0) resulting from the Pitzer fit is also in good agreement with the estimate calculated following the approach described by Grenthe et al.44 (β(0) = −0.32 kg mol−1).§
Fig. 11 compares the experimental and calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s,Tc3O52+ for NaCl and MgCl2 systems, using both SIT and Pitzer approaches. The figure clearly shows that both activity models describe very well experimentally determined log
K′s,Tc3O52+ for NaCl and MgCl2 systems, using both SIT and Pitzer approaches. The figure clearly shows that both activity models describe very well experimentally determined log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s,Tc3O52+ values in dilute to concentrated saline systems, confirming again the good performance of SIT well beyond Im > 3.5 m.
K′s,Tc3O52+ values in dilute to concentrated saline systems, confirming again the good performance of SIT well beyond Im > 3.5 m.
4.2 Weakly acidic to weakly alkaline pH conditions (4 ≤ pHm ≤ 8/11)
The solubility of Tc(IV) follows a pH-independent behaviour at 4 ≤ pHm ≤ 11 and 4 ≤ pHm ≤ 8 in NaCl and MgCl2 or CaCl2 systems, respectively. Provided a solubility-control by TcO2·0.6H2O(s), this observation indicates that a neutral hydrolysis species prevails in the aqueous phase within this pH range. Tc(IV) solubility shows no ionic strength dependency within this pH region, in good agreement with the behaviour expected for neutral species. Based on the available experimental evidence and consistently with the NEA–TDB18 selection, chemical reaction (7) is defined for the control of Tc(IV) solubility within this pH region.| TcO2·0.6H2O(s) + 0.4H2O(l) ⇔ TcO(OH)2(aq) | (7) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s,TcO(OH)2(aq) = log [TcO(OH)2(aq)] K′s,TcO(OH)2(aq) = log [TcO(OH)2(aq)] | (8) |
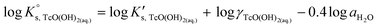 | (9) |
SIT and Pitzer ion interaction coefficients for the neutral TcO(OH)2(aq) species are considered equal to zero. Thus,  is calculated as the average mTc measured within 4 ≤ pHm ≤ 11, accounting also for the small contribution of water activity in eqn (9). The resulting value
is calculated as the average mTc measured within 4 ≤ pHm ≤ 11, accounting also for the small contribution of water activity in eqn (9). The resulting value 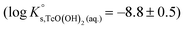 is slightly lower but agrees within the uncertainty with the current NEA–TDB selection
is slightly lower but agrees within the uncertainty with the current NEA–TDB selection 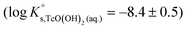 .
.
Note that the formation and predominance of polyatomic species of the type TcnOm(OH)4n–2m(aq) are also consistent with the available experimental evidence. Although the definition of the monomeric TcO(OH)2(aq) species is favoured in the present work in agreement with the NEA–TDB selection, a definitive proof-of-concept for the predominance of this species is still missing.
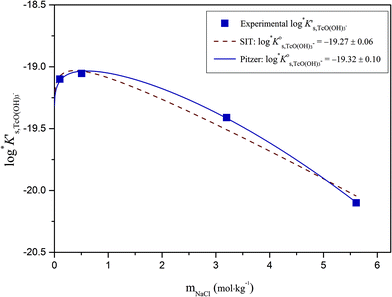
4.3 Alkaline pH conditions (pHm ≥ 11) in NaCl system
Solubility data of Tc(IV) in dilute to concentrated NaCl solutions with pHm ≥ 11 follow a well-defined slope of +1. Considering a solubility-control by TcO2·0.6H2O(s), this observation is properly explained by the predominance in the aqueous phase of the TcO(OH)3− species. This chemical model is consistent with the current NEA–TDB18 selection:| TcO2·0.6H2O(s) + 1.4H2O(l) ⇔ TcO(OH)3− + H+ | (10) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s,TcO(OH)3− = log[TcO(OH)3−] + log[H+] K′s,TcO(OH)3− = log[TcO(OH)3−] + log[H+] | (11) |
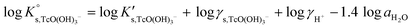 | (12) |
Conditional solubility constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s,TcO(OH)3−) are determined based on experimental solubility data in 0.1–5.0 M NaCl according to eqn (11). The use of eqn (12) allows the extrapolation of log
K′s,TcO(OH)3−) are determined based on experimental solubility data in 0.1–5.0 M NaCl according to eqn (11). The use of eqn (12) allows the extrapolation of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s,TcO(OH)3− to I = 0 and the determination of the corresponding SIT/Pitzer ion interaction parameters.
K′s,TcO(OH)3− to I = 0 and the determination of the corresponding SIT/Pitzer ion interaction parameters.
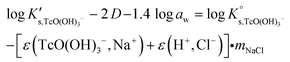 | (13) |
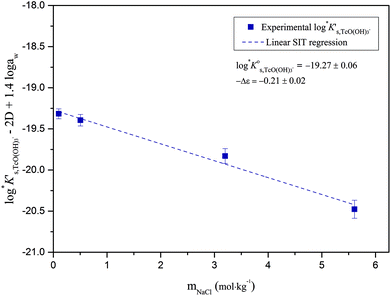
The linear regression (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s,TcO(OH)3− − 2D − 1.4log
K′s,TcO(OH)3− − 2D − 1.4log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aw) vs. mNaCl (SIT-plot) is shown in Fig. 12. The resulting solubility constant at I = 0,
aw) vs. mNaCl (SIT-plot) is shown in Fig. 12. The resulting solubility constant at I = 0, 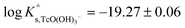 , is in excellent agreement with the current NEA–TDB selection
, is in excellent agreement with the current NEA–TDB selection 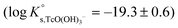 , and represents a very significant contribution in decreasing the associated uncertainty. The ion interaction coefficient ε(TcO(OH)3−, Na+) = (0.09 ± 0.02) kg mol−1 is calculated from the slope of the linear regression (−Δε = −ε(TcO(OH)3−, Na+) − ε(H+, Cl−) = (−0.21 ± 0.02) kg mol−1), considering ε(H+, Cl−) = (0.12 ± 0.01) kg mol−1 as reported by Guillaumont et al. (2003).18 This value is in moderate agreement with SIT ion interaction coefficients expected for a typical monovalent anion ε(X−, Na+) = −(0.05 ± 0.10) kg mol−1.42 Note that positive SIT ion interaction coefficients have been previously reported for anionic hydrolysis species of metal cations with similar ionic radii (e.g. Zr,21 Sn45).
, and represents a very significant contribution in decreasing the associated uncertainty. The ion interaction coefficient ε(TcO(OH)3−, Na+) = (0.09 ± 0.02) kg mol−1 is calculated from the slope of the linear regression (−Δε = −ε(TcO(OH)3−, Na+) − ε(H+, Cl−) = (−0.21 ± 0.02) kg mol−1), considering ε(H+, Cl−) = (0.12 ± 0.01) kg mol−1 as reported by Guillaumont et al. (2003).18 This value is in moderate agreement with SIT ion interaction coefficients expected for a typical monovalent anion ε(X−, Na+) = −(0.05 ± 0.10) kg mol−1.42 Note that positive SIT ion interaction coefficients have been previously reported for anionic hydrolysis species of metal cations with similar ionic radii (e.g. Zr,21 Sn45).
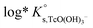 , β(0) and C(Φ) are fitted by minimizing the difference between experimental and modelled log
, β(0) and C(Φ) are fitted by minimizing the difference between experimental and modelled log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s,TcO(OH)3− in 0.1 M, 0.5 M, 3.0 M and 5.0 M NaCl systems, and resulted in:
K′s,TcO(OH)3− in 0.1 M, 0.5 M, 3.0 M and 5.0 M NaCl systems, and resulted in:Excellent agreement is obtained between 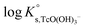 values determined using SIT and Pitzer approaches. The extrapolation of this value to higher ionic strengths using the Pitzer activity model derived in this work results in a very good agreement with experimental log
values determined using SIT and Pitzer approaches. The extrapolation of this value to higher ionic strengths using the Pitzer activity model derived in this work results in a very good agreement with experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s,TcO(OH)3− (Fig. 13). In the case of SIT, minor deviations (≈
K′s,TcO(OH)3− (Fig. 13). In the case of SIT, minor deviations (≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 log-units) appear between experimental and calculated log
0.1 log-units) appear between experimental and calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s,TcO(OH)3− at [NaCl] ≥ 3.0 M.
K′s,TcO(OH)3− at [NaCl] ≥ 3.0 M.
4.4 Alkaline pH conditions (pHm ≥ 8) in MgCl2 and CaCl2 systems
The solubility of Tc(IV) shows a steep increase with a slope of +3 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mTcvs. pHm) in concentrated MgCl2 and CaCl2 solutions with pHm ≥ 8 and solubility control by the TcO2·0.6H2O(s) phase. This observation cannot be explained assuming the only formation of the TcO(OH)3− species, and requires extending the chemical model so far available for Tc(IV) under alkaline conditions. Because of the pH-limitations in MgCl2 systems caused by the precipitation of Mg(OH)2(s) or Mg–OH–Cl(s) (pHmax ≈ 9), chemical, thermodynamic and activity models for MCl2 systems (M = Mg, Ca) were first derived for CaCl2 where a significantly larger pH range can be assessed.
mTcvs. pHm) in concentrated MgCl2 and CaCl2 solutions with pHm ≥ 8 and solubility control by the TcO2·0.6H2O(s) phase. This observation cannot be explained assuming the only formation of the TcO(OH)3− species, and requires extending the chemical model so far available for Tc(IV) under alkaline conditions. Because of the pH-limitations in MgCl2 systems caused by the precipitation of Mg(OH)2(s) or Mg–OH–Cl(s) (pHmax ≈ 9), chemical, thermodynamic and activity models for MCl2 systems (M = Mg, Ca) were first derived for CaCl2 where a significantly larger pH range can be assessed.
The slope of +3 observed in the experimental solubility data indicates the release of 3H+ in the chemical reaction controlling the solubility of Tc(IV) in systems with [CaCl2] ≥ 1.0 M and pHm ≥ 8. Provided the predominance of the solid phase TcO2·0.6H2O(s), a new aqueous species holding the moiety [TcO(OH)5]3− must be defined. Experimental data collected in NaCl–NaOH systems strongly argue for TcO(OH)3− as limiting hydrolysis species forming under alkaline to hyperalkaline pH conditions. The moiety [TcO(OH)5]3− has not been reported in NaCl media and is thus specifically stabilized by Ca2+ or Mg2+, either involving the formation of ternary species of the type Can/Mgn[TcO(OH)5]2n−3 or by strong ion interaction processes. Previous studies focussing on the solubility of Ln(III), An(III/IV/V) and Zr(IV) in concentrated CaCl2 systems have provided unequivocal indications on the formation of ternary Ca–Ln/An/Zr–OH complexes under alkaline pH conditions.21,34,35,46 In most cases, the formation of these species was accompanied by the full occupancy of the coordination sphere of the central metal atom, as also occurs in the moiety [TcO(OH)5]3− (CNTc(IV) = 6). Based on the previous evidence available for An(IV) and Zr(IV), the formation of ternary complexes of the type CanTcO(OH)(2n−3)5 in concentrated CaCl2 solutions is postulated for Tc(IV). The chemical reaction (14) is thus proposed to control the solubility of Tc(IV) under these conditions:
| TcO2·0.6H2O(s) + nCa2+ + 3.4H2O(l) ⇔ CanTcO(OH)(2n−3)5 + 3H+ | (14) |
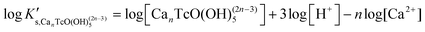 | (15) |
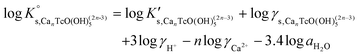 | (16) |
Conditional stability constants for reaction (14) are determined according to eqn (15) from Tc(IV) experimental solubility data gained in 1.0 M, 2.0 M and 4.5 M CaCl2 systems. The value of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K° is calculated by extrapolating the results in high ionic strength to I = 0 according to eqn (16). DFT calculations support the formation and stability of ternary complexes of the type CanTcO(OH)(2n−3)5 with n = 3 (see section 3.4.4). In spite of this and to gain further confidence in the chemical model controlling the chemistry of Tc under these conditions, Tc(IV) solubility data in concentrated [CaCl2] systems with pHm ≥ 8 have been evaluated considering four different chemical models based on eqn (16) with n = 1–4 to justify the quality of the adopted chemical model. Although it is postulated that the stabilization of the moiety [TcO(OH)53−] requires the formation of a new aqueous complex involving the participation of Ca2+, the fifth case with n = 0 is also evaluated for comparison purposes. In the first step, log
K° is calculated by extrapolating the results in high ionic strength to I = 0 according to eqn (16). DFT calculations support the formation and stability of ternary complexes of the type CanTcO(OH)(2n−3)5 with n = 3 (see section 3.4.4). In spite of this and to gain further confidence in the chemical model controlling the chemistry of Tc under these conditions, Tc(IV) solubility data in concentrated [CaCl2] systems with pHm ≥ 8 have been evaluated considering four different chemical models based on eqn (16) with n = 1–4 to justify the quality of the adopted chemical model. Although it is postulated that the stabilization of the moiety [TcO(OH)53−] requires the formation of a new aqueous complex involving the participation of Ca2+, the fifth case with n = 0 is also evaluated for comparison purposes. In the first step, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K° values and ion interaction coefficients are calculated using the SIT approach. In the second step, the best chemical model selected accordingly with the criteria described below, was used to derive
K° values and ion interaction coefficients are calculated using the SIT approach. In the second step, the best chemical model selected accordingly with the criteria described below, was used to derive 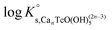 and ion interaction coefficients according to the Pitzer formalism.
and ion interaction coefficients according to the Pitzer formalism.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ks,CanTcO(OH)5(2n−3) are calculated according to eqn (14) and considering n = 0–4 (Table 5). The use of SIT for the determination of
Ks,CanTcO(OH)5(2n−3) are calculated according to eqn (14) and considering n = 0–4 (Table 5). The use of SIT for the determination of 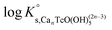 involves the linear regression of (log
involves the linear regression of (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s,CanTcO(OH)5(2n−3) − mD − 3.4log
K′s,CanTcO(OH)5(2n−3) − mD − 3.4log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aw) vs. mCaCl2 (see Fig. A2†). The SIT ion interaction coefficient of the forming species ε(Can[TcO(OH)5]2n−3, Ca2+/Cl−) can be calculated from the slope of the linear regression (−Δε) in combination with ε(H+, Cl−) = (0.12 ± 0.01) kg mol−1 and ε(Ca2+, Cl−) = (0.14 ± 0.01) kg mol−1 as reported in the NEA–TDB.18
aw) vs. mCaCl2 (see Fig. A2†). The SIT ion interaction coefficient of the forming species ε(Can[TcO(OH)5]2n−3, Ca2+/Cl−) can be calculated from the slope of the linear regression (−Δε) in combination with ε(H+, Cl−) = (0.12 ± 0.01) kg mol−1 and ε(Ca2+, Cl−) = (0.14 ± 0.01) kg mol−1 as reported in the NEA–TDB.18
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′ values determined from Tc(IV) solubility data in 1.0, 2.0 and 4.5 M CaCl2 according to chemical reaction (14) and eqn (15) for n = 0–4. log
K′ values determined from Tc(IV) solubility data in 1.0, 2.0 and 4.5 M CaCl2 according to chemical reaction (14) and eqn (15) for n = 0–4. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ko and ε(i,j) values determined using the linear regressions shown in the SIT-plot, Fig. A2
Ko and ε(i,j) values determined using the linear regressions shown in the SIT-plot, Fig. A2
| Species | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′experimental K′experimental![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
Outcome of SIT – plot | |||||
|---|---|---|---|---|---|---|---|
| I | 1.0 M | 2.0 M | 4.5 M | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ko Ko |
j | ε(i,j) | Quality |
a Uncertainty of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′ values determined as ± 0.3. K′ values determined as ± 0.3.
|
|||||||
| [TcO(OH)5]3− | −40.70 | −39.00 | −36.00 | −44.69 ± 0.3 | Ca2+ | −1.93 ± 0.10 | Δ = 0.10 |
| Ca[TcO(OH)5]− | −40.71 | −39.32 | −36.72 | −41.71 ± 0.3 | Ca2+ | −1.61 ± 0.10 | Δ = 0.10 |
| Ca2[TcO(OH)5]+ | −40.72 | −39.64 | −37.44 | −40.65 ± 0.3 | Cl− | −0.60 ± 0.10 | Δ = 0.04 |
| Ca 3 [TcO(OH) 5 ] 3+ | −40.73 | −39.97 | −38.16 | −41.53 ± 0.3 | Cl − | −0.37 ± 0.10 | Δ = 0.00 |
| Ca4[TcO(OH)5]5+ | −40.74 | −40.30 | −38.88 | −44.32 ± 0.3 | Cl− | −0.08 ± 0.20 | Δ = 0.11 |
Table 5 summarizes 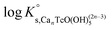 and ε(Can[TcO(OH)5]2n−3, Ca2+/Cl−) determined for the five chemical models evaluated, involving the formation of the binary/ternary CanTcO(OH)(2n−3)5 species with n = 0–4. Table 5 also shows the “quality parameter” (Δ), which is calculated as
and ε(Can[TcO(OH)5]2n−3, Ca2+/Cl−) determined for the five chemical models evaluated, involving the formation of the binary/ternary CanTcO(OH)(2n−3)5 species with n = 0–4. Table 5 also shows the “quality parameter” (Δ), which is calculated as 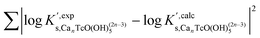 and analyses the goodness of the fit. The final selection of the chemical model for Tc(IV) in concentrated alkaline CaCl2 solutions is based on the criteria described below. Note that a similar strategy was successfully applied by Fellhauer for the evaluation of the ternary system Ca–Np(V)–OH in dilute to concentrated CaCl2 solutions.46,47
and analyses the goodness of the fit. The final selection of the chemical model for Tc(IV) in concentrated alkaline CaCl2 solutions is based on the criteria described below. Note that a similar strategy was successfully applied by Fellhauer for the evaluation of the ternary system Ca–Np(V)–OH in dilute to concentrated CaCl2 solutions.46,47
– Minimization of the “quality parameter” (Δ, Table 5).
– Consistency of SIT ion interaction coefficients. ε(i,j) are known to correlate with the charge of the ion,42 although significant deviations from this trend are expected for polyatomic species or voluminous ternary complexes. ε(Can[TcO(OH)5]2n−3, Ca2+/Cl−) values calculated in the present work (Table 5) are compared with ε(i,j) values reported for Ca–An(III/IV/V)–OH and Ca–Zr(IV)–OH complexes.
– Shape of the plot log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ks,CanTcO(OH)5(2n−3)vs. CaCl2 concentration. The plot should give a smooth shape without jumps or turning points (Fig. A3†).
Ks,CanTcO(OH)5(2n−3)vs. CaCl2 concentration. The plot should give a smooth shape without jumps or turning points (Fig. A3†).
All the chemical models result in a smooth shape of the plot log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′svs. mCaCl2 (Fig. A3†). Chemical models involving the formation of the [TcO(OH)5]3−, Ca[TcO(OH)5]− and Ca4[TcO(OH)5]5+ species led to very large and clearly unrealistic values of ε(i,j) and/or Δ, and consequently were disregarded. The Ca2[TcO(OH)5]+ species shows a relatively low Δ, but retains a very negative SIT ion interaction coefficient. The chemical model including the species Ca3[TcO(OH)5]3+ species has the lowest Δ and holds a less negative SIT ion interaction coefficient (ε(Ca3[TcO(OH)5]3+, Cl−) = −(0.37 ± 0.10) kg mol−1). The latter value is very discrepant with respect to the value estimated according to the charge-analogy concept (ε(M3+,Cl−) = (0.25 ± 0.10) kg mol−1). As discussed above, the applicability of charge analogies for the estimation of ε(i,j) in the case of voluminous complexes has been previously challenged in the literature and is also disregarded in the present case.
K′svs. mCaCl2 (Fig. A3†). Chemical models involving the formation of the [TcO(OH)5]3−, Ca[TcO(OH)5]− and Ca4[TcO(OH)5]5+ species led to very large and clearly unrealistic values of ε(i,j) and/or Δ, and consequently were disregarded. The Ca2[TcO(OH)5]+ species shows a relatively low Δ, but retains a very negative SIT ion interaction coefficient. The chemical model including the species Ca3[TcO(OH)5]3+ species has the lowest Δ and holds a less negative SIT ion interaction coefficient (ε(Ca3[TcO(OH)5]3+, Cl−) = −(0.37 ± 0.10) kg mol−1). The latter value is very discrepant with respect to the value estimated according to the charge-analogy concept (ε(M3+,Cl−) = (0.25 ± 0.10) kg mol−1). As discussed above, the applicability of charge analogies for the estimation of ε(i,j) in the case of voluminous complexes has been previously challenged in the literature and is also disregarded in the present case.
Based on the discussion above and considering the clear inputs obtained from DFT calculations (see section 3.4.4), the chemical model involving the formation of the ternary Ca3[TcO(OH)5]3+ species is selected in the present work.
The same chemical model is considered for the interpretation of experimental observations in concentrated MgCl2 solutions with pHm ≥ 8. Due to limitations in pHm caused by the precipitation of Mg(OH)2(s) or Mg–OH–Cl(s) (pHmax ≈ 9), the increase of Tc(IV) solubility with the slope of +3 is only observed in 4.5 M MgCl2. This allows the only calculation of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s,Mg3TcO(OH)53+ for this ionic strength. In order to overcome the limited data set available, ε(Mg3[TcO(OH)5]3+, Cl−) is considered ≈
K′s,Mg3TcO(OH)53+ for this ionic strength. In order to overcome the limited data set available, ε(Mg3[TcO(OH)5]3+, Cl−) is considered ≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε(Ca3[TcO(OH)5]3+, Cl−), and
ε(Ca3[TcO(OH)5]3+, Cl−), and 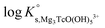 is accordingly calculated using the SIT approach.
is accordingly calculated using the SIT approach.
This value is significantly higher than 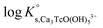 , thus reflecting the earlier (lower pHm values) increase in solubility observed in MgCl2 systems.
, thus reflecting the earlier (lower pHm values) increase in solubility observed in MgCl2 systems.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X− interactions.34,35,44 The binary parameters β(2) and the mixing parameters θ(Ca3[TcO(OH)5]3+, Ca2+) and Ψ(Ca3[TcO(OH)5]3+, Cl−, Ca2+) were set to zero.
X− interactions.34,35,44 The binary parameters β(2) and the mixing parameters θ(Ca3[TcO(OH)5]3+, Ca2+) and Ψ(Ca3[TcO(OH)5]3+, Cl−, Ca2+) were set to zero. 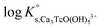 and β(0) were fitted for CaCl2 systems by minimizing the difference between experimental and calculated log
and β(0) were fitted for CaCl2 systems by minimizing the difference between experimental and calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s,Ca3TcO(OH)53+ in 1.0 M, 2.0 M and 4.5 M CaCl2 systems. The resulting values are:
K′s,Ca3TcO(OH)53+ in 1.0 M, 2.0 M and 4.5 M CaCl2 systems. The resulting values are:The value of β(0) can also be estimated for M3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X− interactions according to β(0)MX = 0.366 + εMX·(ln 10)/2
X− interactions according to β(0)MX = 0.366 + εMX·(ln 10)/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 and using ε(Ca3[TcO(OH)5]3+, Cl−) = −0.37 ± 0.1 kg mol−1 as determined in the present study. The resulting estimate (β(0) = −0.0599) is in good agreement with the value obtained in the fit. Fig. 14 shows that both SIT and Pitzer models explain very well log
44 and using ε(Ca3[TcO(OH)5]3+, Cl−) = −0.37 ± 0.1 kg mol−1 as determined in the present study. The resulting estimate (β(0) = −0.0599) is in good agreement with the value obtained in the fit. Fig. 14 shows that both SIT and Pitzer models explain very well log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′s,Ca3TcO(OH)53+ values determined from the experimental solubility data.
K′s,Ca3TcO(OH)53+ values determined from the experimental solubility data.
As in the SIT approach, Pitzer ion interaction parameters determined for Ca3[TcO(OH)5]3+ are used for Mg3[TcO(OH)5]3+ to extrapolate the conditional stability constant at 4.5 M MgCl2 to I = 0 and to calculate 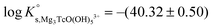 . This value agrees within their uncertainties with
. This value agrees within their uncertainties with 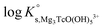 determined using the SIT approach.
determined using the SIT approach.
4.5 Chemical, thermodynamic and activity models for the system Tc4+–Na+–Mg2+–Ca2+–H+–Cl−–OH−–H2O
Tables 6 and 7 summarize the chemical, thermodynamic and (SIT/Pitzer) activity models derived in the present work for the system Tc4+–Na+–Mg2+–Ca2+–H+–Cl−–OH−–H2O. Fig. 15–17 show all experimental solubility data determined in the present work in dilute to concentrated NaCl, MgCl2 and CaCl2 systems, respectively, in combination with thermodynamic calculations performed using the SIT and Pitzer activity models summarized in Tables 6 and 7. The figures show an excellent agreement between experimental and calculated Tc(IV) solubility data, which further extends to experimental solubility data at I ≈ 0 reported in the literature. The present work represents the first comprehensive description of Tc(IV) solubility in dilute to concentrated saline systems, covering acidic to hyperalkaline pH conditions.| Chemical reactions | SIT | Pitzer |
|---|---|---|
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K° K° |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K° K° |
|
| TcO2·0.6H2O(s) + 2/3 H+ ⇔ 1/3Tc3O52+ + 0.93H2O | −1.53 ± 0.15 | −1.50 ± 0.10 |
| TcO2·0.6H2O(s) + 0.4H2O ⇔ TcO(OH)2 | −8.80 ± 0.50 | −8.80 ± 0.50 |
| TcO2·0.6H2O(s) + 1.4H2O ⇔ TcO(OH)3− + H+ | −19.27 ± 0.06 | −19.32 ± 0.10 |
| TcO2·0.6H2O(s) + 3Mg2+ + 3.4H2O ⇔ Mg3[TcO(OH)5]3+ + 3H+ | −40.55 ± 0.50 | −40.32 ± 0.50 |
| TcO2·0.6H2O(s) + 3Ca2+ + 3.4H2O ⇔ Ca3[TcO(OH)5]3+ + 3H+ | −41.53 ± 0.30 | −41.65 ± 0.30 |
| Species | SIT | Pitzer | |||||
|---|---|---|---|---|---|---|---|
| Binary parameters | Mixing parameters | ||||||
| i | j | ε(i,j) | β (0) | β (1) | C (ϕ) | Θ ii′ | Ψ iji′ |
| a Fixed value for the corresponding charge type, according to ref. 44. b Estimated value for the corresponding charge type, according to ref. 42. c Estimated value for the corresponding charge type, according to ref. 48. | |||||||
| Tc3O52+ | Cl− | −0.41 ± 0.05 | −0.3681 | 2.6972 | 0.0063 | 0 | 0 |
| TcO(OH)3− | Na+ | 0.09 ± 0.02 | −0.0087 | 0.3a | 0.035 | 0 | 0 |
| Ca2+ | 0.15b | 0.3c | 1.7c | 0c | 0c | 0c | |
| Ca3[TcO(OH)5]3+ | Cl− | −0.37 ± 0.1 | −0.074 | 4.3a | 0.015 | 0 | 0 |
| Mg3[TcO(OH)5]3+ | Cl− | −0.37 ± 0.1 | −0.074 | 4.3a | 0.015 | 0 | 0 |
| TcO(OH)2(aq) | Na+, Mg2+, Ca2+, Cl− | 0 | 0 | 0 | 0 | 0 | 0 |
5 Summary and conclusions
The solubility and speciation of Tc(IV) were successfully investigated in dilute to concentrated NaCl, MgCl2 and CaCl2 systems using a systematic combination of undersaturation solubility experiments, extensive solid phase characterization, aqueous speciation methods/techniques and DFT calculations. The chemical, thermodynamic and activity models accordingly derived improve and further extend the current NEA–TDB thermodynamic selection for Tc and offer the first experimentally derived comprehensive Pitzer model available for highly saline systems.TcO2·0.6H2O(s) is the solid phase controlling the solubility of Tc(IV) in all the evaluated systems, except under acidic conditions with a very high chloride concentration where the formation of a Tc(IV)–Cl solid phase is hinted from solubility experiments in agreement with the literature. The previously unreported formation of the polynuclear Tc3O52+ species under acidic pH conditions is accepted based on the slope analysis of solubility data gained in the present work and spectroscopic evidence available in the literature. The predominance of this species in the aqueous phase under acidic conditions (instead of TcO2+ + TcO(OH)+) properly explains the experimental observations from dilute to concentrated saline systems, except in very acidic systems with a high chloride concentration where the formation of binary Tc(IV)–Cl or ternary Tc(IV)–O/OH–Cl aqueous species is indicated by spectroscopic techniques. The pH-independent chemical reaction TcO2·0.6H2O(s) + 0.4 H2O(l) ⇔ TcO(OH)2(aq) controls the solubility of Tc(IV) under weakly acidic to alkaline pH conditions. The stability field of TcO(OH)2(aq) decreases in concentrated saline systems due to the greater stabilization of charged species and the formation of new ternary complexes in concentrated alkaline MgCl2 and CaCl2 systems. 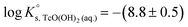 determined in the present work agrees well within the uncertainties with the value currently selected in the NEA–TDB. The solubility of Tc(IV) increases with a slope of +1 (log
determined in the present work agrees well within the uncertainties with the value currently selected in the NEA–TDB. The solubility of Tc(IV) increases with a slope of +1 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mTcvs. pHm) in NaCl systems with pHm ≥ 11, indicating the predominance of TcO(OH)3− as previously selected in the NEA–TDB and decreases about one order of magnitude with increasing ionic strength due to ion interaction processes. A very different behaviour of Tc(IV) is observed in concentrated alkaline MgCl2 and CaCl2 systems, where a steep increase of the solubility with a well-defined slope of +3 is observed. The formation of Mg3[TcO(OH)5]3+ and Ca3[TcO(OH)5]3+ species is proposed based on the slope analysis, model calculations and previous solubility and spectroscopic evidence available for An(IV) and Zr(IV). DFT calculations further support the key role of Ca2+ in stabilizing the highly charged [TcO(OH)5]3− moiety.
mTcvs. pHm) in NaCl systems with pHm ≥ 11, indicating the predominance of TcO(OH)3− as previously selected in the NEA–TDB and decreases about one order of magnitude with increasing ionic strength due to ion interaction processes. A very different behaviour of Tc(IV) is observed in concentrated alkaline MgCl2 and CaCl2 systems, where a steep increase of the solubility with a well-defined slope of +3 is observed. The formation of Mg3[TcO(OH)5]3+ and Ca3[TcO(OH)5]3+ species is proposed based on the slope analysis, model calculations and previous solubility and spectroscopic evidence available for An(IV) and Zr(IV). DFT calculations further support the key role of Ca2+ in stabilizing the highly charged [TcO(OH)5]3− moiety.
The comprehensive thermodynamic model derived in the present work for the system Tc4+–Na+–Mg2+–Ca2+–H+–Cl−–OH−–H2O at T = 25 °C provides an accurate and robust tool for the calculation of Tc(IV) solubility in a diversity of geochemical conditions. This new thermodynamic model represents a significant improvement and is highly relevant for calculating reliable Tc(IV) source term concentrations in the context of safety assessments for nuclear waste repositories.
Acknowledgements
The authors would like to thank D. Fellhauer and A. Baumann (KIT–INE) for their support in the Pitzer calculations and technical assistance, respectively. The contribution of M. Böttle, E. Soballa and S. Heck (KIT–INE) to ICP–OES, SEM–EDS and TG–DTA analyses is highly appreciated. This work was funded by the German Federal Ministry of Economics and Technology (BMWi) under the project of VESPA.References
- J. A. Rard, M. H. Rand, G. Anderegg and H. Wanner, Chemical thermodynamics of technetium, Elsevier, North-Holland, Amsterdam, 1999 Search PubMed.
- V. Metz, H. Geckeis, E. Gonzalez-Robles, A. Loida, C. Bube and B. Kienzler, Radiochim. Acta, 2012, 100, 699–713 CrossRef CAS.
- E. Wieland and L. R. Van Loon, Cementitious Near-Field Sorption Data Base for Performance Assessment of an ILW Repository in Opalinus Clay, PSI-Bericht 03-06, Nuclear Energy and Safety Research Department Laboratory for Waste Management, 2006 Search PubMed.
- C. Bube, V. Metz, E. Bohnert, K. Garbev, D. Schild and B. Kienzler, Phys. Chem. Earth, 2013, 64, 87–94 CrossRef.
- R. E. Meyer, W. D. Arnold, F. I. Case and G. D. Okelley, Radiochim. Acta, 1991, 55, 11–18 CAS.
- T. E. Eriksen, P. Ndalamba, J. Bruno and M. Caceci, Radiochim. Acta, 1992, 58-9, 67–70 Search PubMed.
- N. J. Hess, Y. X. Xia, D. Rai and S. D. Conradson, J. Solution Chem., 2004, 33, 199–226 CrossRef CAS.
- D. J. Liu, J. Yao, B. Wang, C. Bruggeman and N. Maes, Radiochim. Acta, 2007, 95, 523–528 CAS.
- P. Warwick, S. Aldridge, N. Evans and S. Vines, Radiochim. Acta, 2007, 95, 709–716 CrossRef CAS.
- T. Kobayashi, A. C. Scheinost, D. Fellhauer, X. Gaona and M. Altmaier, Radiochim. Acta, 2013, 101, 323–332 CrossRef CAS.
- E. Yalcintas, X. Gaona, A. C. Scheinost, T. Kobayashi, M. Altmaier and H. Geckeis, Radiochim. Acta, 2015, 103, 57–72 CrossRef CAS.
- L. Vichot, G. Ouvrard, G. Montavon, M. Fattahi, C. Musikas and B. Grambow, Radiochim. Acta, 2002, 90, 575–579 CrossRef CAS.
- L. Vichot, M. Fattahi, C. Musikas and B. Grambow, Radiochim. Acta, 2003, 91, 263–271 CrossRef CAS.
- F. Poineau, M. Fattahi, C. Den Auwer, C. Hennig and B. Grambow, Radiochim. Acta, 2006, 94, 283–289 CAS.
- F. Poineau, M. Fattahi and B. Grambow, Radiochim. Acta, 2006, 94, 559–563 CAS.
- F. Poineau, M. Fattahi and B. Grambow, Radiochim. Acta, 2006, 94, 91–95 CAS.
- F. Poineau, M. Fattahi, G. Montavon and B. Grambow, Radiochim. Acta, 2006, 94, 291–299 CAS.
- R. Guillaumont, T. Fanghänel, V. Neck, J. Fuger, D. A. Palmer, I. Grenthe and M. H. Rand, Update on the chemical thermodynamics of uranium, neptunium, plutonium, americium and technetium, Elsevier, North-Holland, Amsterdam, 2003 Search PubMed.
- B. Gorski and H. Koch, J. Inorg. Nucl. Chem., 1969, 31, 3565–3573 CrossRef CAS.
- M. Altmaier, V. Metz, V. Neck, R. Muller and T. Fanghänel, Geochim. Cosmochim. Acta, 2003, 67, 3595–3601 CrossRef CAS.
- M. Altmaier, V. Neck and T. Fanghänel, Radiochim. Acta, 2008, 96, 541–550 CrossRef.
- M. Altmaier, V. Neck and T. Fanghänel, Radiochim. Acta, 2004, 92, 537–543 CrossRef CAS.
- T. Omori, Y. Muraoka and H. Suganuma, J. Radioan. Nucl. Ch. Ar., 1994, 178, 237–243 CrossRef CAS.
- R. Kopunec, F. N. Abudeab and S. Skraskova, J. Radioanal. Nucl. Ch., 1998, 230, 51–60 CrossRef CAS.
- JCPDS, USA (2001), 2001.
- J. Rothe, S. Butorin, K. Dardenne, M. A. Denecke, B. Kienzler, M. Löble, V. Metz, A. Seibert, M. Steppert, T. Vitova, C. Walther and H. Geckeis, Rev. Sci. Instrum., 2012, 83 CrossRef CAS PubMed , 043105.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- S. R. Langhoff, C. W. Bauschlicher, L. G. M. Pettersson and P. E. M. Siegbahn, Chem. Phys., 1989, 132, 49–58 CrossRef CAS.
- E. Breynaert, C. E. A. Kirschhock and A. Maes, Dalton Trans., 2009, 9398–9401 RSC.
- R. Polly, B. Schimmelpfennig, E. Yalcintas, X. Gaona and M. Altmaier, Hydrolysis of Tc(IV) and formation of ternary Na/Ca-Tc(IV)-OH species in NaCl/CaCl2 systems: a quantum chemical study, Migration conference, Santa Fe, USA, 2015 Search PubMed.
- A. A. Müller, H. Bogge and E. Diemann, Inorg. Chem. Commun., 2003, 6, 52–53 CrossRef.
- A. Müller, H. Bogge and E. Diemann, Inorg. Chem. Commun., 2003, 6, 329–329 CrossRef.
- A. Lenz and L. Ojamae, J. Phys. Chem. A, 2006, 110, 13388–13393 CrossRef CAS PubMed.
- V. Neck, M. Altmaier, T. Rabung, J. Lützenkirchen and T. Fanghänel, Pure Appl. Chem., 2009, 81, 1555–1568 CrossRef CAS.
- D. Fellhauer, V. Neck, M. Altmaier, J. Lützenkirchen and T. Fanghänel, Radiochim. Acta, 2010, 98, 541–548 CrossRef CAS.
- B. Brendebach, M. Altmaier, J. Rothe, V. Neck and M. A. Denecke, Inorg. Chem., 2007, 46, 6804–6810 CrossRef CAS PubMed.
- I. Almahamid, J. C. Bryan, J. J. Bucher, A. K. Burrell, N. M. Edelstein, E. A. Hudson, N. Kaltsoyannis, W. W. Lukens, D. K. Shuh, H. Nitsche and T. Reich, Inorg. Chem., 1995, 34, 193–198 CrossRef CAS.
- E. E. Rodriguez, F. Poineau, A. Llobet, A. P. Sattelberger, J. Bhattacharjee, U. V. Waghmare, T. Hartmann and A. K. Cheetham, J. Am. Chem. Soc., 2007, 129, 10244–10248 CrossRef CAS PubMed.
- G. H. Morrison and H. Freiser, Solvent Extraction in Analytical Chemistry, John Willey & Sons, Inc., London, 1957 Search PubMed.
- J. C. Shannon, Database of ionic radii, http://abulafia.mt.ic.ac.uk/shannon/ptable.php Search PubMed.
- H. Wanner, Guidelines for the assignment of uncertainties, Elsevier, F-92130 Issy-les-Moulineaux, France, 1999 Search PubMed.
- W. Hummel, Ionic strength corrections and estimation of SIT ion interaction coefficients, Paul Scherrer Institut, 2009 Search PubMed.
- C. E. Harvie, N. Moller and J. H. Weare, Geochim. Cosmochim. Acta, 1984, 48, 723–751 CrossRef CAS.
- I. Grenthe and I. Puigdomenech, Modelling in aquatic chemistry, Elsevier, Paris, 1997 Search PubMed.
- H. Gamsjäger, T. Gajda, J. Sanster, S. K. Saxena and W. Voigt, Chemical thermodynamics of tin, Elsevier, Issy-les-Moulineaux (France), 2012 Search PubMed.
- D. Fellhauer, PhD, University of Heidelberg, 2013.
- D. Fellhauer, M. Altmaier, X. Gaona, J. Lützenkirchen and T. Fanghänel, Radiochim. Acta, 2016 DOI:10.1515/ract-2015-2490.
- V. Neck, T. Fanghänel and J. Kim, Thermodynamische Modellierung von Technetium in Natürlichen Aquatischen Systemen, FZKA 6340, Forschungszentrum Karlsruhe, Germany, 1999 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6dt00973e |
| ‡ The same trend is reported for the ionic radii of the corresponding metal cations: Tc(IV) = 0.645 Å (CN = 6), Zr(IV) = 0.72 Å (CN = 6), Th(IV) = 1.05 Å (CN = 8).48 |
§ β(0)MX = 0.15 + ε(M,X)·(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10)/2 for M2+ − X– interactions, where ε(M,X) is the SIT ion interaction coefficient determined for the same species. 10)/2 for M2+ − X– interactions, where ε(M,X) is the SIT ion interaction coefficient determined for the same species. |
| This journal is © The Royal Society of Chemistry 2016 |