Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanochemically synthesized fluorides: local structures and ion transport
Florian
Preishuber-Pflügl
and
Martin
Wilkening
Institute for Chemistry and Technology of Materials, DFG-SPP 1415, Graz University of Technology (NAWI Graz), Stremayrgasse 9/Z4, 8010 Graz, Austria. E-mail: preishuber-pfluegl@tugraz.at; wilkening@tugraz.at
First published on 26th April 2016
Abstract
The performance of new sensors or advanced electrochemical energy storage devices strongly depends on the active materials chosen to realize such systems. In particular, their morphology may greatly influence their overall macroscopic properties. Frequently, limitations in classical ways of chemical preparation routes hamper the development of materials with tailored properties. Fortunately, such hurdles can be overcome by mechanochemical synthesis. The versatility of mechanosynthesis allows the provision of compounds that are not available through common synthesis routes. The mechanical treatment of two or three starting materials in high-energy ball mills enables the synthesis not only of new compounds but also of nanocrystalline materials with unusual properties such as enhanced ion dynamics. Fast ion transport is of crucial importance in electrochemical energy storage. It is worth noting that mechanosynthesis also provides access to metastable phases that cannot be synthesized by conventional solid state synthesis. Ceramic synthesis routes often yield the thermally, i.e., thermodynamically, stable products rather than metastable compounds. In this perspective we report the mechanochemical synthesis of nanocrystalline fluorine ion conductors that serve as model substances to understand the relationship between local structures and ion dynamics. While ion transport properties were complementarily probed via conductivity spectroscopy and nuclear magnetic relaxation, local structures of the phases prepared were investigated by high-resolution 19F NMR spectroscopy carried out by fast magic angle spinning. The combination of nuclear and non-nuclear techniques also helped us to shed light on the mechanisms controlling mechanochemical reactions in general.
Introduction
A chemical reaction which is induced by the absorption of mechanical energy is called a mechanochemical reaction. It constitutes its own class of chemical synthesis routes. Chemical reactions are usually driven by other sources of energy such as heat, light or by the difference in the electrochemical potentials of the materials involved, i.e., through electric energy.Mechanochemistry offers access to nanocrystalline compounds and metastable phases that are often characterized by non-equilibrium structures. In many cases these materials cannot be obtained through conventional approaches such as solid state synthesis which require high sintering temperatures, for example. Compared to other preparation routes, mechanosynthesis, e.g., when carried out in high-energy planetary mills, represents a highly versatile way of preparation that benefits from its facile realization and so-called one-pot conditions. This advantages as well as the possibility to synthesize materials with yet inaccessible properties led to a rapid increase of applications of mechanochemical techniques. This growing interest is highlighted by the increasing number of publications reporting on mechanochemical reactions as well as by several comprehensive reviews that appeared over the last couple of years.1–3 While recent reviews focused on, e.g., the synthesis of non-equilibrium oxides, the present one puts emphasis on the preparation of inorganic, nanocrystalline fluorides, i.e., ternary and quaternary ionic conductors. Here, we focus on the direct synthesis of complex fluorides by milling binary fluorides under dry conditions in high-energy ball mills.
Besides the effect of nanostructuring, the impact of mechanical stress yields materials with a high concentration of defects and a large volume fraction of the so-called interfacial regions anticipated to be structurally disordered. In the case of Li+ and F− ionic conductors defects are necessary to facilitate both self-diffusion and long-range ion transport. From an application point of view, fast ion conductors are urgently needed to develop powerful electrochemical sensors or energy storage devices that may also take advantage of fluoride as the main ionic charge carrier.4 In this regard, mechanosynthesis has also been employed for the direct synthesis of current electrode materials for lithium-ion batteries.5–8
For the characterization of materials synthesized via mechanochemical routes, nuclear magnetic resonance (NMR) techniques and impedance spectroscopy have proven as powerful tools to investigate both ion dynamics on short-range as well as long-range length scales. Considering local structures, high-resolution solid-state NMR under conditions of very fast magic angle spinning (MAS) can be used to follow possible microstructural changes taking place as a function of the milling time.
Mechanochemically induced changes: what happens during high-energy ball milling?
The first results on mechanochemically induced reactions were reported by Wilhelm Ostwald, Michael Faraday and Carey Lea.9,10 Lea carried out systematic investigations on silver halides upon exposure to light or mechanical force, which finally led to the differentiation of mechanochemistry as a separate branch in chemical synthesis. Initially this phenomenon was discovered in the area of inorganic solid state chemistry, but applications of this method spread to many other fields including biomaterials, metal organic frameworks, catalysts, organics and pharmaceuticals, in particular.1,9,11In terms of solid state chemistry, such as the direct synthesis of nanocrystalline fluoride ion conductors under dry conditions, the processes during mechanical treatment can affect the starting material in two different ways: (i) altering the defect structure without any chemical reaction induced, i.e., conserving the initial crystal structure and (ii) changing the crystal chemical structure by chemical reactions, that is, inducing a structural conversion by breaking and forming chemical bonds.
Fig. 1 provides an overview of the possible macroscopic and microscopic structural changes taking place during severe high-energy ball milling.12 Shear, friction and impact forces lead to the abrasion and fracture of the solid particles into smaller ones. This drastic reduction in the crystallite size—usually the mean crystallite size reached after some hours of milling is in the order of 20 nm—results in a high ratio between the remaining bulk material and the structurally disordered surface-near regions.13 The bulk regions of a mechanosynthesized phase, however, are also expected to differ from those of the starting material since mechanical impact does not only introduce structural disorder in the boundary layers but also generates defects and dislocations in the interior of the small crystallites.
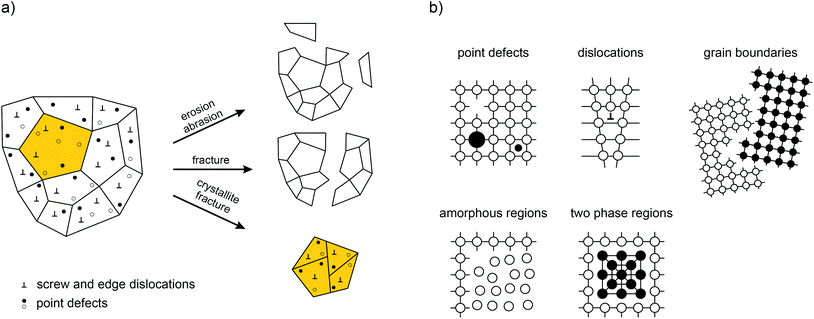 | ||
| Fig. 1 (a) What happens during mechanical treatment? An overview of the complex processes simultaneously taking place during high-energy ball milling. Most importantly, defects are introduced that will significantly govern the properties of the final nanocrystalline and structurally disordered product. (b) Possible defect structures generated in crystalline solids treated mechanically. Illustration adapted from ref. 12. | ||
From the point of view of ion dynamics those ions that are located in or near these interfacial regions often move much faster than those in the bulk material. In favourable cases the quickly jumping ions can be revealed by NMR line shape studies (Fig. 2).14 In particular, this has been demonstrated for single-phase nanocrystalline Li2O and the two-phase composites Li2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X2O3 with x = Al, B.15–17 In the latter, the compaction of two nanocrystalline materials, an ion conductor and an ionic insulator, leads to an interfacial network of homo-contacts (Li2O
X2O3 with x = Al, B.15–17 In the latter, the compaction of two nanocrystalline materials, an ion conductor and an ionic insulator, leads to an interfacial network of homo-contacts (Li2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li2O) and hetero-contacts (Li2O
Li2O) and hetero-contacts (Li2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X2O3), see Fig. 3 for comparison. Compared to the situation in the bulk regions of nano-Li2O the two-component interfacial regions provide fast diffusion pathways in their vicinity.15 The same is anticipated in other dispersed ion conductors such as LiI–Al2O3 which was the first example of its class.18 Other nanostructured ion conductors19,20 also benefit from the so-called non-trivial size effects that are based on the formation of space charge zones21 which in some cases influence the dynamic properties of the whole nanocrystallite, i.e., its interior regions. Maier introduced the term artificial ion conductor to describe the electrochemical situation created in nano-ionics.22,23
X2O3), see Fig. 3 for comparison. Compared to the situation in the bulk regions of nano-Li2O the two-component interfacial regions provide fast diffusion pathways in their vicinity.15 The same is anticipated in other dispersed ion conductors such as LiI–Al2O3 which was the first example of its class.18 Other nanostructured ion conductors19,20 also benefit from the so-called non-trivial size effects that are based on the formation of space charge zones21 which in some cases influence the dynamic properties of the whole nanocrystallite, i.e., its interior regions. Maier introduced the term artificial ion conductor to describe the electrochemical situation created in nano-ionics.22,23
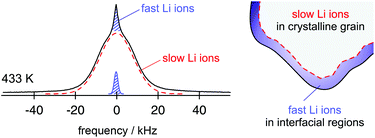 | ||
| Fig. 2 7Li NMR spectrum of nanocrystalline Li2O prepared by high-energy ball milling. The line is composed of two contributions reflecting the slow and the fast ions in either the bulk or in/near the interfacial regions. Figure adapted from ref. 14. | ||
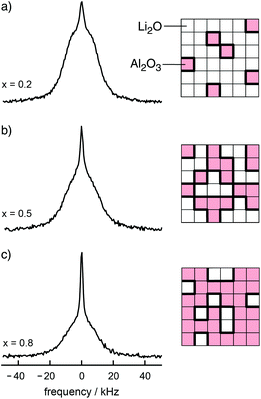 | ||
Fig. 3
7Li NMR spectra of the nanocrystalline composite xLi2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1 − x)Al2O3, (a) x = 0.2, (b) x = 0.5, and (c) x = 0.8. The more hetero-contacts per formula unit of Li2O are formed, the larger is the fraction of the motionally narrowed NMR line superimposing the broad main signal. Figure adapted from ref. 14. (1 − x)Al2O3, (a) x = 0.2, (b) x = 0.5, and (c) x = 0.8. The more hetero-contacts per formula unit of Li2O are formed, the larger is the fraction of the motionally narrowed NMR line superimposing the broad main signal. Figure adapted from ref. 14. | ||
Apart from ion dynamics, the element distribution in grain boundary regions might be different from that in the bulk state. In particular, this holds for non-equilibrium compounds as described by Šepelàk et al.:2 the inhomogeneous distribution of cations in the grain boundaries is referred to as mechanical treatment. The authors presented detailed analysis techniques for such non-equilibrium phenomena in oxides.
The second aspect of mechanochemistry is the direct conversion of the reagents into the desired product without the need for any further processing or purification steps. As mentioned above, it is feasible to prepare materials which are not accessible through conventional synthesis techniques such as thermochemistry, precipitation techniques or sol–gel methods. It is worth mentioning that such metastable phases allow miscibility gaps to be overcome giving rise to solid-solutions being characterized by an enhanced concentration of vacancies, interstitials or other defects that are necessary to enable high ionic conductivities.24
The underlying reaction mechanism of a mechanochemical synthesis is still under discussion. Besides the various microstructural changes taking place, localized reactions induced by heat and pressure are anticipated to lead to the final conversion of the starting material. In contrast to any high temperature solid state reaction, where the entire material is heated to a certain temperature, a mechanochemical reaction is thought to occur at localized spots where the material is stressed by the milling tools. Bowden, Tabor and Yoffe proposed a ‘hot-spot theory’ that suggests temperatures as high as 1000 K for a time period of 10−4 to 10−3 s due to the friction at surfaces of about 1 μm2.25–27 The magma–plasma model predicts even higher temperatures of up to 104 K and a molten-like state of the reactants in the impact zone of the particles.28
The common finding in both theories is a localized development of thermal energy that promotes the solid state reactions. As the reactants are thoroughly mixed on the nm-scale, the diffusion pathways between the reactants are some orders of magnitude smaller as compared to μm-sized grains. For such a localized reaction, the energy delivered by mechanical treatment might be sufficient to completely convert the starting materials into a new product. As an example, for the synthesis of BaMgF4, as is presented below, a quantitative reaction in a planetary ball mill required extremely high rotational speeds.29 The fact that the overall temperature inside the milling beaker is much lower as compared to high temperature solid state methods represents a clear advantage. At low temperatures the transformation of the products into thermodynamically stable phases is suppressed; for example, this concerns phase separations of usually immiscible solids. Hence, mechanosynthesis is indeed a powerful method to prepare highly metastable, i.e., non-equilibrium compounds.
Characterization techniques: making use of X-rays, spins and charge carriers
For the characterization of (nano-)crystalline materials, diffraction techniques such as X-ray powder diffraction (XRPD) are commonly employed to determine the crystal structures. Mechanochemically synthesized materials, however, often show patterns that deviate from single crystalline or coarse grained materials. The broadening of reflections due to extremely small mean crystallite sizes leads to overlapping of the reflections or hides impurities and secondary phases. In addition, the signals can be shifted because of variations of the mean lattice parameters. Moreover, they can show different intensities which complicates a certain determination of the product. The milling process may also yield amorphous fractions lacking in periodicity so they cannot be identified by X-ray diffraction methods.To overcome the drawbacks of X-ray diffraction, solid state NMR is the method of choice to uncover amorphous components and to collect information on local magnetic and electric fields at the nuclear sites. NMR, e.g., is able to determine polyhedral distortions as being a result of mechanical impact. In general, local distortions as well as outspread structural disorder can also be regarded as metastable states of the product obtained. 19F NMR benefits from the excellent receptivity of the fluorine nuclei. The good sensitivity as well as fast spin–lattice relaxation of the 19F nuclei due to relatively strong dipole–dipole interactions results in short acquisition times further underlining the advantages of 19F NMR spectroscopy. In order to achieve a high resolution in the solid state magic angle spinning (MAS) is applied. With current NMR probes spinning speeds as high as 100 kHz are available. Since NMR spectroscopy senses the magnetic environment of each nucleus it is also applicable to amorphous compounds (see below). Thus, it is a valuable tool to help identify by-products or impurities that remain unresolved or as such invisible by XRPD. Fortunately, MAS NMR does not require special sample preparation methods; air sensitive materials can be filled into the desired rotors using a dry box under an inert atmosphere. In particular, fluorine NMR takes advantage of a broad chemical shift range with the result that the individual signals can be well distinguished and, later, assigned to the crystallographic positions.
Besides structural characterisation via XRPD and NMR on both the macroscopic length scale and the angstrom length scale, ion transport properties of mechanosynthesized compounds are of particular interest since they may be largely different from those of their coarse-grained counterparts. Taken together, broadband impedance spectroscopy and solid-state time-domain NMR techniques are powerful tools that enable a complementary characterization of ion dynamics by sensing the hopping processes on different time scales. In terms of jump rates the accessible dynamic window ranges from the Hz to the GHz regime.
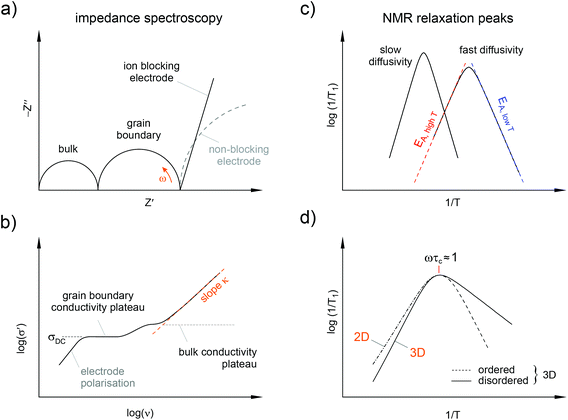
Complex conductivities and dielectric permittivities, if measured over a wide frequency range, contain valuable information on ion hopping dynamics taking place on different length scales. In general, average hopping barriers are available from variable-temperature experiments when analysing the results in the frame of the law of Arrhenius, i.e., by plotting, e.g., log(σ′T) vs. the inverse temperature 1/T; σ′ denotes the real part of the complex conductivity. Nyquist diagrams, which are obtained when the real part (Z′) of the complex impedance is plotted vs. the imaginary part (Z′′), and the analysis of modulus peaks M′′ are helpful to distinguish bulk from grain boundary contributions to the total conductivity. Of course, from the various representations of impedance data (see Fig. 4) electrical relaxation rates can be deduced that are useful for comparisons with results from other micro- and macroscopic techniques.
In many cases NMR relaxometry and NMR exchange spectroscopy are able to complement broadband impedance studies. For example, time-domain NMR spin–lattice relaxation measurements,30,31 if performed in the so-called low-T range of NMR relaxometry, are sensitive to short-range ion dynamics that are usually accessed by AC impedance spectroscopy carried out at sufficiently high frequencies. This regime in NMR relaxometry is characterized by jump rates 1/τ that are much lower than the Larmor frequency applied to carry out the experiment. If we assume an irregularly formed potential landscape that the jumping ion is exposed to, the method senses local jumps of the ions between neighbouring sites in the crystal lattice connected by low energy barriers. In this regime the relaxation rate is also sensitive to correlation effects such as structural disorder and Coulomb interactions of the hopping ions.30,32
At higher temperatures, this is the regime where the mean jump rates exceed the angular Larmor frequency ω0, the spin–lattice relaxation rate is sensitive to long-range ion dynamics. This is because during the time interval 1/ω0 the ions perform many jumps that can be sampled. These hops may also include jump processes where the ions have to surmount higher energy barriers. Provided that all the diffusion processes present contribute to the spin–lattice relaxation rate, the activation energy deduced from measurements in this T-range is comparable with that of DC conductivity measurements. In the case of low-dimensional diffusion, the NMR rates are expected to depend on the Larmor frequency applied. Moreover, the slope of the respective flank is lower than in the case of 3D motion for which no frequency dependence should be observed.30,33
If dynamically distinct processes are stepwise activated with increasing temperature, NMR is able to identify these: if widely separated on the dynamic time window they should show up as multiple relaxation rate peaks in an Arrhenius diagram.34 The maxima allow an almost model-independent estimation of mean jump rates by means of the maximum condition linking ω0 and 1/τ: ω0τ ≈ 1.30 A thorough analysis, however, would require a specific relaxation model to interpret the data further, e.g., in terms of diffusion pathways the ions chose. As mentioned above, if the number density of spins in the interfacial regions is large enough, as it is the case for nanocrystalline ceramics, NMR is able to separately probe ion dynamics of the ions residing in or near these zones.
Applications in electrochemical energy storage
The aforementioned aspects of mechanochemistry makes it a highly promising method to prepare materials useful in electrochemical energy storage, in particular. Besides electrochemical stability, ionic conductivity belongs to the key parameters of a good solid electrolyte. The electrolyte is the region that should guarantee extremely fast ion exchange between the two electrodes of a battery.The same applies to electrode materials as well, both fast ion dynamics and fast insertion kinetics crucially determine the performance of a battery, i.e., to accept (ultra-)high charging rates being necessary for today's portable electronics or electric vehicles, for example. Finally, facile and environmentally friendly preparation methods are needed to avoid hazardous chemicals.
As an example, electrode materials for rechargeable Li-ion batteries with aprotic liquid electrolytes were prepared by mechanochemical synthesis by Liao et al., who tested LiFe2F6 as an intercalation compound.6 A similar approach to use Na3FeF6 as a cathode material in Na-ion batteries was reported by Shakoor and co-workers.5 In terms of solid state batteries, the fast Li+ conducting electrolyte Li7P3S11 can be obtained through ball milling of Li2S and P2S5 followed by a soft annealing step to yield a crystalline product.7,8
Research on anion conduction in solids has a long tradition; it was initiated by an experiment of Michael Faraday in 1834. In his experiments Faraday observed the electrical conductivity of lead fluoride (PbF2) at high temperatures. Around 1975 Schoonman, Kennedy, Hunter and others35 reported on the first results to prepare solid-state electrochemical cells based on F ion chemistry. The large change in free enthalpy in the reactions of fluorine with metals and the potentially high voltage in a battery encouraged researchers to prepare a rechargeable cell based on F ion chemistry in 2011.36 One significant drawback of the system, however, was the low mobility of F ions at ambient temperature which triggered research to develop fast solid fluorine ion conductors. From the point of view of fluorine solid electrolytes, the present paper complements an earlier review by Sorokin and Sobolev that was restricted to ion conductivity in coarse-grained MF2–RF3 fluorides (M = Ca, Sr, Ba, Cd, or Pb; R = Sc, Y, or La–Lu) prepared by solid state synthesis.4
Case studies: ion diffusion in mechanosynthesized complex fluorides
The small size and the single negative charge enable F anions to quickly move in solids. To date, MF2–SnF2 (M = Pb, Ba) systems are considered as the fastest F− conductors.37,38 This property is attributed to their layered structure which is the consequence of the ordering effects of the cations, see Fig. 5. Cation ordering is caused by the steric demand of the unpaired electrons of the Sn atoms.39,40 PbSnF4 and BaSnF4 can be prepared by means of solid state synthesis at high temperatures;41–43 alternatively, the ternary fluorides can be synthesized by mechanochemical means as well.43–46 In the case of BaSnF4, the highest conductivity was reached if a mechanochemical milling route was chosen.43,46 The same holds for SnF2: if treated in a high-energy ball its conductivity can be increased by almost two orders of magnitude.47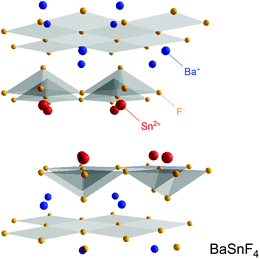 | ||
| Fig. 5 Crystal structure of layered BaSnF4 which belongs to one of the fastest F anion conductors known so far. | ||
Unfortunately, SnF2-based fluorides are highly reactive, i.e., unstable under electrochemical conditions complicating practical applications. Metals from the early groups of the periodic table are considered as more stable and usually possess only one oxidation/reduction state. Usually, the conductivity of these metal fluorides in the form of single crystals or polycrystalline materials is relatively low. It can be enhanced, however, by changing the morphology of the materials, e.g., via nanostructuring including both bottom-up and top-down approaches such as milling.48
In order to increase the number of defects aliovalent doping can be used to facilitate ion dynamics. As an example, mixtures of BaF2 and LaF3 have been extensively studied over the past few years.24,36,49,50 SrF2 represents another substituent to manipulate ion transport in LaF3;51 to the best of our knowledge, such samples have, however, not been prepared mechanochemically as yet. In the following we will present case studies48,50,52–54 including isovalent and aliovalent ion-mixed compounds such as Ba1−xSrxLiF3, Ba1−xCaxF2 and Ba1−xLaxF2+x. Special emphasis will be put on the interplay of (local) structural effects with hopping ion dynamics. Whenever possible comparisons between mechanosynthesized and conventionally prepared materials are drawn.
The inverse perovskite (Ba,Sr)LiF3
The joint milling of cubic BaF2 and LiF results in phase BaLiF3 crystallizing with the inverse perovskite structure (Fig. 6).55 In a normal perovskite the cation with the higher charge is octahedrally coordinated while the cation with the lower charge is cuboctahedrally coordinated, see, e.g., BaTiO3. In BaLiF3, however, the lower charged cation (Li+) is octahedrally coordinated while Ba2+ is located in-between the octahedra. If BaF2 is partially replaced by SrF2 a mixed compound is formed, Ba1−xSrxLiF3, (x can reach values of up to 0.3) that decomposes at elevated temperatures (393 K). Thus, it cannot be prepared by thermochemical routes. Above x > 0.32, X-ray reflections of pure BaF2 and SrF2 appear in the X-ray pattern indicating the upper limit of miscibility. Interestingly, a comparative XRPD and 19F NMR study showed that the mechanochemical reaction proceeds stepwise, starting with the formation of BaLiF3 with the subsequent incorporation of Sr2+ into the ternary fluoride.5219F MAS NMR turned out to be extremely helpful to reveal the local chemical environments of the F nuclei and to unravel the formation mechanism of the quaternary compound.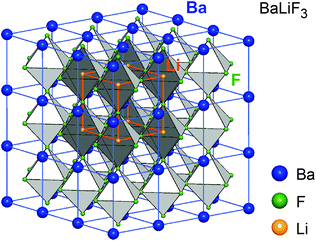 | ||
| Fig. 6 Crystal structure of the inverse perovskite BaLiF3, the smaller Sr-atoms in (Ba,Sr)LiF3 occupy the same sites as Ba. This leads to lattice contraction and local distortions affecting fluorine ion dynamics. Figure adapted from ref. 55. | ||
As an example, in Fig. 7 the 19F MAS NMR spectrum of mechanosynthesized Ba0.74Sr0.26LiF3 is shown. Whereas Sr-free BaLiF3 is characterized by a single NMR line,55 that of earth-alkaline mixed Ba0.74Sr0.26LiF3 is composed of 5 signals representing the different [Sr]a[Ba]b configurations formed (a + b = 4, a,b ∈ ![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) ∪ {0}). Note that in the inverse perovskite structure Ba- and Sr-ions occupy the corner-positions of the cubic unit cells. The face centred fluorine ions span the octahedra that host the lithium ions. The more Sr ions reside in the direct vicinity of 19F the more the isotropic NMR chemical shift value δiso is shifted towards positive ppm values as is illustrated in Fig. 7. As an example, for the [Sr]4 environments in Ba0.74Sr0.26LiF3δiso = 32 ppm is obtained. The areas under the NMR lines, which can be well resolved at spinning speeds as high as 60 kHz, reveal the cation distribution in Ba0.74Sr0.26LiF3.52
∪ {0}). Note that in the inverse perovskite structure Ba- and Sr-ions occupy the corner-positions of the cubic unit cells. The face centred fluorine ions span the octahedra that host the lithium ions. The more Sr ions reside in the direct vicinity of 19F the more the isotropic NMR chemical shift value δiso is shifted towards positive ppm values as is illustrated in Fig. 7. As an example, for the [Sr]4 environments in Ba0.74Sr0.26LiF3δiso = 32 ppm is obtained. The areas under the NMR lines, which can be well resolved at spinning speeds as high as 60 kHz, reveal the cation distribution in Ba0.74Sr0.26LiF3.52
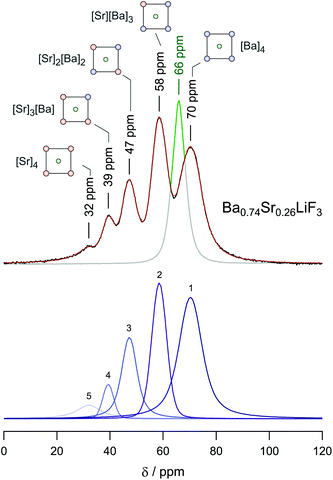 | ||
| Fig. 7 19F MAS NMR spectrum of Ba0.74Sr0.26LiF3 revealing the individual NMR signals of the different environments of the F ions. Since in BaLiF3 the F sites are magnetically equivalent only a single signal shows. Depending on the number of Sr atoms in the direct vicinity of the 19F nucleus the chemical shift ranges from 70 to 32 ppm. Figure taken from ref. 52. | ||
Since Sr2+ is smaller than Ba2+ its incorporation into the BaLiF3 lattice leads to a reduction of the lattice constant with increasing Sr content. Hence, the formation of Ba1−xSrxLiF3 can be followed by the shift of the XRPD reflections of BaLiF3 towards larger diffraction angles. The variations in chemical environments for each fluorine site result in an irregular potential landscape with a distribution of local energy barriers. Obviously, such a distribution facilitates F anion hopping since higher conductivities are reported for the mixed compounds as compared to Sr-free BaLiF3.52 In addition to local strain throughout the bulk structure, disordered regions may be found near the interfacial regions in nanocrystalline Ba1−xSrxLiF3. While the interior of the nanocrystallites reveals an ordered structure, the surface regions are affected by dislocations, as it is shown by the TEM images in Fig. 8.52
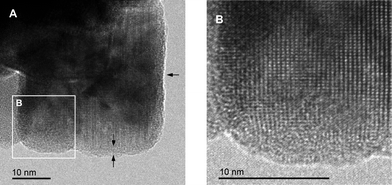 | ||
| Fig. 8 (A) High-resolution TEM image of nanocrystalline (Ba,Sr)LiF3 directly obtained by high-energy ball milling. The enlargement (B) reveals structurally disordered regions at the grain boundaries. Figure taken from ref. 52. | ||
Fluorides crystallizing with a cubic symmetry: (Ba,Ca)F2
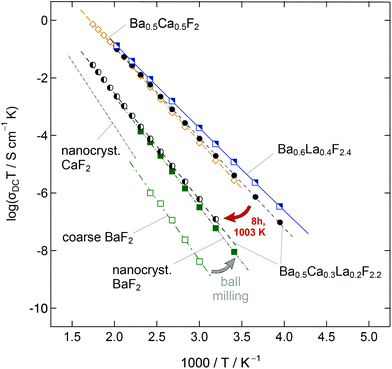
BaF2 and CaF2 do not form a solid solution by high temperature synthesis routes. This observation is due to the large differences in the ionic radii of Ba2+ (1.42 Å) and Ca2+ (1.12 Å). The formation of BaxCa1−xF2, however, can be forced by treating the fluorides in a high-energy planetary ball mill (see Fig. 9).48,54 Isovalent mixing yields a metastable ternary fluoride with a cubic symmetry (Fig. 10a) whose ionic conductivity is about two orders of magnitude higher than that of nanocrystalline, pure BaF2.53 Ion conductivity values derived from impedance spectroscopy are in the order of 1.16 × 105 S cm−1 at 413 K, see also Fig. 10 that shows the variation of conductivity with x.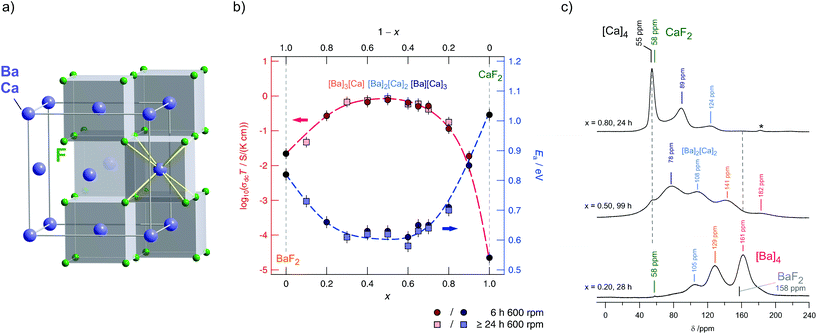 | ||
| Fig. 10 (a) Cubic crystal structure of (Ba,Ca)F2. (b) Variation of conductivity and activation energies for BaxCa1−xF2 samples mechanically prepared by milling the starting materials for 6 h and >24 h in a planetary mill. (c) 19F MAS spectra revealing the local magnetic environments sensed by the F anions. Maximum structural disorder is reached if x = 0.5. Figures (b) and (c) adapted from ref. 53. | ||
If a mixture of BaF2 and CaF2 is milled for sufficiently long in high-energy ball mills, the XRPD unequivocally reveals the formation of a (Ba,Ca)F2 solid solution.53 This results in complex 19F MAS NMR spectra being composed of several NMR lines associated with the [Ba]a[Ca]b environments formed (see Fig. 10c). Differential scanning calorimetry measurements showed that the compound prepared is stable up to ca. 680 K.54 In contrast, lanthanum fluoride forms a stable solution with BaF2. As an example, ionic conductivity in Ba0.5Ca0.3La0.2F2.2, which was prepared under almost the same conditions turns out to be very similar compared to Ba0.5Ca0.5F2. In both cases CaF2 starts to segregate at high temperatures causing the conductivity to drop off. Interestingly, XRPD gave no indications of any LaF3 that was precipitated at a higher T. Thus, the lower conductivity is attributed to crystallite growth, and structural relaxation processes including the ‘healing’ of defects.
Fluorides with a tysonite structure: Ba1−xLaxF2+x
BaF2 and LaF3 are miscible in almost any molar ratio and form stable solutions up to high temperatures which enables thermal as well as mechanochemical syntheses routes. The benefit of mechanochemistry, however, is the creation of defects necessary to yield higher conductivities compared to their highly ordered, crystalline counterparts. Ba0.6La0.4F2.4, which shows the highest conductivity among the Ba1−xLaxF2+x solid solutions,24 was chosen as a model substance to study ion dynamics by both NMR (see Fig. 11) and impedance spectroscopy (Fig. 12).50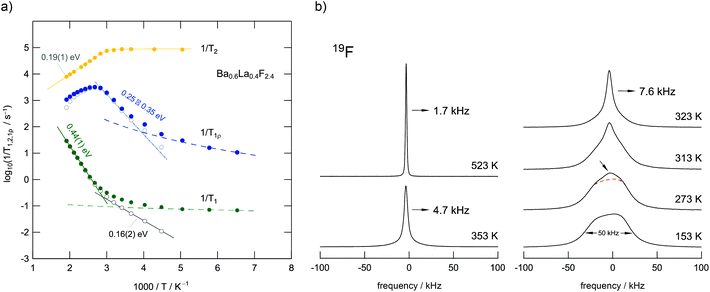 | ||
| Fig. 11 (a) F anion dynamics in Ba0.6La0.4F2.4 as seen via NMR relaxometry. The rates 1/T1 and 1/T1ρ are sensitive to different ionic motions. The same holds for T2 which refers to the transversal decay of magnetization. Most importantly, the 1/T1ρ(1/T) peak can be understood as a superposition of a range of sub-peaks that reflect dynamically distinct diffusion processes occurring in the same temperature range. Presumably, the distribution of activation energies found, i.e., the heterogeneous dynamics seen, results from the local structural disorder introduced by mixing the Ba2+ and La3+ cations that differ in size and charge. (b) 19F NMR lines for Ba0.6La0.4F2.4. At low temperatures, the exchange between the individual F ion positions in the crystal is ‘frozen’ in so that the different environments appear as a superposition of several processes comparable to the relaxation data in Fig. 6. Figure adapted from ref. 50. | ||
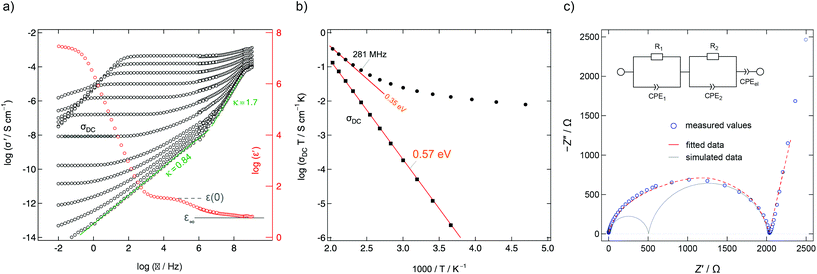 | ||
| Fig. 12 (a) Conductivity isotherms of Ba0.6La0.4F2.4 measured at frequencies ranging from 10 mHz up to 3 GHz (153 K to 513 K in steps of 20 K). At frequencies above 100 MHz the individual isotherms collapse on a high frequency-plateau that shows localized motions of the mobile charge carriers. The ions perform forward–backward jumps due to the short time scale at such frequencies. The chemical environment cannot adjust as fast and the process is almost independent of temperature. (b) Arrhenius diagram highlighting overall DC and AC conductivities determined from data of the real part of the conductivity (σ‘) in the DC regime and at 281 MHz. The latter frequency is similar to the NMR Larmor frequency used to acquire the relaxation rates. Figures adapted from ref. 50. (c) Complex-plane plot of the impedance determining ion transport in Ba0.6La0.4F2.4 at 413 K (10 mHz to 1 GHz). The data can be represented by two R-CPE units (CPE: constant phase element) connected in parallel representing distinct dynamic contributions. Electrode polarization is taken into account with a third CPE. | ||
Mechanosynthesized Ba0.6La0.4F2.4 is characterized by broad XRPD reflections pointing to structural disorder and strain introduced during its preparation.24,50 Static 19F NMR line shapes support this finding; besides the dipolar broadening of the lines recorded can be understood as a superposition of many lines representing the variety of magnetically distinct F environments. Variable-temperature NMR measurements, including line shape studies and relaxation measurements, as well as conductivity measurements reveal complex ion dynamics. Depending on the time scale the NMR method applied is sensitive to the activation energies obtained range from 0.16 eV to 0.44 eV. In particular, the presence of several hopping processes is highlighted in the Arrhenius diagram of Fig. 11 that summarizes NMR relaxometry data on mechanosynthesized Ba0.6La0.4F2.4. While with T1 NMR measurements only the low-T flank of the diffusion-induced rate peak is accessible, the analogous rate 1/T1ρ passes through a maximum; the corresponding peak is, however, unusually broad on the 1/T axis. It directly reflects a wide distribution of ion jump processes occurring on a very similar timescale. Compared to DC conductivity measurements, NMR relaxometry is a probe to uncover local jump processes, i.e., it is possible to reveal the low energy barriers of an irregularly shaped potential landscape that the ions have to surmount.
For comparison, conductivity spectroscopy, if DC plateau values were considered, points to a mean activation energy of 0.57 eV (Fig. 12) being a typical value found for migration processes that are mainly driven by anion vacancies.56 On the other hand, analysing AC conductivities recorded at frequencies similar to the NMR Larmor frequency yields activation energies in agreement with those extracted from NMR (Fig. 12b). At high frequencies σ′ is sensitive to local (forward–backward) jumps, i.e., both methods are able to access dynamic parameters on the same time scale. This similarity is also valid in the regime of very low T: the responses of the two spectroscopic techniques indicate the presence of strictly localized, within-site motions. The latter observation points to a highly irregular distribution of energy barriers in mechanosynthesized Ba0.6La0.4F2.4.50
Channel-structured fluorides: BaMgF4
Besides the formation of structurally disordered solid solutions taking advantage of aliovalent and isovalent ion mixing, mechanosynthesis can be used to prepare functional materials with remarkable purity. BaMgF4, which is a channel-structured ternary fluoride, is accessible via the mechanical treatment of BaF2 and MgF2 under extremely harsh conditions, i.e., at very high rotation speeds.29 Ion transport is influenced by the spatial confinement of the crystal structure. BaMgF4 crystallizes in the orthorhombic Cmc21 structure and consists of strands of corner-sharing MgF6-octahedra that are separated by Ba-ions. These MgF6-octahedra run in parallel with the c-axis of the unit cell and provide a 1-dimensional pathway which is preferred for the conduction of F-ions (see Fig. 13).57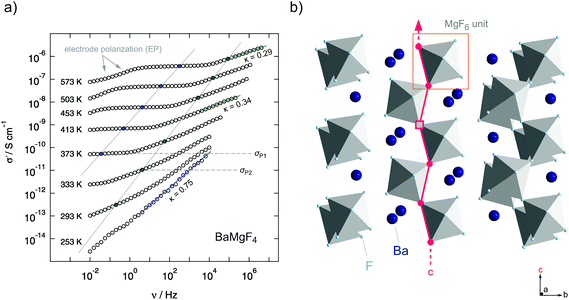 | ||
| Fig. 13 (a) Conductivity isotherms of mechanosynthesized BaMgF4 in a one-pot route. The slope of the isotherms at higher temperatures was close to 0.3 which is associated with low dimensional (1D) transport. (b) Crystal structure of BaMgF4: the corner sharing MgF6-octahedra form a diffusion pathway along the c-axis. Kannan et al. investigated oriented single crystals and reported on the highest conductivity along the c-axis. Figures adapted from ref. 29. | ||
The material, which usually requires high temperatures to be synthesized from a mixture of BaF2 and MgF2,57 could be prepared in a planetary ball mill at rotation speeds as high as 1000 rpm.29 At lower rotation speeds the synthesis remains unsuccessful. We attribute this finding to the strong heat development at the contact region of the milling media (balls/beaker walls) that induces the solid state reaction finally yielding BaMgF4 as the only phase.
The synthesis was followed by XRPD and 19F MAS NMR spectroscopy which is presented in Fig. 14.29 Switching off the mill immediately interrupts the synthesis process; hence, the evolution of the product can directly be followed as a function of the milling time. Interestingly, whereas the XRPD patterns recorded only show reflections of the product formed, 19F MAS NMR reveals that a high amount of the starting materials, MgF2 and BaF2, are still present. Again, this demonstrates the benefits if both methods are used in combination. The increase of the signal intensity in the X-ray powder pattern at low diffraction angles points to the amorphous material that could be attributed to MgF2. Indeed, non-reacted MgF2 is clearly visible in the corresponding 19F MAS NMR spectrum, but is missing or superimposed by the signals of the product in X-ray diffraction. The signal of BaF2 is also likely to be hidden under the broad XRPD reflections of the product. After milling the mixture for three hours the 19F MAS NMR lines attributed to the starting materials completely vanished; according to NMR, at this stage the reaction is complete.
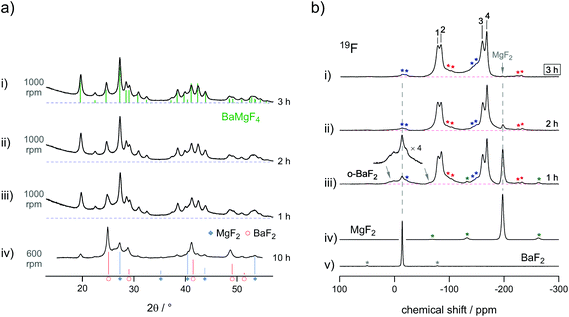 | ||
| Fig. 14 Comparison of the information obtained from (a) X-ray powder diffraction and (b) 19F solid state MAS NMR. The residual starting materials cannot be identified by XRPD (a) but were identified by MAS NMR. The latter one was used to follow the synthesis procedure, which was finished after three hours, as no noteworthy amounts of pure BaF2 or MgF2 could be identified any longer. Figures adapted from ref. 29. | ||
As expected, the MAS NMR spectra show four different lines each representing one of the magnetically non-equivalent F sites in BaMgF4. The lines partly overlap as a result of the local disorder introduced during milling. For comparison, thermochemical approaches or post annealing of the product yield well separated signals due to grain growth and healing of defects.58
It is worth noting that conductivity spectroscopy indeed indicates a quasi-1-dimensional migration pathway that the ions chose to jump over long distances.29 In general, low-dimensional ion transport influences the power law exponent κ describing the dispersive region of the conductivity isotherms (see Fig. 4). In the present case, the low κ values of approximately 0.3 (see the isotherms shown in Fig. 13a) indeed point to F anion migration along the aligned corner-sharing MgF6 units. This finding is in agreement with the results of Kannan et al. who investigated BaMgF4 single crystals.57
Two-dimensional ion conduction: layer-structured BaSnF4
Besides using mechanochemistry to prepare defect-rich materials, it is also a valuable tool to mechanically activate the reactants: the final product is only obtained after a subsequent annealing step. If heat treatment is carried out in a moderate way, defects may be frozen, i.e., partly preserved. The residual defects are anticipated to greatly govern ion transport even in the annealed samples characterized by larger grains. Tetragonal, layer-structured BaSnF4 represents such an example.BaSnF4 is one of the fastest F anion conducting materials known today.38 Similar to BaMgF4, it shows anisotropic conduction characteristics. This behaviour is related to the alternating double-layer structure of BaSnF4 yielding three different types of interlayers built up of either Ba–Ba, Ba–Sn, or Sn–Sn cations. The F anions are distributed between these cation layers with each showing different diffusion characteristics depending on the surrounding cations. Because of the highly ordered environment one can distinguish between fluorine ions located close to Sn-ions or close to Ba-ions. At room temperature, two spin reservoirs were found by 19F MAS NMR spectroscopy, see the work by Grey and co-workers.39 The anions which are distributed in the more rigid Ba–Ba interlayer do not exchange very much with those in the neighbouring Ba–Sn layer; the ions residing in the Ba–Sn layer are the most mobile ones. As was shown for PbSnF4 compounds,59 the occupation of fluorine ions in the Sn–Sn layer is rather low. This observation can be explained by the steric demand of the lone-pairs of the Sn ions.59 Similar anisotropic properties, which will largely affect ion dynamics, are also expected for BaSnF4.
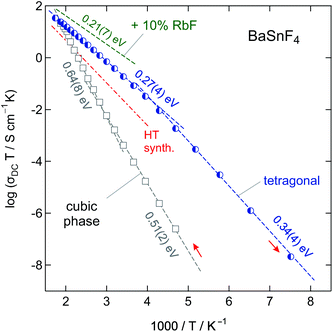
Considering ionic conductivity, the values for mechanochemically synthesized BaSnF4 are the highest reported in the literature so far.46 In contrast to other preparation methods reported, even after the annealing step at 573 K the average crystallite size of BaSnF4 remains small, namely <25 nm according to the equation introduced by Scherrer. This fact might explain the high conductivity found; most likely the remaining defects and large interfacial areas substantially govern F ion dynamics.
To investigate the possible effects of Ba2+-substitution on the conduction behaviour, 10% of BaF2 was replaced with RbF. The comparable ionic radius of Rb+ was expected to be rather compatible with the Ba2+-environment than the smaller Sn2+. The replacement of bivalent Ba2+ with monovalent Rb+ is expected to introduce vacancies and thus to enhance the dynamics of the rigid BaF2-derived sublayer. Indeed, the total conductivity could be increased by about 10% reaching 3 mS cm−1 at room temperature, as it is illustrated in Fig. 15. This value is one of the highest ever reported for BaSnF4.
Summary
This perspective presents a brief overview of the local structures and ion dynamics in defect-rich fluorides recently prepared via mechanochemical routes. Without doubt mechanochemistry, in some cases combined with soft annealing steps, is a powerful synthesis method that enables a facile preparation of complex fluorides, as well as oxides and sulphides that could serve as fast ion conducting materials. It allows a direct preparation of nanocrystalline powders that can be processed in a straightforward way, i.e., without the need for further purification steps. In many cases, due to structural disorder or non-equilibrium effects, the compounds synthesized benefit from improved ion transport properties if compared to conventionally prepared solids. Furthermore, as no high temperatures are needed, metastable compounds can be synthesized that are not accessible by other synthesis routes.Considering fluorine-bearing compounds 19F solid-state MAS NMR, carried out at extremely fast spinning speeds, has been demonstrated as a versatile method to reveal local magnetic structures and hence to shed light on the evolution of the final compounds with increasing milling time. In contrast to X-ray diffraction methods, MAS NMR is not only sensitive to crystalline materials, it is also possible to obtain information about amorphous fractions. In particular, due to the excellent receptivity of the 19F nucleus, fluorides represent highly suitable model compounds to study mechanochemical reactions.
The use of solid state NMR spectroscopy is, however, not limited to the exploration of structural details of disordered solids, but can also be used for the investigation of ion dynamics. In combination with impedance measurements and conductivity investigations the various spin-relaxation methods can be used to study short- as well as long range 19F ion transport. Via the application of both methods the information obtainable ranges from elementary jump processes to long-range (through-going) ion dynamics and contains activation energies, jump rates and diffusion coefficients, respectively. The data retrieved from NMR relaxometry can also provide information on the possible spin reservoirs differing in ion dynamics. This means that in favourable cases a separation of dynamically distinct ions in the bulk and grain boundary regions is possible.
To conclude, a thorough understanding of the formation mechanisms as well as properties of (nano-)crystalline compounds prepared via mechanochemical routes may open the field for future work including the preparation of new fluorides as well as their application in modern energy storage systems, in particular.
Acknowledgements
We thank Stefan Breuer from TU Graz for valuable discussions and help with the preparation of the samples studied. The studies were financially supported by the German Science Foundation DFG within the framework of the Priority Program ‘Crystalline Non-Equilibrium Phases’ (SPP 1415, grant no.: WI 3600 5-2).References
- S. L. James, C. J. Adams, C. Bolm, D. Braga, P. Collier, T. Friscic, F. Grepioni, K. D. Harris, G. Hyett, W. Jones, A. Krebs, J. Mack, L. Maini, A. G. Orpen, I. P. Parkin, W. C. Shearouse, J. W. Steed and D. C. Waddell, Chem. Soc. Rev., 2012, 41, 413–447 RSC.
- V. Šepelàk, A. Düvel, M. Wilkening, K. D. Becker and P. Heitjans, Chem. Soc. Rev., 2013, 42, 7507–7520 RSC.
- P. Balaz, M. Achimovicova, M. Balaz, P. Billik, Z. Cherkezova-Zheleva, J. M. Criado, F. Delogu, E. Dutkova, E. Gaffet, F. J. Gotor, R. Kumar, I. Mitov, T. Rojac, M. Senna, A. Streletskii and K. Wieczorek-Ciurowa, Chem. Soc. Rev., 2013, 42, 7571–7637 RSC.
- N. I. Sorokin and B. P. Sobolev, Crystallogr. Rep., 2007, 52, 842–863 CrossRef CAS.
- R. A. Shakoor, S. Y. Lim, H. Kim, K.-W. Nam, J. K. Kang, K. Kang and J. W. Choi, Solid State Ionics, 2012, 218, 35–40 CrossRef CAS.
- P. Liao, J. Li and J. R. Dahn, J. Electrochem. Soc., 2010, 157, A355–A361 CrossRef CAS.
- K. Minami, A. Hayashi and M. Tatsumisago, J. Am. Ceram. Soc., 2011, 94, 1779–1783 CrossRef CAS.
- D. Wohlmuth, V. Epp and M. Wilkening, ChemPhysChem, 2015, 16, 2582–2593 CrossRef CAS PubMed.
- W. Jones and M. D. Eddleston, Faraday Discuss., 2014, 170, 9–34 RSC.
- L. Takacs, J. Mater. Sci., 2004, 39, 4987–4993 CrossRef CAS.
- C. R. Hickenboth, J. S. Moore, S. R. White, N. R. Sottos, J. Baudry and S. R. Wilson, Nature, 2007, 446, 423–427 CrossRef CAS PubMed.
- U. Hoffmann, C. Horst and U. Kunz, in Integrated Chemical Processes, ed. K. Sundmacher, A. Kienle and A. Seidel-Margenstern, Wiley, Weinheim, 2005, ch. 14, p. 409 Search PubMed.
- A. Chadwick and S. Savin, Solid State Ionics, 2006, 177, 3001–3008 CrossRef CAS.
- P. Heitjans and M. Wilkening, Mater. Res. Bull., 2009, 34, 915–922 CrossRef CAS.
- P. Heitjans and S. Indris, J. Phys.: Condens. Matter, 2003, 15, R1257–R1289 CrossRef CAS.
- S. Indris and P. Heitjans, J. Non-Cryst. Solids, 2002, 307, 555–564 CrossRef.
- M. Wilkening, S. Indris and P. Heitjans, Phys. Chem. Chem. Phys., 2003, 5, 2225–2231 RSC.
- C. C. Liang, J. Electrochem. Soc., 1973, 120, 1289–1292 CrossRef CAS.
- N. Sata, K. Eberman, K. Eberl and J. Maier, Nature, 2000, 408, 946–949 CrossRef CAS PubMed.
- J. Maier, J. Phys. Chem. Solids, 1985, 46, 309–320 CrossRef CAS.
- J. Maier, Prog. Solid State Chem., 1995, 23, 171–263 CrossRef CAS.
- J. Maier, Phys. Chem. Chem. Phys., 2009, 11, 3011–3022 RSC.
- J. Maier, Nat. Mater., 2005, 4, 805–815 CrossRef CAS PubMed.
- A. Düvel, J. Bednarcik, V. Šepelák and P. Heitjans, J. Phys. Chem. C, 2014, 118, 7117–7129 Search PubMed.
- F. P. Bowden and D. Tabor, The Friction and Lubrication of Solids, Clarendon Press, Oxford, 1958 Search PubMed.
- F. P. Bowden and A. Yoffe, Initiation and Growth of Explosion in Liquids and Solids, Cambridge University Press, Cambridge, 1952 Search PubMed.
- F. P. Bowden and A. Yoffe, Fast Reactions in Solids, Butterworths, London, 1958 Search PubMed.
- P. A. Thiessen, K. Meyer and G. Heinicke, Grundlagen der Tribochemie, Akademie-Verlag, Berlin, 1967 Search PubMed.
- F. Preishuber-Pflügl and M. Wilkening, Dalton Trans., 2014, 43, 9901–9908 RSC.
- M. Wilkening and P. Heitjans, ChemPhysChem, 2012, 13, 53–65 CrossRef CAS PubMed.
- A. Kuhn, M. Kunze, P. Sreeraj, H. D. Wiemhöfer, V. Thangadurai, M. Wilkening and P. Heitjans, Solid State Nucl. Magn. Reson., 2012, 42, 2–8 CrossRef CAS PubMed.
- A. Kuhn, S. Narayanan, L. Spencer, G. Goward, V. Thangadurai and M. Wilkening, Phys. Rev. B: Condens. Matter, 2011, 83, 094302 CrossRef.
- V. Epp and M. Wilkening, Phys. Rev. B: Condens. Matter, 2010, 82, 020301 CrossRef.
- A. Kuhn, P. Sreeraj, R. Pöttgen, H. D. Wiemhöfer, M. Wilkening and P. Heitjans, J. Am. Chem. Soc., 2011, 133, 11018–11021 CrossRef CAS PubMed.
- J. Schoonman, J. Electrochem. Soc., 1976, 123, 1772–1775 CrossRef CAS.
- M. Anji Reddy and M. Fichtner, J. Mater. Chem., 2011, 21, 17059–17062 RSC.
- A. V. Chadwick, E.-S. Hammam, D. van der Putten and J. H. Strange, Cryst. Lattice Defects Amorphous Mater., 1987, 15, 303–308 CAS.
- L. N. Patro and K. Hariharan, Solid State Ionics, 2013, 239, 41–49 CrossRef CAS.
- S. Chaudhuri, F. Wang and C. P. Grey, J. Am. Chem. Soc., 2002, 124, 11746–11757 CrossRef CAS PubMed.
- G. Dénès, T. Tyliszczak and P. Hitchcock, J. Solid State Chem., 1991, 91, 1–15 CrossRef.
- G. Dénès, T. Birchall, M. Sayer and M. F. Bell, Solid State Ionics, 1984, 13, 213–219 CrossRef.
- G. Dénès, J. Hantash, A. Muntasar, P. Oldfield and A. Bartlett, Hyperfine Interact., 2007, 170, 145–158 CrossRef.
- L. N. Patro and K. Hariharan, Mater. Res. Bull., 2011, 46, 732–737 CrossRef CAS.
- M. M. Ahmad and K. Yamada, Appl. Phys. Lett., 2007, 91, 052912 CrossRef.
- M. M. Ahmad, Y. Yamane and K. Yamada, J. Appl. Phys., 2009, 106, 074106 CrossRef.
- F. Preishuber-Pflügl, V. Epp, S. Nakhal, M. Lerch and M. Wilkening, Phys. Status Solidi C, 2015, 12, 10–14 CrossRef.
- L. N. Patro and K. Hariharan, Mater. Lett., 2012, 80, 26–28 CrossRef CAS.
- B. Ruprecht, M. Wilkening, S. Steuernagel and P. Heitjans, J. Mater. Chem., 2008, 18, 5412–5416 RSC.
- C. Rongeat, M. A. Reddy, R. Witter and M. Fichtner, J. Phys. Chem. C, 2013, 117, 4943–4950 CAS.
- F. Preishuber-Pflügl, P. Bottke, V. Pregartner, B. Bitschnau and M. Wilkening, Phys. Chem. Chem. Phys., 2014, 16, 9580–9590 RSC.
- H. Geiger, G. Schon and H. Stork, Solid State Ionics, 1985, 15, 155–158 CrossRef CAS.
- A. Düvel, S. Wegner, K. Efimov, A. Feldhoff, P. Heitjans and M. Wilkening, J. Mater. Chem., 2011, 21, 6238–6250 RSC.
- A. Düvel, B. Ruprecht, P. Heitjans and M. Wilkening, J. Phys. Chem. C, 2011, 115, 23784–23789 Search PubMed.
- B. Ruprecht, M. Wilkening, A. Feldhoff, S. Steuernagel and P. Heitjans, Phys. Chem. Chem. Phys., 2009, 11, 3071–3081 RSC.
- A. Düvel, M. Wilkening, R. Uecker, S. Wegner, V. Šepelák and P. Heitjans, Phys. Chem. Chem. Phys., 2010, 12, 11251–11262 RSC.
- D. R. Figueroa, A. V. Chadwick and J. H. Strange, J. Phys. C: Solid State Phys., 1977, 11, 55–73 CrossRef.
- C. V. Kannan, K. Shimamura, H. R. Zeng, H. Kimura, E. G. Villora and K. Kitamura, J. Appl. Phys., 2008, 104, 114113 CrossRef.
- G. Scholz, S. Breitfeld, T. Krahl, A. Düvel, P. Heitjans and E. Kemnitz, Solid State Sci, 2015, 50, 32–41 CrossRef CAS.
- R. Kanno, K. Ohno, H. Izumi, Y. Kawamoto, T. Kamiyama, H. Asano and F. Izumi, Solid State Ionics, 1994, 70, 253–258 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |