Open Access Article
Open Access ArticleThe roles of 4f- and 5f-orbitals in bonding: a magnetochemical, crystal field, density functional theory, and multi-reference wavefunction study†
W. W.
Lukens
*a,
M.
Speldrich
*b,
P.
Yang
*c,
T. J.
Duignan
d,
J.
Autschbach
*d and
P.
Kögerler
 be
be
aChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA, USA. E-mail: wwlukens@lbl.gov
bInstitute of Inorganic Chemistry, RWTH Aachen University, Aachen, Germany. E-mail: manfred.speldrich@ac.rwth-aachen.de
cTheoretical Division, Los Alamos National Laboratory, Los Alamos, NM, USA. E-mail: pyang@lanl.gov
dDepartment of Chemistry, University at Buffalo, State University of New York, Buffalo, NY, USA. E-mail: jochena@buffalo.edu
eJülich-Aachen Research Alliance (JARA-FIT) and Peter Grünberg Institute (PGI-6), Forschungszentrum Jülich, 52425 Jülich, Germany
First published on 31st May 2016
Abstract
The electronic structures of 4f3/5f3 Cp′′3M and Cp′′3M·alkylisocyanide complexes, where Cp′′ is 1,3-bis-(trimethylsilyl)cyclopentadienyl, are explored with a focus on the splitting of the f-orbitals, which provides information about the strengths of the metal–ligand interactions. While the f-orbital splitting in many lanthanide complexes has been reported in detail, experimental determination of the f-orbital splitting in actinide complexes remains rare in systems other than halide and oxide compounds, since the experimental approach, crystal field analysis, is generally significantly more difficult for actinide complexes than for lanthanide complexes. In this study, a set of analogous neodymium(III) and uranium(III) tris-cyclopentadienyl complexes and their isocyanide adducts was characterized by electron paramagnetic resonance (EPR) spectroscopy and magnetic susceptibility. The crystal field model was parameterized by combined fitting of EPR and susceptibility data, yielding an accurate description of f-orbital splitting. The isocyanide derivatives were also studied using density functional theory, resulting in f-orbital splitting that is consistent with crystal field fitting, and by multi-reference wavefunction calculations that support the electronic structure analysis derived from the crystal-field calculations. The results highlight that the 5f-orbitals, but not the 4f-orbitals, are significantly involved in bonding to the isocyanide ligands. The main interaction between isocyanide ligand and the metal center is a σ-bond, with additional 5f to π* donation for the uranium complexes. While interaction with the isocyanide π*-orbitals lowers the energies of the 5fxz2 and 5fyz2-orbitals, spin–orbit coupling greatly reduces the population of 5fxz2 and 5fyz2 in the ground state.
Introduction
The electronic structures of actinide and lanthanide complexes have been the subject of considerable recent attention due largely to improvements in computational techniques that allow accurate calculations of their electronic structures and to advanced spectroscopic techniques, including ligand K-edge X-ray absorption spectroscopy, which allow covalency to be deduced.1–8 The practical reason for the interest in f-element electronic structure is using a better understanding of f-orbital bonding to improve chemical separations: separation of technologically important Nd, Sm, Eu, Dy, and Tb; separation of lanthanides from Am and Cm in spent nuclear fuel reprocessing; and the particularly difficult separation of Am from Cm. The similar ionic radii of these trivalent metal ions result in small separation factors using conventional separations based on “hard” extractants, such as tributylphosphate or di-(2-ethylhexyl) phosphoric acid.9,10 While such separations are possible, they require many separation stages, and better understanding of f-orbital bonding may improve these separations.10Common approaches to studying bonding in actinides and lanthanides are comparing ions with either similar ionic radii, e.g., Ce(III) vs. U(III), or similar electronic structures, e.g., Nd(III) vs. U(III). In the latter case, the main difference is the larger radial extent of the 5f-orbitals relative to the 4f-orbitals. More recently, the relative energies of the ligand and metal orbitals have received increased attention due to their roles in increasing metal-ligand orbital mixing by ‘accidental degeneracy’ (increased mixing due to the similar ligand and metal orbital energies).6–8,11 A particularly attractive and well-studied system for the comparison of 4f and 5f bonding are the tris(cyclopentadienyl) complexes, Cp3M, where Cp is cyclopentadienyl or a substituted cyclopentadienyl ligand and M is a lanthanide or actinide element. In addition to the parent Cp3M complexes, the isocyanide adducts provide additional information about the roles of the 4f and 5f-orbitals. Conejo et al. studied isocyanide adducts of Cp3Ce and Cp3U and concluded that Cp3U was a better π-donor towards isocyanide ligands than Cp3Ce.12
The electronic structures of Cp3Nd (4f3) complexes have been extensively studied by Amberger and co-workers using UV-Vis-NearIR spectroscopy in conjunction with crystal field modeling to determine the splitting of the 4f-orbitals due interactions with the ligands.13–19 This system is particularly amenable to crystal field analysis since the charge-transfer bands and the 4f–5d transitions are in the UV, which provides a wide window for observing the weak f–f transitions on which the analysis is based. In favorable cases, up to 80 transitions have been assigned, which allows many parameters to be varied during crystal field modeling.20 In Cp3Nd, the fy(3x2−y2)-orbital (a′2 in D3h symmetry) interacts with one set of the Cp highest occupied molecular-orbitals (HOMOs). The destabilization of this orbital may be seen in the experimentally derived molecular-orbital (MO) diagram, which is determined by performing a crystal field calculation for an f1 ion with no spin–orbit coupling using the crystal field parameters determined for the Cp3Nd complex.14,16,18,19 The role of this orbital in bonding may also be observed by photoelectron spectroscopy although the effect is more pronounced in the Cp3M+ molecular cations.21 Amberger's work provides an excellent basis for understanding the electronic structures of neodymium complexes and a starting point for exploring the electronic structures of the uranium complexes.
In addition to the spectroscopically observable f–f transitions, the magnetic properties of Cp3Nd could be used to model the crystal field, which would avoid the difficulty of observing and assigning the f–f transitions. However, magnetic data generally contains less information. The number of independent data in powder magnetic susceptibility measurements may be determined conservatively using van Vleck's theorem (eqn (1)), where the energy of state Ei in a magnetic field, H, is Ei = E(0)i + HE(1)i + H2E(2)i + higher order terms.22,23
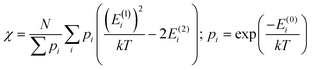 | (1) |
To second order, the ground state provides two independent data (E(1)0 and E(2)0), and each excited state that is appreciably thermally populated provides three additional independent data (E(0)i, E(1)i, E(2)i). Electron paramagnetic resonance (EPR) spectroscopy can provide additional information. Due to the limited independent data in magnetic measurements, refining all parameters in a crystal field analysis is not possible. However, performing an analysis to determine specific information, such as the splitting of the f-orbitals, may be possible.
The electronic structures of Cp3U (5f3) complexes have not received extensive spectroscopic study.24 The 5f–6d transitions are in the visible and tail into the near IR, which makes observing and assigning the weak f–f transitions difficult. Like Cp3Nd, Cp3U has three unpaired f electrons, and magnetic measurements can provide information about its electronic structure. For instance, this approach has been effectively used to determine the oxidation states of uranium in K6Cu12U2S15 from its magnetic susceptibility.25 While spectroscopic studies of Cp3U electronic structure are few, this system has been studied computationally starting with an MO description of the bonding in the Cp3U+ fragment.26 Bonding in Cp3U, its Lewis base adducts, and the lanthanide analogs were studied using Xα-SW methodology.27–30 More recently, bonding between Cp3U and CO has been studied using DFT,31 and covalency in Cp3U and its transuranic analogues has been studied by Kaltsoyannis.8 Overall, these studies suggest that the 5f-orbitals do not participate extensively in bonding with two important exceptions. As observed in Cp3Nd, the Cp3U fy(3x2−y2)-orbital interacts with one set of the Cp HOMOs. In addition, the fz3-orbital can interact when an additional ligand is coordinated along the C3 axis. Interestingly, the fxz2 and fyz2-orbitals, which could form a back-bond with π-acceptor ligands, such as CO, are only weakly stabilized, and work by Maron et al. suggests that backbonding by the 5f-electrons to the ligand π-acceptor-orbitals does not greatly stabilize these complexes.31 On the other hand, DFT and multi-reference wavefunction calculations have indicated strong, covalent π-interactions in Cp3UIV–NO involving the 5f π-orbitals and antibonding π*-orbitals of the NO ligand, such that the ground state is non-magnetic.32,33
In this manuscript, we report the syntheses of complexes Cp′′3M and Cp′′3M·L, where Cp′′ is 1,3-bis-(trimethylsilyl)cyclopentadienyl, M = La, Nd, U, and L is tert-butylisocyanide (tBuNC) or cyclohexylisocyanide (CyNC). The complexes (1: Cp′′3Nd; 2: Cp′′3Nd·tBuNC; 3: Cp′′3Nd·CyNC; 4: Cp′′3U; 5: Cp′′3U·tBuNC; 6: Cp′′3U·CyNC; 7: Cp′′3La; 8: Cp′′3La·tBuNC) were characterized using IR spectroscopy (1–8), EPR spectroscopy (1–6), and magnetic susceptibility (1–6). The electronic structures of the complexes were determined from the magnetic data (magnetic susceptibility and EPR spectra) using the full crystal field model implemented in the computational framework CONDON.34 The electronic structures of (1–6) were also determined computationally by density functional theory (DFT) and multireference wavefunction calculations. The goals of this study were to determine whether the electronic structures of these compounds may be determined using magnetic data and “free ion” parameters taken from similar compounds. The results of the analysis are compared with previous crystal field analyses of Cp3Nd complexes and with computational models. The roles of the 4f and 5f-orbitals in the parent Cp′′3M complexes and their interactions with the electron-accepting isocyanide ligands are discussed.
Experimental
Synthetic procedures
Syntheses were performed using Schlenk and inert atmosphere glovebox techniques. Solvents were freshly distilled from sodium/benzophenone ketyl. tBuNC and CyNC were obtained commercially, dried over Na and degassed before use. Cp′′H was prepared as previously described except that cyclopentadienyl and trimethylsilylcyclopentadienyl anions were prepared using potassium metal rather than butyllithium.35 Cp′′3U·tBuNC (5) was prepared as previously reported.12 Cp′′3Nd (1), Cp′′3U (4) and Cp′′3La (7) were previously prepared by different routes.12,36 Nd[N(SiMe3)2]3 and La[N(SiMe3)2]3 were prepared as described by Bradley et al.37 Examples of the synthesis of Cp′′3M and the base adducts are given here, and full details are provided in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 (2.00 g, 3.20 mmol) was dissolved in 50 mL of toluene, and Cp′′H (2.53 mL, 2.15 g, 10.2 mmol) was added by syringe. The solution was heated to 110 °C. After stirring for 5 days, the color had changed from blue to green. The toluene was slowly removed under vacuum at 100 °C giving oily, green blocks. The blocks were dissolved in 50 mL of hexane, and the solution was filtered. The volume of the solution was reduced to ca. 25 mL. Cooling to −20 °C produced large, light green prisms (1.68 g, 68%). MP: 191–196 °C. 1H NMR, δ = 33.70 (1H, FWHM = 27 Hz), 15.15 (2H, FWHM = 35 Hz), −7.53 (18H, FWHM = 5 Hz) ppm. IR: 3050(w), 1320(w), 1245(s), 1209(w), 1201(w), 1079(s), 920(s), 833(s), 778(s), 751(s), 690(m), 641(m), 621(m) cm−1. MS (M − CH3)+, m/z (calc, found): 754(63, 63), 755(70, 70), 756(100, 100), 757(78, 79), 758(84, 84), 759(47, 46), 760(37, 36), 761(18, 18), 762(22, 21), 763(12, 11). Anal. Calc for C33H63Si6Nd: 51.3; H, 8.22%. Found: C, 50.3; H, 8.29%. Note: elemental analyses for complexes of the Cp′′ ligand are usually low in C, presumably due to the formation of SiC.
37 (2.00 g, 3.20 mmol) was dissolved in 50 mL of toluene, and Cp′′H (2.53 mL, 2.15 g, 10.2 mmol) was added by syringe. The solution was heated to 110 °C. After stirring for 5 days, the color had changed from blue to green. The toluene was slowly removed under vacuum at 100 °C giving oily, green blocks. The blocks were dissolved in 50 mL of hexane, and the solution was filtered. The volume of the solution was reduced to ca. 25 mL. Cooling to −20 °C produced large, light green prisms (1.68 g, 68%). MP: 191–196 °C. 1H NMR, δ = 33.70 (1H, FWHM = 27 Hz), 15.15 (2H, FWHM = 35 Hz), −7.53 (18H, FWHM = 5 Hz) ppm. IR: 3050(w), 1320(w), 1245(s), 1209(w), 1201(w), 1079(s), 920(s), 833(s), 778(s), 751(s), 690(m), 641(m), 621(m) cm−1. MS (M − CH3)+, m/z (calc, found): 754(63, 63), 755(70, 70), 756(100, 100), 757(78, 79), 758(84, 84), 759(47, 46), 760(37, 36), 761(18, 18), 762(22, 21), 763(12, 11). Anal. Calc for C33H63Si6Nd: 51.3; H, 8.22%. Found: C, 50.3; H, 8.29%. Note: elemental analyses for complexes of the Cp′′ ligand are usually low in C, presumably due to the formation of SiC.
Physical measurements
IR spectra were recorded as Nujol mulls between CsI plates using a Perkin Elmer 283 spectrometer. NMR spectra were recorded in C6D6 using a Jeol FX-90Q spectrometer. Electron paramagnetic resonance (EPR) spectra were obtained below 5 K with a Varian E-12 spectrometer equipped with a liquid helium cryostat, an EIP-547 microwave frequency counter, and a Varian E-500 gaussmeter, which was calibrated using 2,2-diphenyl-1-picrylhydrazyl (DPPH, g = 2.0036). The low temperature EPR spectra were fit using a version of the code ABVG38 modified to fit spectra in the frequency regime as suggested by Pilbrow39 and to fit spectra using the downhill simplex method.40 Magnetic measurements were conducted in a 7 T Quantum Design MPMS magnetometer utilizing a superconducting quantum interference device (SQUID). Between 50 and 100 mg of sample were contained in a KelF capsule, which was sealed with silicone grease. The data are corrected for the diamagnetism of the capsule. The data are also corrected for the overall diamagnetism of the molecule using Pascal constants.Crystal field model (CONDON)34
To analyze the magnetic characteristics of the title compounds, we focus on the splitting and mixing of the relevant multiplet energy levels, mainly those of 4I9/2 and 4I11/2 for these f3 complexes, considering all relevant interactions. Electrons in filled, inner shells are not included.A magnetically isolated, f3 metal ion in a ligand environment with a specific point symmetry is described by the following Hamiltonian in the presence of an external magnetic field:
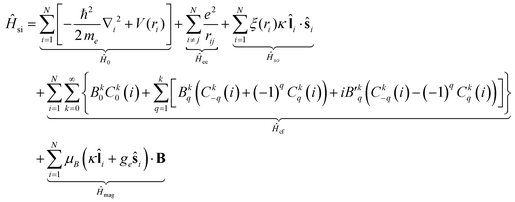 | (2) |
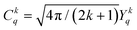 denote the spherical tensors, which are directly related to the spherical harmonics Ykq and Bkq (Wybourne's notation).44 As with Ĥ0, the spherically symmetric term B00C00 does not change the relative energies of the states and is not included. The summation (i) is carried out over the number of electrons, N. For f-electrons, terms in the expansion with k > 6 are zero, and all terms with odd k values are zero due to the orthogonality relations of the spherical harmonics. The values of k and q for which Bkq is not zero are determined by the point symmetry of the metal ion site.
denote the spherical tensors, which are directly related to the spherical harmonics Ykq and Bkq (Wybourne's notation).44 As with Ĥ0, the spherically symmetric term B00C00 does not change the relative energies of the states and is not included. The summation (i) is carried out over the number of electrons, N. For f-electrons, terms in the expansion with k > 6 are zero, and all terms with odd k values are zero due to the orthogonality relations of the spherical harmonics. The values of k and q for which Bkq is not zero are determined by the point symmetry of the metal ion site.
The temperature dependence of thermodynamic parameters (susceptibility, specific heat contributions, etc.) in an applied magnetic field, B, is introduced by Ĥmag shown in eqn (2).34,45,46 The component of the molar magnetization in direction α = x, y, z of the applied field B, Mm,α, is determined using Boltzmann statistics (eqn (3)).
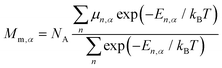 | (3) |
The molar magnetic susceptibility along α is calculated as χm,α = μ0Mm,α/|B| (μn,α = μn⋅B/|B|), which is also accurate at higher magnetic fields where the magnetization is not linear with respect to the field, as we are including not only the multiplet ground state but the entire multiplet energy spectrum. The mean value χm,av is given by the averaged sum of its principal components, χm,av = (χxx + χyy + χzz)/3 = tr(χm)/3.47 Since the trace of a tensor is independent of the choice of the basis, any basis may be selected as long as the three diagonal elements of χm are calculated in that basis and averaged to obtain χm,av.
Density functional theory computational details
First principles calculations were performed using PBE0 exchange–correlation functional48,49 implemented in the Amsterdam Density Functional (ADF 2014.07) program.50–52 Scalar relativistic effects were taken into account by the ZORA formalism to the Dirac equation.53 TZ2P basis sets with small cores were used for geometry optimization and QZ4P were used for property analysis.54 The syntheses of these compounds were carried out in hexane. Since hexane is a non-polar solvent and the complexes themselves are neutral in charge, solvation has little effect on the structures and binding energies of these complexes. Results comparing molecular properties of (C5H5)3Nd·tBuNC (2′) in the gas phase and in hexane are given in Table S5 (ESI†).Multi-reference wavefunction computations
Relativistic ab initio wavefunction calculations were carried out for complexes 2′ (Nd(III)) and 5′ (U(III)) with a developer's version of the Molcas program similar to release 8.55 The second-order Douglas–Kroll–Hess scalar relativistic Hamiltonian56 was employed in the calculations without spin–orbit (SO) coupling, along with all-electron ANO-RCC Gaussian-type basis sets contracted to TZP (DZ for H) quality (U = 26s23p17d13f5g3h/9s8p6d4f2g1h; Nd = 25s22p15d11f4g2h/12s11p8d7f4g2h, C, N = 14s9p4d3f2g/4s3p2d1f; H = 8s/2s). The computations used state-averaged Complete Active Space Self Consistent Field (CASSCF) wavefunctions.57 Spin–orbit (SO) coupling was treated by state interactions between the CASSCF wavefunctions, using a modified version of the Restricted Active Space State Interaction (RASSI) program.58,59 For brevity, the scalar relativistic or ‘spin-free’ (SR, i.e. not including SO coupling) and the calculations with SO coupling are referred to as SCF-SR and SCF-SO, respectively. The magnetic data were calculated according to ref. 60–63. For a combined visual inspection of the electronic states, natural-orbitals of the SO wavefunctions were generated as explained in ref. 55, 64, and 65. The active spaces for the complexes were the 3 unpaired f electrons in the seven 4f- or 5f-orbitals.Results
Synthesis and IR spectroscopy
Cp′′3M complexes were prepared by the reaction of M[N(SiMe3)2]3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37,66 with Cp′′H in toluene followed by recrystallization from hexane. The properties of Cp′′3M are identical to those previously reported.12,36 The base adducts were prepared by adding the ligand to a hexane solution of Cp′′3M. The reactions are rapid, and the 1
37,66 with Cp′′H in toluene followed by recrystallization from hexane. The properties of Cp′′3M are identical to those previously reported.12,36 The base adducts were prepared by adding the ligand to a hexane solution of Cp′′3M. The reactions are rapid, and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct is the only product as determined by elemental analysis, NMR and IR spectroscopy, and the yield of the reaction.
1 adduct is the only product as determined by elemental analysis, NMR and IR spectroscopy, and the yield of the reaction.
The IR stretching frequencies of isocyanide ligands and carbon monoxide coordinated to Cp3U have been previously investigated, and Cp3U complexes were found to act as effective π-donors towards isocyanide ligands.12 The CN stretching frequency of the coordinated isocyanide ligand reflects the relative roles of the metal center as a σ-acceptor and a π-donor. Interaction between unoccupied metal orbitals and the filled isocyanide σ-orbital increases the CN stretching frequency, and π-donation from occupied metal orbitals into the unoccupied π*-orbitals lowers the stretching frequency.67 In Cp′′3La·tBuNC (8), the CN stretching frequency increases by ∼30 cm−1 relative to the free ligand, suggesting that tBuNC acts only as a σ-donor in this complex as one would expect since the La(III) center has no f-electrons to donate to the isocyanide π*-orbitals. Interestingly, the CN stretching frequency of the Cp′′3Nd adduct is identical to that of Cp′′3La, which strongly suggests that the Nd 4f electrons do not to back-bond to the ligand. Similar behavior has been observed previously in isocyanide adducts of Cp3Ce.12 On the other hand, the CN stretching frequency for the Cp′′3U adduct is significantly lower in energy than in either lanthanide complex, which suggests that the 5f electrons, unlike the 4f electrons, can back-bond with the isocyanide π*-orbitals (Table 1).
DFT calculation results
DFT calculations were employed to provide insights into the energetics of ligand binding and to provide a benchmark for comparison of the experimental MO schemes determined by crystal field fitting. The tBuNC system is used as an example herein. In these calculations, the Cp′′ ligand was simplified to C5H5 to reduce the computational cost while maintaining its chemical nature. To understand the bonding interactions between the isocyanide ligand and the metal center, we conducted hybrid DFT calculations of free tBuNC ligand, (C5H5)3Nd·tBuNC (2′), and (C5H5)3U·tBuNC (5′). The selected geometric parameters of the optimized structures are listed in Table 2. Since no crystal structures of these metal compounds are available for direct comparison, the CN stretching frequency was used as the reference. The vibrational analyses show that these optimized geometries are in good agreement with experimental results by correctly predicting the changes of CN stretching frequency upon ligand binding. The binding of tBuNC to the (C5H5)3Nd increases the CN stretching frequency by 20 cm−1 compared to the free ligand, which is in good agreement with the 32 cm−1 increase observed experimentally. In contrast, the coordination of tBuNC to (C5H5)3U decreases the CN stretching frequency by 64 cm−1 and lengthens the CN bond by 0.05 Å. The experimental data also shows a decrease but with a much smaller magnitude of 6 cm−1. This decrease is due to the back-donation of 5f electrons to the ligand π*-orbitals in (C5H5)3U·tBuNC (vide infra), which results in stronger metal ligand bonding in the trivalent uranium complex. The binding energies of tBuCN further verify this conclusion by giving −21.77 kcal mol−1 for Cp3U and −16.37 kcal mol−1 for Cp3Nd, respectively.| tBuNC | (C5H5)3Nd·tBuNC (2′) | (C5H5)3U·tBuNC (5′) | |
|---|---|---|---|
| M–C (Å) | — | 2.603 | 2.466 |
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N (Å) N (Å) |
1.170 | 1.165 | 1.175 |
| N–C (tBu) (Å) | 1.436 | 1.439 | 1.436 |
| Angle (CNC) | 179.8° | 178.7° | 179.4° |
| CN stretching freq. calc (cm−1) | 2178 | 2198 | 2114 |
| CN stretching freq. expt (2 and 5) (cm−1) | 2146 | 2178 | 2140 |
| Ligand binding energy (kcal mol−1) | — | −16.37 | −21.77 |
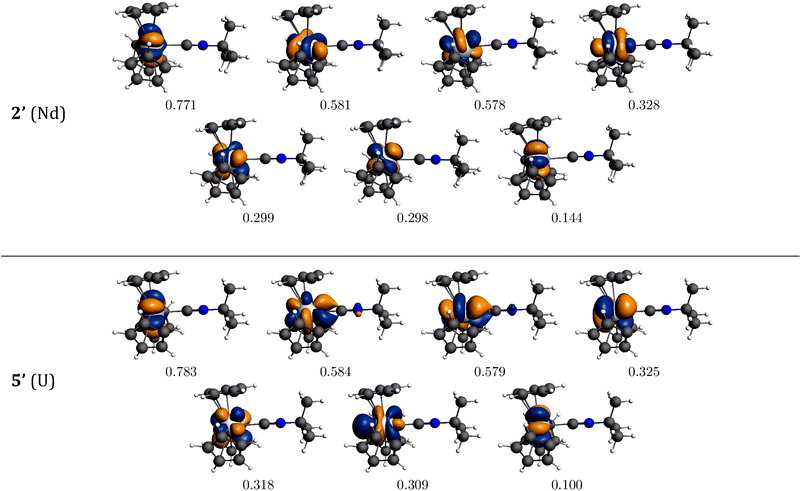
The bonding interaction of the isocyanide ligand with the trivalent metal center is dominated by the σ-donation to the dz2-orbital, shown in Fig. 1. In 2′, the 4f electrons are almost exclusively localized at the Nd center in singly occupied molecular orbitals (SOMOs) and result in the spin density of 3.0. SOMOs 1–3 are mainly fxz2, fz3 and fx(x2−3y2), respectively, and are nearly degenerate. In 2′, the f-orbital coordinate system is not aligned with the molecular C3 axis (fz3, SOMO-2 in Fig. 1, does not lie on the C3 axis). With respect to the C3 axis, SOMO-2 has π symmetry and corresponds to fyz2 due to the change in coordinate system. Interestingly, the ordering of the orbitals is the same as if back-bonding were important; that is, the lowest lying SOMOs are those with the proper symmetry to interact with the tBuNC π*-orbitals. Nevertheless, the SOMOs depicted in Fig. 1 illustrate that the 4f electrons have little or no overlap with the tBuNC ligand and do not back donate to the ligand as reflected by the spin density and the experimental and calculated values of v(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N).
N).
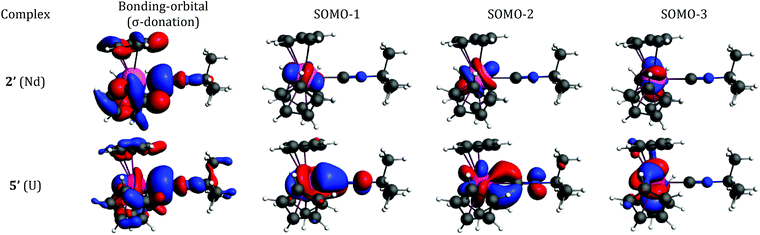 | ||
| Fig. 1 Bonding analysis of (C5H5)3Nd·tBuNC (2′) and (C5H5)3U·tBuNC (5′) from DFT calculations. Isosurfaces at ±0.03 atomic units for both 2′ and 5′. | ||
Unlike the 4f-orbitals, the 5f-orbitals display strong overlap with the ligand π*-orbitals. The lowest lying-orbitals in 5′, SOMO-1 and SOMO-2 are those with π-symmetry with respect to the molecular 3-fold axis (mainly fxz2 and fyz2). SOMO-3 is an orbital with ϕ-symmetry, fx(x2−3y2), which has no overlap with either the Cp or isocyanide ligands. The 5f electrons back-donate to the π*-orbitals of the ligand (Fig. 1), which reduces the spin density at the uranium center to 2.68. As a consequence, the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond distance is lengthened, and the C
N bond distance is lengthened, and the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretching mode is decreased. The calculated reduction in v(C
N stretching mode is decreased. The calculated reduction in v(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N) in 5′ is large compared to experiment (64 cm−1versus 6 cm−1), especially in light of the agreement between the calculated and experimental values in 2′. This difference may be attributed to spin–orbit coupling as addressed below.
N) in 5′ is large compared to experiment (64 cm−1versus 6 cm−1), especially in light of the agreement between the calculated and experimental values in 2′. This difference may be attributed to spin–orbit coupling as addressed below.
EPR, magnetism and crystal field modeling
In general, it is more difficult to interpret the spectra and magnetic behavior of actinide compounds than lanthanide compounds. In lanthanides, electron repulsion (Hee ≈ 105 cm−1), is much stronger than either spin–orbit coupling (Hso ≈ 103 cm−1) or crystal field potential (Hcf ≈ 103 cm−1). Consequently, lanthanide electronic structure is well described by Russell–Saunders coupling, where L, S, and J are ‘good’ quantum numbers. In actinides, Hee is weaker and Hso and Hcf are much stronger than in the lanthanides. As a result, L, S, and J are not ‘good’ quantum numbers, and Russell–Saunders coupling is no longer accurate.69 U(III) has three unpaired 5f electrons, with a 4I (S = 3/2, L = 6) ground state and total angular momentum, J = 9/2; this leads to a 4I9/2 ground state (ground multiplet) in Russell–Saunders coupling. Strong spin–orbit coupling mixes other J = 9/2 states into the 4I9/2 ground state. Previous spectroscopic studies of U(III) ions show that the “free ion” ground state has a significant 2H9/2 (15.2%) character.69 This mixing of excited terms into the ground state is a result of the breakdown of Russell–Saunders coupling, and renders it difficult to model variable temperature magnetic susceptibility.70,71The impact of the ligand field on electronic structure is significantly larger in the actinides than in the lanthanides because the greater radial extent of the 5f-orbitals allows better metal ligand overlap. The ligand field removes the (2J + 1)-fold degeneracy of the ground state giving rise to 2J + 1 sublevels with mJ = −J, −J + 1, … , J. The degeneracies of the resulting mJ sublevels are determined by the site symmetry of the metal ion. The energies of the mJ sublevels depend on the orientation and strength of the ligand field. The ligand field also allows excited states with J ± 1 to mix into the ground state. The aforementioned mixing of excited states into the “free ion” ground state complicates the mixing and splitting of the 5f-orbitals. The degree of mixing depends on the relative strengths of the single ion effects (Hee, Hso, Hcf), which can produce complex electronic structures for actinide complexes. In many cases, energies of the lowest sublevels are smaller than kT at room temperature, and the effective magnetic moment, μeff, is highly temperature dependent. Because the single-ion effects (Hee, Hso, Hcf) are similarly strong in actinide complexes, using a perturbation approach to model the crystal field is inaccurate. To determine the 5f electronic structure from physical measurements, the full Hamiltonian (eqn (2)) must be diagonalized with respect to all single-ion effects simultaneously.
To assess whether our approach to the magnetic structures of Cp′′3Nd (1), Cp′′3U (4), and their isocyanide adducts is effective, the parameters determined by modeling the magnetic properties are compared with DFT computational results and crystal field parameters previously obtained by fitting the energies of the f–f transitions. The parameters that we are primarily interested in are the crystal field parameters (Bkq), which reflect f-orbital splitting and the strength of their bonding interactions with the ligands.
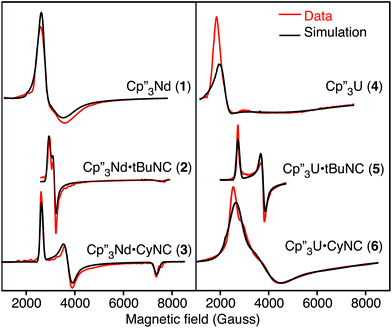
The EPR spectra of the neodymium and uranium complexes are shown in Fig. 2 and their g-values, determined by fitting the spectra, are given in Table 3. The spectra of Cp′′3Nd·L are easily interpreted since the individual g-components are distinct. Both spectra are nearly axial with that of 3 showing slightly more distortion than that of 2. The EPR spectra of all the neodymium complexes are remarkably similar to each other. While the spectrum of 1 appears quite different from those of 2 and 3, the main difference is that the spectrum of 1 is much broader. The other difference is that g|| of 1 is at a field greater than 1 T and is not observed. The EPR spectrum of 4 is similar to that of 1, except that it is somewhat broader and g⊥ is greater. The spectra of 5 and 6 are somewhat similar to 2 and 3.
| Complex | g 1 | g 2 | g 3 | g || (expt)a | g ⊥ (expt)a | g || (calc)b | g ⊥ (calc)b |
|---|---|---|---|---|---|---|---|
| a The high field component is assigned to g|| with respect to the pseudo-C3 axis of the molecule, and the low field g-components are averaged to give g⊥ based on the work by Amberger and coworkers. b From the crystal field model derived from CONDON simulations. | |||||||
| 1 | 2.44 | 2.06 | <0.7 | <0.7 | 2.25 | 0.69 | 2.27 |
| 2 | 2.25 | 2.08 | 0.87 | 0.87 | 2.17 | 1.02 | 2.17 |
| 3 | 2.51 | 1.77 | 0.89 | 0.89 | 2.14 | 0.90 | 2.22 |
| 4 | 3.03 | 2.31 | <0.7 | <0.7 | 2.69 | 0.45 | 2.75 |
| 5 | 2.42 | 1.75 | <0.7 | <0.7 | 2.09 | 0.81 | 2.12 |
| 6 | 2.40 | 1.68 | 1.04 | 1.04 | 2.04 | 1.06 | 2.06 |
Least-squares fits from CONDON crystal field calculations
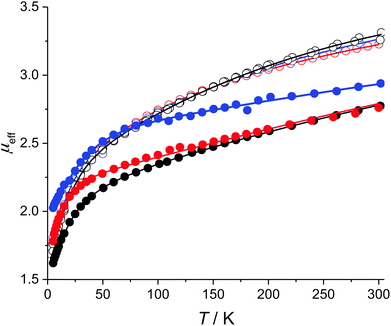
The low-field magnetic DC susceptibility data for 1–6 are illustrated in Fig. 3. In all cases, μeff is strongly temperature dependent, which is consistent the presence of low-lying mJ sublevels that are populated below 300 K. The neodymium complexes have nearly identical magnetic susceptibilities from 2 to 300 K, which suggests that coordination of the isocyanide ligands to 1 only weakly perturbs the electronic structures of the thermally populated states. In contrast, the magnetic susceptibility curves of 4–6 are quite different from each other, which suggests that the electronic structures of the uranium complexes are more strongly perturbed by the addition of an isocyanide ligand. This qualitative difference between the Nd and U complexes reflects the greater radial extent of the 5f-orbitals relative to the 4f-orbitals.As noted above, modeling the temperature-dependent magnetic moments of 1–6 requires accounting for all single-ion effects including determining the approximate starting values for the crystal field parameters (Bkq), spin–orbit coupling (ζ), and Slater–Condon electron–electron repulsion parameters (Fn). For both U and Nd, the values of ζ and Fn were taken from those determined for Tp3M, where Tp is hydrotris(1-pyrazolyl)borato, since this is the only system for which parameters are available for both Nd(III) and U(III).15 Starting values of Bkq were taken from (C5HMe4)3Nd and Tp3U for the neodymium and uranium compounds, respectively.13,15 To avoid over parameterizing the fit, only Bkq are varied while the values of ζ, F2, F4, and F6 were fixed. The fixed parameters mainly reflect the overall covalency in the complex and are not expected to vary significantly between Cp′′3M and Cp′′3M·L; moreover, these parameters do not directly affect the splitting of the f-orbitals—as such, fixing ζ, F2, F4, and F6 to appropriate values should not significantly impact the crystal field parameters, which are the focus of this study.
To reduce the number of crystal field parameters, the site symmetries of Cp′′3M and Cp′′3M·L are assumed to be D3h and C3v, respectively, which leads to the crystal field Hamiltonians given in eqn (4) and (5).
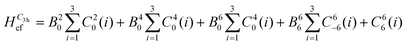 | (4) |
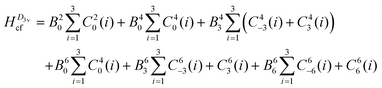 | (5) |
Using these crystal field Hamiltonians, the magnetic susceptibility and EPR values of 1–6 were fitted using CONDON to determine the values of the crystal field parameters. The fitting results are shown in Fig. 3, and the modeling parameters are given in Table 4. The values of Bkq determined for 1 may be compared with those of other Cp3Nd complexes with bulky Cp ligands. As shown in Table S1,† crystal field parameters are very similar for all complexes, which supports the notion that the Bkq determined by modeling the magnetic data are consistent with those determined by fitting the energies of the excited states. The average relative uncertainty in the values of Bkq in Table 4 is 10%, which is approximately twice as large as the uncertainty in the values of Bkq determined by fitting optical data.20 The greater uncertainty is due, in part, to the limitation on the number of variables in the CONDON fit imposed by the independent data available in magnetic data. Nevertheless, the uncertainties in the values of Bkq determined by fitting the magnetic data are small relative to the values of Bkq.
| Cp′′3Nd (1) | Cp′′3Nd·tBuNC (2) | Cp′′3Nd·CyNC (3) | Cp′′3U (4) | Cp′′3U·tBuNC (5) | Cp′′3U·CyNC (6) | |
|---|---|---|---|---|---|---|
a Quality of fit: 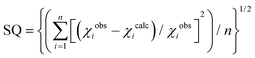 . .
|
||||||
| F 2 | [71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 714] 714] |
[71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 714] 714] |
[71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 714] 714] |
[36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 305] 305] |
[36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 305] 305] |
[36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 305] 305] |
| F 4 | [52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 182] 182] |
[52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 182] 182] |
[52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 182] 182] |
[26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 452] 452] |
[26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 452] 452] |
[26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 452] 452] |
| F 6 | [35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 286] 286] |
[35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 286] 286] |
[35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 286] 286] |
[23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130] 130] |
[23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130] 130] |
[23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130] 130] |
| ζ | [881] | [881] | [881] | [1516] | [1516] | [1516] |
| B 20 | −3184 ± 56 | −1395 ± 13 | −2781 ± 13 | −777 ± 189 | −3165 ± 103 | −3660 ± 135 |
| B 40 | 1597 ± 25 | 828 ± 91 | 733 ± 186 | 6418 ± 830 | 5890 ± 631 | 2744 ± 336 |
| B 43 | — | −156 ± 79 | −557 ± 176 | — | −2410 ± 251 | −1280 ± 276 |
| B 60 | 973 ± 27 | 1199 ± 45 | 925 ± 149 | 752 ± 21 | 5700 ± 141 | 4705 ± 318 |
| B 63 | — | −475 ± 18 | −672 ± 47 | — | 3650 ± 204 | 3250 ± 142 |
| B 66 | −2665 ± 43 | −1697 ± 15 | −1959 ± 89 | −8220 ± 215 | −1160 ± 76 | −2290 ± 127 |
| ΔE | 60.2 | 63.0 | 62.1 | 90.0 | 49.0 | 73.0 |
| LFOS, 4I | 7161 | 6840 | 6968 | 9400 | 9370 | 9460 |
| LFOS, 4I9/2 | 1110 | 781 | 780 | 1514 | 1720 | 1570 |
| Ground state (mJ) | ∓5/2 (67%) | ∓5/2 (68%) | ∓5/2 (64%) | ∓5/2 (53%) | ∓5/2 (45%) | ∓5/2 (61%) |
| ±7/2 (32%) | ±7/2 (27%) | ±7/2 (25%) | ±7/2 (46%) | ±1/2 (44%) | ±7/2 (10%) | |
| ±1/2 (4%) | ±1/2 (9%) | ±1/2 (26%) | ||||
| SQa | 0.007 | 0.008 | 0.009 | 0.010 | 0.010 | 0.010 |
Discussion
In the following paragraphs, we compare the electronic structures of 1–6 as determined by DFT and the parameters in Table 4. The structures will be analyzed in two ways. The electronic structures of the f3 systems including the energies and crystal field wavefunctions of the mJ substates of 4I9/2 will be discussed. In addition, the experimental MO scheme in the absence of spin–orbit coupling (nonrelativistic MO scheme) can be derived by diagonalizing the energy matrices of an f1 ion using the ligand field parameters given in Table 4 with ζ equal to zero. As shown by Amberger and coworkers, this approach produces an experimentally derived MO description of the splitting of the f-orbitals due to interaction with the ligands. The orbitals in the MO scheme are labeled by the f-orbital with the largest contribution. These MO schemes may be directly compared with the DFT computational results, which do not explicitly include spin–orbit coupling. Based on these MO-schemes, we discuss changes in the metal–ligand bonding between the actinides and lanthanides.Cp′′3M (1 and 4)
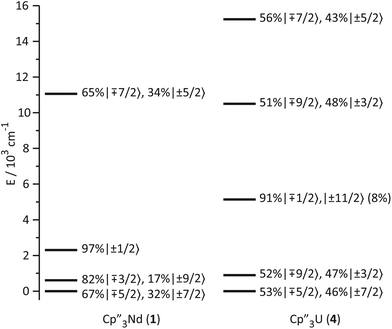
The low-lying excited states (substates of 4I9/2) of 1 and 4 are shown in Fig. 4, and their ground state, crystal field wavefunctions are similar. In both, the ground state is a mixture of mJ = ∓5/2 and ±7/2. In 4, there is a greater degree of mixing and larger splitting of the mJ substates, a consequence of the greater radial extent of the 5f-orbitals relative to the 4f-orbitals.A more detailed understanding of the bonding in these complexes may be obtained by examining the splitting of the f-orbitals illustrated in Fig. 5. In D3h symmetry, the crystal field only splits the orbitals but does not mix them (Table S2†). In 1, a single orbital, fy(3x2−y2), interacts significantly with the ligand-orbitals, while the other f-orbitals show little interaction. This result is consistent with previous crystal field studies, which show essentially the same splitting of the 4f-orbitals and a similar ordering (the relative order of the nearly degenerate fz3 and (fxyz, fz(x2−y2))-orbitals varies).14,16,17 In 4, the splitting of the f-orbitals is approximately twice as large as that in 1, which can be attributed to the greater radial extent of the 5f-orbitals. As in 1, the most strongly destabilized-orbital is fy(x2−3y2); however, the fz3-orbital is also destabilized. As previously shown, the fy(x2−3y2) is ideally configured to interact with the HOMO of the Cp ligands.24,26,28 In addition, none of the 6d-orbitals has the appropriate symmetry, a′2, to interact with this Cp MO. The same is true for the fz3-orbital, which can interact with the Cp HOMO with a′′2 symmetry via the two equatorial lobes. The overlap with fz3 is not as large as with fy(x2−3y2) since the lobes of the latter point directly at the Cp ligands. That these f-orbitals interact most strongly with the ligands may be viewed as a consequence of the FEUDAL (“f's essentially unaffected, d's accommodate ligands”) principle in which bonding in actinide and lanthanide ions largely involves the d-orbitals.72 The f-orbitals only participate substantially in bonding when no d-orbital possesses the appropriate symmetry to interact with the ligand MOs.
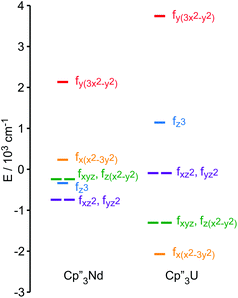 | ||
| Fig. 5 Comparison of the experimentally-based, crystal field MO schemes of Cp′′3Nd (1, left) and Cp′′3U (4, right). MO schemes are plotted with their barycenters at 0 cm−1. | ||
Cp′′3Nd·L (2 and 3)
As noted above, the similarity among the EPR g-values and the magnetic susceptibilities of 1–3 strongly suggest that coordination of the isocyanide ligand to the Nd ion has little effect on the thermally populated states. As illustrated in Fig. 6, the ground states change little upon coordination of the ligand. The main change is that a small amount of mJ = ±1/2 character is mixed into the ground state; otherwise, the ground state crystal field wavefunctions and the energies and wavefunctions of the low-lying excited states are similar to those of 1.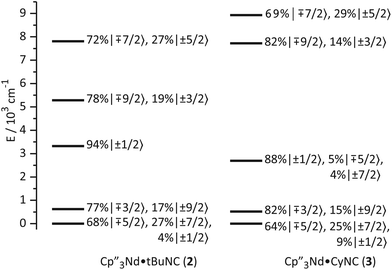 | ||
| Fig. 6 Ligand-field splitting and the composition of mJ substates (in the absence of an applied magnetic field) of 2 and 3. | ||
A more detailed picture of the change in electronic structure of the Nd center upon coordination of an isocyanide ligand along the z-axis emerges from the splitting of the f-orbitals (Fig. 7). The identities of the low-lying-orbitals determined by crystal field fitting may be compared with those determined by DFT (Fig. 1) using the coordinate system defined by the molecular C3 axis as the z axis. SOMO-1 and SOMO-2 in Fig. 1 correspond to the degenerate fxz2 and fyz2-orbitals in Fig. 7 since they have π symmetry with respect to the C3 axis. Both the crystal field fit and calculation provide the same ordering of the lowest energy f-orbitals (fxz2,fyz2) < fx(x2−3y2) in 2. The ordering in 3 is slightly different; fxz2 and fyz2 are lowest in energy, but the ordering of the next highest orbital is fz3. Nevertheless, the agreement between the DFT calculation and the experimentally derived MO supports the accuracy of the crystal field model for 2 and 3.
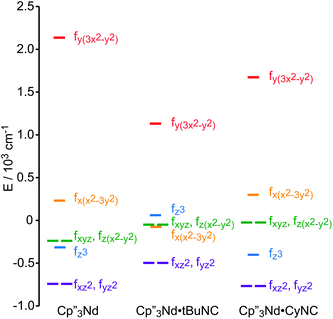 | ||
| Fig. 7 Experimentally-based, crystal field MO schemes of the Nd complexes 1, 2 and 3. MO schemes are plotted with their barycenters at 0 cm−1. | ||
The highest and lowest lying orbitals are unchanged upon coordination of the ligand; however, the total splitting of the f-orbitals is decreased as previously observed for (C5H5)3Nd isocyanide adducts.16 The reduction in f-orbital splitting seems to suggest that coordination of an additional ligand weakens the overall interaction between the f-orbitals and the ligands. However, the splitting of the f-orbitals reflects the anisotropy of their interactions with ligands as well as the strength of those interactions (a spherically symmetric crystal field does not split the orbitals regardless of the strength of the interaction). Coordination of an isocyanide ligand to Cp′′3Nd makes the system less anisotropic. Previous work by Schulz et al. shows that coordination of a second ligand along the z-axis, to form a pseudo-trigonal bipyramidal complex, further decreases the splitting of the f-orbitals.19 Both experimentally and computationally, coordination of the isocyanide ligand does not greatly destabilize the fz3-orbital relative to 1 and does not stabilize the (fxz2,fyz2)-orbitals that could interact with the π*-orbital of the ligand in agreement with the SOMOs illustrated in Fig. 1. In short, coordination of an isocyanide ligand to 1 does little except make the ligand field slightly more isotropic.
Cp′′3U·L (5 and 6)
The bonding in the uranium base adducts is distinct from the neodymium system. The crystal field wavefunctions and energies of the ground state and low-lying excited states are similar in 5 and 6 as shown in Fig. 8. As in 3 and 4, the lower symmetry of the isocyanide adducts results in mixing of mJ = ±1/2 character into the ground state; however, a greater degree of mixing occurs in 5 and 6.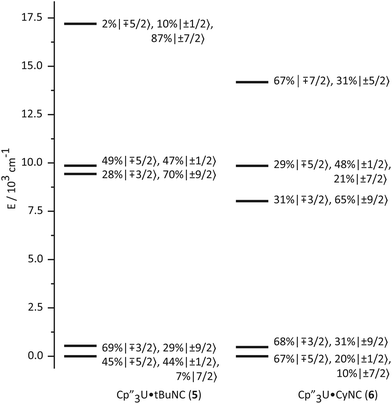 | ||
| Fig. 8 Ligand-field splitting and the composition of mJ substates (in the absence of an applied magnetic field) of Cp′′3U·tBuNC (5, left) and Cp′′3U·CyNC (6, right). | ||
The effect of the addition of an isocyanide ligand upon the 5f-orbitals is illustrated in Fig. 9. As in the Nd system, DFT and experiment provide the same lowest lying orbitals, fxz2 and fyz2. The next lowest lying orbital is different in 5 and 6, where 6 displays the same ordering as the DFT calculation. The agreement between theory and experiment suggests that determining the crystal field parameters using magnetic data provides an accurate description of the 5f-orbital splitting. As in the Nd system, addition of a ligand decreases the total splitting of the f-orbitals. Unlike the Nd system, coordination of an isocyanide ligand changes the ordering of the U 5f-orbitals. In both 5 and 6, fz3 is strongly destabilized, which is consistent with a significant interaction with the ligand σ-donor orbital; however, the main interaction is between 6dz2 and the ligand σ-orbital as shown in Fig. 1. In addition, both experiment and calculation show that fxz2 and fyz2 are stabilized in 5 and 6 relative to 4 due to interaction with the isocyanide π*-orbitals. These results are consistent with significant participation of the 5f-orbitals in bonding with the isocyanide ligand, which was not the case in the Nd system.
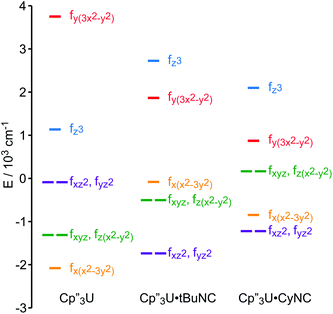 | ||
| Fig. 9 Comparison of the experimentally-based, crystal field MO schemes (splitting of the f-orbitals) of 4, 5 and 6. MO schemes are plotted with their barycenters at 0 cm−1. | ||
Role of the f-orbitals in bonding
The MO schemes in Fig. 4, 6, and 9 allow one to evaluate f-orbital bonding. Using second-order perturbation theory and the Wolfsberg–Helmholz approximation,73,74 the stabilization of the ligand orbitals, ΔEL, is related to the destabilization of the metal orbitals, ΔEM, by ΔEL ≈ ΔEM(EM/EL)2, where EM and EL are the energies of the metal and ligand orbitals, respectively.74,75 For Nd(III) and U(III), EM can be estimated using 1/3 of the third atomic ionization potentials, giving 7.4 eV and 6.6 eV, respectively.76,77 These values are in good agreement with the experimental ionization potentials of (C5H5)3Nd, 7.4 eV, and (C5H5)3U(thf), 6.4 eV.21,24 The ionization potential of tBuNC is 10.8 eV. While the ionization potential of Cp′′ radical is unknown, that of Cp′′H is 8.05 eV, which is 0.56 eV smaller than the parent, cyclopentadiene.78 Assuming that the effect of the –SiMe3 groups is similar in the cyclopentadienyl radial, for which the IE is 8.43 eV, the estimated value of EL is 7.9 eV for Cp′′ radical.79The contribution of the f-orbitals to bonding between the metal and Cp′′ ligands may be evaluated using the MO scheme in Fig. 5 assuming that the lowest energy-orbitals are essentially non-bonding. From the destabilization of the fy(3x2−y2)-orbital, 2860 cm−1 and 5824 cm−1 in 1 and 4, respectively, the stabilization of the a′2 Cp-orbitals are estimated to be 2520 cm−1 and 4070 cm−1, respectively. In 1 and 4, stabilization of the doubly occupied a′2 Cp-orbitals by interaction with f-orbitals contributes 14 kcal mol−1 and 23 kcal mol−1, respectively, to the bond between the metal and three Cp′′ ligands.
The bonding between the metal center and the isocyanide ligands may be similarly examined using the energy of fy(3x2−y2) as a reference. The energy of this orbital should be largely unaffected by coordination of the isocyanide ligand because it has no overlap with the incoming ligand, and because the steric bulk of the Cp′′ ligands prevents them from adopting a different coordination geometry when the isocyanide ligand coordinates to the metal center as illustrated by the structures of Cp′′3Ce and Cp′′3Ce·tBuNC.80 The main f-orbital interaction with the isocyanide ligand is stabilization of the isocyanide σ-orbital by fz3. Using fy(3x2−y2) as a reference, the change in the energy of the fz3-orbital can be used to estimate how effectively the f-orbitals stabilize the bond between Cp′′3M and L. In 2 and 3, fz3 is destabilized by 1360 cm−1 and 340 cm−1, relative to 1, and in 5 and 6, fz3 is destabilized by 3480 cm−1 and 3850 cm−1, relative to 4. Interaction with the fz3-orbital contributes 4 kcal mol−1 and 1 kcal mol−1 to the stability of 2 and 3, respectively, and 7 kcal mol−1 and 8 kcal mol−1 in 5 and 6, respectively. In other words, the increased overlap in Cp′′3U strengthens the σ-bond with the isocyanide ligand by 5 kcal mol−1 relative to Cp′′3Nd, which is in agreement with the 5.4 kcal mol−1 difference in bond strength determined by DFT (Table 2). The contribution of π-back bonding to the stability of the complexes cannot be readily estimated because the populations of the f-orbitals are more difficult to quantify than that of the ligand orbitals.
Multi-reference wavefunction calculations
The natural orbitals (NOs) for the open metal shells generated from the SCF-SO ab initio wavefunctions reflect the expected lack of covalent interactions in the Nd complex 2′ and they indicate covalency involving the U 5f π-orbitals and π*-orbitals of the axial ligand in the U complex 5′ (Fig. 10). Covalent character of the 5f σ NO is not evident. Fig. 11 shows contour line plots of the two NOs involved in π back-bonding, and illustrates the U–C bonding and C–N antibonding character more clearly. Due to the principal pseudo symmetry axis being lower than 7-fold, the NOs for the Nd complex show some mixing among the σ π δ and ϕ symmetric f-orbitals (classification with respect to rotational symmetry along the principal axis), similar to what is found in the DFT calculations.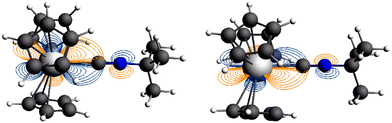 | ||
| Fig. 11 Contour line plots of the two π-bonding NOs of 5′ of Fig. 10 in perpendicular cut planes. Contour lines from ±0.01 to ±1 atomic units with logarithmic spacing. | ||
In a scalar relativistic (SR) calculation, i.e. without SO coupling, the ground states are spin quartets related to the 4I9/2 ion level. These mix with of other J = 9/2 levels due to SO coupling, and with levels having different values of J due to the low symmetry of the ligand field—as already mentioned. The characterization of the calculated electronic ground states in terms of their metal ion level parentages in Table 5 shows that spin-quartet states derived from the 4I9/2 ion levels dominate the two-fold degenerate ground states of the two complexes, with SO coupling causing less than 10% mixing of higher energy spin-doublets into the ground state. It is important to note that the NOs in Fig. 10 were calculated for the ground states including SO effects. When SO coupling is taken into consideration, π and ϕ symmetry f-orbitals couple with those of σ and δ symmetry, and occupation may shift accordingly among these orbitals. Nevertheless, f-orbitals with π and ϕ symmetry relative to the axial ligand, which have occupations of 1 in the SR DFT calculations, also have the largest occupations in the SO wavefunction calculations, as shown in Fig. 10. However, due to SO coupling as well as multi-configurational character of the SCF-SR states, for 5′, the formal U–ligand bond order is less than in the DFT calculation because the combined occupation of the 5f π-bonding-orbitals is only about 1.2 electrons. This difference is presumably the main cause of the deviation between the calculated reduction in ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N) upon coordination to Cp′′3U (64 cm−1) compared with the experimental value (6 cm−1). Spin–orbit coupling diminishes the f-electron contribution to back bonding in agreement with the earlier studies by Maron et al. and Gendron et al.31,32
N) upon coordination to Cp′′3U (64 cm−1) compared with the experimental value (6 cm−1). Spin–orbit coupling diminishes the f-electron contribution to back bonding in agreement with the earlier studies by Maron et al. and Gendron et al.31,32
| g || | g ⊥ | g || | g ⊥ | ||
|---|---|---|---|---|---|
| Complex | Weight 2S+1LJ | (exp) | (calc) | ||
| 2′ | 97.9 4I9/2, 2.0 2H9/2 | 0.87 | 2.25 | 1.12 | 2.22 |
| 5′ CNC linear | 91.6 4I9/2, 6.6 2H9/2 | <0.7 | 2.09 | 0.61 | 1.97 |
| 5′ CNC bent | 91.7 4I9/2, 6.2 2H9/2 | 1.45 | 1.31 | ||
For both 2′ and 5′, there is reasonably good agreement between the experimental and crystal-field derived EPR g-factors (Table 3) and those from the ab initio calculations (Table 5). In order to match the experimental g-factors more closely, the calculations would likely need to employ a model for the environment of the complex in the solid including crystal packing effects on its structure.59 Because of the π interactions with the axial ligand, the g-factors are highly sensitive to structural distortions. When the t-butyl group is bent somewhat out of its axial position, the ground state composition does not change dramatically in terms of the contributions from the 4I9/2 and 2H9/2 states. However, the U–tBuNC π bonding character increases significantly (Fig. S2†), and the parallel g-factor increases strongly, while the average of the perpendicular components decreases somewhat. Deviations between the calculation and experiment can also be attributed to the missing treatment of the dynamic electron correlation and the size of the active space.
Conclusions
The electronic structures of 1–6 have been studied by a combination of magnetochemistry, crystal field modeling and DFT and ab initio CAS wavefunction calculations. The crystal field model was parameterized using experimental EPR and magnetic susceptibility data. Since these magnetic data do not contain many independent data points, only the crystal field strength parameters, Bkq, were allowed to vary, and the other parameters were adopted from studies of related compounds. Despite the limited number of independent fitting parameters, the results for the Nd systems agree with those previously derived from optical data. In addition, the experimentally derived MO schemes are in good agreement with those determined by DFT. Using the magnetic data allows the f-orbital splitting of Cp′′3U and its base adducts to be evaluated experimentally for the first time. Both experiment and theory clearly show that the 4f-orbitals do not participate significantly in bonding except for the 4fy(3x2−y2)-orbital. On the other hand, crystal field theory, DFT, and ab initio CAS wavefunction calculations show that the 5f-orbitals appear to participate in bonding to the isocyanide ligands as well as the Cp ligands.This comparative study showcases the strengths and limitations of simple scalar relativistic (SR) orbital, single-reference descriptions (i.e. single electron MO diagrams) to characterize the bonding in f-metal complexes. For instance, while such a model may reveal the role of the f-orbitals in bonding, it does not take into account the strong mixing of the occupied f-orbitals by spin–orbit coupling, or deviations from formal occupations due to a multi-reference nature of the electronic state, which may be important for a full description of the bonding or magnetic behavior. Such information can be obtained without semi-empirical parameters from natural-orbitals generated from multi-reference wavefunctions including SO effects, or similar types of analysis tools for complex wavefunctions. For instance, CAS calculations confirm the presence of π bonding between the uranium center and the isocyanide ligands, but with less than the formal U–L bond order because the ground state electron density of the open 5f shell has contributions – to varying degrees – from all seven 5f-orbitals.
Motivated by these findings, future implementations of CONDON will include the conversion of the micro state, |mJ〉 basis into the real-orbitals (e.g. fxz2) of the ground state, assigning a ligand field splitting to the real-orbitals and identifying the orbitals based on the occupied micro states.
Acknowledgements
The authors thank Prof. Richard A. Andersen for guidance on synthesis and for many discussions on the role of f-orbitals in bonding. We thank Norman M. Edelstein and Nicola Magnani for helpful discussions on crystal field modeling. The DFT calculations were performed using the Molecular Science Computing (MSC) Facilities in the William R. Wiley Environmental Molecular Sciences Laboratory (EMSL), a national scientific user facility sponsored by the U.S. DOE BER and located at Pacific Northwest National Laboratory. Portions of this work (Lukens and Yang) were supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Chemical Sciences, Biosciences, and Geosciences Division (CSGB), Heavy Element Chemistry Program and were performed at Lawrence Berkeley National Laboratory under contract No. DE-AC02-05CH11231 and at Los Alamos National Laboratory under contract No. DE-AC52-06NA25396 (operated by Los Alamos National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy). Portions of this work were supported by the ACalNet program (DAAD (German Academic Exchange Service)) and by ERC StG 308051 – MOLSPINTRON. The CAS calculations were carried out by TD and JA at the University at Buffalo Center for Computational Research. JA and TD acknowledge support from the U.S. Department of Energy, Office of Basic Energy Sciences, Heavy Element Chemistry program, under grant DE-SC0001136 (formerly DE-FG02-09ER16066), and Dr Frédéric Gendron for assistance with the computations.Notes and references
- S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, D. L. Clark, S. D. Conradson, S. A. Kozimor, R. L. Martin, D. E. Schwarz, D. K. Shuh, G. L. Wagner, M. P. Wilkerson, L. E. Wolfsberg and P. Yang, J. Am. Chem. Soc., 2012, 134, 5586–5597 CrossRef CAS PubMed.
- M. W. Loble, J. M. Keith, A. B. Altman, S. C. E. Stieber, E. R. Batista, K. S. Boland, S. D. Conradson, D. L. Clark, J. L. Pacheco, S. A. Kozimor, R. L. Martin, S. G. Minasian, A. C. Olson, B. L. Scott, D. K. Shuh, T. Tyliszczak, M. P. Wilkerson and R. A. Zehnder, J. Am. Chem. Soc., 2015, 137, 2506–2523 CrossRef CAS PubMed.
- W. Xiao-Dong, M. W. Loble, E. R. Batista, E. Bauer, K. S. Boland, A. K. Burrell, S. D. Conradson, S. R. Daly, S. A. Kozimor, S. G. Minasian, R. L. Martin, T. M. McCleskey, B. L. Scott, D. K. Shuh and T. Tyliszczak, J. Electron Spectrosc. Relat. Phenom., 2014, 194, 81–87 CrossRef.
- S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, D. L. Clark, S. A. Kozimor, R. L. Martin, D. K. Shuh and T. Tyliszczak, Chem. Sci., 2014, 5, 351–359 RSC.
- L. P. Spencer, P. Yang, S. G. Minasian, R. E. Jilek, E. R. Batista, K. S. Boland, J. M. Boncella, S. D. Conradson, D. L. Clark, T. W. Hayton, S. A. Kozimor, R. L. Martin, M. M. MacInnes, A. C. Olson, B. L. Scott, D. K. Shuh and M. P. Wilkerson, J. Am. Chem. Soc., 2013, 135, 2279–2290 CrossRef CAS PubMed.
- I. D. Prodan, G. E. Scuseria and R. L. Martin, Phys. Rev. B: Condens. Matter, 2007, 76, 4 Search PubMed.
- M. L. Neidig, D. L. Clark and R. L. Martin, Coord. Chem. Rev., 2013, 257, 394–406 CrossRef CAS.
- N. Kaltsoyannis, Inorg. Chem., 2013, 52, 3407–3413 CrossRef CAS PubMed.
- F. Xie, T. A. Zhang, D. Dreisinger and F. Doyle, Miner. Eng., 2014, 56, 10–28 CrossRef CAS.
- G. Modolo, A. Wilden, A. Geist, D. Magnusson and R. Malmbeck, Radiochim. Acta, 2012, 100, 715–725 CrossRef CAS.
- S. Fortier, J. R. Walensky, G. Wu and T. W. Hayton, J. Am. Chem. Soc., 2011, 133, 11732–11743 CrossRef CAS PubMed.
- M. D. Conejo, J. S. Parry, E. Carmona, M. Schultz, J. G. Brennann, S. M. Beshouri, R. A. Andersen, R. D. Rogers, S. Coles and M. Hursthouse, Chem. – Eur. J., 1999, 5, 3000–3009 CrossRef.
- H. D. Amberger and H. Reddmann, Z. Anorg. Allg. Chem., 2007, 633, 443–452 CrossRef CAS.
- H. D. Amberger, H. Reddmann, T. J. Mueller and W. J. Evans, J. Organomet. Chem., 2011, 696, 2829–2836 CrossRef CAS.
- C. Apostolidis, A. Morgenstern, J. Rebizant, B. Kanellakopulos, O. Walter, B. Powietzka, M. Karbowiak, H. Reddmann and H. D. Amberger, Z. Anorg. Allg. Chem., 2010, 636, 201–208 CrossRef CAS.
- S. Jank, H. Reddmann, H. D. Amberger and C. Apostolidis, J. Organomet. Chem., 2004, 689, 3143–3157 CrossRef CAS.
- H. Reddmann, H. Schultze, H. D. Amberger, G. V. Shalimoff and N. M. Edelstein, J. Organomet. Chem., 1991, 411, 331–345 CrossRef CAS.
- H. Reddmann, M. Karbowiak, H. D. Amberger and J. Drozdzynski, Z. Anorg. Allg. Chem., 2006, 632, 1953–1955 CrossRef CAS.
- H. Schulz, H. Reddmann, H. D. Amberger, B. Kanellakopulos, C. Apostolidis, J. Rebizant and N. M. Edelstein, J. Organomet. Chem., 2001, 622, 19–32 CrossRef CAS.
- H. D. Amberger, H. Schultze and N. M. Edelstein, Spectrochim. Acta, Part A, 1986, 42, 657–667 CrossRef.
- M. Coreno, M. de Simone, J. C. Green, N. Kaltsoyannis, R. Coates, C. Hunston, N. Narband and A. Sella, Dalton Trans., 2014, 43, 5134–5141 RSC.
- J. H. van Vleck, in Nobel Lectures, Physics 1971-1980, ed. S. Lundqvist, World Scientific Publishing, Singapore, 1992 Search PubMed.
- J. H. van Vleck, The Theory of Electric and Magnetic Susceptibilities, Oxford University Press, London, 1932 Search PubMed.
- J. C. Green, M. R. Kelly, J. A. Long, B. Kanellakopulos and P. I. W. Yarrow, J. Organomet. Chem., 1981, 212, 329–340 CrossRef CAS.
- H. Schilder, M. Speldrich, H. Lueken, A. C. Sutorik and M. G. Kanatzidis, J. Alloys Compd., 2004, 374, 249–252 CrossRef CAS.
- K. Tatsumi and A. Nakamura, J. Organomet. Chem., 1984, 272, 141–154 CrossRef CAS.
- B. E. Bursten, L. F. Rhodes and R. J. Strittmatter, J. Less-Common Met., 1989, 149, 207–211 CrossRef.
- B. E. Bursten, L. F. Rhodes and R. J. Strittmatter, J. Am. Chem. Soc., 1989, 111, 2756–2758 CrossRef CAS.
- B. E. Bursten, L. F. Rhodes and R. J. Strittmatter, J. Am. Chem. Soc., 1989, 111, 2758–2766 CrossRef CAS.
- R. J. Strittmatter and B. E. Bursten, J. Am. Chem. Soc., 1991, 113, 552–559 CrossRef CAS.
- L. Maron, O. Eisenstein and R. A. Andersen, Organometallics, 2009, 28, 3629–3635 CrossRef CAS.
- F. Gendron, B. Le Guennic and J. Autschbach, Inorg. Chem., 2014, 53, 13174–13187 CrossRef CAS PubMed.
- N. A. Siladke, K. R. Meihaus, J. W. Ziller, M. Fang, F. Furche, J. R. Long and W. J. Evans, J. Am. Chem. Soc., 2012, 134, 1243–1249 CrossRef CAS PubMed.
- J. van Leusen, M. Speldrich, H. Schilder and P. Kögerler, Coord. Chem. Rev., 2015, 289–290, 137–148 CrossRef CAS.
- E. W. Abel and S. Moorhouse, J. Organomet. Chem., 1971, 29, 227–232 CrossRef CAS.
- Z. W. Xie, K. L. Chui, Z. X. Liu, F. Xue, Z. Y. Zhang, T. C. W. Mak and J. Sun, J. Organomet. Chem., 1997, 549, 239–244 CrossRef CAS.
- D. C. Bradley, J. S. Ghotra and F. A. Hart, J. Chem. Soc., Dalton Trans., 1973, 1021–1027 RSC.
- C. Daul, C. W. Schlapfer, B. Mohos, J. Ammeter and E. Gamp, Comput. Phys. Commun., 1981, 21, 385–395 CrossRef CAS.
- J. R. Pilbrow, Transition Ion Paramagnetic Resonance, Oxford University Press, Oxford, 1990 Search PubMed.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in Fotran 77 the Art of Scientiic Computing Second Edition, Cambridge University Press, Cambridge, 1992 Search PubMed.
- G. Racah, Phys. Rev., 1942, 62, 438–462 CrossRef CAS.
- J. C. Slater, Quantum Theory of Atomic Structure. 1 (1960), McGraw-Hill Interamericana, 1960 Search PubMed.
- E. U. Condon and G. H. Shortley, The Theory of Atomic Spectra, Cambridge University Press, 1970 Search PubMed.
- B. G. Wybourne, Spectroscopic Properties of Rare Earths, Wiley, New York, London, Sydney, 1965 Search PubMed.
- H. Schilder and H. Lueken, J. Magn. Magn. Mater., 2004, 281, 17–26 CrossRef CAS.
- M. Speldrich, H. Schilder, H. Lueken and P. Kögerler, Isr. J. Chem., 2011, 51, 215–227 CrossRef CAS.
- H. Lueken, Magnetochemie: Eine Einführung in Theorie und Anwendung, Vieweg+Teubner Verlag, 2013 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed.
- ADF 2013, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands Search PubMed.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galvan, N. Ferre, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. X. Ma, P. A. Malmqvist, T. Muller, A. Nenov, M. Olivucci, T. B. Pedersen, D. L. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Marti, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- A. Wolf, M. Reiher and B. A. Hess, J. Chem. Phys., 2002, 117, 9215–9226 CrossRef CAS.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- P. A. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- F. Gendron, D. Paez-Hernandez, F. P. Notter, B. Pritchard, H. Bolvin and J. Autschbach, Chem. – Eur. J., 2014, 20, 7994–8011 CrossRef CAS PubMed.
- H. Bolvin, ChemPhysChem, 2006, 7, 1575–1589 CrossRef CAS PubMed.
- S. Vancoillie, P. A. Malmqvist and K. Pierloot, ChemPhysChem, 2007, 8, 1803–1815 CrossRef CAS PubMed.
- S. Vancoillie, L. Rulisek, F. Neese and K. Pierloot, J. Phys. Chem. A, 2009, 113, 6149–6157 CrossRef CAS PubMed.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 22 CrossRef PubMed.
- J. Autschbach, Comments Inorg. Chem., 2016, 36, 214–244 CrossRef.
- F. Gendron, B. Pritchard, H. Bolvin and J. Autschbach, Dalton Trans., 2015, 44, 19886–19900 RSC.
- R. A. Andersen, Inorg. Chem., 1979, 18, 1507–1509 CrossRef CAS.
- F. A. Cotton and F. Zingales, J. Am. Chem. Soc., 1961, 83, 351–355 CrossRef CAS.
- I. Ugi and R. Meyr, Chem. Ber./Recl., 1960, 93, 239–248 CrossRef CAS.
- W. T. Carnall and B. G. Wybourne, J. Chem. Phys., 1964, 40, 3428–3433 CrossRef CAS.
- C. Miyake, in Handbook on the Physics and Chemistry of the Actinides, ed. A. J. Freeman, G. H. Lander and C. Keller, North-Holland, 1991, ch. 6, vol. 6, p. 337 Search PubMed.
- T. H. Siddall, in Theory and Applications of Molecular Paramagnetism, ed. E. A. Boudreaux and L. N. Mulay, Wiley, 1976, p. 317 Search PubMed.
- B. E. Bursten, E. J. Palmer and J. L. Sonnenberg, in Recent Advances in Actinide Science, ed. R. Alvares and I. May, Royal Society of Chemistry, London, 2006 Search PubMed.
- M. Wolfsberg and L. Helmholz, J. Chem. Phys., 1952, 29, 837–843 CrossRef.
- J. K. Burdett, J. Am. Chem. Soc., 1979, 101, 580–583 CrossRef CAS.
- W. W. Lukens, N. M. Edelstein, N. Magnani, T. W. Hayton, S. Fortier and L. A. Seaman, J. Am. Chem. Soc., 2013, 135, 10742–10754 CrossRef CAS PubMed.
- X. Y. Cao and M. Dolg, J. Mol. Struct. (THEOCHEM), 2004, 673, 203–209 CrossRef CAS.
- X. Y. Cao and M. Dolg, J. Mol. Struct. (THEOCHEM), 2002, 581, 139–147 CrossRef CAS.
- H. Bock and W. Kaim, J. Am. Chem. Soc., 1980, 102, 4429–4438 CrossRef CAS.
- H. J. Wörner and F. Merkt, J. Chem. Phys., 2007, 127 CrossRef PubMed , 034303.
- S. D. Stults, R. A. Andersen and A. Zalkin, Organometallics, 1990, 9, 115–122 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis details, comparison of crystal field parameters, occupation of micro states. See DOI: 10.1039/c6dt00634e |
| This journal is © The Royal Society of Chemistry 2016 |