The photochemistry of mono- and dinuclear cyclometalated bis(tridentate)ruthenium(II) complexes: dual excited state deactivation and dual emission

Abstract

The synthesis and characterization of a series of weakly emissive mononuclear cyclometalated [Ru(dpb-R)(tpy)]⁺ complexes with functional groups R of varying electron-donating characters at the dpb ligand are described (dpbH = 1,3-di(2-pyridyl)benzene, tpy = 2,2′;6′,2′′-terpyridine, 1⁺: R = NHCOMe, 2⁺: R = NH₂, 3⁺: R = COOEt, 4⁺: R = COOH). Steady-state emission spectroscopy in the temperature range between 298 K and 77 K revealed a previously unrecognized excited state deactivation pathway via low-lying triplet ligand-to-ligand (³LL′CT) charge transfer states in addition to the well-known pathway via³MC states. Thermal activation barriers for depopulation of the emissive metal-to-ligand charge transfer (³MLCT) states via the ³MC (metal-centered) and ³LL′CT states were determined experimentally for complexes 1⁺ and 3⁺. The experimental results were further corroborated by calculating the respective ³MLCT–³LL′CT and ³MLCT–³MC transition states and their energies with density functional theoretical methods. The R substituent modifies the energy difference between the ³MLCT and ³LL′CT states and the corresponding activation barrier but leaves the analogous ³MLCT/³MC energetics essentially untouched. Additionally, the dinuclear complex [(tpy)Ru(dpb-NHCO-dpb)Ru(tpy)]²⁺, 6²⁺, containing a biscyclometalating bridge was devised. Despite the asymmetric nature induced by the amide bridge, the mixed-valent cation 6³⁺ is ascribed to Robin–Day class II with a broad and intense intervalence charge-transfer (IVCT) absorption (λ_max = 1165 nm). Upon optical excitation, the Ru^II/Ru^II complex 6²⁺ exhibits dual emission in liquid solution from two independently emitting ³MLCT states localized at the two remote [Ru(tpy)] fragments. No equilibration via Dexter energy transfer is possible due to their large distance and short excited state lifetimes.

---

Introduction

Polypyridine complexes of ruthenium(II) have been known and studied for the past sixty years.^1,2 Although the fundamentals of their photo- and electrochemical properties are well understood,^3–7 research efforts have not diminished over the last few years mainly due to a widespread potential for applications for this class of metal complexes. These vary from photoredox catalysis,^8–12 over light sensitization in dye-sensitized solar cells,¹³ and sensing applications in biological^14,15 and chemical¹⁶ contexts to optoelectronics.¹⁷

The prototype of this class of complexes is [Ru(bpy)₃]²⁺ (bpy = 2,2′-bipyridine), whose photophysical properties have been extensively studied and are well understood. Under visible light irradiation, excitation into a singlet metal-to-ligand charge transfer (¹MLCT) state occurs (λ_max = 452 nm, ε_max = 14.6 M⁻¹ cm⁻¹).^1,3 This state undergoes rapid and quantitative intersystem crossing onto the triplet hypersurface^18,19 populating a long-lived ³MLCT state that is phosphorescent at room temperature (λ_em = 621 nm, ϕ = 0.095, τ = 855 ns in MeCN).^20,21 Upon cooling, both, emission quantum yield and excited state lifetime, increase drastically. Using lifetime measurements at varying temperatures, T. J. Meyer and coworkers showed that this temperature dependence is due to a thermally accessible d–d excited state (metal centered, ³MC) that rapidly undergoes vibrational relaxation into the ground state (¹GS).^20,22 Additionally, this excited state is dissociative in nature and enables [Ru(bpy)₃]²⁺ to undergo photosubstitution reactions.^20,22,23

To suppress these reactions and also to circumvent the chiral nature of [Ru(bpy)₃]²⁺ stronger chelating, tridentate ligands such as tpy (tpy = 2,2′;6′,2′′-terpyridine) were introduced in bis(tridentate)ruthenium(II) complexes.^5,24 Their meridional coordination geometry²⁵ allows the functionalization of the ligand periphery without resulting in stereoisomers. A major drawback of these complexes compared to their bpy counterparts is the almost complete lack of emission at room temperature (ϕ = 5 × 10⁻⁶).^5,26 Due to the weaker ligand field caused by the smaller bite angle of the terpyridine ligand (N–Ru–N ≈ 79°), the emissive ³MLCT states of [Ru(tpy)₂]²⁺ are very efficiently depopulated via low-lying ³MC states.²⁴ Upon cooling, thermal depopulation of the emissive state is retarded yielding bright luminescence at 77 K (λ_em = 599 nm, ϕ = 0.48, τ = 110 μs in MeOH/EtOH).²⁷

Various attempts have been made to regain room temperature luminescence from bis(tridentate)ruthenium(II) complexes. By introducing an electron-donating functional group on one of the terpyridine ligands, the energy of the ³MC state is increased with respect to the ³MLCT state energy rather selectively.⁵ Similarly, electron-accepting functionalities lower the ³MLCT state energy.⁵ Combining these two approaches in a push–pull system, the activation barrier for depopulation of the emissive ³MLCT state is increased. As a result, room temperature quantum yields of up to 0.003 and excited state lifetimes of 50 ns are achieved.^5,28–31 Since the coordination mode of the tpy ligand with five-membered chelate rings only allows for rather constrained geometries around the metal center with small bite angles, several research groups focussed on expanding the ligand backbone to increase the overlap between the ruthenium d orbitals of the e_g set and the nitrogen lone pairs. This yields an enlarged ligand field splitting and thus makes ³MC states as deactivation pathway thermally less accessible at room temperature.^32–35 Following this concept, bis(tridentate)ruthenium(II) complexes were synthesized with optical properties comparable to those of [Ru(bpy)₃]²⁺ (ϕ = 0.30, τ = 3.3 μs).³³

In a very similar approach, by introduction of very strong σ-donors in the coordination sphere, the ligand field splitting can be increased compared to [Ru(tpy)₂]²⁺. Conceptually, this was shown by Berlinguette and Schubert using N-heterocyclic carbene containing tridentate ligands (C^N^C coordination mode) with quantum yields of 0.11 and excited state lifetimes of up to 8 μs.³⁶ Disappointingly, attempts using 1,3-di(2-pyridyl)benzene (dpbH), deprotonated in the 2-position of the central benzene ring, as a strong cyclometalating σ-donor ligand in conjunction with tpy as a π-accepting ligand ([Ru(dpb)(tpy)]⁺), gave only very weakly emissive complexes.^30,37–40 This was originally ascribed to a very small activation barrier for thermal depopulation of the emissive ³MLCT state via low-lying ³MC states since the cyclometalation at the central position of the dpb ligand merely shifts one of the ³MC states to a higher energy.³⁰ Recently, we have suggested that the introduction of a very strong push–pull arrangement across the metal center additionally gives rise to low-lying triplet ligand-to-ligand charge transfer (³LL′CT) states.⁴⁰ Since the involved ligands are orthogonal to one another in the meridional coordination geometry, so are the spin-carrying orbitals. Hence, emission from such ³LL′CT states is symmetry-forbidden and leads to efficient radiationless deactivation of the excited state.

To further study this phenomenon and to elaborate a general view, the work presented herein devised four cyclometalated ruthenium complexes [Ru(dpb-R)(tpy)]⁺ with varying substituents at the 5-position of the dpb ligand (R = NHCOMe, 1⁺; R = NH₂, 2⁺; R = COOEt, 3⁺; R = COOH, 4⁺). Using these, it is possible to systematically study the impact of varying push–pull strengths across the metal center on the ground and excited state properties of these cyclometalated complexes. By employing steady-state emission spectroscopy, we demonstrate that the occurrence of low-energy ³LL′CT states is a common theme in cyclometalated bis(tridentate)ruthenium complexes providing a second excited state deactivation pathway in addition to the well-known pathway mediated by ³MC states.

Additionally, the presence of free amino and carboxylic acid groups allows the straightforward formation of a dinuclear complex with an amide-linked biscyclometalating bridging ligand ([(tpy)Ru(dpb-NHCO-dpb)Ru(tpy)]²⁺ (6²⁺) that we synthesized and studied as well. Dinuclear bisruthenium complexes received wide interest since the discovery of the mixed-valent Creutz–Taube ion, [(NH₃)₅Ru(μ-pz)Ru(NH₃)₅]⁵⁺ (pz = pyrazine).^41–43 The ruthenium oxidation states within this mixed-valent complex cannot be assigned unambiguously. Depending on the spectroscopic method either 2+/3+ or 2.5+/2.5+ is obtained.^44–47 Dinuclear mixed-valent complexes are assigned to three different groups based on Robin's and Day's classification.⁴⁸ Systems with entirely localized valences and no electronic coupling between the redox centers in the mixed-valent state are referred to as Robin–Day class I, and systems with entirely delocalized valences are assigned as class III. Class II describes valence-localized complexes with measurable electronic interactions between the redox sites. The theoretical basis for an accurate physicochemical treatment of Robin–Day class II complexes was laid by Hush^49–51 describing the photochemical electron transfer occurring between the donor and acceptor sites [Mⁿ⁺ − M⁽ⁿ⁺¹⁾⁺ → M⁽ⁿ⁺¹⁾⁺ − Mⁿ⁺]. This process yields an intervalence charge transfer (IVCT) absorption that is typically observed in the Near Infrared (NIR) region of the electronic absorption spectrum of a Robin–Day class II compound. According to Marcus–Hush theory, this IVCT band is correlated with the electronic coupling parameter V_ab between the redox centers calculated as: V_ab = 2.06 × 10⁻²[small nu, Greek, tilde]_max·ε_max·[small nu, Greek, tilde]_1/2)^1/2r⁻¹ with the absorption maximum [small nu, Greek, tilde]_max in cm⁻¹, the extinction coefficient ε_max at [small nu, Greek, tilde]_max in M⁻¹ cm⁻¹, the full width at half maximum [small nu, Greek, tilde]_1/2 in cm⁻¹ and the donor–acceptor distance r in Å.^47,52

Several amide-bridged dinuclear bis(terpyridine)ruthenium(II) complexes and their mixed-valent counterparts have been described in the literature.^53–55 While the back-to-back linked (n = 0) or phenylene-extended (n = 1–2) dinuclear bis(terpyridine)ruthenium(II) complexes [(ttpy)Ru(tpy-(1,4-C₆H₄)_n-tpy)Ru(ttpy)]⁴⁺ (ttpy = 4′-tolylterpyridine, 1,4-C₆H₄ = para-phenylene) exhibit electronic coupling of the metal centers in the mixed-valent state to a small extent (n = 0: V_ab = 0.047 eV, n = 1: V_ab = 0.030 eV, n = 2: V_ab = 0.022 eV),^56,57 the introduction of an amide bridge seems to reduce the molecular and redox-chemical symmetry enough to prevent the electronic interactions entirely.^54,55 In the cyclometalated analogue of the dinuclear back-to-back linked bis(terpyridine)ruthenium complex, [(ttpy)Ru(dpb-dpb)Ru(tpy)]²⁺, on the other hand, the metal–metal interaction is increased to V_ab = 0.127 eV.^58,59 This increase was attributed to an energy shift of the bridge's frontier orbitals to better match those of the metal centers.^59,60 In this work, we study to what extent the insertion of an NHCO group into the bridge reduces the electronic coupling between the metal centers in the mixed-valent state 6³⁺ and the interaction of the triplet excited states of 6²⁺.

Results and discussion

Synthesis and characterization of mono- and dinuclear complexes

The synthesis (Scheme 1) of the target mononuclear complexes was carried out following a previously described synthetic route starting from RuCl₃(tpy).^40,58 In the first step, this precursor is activated by chloride abstraction using silver tetrafluoroborate. The resulting solvent complex intermediate was subsequently treated with the respective dipyridylbenzene ligand L1 or L2 ⁴⁰ to give the amide or ester substituted [Ru(dpb-R)(tpy)]⁺ complexes 1(PF₆) and 3(PF₆) in good yields. Cleavage of the functional groups for the liberation of free amine or carboxylic acid was achieved in aqueous methanolic solutions using sodium hydroxide as a base and hydrazine as a reductant to prevent oxidative decomposition. This hydrolysis protocol gives comparable yields to the hydrolysis of structurally related ruthenium complexes by trimethylamine employed by Berlinguette and coworkers.⁶¹

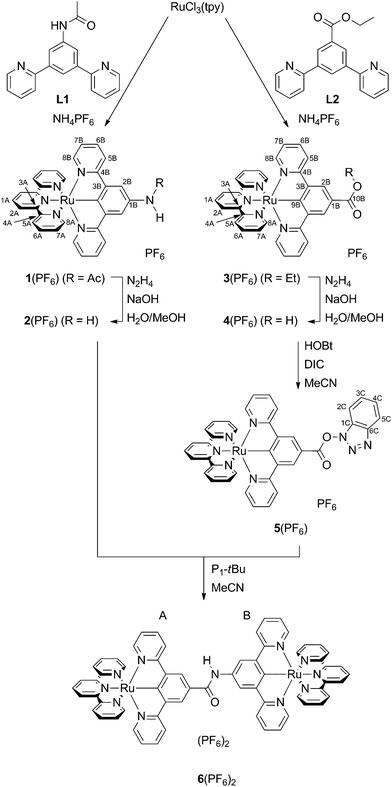Scheme 1 Synthesis of the mononuclear complexes 1(PF₆)–5(PF₆) and the dinuclear complex 6(PF₆)₂ from RuCl₃(tpy). Atom numbering for NMR assignment is included.

In order to accomplish the coupling reaction between the free acid and the amine moieties of 2⁺ and 4⁺ to the dinuclear complex 6²⁺, activation of the acid component is necessary. This was achieved similarly to a previously employed technique using N-hydroxybenzotriazole (HOBt) and N,N′-diisopropylcarbodiimide (DIC).^55,62 Compared to the amide coupling reaction between bis(terpyridine)ruthenium(II) amino acid derivatives described previously,^54,55 the coupling had to be performed at elevated temperatures, possibly attributed to the reduced acidity of the amino functionality and relatively weak nucleophilicity of the OBt ester compared to other active esters.

All complexes were characterized using 1D- and 2D-NMR techniques (ESI, Fig. S1–S14†) as well as ESI and high-resolution ESI mass spectrometry (ESI, Fig. S15†). The purity of all compounds under study was confirmed by elemental analyses. Successful amide cleavage (1(PF₆) → 2(PF₆)) is proven by the disappearance of the NH (8.62 ppm) and CH₃ (2.23 ppm) resonances in the proton NMR spectrum of 2(PF₆). Simultaneously, a new significantly broadened resonance appears at 4.24 ppm indicating the presence of a free amino group. Similarly, ester saponification (3(PF₆) → 4(PF₆)) yields a loss of the characteristic CH₂ and CH₃ proton resonances of the ethyl group while essentially leaving the aromatic region of the ¹H NMR spectrum unaffected. For the hydroxybenzotriazole ester 5(PF₆), the resonances of the dipyridylbenzene ligand, predominantly those in the 2B-position, are shifted to a lower field. This is in agreement with the formation of a more electron-deficient species that is activated towards nucleophilic attack.

Interestingly, the functional group attached to the dpb ligand strongly affects the ¹³C chemical shift of the coordinating carbon atom. While this resonance is found at 239.5 ppm in complex 5(PF₆) with the strongly electron-withdrawing COOBt substituent, it is shifted upfield to 233 ppm in complexes 3(PF₆) and 4(PF₆) with COOEt and COOH functional groups. In the N-substituted complexes, it is found at even lower chemical shifts, namely at 217.2 ppm for 1(PF₆) and at 208.9 ppm for 2(PF₆). This also reflects the electrochemistry at the ruthenium center (vide infra).

Evidence for the success of the amide coupling between 2(PF₆) and 5(PF₆) is gained from the ¹H NMR spectrum of 6(PF₆)₂. The proton resonance at low field (9.63 ppm) with an integral of a single proton indicates the presence of an amide bridge. Additionally, all aromatic signal sets occur four times in a 1 : 1 : 1 : 1 ratio. Although the resonances of the two terpyridine ligands are distinguishable due to the different substituents at the remote dpb ligands, an unambiguous assignment to one of the two capping ligands is impossible. The ESI mass spectrum, which shows the required peaks at m/z = 586.6 for 6²⁺ and at 1318.3 for 6(PF₆)⁺ with isotope patterns characteristic for a complex containing two ruthenium atoms, gives additional support to the successful formation of the dinuclear complex.

IR spectroscopy further confirms all structures under study (ESI, Fig. S16†). All the complexes exhibit an intense IR absorption at 843 cm⁻¹ arising from P–F stretching vibrations within the PF₆⁻ counterion. The amino-substituted complex 2⁺ shows a broad, intense absorption at 3420 cm⁻¹ arising from N–H stretching vibrations of the NH₂ group. The amide containing complexes 1⁺ and 6²⁺ exhibit a broad absorption band at around 3220–3230 cm⁻¹ ascribed to the N–H stretch along with intense C=O vibrations at 1650 cm⁻¹ and 1635 cm⁻¹, respectively. Similar C=O vibrations are observed for the carboxy-substituted complexes 3⁺ and 4⁺, with that of the ester occurring at 1695 cm⁻¹ and that of the carboxylic acid at 1665 cm⁻¹. Additionally, the carboxylic acid 4⁺ exhibits a broad absorption at 3440 cm⁻¹ (O–H stretch) along with absorptions in the range between 3000 and 2300 cm⁻¹ typical for carboxylic acids.

Electrochemical properties of complexes 1(PF₆)–4(PF₆) and 6(PF₆)₂

The cyclic voltammograms of the complexes 1(PF₆)–4(PF₆) and 6(PF₆)₂ are depicted in Fig. 1 and the respective electrochemical data are summarized in Table 1. For all mononuclear complexes, 1(PF₆)–4(PF₆), a single reversible oxidation is observed in the range between −0.2 V and 0.28 V versus the ferrocene/ferrocenium redox couple. It is ascribed to the Ru^II/Ru^III couple. The electrochemical data of the ethyl ester-substituted complex 3(PF₆) agree well with those of the methyl ester reported in the literature.³⁰ With increasing electron-accepting properties of the respective substituent, this redox process is shifted to higher potentials by almost 500 mV. This suggests a strong contribution of the dpb ligand to the highest occupied molecular orbital (HOMO) of these complexes.

Fig. 1 Cyclic voltammograms of 1(PF₆)–4(PF₆) and 6(PF₆)₂ in MeCN with 0.1 mol l⁻¹ [nBu₄N][PF₆] as the supporting electrolyte.

Table 1 Electrochemical data of complexes 1(PF₆)–4(PF₆) and 6(PF₆)₂, obtained from 0.1 mol l⁻¹ [nBu₄N][PF₆] containing acetonitrile solution. Potentials are referenced against the FcH/FcH⁺ couple. Energy differences E_HOMO − E_LUMO are obtained from DFT calculations (see the MO diagram in Fig. 2)

	E ox,1/V	E ox,2/V	E ox,3/V	E red,1/V	E red,2/V	E ox,1 − Ered,1/V	E LUMO − EHOMO/eV
a Reversible, E1/2 given. b Irreversible, anodic peak potential given. c Irreversible, cathodic peak potential given.
1(PF6)	0.06 ([Ru–dpb]/[Ru–dpb]^+)^a	0.86 ([Ru–dpb]^+/[Ru–dpb]^2+)^b	—	−1.93 (tpy/tpy^−)^a	−2.54^c	1.99	2.72
2(PF6)	−0.20 ([Ru–dpb]/[Ru–dpb]^+)^a	0.35 ([Ru–dpb]^+/[Ru–dpb]^2+)^a	—	−1.95 (tpy/tpy^−)^a	−2.48^c	1.75	2.48
3(PF6)	0.28 ([Ru–dpb]/[Ru–dpb]^+)^a	1.49 ([Ru–dpb]^+/[Ru–dpb]^2+)^b	—	−1.87 (tpy/tpy^−)^a	−2.40^c	2.15	2.98
4(PF6)	0.28 ([Ru–dpb]/[Ru–dpb]^+)^a	1.42 ([Ru–dpb]^+/[Ru–dpb]^2+)^b	—	−1.86 (tpy/tpy^−)^a	−2.50^c	2.14	2.99
6(PF6)2	0.05 ([Ru–Ru]/[Ru–Ru]^+)^a	0.29 ([Ru–Ru]^+/[Ru–Ru]^2+)^a	1.58 ([Ru–Ru]^2+/[Ru–Ru]^3+)^b	−1.85 (2 e^−, tpy/tpy^−)^a	−2.51^c	1.90	2.64

---

Density functional theory (DFT) calculations further illustrate and enlighten these experimental findings. We have shown previously⁴⁰ that the B3LYP functional⁶³ along with a split-valence double-ξ basis set and polarization functions on all non-hydrogen atoms (def2-SV(P))^64–66 provides reasonable access to the electronic properties of the numerous charge transfer states of the complexes under study when combined with the ZORA relativistic approximation⁶⁷ and a continuum solvent model (COSMO).⁶⁸

Indeed, DFT calculations for the singlet ground states of the respective cationic complexes nicely reproduce the dependence of the energy of the HOMO from the substitution pattern (Fig. 2). Additionally, the shape of the HOMO parallels that of the doublet spin density of the Ru^III complexes 1²⁺–4²⁺ (ESI, Table S2†) supporting the fact that oxidation occurs on both the metal site and the dpb ligand. At substantially higher potentials, a second, irreversible oxidation is observed. It is again assigned to a mixed metal/dpb ligand oxidation yielding a [Ru(dpb)]³⁺ state as suggested previously by DFT calculations for analogous complexes.⁴⁰ The dependence of this second oxidation from the substitution pattern is even more pronounced so that its potential ranges from 0.35 V for amine-substituted 2(PF₆) to 1.49 V for ester-substituted 3(PF₆).

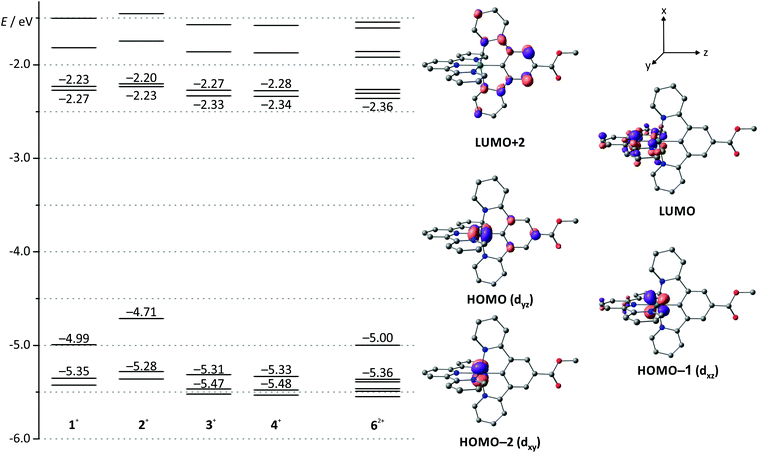Fig. 2 Molecular orbital energy diagram of complexes 1(PF₆)–4(PF₆) and 6(PF₆)₂ obtained from DFT calculations (B3LYP, def2-SV(P), COSMO (acetonitrile), ZORA). Frontier orbitals are depicted exemplary for 3(PF₆) since the shape of the respective orbital varies only marginally among the mononuclear complexes (see also ESI, Table S1†). Hydrogen atoms are omitted for clarity.

All four mononuclear complexes exhibit one reversible and several unresolved irreversible reductions. According to DFT calculations on the ground and the one-electron reduced states of 1⁺–4⁺ (1⁰–4⁰), the first reduction is ascribed to a tpy-centered reduction (ESI, Table S2†). The COOH-substituted complex 4(PF₆) shows a stripping peak upon reoxidation following the first reduction. We ascribe this phenomenon to precipitation of the neutral complex moiety [Ru^II(dpb⁻-COOH)(tpy⁻)] 4⁰ on the electrode surface and subsequent redissolution after reoxidation to 4⁺.⁵⁵

Due to the orthogonal mer-coordination of the two tridentate ligands, the electronic influence of the different functional groups attached to the dpb ligand on the tpy ligand is reduced to a minor inductive effect. Consequently, the first reduction occurs at very similar potentials for all four complexes in the range between −1.86 (COOH-substituted 4(PF₆)) and −1.95 V (NH₂-substituted 2(PF₆)) spanning just 90 mV. Accordingly, the HOMO–LUMO gap, which is closely correlated to the difference of the redox potentials of the first reduction and oxidation, varies considerably in the order 4⁺ ≈ 3⁺ > 1⁺ > 2⁺ (Table 1). This trend is in excellent agreement with DFT calculations (Fig. 2 and Table 1).

All complexes exhibit follow-up oxidation peaks in the range between −1 and −0.5 V once reduction has been carried out beyond −2 V. We had observed such behaviour previously both in mono- and dinuclear bis(terpyridine)ruthenium(II) complexes and cyclometalated ruthenium complexes bearing amide functionalities. We had suggested that these follow-up oxidations are associated with species that are formed after reduction of the substantially acidified amide NH proton (hydrogen formation).⁵⁵ The observation of similar processes in complexes such as 3(PF₆) and 4(PF₆) lacking NH functionalities contradicts this hypothesis. In fact, such more or less pronounced follow-up reoxidation peaks can be found for a large variety of tpy containing complexes of different metals such as chromium,⁶⁹ manganese,⁷⁰ and ruthenium,³⁵ once a sufficient number of reduction events have taken place at the tpy unit. The triplet spin densities of the twofold reduced complexes 1¹⁻–4¹⁻ do not provide further hints on possible follow-up reactions (ESI, Table S2†). Compared to the respective ¹GS structures, their geometries are undistorted with a spin density homogeneously distributed over all three pyridine rings of the terpyridine ligand.

For the dinuclear complex 6(PF₆)₂, cyclovoltammetric studies reveal a single reversible two-electron reduction, as evidenced from square-wave voltammetry, followed by an intense stripping peak. Again, this stripping peak arises from precipitation of the large uncharged complex 6⁰ on the electrode surface and redissolution after reoxidation to 6²⁺. The first, unsplit reduction processes are ascribed to tpy-centered reductions occurring at both terminal ligands of the bimetallic complex as evidenced from DFT calculated triplet spin densities of 6⁰ (ESI, Table S3 and Fig. S17†). Additionally, two reversible oxidation processes at 0.05 and 0.29 V, respectively, are observed. Based on the redox potentials of the mononuclear complexes, these can be ascribed to a primary oxidation of the NH-substituted complex fragment followed by oxidation of the CO-substituted moiety. Interestingly, the difference of the two oxidation potentials is slightly increased by 20 mV compared to that of the mononuclear complexes 1⁺ and 3⁺ (240 versus 220 mV, Table 1). This might be due to spatial charge accumulation or to a weak electronic communication between the two complex fragments in the mixed-valent state 6³⁺. Missing shifts of the electrochemical potentials of asymmetric dinuclear complexes compared to similar mononuclear complexes or negligible splittings between the Ru^IIRu^II/Ru^IIRu^III and the Ru^IIRu^III/Ru^IIIRu^III oxidation potentials in symmetrical complexes have already been observed with other bimetallic bis(tridentate)ruthenium complexes.^53–55,57 Some of these were accompanied by a weak electronic interaction between the Ru centers while others showed no metal–metal interaction. These examples illustrate that a clear conclusion as to whether electronic communication occurs between the metal centers of the complex fragments is impossible purely based on these electrochemical data.⁷¹ UV-Vis spectroscopy studies on the mixed-valent species 6³⁺ will provide deeper insight into that matter (vide infra).

UV-Vis spectroscopic properties of complexes 1(PF₆)–4(PF₆) and 6(PF₆)₂

The absorption spectra of all mononuclear complexes (Fig. 3) exhibit very similar features. Besides intense transitions in the UV region attributed to π–π* transitions within the ligands, four discernible absorption bands are observed in the visible range between 350 and 650 nm. DFT calculations^30,39 and resonance Raman spectroscopy studies⁴⁰ suggest that such bands characteristic for cyclometalated ruthenium complexes containing polypyridine and N^C, N^C^N or N^N^C ligands arise from metal-to-ligand charge transfer transitions (¹MLCT) involving both the polypyridine and the cyclometalating ligand as electron accepting sites.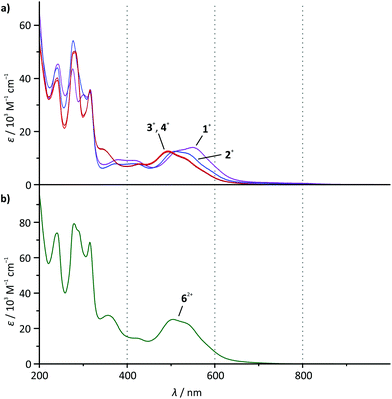

Fig. 3 UV-Vis absorption spectra of (a) 1(PF₆)–4(PF₆) and (b) 6(PF₆)₂ in dry acetonitrile solution at room temperature (c = 2 × 10⁻⁵ mol l⁻¹).

As the visible-range absorption bands are governed by ¹MLCT transitions involving both ligands, variation of the functional group on the cyclometalating ligand greatly affects the position of the low-energy absorption maximum (Table 2). While the ester- or acid-substituted complexes 3⁺ and 4⁺ exhibit absorption maxima at 493 nm, the respective maximum of amide-substituted 1⁺ is observed at 509 nm and that of the amine complex 2⁺ is found at 550 nm (Fig. 3). This trend is in good agreement with the HOMO–LUMO gap (Table 1 and Fig. 2) in this series of complexes. In contrast, DFT calculations reveal that the most intense Ru → tpy MLCT transitions (HOMO−1 (d_xz) → LUMO) are not responsible for the observed trend since they appear at very similar energies for all four complexes (transition 5 in ESI, Tables S4–S7†). This is easily understood based on a closer examination of the orbitals of the complexes 1⁺–4⁺ involved in this transition (Fig. 2 and ESI, Table S1†): the symmetry of the LUMO (tpy) only allows for constructive interference with the d_xz orbital of the metal (HOMO−1). On the other hand, both, HOMO−1 and LUMO are perpendicular to the Ru d_yz orbital and the dpb π-orbital which strongly contribute to the HOMO. Hence, the dpb functional group's impact on the involved orbitals is again reduced to a minor inductive effect explaining the weak dependence of the Ru → tpy MLCT transitions on the dpb substituent.

Table 2 Experimental UV-Vis absorption and emission data of the mononuclear complexes 1(PF₆), 2(PF₆), 3(PF₆), and 4(PF₆) as well as the dinuclear complex 6(PF₆)₂. Absorption and emission data are obtained from (deaerated) acetonitrile solution, and low-temperature emission data are recorded in butyronitrile. Excitation wavelengths are given in parentheses where wavelength dependence of the emission maximum was observed, otherwise λ_exc = 500 nm

	λ max/nm (ε/10^3 M^−1 cm^−1)	λ em/nm at 298 K	λ em/nm at 155 K	λ em/nm at 77 K	ϕ at 298 K
1(PF6)	533 (11.9, sh), 509 (12.5), 419 (7.9), 373 (7.9), 315 (34.8)	800	798	736	8 × 10^−6
2(PF6)	550 (12.9), 519 (12.9, sh), 417 (9.1), 379 (9.4), 316 (35.8)	780	768	731	<2 × 10^−6
3(PF6)	529 (9.9, sh), 493 (12.3), 428 (7.6), 343 (13.5), 315 (35.3)	744	738	708	14 × 10^−6
4(PF6)	529 (10.2, sh), 493 (12.7), 429 (7.8), 343 (13.3), 315 (35.6)	744	738	709	15 × 10^−6
6(PF6)2	530 (23.4, sh), 504 (25.1), 422 (14.6), 356 (27.4), 315 (68.7)	756 (480), 772 (560)	746	736	9 × 10^−6

---

The strong bathochromic shift of the experimental absorption maximum accompanying the more electron-donating N-acetyl amino and amino substituents at the dpb ligand in fact arises from symmetry-allowed d_yz(Ru) → dpb MLCT transitions. Especially the HOMO → LUMO+2 transition plays a key role within the absorption characteristics (transition 6 in Tables S4–S7†). These transitions are calculated at 486 (1⁺), 507 (2⁺), and 456 nm (3⁺ and 4⁺), respectively, and they nicely reproduce the trends within the absorption maxima of the respective complexes (Table 2). This fully confirms that the two main ¹MLCT transitions in the visible range of the electronic spectrum, namely d_xz(Ru) → tpy and d_yz(Ru) → dpb, are electronically decoupled for simple symmetry reasons.

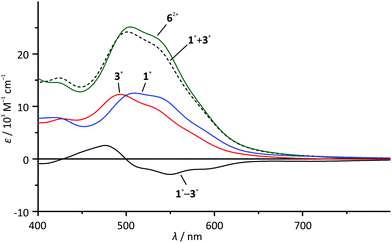
At first sight, the absorption spectrum of the dinuclear complex 6²⁺ resembles the absorption spectra of the carboxy-substituted mononuclear complexes 3⁺ and 4⁺ with roughly doubled extinction coefficients due to its dinuclear nature (Fig. 3). A closer inspection reveals that the spectrum of the dinuclear complex is much better reproduced by a 1 : 1 superposition of the absorption spectra of the ester- and the amide-substituted mononuclear complexes 1⁺ and 3⁺ (Fig. 4). This suggests that the dinuclear compound 6²⁺ consists of two essentially non-interacting bis(tridentate)ruthenium(II) fragments connected via an amide bond. Indeed, this is underlined by time-dependent DFT calculations which reveal that all charge transfer excitations >400 nm between the two complex fragments have negligible oscillator strengths and should play no role in the observed absorption features (Table S8†). Similar observations have previously been made for other amide-linked dinuclear ruthenium(II) complexes with tridentate ligands.^53–55 Since in this study the visible absorption-spectroscopic fingerprints of the two subunits are more distinct than in the literature-known bimetallic examples, the superimposed nature of the absorption bands of 6²⁺ is more obvious. In principle, the two [Ru(dpb)(tpy)]⁺ subunits are essentially uncoupled in the Ru^IIRu^II state.

Fig. 4 Visible range of the absorption spectra of 1⁺ (blue), 3⁺ (red) and 6²⁺ (green) in dry acetonitrile solution as well as superposition (1⁺ + 3⁺) (black, dashed line) and difference spectra (3⁺ − 1⁺) (black, solid line).

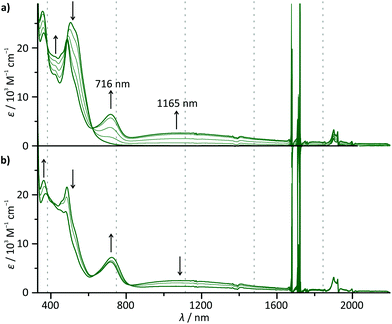
To probe the metal–metal interaction in the mixed-valent state 6³⁺, careful in situ chemical oxidation of 6(PF₆)₂ in acetonitrile solution was carried out using (NH₄)₂[Ce(NO₃)₆] as an oxidant (E ≈ 0.8–0.9 V).⁷² Its oxidation potential is high enough to allow for a stepwise double oxidation of 6²⁺ to the bis(ruthenium(III)) complex 6⁴⁺. Absorption spectra (Fig. 5) were recorded each time after addition of 0.25 equivalents of the oxidant. A broad, symmetrical absorption band appears in the near infrared (NIR) region of the absorption spectrum upon addition of 0 → 1 equivalents of the oxidant with an absorption maximum at 1165 nm (8585 cm⁻¹, ε_max = 2620 M⁻¹ cm⁻¹, full width at half maximum [small nu, Greek, tilde]_1/2 = 6020 cm⁻¹). Simultaneously, a second, significantly sharper band appears in the red region (maximum at 716 nm). A set of isosbestic points is observed for the oxidation of 6²⁺ to 6³⁺ at 233, 326, 335, 486, and 619 nm indicating a clean reaction without side products. Upon addition of more oxidant (1 → 1.5 eq.), a new set of isosbestic points is observed at 273, 325, 335, 638, and 810 nm. Hence, the reaction 6²⁺ → 6³⁺ → 6⁴⁺ occurs stepwise as expected from the separation of the first and second oxidation waves in the cyclic voltammogram of 6²⁺. Simultaneously, the intensity of the NIR band decreases while the band in the red region rises further. Interestingly, upon addition of more oxidant (1.5 → 2 eq.), the isosbestic points are lost and a new absorption band appears at around 940 nm (ESI, Fig. S18†). We ascribe this to the decomposition of the highly charged complex 6⁴⁺ on the timescale of the measurement (about 45 minutes).

Fig. 5 UV-Vis-NIR absorption spectra of 6²⁺ in acetonitrile solution upon addition (a) of 0 → 1 equivalents of (NH₄)₂[Ce(NO₃)₆] as an oxidant and (b) of 1 → 1.5 equivalents of (NH₄)₂[Ce(NO₃)₆] as an oxidant. Spectra are recorded after addition of 0.25 equivalents each time.

The fact, that the NIR band is only present in the mixed-valent state 6³⁺, allows for the conclusion that it arises from an intervalence charge transfer (IVCT) process between the two metal centers Ru^II → Ru^III. The absorption band in the red spectral region on the other hand is ascribed to ligand-to-metal (LMCT) transitions in the newly formed Ru^III fragment (dpb → Ru). This is supported by TD-DFT calculations which predict such a symmetry allowed IVCT transition (d_yz(Ru) + dpb-CO → d_yz(Ru) + dpb-NH) to occur at a wavelength of 1395 nm and LMCT excitations at around 630 nm for 6³⁺ (ESI, Table S9†). Additionally, the absorption spectra of the mononuclear complexes 1⁺ and 3⁺ exhibit very similar LMCT bands in the range between 600 and 800 nm upon oxidation under the same conditions (ESI, Fig. S19†). In particular, the excellent agreement between the LMCT maximum of 1²⁺ (720 nm) and 6³⁺ (716 nm) underlines that the first oxidation of 6²⁺ occurs at the N-substituted [Ru(dpb)(tpy)]⁺ fragment.

Although a straight-forward Hush analysis of the band shape and energy of the IVCT band is formally not correct due to the energy difference ΔG₀ of the two valence isomers [(tpy)Ru^II(dpb-NHCO-dpb)Ru^III(tpy)]³⁺ and [(tpy)Ru^III(dpb-NHCO-dpb)Ru^II(tpy)]³⁺, the latter being the lower energy isomer, we analysed the IVCT band to obtain a rough estimate of the electronic coupling parameter V_ab (ESI, Fig. S20†).^49,73 As the donor–acceptor distance r_MM, the Ru–Ru distance of 13.1 Å (from DFT calculation) was taken into account despite the fact that the involved orbitals are substantially delocalized towards the cyclometalated bridging ligand, thus rendering the effective charge transfer distance smaller.^{59,60,74–76} As using a too large value for r_MM will underestimate the electronic coupling parameter, the calculated V_ab value of 580 cm⁻¹ represents a lower limit. This coupling in 6³⁺ is roughly half as strong as in the back-to-back linked symmetrical dinuclear complex [(ttpy)Ru(dpb-dpb)Ru(ttpy)]³⁺ (ttpy = 4′-tolylterpyridine).⁵⁹ We attribute this weakening to the redox asymmetry introduced by the amide bridge in 6³⁺. Simultaneously, the NHCO group increases the donor–acceptor distance and reduces the orbital overlap between the two complex moieties. Clearly, the mixed-valent complex 6³⁺ has to be assigned to the Robin–Day class II with localized valencies and a moderate electronic coupling between the complex subunits.⁴⁸ The activation barrier for thermal electron transfer can be calculated when the strength of electronic coupling and the energy difference ΔG₀ of the two valence isomers are known.⁵² The latter can be estimated based on the difference in redox potentials of the Ru^II/Ru^III couple of the two complex subunits. Since for 6²⁺, this difference is shifted towards larger values due to charge accumulation and the resonance stabilization of the mixed-valent species 6³⁺, we used the difference in Ru^II/Ru^III redox potentials of the mononuclear complexes 1⁺ and 3⁺ to estimate ΔG₀ as 0.22 eV (1775 cm⁻¹, 21 kJ mol⁻¹).⁵² This yields an activation barrier of the electron transfer from [(tpy)Ru^III(dpb-NHCO-dpb)Ru^II(tpy)]³⁺ to [(tpy)Ru^II(dpb-NHCO-dpb)Ru^III(tpy)]³⁺ of 2190 cm⁻¹ (26 kJ mol⁻¹).

The electronic coupling in 6³⁺ is in contrast to the amide bridged dinuclear ruthenium complex [(EtOOC-tpy)Ru^II(tpy-NHCO-tpy)Ru^III(tpy-NHCOMe)]⁵⁺.⁵⁵ Based on a simple molecular orbital consideration, the electronic coupling occurs via a superexchange mechanism involving the bridge's frontier orbitals.^77,78 In the bis(terpyridine)ruthenium system, these are well separated in energy from the donor and acceptor orbitals at the metal centers. Thus, the tunnel barrier for electron transfer is much higher than in 6³⁺ leading to no detectable electronic interaction in the former. In contrast, the mediating bridge orbitals of 6³⁺ are already mixed into the ground state donor and acceptor orbitals of the metal centers, significantly increasing the electronic coupling in 6³⁺.⁵⁵ Obviously, cyclometalating bridging ligands enable electronic communication in mixed-valent Ru^II/Ru^III complexes.^59,60,75,76

Emission spectroscopy and triplet excited states of complexes 1(PF₆)–4(PF₆)

All four mononuclear complexes 1(PF₆)–4(PF₆) exhibit very weak room temperature emission in the red spectral range (Fig. 6 and Table 2). The carboxy-substituted complexes 3⁺ and 4⁺ show the highest energy emission along with the highest phosphorescence quantum yield. Both are in excellent agreement with the values for the methyl ester complex reported by van Koten and coworkers.³⁰ Interestingly, the phosphorescence of these complexes is not quenched by oxygen present during the measurement. This is attributed to very short excited state lifetimes in the picosecond range that are too short for bimolecular quenching processes by triplet oxygen to occur. Indeed, attempts to measure the luminescence lifetimes by time-correlated single photon counting failed underlining that the excited state lifetimes at room temperature are well below one nanosecond.

Fig. 6 Normalized steady-state emission spectra of 1(PF₆)–4(PF₆) (λ_exc = 500 nm) (a) at room temperature in degassed acetonitrile solution, (b) at 155 K in liquid butyronitrile solution and (c) at 77 K in a frozen butyronitrile matrix.

The shape of the emission band of the two COOR-substituted compounds 3⁺ and 4⁺ is very similar to that of many other (polypyridine)ruthenium(II) complexes with a vibronic progression resulting in a typical low-energy shoulder.^2,27,31,40 The emission band shape of the N-substituted complexes 1⁺ and 2⁺ on the other hand is different. Spectral decomposition in separate Gaussian shaped bands (ESI, Fig. S21†) suggests that 0–1 and especially 0–2 transitions dominate in these complexes at room temperature. The 0–0 transition, which typically is quite strong in other [Ru(dpb)(tpy)]⁺-complexes at room temperature, apparently is of less relevance in complexes with dpb-NHR ligands (ESI, Fig. S21†). Consequently, in a solid butyronitrile matrix at 77 K, a more pronounced hypsochromic shift is observed for complexes 1⁺ (1085 cm⁻¹) and 2⁺ (860 cm⁻¹) than for 3⁺ and 4⁺ (580 cm⁻¹). At 77 K in frozen butyronitrile solution, the carboxy-substituted complexes 3⁺ and 4⁺ emit at a wavelength of 708–709 nm, while the amido- and amino-substituted complexes 1⁺ and 2⁺ emit at 736 and 731 nm, respectively. The similarity in the emission energy of the latter two complexes is remarkable and not straight-forwardly understood from a simple consideration of the HOMO–LUMO gap of the respective complexes (Table 1).

In order to gain a deeper understanding of the excited state properties of the respective complexes, DFT calculations on the excited triplet states were performed. The symmetry allowed emission of (polypyridine)ruthenium(II) complexes arises from a low-energy ³MLCT state. It exhibits spin density both at the metal site and the π-accepting polypyridine ligand. In fact, in cyclometalated complexes of the type [Ru(dpb-R¹)(tpy-R²)],⁺ the LUMO of the terpyridine is always involved in the ³MLCT emissive state as well.⁴⁰ Consequently, geometry optimizations were performed on the triplet states of all complexes under study yielding the respective ³MLCT states (Fig. 7). Despite the fact that these states are distorted to some extent compared to the singlet ground states (¹GS) (vide infra), it is obvious from the respective spin densities that the ³MLCT states are composed of HOMO−1 (d_xz(Ru)) as the electron donor and LUMO as the electron acceptor. Similar to the previous discussion concerning the ¹MLCT excitations (vide supra), this orbital parentage of the ³MLCT state results in rather similar ³MLCT-¹GS energy gaps despite the strongly varying HOMO (d_yz + π_dpb)–LUMO gaps.

Fig. 7 Jablonski diagram of the triplet states of complexes 1⁺–4⁺ including DFT spin density plots (B3LYP, def2-SV(P), COSMO (acetonitrile), ZORA; contour value: 0.01). ³MLCT energies are given as experimental 0–0 emission energies, ³LL′CT and ³MC energies are calculated based on DFT derived Gibbs free energies relative to the respective ³MLCT energy and given in kJ mol⁻¹. Hydrogen atoms are omitted for clarity.

Insight into excited state deactivation pathways can be gained from temperature dependent measurements of excited state lifetimes or quantum yields. Seminal work by T. J. Meyer and co-workers²² revealed a metal-centered ³MC state as a thermally accessible state in [Ru(bpy)₃]²⁺. This state depopulates the emissive ³MLCT state and substantially shortens its lifetime at room temperature. In strongly push–pull substituted cyclometalated complexes such as [Ru(dpb-NHCOMe)(tpy-COOEt)],⁺ a second pathway via a low-energy ligand-to-ligand (dpb → tpy) charge transfer (³LL′CT) state is accessible that prevents emission entirely.⁴⁰

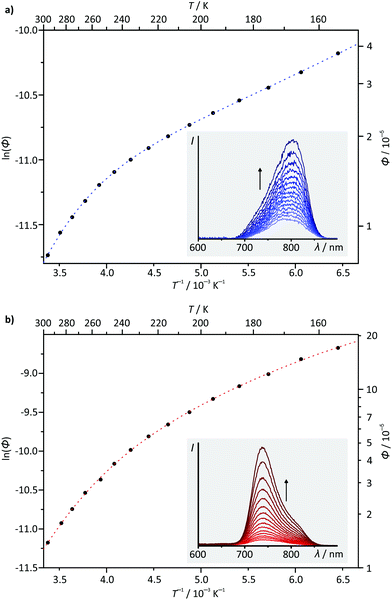
Temperature-dependent steady-state emission spectra were recorded for complexes 1(PF₆) and 3(PF₆) in butyronitrile solution in the temperature range between 298 K and 155 K (Fig. 8). Due to the low quantum yield of complex 2(PF₆) and the spectroscopic similarity of 3(PF₆) and 4(PF₆), 2(PF₆) and 4(PF₆) were not considered in this variable temperature (VT) emission study. Interestingly, the VT emission plots ln(ϕ) vs. T⁻¹ obtained for complexes 1(PF₆) and 3(PF₆) differ qualitatively from those of [Ru(bpy)₃](PF₆)₂ (ESI, Fig. S22 and S23†) and the structurally related complex [Ru(dpb-COOEt)(tpy-NHCOMe)](PF₆).⁴⁰ The shape of the curves clearly is not linear as has been found for [Ru(dpb-COOEt)(tpy-NHCOMe)]⁺.⁴⁰ Meyer's equation^22,23 which assumes a single thermally activated deactivation pathway (³MC) for the emissive ³MLCT state fails to reproduce the shape of the VT emission plots of 1⁺ and 3⁺ as well, while it perfectly fits the VT emission plot of [Ru(bpy)₃]²⁺ (ESI, Fig. S22 and S23†).

Fig. 8 Variable-temperature emission plots of ln(ϕ) vs. T⁻¹ for complexes (a) 1(PF₆) and (b) 3(PF₆) including fit curves (dashed lines; see the text for fit function and parameters). The insets show emission spectra in the range between 298 K and 155 K.

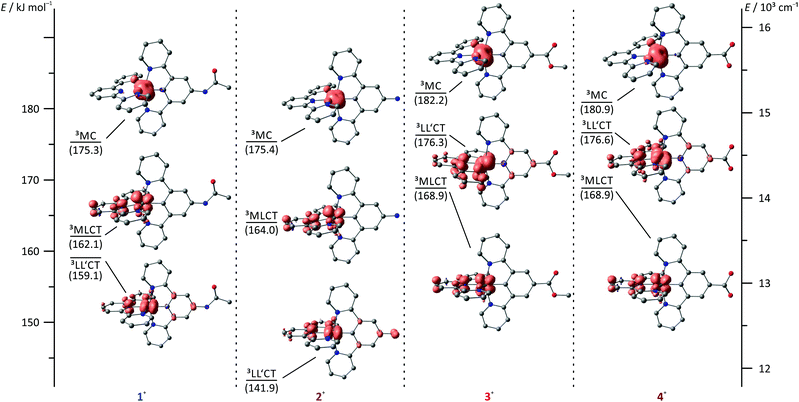
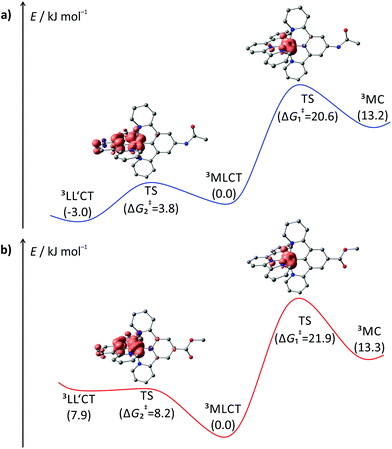
A rational explanation for this behaviour was found upon extended DFT examination of the triplet potential energy surface. Besides the emissive ³MLCT state, two additional low-energy triplet states could be localized as local minima for all four complexes 1⁺–4⁺. These are assigned as ³MC states with a spin density essentially found on the metal site and as ³LL′CT states in which the tpy ligand can be formally regarded as singly reduced while the Ru–dpb moiety carries an electron hole.⁴⁰ This latter low-energy state was considered responsible for the lack of emission from the strongly donor–acceptor substituted complex [Ru(dpb-NHCOMe)(tpy-COOEt)]⁺ because the orthogonality of the orbitals of the electron and hole prevents the radiative recombination from the ³LL′CT state.⁴⁰

Remarkably, all triplet states exhibit characteristic distortions compared to the geometry of the respective singlet ground state structures with a strong resemblance between the COOR-substituted complex on one side and the NHR-substituted complex on the other (Fig. 7). In the ³MLCT states of complexes 3⁺ and 4⁺, the arrangement of the ligand periphery is essentially unaltered while the metal center is shifted towards the tpy ligand. The Ru–N^tpy central bond length is shortened by 2 pm (¹GS: 204 pm, ³MLCT: 206 pm for 3⁺ and 4⁺) while the Ru–C^dpb bond is elongated by 4 pm in both cases (¹GS: 195 pm, ³MLCT: 199 pm for 3⁺ and 4⁺). This is in agreement with an increased coulombic interaction between the formally oxidized Ru and reduced tpy ligands upon population of the ³MLCT state and has been described before for other polypyridine ruthenium complexes.^35,40 All Ru–N bonds involving the four peripheral pyridines are nearly unaffected with similar bond lengths between 210 pm and 212 pm in all cases. This is in stark contrast to the geometry of the ³MLCT state of both 1⁺ and 2⁺. Here, the ligand periphery is substantially distorted compared to the ¹GS geometry: the central pyridine ring of the tpy unit is offset from the plane perpendicular to the dpb ligand with a central N^tpy–Ru–C^dpb bond angle of just 167°. At the same time, one of the two peripheral pyridine rings of the dpb unit is shifted away from the metal center to some extent yielding a long Ru–N bond of 219 pm while the trans Ru–N bond is shortened to 209 pm (from 212 pm in the ¹GS of 1⁺ and 2⁺). A similar shift of the metal center towards the tpy ligand as observed for 3⁺ and 4⁺ is also found for 1⁺ and 2⁺. This difference in the geometry of the ³MLCT states between the NHR- and COOR-substituted complexes might explain the dominance of 0–2 transitions in the emission spectra of 1⁺ and 2⁺ as it corresponds to a larger horizontal offset on the ¹GS-³MLCT reaction coordinate.

In the ³LL′CT states again a clear distinction is found between the geometries of complexes 1⁺ and 2⁺ on one side and 3⁺ and 4⁺ on the other. The ³LL′CT geometries of complexes 1⁺ and 2⁺ appear essentially undistorted compared to the ¹GS structures with a slight elongation of the central Ru–N^tpy bond by about 4 pm.⁴⁰ A similar shift is observed in the ³LL′CT states of complexes 3⁺ and 4⁺. Yet, in their ³LL′CT geometries, the tpy ligand is twisted by about 8° out of the plane perpendicular to the dpb ligand.

The ³MC states of all four complexes appear structurally similar with immensely elongated bond lengths between Ru and the tpy nitrogen atoms (central Ru–N^tpy bonds: 225–227 pm, peripheral Ru–N^tpy bonds: 235–237 pm). This distortion is accompanied by a tilt of the peripheral pyridine rings compared to the central one within the tpy unit by 9–11°. The dpb ligand on the other side is undistorted with typical Ru–dpb bond lengths (central Ru–C^dpb bonds: 195–196 pm, peripheral Ru–N^dpb bonds: 215–217 pm).

Based on DFT calculated Gibbs free energies, the ³LL′CT state is the triplet ground state of the NHR-substituted complexes 1⁺ and 2⁺ (Fig. 7) followed by the ³MLCT and ³MC states. This order is identical to that of the strongly donor–acceptor substituted complex [Ru(dpb-NHCOMe)(tpy-COOEt)]⁺.⁴⁰ In complexes 3⁺ and 4⁺, in which the donor strength of the dpb ligand is weakened by the COOR substituents, the order of ³MLCT and ³LL′CT is inverted. Increasing the push–pull substitution of a given heteroleptic [Ru(dpb)(tpy)]⁺ complex will lower the energy of a donor–acceptor charge-separated state, here the ³LL′CT state, relative to the other excited states. Remarkably, the trends of the geometrical features of the various states can be related to their relative energies. While for 1⁺ and 2⁺, the ³LL′CT state is the least distorted compared to the ¹GS geometries, for 3⁺ and 4⁺ this is true for the ³MLCT state instead.

Considering the relative energies of the various triplet states, it is apparent that the emissive ³MLCT state is flanked by two non-emissive states (³MC and ³LL′CT) for all four complexes. Both are thermally accessible, instead of just a single state (³MC) as in [Ru(bpy)₃](PF₆)₂. The presence of a second non-emissive state at low energy gives rise to an additional excited state deactivation pathway.⁴⁰ This is important for the interpretation of the temperature dependence of the emission spectra of 1(PF₆) and 3(PF₆) (Fig. 8). In fact, a second exponential term needs to be taken into account, compared to Meyer's original equation which accounts for a single depopulating state.^22,23 Including a second state yields the following equation (for derivation see the ESI†):

ln(ϕ) = ln(k_r) − ln[k_r + k_nr + k₁ exp(−ΔE₁/RT) + k₂ exp(−ΔE₂/RT)].

The rate constants k_r and k_nr describe the radiative and non-radiative decays (³MLCT → ¹GS), ΔE₁ corresponds to the activation barrier for surface crossing from the ³MLCT to the ³MC state (ΔE₁ = ΔG^‡₁) and k₁ is the rate constant for this surface crossing at infinite temperature as shown by Meyer.²²

An analogous equation was previously used by Balzani and coworkers to describe the photodynamics of complexes of the [Ru(bpy)₃]²⁺ family.^79,80 In these cases, ΔE₁ corresponds to the barrier for the thermally activated ³MLCT → ³MC surface crossing while ΔE₂ (typically <1 kJ mol⁻¹) is interpreted as the energy separation between multiple close-lying ³MLCT states split by spin–orbit coupling.^80–82

In the present study, ΔE₂ can be interpreted either as the energy difference ΔG₀ of the ³MLCT and ³LL′CT states in thermal equilibrium or the activation barrier ΔG^‡₂ for the surface crossing from the ³MLCT to the ³LL′CT state (see the ESI† for in-depth elaboration). This depends on the relative rate constants for the reverse internal conversion ³LL′CT → ³MLCT and the non-radiative intersystem crossing (ISC) to the ground state (³LL′CT → ¹GS). Upon cooling of solutions of all four mononuclear complexes, even complexes 1⁺ and 2⁺, in which the emissive ³MLCT state is not the triplet ground state, the emission intensity increases. This corroborates that ³MLCT and ³LL′CT cannot be in thermal equilibrium at least in complexes 1⁺ and 2⁺. For complexes 3⁺ and 4⁺, this conclusion cannot be drawn purely based on the temperature dependence of the emission quantum yield, since both, the energy difference of the ³MLCT and ³LL′CT states and the activation barrier ΔG^‡₂, are positive. Based on the DFT calculated energies of the activation barriers for the ³MLCT–³LL′CT surface crossing and the experimentally determined ΔE₂ values (vide infra), however, it is plausible, that also for complexes 3⁺ and 4⁺, the surface crossing into the ³LL′CT state is irreversible and followed by rapid relaxation into the singlet ground state. Consequently, ΔE₂ is identified in analogy to ΔE₁ = ΔG^‡₁ as the activation barrier ΔG^‡₂ for the thermal depopulation of the ³MLCT via the ³LL′CT states.

Based on the very similar 0–0 emission energies which should give similar rate constants for the non-radiative decay (³MLCT → ¹GS), the large differences in the phosphorescence quantum yields of the four complexes 1⁺–4⁺ are quite unexpected (Table 2).^83–85 Yet, combining the ln(ϕ) vs. T⁻¹ plots with the relative energies of the involved states as determined by DFT provides an explanation. For complexes 3⁺ and 4⁺ the relatively high quantum yield is associated with the emissive ³MLCT state being the triplet ground state. For 1⁺ and 2⁺ on the other hand, the non-emissive ³LL′CT state becomes the triplet ground state giving rise to a deactivation pathway with a potentially very low activation barrier ΔG^‡₁. Due to the small experimentally accessible temperature range, the fit using the biexponential equation given above is overparametrized. Consequently, quantitative results have to be considered very carefully. For 1⁺, activation barriers of ΔG^‡₁ = 21.7 and ΔG^‡₂ = 2.1 kJ mol⁻¹ are obtained from the fit, while for 3⁺, the activation barriers are ΔG^‡₁ = 23.1 and ΔG^‡₂ = 6.2 kJ mol⁻¹. Based on the calculated energies of the various triplet states (Fig. 7), it is reasonable to assume that the higher activation barriers ΔG^‡₁ of >20 kJ mol⁻¹ are associated with the deactivation via the ³MC state (vide infra). ΔG^‡₂ is very similar for both the NHR- and COOR-substituted complex types, corroborating that the substitution pattern at the cyclometalating ligand only has a marginal effect on the ligand field splitting in the [Ru(dpb-R)(tpy)]⁺ type of complexes. The second activation barrier ΔG^‡₂ of 1⁺ is only one third of that of 3⁺. Hence, thermal deactivation via³LL′CT states is significantly accelerated by the presence of an electron donating substituent at the dpb ligand explaining the substantially lower quantum yield of the former. Substituents at the tpy ligand on the other hand are expected to influence both activation barriers but especially ΔG^‡₁ between the ³MLCT and ³MC states since the substituents at the tpy ligand significantly impact the ³MLCT energy.

To gain a better understanding of the excited state processes, we performed DFT based geometry optimizations to find the transition states connecting the ³MLCT and the ³MC states on one side and the ³MLCT and ³LL′CT states on the other. All four transition states could be localized successfully and their nature confirmed by the presence of a single negative vibrational frequency representing the reaction coordinate of the respective transition (Fig. 9). Subsequent spin density calculations further confirmed the nature of the localized states as the desired transition states. For both complexes, 1⁺ and 3⁺, the spin density of the ³MLCT–³LL′CT transition state shows contributions of both ligands and, predominantly, the metal center. Remarkably, the spin carrying orbital at the metal center neither corresponds to the d_xy orbital as in the ³MLCT state nor to the d_yz orbital as in the ³LL′CT state but is a linear combination of both. This further underlines the transition state character of the localized state. Similarly, the ³MLCT–³MC transition states of 1⁺ and 3⁺ show a substantial amount of spin density at the metal center (1.46 electrons based on Mulliken's spin population analysis). But instead of the nitrogen lone pairs, a tpy π*-orbital (LUMO of 1⁺ and 3⁺) contributes to this transition state. The DFT calculated transition state energies ΔG^‡₁(DFT) and ΔG^‡₂(DFT) and G^‡₁(exp.) and ΔG^‡₂(exp.) extracted from the fits of the ln(ϕ) vs. T⁻¹ plots show remarkable agreement with deviation as small as ±2 kJ mol⁻¹. This suggests that despite the narrow temperature range of the VT measurement and their very low quantum yields and short excited state lifetimes, a very reasonable description of the excited state deactivation processes can be obtained for these cyclometalated complexes.

Fig. 9 Profile of the triplet hypersurface of (a) 1⁺ and (b) 3⁺ obtained from DFT calculations (B3LYP, def2-SV(P), ZORA, COSMO (acetonitrile)). Gibbs free energies are given in kJ mol⁻¹ relative to the emissive ³MLCT state (G_MLCT = 0 kJ mol⁻¹). Spin densities of the transition states (TS) are given at a contour value of 0.01. Hydrogen atoms are omitted for clarity.

In summary, dpb ligands in bis(tridentate)ruthenium(II) complexes indeed induce high-energy ³MC states, but give rise to low-energy ³LL′CT states. As for both states, emission is symmetry-forbidden, both contribute to the rapid excited state deactivation observed for these types of complexes. The combination of two [Ru(dpb)(tpy)]⁺ emitters is discussed in the next chapter.

Emission spectroscopy and triplet excited states of complex 6(PF₆)₂

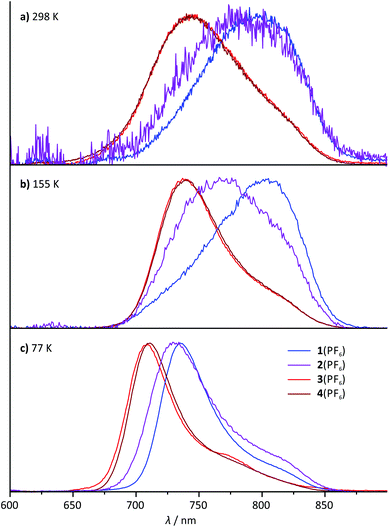
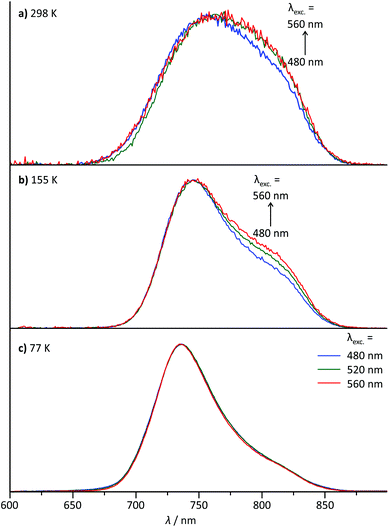
For the dinuclear complex 6²⁺, a broadened emission spectrum is obtained at room temperature compared to the formally constituting mononuclear complexes 1⁺ and 3⁺ (Fig. 10). Additionally, the position of the emission maximum is dependent on the excitation wavelengths and shifts from 756 nm upon excitation at 480 nm to 772 nm when being irradiated at 560 nm (Fig. 10 and Table 2). Measurement at 155 K in butyronitrile yields substantially sharpened emission spectra with an emission maximum at 746 nm and a pronounced shoulder at 800 nm. The intensity of this shoulder increases upon increasing the excitation wavelength from 480 to 560 nm. The blueshift of the emission maximum (180 cm⁻¹) upon freezing the butyronitrile solution of 6²⁺ is much smaller than that of all mononuclear complexes under study.

Fig. 10 Normalized steady-state emission spectra of 6(PF₆)₂ at varying excitation wavelengths (a) at room temperature in degassed acetonitrile solution, (b) at 155 K in liquid butyronitrile solution and (c) at 77 K in a frozen butyronitrile matrix.

A wavelength dependence of the emission maximum from the excitation energy is very atypical for polypyridineruthenium(II) complexes. We ascribe this behaviour to two independent emission processes in solution involving the two complex subunits of 6²⁺. In fact, similar dual emission processes have previously been invoked to explain the emission wavelength dependence from the excitation energy.^86–89 Unfortunately, attempts to measure the excited state lifetimes by time-correlated single photon counting failed in this case due to the very rapid excited state decay of 6²⁺. Hence, no evidence for a biexponential character of the excited state decay, which would support the presence of a dual emission mechanism, could be obtained.

However, a reasonable explanation for the dual emission of 6²⁺ can be given based on its absorption characteristics. As shown above, the visible range of the absorption spectrum of 6²⁺ is composed of ¹MLCT excitations localized on one of the two complex halves. Upon intersystem crossing and vibrational relaxation, d_xz(Ru) → tpy ³MLCT states are populated. Two such triplet excited states are conceivable, namely ³[(tpy⁻)Ru^III(dpb-NHCO-dpb)Ru^II(tpy)]²⁺ and ³[(tpy)Ru^II(dpb-NHCO-dpb)Ru^III(tpy⁻)]²⁺, with the triplet spin density localized on opposing [Ru(tpy)] fragments (ESI, Fig. S24†). Via double electron transfer from Ru^II to Ru^III and from tpy⁻ to tpy (Dexter energy transfer), these states could interconvert.^90,91 Apparently, due to the large distance between the two [Ru(tpy)] moieties (r_RuRu = 13 Å, r_tpy,tpy ≈ 20 Å), Dexter energy transfer, whose rate constant decays exponentially with distance, is rather slow between the complex subunits. All other radiative and non-radiative relaxation pathways of triplet 6²⁺ are extremely fast (below 1 ns as evidenced from time-resolved emission spectroscopy). Consequently, in fluid solution, emission occurs faster than thermal equilibration between the two emissive ³MLCT states. If equilibration was faster than emission, the ³[(tpy⁻)Ru^III(dpb-NHCO-dpb)Ru^II(tpy)]²⁺ state would be favoured over ³[(tpy)Ru^II(dpb-NHCO-dpb)Ru^III(tpy⁻)]²⁺ thermodynamically and would yield single emission at around 800 nm, but this is not observed.

Given that the two ³MLCT states are not in thermal equilibrium, it should be possible to selectively populate one or the other excited state by irradiation into one of the two complex subunits. Since in the absorption spectrum of 6²⁺ the absorption bands of the two fragments [(tpy)Ru(dpb-NHR)] and [(ROC-dpb)Ru(tpy)] overlap substantially, it is not possible to excite them with 100% selectivity (Fig. 4). But by changing the excitation wavelength it is possible to gradually tune the ratio at which the two building blocks are excited. The difference spectrum of the two mononuclear complexes 1⁺ and 3⁺ carrying similar functional groups as the two subunits of 6²⁺ (Fig. 4) gives an idea where a maximum difference of absorption can be expected between the NH- and CO-substituted [Ru(dpb)(tpy)]⁺ complex subunits. This difference spectrum reveals a maximized and minimized absorption of the COR-substituted complex at around 480 and 560 nm, respectively. This is in excellent agreement with the above mentioned minimum and maximum of the shoulder at 800 nm in the emission spectrum of 6²⁺ at 155 K. Additionally, the difference spectrum of the emission spectra recorded at 155 K with λ_exc = 480 and 560 nm reveals a band with a maximum at 800 nm (ESI, Fig. S25†) that resembles the emission band of 1⁺ at that temperature (Fig. 6b). These observations strongly support that dual emission occurs from two uncoupled ³MLCT excited states of the dinuclear complex 6²⁺ in solution.

The origin of this dual emission process is markedly different than that observed for the structurally similar amide-bridged dinuclear complex [(EtOOC-tpy)Ru(tpy-NHCO-tpy)Ru(tpy-NHCOMe)]⁴⁺.⁵⁵ In the latter, the involved emissive states are sufficiently long-lived and at a significantly shorter distance to allow for thermal equilibration prior to emission. Since the emissive states [(EtOOC-tpy)Ru^II(tpy-NHCO-tpy⁻)Ru^III(tpy-NHCOMe)]⁴⁺ and [(EtOOC-tpy)Ru^III(tpy-NHCO-tpy⁻)Ru^II(tpy-NHCOMe)]⁴⁺ are very similar in energy, occupation between the two is Boltzmann distributed leading to dual emission at room temperature.

Interestingly, upon freezing of the butyronitrile solution of 6²⁺, single emission is observed arising from the NHR-substituted subunit as judged from the position of the emission maximum as well as the independence of the emission band shape from the excitation wavelength (Fig. 10c). This loss of dual emission can be traced back to the change in the rate constants involved with the excited state decay. Upon freezing the solvent matrix around a given luminescent dye, both non-radiative vibrational relaxation and emissive decay are slowed down substantially. This is because they are typically accompanied by geometrical rearrangements of the dye and the environment and such rearrangements are much more difficult in a rigid solvent cage. The rate for intramolecular Dexter energy transfer on the other hand is not significantly diminished upon freezing of the solvent.^92,93 Consequently, in frozen solution, the two ³MLCT states of 6²⁺ equilibrate thermally prior to emission from the lower-energy ³[(tpy⁻)Ru^III(dpb-NHCO-dpb)Ru^II(tpy)]²⁺ state following Kasha's rule.⁹⁴

Experimental

General procedures

Chemicals were obtained from commercial suppliers and used without further purification. Air- or moisture-sensitive reactions were performed in dried glassware under an inert gas atmosphere (argon, quality 4.6). Acetonitrile was refluxed over CaH₂ and distilled under argon prior to use. The ligands N-acetyl-3,5-dipyrid-2′-ylaniline L1 ⁴⁰ and ethyl 3,5-dipyrid-2′-ylbenzoate L2 ⁴⁰ as well as RuCl₃(tpy)⁹⁵ were synthesized following the literature-known procedures. Infrared spectra were recorded on a Varian Excalibur Series 3100 FT-IR spectrometer using KBr disks. IR absorption band intensities are classified as s (strong), m (medium) and w (weak). UV/Vis spectra were recorded on a Varian Cary 5000 spectrometer in 1 cm cuvettes. Emission spectra were recorded on a Varian Cary Eclipse spectrometer. Quantum yields were determined by comparing the areas under the emission spectra on an energy scale recorded for solutions of the samples and a reference with matching absorbances (ϕ([Ru(bipy)₃]Cl₂) = 0.094 in deaerated MeCN).²¹ Experimental uncertainty is estimated to be 15%. Low temperature emission spectra were recorded using an Oxford Instruments Optistat DN cryostat with cooling by liquid N₂. ESI⁺ and high resolution ESI⁺ mass spectra were recorded on a Micromass QTof Ultima API mass spectrometer with analyte solutions in acetonitrile. Elemental analyses were performed in the microanalytical laboratory of the Chemical Institutes of the University of Mainz. NMR spectra were obtained with a Bruker Avance II 400 spectrometer at 400.31 (¹H) and 100.66 (¹³C) at 25 °C. Chemical shifts δ [ppm] are reported with respect to residual solvent signals as internal standards (¹H, ¹³C): CD₃CN δ(¹H) = 1.94 ppm, δ(¹³C) = 1.32 and 118.26 ppm.⁹⁶ Electrochemical experiments were performed with a BioLogic SP-50 voltammetric analyzer at a sample concentration of 10⁻³ mol l⁻¹ using platinum wire as working and counter electrodes and a 0.01 mol l⁻¹ Ag/AgNO₃ reference electrode. Measurements were carried out at a scan rate of 100 mV s⁻¹ for cyclic voltammetry experiments and at 10 mV s⁻¹ for square-wave voltammetry experiments using 0.1 mol l⁻¹ [nBu₄N][PF₆] as the supporting electrolyte in acetonitrile. Potentials are given relative to the ferrocene/ferrocenium couple (0.40 V vs. SCE, E_1/2 = 0.09 ± 5 mV under the given conditions).⁷²

Density functional theory calculations

DFT calculations were carried out using the ORCA program package (version 3.0.2).⁹⁷ Tight convergence criteria were chosen for all calculations (keywords TightSCF and TightOpt, convergence criteria for the SCF part: energy change 1.0 × 10⁻⁸ E_h, 1-El. energy change 1.0 × 10⁻⁵ E_h, orbital gradient 1.0 × 10⁻⁵, orbital rotation angle 1.0 × 10⁻⁵, DIIS error 5.0 × 10⁻⁷; for geometry optimizations: energy change: 1.0 × 10⁻⁶ E_h, max. gradient 1.0 × 10⁻⁴ E_h per bohr, RMS gradient 3.0 × 10⁻⁵ E_h per bohr, max. displacement 1.0 × 10⁻³ bohr, RMS displacement 6.0 × 10⁻⁴ bohr). All calculations employ the resolution of identity (Split-RI-J) approach for the coulomb term in combination with the chain-of-spheres approximation for the exchange term (COSX).^98,99 All calculations were performed using the hybrid functional B3LYP⁶³ in combination with Ahlrichs’ split-valence double-ξ basis set def2-SV(P) which comprises polarization functions for all non-hydrogen atoms.^64,65 Relativistic effects were calculated at the zeroth order regular approximation (ZORA) niveau.⁶⁷ The ZORA keyword automatically invokes relativistically adjusted basis sets.¹⁰⁰ To account for solvent effects, a conductor-like screening model (COSMO) modelling acetonitrile was used in all calculations.⁶⁸ TD-DFT calculations with at least 50 vertical transitions were carried out based on the def2-SV(P) optimized geometry of the respective complex. Explicit counterions and/or solvent molecules were not taken into account in all cases. To reduce the computational cost, methyl instead of ethyl groups at the ester moiety were used throughout all calculations.

Synthesis of [Ru(dpb-NHCOCH₃)(tpy)](PF₆) 1(PF₆). RuCl₃(tpy) (250 mg, 0.567 mmol, 1 eq.) and AgBF₄ (320 mg, 1.64 mmol, 2.9 eq.) were dissolved in dry acetone (20 ml) and heated to reflux for 2 h in the dark. The mixture was left to stand for 1 h and filtered through a syringe filter before removing the solvent under reduced pressure. The dark residue was dissolved in nBuOH (20 ml) and N-acetyl-3,5-dipyrid-2′-ylaniline L1 (197 mg, 0.680 mmol, 1.2 eq.) was added. The resulting mixture was heated to reflux for 16 h to give a dark purple solution. After the removal of the solvent under reduced pressure, the residue was dissolved in a minimal amount of acetonitrile (5 ml). Upon addition of a solution of NH₄PF₆ (220 mg, 1.35 mmol, 2.4 eq.) in water (1 ml) followed by slow addition of more water (80 ml), a black solid precipitated which was filtered off. Column chromatography on silica gel (CHCl₃ : MeOH = 7 : 1) afforded [Ru(dpb-NHCOCH₃)(tpy)](PF₆) 1(PF₆) as a dark purple solid. Yield: 175 mg (0.228 mmol, 40%). Anal. Calc. for C₃₃H₂₅F₆N₆OPRu (767.6)·H₂O: C, 50.45; H, 3.46; N, 10.70. Found: C, 50.62; H, 3.31; N, 10.46. MS(ESI⁺): m/z (%) = 623.1 (100) [M − PF₆]⁺. HR-MS(ESI⁺, m/z): Calcd for C₃₃H₂₅N₆ORu [M − PF₆]⁺: 617.1166; Found: 617.1177. ¹H NMR (CD₃CN): δ [ppm] = 8.73 (d, ³J_HH = 8 Hz, 2H, H^2A), 8.62 (s, 1H, NH), 8.44–8.35 (m, 4H, H^2B, H^5A), 8.24 (t, ³J_HH = 8 Hz, 1H, H^1A), 8.05 (d, ³J_HH = 8 Hz, 2H, H^5B), 7.67 (dt, ³J_HH = 8 Hz, ⁴J_HH = 1 Hz, 2H, H^6A), 7.59 (dt, ³J_HH = 8 Hz, ⁴J_HH = 1 Hz, 2H, H^6B), 7.11 (d, ³J_HH = 5 Hz, 2H, H^8A), 7.01 (d, ³J_HH = 5 Hz, 2H, H^8B), 6.94 (m, 2H, H^7A), 6.64 (m, 2H, H^7B), 2.23 (s, 3H, H¹¹). ¹³C{¹H} NMR (CD₃CN): δ [ppm] = 217.2 (C^9B), 169.6 (C¹⁰), 169.4 (C^4B), 160.1 (C^4A), 155.3 (C^8A), 154.0 (C^3A), 152.9 (C^8B), 142.5 (C^3B), 136.4 (C^6B), 135.9 (C^6A), 133.6 (C^1B), 132.7 (C^1A), 127.2 (C^7A), 124.4 (C^5A), 123.2 (C^2A), 122.5 (C^7B), 120.6 (C^5B), 117.8 (C^2A), 24.3 (C¹¹). IR (KBr disk): [small nu, Greek, tilde] [cm⁻¹] = 3230 (m, N–H amide), 1650 (s, C=O amide), 1600 (m, C=C), 1520 (w, amide II), 843 (s, P–F).

Synthesis of [Ru(dpb-NH₂)(tpy)](PF₆) 2(PF₆). [Ru(dpb-NHCOCH₃)(tpy)](PF₆) 1(PF₆) (113 mg, 0.147 mmol) was added to a mixture of water (20 ml), methanol (20 ml), hydrazine monohydrate (1 ml) and sodium hydroxide (1 g) and heated to reflux for 16 h. After removal of the solvent under reduced pressure, the dark residue was dissolved in a minimal amount of acetonitrile (5 ml) followed by addition of a solution of NH₄PF₆ (153 mg, 0.939 mmol, 6.75 eq.) in water (80 ml). The precipitate was filtered off and washed with water (2 × 5 ml) and diethyl ether (2 × 15 ml) giving [Ru(dpb-NH₂)(tpy)](PF₆) 2(PF₆) as a purple solid. Yield: 92 mg (0.127 mmol, 86%). Anal. Calc. for C₃₁H₂₃F₆N₆PRu (725.6)·0.5H₂O: C, 50.69; H, 3.29; N, 11.58. Found: C, 50.82; H, 3.05; N, 11.34. MS(ESI⁺): m/z (%) = 581.1 (100) [M − PF₆]⁺. HR-MS(ESI⁺, m/z): Calcd for C₃₁H₂₃N₆Ru [M − PF₆]⁺: 575.1060; Found: 575.1071. ¹H NMR (CD₃CN): δ [ppm] = 8.72 (d, ³J_HH = 8 Hz, 2H, H^2A), 8.40 (d, ³J_HH = 8 Hz, 2H, H^5A), 8.20 (t, ³J_HH = 8 Hz, 1H, H^1A), 8.00 (d, ³J_HH = 8 Hz, 2H, H^5B), 7.74 (s, 2H, H^2B), 7.67 (t, ³J_HH = 8 Hz, 2H, H^6A), 7.56 (t, ³J_HH = 8 Hz, 2H, H^6B), 7.18 (d, ³J_HH = 5 Hz, 2H, H^8A), 6.97 (dd, ³J_HH = 5 Hz, 8 Hz, 2H, H^7A), 6.93 (d, ³J_HH = 5 Hz, 2H, H^8B), 6.58 (dd, ³J_HH = 5 Hz, 8 Hz, 2H, H^7B), 4.24 (s, 2H, NH₂). ¹³C{¹H} NMR (CD₃CN): δ [ppm] = 208.9 (C^9B), 169.9 (C^94B), 160.3 (C^4A), 155.2 (C^8A), 154.3 (C^3A), 152.8 (C^8B), 143.6 (C^1B), 142.6 (C^3B), 136.2 (C^6B), 135.5 (C^6A), 132.0 (C^1A), 127.2 (C^7A), 124.2 (C^5A), 123.2 (C^2A), 122.0 (C^7B), 120.4 (C^5B), 113.0 (C^2B). IR (KBr disk): [small nu, Greek, tilde] [cm⁻¹] = 3420 (m, N–H amine), 1600 (m, C=C), 843 (s, P–F).

Synthesis of [Ru(dpb-COOC₂H₅)(tpy)](PF₆) 3(PF₆). [RuCl₃(tpy)] (250 mg, 0.567 mmol, 1 eq.) and AgBF₄ (320 mg, 1.64 mmol, 2.9 eq.) were dissolved in dry acetone (20 ml) and heated to reflux for 2 h in the dark. The mixture was left to stand for 1 h and filtered through a syringe filter before removing the solvent under reduced pressure. The dark residue was dissolved in nBuOH (20 ml) and ethyl 3,5-dipyrid-2′-ylbenzoate L2 (207 mg, 0.680 mmol, 1.2 eq.) was added. The resulting mixture was heated to reflux for 16 h to give a dark purple solution. After removal of the solvent under reduced pressure, the residue was dissolved in a minimal amount of acetonitrile (5 ml). Upon addition of a solution of NH₄PF₆ (220 mg, 1.35 mmol, 2.4 eq.) in water (1 ml) followed by slow addition of more water (80 ml), a dark red solid precipitated that was filtered off and washed with water (2 × 5 ml) and diethyl ether (2 × 15 ml). Column chromatography on silica gel (CHCl₃ : MeOH = 7 : 1) afforded [Ru(dpb-COOC₂H₅)(tpy)](PF₆) 3(PF₆) as a dark red solid. Yield: 229 mg (0.293 mmol, 52%). Anal. Calc. for C₃₄H₂₆F₆N₅O₂PRu (782.6): C, 52.18; H, 3.35; N, 8.95. Found: C, 52.01; H, 3.34; N, 8.65. MS(ESI⁺): m/z (%) = 638.1 (100) [M − PF₆]⁺. HR-MS(ESI⁺, m/z): Calcd for C₃₄H₂₆N₅O₂Ru [M − PF₆]⁺: 632.1162; Found: 632.1173. ¹H NMR (CD₃CN): δ [ppm] = 8.85 (s, 2H, H^1B), 8.74 (d, 2H, ³J_HH = 8 Hz, H^2A), 8.42 (d, 2H, ³J_HH = 8 Hz, H^5A), 8.30 (t, 1H, ³J_HH = 8 Hz, H^1A), 8.27 (d, 2H, ³J_HH = 8 Hz, H^5B), 7.74–7.56 (m, 4H, H^6A, H^6B), 7.13–7.04 (m, 4H, H^8A, H^8B), 6.91 (t, 2H, ³J_HH = 7 Hz, H^7A), 6.72 (t, 2H, ³J_HH = 7 Hz, H^7B), 4.52 (q, 2H, ³J_HH = 7 Hz, H¹¹), 1.52 (t, 3H, ³J_HH = 7 Hz, H¹²). ¹³C{¹H} NMR (CD₃CN): δ [ppm] = 232.8 (C^9B), 168.9 (C^4B), 168.6 (C^10B), 159.8 (C^4A), 155.4 (C^8A), 153.5 (C^3A), 152.8 (C^8B), 143.1 (C^3A), 136.7 (C^6B), 136.4 (C^6A), 133.8 (C^1A), 127.3 (C^7A), 124.6 (C^2B), 124.5 (C^6A), 123.3 (C^2A), 123.0 (C^7B), 120.9 (C^1B), 61.5 (C¹¹), 14.9 (C¹²). IR (KBr disk): [small nu, Greek, tilde] [cm⁻¹] = 1695 (s, C=O ester), 1600, 1582 (m, C=C), 843 (s, P–F).

Synthesis of [Ru(dpb-COOH)(tpy)](PF₆) 4(PF₆). [Ru(dpb-COOC₂H₅)(tpy)](PF₆) 3(PF₆) (154 mg, 0.197 mmol) was added to a mixture of water (20 ml), methanol (20 ml), hydrazine monohydrate (1 ml) and sodium hydroxide (1 g) and heated to reflux for 16 h. After removal of the solvent under reduced pressure, the dark residue was dissolved in a minimal amount of acetonitrile (5 ml) followed by slow addition of 1 mol per l aqueous H₂SO₄ to adjust the pH to 1. Upon addition of a solution of NH₄PF₆ (145 mg, 0.890 mmol, 4.5 eq.) in water (40 ml) the product precipitated. The complex was filtered off and washed with water (2 × 5 ml) and diethyl ether (2 × 15 ml). Column chromatography on silica gel (CHCl₃ : MeOH = 5 : 1) afforded [Ru(dpb-COOH)(tpy)](PF₆) 4(PF₆) as a dark red solid. Yield: 82 mg (0.109 mmol, 55%). Anal. Calc. for C₃₂H₂₂F₆N₅O₂PRu (754.6): C, 50.93; H, 2.94; N, 9.28. Found: C, 50.64; H, 2.51; N, 9.42. MS(ESI⁺): m/z (%) = 610.1 (100) [M − PF₆]⁺. HR-MS(ESI⁺, m/z): Calcd for C₃₂H₂₂N₅O₂Ru [M − PF₆]⁺: 604.0849; Found: 604.0873. ¹H NMR (CD₃CN): δ [ppm] = 8.85 (s, 2H, H^2B), 8.74 (d, ³J_HH = 8 Hz, 2H, H^2A), 8.42 (d, ³J_HH = 8 Hz, 2H, H^5A), 8.33–8.24 (m, 3H, H^1A, H^5B), 7.74–7.67 (m, 2H, H^6A), 7.67–7.60 (m, 2H, H^6B), 7.13–7.05 (m, 4H, H^8A, H^8B), 6.91 (ddd, ³J_HH = 7 Hz, 6 Hz, ⁴J_HH = 1 Hz, 2H, H^7A), 6.72 (ddd, ³J_HH = 7 Hz, 6 Hz, ⁴J_HH = 1 Hz, 2H, H^7B). ¹³C{¹H} NMR (CD₃CN): δ [ppm] = 233.3 (C^9B), 169.4 (C¹⁰), 168.9 (C^4B), 159.8 (C^4A), 155.5 (C^8A), 153.5 (C^3A), 152.8 (C^8B), 143.2 (C^3B), 136.7 (C^6B), 136.4 (C^6A), 133.9 (C^1A), 127.4 (C^7A), 125.0 (C^2B), 124.6 (C^5A), 123.4 (C^2A), 123.1 (C^7B), 122.4 (C^1B), 121.0 (C^5B). IR (KBr disk): [small nu, Greek, tilde] [cm⁻¹] = 3440 (s, O–H acid), 1665 (s, C=O acid), 1602, 1579 (m, C=C), 843 (s, P–F).

Synthesis of [Ru(dpb-COOBt)(tpy)](PF₆) 5(PF₆). [Ru(dpb-COOC₂H₅)(tpy)](PF₆) 4(PF₆) (42 mg, 0.056 mmol, 1 eq.), N,N′-diisopropylcarbodiimide (15 mg, 0.119 mmol, 2.1 eq.) and N-hydroxybenzotriazole (HOBt, 18 mg, 0.117 mmol, 2.1 eq.) were dissolved in dry acetonitrile (20 ml) and stirred for 16 h at room temperature. After removal of the solvent under reduced pressure, the dark residue was dissolved in acetonitrile (5 ml). The product was precipitated by addition of NH₄PF₆ (95 mg, 0.583 mmol, 10.4 eq.) and water (50 ml), filtered off and washed with water (2 × 5 ml) and diethyl ether (2 × 15 ml). [Ru(dpb-COOBt)(tpy)](PF₆) 5(PF₆) was obtained as a dark red solid. Yield: 45 mg (0.052 mmol, 92%). Anal. Calc. for C₃₈H₂₅F₆N₈O₂PRu (871.69): C, 52.36; H, 2.89; N, 12.85. Found: C, 52.42; H, 2.53; N, 12.54. MS(ESI⁺): m/z (%) = 699.1 (11) [M − PF₆ − N₂]⁺, 727.1 (100) [M − PF₆]⁺, 1599.2 (8) [2M − PF₆]⁺. HR-MS(ESI⁺, m/z): Calcd for C₃₈H₂₅N₈O₂Ru [M − PF₆]⁺: 721.1176; Found: 721.1192. ¹H NMR (CD₃CN): δ [ppm] = 9.05 (s, 2H, H^2B), 8.77 (d, 2H, ³J_HH = 8 Hz, H^2A), 8.44 (d, 2H, ³J_HH = 8 Hz, H^5A), 8.35 (t, 1H, ³J_HH = 8 Hz, H^1A), 8.34 (d, 2H, ³J_HH = 8 Hz, H^5B), 8.16 (d, 1H, ³J_HH = 9 Hz, H^2C), 7.83 (d, 1H, ³J_HH = 8 Hz, H^5C), 7.77–7.66 (m, 5H, H^6A, H^6B, H^4C), 7.58 (t, 1H, H^3C), 7.20 (d, 2H, ³J_HH = 5 Hz, H^8B), 7.13 (d, 2H, ³J_HH = 5 Hz, H^8A), 6.96 (t, 2H, ³J_HH = 6 Hz, H^7A), 6.80 (t, 2H, ³J_HH = 6 Hz, H^7B). ¹³C{¹H} NMR (CD₃CN): δ [ppm] = 239.5 (C^9B), 168.2 (C^4B), 165.7 (C¹⁰), 159.7 (C^4A), 155.5 (C^8A), 153.3 (C^3A), 152.9 (C^8B), 144.5 (C^1C), 144.2 (C^3B), 137.0 (C^6B), 136.9 (C^6A), 134.8 (C^1A), 130.1 (C^4C), 127.5 (C^7A), 126.2 (C^3C), 124.9 (C^2B), 124.8 (C^5A), 123.6 (C^7B), 123.5 (C^2A), 121.3 (C^2C), 121.1 (C^6C), 115.4 (C^1B), 110.0 (C^5C).

Synthesis of [(tpy)Ru(dpb-NHCO-dpb)Ru(tpy)](PF₆)₂6(PF₆)₂. In separate Schlenk flasks, [Ru(dpb-NH₂)(tpy)](PF₆) 2(PF₆) (35 mg, 0.048 mmol, 1 eq.) and [Ru(dpb-COOBt)(tpy)](PF₆) 5(PF₆) (42 mg, 0.048 mmol, 1 eq.) were dissolved in dry acetonitrile (10 ml). Molecular sieves (3 Å) were added and the mixtures were left to stand overnight to remove crystal water. Both solutions were then combined in a third Schlenk flask and tert-butylimino-tris(dimethylamino)phosphorane (P₁-tBu) (34 mg, 0.144 mmol, 3 eq.) was added. The resulting solution was stirred at 50 °C for 16 h. After quenching the reaction by addition of NH₄PF₆ (180 mg, 1.10 mmol, 23 eq.) dissolved in water (2 ml), the solution was concentrated to 5 ml and the product was triturated by addition of water (80 ml). The precipitate was filtered off, washed with water (2 × 5 ml) and diethyl ether (2 × 15 ml) and purified by column chromatography on silica gel (CHCl₃ : MeOH = 7 : 1) affording [(tpy)Ru(dpb-NHCO-dpb)Ru(tpy)](PF₆)₂6(PF₆)₂ as a dark red solid. Yield: 14 mg (0.0096 mmol, 20%). Anal. Calc. for C₆₃H₄₃F₁₂N₁₁OP₂Ru₂ (1462.16)·4H₂O: C, 49.32; H, 3.35; N, 10.04. Found: C, 49.39; H, 3.76; N, 10.36. MS(ESI⁺): m/z (%) = 296.6 (3) [M − 2PF₆]⁴⁺, 390.8 (17) [M − 2PF₆]³⁺, 586.6 (100) [M − 2PF₆]²⁺, 1318.3 (5) [M − PF₆]⁺. HR-MS(ESI⁺, m/z): Calcd for C₆₃H₄₃N₁₁ORu₂ [M − 2PF₆]²⁺: 586.5885; Found: 586.5884. ¹H NMR (CD₃CN): δ [ppm] = 9.63 (s, 1H, NH), 9.09 (s, 2H, H^2A), 8.83 (s, 2H, H^2B), 8.80–8.74 (m, 4H, H^2,tpy), 8.44 (m, 4H, H^5,tpy), 8.39 (d, ³J_HH = 8 Hz, 2H, H^5A), 8.32 (t, ³J_HH = 8 Hz, 1H, H^1,tpy), 8.28 (t, ³J_HH = 8 Hz, 1H, H^1,tpy), 8.18 (d, ³J_HH = 8 Hz, 2H, H^5B), 7.76–7.65 (m, 6H, H^6,tpy, H^6A), 7.65–7.59 (m, 2H, H^6B), 7.19–7.10 (m, 6H, H^8,tpy, H^8A), 7.07 (d, ³J_HH = 6 Hz, 2H, H^8B), 6.96–6.88 (m, br, 4H, H^7,tpy), 6.75 (m, 2H, H^7A), 6.68 (m, 2H, H^7B). ¹³C{¹H} NMR (CD₃CN): δ [ppm] = 230.3 (C^9A), 217.9 (C^9B), 169.6 (C^5B), 169.3 (C^5A), 168.0 (C¹⁰), 160.2, 160.0 (C^4,tpy), 155.3, 155.2 (C^8,tpy), 154.0, 153.6 (C^3,tpy), 153.0 (C^8A, C^8B), 143.2 (C^3A), 142.7 (C^3B), 136.8, 136.5, 136.4, 136.0 (C^6,tpy, C^6A, C^6B), 133.9 (C^1B), 133.8, 132.9 (C^1,tpy), 127.9 (C^1A), 127.3 (C^7,tpy), 124.6, 124.4 (C^5,tpy), 123.4, 123.3 (C^2,tpy), 123.3 (C^2A), 123.0 (C^7A), 122.6 (C^7B), 120.9 (C^8A), 120.7 (C^8B), 118.9 (C^2B). IR (KBr disk): [small nu, Greek, tilde] [cm⁻¹] = 3220 (m, N–H amide), 1635 (s, C=O amide), 1599, 1582 (m, C=C), 1517 (w, amide II), 843 (s, P–F).

Conclusions

The electrochemical, UV-Vis and excited state properties of a series of [Ru(dpb-R)(tpy)]⁺ type of complexes was systematically studied. The visible range absorption bands of these complexes are dominated by two electronically decoupled ¹MLCT transitions either involving the dpb ligand (d_yz(Ru) → dpb) or the tpy ligand (d_xz(Ru) → tpy). These excitations are followed by intersystem crossing populating an emissive [Ru⁺(tpy⁻)] ³MLCT state in all cases. This state, however, is rapidly depopulated at room temperature via two additional low-energy triplet excited states yielding very low luminescence quantum yields and short excited state lifetimes. VT steady-state emission spectroscopy and extended DFT calculations revealed their nature as ³LL′CT and ³MC states yielding a biexponential dependence of the quantum yield on the temperature. While the ³MC state has been known as a parasitic channel for non-radiative decay in (polypyridine)ruthenium(II) complexes for over 30 years,²² the observation of a ³LL′CT state in such ruthenium complexes is unprecedented to the best of our knowledge. We previously referred to the ³LL′CT state as a spectroscopically undetectable state (“dark” state).⁴⁰ However, the characteristic temperature dependence of the quantum yield clearly is spectroscopic evidence for its presence. Also for the bis(tridentate)iridium(III) complex [Ir(dpx)(tpy)]²⁺ (dpxH = 1,5-di(2-pyridyl)-2,4-xylene), a ³LL′CT state is suggested to be responsible for its low luminescence quantum yield.¹⁰¹ Based upon the findings of this study, we believe that the excited state deactivation in this cyclometalated iridium complex occurs in an analogous manner via thermal depopulation of the emissive state via³LL′CT states.

Remarkably, for the acceptor-substituted complexes 3⁺ and 4⁺, the ³LL′CT state resides higher in energy than the ³MLCT state, while for the donor-substituted complexes 1⁺ and 2⁺, it is found to be the lowest triplet state. As a consequence, faster deactivation of the emissive ³MLCT states is observed in the latter complexes associated with substantially lowered emission quantum yields compared to complexes 3⁺ and 4⁺. But, since emission is observed for 1⁺ and 2⁺ with increasing quantum yields at lower temperatures, deactivation via the ³LL′CT state is a thermally activated process and the ³MLCT and ³LL′CT states are not in thermal equilibrium.

Upon oxidation of the dinuclear complex 6²⁺ to its mixed-valent counterpart 6³⁺, an intense NIR band is detected indicating a photochemical Ru^II → Ru^III charge transfer across the asymmetric biscyclometalating bridging ligand. Despite the substantial redox asymmetry of the two complex subunits bearing NH- and CO-substituents, a strong electronic communication between the donor and acceptor sites of 6³⁺ is observed. In the excited state of 6²⁺ however, the two complex fragments appear electronically uncoupled with dual emission occurring from ³MLCT states localized at the two remote [Ru(tpy)] moieties. This “anti-Kasha” behaviour is explained based on the long metal–metal distance and the very rapid excited state decay (emissive and non-emissive) that prevents thermal equilibration in solution via energy transfer entirely. Just upon freezing of the solution, the excited states become sufficiently long-lived to allow for thermalization, so that Kasha's rule is obeyed.

In summary, we were able to show spectroscopically and computationally that the introduction of N^C^N cyclometalating ligands in bis(tridentate)ruthenium(II) complexes gives rise to low-lying ³LL′CT states that allow for efficient thermal depopulation of the emissive ³MLCT state. Furthermore, we believe that the existence of ³LL′CT states in polypyridine transition metal complexes is more general. As their energy is strongly dependent on the substitution pattern, they become particularly relevant in strong push–pull systems and can interfere with luminescence processes and shorten the excited state lifetimes substantially.

Additionally, in mixed-valent dinuclear ruthenium complexes such as 6³⁺, the biscyclometalating bridge was shown to be an excellent mediator for photochemical electron transfer between the redox sites even in the presence of a substantial redox asymmetry. The triplet excited states of 6²⁺, however, are electronically uncoupled due to the large spatial separation of the emissive [Ru(tpy)] moieties and their short excited state lifetimes induced by the cyclometalating bridge.

Acknowledgements

Parts of this research were conducted using the supercomputer MOGON and advisory services offered by Johannes Gutenberg Univ. Mainz (http://www.hpc.uni-mainz.de), which is a member of the AHRP and the Gauss Alliance e.V. This work was financially supported by the Deutsche Forschungsgemeinschaft (GSC 266, Materials Science in Mainz, scholarship for C. K.).

Notes and references

1. J. P. Paris and W. W. Brandt, J. Am. Chem. Soc., 1959, 81, 5001–5002.
2. F. E. Lytle and D. M. Hercules, J. Am. Chem. Soc., 1969, 91, 253–257.
3. K. Kalyanasundaram, Coord. Chem. Rev., 1982, 46, 159–244.
4. A. Juris, V. Balzani, F. Barigelletti, S. Campagna, P. Belser and A. von Zelewsky, Coord. Chem. Rev., 1988, 84, 85–277.
5. M. Maestri, N. Armaroli, V. Balzani, E. C. Constable and A. M. W. C. Thompson, Inorg. Chem., 1995, 34, 2759–2767.
6. V. Balzani and A. Juris, Coord. Chem. Rev., 2001, 211, 97–115.
7. S. Campagna, F. Puntoriero, F. Nastasi, G. Bergamini and V. Balzani, Top. Curr. Chem., 2007, 280, 117–214.
8. D. M. Hedstrand, W. H. Kruizinga and R. M. Kellogg, Tetrahedron Lett., 1978, 19, 1255–1258.
9. H. D. Abruna, A. Y. Teng, G. J. Samuels and T. J. Meyer, J. Am. Chem. Soc., 1979, 101, 6745–6746.
10. I. Okura and N. Kim-Thuan, J. Mol. Catal., 1979, 5, 311–314.
11. J.-M. Lehn and R. Ziessel, Proc. Natl. Acad. Sci. U. S. A., 1982, 79, 701–704.
12. J. W. Tucker and C. R. J. Stephenson, J. Org. Chem., 2012, 77, 1617–1622.
13. B. O'Regan and M. Grätzel, Nature, 1991, 353, 737–740.
14. M. G. Sasso, F. H. Quina and E. J. Bechara, Anal. Biochem., 1986, 156, 239–243.
15. K. K.-W. Lo, T. K.-M. Lee, J. S.-Y. Lau, W.-L. Poon and S.-H. Cheng, Inorg. Chem., 2008, 47, 200–208.
16. P. D. Beer, Z. Chen, A. J. Goulden, A. Grieve, D. Hesek, F. Szemes and T. Wear, J. Chem. Soc., Chem. Commun., 1994, 1269–1271.
17. H. J. Bolink, L. Cappelli, E. Coronado and P. Gaviña, Inorg. Chem., 2005, 44, 5966–5968.
18. J. N. Demas and D. G. Taylor, Inorg. Chem., 1979, 18, 3177–3179.
19. S. Yoon, P. Kukura, C. M. Stuart and R. A. Mathies, Mol. Phys., 2006, 104, 1275–1282.
20. J. V. Caspar and T. J. Meyer, J. Am. Chem. Soc., 1983, 105, 5583–5590.
21. K. Suzuki, A. Kobayashi, S. Kaneko, K. Takehira, T. Yoshihara, H. Ishida, Y. Shiina, S. Oishi and S. Tobita, Phys. Chem. Chem. Phys., 2009, 11, 9850–9860.
22. B. Durham, J. V. Caspar, J. K. Nagle and T. J. Meyer, J. Am. Chem. Soc., 1982, 104, 4803–4810.
23. J. van Houten and R. J. Watts, Inorg. Chem., 1978, 17, 3381–3385.
24. J. P. Sauvage, J. P. Collin, J. C. Chambron, S. Guillerez, C. Coudret, V. Balzani, F. Barigelletti, L. de Cola and L. Flamigni, Chem. Rev., 1994, 94, 993–1019.
25. K. Lashgari, M. Kritikos, R. Norrestam and T. Norrby, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1999, 55, 64–67.
26. J. R. Winkler, T. L. Netzel, C. Creutz and N. Sutin, J. Am. Chem. Soc., 1987, 109, 2381–2392.
27. M. L. Stone and G. A. Crosby, Chem. Phys. Lett., 1981, 79, 169–173.
28. K. Heinze, K. Hempel and M. Beckmann, Eur. J. Inorg. Chem., 2006, 2006, 2040–2050.
29. K. Heinze, K. Hempel and A. Breivogel, Z. Anorg. Allg. Chem., 2009, 635, 2541–2549.
30. S. H. Wadman, M. Lutz, D. M. Tooke, A. L. Spek, F. Hartl, R. W. A. Havenith, G. P. M. van Klink and G. van Koten, Inorg. Chem., 2009, 48, 1887–1900.
31. A. Breivogel, C. Kreitner and K. Heinze, Eur. J. Inorg. Chem., 2014, 2014, 5468–5490.
32. M. Abrahamsson, M. Jäger, T. Österman, L. Eriksson, P. Persson, H.-C. Becker, O. Johansson and L. Hammarström, J. Am. Chem. Soc., 2006, 128, 12616–12617.
33. F. Schramm, V. Meded, H. Fliegl, K. Fink, O. Fuhr, Z. Qu, W. Klopper, S. Finn, T. E. Keyes and M. Ruben, Inorg. Chem., 2009, 48, 5677–5684.
34. A. Breivogel, C. Förster and K. Heinze, Inorg. Chem., 2010, 49, 7052–7056.
35. A. Breivogel, M. Meister, C. Förster, F. Laquai and K. Heinze, Chem. – Eur. J., 2013, 19, 13745–13760.
36. D. G. Brown, N. Sanguantrakun, B. Schulze, U. S. Schubert and C. P. Berlinguette, J. Am. Chem. Soc., 2012, 134, 12354–12357.
37. M. Beley, J. P. Collin and J. P. Sauvage, Inorg. Chem., 1993, 32, 4539–4543.
38. S. H. Wadman, J. M. Kroon, K. Bakker, M. Lutz, A. L. Spek, G. P. M. van Klink and G. van Koten, Chem. Commun., 2007, 1907–1909.
39. P. G. Bomben, K. C. D. Robson, P. A. Sedach and C. P. Berlinguette, Inorg. Chem., 2009, 48, 9631–9643.
40. C. Kreitner, E. Erdmann, W. W. Seidel and K. Heinze, Inorg. Chem., 2015, 54, 11088–11104.
41. C. Creutz and H. Taube, J. Am. Chem. Soc., 1969, 91, 3988–3989.
42. W. Kaim, A. Klein and M. Glöckle, Acc. Chem. Res., 2000, 33, 755–763.
43. W. Kaim and G. K. Lahiri, Angew. Chem., 2007, 119, 1808–1828 ( Angew. Chem., Int. Ed. , 2007 , 46 , 1778–1796 ).
44. U. Fuerholz, H. B. Buergi, F. E. Wagner, A. Stebler, J. H. Ammeter, E. Krausz, R. J. H. Clark, M. J. Stead and A. Ludi, J. Am. Chem. Soc., 1984, 106, 121–123.
45. L. T. Zhang, J. Ko and M. J. Ondrechen, J. Am. Chem. Soc., 1987, 109, 1666–1671.
46. S. P. Best, R. J. H. Clark, R. C. S. McQueen and S. Joss, J. Am. Chem. Soc., 1989, 111, 548–550.
47. B. S. Brunschwig, C. Creutz and N. Sutin, Chem. Soc. Rev., 2002, 31, 168–184.
48. M. B. Robin and P. Day, Adv. Inorg. Chem., 1968, 10, 247–422.
49. N. S. Hush, Prog. Inorg. Chem., 1967, 8, 391–444.
50. N. S. Hush, Electrochim. Acta, 1968, 13, 1005–1023.
51. N. S. Hush, Coord. Chem. Rev., 1985, 64, 135–157.
52. B. S. Brunschwig and N. Sutin, Coord. Chem. Rev., 1999, 187, 233–254.
53. G. D. Storrier and S. B. Colbran, Inorg. Chim. Acta, 1999, 284, 76–84.
54. A. Breivogel, K. Hempel and K. Heinze, Inorg. Chim. Acta, 2011, 374, 152–162.
55. C. Kreitner, M. Grabolle, U. Resch-Genger and K. Heinze, Inorg. Chem., 2014, 53, 12947–12961.
56. E. C. Constable and M. D. Ward, J. Chem. Soc., Dalton Trans., 1990, 1405–1409.
57. J.-P. Collin, P. Lainé, J.-P. Launay, J.-P. Sauvage and A. Sour, J. Chem. Soc., Chem. Commun., 1993, 434–435.
58. M. Beley, J. P. Collin, R. Louis, B. Metz and J. P. Sauvage, J. Am. Chem. Soc., 1991, 113, 8521–8522.
59. C. Patoux, J.-P. Launay, M. Beley, S. Chodorowski-Kimmes, J.-P. Collin, S. James and J.-P. Sauvage, J. Am. Chem. Soc., 1998, 120, 3717–3725.
60. J.-Y. Shao and Y.-W. Zhong, Chem. – Eur. J., 2014, 20, 8702–8713.
61. K. C. D. Robson, B. D. Koivisto, A. Yella, B. Sporinova, M. K. Nazeeruddin, T. Baumgartner, M. Grätzel and C. P. Berlinguette, Inorg. Chem., 2011, 50, 5494–5508.
62. W. König and R. Geiger, Chem. Ber., 1970, 103, 788–798.
63. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
64. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
65. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
66. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
67. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
68. S. Sinnecker, A. Rajendran, A. Klamt, M. Diedenhofen and F. Neese, J. Phys. Chem. A, 2006, 110, 2235–2245.
69. M. C. Hughes and D. J. Macero, Inorg. Chem., 1976, 15, 2040–2044.
70. S. Romain, C. Baffert, C. Duboc, J.-C. Leprêtre, A. Deronzier and M.-N. Collomb, Inorg. Chem., 2009, 48, 3125–3131.
71. R. F. Winter, Organometallics, 2014, 33, 4517–4536.
72. N. G. Connelly and W. E. Geiger, Chem. Rev., 1996, 96, 877–910.
73. C. Creutz, M. D. Newton and N. Sutin, J. Photochem. Photobiol., A, 1994, 82, 47–59.
74. J.-P. Launay, Chem. Soc. Rev., 2001, 30, 386–397.
75. L. Wang, W.-W. Yang, R.-H. Zheng, Q. Shi, Y.-W. Zhong and J. Yao, Inorg. Chem., 2011, 50, 7074–7079.
76. W.-W. Yang, L. Wang, Y.-W. Zhong and J. Yao, Organometallics, 2011, 30, 2236–2240.
77. D. E. Richardson and H. Taube, J. Am. Chem. Soc., 1983, 105, 40–51.
78. M. Natali, S. Campagna and F. Scandola, Chem. Soc. Rev., 2014, 43, 4005–4018.
79. F. Barigelletti, A. Juris, V. Balzani, P. Belser and A. von Zelewsky, Inorg. Chem., 1983, 22, 3335–3339.
80. A. Juris, F. Barigelletti, V. Balzani, P. Belser and A. von Zelewsky, Inorg. Chem., 1985, 24, 202–206.
81. G. A. Crosby, Acc. Chem. Res., 1975, 8, 231–238.
82. F. Barigelletti, A. Juris, V. Balzani, P. Belser and A. von Zelewsky, J. Phys. Chem., 1986, 90, 5190–5193.
83. R. Englman and J. Jortner, Mol. Phys., 1970, 18, 145–164.
84. J. V. Caspar, E. M. Kober, B. P. Sullivan and T. J. Meyer, J. Am. Chem. Soc., 1982, 104, 630–632.
85. J. V. Caspar and T. J. Meyer, J. Phys. Chem., 1983, 87, 952–957.
86. K. A. King and R. J. Watts, J. Am. Chem. Soc., 1987, 109, 1589–1590.
87. T. E. Keyes, Chem. Commun., 1998, 889–890.
88. E. C. Glazer, D. Magde and Y. Tor, J. Am. Chem. Soc., 2007, 129, 8544–8551.
89. Y. Chen, X. Zhou, X.-H. Wei, B.-L. Yu, H. Chao and L.-N. Ji, Inorg. Chem. Commun., 2010, 13, 1018–1020.
90. D. L. Dexter, J. Chem. Phys., 1953, 21, 836–850.
91. F. Barigelletti, L. Flamigni, V. Balzani, J.-P. Collin, J.-P. Sauvage, A. Sour, E. C. Constable and A. M. W. C. Thompson, J. Am. Chem. Soc., 1994, 116, 7692–7699.
92. V. Grosshenny, A. Harriman and R. Ziessel, Angew. Chem., 1995, 107, 1211–1214 ( Angew. Chem. Int. Ed. , 1995 , 34 , 1100–1102 ).
93. B. Schlicke, P. Belser, L. de Cola, E. Sabbioni and V. Balzani, J. Am. Chem. Soc., 1999, 121, 4207–4214.
94. M. Kasha, Discuss. Faraday Soc., 1950, 9, 14–19.
95. B. P. Sullivan, J. M. Calvert and T. J. Meyer, Inorg. Chem., 1980, 19, 1404–1407.
96. G. R. Fulmer, A. J. M. Miller, N. H. Sherden, H. E. Gottlieb, A. Nudelman, B. M. Stoltz, J. E. Bercaw and K. I. Goldberg, Organometallics, 2010, 29, 2176–2179.
97. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
98. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109.
99. R. Izsák and F. Neese, J. Chem. Phys., 2011, 135, 144105.
100. D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919.
101. A. J. Wilkinson, H. Puschmann, J. A. K. Howard, C. E. Foster and J. A. G. Williams, Inorg. Chem., 2006, 45, 8685–8699.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6dt00384b

---