The unusual metal ion binding ability of histidyl tags and their mutated derivatives

Abstract

Polyhistidine-tags are often used for the affinity purification of polyhistidine-tagged recombinant proteins. These sequences are also found in nature and are often highly conserved across different species. However, their exact role in the biological systems is not clear. The purpose of this work is to shed light on the behavior of poly-His sequences in their interactions with metal ions. This work illustrates the first study of novel poly-(His–Ala) peptides that bind Cu(II) applying both experimental techniques and extensive computational tools. The studied novel peptides are analogues of the short protected fragment of the pHpG (EDDH₉GVG₁₀) peptide, which was found in the venom of Atheris squamigera. Our study presents the properties of metal ion binding-histidine tag complexes and their mutated derivatives. The Cu(II) binding ability in pHG (Ac-EDDH₉G-NH₂) is more efficient than in the mutated derivatives, although the number of imidazoles that bind to Cu(II) ions are similar. Finally, the formation of an α-helical structure is observed in pHG and in one of the mutated derivatives, indicating the importance of the sequence in the poly-(His-Ala) tags.

---

Introduction

Nature has developed histidine rich proteins (HRPs) in many living organisms.¹ They are found in bacterial chaperones,² snake venoms³ and human genome.⁴ Often, they play a crucial role in many life functions.⁵ A special group of HRPs are sequences with His-tag motifs and in the last few decades around 700 of such natural peptides have been discovered.^1,4 The His-tag is an excellent ligand for metal ions, but its functional mechanisms are more complicated than that of a simple chelating agent and therefore have not been yet fully elucidated. Chelating properties of histidine rich proteins are the basis of one of the most effective methods of protein purification. Immobilized Metal Ion Affinity Chromatography (IMAC) makes use of the strong complex-formation capabilities of natural or artificial sequences of histidines (usually His₆-tag).^6,7 The imidazole nitrogens of histidines play a role as donor groups that have the ability to form coordination bonds with transition metals immobilized onto a chromatographic support such as Ni(II), Cu(II), Co(II), Zn(II).⁸

Recently, the interest in HRP studies has been increased, especially for a large class of proteins with poly-His–poly-Gly (pHpG) sequences, which are found in the venom of snakes.^3,9 For example, the EDDHHHHHHHHHGVGGGGGGGGGG (pHpG) sequence appears in the venom of Atheris squamigera, an African viper. It has been proposed that such peptides may block the metalloproteinases contained in the poison, and therefore do not cause damage to the venom gland.^3,10

Recently, we have studied the short protected fragment of the pHpG peptide from the Atheris squamigera venom: Ac-EDDHHHHHHHHHG-NH₂ (pHG) using experimental techniques and computational tools.¹¹ We have shown that the multiple histidine residues in this peptide fragment are very efficient metal ion chelators with very high affinities toward Cu(II), Ni(II) and Zn(II) ions in comparison with other histidine rich proteins. Furthermore, the interactions of metal ions with the pHG peptide have shown a very unusual behavior of this system.¹¹ First, various sets of three imidazoles from the His₉-tag in pHG can bind metal ions in different ways along the sequence and consequently form polymorphic binding states. Second, the formation of a regular α-helical structure has been observed when a metal binds to the peptide molecule. Polymorphism allows metal ions to ‘move along’ the polyhistidine fragments, which serve as a metal ion transporting pathway. Our previous studies on copper complexes with the His₆-tag have shown similar results: the presence of polymorphic binding states (with the participation of maximum two His residues in metal ion binding) and the formation of helical structures for some binding modes.^12,13

Since our recent studies on the specificity of the metal ion interactions with His-tags containing 6 or 9 His residues have shown very unusual behavior and incredible efficiency of binding metal ions,^11,12,14 this work extends our studies to new analogues in which the His residues mutated to Ala residues. Therefore the aim of this study is to examine the properties and the structural characterization of these new poly-(His–Ala) analogues of the pHG peptide.

To provide an insight into the mechanisms through which the Cu(II) binds non-adjacent His or alternate His residues in poly-His peptides, this study is focused on two new poly-His peptides that are derived from mutations of Ala of the pHG peptide. The first peptide consists of four His residues alternating with five Ala residues: Ac-EDDAHAHAHAHAG-NH₂ (L1) and the second peptide consists of five His residues alternating with four Ala residues: Ac-EDDHAHAHAHAHG-NH₂ (L2). These two analogues contain a lower number of histidines with respect to the original peptide pHG; but, more importantly, histidines are not consecutive. In fact, it has been already reported in the literature that not only the number of histidines in the sequence, but also their relative position influences the stability and the structure of the complexes.^15–18

This work presents a combination of experimental techniques and computational tools used to investigate the interactions of Cu(II) with each one of these two peptides. This is the first study that shows the coordination abilities of mutated sequences of pHG peptide derivatives towards the Cu(II) ion and the comparison of their properties to the original sequence with consecutive histidines.

Results and discussion

Peptide L1 consists of seven groups of acidic/basic sites and peptide L2 consists of eight groups of acidic/basic sites

Each one of the peptides L1 and L2 was protected in the N-terminus by acetylation and in the C-terminus by amidation. L1 consists of seven groups of acidic/basic sites: one glutamic acid, two aspartic acids and four histidines. On the other hand, L2 consists of eight groups of acidic/basic sites: one glutamic acid, two aspartic acids and five histidines. The protons of the peptide bonds cannot spontaneously be released in the pH range explored by potentiometry, since they are very weak acids (pK_a ≈ 15);¹⁹ but they can be displaced by Cu(II) at a suitable pH value, to form complexes. The potentiometric titrations on L1 and L2 peptides, in the absence or in the presence of Cu(II), allow the measurement of the overall protonation constants (β) and the corresponding step dissociation constants (K_a) (Tables 1, 2 and Fig. S1, S2†). The most acidic protons are those of the side carboxylic groups of Asp and Glu residues (pK_a range 2.53–4.26), while the pK_a values of the histidines range from 5.61 to 7.89. This result is in a very good agreement with the literature values obtained for similar systems.^11,12,18,20 Obviously, one cannot assign the exact pK_a value for each His residue in each peptide, due to the partial superimposition of the protonation equilibria. Therefore, the data that are presented in Tables 1 and 2 have to be considered as macro-constants, which is different than the exact micro-constant of each single site. However, one can hypothesize that the histidines that are closer to the negative charges of the deprotonated acidic amino acids (at the N-terminus) are more basic. The His residues at the opposite site of the peptide, for electrostatic reasons and also due to the higher probability of intramolecular H-bond formation are less basic and thus demonstrate more acidic properties.

Table 1 Protonation constants for the peptide L1, at T = 298 K and I = 0.1 mol dm⁻³ (KCl). Standard deviations in the last figure in parentheses

Species	Log β	pKa	Residue
LH^2−	7.89 (6)	7.89	His
LH2^−	14.47 (6)	6.58	His
LH3	20.98 (7)	6.51	His
LH4^+	26.59 (7)	5.61	His
LH5^2+	30.9 (1)	4.3	Glu
LH6^3+	34.5 (1)	3.6	Asp
LH7^4+	37.2 (1)	2.7	Asp

---

Table 2 Protonation constants for the peptide L2, at T = 298 K and I = 0.1 mol dm⁻³ (KCl). Standard deviations in the last figure in parentheses

Species	Log β	pKa	Residue
LH^2−	7.72 (3)	7.72	His
LH2^−	14.54 (3)	6.82	His
LH3	21.17 (4)	6.63	His
LH4^+	27.14 (4)	5.97	His
LH5^2+	32.75 (5)	5.61	His
LH6^3+	37.01 (6)	4.26	Glu
LH7^4+	40.70 (7)	3.69	Asp
LH8^5+	43.24 (1)	2.53	Asp

---

The ratios Cu(II) : L1 and Cu(II) : L2 in solution are 1 : 1

The potentiometric measurements, under the experimental conditions adopted here (metal to peptide ratio 1 : 1.1, millimolar concentrations) revealed seven protonated mononuclear Cu(II) complexes for each one of the peptides L1 and L2. The distribution diagrams are shown in Fig. 1 and 2 and the corresponding stability constants are reported in Tables S1 and S2.† The formation of some of these seven protonated mononuclear Cu(II) complexes has been confirmed by the mass spectra (MS) (Fig. S3–S11†). Under conditions of metal excess (M : L = 2 : 1) protonated binuclear Cu(II) complexes were formed (Fig. S7 and S11, ESI†). This result is not surprising due to the relatively large number of donor sites that are available in the two peptides, and this finding can be the subject of a further investigation. However, when the metal-to-peptide ratio is approximately 1 : 1, as it is the case for the thermodynamic measurements performed in the current study, no polynuclear complex has been detected.

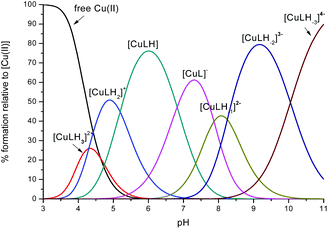Fig. 1 Representative distribution diagram for the peptide L1 with Cu(II); = 6 × 10⁻⁴ mol dm⁻³; metal/peptide ratio = 1 : 1.1.

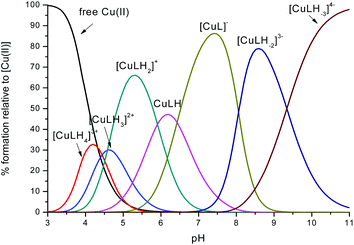Fig. 2 Representative distribution diagram for the peptide L2 with Cu(II); = 6 × 10⁻⁴ mol dm⁻³; metal/peptide ratio = 1 : 1.1.

The coordination mode of Cu(II) with L1/L2 is affected by the pH: a comparison between L1 and L2

The first Cu(II) complex identified with L1 is [CuLH₃]²⁺. Two hypotheses are proposed for two different possible modes for the coordination of this species with Cu(II): first, the Cu(II) binds one histidine and the carboxylate group of the glutamic acid (1N_im; COO–). In fact, at pH about 3, when the species [CuLH₃]²⁺ begins to form, the glutamic acid, characterized by a pK_a value of ∼4.3, can be deprotonated only if it binds to Cu(II). Second, the binding to Cu(II) occurs via two histidines (2N_im) while the glutamic acid is still protonated. The second hypothesis is supported by the UV-Vis data (Table S3† and Fig. 3): the wavelength of the maximum absorption at pH 4.5 shows a good agreement with the expected values for a complex where Cu(II) binds to two imidazole nitrogens.^11,19,21,22 This hypothesis is also supported by EPR data (Table S3 and Fig. S12†).²³ However, the charge transfer signal observed at 254 nm in the CD spectra (Table S3† and Fig. 4) can be due to the coordination of Cu(II) either with the carboxylic group of the glutamic acid or with the imidazole groups of the histidines.²⁴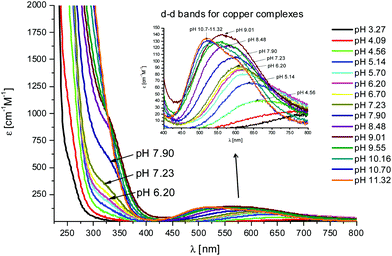

Fig. 3 UV-Vis spectra at different pH values for the system Cu(II)/L1; = 5 × 10⁻⁴ mol dm⁻³; M/L ratio = 1.1.1.

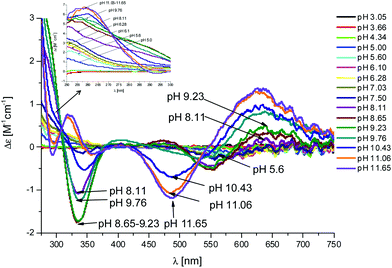Fig. 4 CD spectra at different pH values for the system Cu(II)/L1; = 5 × 10⁻⁴ mol dm⁻³; M/L ratio = 1.1.1.

In the complex [CuLH] prevailing at pH ≈ 6, L1 is monoprotonated. The fourth His is still protonated, i.e. cannot bind Cu(II). A pK_a value of 6.82 characterizes the deprotonation of the species [CuLH] to form the species [CuL]⁻, which is the most abundant complex at physiological pH. This pK_a value is compatible with the coordination to Cu(II) either by an amide nitrogen or by His11 (Tables S1 and S2†). The latter hypothesis implies that the species [CuL]⁻ has a coordination of Cu(II) with four imidazoles (4N_im). However, observing the visible portion of the CD spectra for the system Cu(II)/L1, at a pH higher than 5 the onset of a weak but detectable d–d band at 570–580 nm can be observed (Table S4†). This may be a clue that an amide nitrogen is involved in the coordination. Since the amides are closer to the chiral centers of the peptide more than the imidazole side chains, it is expected to get more intense CD signals. At the same time, the UV-Vis spectra show a further blue-shift of the absorption band to 603 nm (pH 7.2–7.9) and the EPR A_II value increases from 173 to 186 G. Therefore, the coordination mode proposed for the species [CuL]⁻ of L1 is (3N_im, N⁻), where N⁻ refers to the deprotonated nitrogen of a peptide bond. It is therefore proposed that the fourth His residue should remain protonated. The deprotonation of [CuL]⁻, leading to the formation of the subsequent [CuLH₋₁]²⁻ species, is characterized by a pK_a value of 7.87 which is very close to the value that is measured for His11 in the free peptide (7.89, Table 1). This value suggests that no interaction occurs between this imidazole and Cu(II) and that the complex geometry remains with three imidazoles and a nitrogen (3N_im, N⁻). Finally, at higher pH values the species [CuLH₋₂]³⁻ and [CuLH₋₃]⁴⁻ are formed. Spectroscopic data suggest that at these higher pH values the deprotonated amides gradually substitute imidazole nitrogens, forming a (2N_im, 2N⁻) and (N_im, 3N⁻) complex, respectively.

In the case of L2, the first species which is formed is the complex [CuLH₄]³⁺ (Fig. 2). Also in this case, the coordination hypothesis is 2N_im, as suggested by spectroscopic data (Table S4,†Fig. 5, 6 and S13†).

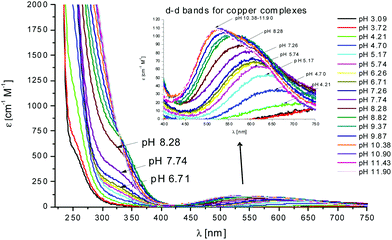Fig. 5 UV-Vis spectra at different pH values for the system Cu(II)/L2; = 5 × 10⁻⁴ mol dm⁻³; M/L ratio = 1.1.1.

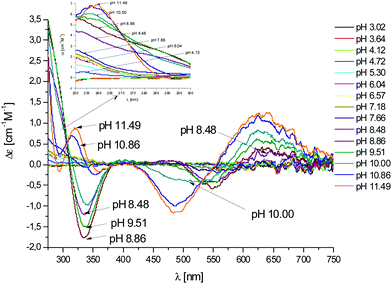Fig. 6 CD spectra at different pH values for the system Cu(II)/L2; = 5 × 10⁻⁴ mol dm⁻³; M/L ratio = 1.1.1.

In this case, CD spectra suggest that the first coordination of an amide nitrogen occurs only at pH 8.5 (Table S4†). The species [CuLH] which is formed at around pH 5 (corresponding to [CuL]⁻ in the case of L1) is expected to exhibit a coordination of four imidazoles (4N_im) with Cu(II) and not with three imidazoles and nitrogen (3N_im, N⁻), as proposed for L1. This can suggest that the interactions between Cu(II) and the backbone of the peptide is shielded by the additional histidine residue in L2.

The pK_a value of 6.43 characterizes the formation of the species [CuL]⁻ of L2 (Fig. 2). Two possible coordination modes are available: first, an axial coordination should take place, to form a square pyramidal species (5N_im). Second, the substitution of a N_im donor atom in the equatorial position would occur, with the possible shift of the latter to the axial position, to form a square pyramid again but with the (3N_im, N⁻) coordination in the equatorial plane, similarly as seen for L1 at physiological pH. On the basis of the available spectroscopy data, the second possible coordination mode is more likely at physiological pH.

In summary, at physiological pH, the spectroscopy data suggest that in peptide L1 the Cu(II) binds either to (2N_im, 2N⁻) or (3N_im, N⁻), in a preference to the coordination mode of (3N_im, N⁻). In peptide L2 the Cu(II) binds to (3N_im, N⁻) at physiological pH.

Cu(II) prefers to bind three imidazole groups both in peptides L1 and L2

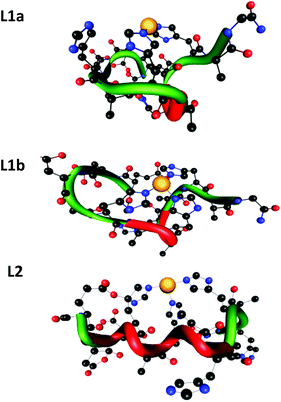
To examine the hypotheses that had been suggested by the spectroscopy data, we applied the DFT level of theory to search the coordination mode for both peptides L1 and L2. Our calculations have shown that there are two possible coordination modes of Cu(II) for peptide L1 (L1a and L1b) and one possible coordination mode of Cu(II) for peptide L2 (Fig. 7).

Fig. 7 The two minimized structures of peptide L1: L1a and L1b, and the minimized structure of peptide L2. The tubes illustrate the backbone of the peptides; red fragments indicate regular helical structures.

The minimized structures of L1a and L1b exhibited interactions of Cu(II) with two and three imidazole groups, respectively. In L1a, Cu(II) strongly binds two histidines: His7 and His11 (Cu(II)–His7 and Cu(II)–His11 distances are: 1.832 Å and 1.835 Å, respectively). In L1b, Cu(II) binds three histidines: two histidines His7 and His11 strongly interact Cu(II) (Cu(II)–His7 and Cu(II)–His11 distances are: 1.849 Å and 1.841 Å, respectively) and a third histidine His5 binds to Cu(II) with relatively lower interactions than His7 and His11 (Cu(II)–His5 distance is ∼0.5 Å longer than those of His7 and His11) (Table S5†). Yet, the third imidazole group of His5 that binds Cu(II) in L1b provides a better stabilization, as we obtained from the DFT calculations: L1b is relatively more stable than L1a by 47.2 kcal mol⁻¹.

The minimized structure of peptide L2 illustrated three imidazole groups that bind Cu(II): Cu–His4 and Cu–His10 with bond lengths of around 1.9 Å and Cu–His6 with a slightly longer bond length: 2.1 Å (Table S6†). It should be noted here that the bond length ranges of all Cu(II)–His that have been found in L1a, L1b and L2 peptides demonstrate the typical strong bonds of Cu(II) that bind residues in peptide complexes, as we also previously have shown.^11,12,14,25 Interestingly, the DFT predictions show an excellent agreement with the experimental observation for both peptides at physiological pH.

The structural differences between peptides L1 and L2

In structural models L1a and L1b the backbone of the peptide and the side chains stabilize the structure by forming an extensive network of six hydrogen bonds (Scheme 1 and Table S7†). In model L1a, only one hydrogen bond fits to demonstrate a regular helix, while the more stable model L1b has two hydrogen bonds that fit to illustrate a 3₁₀ type helix structure. Interestingly, in both peptides the helix is formed only in domains that the Cu(II) binds (Scheme 1).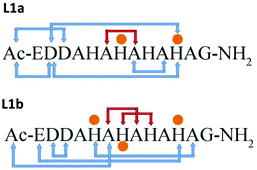

Scheme 1 Hydrogen bond networks (blue arrows) in the structural models of L1a and L1b. Orange dots illustrate the residues that bind Cu(II). Red arrows show a regular helix.

The minimized structure L2 shows a more branched network of hydrogen bonds: ten hydrogen bonds, almost twice than the structural models L1a and L1b (Scheme 2). Most of the hydrogen bond networks contribute to the formation of helical structures: both 3₁₀ helix and α-helical structures (Table S8†). L2 illustrates two cooperative hydrogen bond chains: one is a typical of 3₁₀ helix: D3–A5–A7–A9 and the second typical of the α-helical structure: H4–H6–H8.

Scheme 2 Hydrogen bonds and metal–peptide connections (orange dots). Red arrows show regular helix hydrogen bonds.

Similarly as we found for L1a and L1b, in the minimized structure L2 all the hydrogen bonds are formed in the domains along the peptide that the Cu(II) binds (Scheme 2). According to the DFT calculations, ∼50% of the domains in L2 exhibit 3₁₀ helix properties. We expect α-helical regular structures in peptides longer than 19–21 residues, but the 3₁₀ helices shall be energetically preferred over α-helixes.²⁶

The DFT calculations for the structural models of L1a, L1b and L2 were performed in the gas phase; nevertheless, they can provide good initial structures to run MD simulations for solvated Cu(II)–peptide complexes and mimic the experimental conditions. The simulated structural models can then be compared to the experimental observations performed in solution.

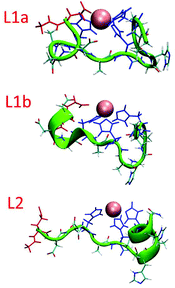
The simulated models for the complexes formed by L1 and L2 peptides are shown in Fig. 8. We applied the DSSP analysis to determine the properties of the secondary structure of these complexes. One can see that during the MD simulations of L1a there are no properties of the α-helical structure, while L1b has slight properties of the α-helical structure that appears at the end of the simulations (Fig. S14†). On the other hand, the complex L2 shows α-helical properties that appear along most of the MD simulations (Fig. S14†). The percentages of the α-helical properties for each residue along these structures are seen in Fig. 9. While the complex L1b demonstrates a small percentage of a short α-helix structure in the N-terminal (Asp2–His5), the complex L2 shows a relatively large percentage of a relatively long α-helical structure in the C-terminal (Ala7–His12). The α-helical structures of these peptides in the domains along the sequences can also be seen from the STRIDE analysis (Fig. 8), which is similar to the DSSP analysis.

Fig. 8 Simulated Cu(II)–peptide complexes demonstrating α-helical structures. The helical structural properties were obtained according to the STRIDE algorithm. The residues that bind Cu(II) in the peptides: His (blue) and Glu1 (red).

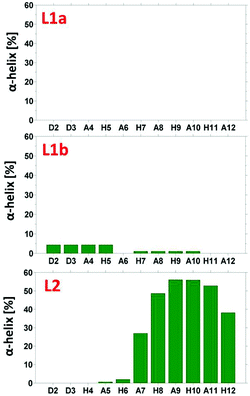Fig. 9 The percentage of α-helical properties of residues for the peptide models using the DSSP analysis.

An estimation of the energies and the populations of L1a and L1b indicates that the structure of L1b is strongly more stable than the structure of L1a (Fig. S15 and Table S9†), as predicted by the DFT level of theory. Therefore, we suggest that there is a slight preference for the formation of an α-helix structure in the N-terminal of the L1 peptide, when it binds to Cu(II). Finally, the MD simulations illustrate the formation of an α-helix structure in the C-terminal of the L2 peptide when it binds to Cu(II).

The differences in metal–peptide coordination between peptides L1 and L2

Interestingly, while starting with the coordination obtained from the DFT calculations, during the MD simulations the coordination has slightly changed. In L1a, the Glu1 residue also binds Cu(II), and in some cases replaces the His5 (Fig. 10 and S16†). Therefore, the three possible coordination modes with Cu(II) are: (1) His5, His7 and His11, (2) Glu1, His7 and His11 and a slight preference for (3) Glu1, His5, His7 and His11. This result confirms the experimental hypothesis that Cu(II) binds to the carboxylic groups of Glu in the L1 peptide. On the other hand, there is only one possible coordination with Cu(II) for L1b: His5, His7 and His11. The population analysis suggests that there may be a slight probability that Glu1 interacts with Cu(II), in the case of peptide L1. Finally, for L2 there is only one possibility for coordination with Cu(II): His4, His6 and His10. This result is in agreement with the experimental observation that suggested that Glu1 may bind to L1, but no evidence has been suggested by the experiment for the binding of Glu1 to Cu(II) in L2.

Fig. 10 A snapshot from the MD simulations for peptide L1a illustrates coordination with Glu1, His7 and His11 (His5 is replaced by Glu1).

Comparisons of the stabilities of the complexes Cu(II)–L1 and Cu(II)–L2 with other complexes with His-rich peptides

In order to compare the relative stability of the complexes formed by L1 and L2 in the pH range studied, one can apply competition plots taking into account different pairs of systems. The competition plots were calculated for equimolar concentrations of ligands and metal ions. It is important to note that only binary complexes are considered, as obtained from the studies.

Fig. 11 illustrates the competition between L1 and L2 to form complexes with Cu(II). One can see that L2, which contains five His residues, forms distinctly more stable complexes than L1 along the whole pH range. This result confirms our previous observation that larger numbers of His residues reveal a better coordination with metals.^11,12,14 Interestingly, the experimental data, the DFT calculations and the MD simulations have shown that Cu(II) is more likely to interact with three histidines in L2 than in L1. The three histidines coordinated and slightly more branched than hydrogen bond networks contribute to a higher stability of the complex Cu(II)–L2.

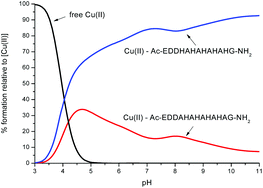Fig. 11 A competition plot for a ternary solution containing equimolar concentrations (1 mM) of Cu(II), L1 and L2.

In order to better shed light on the role of the number of His residues in the ability of Cu(II) to bind the peptide, we further investigated the competition between each one of the studied peptides L1 and L2 with other similar peptides with poly-His sequences. Four poly-His peptides were studied: (i) the peptide Ac-THHHHAHGG-NH₂, which is a protected fragment of the Hpn protein that is secreted by Helicobacter pylori¹⁸ and consists of five His residues, four of which are consecutive (Fig. S18†); (ii) a fragment of the prion protein of zebrafish (zp-PrP63-87),²⁷ which consists of seven His residues, six of which are separated by two amino acids (Fig. S19†); (iii) a pHG peptide,¹¹ which consists of nine consecutive His residues (His₉-tag) (Fig. 12) and (iv) a His₆-tag,¹² commonly used in IMAC chromatography (Fig. S20†).

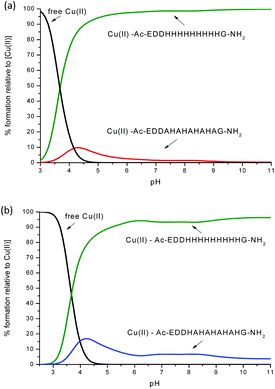Fig. 12 Competition plot for a ternary solution containing equimolar concentrations (1 mM) of: (a) Cu(II), L1 and Ac-EDDH₉G-NH₂ (pHG); (b) Cu(II), L2 and Ac-EDDH₉G-NH₂ (pHG).

One can see from Fig. 12 and S18–S20† that the peptides with a larger number of histidines in the sequence have a better ability to bind the Cu(II) ion. For example, the competition plots that compare the pHG peptide with peptides L1 and L2 show that pHG binds Cu(II) ions more effectively than L1 and L2 (Fig. 12). It is important to note that in pHG with L1 and L2 peptides Cu(II) binds a maximum of three imidazole groups. Interestingly, in all peptides metal ions induce the formation of α-helix. The surprising difference in the efficiency of metal ion binding may be due to the occurrence of polymorphic states in the case of Cu(II)–pHG (twelve of various structures) and a much better defined secondary structure of the α-helix, stabilized by the richer network of hydrogen bonds between the imidazole rings in most of these complexes.¹¹

Similar effects are observed when comparing L1 and L2 complexes with the Cu(II)–His₆-tag system (Fig. S20†). The peptide with six histidines is the most effective, but more interestingly, in these complexes we have differences in coordination modes before involvement of the amide nitrogen in the metal ion binding: {2N_im} (His₆-tag) and {3N_im} (L1 and L2). The MD simulations and DFT calculations have shown an ensemble of polymorphic states for the Cu(II)–His₆-tag complex and a preference for the formation of the α-helix structure.¹²

Finally, for peptides with a similar number of His residues, the alternate sequence of His and Ala as in peptide L2 provides a more stable complex than the non-alternating sequence His and Ala, as seen in peptide Ac-THHHHAHGG-NH₂ (Fig. S18b†). It is likely that in the peptide Ac-THHHHAHGG-NH₂ the His residues are too close to each other to contemporarily bind Cu(II), while in L2 the His residues that bind Cu(II) are not close to each other, i.e. not continuous.

Conclusions

This work illustrates two novel Ala mutated analogue peptides of the short protected pHpG peptide from Atheris squamigera venom: Ac-EDDHHHHHHHHHG-NH₂ (pHG) using extensive experimental techniques and computational tools. Our study leads to several conclusions. First, peptides that consist of repeated sequences of alternating histidines and alanines have the ability to strongly bind Cu(II). Second, the number of histidines and their location along the sequence affect the stability of the peptide complexes. Peptides with a relatively large number of His residues show a relatively better stability, i.e. they bind the Cu(II) stronger than peptides with a smaller number of His residues. Third, the binding ability of the His tag of pHG that consists of nine consecutive His residues is strongly more effective than the two novel Ala mutated analogue peptides that have been investigated here, although the number of imidazoles that coordinate to Cu(II) is similar. Fourth, the metal ion binding to the two Ala mutated analogue peptides induces the formation of the α-helical structure. Yet, the formation of the α-helical structure in the original pHG peptide is more remarkable compared with these two peptides. This can be explained due to the relatively small number of hydrogen-bonding networks in the two peptides compared with the pHG peptide. These differences could be critical for complex stability.

On the basis of the obtained results we suggest that there are strong dependencies between the number and positions of histidines along the histidine-rich sequences and their ability to coordinate metal ions and the stability of the complexes. Furthermore, in longer sequences of poly-His peptides the quantity of possible polymorphic states and the possibility to induce the formation of helical structures are increased. Finally, we propose that the extremely efficient metal ion binding properties that induce the formation of a regular helical structure in the unstructured His-tag peptides may be important for the biological behavior of peptides and proteins containing such sequences.

Experimental methods

Peptide synthesis and purification

The peptides Ac-EDDAHAHAHAHAG-NH₂ (L1) and Ac-EDDHAHAHAHAHG-NH2 (L2) were synthesized in the solid phase using the Fmoc/tBu strategy²⁸ with an automatic solid phase peptide synthesizer Syro II (Biotage, Uppsala Sweden). Protected amino acids, resins and reagents for the solid phase peptide synthesis were purchased from Novabiochem (Laufelfingen, Switzerland) or Iris Biotech (Marktredwitz, Germany). The resin 4-(2′,4′-dimethoxyphenyl-Fmoc-aminomethyl)-phenoxyacetamido-norleucyl-MBHA (Rink amide MBHA resin) was used as a solid support. Fmoc-amino acids (4-fold excess) were sequentially coupled to the growing peptide chain using DIPCDI/HOBt (N,N′-diisopropylcarbodiimide/1-hydroxybenzotriazole) (4-fold excess) as the activating mixture for 1 h at room temperature. Cycles of deprotection of Fmoc (40% piperidine/N,N-dimethylformamide) and coupling with the subsequent amino acids were repeated until the desired peptide-bound resin was completed. N-terminal acetylation has been performed with acetic anhydride (0.5 M) in the presence of N-methylmorpholine (0.25 M) (3 : 1 v/v; 2 mL/0.2 g of resin) as the last synthetic step.

The protected peptide-resin was treated with reagent B²⁹ (trifluoroacetic acid (TFA)/H₂0/phenol/triisopropylsilane 88 : 5 : 5 : 2; v/v; 10 mL/0.2 g of resin) for 1.5 h at room temperature. After filtration of the resin, the solvent was concentrated in vacuo and the residue triturated with ethyl ether. Crude peptides were purified by preparative reversed-phase HPLC using a Water Delta Prep 3000 system with a Jupiter column C₁₈ (250 × 30 mm, 300 A, 15 μm spherical particle size). The column was perfused at a flow rate of 20 mL min⁻¹ with a mobile phase containing solvent A (5%, v/v, acetonitrile in 0.1% TFA), and a linear gradient from 0 to 20% of solvent B (60%, v/v, acetonitrile in 0.1% TFA) over 25 min for the elution of peptides. Analytical HPLC analyses were performed on a Beckman 116 liquid chromatograph equipped with a Beckman 166 diode array detector. The analytical purity of the peptides was determined using a Luna C₁₈ column (4.6 × 100 mm, 3 μm particle size) with the above solvent system (solvents A and B) programmed at a flow rate of 0.5 mL min⁻¹ using a linear gradient from 0% to 40% B over 25 min. All analogues showed ≥95% purity when monitored at 220 nm. The molecular weight of the final compounds was determined by using a mass spectrometer ESI Micromass ZMD-2000.

Potentiometric measurements

Stability constants for proton and metal complexes were measured by means of potentiometric titration curves registered over the pH range 2.5–11, using a total volume of about 1.5 cm³. The pH-metric titrations were performed with a MOLSPIN EA940 pH-meter system equipped with a Mettler-Toledo InLab® Micro, glass-body, micro combination pH electrode, calibrated in proton concentrations using HCl.³⁰ An alkali was added with a 0.250 or 0.500 cm³ micrometer syringe, previously calibrated by both weight titration and the titration of standard materials. Constant-speed magnetic-stirring was applied throughout. The temperature of the titration cell was maintained at 298.2 ± 0.1 K by using a circulation thermostat. High purity grade argon was gently blown over the test solution in order to maintain an inert atmosphere. The peptide concentration was about 6 × 10⁻⁴ mol dm⁻³, the metal-to-peptide ratio was 1 : 1.1. CuCl₂ was an extra pure product (Sigma-Aldrich); the concentration of its stock solution was determined by ICP-MS. The carbonate-free stock solution of NaOH 0.1 mol dm⁻³ was purchased from Sigma-Aldrich and then potentiometrically standardized with potassium hydrogen phthalate as the primary standard. The HCl stock solution was prepared by diluting concentrated HCl (Sigma-Aldrich) and then standardized with NaOH. All sample solutions were prepared with freshly doubly distilled water. The ionic strength was adjusted to 0.1 mol dm⁻³ by adding KCl (Sigma-Aldrich). Grade A glassware was employed throughout.

The standard potential and the slope of the electrode couple were computed by means of Glee³¹ or SUPERQUAD³² programs. The purities and the exact concentrations of the peptide solutions were determined either by the Gran method³³ or by using the SUPERQUAD program. The HYPERQUAD program³⁴ was instead employed for the calculation of the overall (β) stability constant, referred to the following equilibrium (1):

pM + qL + rH ⇄ M_pL_qH_r (1)

(charges were omitted; p might also be 0 and r can be negative).

The associated standard deviations (referring to random errors only), are reported in parentheses in the Tables below as uncertainties on the last significant figure. The speciation and competition diagrams were computed with the HYSS program.³⁵

Spectroscopic measurements

The absorption spectra were recorded on a Varian Cary 300 Bio spectrophotometer, in the range 200–800 nm, using a quartz cuvette with an optical path of 1 cm. Circular dichroism (CD) spectra were recorded on a Jasco J 715 spectropolarimeter in the 225–800 nm range, using a quartz cuvette with an optical path of 1 cm in the visible and near-UV range or with a cuvette with an optical path of 0.1 cm in the wavelength range under 300 nm and 0.01 cm in the wavelength range 190–230. Electron paramagnetic resonance (EPR) spectra were recorded in liquid nitrogen on a Bruker ELEXSYS E500 CW-EPR spectrometer at X-band frequency (9.5 GHz) and it was equipped with an ER 036TM NMR Teslameter and E41 FC frequency counter. The peptides were prepared in a water solution of HCl at I = 0.1 mol dm⁻³ (KCl). The concentration of Cu(II) was 1 × 10⁻³ mol dm⁻³ in a molar ratio M/L 1 : 1.1. Ethylene glycol (30%) was used as a cryoprotectant for EPR measurements. The EPR parameters were analysed by computer simulation of the experimental spectra using Bruker's WIN-EPR SIMFONIA Software Version 1.2. The pH was adjusted with appropriate amounts of HCl and NaOH solutions.

The concentration of solutions used for UV-Vis and CD studies was similar to those employed in the potentiometric experiment. The UV-Vis, CD and EPR spectroscopic parameters were calculated from the spectra obtained at the pH values corresponding to the maximum concentration of each particular species, on the basis of distribution diagrams.

Mass spectrometric measurements

High-resolution mass spectra were recorded on a BrukerQ-FTMS spectrometer (Bruker Daltonik, Bremen, Germany), equipped with an Apollo II electrospray ionization source with an ion funnel. The mass spectrometer was operated both in the positive and in the negative ion modes. The instrumental parameters were as follows: scan range m/z 400–1600, dry gas-nitrogen, temperature 170 °C, capillary voltage 4500 V, ion energy 5 eV. Capillary voltage was optimized to the highest S/N. The small changes of voltage (±500 V) did not significantly affect the optimized spectra. Instrumental parameters for a Bruker MicrOTOF-Q were as follows: scan range m/z 250–2000, dry gas-nitrogen, temperature 200 °C, ion source voltage 4500 V, collision energy 10 eV. The samples (metal/peptide in a 1 : 1.1 stoichiometry, [peptide]_tot = 5 × 10⁻⁴ mol dm⁻³) were prepared in a 1 : 1 MeOH–H₂O mixture at pH 4.5. The samples were infused at a flow rate of 3 μL min⁻¹. The instrument was calibrated externally with the Tunemix™ mixture (Bruker Daltonik, Germany) in the quadratic regression mode. Data were processed by using the Bruker Compass Data Analysis 4.0 program. The mass accuracy for the calibration was better than 5 ppm, enabling together with the true isotopic pattern (using SigmaFit) an unambiguous confirmation of the elemental composition of the obtained complex.

Computational methods

Density functional theory (DFT) calculations

Density functional theory has been successfully used to investigate the structure and properties of peptides and peptide complexes.^36–41 We performed DFT studies on Cu(II) cations in the 1 : 1 complex with capped Ac-EDDAHAHAHAHAG-NH₂ (L1) and Ac-EDDHAHAHAHAHG-NH₂ (L2) peptides. The starting structure of the peptide for DFT calculations was generated on the basis of the amino acid sequence after 75 ps simulation at 300 K, without cutoffs using BIO+ implementation of the CHARMM force field. All calculations were performed with the Gaussian 09 ⁴² suite of programs using the M06 ⁴³ hybrid functional and the triple-zeta 6-311G basis set. In the peptide structures imidazole nitrogens are not protonated and thus available for coordination, while amide nitrogens bear their proton and cannot bind the metal ion. This situation is similar to that of a metal/peptide solution at pH approximately 5.

Molecular dynamics (MD) simulations

Constructed models. We applied the structural models that had been obtained from the DFT calculations to run MD simulations: concerning the Cu(II) complexes with peptide L1, two main structures involving side imidazole rings have been suggested by DFT (L1a and L1b) while for peptide L2 there is only one structure (L2). According to the DFT, in the case of structure L1a, the Cu(II) binds His5, His7 and His11 while in the case of complex L1b, the Cu(II) binds only His7 and His11. On the other hand, in the structure L2, the Cu(II) binds 3 His residues: His4, His6 and His10.

Molecular dynamics (MD) simulation protocol

The three models were first minimized as previously described for amyloids and other peptides.^44–50 MD simulations of the solvated models were performed in the NPT ensemble using NAMD⁵¹ with the CHARMM27 force-field.^52,53 The models were energy minimized and explicitly solvated in a TIP3P water box^54,55 with a minimum distance of 15 Å from each edge of the box. Each water molecule within 2.5 Å of the models was removed. Counter ions were added at random locations to neutralize the model charge. The Langevin piston method^56,57 with a decay period of 100 fs and a damping time of 50 fs was used to maintain a constant pressure of 1 atm. A temperature of 310 K was controlled by a Langevin thermostat with a damping coefficient of 10 ps.⁵¹ The short-range van der Waals interactions were calculated using the switching function, with a twin range cut-off of 10.0 and 12.0 Å. Long-range electrostatic interactions were calculated using the particle mesh Ewald method with a cutoff of 12.0 Å.^58,59

The equations of motion were integrated using the leapfrog integrator with a step of 1 fs. The solvated systems were energy minimized for 2000 conjugated gradient steps, where the hydrogen bonding distance between the β-sheet in each oligomer was fixed in the range 2.2–2.5 Å. The counter ions and water molecules were allowed to move. The hydrogen atoms were constrained to the equilibrium bond using the SHAKE algorithm.⁶⁰

The minimized solvated systems were energy minimized for 5000 additional conjugate gradient steps and 20 000 heating steps at 250 K, with all atoms being allowed to move. Then, the system was heated from 250 K to 310 K for 300 ps and equilibrated at 310 K for 300 ps. All simulations were run for 30 ns at 310 K. The temperature of 310 K had been applied to test the stabilities of all the variant models. Parameterizations for the Cu(II)–peptide complexes had been performed for all MD simulations. The force constant values for the Cu(II)–N atom and Cu(II)–O atom are in the range of 25–50 kcal mol⁻¹ Å⁻².

Generalized born method with molecular volume (GBMV)

The relative conformational energies can be compared only for models that have the same sequence and number of peptides, thus the relative conformational energies had been computed only for the two models of L1. To obtain the relative conformational energies of these two models, the model trajectories of the last 5 ns were first extracted from the explicit MD simulations excluding the water molecules – a total of 500 conformations for each model. The solvation energies of all conformations were calculated using the GBMV.^61,62

In the GBMV calculations, the dielectric constant of water was set to 80. The hydrophobic solvent-accessible surface area (SASA) term factor was set to 0.00592 kcal (mol Å)⁻¹. Each conformation was minimized using 1000 cycles, and the conformational energy was evaluated by grid-based GBMV.

A total of 1000 conformations (500 for each model) were used to construct the energy landscapes of the two models and to evaluate the conformer probabilities by using Monte Carlo (MC) simulations. In the first step, one conformation of conformer i and one conformation of conformer j were randomly selected. Then, the Boltzmann factor was computed as e^{−(E_j−E_i)/kT}, where E_i and E_j are the conformational energies evaluated using the GBMV calculations for conformations i and j, respectively, k is the Boltzmann constant and T is the absolute temperature (298 K used here). If the value of the Boltzmann factor was larger than the random number, then the move from conformation i to conformation j was allowed. After 1 million steps, the conformations ‘visited’ for each conformer were counted. Finally, the relative probability of model n was evaluated as P_n = N_n/N_total, where P_n is the population of model n, N_n is the total number of conformations visited for model n, and N_total is the total steps. The advantages of using MC simulations to estimate conformer probability lie in their good numerical stability and the control that they allow for transition probabilities among several conformers.

A total of 1000 conformations of these two models (500 conformations for each model) were used to construct the energy landscape (Table S9†). The pair of these two models is likely to present may be only a very small percentage of the ensemble. Nevertheless, the carefully selected models cover the most likely structures.

Assigning a secondary structure to amino acids by the DSSP algorithm

The DSSP algorithm is the standard method for assigning the secondary structure to the amino acids of a protein or a peptide, given the atomic-resolution coordinates of the protein or the peptide. It does this by reading the position of the atoms in a protein (the ATOM records in a PDB file) followed by calculation of the hydrogen bond energy between all atoms. The best two hydrogen bonds for each atom are then used to determine the most likely class of the secondary structure for each residue in the protein or the peptide. We applied the DSSP algorithm that is embedded in the CHARMM software.⁶³

The DSSP algorithm provides information on specific domains that illustrate an α-helix and a β-sheet. It does not distinguish between various types of α-helixes, such as the 3₁₀ helix, α-helix, etc.

Acknowledgements

This research was supported by grant no. 2011128 from the United States-Israel Binational Science Foundation (BSF) and by MNiSW project 4478/E-344/S/2014. All simulations were performed using the high-performance computational facilities of the Miller lab in the BGU HPC computational center. The support of the BGU HPC computational center staff is greatly appreciated. Financial support from the University of Ferrara (FAR 2013) is gratefully acknowledged.

References

1. M. Rowinska-Zyrek, D. Witkowska, S. Potocki, M. Remelli and H. Kozlowski, New J. Chem., 2013, 37, 58–70.
2. D. Witkowska, M. Rowinska-Zyrek, G. Valensin and H. Kozlowski, Coord. Chem. Rev., 2012, 256, 133–148.
3. S. C. Wagstaff, P. Favreau, O. Cheneval, G. D. Laing, M. C. Wilkinson, R. L. Miller, R. Stoecklin and R. A. Harrison, Biochem. Biophys. Res. Commun., 2008, 365, 650–656.
4. E. Salichs, A. Ledda, L. Mularoni, M. M. Alba and S. de la Luna, PLoS Genet., 2009, 5.
5. T. Cheng, W. Xia, P. Wang, F. Huang, J. Wang and H. Sun, Metallomics, 2013, 5, 1423–1429.
6. K. Terpe, Appl. Microbiol. Biotechnol., 2003, 60, 523–533; K. Terpe, Appl. Microbiol. Biotechnol., 2003, 60, 523–533.
7. D. S. Waugh, Trends Biotechnol., 2005, 23, 316–320.
8. H. L. Liu, Y. Ho and C. M. Hsu, J. Biomol. Struct. Dyn., 2003, 21, 31–41.
9. P. Favreau, O. Cheneval, L. Menin, S. Michalet, H. Gaertner, F. Principaud, R. Thai, A. Menez, P. Bulet and R. Stocklin, Rapid Commun. Mass Spectrom., 2007, 21, 406–412.
10. S. C. Wagstaff, L. Sanz, P. Juarez, R. A. Harrison and J. J. Calvete, J. Proteomics, 2009, 71, 609–623.
11. J. Watly, E. Simonovsky, N. Barbosa, M. Spodzieja, R. Wieczorek, S. Rodziewicz-Motowidlo, Y. Miller and H. Kozlowski, Inorg. Chem., 2015, 54, 7692–7702.
12. J. Watly, E. Simonovsky, R. Wieczorek, N. Barbosa, Y. Miller and H. Kozlowski, Inorg. Chem., 2014, 53, 6675–6683.
13. E. Simonovsky, H. Kozlowski and Y. Miller, RSC Adv., 2015, 5, 104551–104555.
14. F. Pontecchiani, E. Simonovsky, R. Wieczorek, N. Barbosa, M. Rowinska-Zyrek, S. Potocki, M. Remelli, Y. Miller and H. Kozlowski, Dalton Trans., 2014, 43, 16680–16689.
15. D. Valensin, L. Szyrwiel, F. Camponeschi, M. Rowinska-Zyrek, E. Molteni, E. Jankowska, A. Szymanska, E. Gaggelli, G. Valensin and H. Kozlowski, Inorg. Chem., 2009, 48, 7330–7340.
16. A. Janicka-Klos, P. Juszczyk, Z. Grzonka and H. Kozlowski, Polyhedron, 2008, 27, 1511–1516.
17. M. Orfei, M. C. Alcaro, G. Marcon, M. Chelli, M. Ginanneschi, H. Kozlowski, J. Brasun and L. Messori, J. Inorg. Biochem., 2003, 97, 299–307.
18. D. Witkowska, R. Politano, M. Rowinska-Zyrek, R. Guerrini, M. Remelli and H. Kozlowski, Chem – Eur. J., 2012, 18, 11088–11099.
19. H. Sigel and R. B. Martin, Chem. Rev., 1982, 82, 385–426.
20. L. D. Pettit and H. K. J. Powell, The IUPAC Stability Constants Database, Royal Society of Chemistry, London, 1992–2000.
21. E. J. Billo, Inorg. Nucl. Chem. Lett., 1974, 10, 613–617.
22. E. Prenesti, P. G. Daniele, M. Prencipe and G. Ostacoli, Polyhedron, 1999, 18, 3233–3241.
23. J. Peisach and W. E. Blumberg, Arch. Biochem. Biophys., 1974, 165, 691–708.
24. P. G. Daniele, E. Prenesti and G. Ostacoli, J. Chem. Soc., Dalton Trans., 1996, 3269–3275.
25. N. M. Chiera, M. Rowinska-Zyrek, R. Wieczorek, R. Guerrini, D. Witkowska, M. Remelli and H. Kozlowski, Metallomics, 2013, 5, 214–221.
26. R. Wieczorek and J. J. Dannenberg, J. Am. Chem. Soc., 2004, 126, 14198–14205.
27. L. Szyrwiel, E. Jankowska, A. Janicka-Klos, Z. Szewczuk, D. Valensin and H. Kozlowski, Dalton Trans., 2008, 6117–6120.
28. N. L. Benoiton, Chemistry of Peptide Synthesis, Taylor & Francis, London, 2005, pp. 125–154.
29. N. A. Solé and G. Barany, J. Org. Chem., 1992, 57, 5399–5403.
30. H. M. Irving, M. G. Miles and L. D. Pettit, Anal. Chim. Acta, 1967, 38, 475–488.
31. P. Gans and B. O'Sullivan, Talanta, 2000, 51, 33–37.
32. P. Gans, A. Sabatini and A. Vacca, J. Chem. Soc., Dalton Trans., 1985, 1195–1200.
33. G. Gran, Acta Chem. Scand., 1950, 4, 559–577.
34. P. Gans, A. Sabatini and A. Vacca, Talanta, 1996, 43, 1739–1753.
35. L. Alderighi, P. Gans, A. Ienco, D. Peters, A. Sabatini and A. Vacca, Coord. Chem. Rev., 1999, 184, 311–318.
36. A. Masson, M. Z. Kamrath, M. A. S. Perez, M. S. Glover, U. Rothlisberger, D. E. Clemmer and T. R. Rizzo, J. Am. Soc. Mass Spectrom., 2015, 26, 1444–1454.
37. R. Walesa, D. Man, G. Engel, D. Siodlak, T. Kupka, T. Ptak and M. A. Broda, Chem. Biodiversity, 2015, 12, 1007–1024.
38. E. Gumienna-Kontecka, G. Berthon, I. O. Fritsky, R. Wieczorek, Z. Latajka and H. Kozlowski, J. Chem. Soc., Dalton Trans., 2000, 4201–4208.
39. P. Salvador, R. Wieczorek and J. J. Dannenberg, J. Phys. Chem. B, 2007, 111, 2398–2403.
40. M. Rudowska, R. Wieczorek, A. Kluczyk, P. Stefanowicz and Z. Szewczuk, J. Am. Soc. Mass Spectrom., 2013, 24, 846–856.
41. G. Pohl, A. Asensio and J. J. Dannenberg, Biochemistry, 2014, 53, 617–623.
42. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2009.
43. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
44. V. Wineman-Fisher, R. Simkovitch, S. Shomer, R. Gepshtein, D. Huppert, M. Saif, K. Kallio, S. J. Remington and Y. Miller, Phys. Chem. Chem. Phys., 2014, 16, 11196–11208.
45. N. Zeytuni, R. Uebe, M. Maes, G. Davidov, M. Baram, O. Raschdorf, M. Nadav-Tsubery, S. Kolusheva, R. Bitton, G. Goobes, A. Friedler, Y. Miller, D. Schueler and R. Zarivach, PLoS One, 2014, 9.
46. Y. Raz, B. Rubinov, M. Matmor, H. Rapaport, G. Ashkenasy and Y. Miller, Chem. Commun., 2013, 49, 6561–6563.
47. Y. Raz and Y. Miller, PLoS One, 2013, 8.
48. Y. Raz, J. Adler, A. Vogel, H. A. Scheidt, T. Haupl, B. Abel, D. Huster and Y. Miller, Phys. Chem. Chem. Phys., 2014, 16, 7710–7717.
49. V. Wineman-Fisher, Y. Atsmon-Raz and Y. Miller, Biomacromolecules, 2014, 16, 156–165.
50. Y. Miller, B. Y. Ma and R. Nussinov, Coord. Chem. Rev., 2012, 256, 2245–2252.
51. L. Kale, R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan and K. Schulten, J. Comput. Phys., 1999, 151, 283–312.
52. A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616.
53. B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, J. Comput. Chem., 1983, 4, 187–217.
54. M. W. Mahoney and W. L. Jorgensen, J. Chem. Phys., 2000, 112, 8910–8922.
55. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
56. K. Tu, D. J. Tobias and M. L. Klein, Biophys. J., 1995, 69, 2558–2562.
57. S. E. Feller, Y. H. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613–4621.
58. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
59. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
60. J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
61. M. S. Lee, F. R. Salsbury and C. L. Brooks, J. Chem. Phys., 2002, 116, 10606–10614.
62. M. S. Lee, M. Feig, F. R. Salsbury and C. L. Brooks, J. Comput. Chem., 2003, 24, 1348–1356.
63. W. Kabsch and C. Sander, Biopolymers, 1983, 22, 2577–2637.

---

Footnotes

† Electronic supplementary information (ESI) available: Spectroscopy measurement, DFT and MD data. See DOI: 10.1039/c5dt04747a

‡ These authors contributed equally to this work.

---